1   Introduction

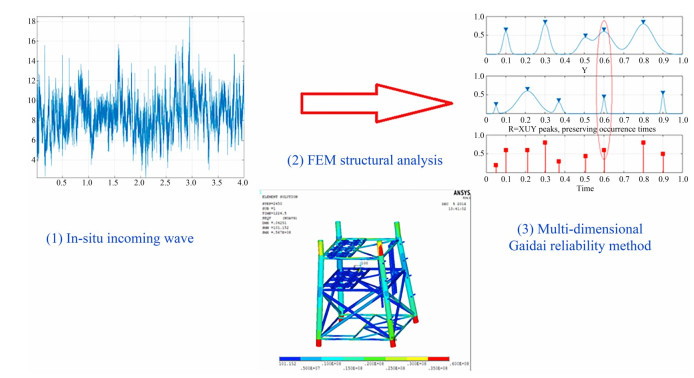
This work examines the responses of an offshore Jacket platform to drag-dominated hydrodynamic forces that act on its support structure. Operating Well Head Platform B Jacket platform, which is located 50 km offshore in the Bohai Bay BZ25-1 oilfield, is chosen for this study. Bohai Bay is the only inner sea in China. In recent years, it has attracted considerable industrial and research interest due to increased scientific and economic activities, particularly within ocean renewable energy, marine engineering, and the offshore oil and gas industry. In situ environmental parameters at the Bohai Sea are the primary input for offshore structural and reliability studies (Lv et al., 2014; Wang et al., 2012). These parameters for Bohai Bay operational venues are usually processed according to Det Norske Veritas offshore engineering standards (DNV-RPH103, 2017; DNV-RP-C205, 2021). Using traditional engineering reliability methodologies to predict the reliability and risks of multidimensional structural systems is often challenging (Zhao and Ono, 1999; Thoft-Christensen and Murotsu, 1986; Tian et al., 2019). Challenges arise not only from the high number of system degrees of freedom (DOFs) but also from the nonlinear cross-correlations between critical/key components of the system. Direct numerical Monte Carlo (MC) simulations or adequate mea‐ surements can be used to determine reliability-based design parameters for complex nonlinear structural systems (Gaidai et al., 2022a; Balakrishna et al., 2022), but the required datasets are often quite limited. Other contemporary approaches for system reliability studies can be found in (Feng et al., 2022; Zhu et al., 2023). Thus, for many nonlinear, highly dimensional engineering dynamic systems, experimental and computational methods may not always provide an affordable way to assess structural risks, especially for long return periods as required by contemporary design. The novel Gaidai reliability methodology advocated here is especially suitable for complex nonlinear structural systems. It utilizes available datasets in a quite efficient way, which reduces efforts associated with either measurements or numerical calculations. This study explores the stresses in the support structure of an offshore Jacket. These stresses are monitored simultaneously in various critical/hotspot locations under realistic in situ environmental loads. Notably, no model simplifications or linearization of nonlinear effects is required for the analysis.

Figure 1 presents the location of the Jacket platform in the Bohai Sea area, as well as the environmental wave height/period contour lines.

Figure  1  Geographical contours of wave height and wave period in Bohai Bay obtained on an annual basis (Lv et al., 2014); the star marks the location of the Jacket platform

Download: Full-Size Img

Figure 2 illustrates a Jacket platform that is comparable to the Jacket studied here. Figure 3 shows the flowchart for long-term MC statistical/reliability analysis.

Figure  2  Example of an offshore Jacket platform

Download: Full-Size Img

Figure  3  Flowchart for long-term environmental statistical/reliability analysis

Download: Full-Size Img

In contrast to univariate/bivariate statistical approaches, the multivariate strategy accounts for stresses at several crucial Jacket support locations and considers intrinsic stress dependence/coupling. The latter is an obviously important feature for offshore engineers, particularly during the design phase. The key contributions of this study are summarized as follows:

• Realistic offshore engineering installation has been studied using a novel system reliability methodology;

• Structural damage risks have been assessed using a multi-state spatiotemporal assessment model;

• Confidence intervals (CIs) for estimated return periods of interest have been provided.

To provide a historical perspective for the current study, the following chronology can be referred to:

1987: System Reliability of Offshore Jacket Structures by Ideal Plastic Analysis

1990: Wave Loading Effect in Offshore Structural Reliability

1998: Reliability-based Design Format for Jacket Platforms Under Wave Loads

2003: System Reliability of Jack-up Structures Based on Fatigue Degradation

2009: Reliability-based Earthquake Design of Jackettype Offshore Platforms Considering Pile – Soil – Structure Interaction

2011: System Failure Probability of Offshore Jack-Up Platforms in the Combination of Fatigue and Fracture

2012: Structural Reliability of Offshore Platforms Considering Fatigue Damage and Different Failure Scenarios

2014: Seismic Reliability of a Fixed Offshore Platform Against Collapse

2018: Probabilistic Seismic Collapse Analysis of Jacket Offshore Platforms (Ali et al., 2016;Raheem et al., 2022a).

Alternative probabilistic design approaches for offshore platforms, as well as their structural elements, can be found in (Raheem et al., 2022b; Raheem et al., 2020a; Raheem et al., 2020b; Nassiraei and Rezadoost, 2022; Ahmadi, 2016; Nassiraei Rezadoost, 2020; Zavvar et al., 2023). However, estimating the design failure, damage probability, and risks of multivariate systems is often challenging in complex engineering contexts (Smith et al., 1990; Coles and Tawn, 1994).

2   Gaidai reliability method

We consider a piecewise jointly stationary dynamic system with multiple DOFs (MDOFs) and key/critical components X (t), Y (t), Z (t), …, These components are part of the system's dynamic MDOF time records (X (t), Y (t), Z (t), …), which are observed, recorded, or measured over a sufficient (representative) timelapse (0, T). The global maximum of the key/critical component in the 1D system is denoted here as $X_T^{\max }=\max _{0 \leqslant t \leqslant T} X(t), Y_T^{\max }=\max _{0 \leqslant t \leqslant T} Y(t)$, $Z_T^{\max }=\max _{0 \leqslant t \leqslant T} Z(t)$, … for the entire timelapse (0, T). By "suitably long" (representative) timelapse T, we essentially refer to a sufficiently large value of T with respect to the auto-correlation and relaxation times of the dynamic sys tem. Let X₁, …, X_NX be the local maxima for the key process component X (t) in the dynamic system at discrete time instants, which temporally increase $t_1^X<\cdots<t_{N_x}^X$ within (0, T). Definitions for the remaining key components of the MDOF dynamic system, Y (t), Z (t), … with Y₁, …, Y_NY; Z₁, …, Z_NZ, are quite similar. For ease of use, we assume that all local maxima of the key components in the dynamic system are non-negative. The goal is to accurately determine the hazard/failure risk of the dynamic Jacket system. We target the hazard/failure risk/probability of the dynamic system:

The risk is related to the survival probability of the target system, which is denoted as P and expressed as

It represents the probability that the critical/key compo‐ nents (e.g., η_X, η_Y, η_Z, …) of the target dynamic system do not exceed their respective values. ∪ denotes the logical unity operation, and $p_{X_T^{\max }, Y_T^{\max }, Z_T^{\max }, \ldots}$ corresponds to the joint probability density function (PDF) of the global maxima of these components over the observational timelapse (0, T). Next, the vector of the MDOF dynamic system (X (t), Y (t), Z (t), …) is scaled to its nondimensional ver‐ sion: ($\tilde{X}, \tilde{Y}, \tilde{Z}, \ldots$), where $\tilde{X}=\frac{X}{\eta_X}, \tilde{Y}=\frac{Y}{\eta_Y}, \tilde{Z}=\frac{Z}{\eta_Z}$. The joint PDF of the latter dynamic Jacket system cannot be directly assessed due to the high dimensionality of the system and the limitations of the underlying raw dataset. More specifically, the dynamic system is considered to have failed/ damaged or entered a state of hazard when any of the following conditions occur: the key component X (t) exceeds η_X, or Y (t) exceeds η_Y, or Z (t) exceeds η_Z; equivalently, when $\tilde{X}, \tilde{Y}, \tilde{Z}, \ldots$ exceed 1. We arrange the local maxima time instants of the key components in the system as [$t_1^X<\cdots<t_{N_X}^X ; t_1^Y<\cdots<t_{N_Y}^Y ; t_1^Z<\cdots<t_{N_z}^Z$]. We merge them into a single temporal vector, t₁ ≤ … ≤ t_N, in a monotonously nondecreasing temporal order, with $t_N=\max \left\{t_{N_x}^X, t_{N_z}^Y, t_{N_z}^Z, \cdots\right\}$, N ≤ N_X + N_Y + N_Z + … Local maxima of each load/response of key components in the MDOF dynamic system, namely, X (t), or Y (t), or Z (t), are represented with their occurrence times t_j. The local maxima of the 1D key components ($) in the system are combined/coalesced and coherent with the merged/coalesced temporal vector t₁ ≤ … ≤ t_N. These local maxima form a temporally increasing vector of the synthetic nondimensional system R(t) ≡ $\vec{R}$ = (R₁, R₂, …, R_N), with $R_j=\max \left\{\left(\tilde{X}_j \mid \exists j_X, t_{j_x}^X=t_j\right), \left(\tilde{Y}_j \mid \exists j_Y, t_{j_Y}^Y=t_j\right)\right.$, $\left.\left(\tilde{Z}_j \mid \exists j_Z, t_{j_z}^Z=t_j\right), \cdots\right\} \text { for } j=1, \cdots, N \text {. }$

A "scaling" parameter 0 < λ ≤ 1 is introduced to artifi cially reduce hazard, limit, or risk values for all nondimensional key components of the system. The survival probability of the system P(λ) is defined as a smooth function of the scaling parameter λ, with P ≡ P(1) according to Eq. (1). To account for the dependency between neighboring R_j, the following memory approximation (conditioning level k) is implemented:

By tracking each individual hazard, failure, or risk event that occurs locally prior to time, the intention is now to prevent cascading or clustering of intercorrelated exceedances in the FPSO system. Given that the MDOF dynamic process R(t) has been considered to be piecewise ergodic and quasi-stationary, the probability/risk is p_k(λ) $\text { := }$ Prob {R_j > λ | R_{j − 1} ≤ λ, …, R_{j − k} ≤ λ} for j > k. This probability/ risk becomes independent of j and solely dependent on the conditioning level k. As a result, the non-exceedance (survival) probability can be approximately calculated using the Poisson assumption.

Notably, Eq. (3) follows from Eq. (2) if we neglect Prob $\left(R_1 \leqslant \eta_1^\lambda\right) \approx 1$, given that the design failure/damage probability is of a small order of magnitude, with $N \gg k$. Eq. (4) is comparable to a popular mean up-crossing rate (MUR) equation for the hazard/failure probability/risk (probability of exceedance). As for the conditioning parameter k, convergence is present.

A popular non-exceedance (survival) probability rela‐ tionship with a matching MUR rate function results from Eq. (4) for k = 1, which can be expressed as

where ν⁺ (λ) denotes the MUR of the risk level λ. The nondimensional vector R(t) is assembled from the critical/key components of the scaled FOWT system with MDOF $\left(\frac{X}{\eta_X}, \frac{Y}{\eta_Y}, \frac{Z}{\eta_Z}, \cdots\right)$. Eq. (4) transforms into a popular nonexceedance probability relationship with the correspond‐ ing MUR function:

where ν⁺ (λ) is the MUR of the dynamic response level λ for the vector of the nondimensional dynamic Jacket system R(t) introduced above. The Rice's formula, which is given by Eq. (7), yields the MUR, with p_RṘ being the joint PDF for (R, Ṙ) and Ṙ being the time derivative R' (t) (Madsen et al., 1986).

Figure  4  Illustration of the process of combining two exemplary processes, namely, X and Y, into a new synthetic vector R(t)

Note: The red ellipse highlights the ease of simultancous maxima for two different components of the Jacket system

Download: Full-Size Img

In the abovementioned cases, the stationarity assumption is used (Gaidai et al., 2023a; Liu et al., 2023). The proposed methodology can also treat various nonstationary cases. The following is an example of the possible application of the suggested technique to nonstationary circumstances. Given an in-situ scatter diagram consisting of m = 1, …, M environmental sea states, each short-term environmental state has individual occurrence probabilities q_m, such that $\sum_{m=1}^M q_m=1$. The corresponding long-term equation is

where p_k (λ, m) is the same function as in Eq. (6). However, it corresponds to a specific short-term environmental state, which is indexed with a number m. The abovementioned presented p_k (λ) functions are often regular in their distri‐ bution tail, particularly for extreme values of λ approaching 1. For λ ≥ λ_{cut − on}, the PDF tail behaves similar to exp{ −(aλ + b) ^c + d} with a, b, c, d as four fitted constants. It matches the appropriate PDF tail cut-on λ_{cut − on} value. The optimal values of the four parameters a, b, c, d may be determined using the sequential quadratic programming technique implemented in the Numerical Algorithm Group library (Numerical Algorithms Group, 2010). Compared with traditional MC-based methods for MDOF offshore systems, the Gaidai reliability methodology suggested in this study can conduct reliability assessment on MDOF systems with no practically limited number of DOFs (NDOFs), as shown in the integral in Eq. (2). Thus, this approach cannot be straightforwardly compared with classic reliability methods, which typically cover only dynamic systems with NDOF ≤ 2.

Figure 5 schematically illustrates the suggested structural reliability approach for MDOF Jacket systems. This method consists of three distinct steps: in-situ environmental input, structural dynamic analysis (including key hotspot stress locations), and application of the Gaidai multidimensional structural reliability method.

Figure  5  Structural reliability approach for MDOF Jacket systems

Download: Full-Size Img

3   Environmental, structural, and material models

Using ANSYS Finite Element Method (FEM) software version 2022 R2 (22.2), the offshore Jacket platform is modeled as an MDOF 4D structure (Gaidai and Xing, 2022). To create an accurate wave scatter map for the Bohai Bay region, satellite-based worldwide wave statistics is employed. The Global Wave Statistics Online (Stansberg et al., 2013) dataset is utilized. With the use of an in-place star, Figure 1 illustrates the geographical PDF of wave heights and wave periods for the Bohai Bay Jacket in situ zone.

Table 1 presents the presumed in situ directional proba bilities of wind waves in Bohai Bay, which are averaged over 1 year. For each ambient sea condition, 3-h stationary storm MC simulations are performed. The sea/ocean state scatter diagram for the Bohai Bay area is taken from (Stansberg et al., 2013), which is averaged for the whole year and per all directions. For each sea/ocean state (H_s, T_z), zero crossing period T_z is assumed to be approximately linearly related with the spectral peak wave period T_p, which follows the rule in DNV (DNV-RP-H103, 2017). One-sided wave elevation power spectral density, which is provided by the Joint North Sea Wave Project wave spectrum, is used to specify stationary sea/ocean conditions η (t), with the PSD denoted here by S_η⁺ (ω), ω > 0

where g = 9.81 m/s²; ω_p is the peak frequency in rad/s; α, γ, and σ are parameters related to the spectral shape; σ = 0.07 when ω ≤ ω p; and σ = 0.09 when ω > ω_p. For Bohai Bay, the in situ parameter γ is chosen to be equal (Wang et al., 2012). The parameter α is determined from equation $\alpha=5.06\left(\frac{H_s}{T_p^2}\right)^2(1-0.287 \ln \gamma)$, with H_s being the significant wave height and T_p = 2π/ω_p being the spectral peak wave period. The Jacket platform is modeled using ANSYS FEM software and utilized as a nonlinear MDOF structure. Figure 6 depicts the investigated Jacket platform that operates on the Bohai continental shelf. Von Mises (VM) stresses of the Jacket system are utilized in this investigation, and the structural material is steel with stresses below the yield level (i. e., no plastic/irreversible deformations). A convergence check is conducted to determine the proper timestep. Response time histories are simulated using the ANSYS FEM software (ANSYS theory reference, Release 5.6, 1994). The dynamic Jacket model presumes discrete node placement from the Jacket deck MDOF structure down to the seafloor, which distributes lumped hydrodynamic forces that act on the Jacket platform. The lumped parameter model can be expressed in the following dynamic vector form:

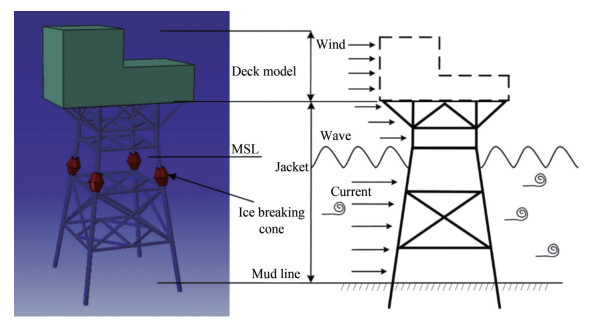Figure  6  Jacket structural loadings (Tian X et al., 2019)

Download: Full-Size Img

where M, C, and K are constant matrices (geometric nonlin‐ earity is not modeled). The response vector X = (X₁, …, X_N)^T consists of components X_k = X_k(t), k = 1, …, N, with each component being the k-th DOF and N being the number DOFs in the FEM model. F_in and F_d are the inertia and drag force components, respectively. The dynamic equation is solved through the full integral method, which accounts for geometrical nonlinearities. The structural MDOF model of the Jacket platform focuses on accurately describing the deformation characteristics of the Jacket legs, especially critical tubular support elements. These elements are modeled by equivalent beam, tubular, or shell structural elements.

For the entire Jacket MDOF structure (Figure 6), especially its area above the sea floor mudline, proper FEM models are utilized. Jacket legs extend 90 m below the seabed mudline, and the average depth of the water is 17 m. The airgap between the lowest deck and the mean water level is about 12 m.

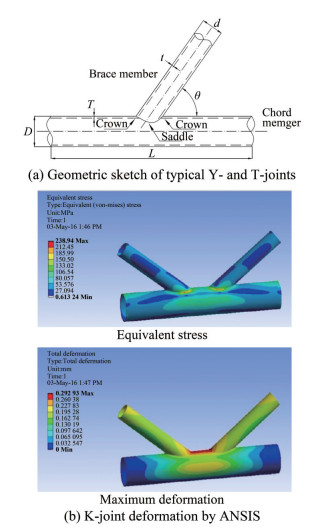
Common T, Y, and K-joints of Jacket offshore platforms are shown in Figure 7.

Figure  7  Examples of welded tubular joints.

Download: Full-Size Img

The soil is modeled following the p − y curve method (API Recommended Practice for Planning, 2002). For sand, the equation is

where A = 0.9 represents the cyclic loading, P_U is the soil resistance level limit of the pile side for the unit area, K is the initial modulus of the subgrade reaction, H refers to the depth below the surface of the Jacket pile in the mud, and Y denotes the lateral deformation of the pile. In the ANSYS FEM analysis, the tubes and weld joints of the Jacket leg are made of steel. The properties of these mate‐ rials are presented in Table 2.

4   Results

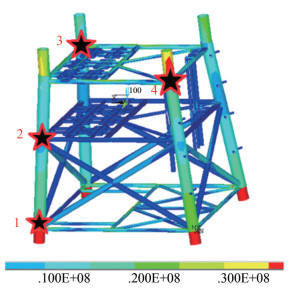
Statistical findings for the VM stresses of the selected Jacket tubular support member are presented in this section. Figure 8 illustrates the Jacket with four critical (i.e., hotspot) stress locations being selected.

Figure  8  Illustration of the slightly deformed part of the Jacket with four critical VM stress monitoring locations. The stresses (hotspots) are indicated using colors

Download: Full-Size Img

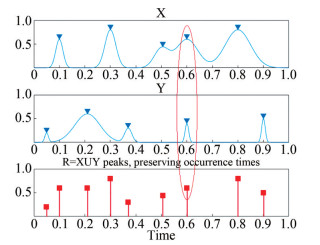
Figure 8 illustrates the part of the Jacket with four stress monitoring locations. Stresses due to external (wave) loadings are computed using ANSYS FEM software, and VM stresses are highlighted using colors. The failure, hazard, or risk limits are all equal to 1. Four measured or simulated time series with local maxima from the key components in the system are kept in temporally nondecreasing order and combined into a synthetic vector R for the Jacket system (Gaidai et al., 2023b; Gaidai et al., 2023c; Gaidai et al., 2023n;Sun et al., 2023a; Yakimov et al., 2023a;Yakimov et al., 2023b;Yakimov et al., 2023c).

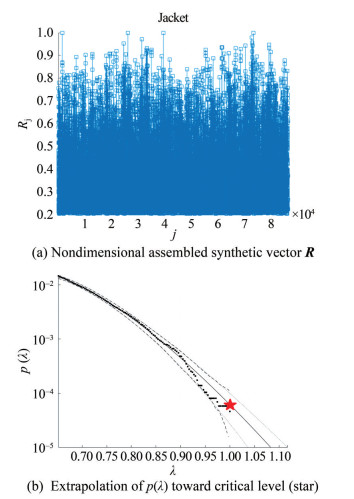
Figure 9(a) presents an example of a nondimensional assembled vector R, which consists of assembled local Jacket stresses at four critical or hotspot locations (Figure 8). λ_{cut − on} = 0.6 cut-on limit is selected as an example given that lower values λ < λ_{cut − on} are clearly irrelevant for extrapolation of the desired failure or hazard PDF tail. Notably, λ = 1 (Gaidai et al., 2023d; Gaidai et al., 2023e; Gaidai et al., 2023f; Gaidai et al., 2023g; Gaidai et al., 2023h; Gaidai et al., 2023i; Gaidai et al., 2023j; Gaidai et al., 2023k; Gaidai et al., 2023l; Gaidai et al., 2023m; Sun et al., 2023b; Gaidai et al., 2024a). The system vector R does not have physical meaning on its own because it is purely synthetic. Index j represents a running index of local maxima for key components in the system, which are sorted in temporally nondecreasing order (Numerical Algorithms Group, 2010).

Figure  9  Assembled vector R and corresponding extrapolation.

Note: Empirical data (^*), extrapolation (solid line), and extrapolated empirical 95% CI (two dotted lines)

Download: Full-Size Img

Figure 9(b) presents extrapolation following Eq. (9) toward target failure or hazard level λ = 1. Two dotted lines indicate the 95% extrapolated CI. According to Eq. (6), the function p(λ) is directly related to the failure/hazard risk/ probability of the target system 1 − P from Eq. (1). Following Eq. (5), the failure/hazard probability/risk of the dynamic Jacket system 1 − P ≈ 1 − P_k(1) can now be estimated. In Eq. (4), the parameter N corresponds to the total number of local maxima of system components within the synthetic vector R (Gaidai et al., 2024b; Gaidai et al., 2024c; Gaidai et al., 2024d; Gaidai et al., 2024e).

Figure 9(b) exhibits reasonably narrow 95% CIs even when the underlying dataset is limited.

Figure 9(b) shows extrapolation over approximately five decimal orders of magnitude, which corresponds to a 10⁵ efficiency compared with MC simulation. When simulating a complex MDOF system using MC, the number of key dimensions or components of the system can become computationally prohibitive (Gaidai et al., 2024f; Gaidai et al., 2024g).

We deploy an alternative multivariate reliability method to cross-validate the Gaidai multivariate reliability method without performing extensive direct MC simulations. To the best of our knowledge, no reliability method is available at present to treat systems with dimensions NDOF > 2. Notably, the Gaidai multivariate reliability method can handle NDOF = ∞. Thus, cross-validation should be performed for NDOF = 2, which considers only the two most critical hotspot stresses. For cross-validation of the Gaidai multivariate reliability method, we refer to a recent study on a 2D Jacket system (i.e., with only two stresses selected) and the modified four-parameter Weibull bivariate method (Sun et al., 2023a).

The advocated Gaidai reliability methodology offers practical engineering benefits by effectively utilizing raw, unfiltered measured or simulated datasets. Its ability to handle the multidimensionality of dynamic systems, as well as accurate extrapolation tools, allows for analysis even when based on a relatively limited dataset.

Figure 9(b) demonstrates the extrapolation depth, which refers to the number of decimal orders of magnitude covered by extrapolation. In other words, it indicates how much CPU time can be saved.

5   Concluding remarks

Traditional reliability methods are not readily applicable to complex systems with a large number of key crosscorrelated components. The ability of the Gaidai multivariate reliability method to assess the reliability of highdimensional nonlinear dynamic systems is its main practical benefit. This work examines dynamic hotspot stresses at several support structure locations of an offshore Jacket platform. The Jacket support structure is modeled as a multidimensional engineering dynamic system. The theoretical rationale of the Gaidai multivariate reliability method is briefly presented. Although the reliability of Jacket structures can be analyzed through direct measurement or extensive MC simulations, the complexity and high dimensionality of dynamic systems require the development of novel, accurate, yet robust techniques. These approaches should be capable of handling even limited underlying datasets while making optimal use of them. The methodology employed in this study demonstrates efficacy across various intricate nonlinear engineering systems. The main goal of this research is to propose an all-purpose, trustworthy, and user-friendly multidimensional reliability strategy for offshore engineers. The suggested method produces reasonably narrow CIs. As a result, the proposed method can be used at the design stage for a wide range of nonlinear dynamic systems. The Gaidai multivariate reliability method is compared with the well-established bivariate Weibull method for validation. The Gaidai multivariate reliability method can be used not only for offshore Jacket platforms but also for other offshore engineering structures.