1   Introduction

The study of inlet and outlet hydrodynamics has a history of over 100 years. In the past, research focused on water inflow, and research on effluent dynamics was relatively scarce. The importance of water outflow issues is evident in many practical problems, such as fish jumping out of the water (Khosronejad et al., 2020), submarines floating (Yang et al., 2017), and amphibious vehicles exiting the water (Liu et al., 2023).

In terms of research methods, the previous research work of several scholars was mainly divided into experimental, simulation, and theoretical research. Different research methods have their advantages and disadvantages. For example, experimental research can more accurately capture the force changes and flow field evolution during the outflow process of structures; however, its experimental difficulty is relatively high. By contrast, theoretical research is easier to implement; however, its accuracy needs to be improved.

To better address the issue of underwater vehicles, a large number of scholars have conducted in-depth theoretical research in this field. Tassin et al. (2013) investigated the two-dimensional water inflow and outflow of objects whose shape changes in a specified manner over time through analysis and numerical modeling. An improved von Karman method was proposed to describe the effluent stage, and a reasonable derivation of the effluent model used in marine engineering was conducted. Shams et al. (2017) established a semi-analytical model to analyze the entire hydroelastic impact of wedges from the inlet stage to the outlet stage, describe the structural dynamics using the Euler–Bernoulli beam theory, estimate the hydrodynamic loads using the potential flow theory, obtain a closedform reduced modal model using the Galerkin method, and find an approximate solution using the Newmark-type integral format. Korobkin et al. (2017) addressed the flow caused by a rigid plate of finite length, which initially came into contact with a horizontal water surface and then began to move upward with a constant acceleration. Negative hydrodynamic pressure is applied on the lower surface of the plate, and water flows on the plate because of the generated suction. Theoretical research can analyze in detail the disturbance of a certain influencing factor on the overall state.

Compared with theoretical research, numerical simulation can more intuitively display the motion state and parameter distribution. Numerical simulation has been widely used in previous research on water exit issues. Hao et al. (2019) conducted a numerical study of the threedimensional outflow of spheres with different vertical velocities using the lattice Boltzmann method. Gravity is introduced in the form of the calculated equilibrium distribution of velocity changes while ignoring surface tension. Bettle et al. (2009) analyzed the roll instability observed in small and medium-sized submarines with rising buoyancy, coupled the computational fluid dynamics Reynolds-averaged Navier–Stokes (RANS) solver with the six-degree-offreedom solid motion equation of a submarine, and provided a detailed overview of the theoretical framework and numerical implementation, particularly the fluid rigid body interaction method, combined with control, propulsion, and ballast blowing models. The submarine-specific model is traditional. Meanwhile, RANS flow field prediction is compared with coefficient-based models and validated based on steady-state wind tunnel data spanning the initial flow conditions of interest. Ni and Wu (2017) investigated the free water outlet of a buoyant sphere that is initially completely submerged in axisymmetric flow, driven by the difference between vertical flow force and gravity. The fluid is assumed to be an incompressible viscous fluid, and the flow is unreasonable. Velocity potential theory is adopted, and completely nonlinear boundary conditions are applied on free surfaces. Moshari et al. (2014) conducted a numerical analysis of the two-dimensional and three-dimensional buoyancy-driven outlets of a cylinder and used the code based on finite volume discretization and fluid volume format for two-phase flow to solve for the nonlinear free-surface deformation caused by buoyancy during the outflow process of a cylinder. Chen and Huang (2024) proposed a new design method for autonomous underwater helicopters based on interdisciplinary collaborative optimization and conducted simulation research. Panahi (2012) attempted to introduce a finite-volume-based moving mesh algorithm to simulate such problems in viscous incompressible twophase media. This algorithm adopts a step-by-step approach to handle the coupling problem between pressure and velocity fields. Chu et al. (2010) simulated the outflow process of a cylinder. When the water body approaches the free surface, cavities first form at the nose and tail of the water body and then collapse as the water passes through the surface. The interaction between the free surface and the cavity was simulated, and the high pressure generated by the collapse of the cavity was captured. Chen et al. (2023) conducted a simulation study of the cavitation flow around the elliptical disk-shaped cavitation device of a nonrotating underwater vehicle. Guo et al. (2023) conducted numerical simulations of the process of cylindrical outflow, analyzing the evolution characteristics of the cavity, stress characteristics, and surrounding flow details during the process. The reliability of the model was determined through grid convergence analysis. Panahi (2012) attempted to introduce a finite-volume-based moving mesh algorithm to simulate such problems in viscous incompressible twophase media. Song et al. (2023) conducted numerical simulations of the gliding motion and hydrodynamic performance of a seaplane in still water and waves. Zhang (2010) used a new level set immersed boundary method to analyze the interaction between free surface flow and structure. By combining the improved immersed boundary method with the free surface capture scheme implemented in the Navier–Stokes solver, the interaction between fluid flows with free surfaces and moving bodies of nearly any shape can be modeled. A new algorithm has been proposed to locate precise force points near solid boundaries, providing accurate numerical solutions. Numerical simulation can demonstrate the changes in the flow field during the outflow process of the vehicle.

In the research process, experimental research has unique advantages over theoretical derivation and numerical simulation, such as the accuracy and intuitiveness of experimental phenomena. Truscott et al. (2016) presented the pop-up height of rising buoyant spheres over a range of release depths and Reynolds numbers. Breton et al. (2020) experimentally investigated the evolution of wetting surfaces and hydrodynamic forces of objects initially floating on the water's surface during the outflow process, as well as during combined inflow and outflow processes. A set of water exit equipment was designed by Wu et al. (2017), and a series of experiments on the water exit of a sphere were conducted to analyze the free-surface deformation and its dynamic change, such as break up. Fu et al. (2018) conducted experimental research on slender objects vertically emerging from water using high-speed cameras, explored the formation, development, and collapse mechanisms of cavities around slender bodies, and analyzed the dynamic characteristics of the shoulder and tail cavities when a low-speed body exits water at different water depths and initial velocities. Wu et al. (2018) investigated the entire process of free water withdrawal and return in a completely submerged sphere with a density slightly lower than water through model experiments. In their experiment, an initially stationary object with a density slightly lower than that of water is released underwater. Pan et al. (2024) conducted experimental research on controllable flexible-body extension-driven fins inspired by swimming frog fins and analyzed their hydrodynamic characteristics. Munns (2013) investigated the ejection heights of rising buoyancy balls at a series of different release depths, as well as the accompanying velocities and accelerations near the free surface. He focuses on the ejection height, velocity, and acceleration at the exit of the free surface and vortex shedding to further define the motion state experienced by the rising buoyant sphere. Kartal and Cantekin (2024) conducted experimental research on autonomous underwater pipeline damage detection, localization, and pipeline tracking for unmanned underwater vehicles. Horowitz and Williamson (2010) investigated the effect of the Reynolds number on the dynamics and vortex formation patterns of the free rise or fall of a sphere in a fluid. Since Newton first reported on the oscillation of a free-falling body, the fundamental question of whether a sphere will vibrate as it rises or falls has been a topic of considerable research, and the mass ratio is an important parameter in defining when vibration occurs. Xing et al. (2024) conducted experimental research on the hydrodynamic performance of biomimetic manta ray underwater vehicles at different forward propulsion modes. Veldhuis et al. (2009) investigated the free ascent behavior of a sphere in Newtonian fluids when the ratio of its density to the density of the surrounding fluid is approximately 0.02. Horowitz and Williamson (2008) investigated the dynamics and vortex wake mode of a sphere freely rising or falling in a fluid. A new vortex formation pattern, which includes four vortex rings formed in each cycle and is different from the previous vortex patterns of fixed and tethered objects, has been discovered. Wei et al.(2022a, b, c) conducted an experimental study of the fluid dynamics of hybrid unmanned aerial underwater vehicles during water–air cross-medium processes. Experimental research, as a commonly used research method, is widely used in the study of the water exit of spacecraft.

In the past, scholars have conducted extensive research on the ascent and descent of powered objects. This study focuses on the research on the kinematic and dynamic characteristics of the upward movement of a positively buoyant cylinder experimentally. The pop-up height above the free surface of a rising buoyant cylinder is examined. Experimental correlations between pop-up height and release depth will be drawn for cylinders of varying diameters. Section 2 presents the experimental methods used herein. Section 3 provides the experimental results and discussion. Section 4 summarizes the conclusions drawn in this study.

2   Experimental apparatus and image processing methods

The experiment is conducted in a closed laboratory, avoiding interference from natural light and air disturbance. The changes in the shape of cylindrical motion are recorded using a high-speed camera, and the trajectory of cylindrical motion is analyzed through image processing.

2.1   Introduction to the experimental parameters

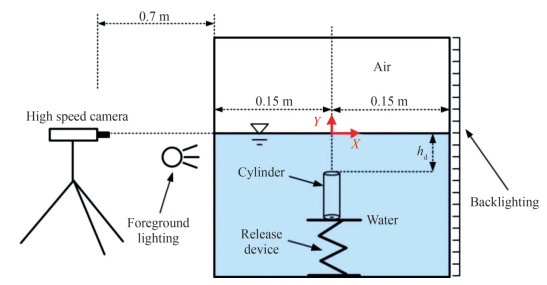
The experiment is conducted in acrylic water tanks with lengths, widths, and heights of 0.3, 0.6, and 0.6 m, respectively. The thickness of the water tank is 10 mm, and the water depth is 0.4 m. The layout of the high-speed camera and water tank is shown in Figure 1. The focus of the highspeed camera is level with the free liquid surface, and its horizontal distance from the cylindrical motion trajectory is 0.85 m. The minimum distance between the cylindrical motion trajectory and the water tank wall is 0.15 m, which can avoid the wall effects. The background and front light sources are used for supplementary lighting. As sketched in Figure 1, the cylinder is launched through an electromagnetic release device. The actual view of the layout is shown in Figure 2. The cylinder is connected to the release mechanism through an electromagnet. By power-off control, the cylinder can be released vertically or horizontally. The intersection point between the trajectory of the cylinder and the free liquid surface is defined as the origin, and the direction of cylindrical motion is defined as the positive Y-axis direction.

Figure  1  Sketch of the experimental setup

Download: Full-Size Img

Figure  2  Panorama of the experimental setup

Download: Full-Size Img

Three typical cylinders were used in the experiments. The specific parameters are shown in Table 1. The diameters of the cylinders are 40, 50, and 75 mm, and the length of the cylinders is 200 mm. The masses of the cylinders are 110, 170, and 340 g. Furthermore, the density ratio is the ratio of the cylinder density to the water density, where water density is taken as 998.2 kg/m³.

2.2   Image acquisition and processing

Referring to Figures 1 and 2, further details of the experimental setup and image acquisition are as follows: One high-speed camera imaged side views perpendicular to the side of the tank. The cameras were calibrated for parallax using a standard grid image technique. Fluorescent light banks provided backlighting to increase contrast. Highspeed cameras recorded images at 1 600 frame/s with a resolution of 512×1 024 for the (above water) pop-up images. The field of view of the pop-up images was 25×50 cm² (yielding a 20.5 pixels cm−1 magnification).

The data from raw high-speed images are extracted by image processing ballistic and pop-up events. The position data are extracted from the original high-speed image using a spherical tracking image processing algorithm. The velocity and acceleration are inferred from the position data: after fitting the position data with a second-order polynomial, the first and second derivatives of the fitted curve generate the velocity and acceleration data, respectively. The velocity of a cylinder on a free surface is obtained by interpolation of existing data.

3   Discussion of experimental results and analysis of hydrodynamic characteristics

This section will discuss and analyze the statistical and hydrodynamic characteristics of the cylinder during its buoyancy process. By conducting a statistical analysis of the behavior of cylindrical motion, corresponding motion laws can be obtained. This study has conducted over 200 sets of experimental cases. To ensure the accuracy and malignancy of the experiment, each typical case must be repeated at least five times.

3.1   Dynamic characteristics of vertical release

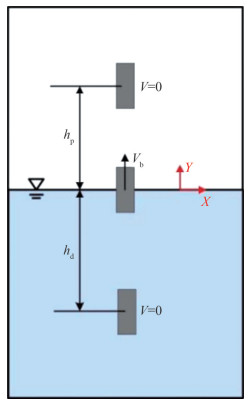
The measurement methods of the pop-up height h_p and release depth h_d are shown in Figure 3. The pop-up height h_p is defined as the maximum height attained by the center of the cylinder above the undisturbed free surface. The popup height is to be determined as a function of the primary parameters of the problem: h_p = f (h_d, D, ρ_s, ρ, μ, σ, g), where h_d is the release depth (the center of the cylinder below the free surface), D is the sphere diameter, ρ_s is the cylinder density, ρ is the fluid density, μ is the fluid dynamic viscosity, σ is the fluid surface tension, and g is the gravity. Choosing D, ρ, and g as the repeating variables, dimensionless groups are formed as follows:

Figure  3  Schematic diagram of cylindrical water exit

Download: Full-Size Img

where m^* is the mass ratio, Ar is the Archimedes number, and Bo is the Bond number.

During the upward movement, the velocity of the cylinder in both the starting and ending states is 0. The velocity at which the center of mass of a cylinder reaches the position of the original stationary free liquid surface is defined as V_b. The definition of the breach Froude number is Fr_b = V_b² / (gD), where D is the diameter of the cylinder.

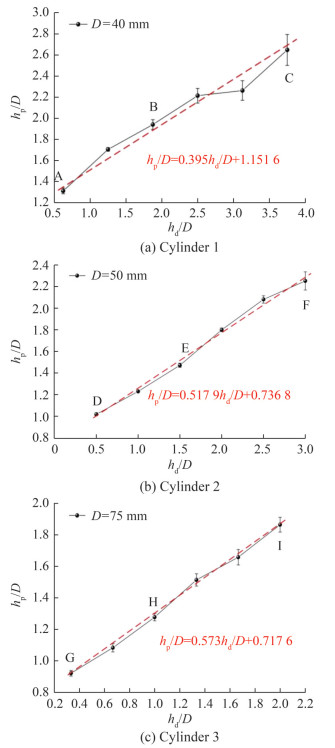
Figure 4 shows the schematic diagram of the variation of the cylinder's pop-up height with the release depth. Within the scope of this experiment, the pop-up heights of the three typical cylinders all increase with the increase of the release depth. The growth process shows nearly linear changes. The rate of change increases with the diameter of the cylinder.

Figure  4  Schematic diagram of the variation of the cylinder's popup height with the release depth

Download: Full-Size Img

Figure 5 shows the visual images of typical cases at pop-up height, which are marked in Figure 4. The figure shows the position and posture of the cylinder popping out at different release depths. The centroid positions of all cases shown in the figure exceed the original stationary free liquid surface.

Figure  5  Visual images of typical cases at pop-up height

Download: Full-Size Img

The image display of the vertical release cylinder water exit process for the typical cases is shown in Figure 6. The graph shows that the rising speed and height of the cylinder vary with different release depths. For Case F, the top of the cylinder first breaks through the water's surface and then reaches its highest point, accompanied by the shedding of water droplets during this process. The cylinder loses stability and falls back to the water's surface after reaching its highest point. Because of space limitations, it was not presented in the text.

Figure  6  Image display of the vertical release cylinder water exit process

Download: Full-Size Img

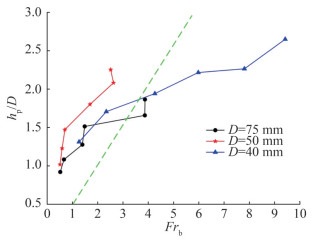
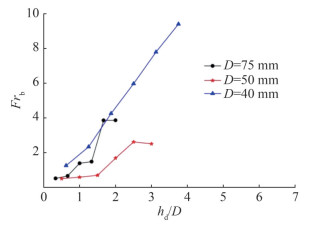
Figure 7 shows the pop-up height h_p/D versus breach Froude number Fr_b = V_b²/(gD) for Cylinders 1–3, and Figure 8 shows the breach Froude number Fr_b = V_b²/(gD) versus release depth h_d/D for Cylinders 1–3. Based on Figure 3, without considering the influence of hydrodynamic forces on the cylinder, the relationship between pop-up height h_p/D and breach Froude number Fr_b can be expressed as follows:

Figure  7  Pop-up height h_p/D versus breach Froude number Fr_b =V²b /(gD) for Cylinders 1–3

Download: Full-Size Img

Figure  8  Breach Froude number Fr_b = V_b²/(gD) versus release depth h_d/D for Cylinders 1–3

Download: Full-Size Img

which is denoted by the green dashed line in Figure 7. Given the effects of water splashing, surface pressure, and surface tension, a certain deviation between the derived formula and the actual measured values is detected.

3.2   Dynamic characteristics of horizontal release

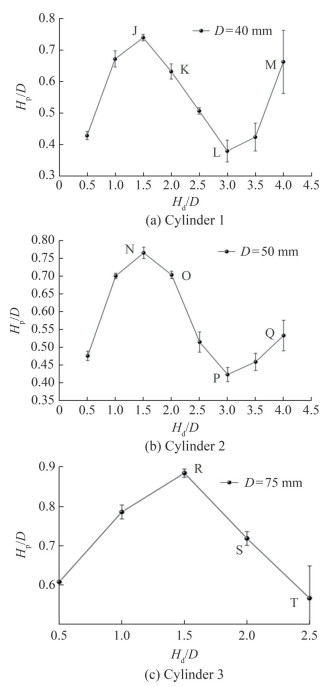
In contrast to the vertical release of cylinders, significant differences in the motion state of the cylinder during the horizontal release process are detected. The most important part is the height at which the cylinder pops out. Figure 9 shows the schematic diagram of the variation of the cylinder's pop-up height with the release depth for the horizontal release process. The graph shows that the pop-up height exhibits an irregular curve with the release depth and reaches its maximum or minimum values during the change process. For the three cylinders, the pop-up height reaches its maximum value at the release depth h_d/D = 1.5. The appearance of the minimum pop-up height is reflected in both Cylinders 1 and 2, both occurring at the release depth h_d/D = 3. For Cylinder 3, because of the limitations of the experimental conditions, the occurrence of the minimum ejection height was not captured.

Figure  9  Schematic diagram of the variation of the cylinder's popup height with the release depth

Download: Full-Size Img

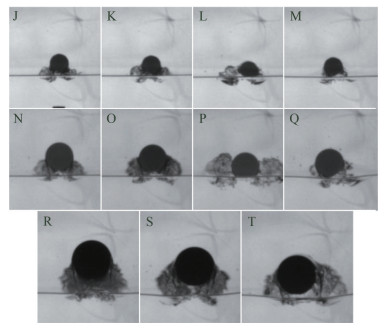
Figure 10 shows the visual images of typical cases at pop-up height for horizontal release, which are marked in Figure 9. The graph shows that the pop-up state of the cylinder is significantly distinct at different release depths, mainly manifested in splashing water and pop-up height. In the vast majority of cases, the cylinder has completely ejected from the water's surface. In a small number of cases, a portion of the cylinder is still submerged underwater, such as in Case L.

Figure  10  Visual images of typical cases at pop-up height for horizontal release

Download: Full-Size Img

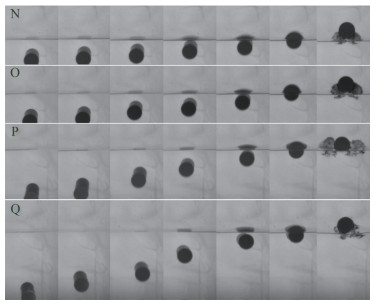
The image display of the horizontal release cylinder water exit process for typical cases is shown in Figure 11. The figure shows that the entire process of the cylinder releasing from different depths and floating out of the water's surface includes the cylinder arching the water's surface and splashing water. Because of the different flow field disturbances generated during the underwater movement of a cylinder, the pop-up height and motion shape of the cylinder are different when it comes out of the water.

Figure  11  Image display of the horizontal release cylinder water exit process

Download: Full-Size Img

4   Conclusions

In this study, the process of a positively buoyant cylinder emerging from the water's surface is investigated through experiments. The movement shape and flow field changes of the cylinder are recorded using a high-speed camera. Digital image processing methods are used to statistically analyze the hydrodynamics of cylindrical water flow. This study conducted two sets of experiments, namely the vertical and horizontal release of the cylinder. The results indicate that, within the experimental range, a positive correlation between the pop-up height of the vertical release cylinder and the release depth is detected. During the horizontal release process of the cylindrical model, the height of the model ejected irregularly varies with the release depth, and the change curve reaches the maximum and minimum values.

This study conducted relevant research on the phenomenon and motion law of water discharge in a cylindrical model through high-speed camera experiments. Because of the limitations of the experimental conditions, factors, such as wake turbulence that affect the motion state of the cylindrical model, have not been comprehensively analyzed. Further in-depth research can be conducted using different methods, such as particle image velocimetry. In addition, numerical simulation and theoretical derivation of the water discharge process of the model can provide a more detailed analysis of its working principle.