1   Introduction

Ships are important in safeguarding national marine territory and serve as the forefront of each country's maritime operations. As the diversity of maritime tasks increases, a diverse range of specialized vessels has emerged to cater to these varying operational needs. In general, ships can be classified into two categories according to their displacement in water: displacement and non-displacement ships. Displacement ships, such as military aircraft carriers Figure 1(a) and civilian bulk carriers Figure 1(b), rely entirely on buoyancy to support their weight. Conversely, non-displacement ships, such as planning boats, hydrofoil boats Figure 2(a), and hovercrafts Figure 2(b), utilize dynamic pressure, air cushions, or other innovative methods to support their hulls, which avoids reliance on buoyancy.

Figure  1  Displacement ships

Download: Full-Size Img

Figure  2  Non-displacement ships

Download: Full-Size Img

In the execution of maritime missions, various types of ships are susceptible to underwater weapons, such as torpedoes, which can greatly threaten ships' operational viability. Given the dual imperatives of national coastal defense, that is, the need for protective measures and offensive capabilities, current research on ship damage resulting from underwater explosion (UNDEX) has adopted a balanced approach, which encompasses the "spear" and "shield" perspectives (Zhang et al., 2023b). On the offensive side, researchers have examined the conditions that optimize the efficiency of strikes against ships. On the defensive side, researchers have attempted to determine which design can minimize the damage to ships under the action of explosion shock and can lead to a longer service life (Yao et al., 2016). In addition to the instantaneous structural damage, the effects of UNDEX on ships exist in the aspects of the safety of the ship's personnel and equipment and the stability of the ship's navigation. The shock generated by UNDEX can inflict varying degrees of harm on the personnel and equipment aboard, which potentially leads to irreparable damages (Zhou et al., 2019; Rakotomalala et al., 2021). Moreover, the intricate interplay among the free surface, the explosion shock wave, and the resulting bubbles generates disturbances that manifest in phenomena such as cavitation, bubble plumes, and explosion-induced water waves (Swisdak, 1978; Li et al., 2012; Saade et al., 2021; Zhou et al., 2024). These disturbances can significantly affect the navigation of ships in the vicinity.

This study aims to review research pertaining to the progress of ship damage and stability under the influence of UNDEX load. The main contents are as follows. First, studies on UNDEX load are reviewed, which are segmented into two primary components: shock wave and bubble stage loads. Second, research on ship damage caused by UNDEX is reviewed from two aspects: underwater contact and noncontact explosions. Third, research on the stability of ship navigation influenced by UNDEX is reviewed from natural factors, ship's internal factors, and explosion factors. Finally, this study is summarized, and relevant suggestions and prospects are proposed.

2   UNDEX load

The process of UNDEX is accompanied by many complex physical phenomena, including the transmission of shock waves, the pulsation and collapse of bubbles, the formation of water jets, and the occurrence of local cavitation (Cole, 1948; Zamyshlyayev and Yakovlev, 1973). When an explosive detonates, a violent chemical reaction within the explosive material releases a large amount of energy and rapidly radiates outward. The initial velocity of the shock wave in water is approximately three to five times that of the sound velocity in water. With the increase in the propagation distance, the energy of the shock wave gradually dissipates, and the velocity drops to the sound velocity in water. The shock wave gradually turns into a sound wave. Concurrently, an air mass with high temperature and pressure generated by detonation forcibly expels the surrounding water medium, which leads to the formation of a rapidly expanding bubble. Notably, the expansion rate of this bubble is inferior to that of the transmission speed of the shock wave. Given that the internal pressure of the initial bubble is significantly higher than that of the surrounding flow field, the pressure difference drives the volume of the bubble to expand, which is accompanied by a gradual pressure decrease inside the bubble. When the internal pressure of the bubble is equal to the pressure of the flow field, the inertia of water continues the expansion, which results in an increase in the volume of the bubble and a lower pressure of the internal bubble than the external flow field. This process continues until the bubble attains its maximum volume, at which point the water in the flow field commences to compress the bubble. When the bubble reaches its minimum volume, it emits the first pulsation pressure. This pressure initiates a repetitive pulsation cycle of "expansion–contraction". This process repeats until the energy of the bubble is exhausted or the bubble rises to the free surface, which releases the remaining energy (Jin et al., 2017). The loads from the shock wave and bubble pulsation are shown in Figure 3. In addition, cavitation areas appear near the wall or free surface due to the sparse wave generated by the shock wave propagating to the interface. Uneven stress causes the bubbles near the wall or nonspherical ones to form a jet, which can inflict localized damage on structures and potentially affect the ship's stability (Wang et al., 2018). For the shaped charge projectile, apart from the loads from the shock wave and bubble pulsation, the load caused by the high-speed shaped penetrator generated by the explosion should also be considered (Zhang et al., 2022).

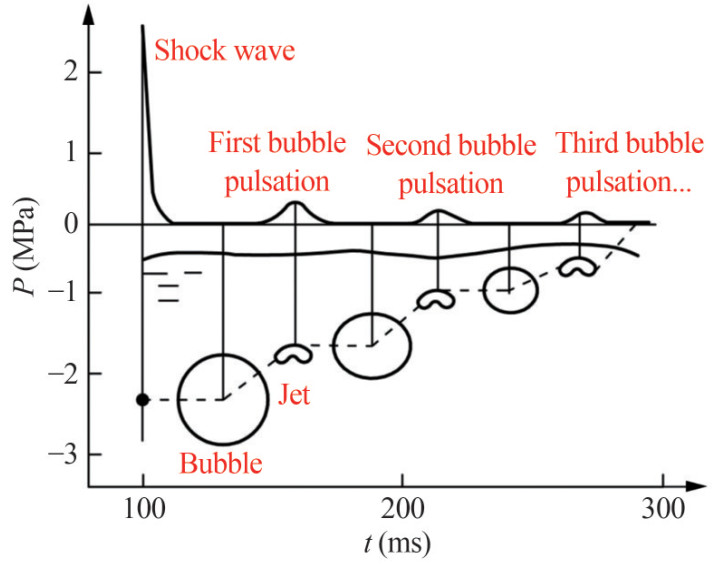Figure  3  Shock wave and bubble pulse of underwater explosive (Jin et al., 2009)

Download: Full-Size Img

From the perspective of TNT explosive energy, the cumulative energy released during the shock wave propagation and subsequent bubble pulsation stages closely approximates the total detonation energy of the explosive. Therefore, this study mainly focuses on the loads from the shock wave and bubble pulsation.

2.1   Shock wave load

During the Second World War, which was driven by the United States and the Soviet Union, an extensive array of UNDEX tests were conducted by various nations to meet wartime needs. Past the war, scientists have summarized and analyzed the vast trove of test data amassed during this period, which resulted in the derivation of a series of empirical formulas for UNDEX load. For example, Cole (1948) first proposed the empirical formulas of shock wave load and bubble pulsation load generated by UNDEX. Based on Cole's work, Zamyshlyayev and Yakovlev (1973) improved the empirical formulas of shock wave and bubble pulsation loads by accounting for the load characteristics of near-field explosion. The formulas of shock wave load that varies with time p(t) given by Zamyshlyayev are as follows:

where p_m is the peak pressure of the shock wave, θ is the attenuation constant, W is the weight of TNT, D is the detonation distance, and R₀ is the initial radius of the explosive.

Zhang et al. (2023a) proposed a new method based on the weakly compressible assumption for quick estimation of shock wave pressure in the far field. The pressure history at location r can be expressed as follows:

where p_∞ is the pressure at infinity, R_s is the radius of the shock front, and δp is obtained from Equation (5).

where L_p is the length of the computational domain, G is the flux, ζ = (r−R_e) /L_p represents the mapping relationship, Re is the left end of the computational domain, and c_∞ is the speed of sound in the infinite liquid.

Measuring shock wave pressure in UNDEX tests is difficult due to the limitation of test equipment. Data acquisition equipment and sensors require high sampling frequency and a large range due to the short pulse width, high frequency, and large peak value of explosion signals (Cui, 2019). The progress of science and technology and the continuous upgrading of test equipment have greatly expanded the research on shock waves generated by UNDEX. The advent of high-speed photography technology has enabled researchers to capture the intricate phenomena of UNDEX, which helped obtain the propagation trajectory and elucidate the propagation laws of shock waves (Kira et al., 1999; Saito et al., 2003; Gao et al., 2003; Berger et al., 2015), and determine the relationship between shock wave velocity and detonation distance (Liddiard and Forbes, 1982). Figure 4 shows a UNDEX shock wave interacting with the gauze layer captured using a high-speed camera. The majority of the shock wave penetrates the gauze layer, while a small part of the shock wave is reflected. Different types of sensors are widely used in UNDEX tests, such as PVDF pressure sensing technology (Zhou et al., 2024), piezoelectric sensing technology (Si et al., 2020), manganin piezo-resistance measurement technology (An et al., 2011), and Hopkinson bar measurement technology (Cui, 2019). These advanced sensors have significantly improved the accuracy and depth of UNDEX research.

Figure  4  Shock wave and bubble captured using a high-speed camera (Zhang et al., 2023a)

Download: Full-Size Img

The advancement and development of computer technology and modern simulation technology have encouraged numerous domestic and international scholars to use numerical methods for exploring the UNDEX phenomena. The utilized numerical methods include the discontinuous Galerkin (DG) method (Wang, 2017), the finite difference method (FDM) (Su et al., 2013), the finite volume method (FVM), the finite element method (FEM) (Gao et al., 2020), and the smoothed particle method (SPH) (Li et al., 2023). FEM, FDM, FVM, and DG are commonly used spatial discretization methods for discrete fluid equations. FDM can transform differential problems into algebraic ones. It has a simple format and is beneficial for constructing highorder equations. However, FDM has difficulty dealing with complex grids and boundaries. FVM has a strong ability to deal with irregular computational domains. However, its calculation accuracy is low, and the calculation is more complicated when performing high-order approximation. FEM is suitable for irregular computational domains and has high calculation accuracy. However, its calculation amount is larger than that of FDM and FVM, and it performs poorly in capturing strong discontinuities in the computational domain. DG has the advantages of FEM and FVM. It has a compact computing structure and can easily capture the strong discontinuity in the computational domain. The calculation is stable, but many unknown parameters exist in the solution process, which makes the solution work intensive. The abovementioned methods are often calculated based on grids, and they often encounter computational difficulties, such as large distortions, deformable boundaries, and interface movement caused by cavitation. Meshfree methods, which are based on particles, have been developed in UNDEX simulation to solve the aforementioned problems. These methods discretize the continuum with a series of nodes without any connecting mesh. Physical and material properties are assigned to these nodes. The most common examples of such methods are SPH and lattice Boltzmann method (LBM).

Upon analyzing the numerical simulation data, predictive formulas for the shock wave load resulting from underwater contact explosions have been obtained. For example, Ming (2014) used the SPH method, and Wang (2017) utilized the DG method to provide the prediction formula for shock wave load within a range of 2–6 charge radii. In addition, Wang (2014) obtained a prediction formula for near-field explosion loads by utilizing the FDM within the AutoDyn calculation program.

2.2   Bubble pulsation load

Rayleigh (1917) clearly demonstrated the motion characteristics of spherical bubbles and established the motion equation of bubble expansion and contraction within an incompressible, inviscid, and irrotational fluid environment. Subsequently, Plesset (1949) enhanced the Rayleigh equation and then proposed the Rayleigh-Plesset (RP) equation.

where R is a function of the bubble radius of time, $\dot{R} $ and $\ddot{R} $ are the first and second derivatives of R to time, ρ is the fluid density, P_g the pressure at the bubble boundary, and P is the given external pressure of bubble.

However, the RP equation disregards the compressibility of the flow field, which results in an unrealistic situation where the maximum radius of the bubble does not decay during repeated pulsation. Therefore, Keller and Kolodner (1956), Keller and Miksis (1980), Prosperetti and Lezzi (1986), and Lezzi and Prosperetti (1987) successively proposed the motion equations for a single bubble considering the compressibility of the flow field. The expression is shown in Equation (7).

where H is the enthalpy difference at the bubble surface, and p(t) is the (spherically symmetric part of the) liquid pressure at the bubble site in the absence of the bubble.

Building upon these foundations, Geer and Hunter (2002) proposed a pulsation equation for spherical bubbles that accounts for the influence of the external flow field and the effect of internal gas fluctuations within the bubble. Liu (2002) obtained the analytical formula for the entire stage of shock wave and bubble pulsation by using a semi-empirical and semi-analytical formula. This formula avoids a large number of differential and integral operations in the traditional bubble motion equation, and its calculation amount is significantly reduced. However, the intricacies of actual bubble behavior in natural settings are multifaceted, which is manifested in the emergence of bubbles in groups and affections by factors such as boundaries, water depth, gravity, environmental flow fields, and compressibility. Zhang et al. (2023a) established the unified theory for bubble dynamics and proposed bubble dynamics equations that can simultaneously consider the effects of multiple factors for the first time. The expression is shown in Equation (8). This equation delineates the fundamental principles of bubble motion in nature and addresses the challenges of theoretically predicting bubble dynamics across diverse sources, scales, and environmental conditions.

where C is the sound velocity in the flow field, and dF/dt is determined according to different physical problems. The bubble pulsation load at an arbitrary location in fluid r = (r, θ) can be calculated once the bubble motion is solved. The formula for the pressure at r is shown in Equation (9).

where P_a is the ambient pressure at the bubble center.

The motion of nonspherical bubbles is mainly studied by numerical methods. The boundary element method (BEM) (Luo et al., 2022; Liu et al., 2024) is a widely used numerical method at present. It has high computational efficiency and produces accurate results, which make it suitable for tackling intricate bubble dynamics in scenarios involving near walls, free surfaces, and multiple bubbles. Based on the boundary integral method considering the compressibility of the flow field, Liu et al. (2024) calculated and verified the bubble pressure in the free field by constructing a new form of solving the auxiliary function. They also discussed the pressure characteristics of nonspherical bubbles. This method is shown in Figure 5.

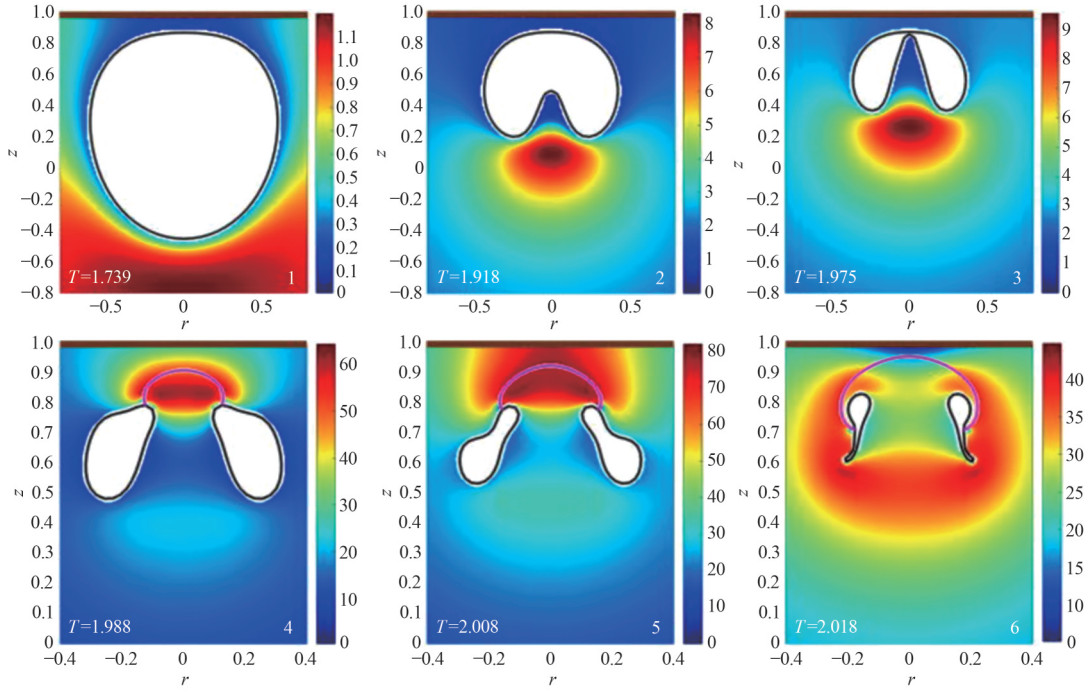Figure  5  Bubble shape and its surrounding pressure distribution near the rigid wall obtained by the boundary integral method that considers the compressibility of the flow field (the color scale on the right side of each frame represents pressure, the black solid lines are bubble surfaces, the magenta lines are cut surfaces, and the brown thick solid lines on the top are the rigid wall) (Liu et al., 2024)

Download: Full-Size Img

Other examples of numerical methods are domain solution methods, which mainly solve the Euler equation by utilizing interface tracking methods. Domain solution methods mainly include the Eulerian FEM (Qin et al., 2024), FVM (Liu et al., 2018a), FDM (Su et al., 2013), the DG method (Park, 2008), and LBM (Yapar and Basu, 2022). The boundary tracking method is used in conjunction with the domain solution method, including the volume of fluid method, the level-set method, and the front tracking method.

Based on the theories and numerical methods above, the phenomena of bubble jets and collapse caused by nonspherical bubbles have been discussed. The velocity of the bubble jet generated by the nonspherical bubble, the peak value, and the distribution of the load acting on the structure have been discussed. The load of the bubble jet on the structure is related to the velocity and sound velocity, and the damage to the structure is related to the material (Wang et al., 2005; Ming, 2014). However, another study found that a higher jet velocity does not necessarily result in a higher impact pressure, given that the impact pressure also depends on the distance between the wall and the jet front at the touchdown moment. For smaller distances, a more concentrated pressure loading on the material surface is obtained, which causes greater damage to the structure (Hsiao et al., 2014). In addition, when the bubble jet penetrates the surface of a bubble, a toroidal bubble forms. The speed of the bubble jet emerging at the end of the bubble collapse reaches hundreds of meters per second. Thus, the external liquid compressibility and the internal gas wave effect cannot be ignored. Research showed that an increase in buoyancy parameter causes improvements in equivalent radius, centroid displacement, and remaining total energy of toroidal bubble due to gravity. The internal gas wave effect causes declines in the equivalent radius and remaining total energy of the toroidal bubble due to gravity (Xiao et al., 2019). Based on Taylor's plate theory and a large amount of experimental data, the empirical formula for bubble collapse load is modified, which can lay a foundation for future tests of UNDEX near structures (Wang et al., 2023).

The aforementioned studies have primarily focused on the underwater manifestations of UNDEX, such as bubble jets and collapse, as well as their load impacts on the submerged components of displacement ships. However, the impact of the explosion is felt not only underwater but also above the free surface, as shown in Figure 6. Different from displacement ships, the effects on non-displacement ships, with their main hulls perched above the free surface, predominantly come from the disturbances above the free surface. For example, as the bubble ascends and causes the free surface to arch, a water plume is generated, which is accompanied by cavitation (Figure 7). Moreover, a highspeed water jet is formed on the free surface, which can affect the suspended bulkheads or the bottom of ships.

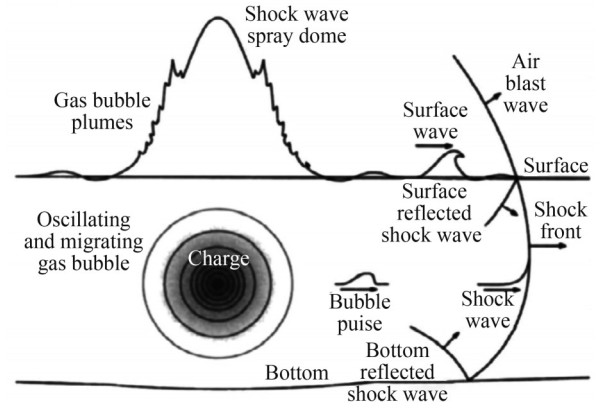Figure  6  Physical phenomena of UNDEX (Tupper, 2013)

Download: Full-Size Img

Figure  7  Water plume accompanied by cavitation (Gung, 2021)

Download: Full-Size Img

For an extended period, the morphology and formation mechanisms of free surface phenomena resulting from UNDEX, such as water plumes and activation, have attracted considerable attention. Research showed that different forms of water plumes are generated when different depths of the explosive are considered (Kedrinskii, 2005; Costanzo et al., 2011; Li and Rong, 2011; Zhang et al., 2016), as shown in Figure 8. In the later stage of UNDEX, the water plume undergoes a rebound downward, which causes disturbances at the free surface; these disturbances propagate as waves outward (Li et al., 2010).

Figure  8  Schematics of the effect of UNDEX (Zhang et al., 2016)

Download: Full-Size Img

Cui et al. (2016) studied the dynamic behavior of bubbles under gravity and different boundary conditions by small-charge UNDEX experiments. They analyzed the characteristics of related pressure pulses and revealed the causes of cavitation under the free surface (Figure 9). Huang et al. (2024) found that cavitation exists in the shock wave and bubble pulsation stages. Then, they investigated the influence of the stand-off distance and charge weight on the cavitation area and load characteristics.

Figure  9  Free surface cavitation and bubble dynamics of near-surface UNDEX (Cui et al., 2016)

Download: Full-Size Img

Although researchers have begun to study these phenomena very early, the results remain focused on the morphology and formation mechanism. The load introduced by these phenomena is still unclear, which requires further investigation and research efforts.

3   Ship damage caused by UNDEX

Exploring the influences of UNDEX on ships and other structures is a primary aim of the research on the distribution and mechanism of UNDEX loads. Among these influences, ship damage stands out as the most immediate and devastating consequence. Since World War II, researchers from various nations have extensively discussed the damage to ships and the failure mode of their structures under UNDEX. The UNDEX process is accompanied by many complex physical phenomena. The effects of UNDEX on ships are often the coupling of multiple forms of action, such as the coupling of shock wave and bubble load, the coupling of shock wave and cavitation load, or the coupling of boundary and explosion load (Figure 10).

Figure  10  Schematics of the effect of UNDEX (Yapar and Basu, 2022)

Download: Full-Size Img

The scope of explosion damage to the structure shows that it can be divided into local and overall damages. Local damage is usually caused by contact explosion or close-in explosion, which greatly impacts local structures, such as large plastic deformation and tearing (Figure 11). The overall damage often occurs in the mid and far-field explosion, which affects the entire hull, such as whipping motion, and even the hull breaking in some cases (Figure 12).

Figure  11  Local damage on HMS Boxer, F92 (Wang, 2015)

Download: Full-Size Img

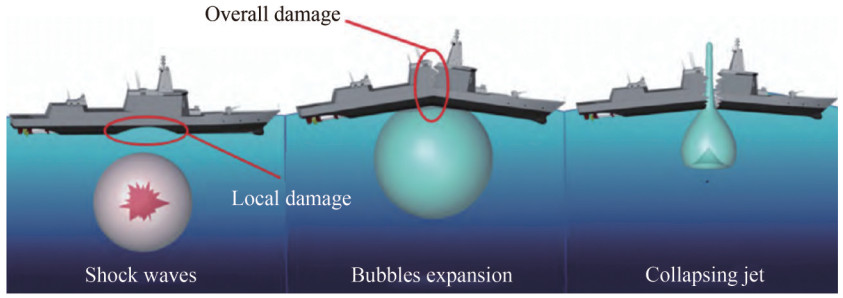Figure  12  Schematic of the ship's overall damage (Zhang et al., 2023b)

Download: Full-Size Img

When local damage occurs on the ship, the load it receives is mainly a combination of shock waves, bubble pulsation, and high-speed fragment loads. Detonations breach the structures, which poses serious threats to the vitality of ships (Rajendran and Narasimhan, 2001; 2006). Research on local damage is mainly based on numerical and experimental methods. Researchers have often simplified the structure (Cole, 1948; Geers, 1969) to complete their investigation, such as light plates (Zhou et al., 2024; Zhang et al., 2017), stiffened plates (Mu et al., 2008), and cylindrical shells (Xiao, 2014). Subsequently, more complex structures, like cabin models and real ships, have been used in UNDEX tests (Figure 13).

Figure  13  Local damage caused by UNDEX to different test objects

Download: Full-Size Img

Several researchers, such as Nurick et al. (1995; 1996), Brett and Yiannakopoulos (2008), and Langdon et al. (2005), conducted a series of experiments to explore the damage inflicted upon different simplified structures subjected to UNDEX loads. The different dynamic responses and damage of the structure under near-field explosion have been obtained. The analysis showed that, although the peak value of the bubble pulsation load is much smaller than that of the shock wave load, it has a greater influence on the damage and dynamic response of the structure. The spatial characteristics of the explosion load also change the response of structures, which makes the study of multiexplosive source explosion more important. In addition, researchers have found a phenomenon that, although the stiffener can reduce the overall structure deformation, the additional stiffness in this highly strained region leads to premature tearing. Chen (2019), based on previous research on the damage to different structures, established a method for engineering prediction of plate and cylindrical shell damage by theoretical derivation and a large number of experimental data combined with numerical methods. Wu et al. (2020) conducted a close-in UNDEX test on a largescale cabin model. They demonstrated that the close-in UNDEX seriously damages the cabin structure. However, the damage range is limited. Thus, the damage to the cabin model is still dominated by local damage.

In theory and numerical simulation studies, Florence (1977), Jones and Oliveira (1980), and Shen and Jones (1993) used the maximum normal stress criterion and Tresca yield criterion to investigate the dynamic response of plastic circular plates under different loads and boundary conditions. Simple formulas were obtained for the permanent central deflection under different pressures and loaded areas. However, studying the deformation and damage of underwater structures only by using light plates is insufficient. Based on the abovementioned research, Liu et al. (2001) and Zhu et al. (2003) introduced a new concept of relative stiffness of stiffeners, analyzed the influence of stiffeners on crevasses, and proposed and refined a formula for estimating the length of crevasses. In Yang (2015), a crevasse's diameter calculation method was developed using a rigid–plastic cross-beam mechanical model based on the theorem of momentum and the principle of conservation of energy. This method fills the gap in estimating the size of the crevasse by considering the influence of charge stand-off distance in near-field contact UNDEX. In addition to the calculation formula of deformation and crevasse, researchers have studied the influence of the structure on local damage caused by UNDEX. Gong and Lam (2006) used an explicit finite element approach interfaced with the BEM to explore the attenuation of a floating cylindrical shell under UNDEX. The effective structural damping and stiffness of the floating structure and the bulk cavitation effects near the free surface were considered in this study. The authors provided suggestions on structure design for protection and shock attenuation. Gao et al. (2020) simulated deformation and damage to a cylindrical shell– water–cylindrical shell (CWC) structure subjected to UNDEX loading. The results showed that the CWC structure can remarkably facilitate the structural explosion resistance capacity, and it exhibits great difficulty in completing penetration.

The development of technologies has made the shaped charge projectile an indispensable part of underwater weapons. For a shaped charge, in addition to shock wave and bubble pulsation loads, a high-speed shaped penetrator is produced in the process of its UNDEX (Zhang et al., 2022), which can impose severe local damage on the structure. In this case, the coupled damage on the structure is more serious than the damage under shock wave or bubble pulsation load (Zhang et al., 2024).

Overall damage is a prevalent threat in naval warfare. It is mainly formed in the shock wave and bubble pulsation stages, which can inflict overall deformation. It is mainly reflected in the whipping response of the entire ship. After the explosion, the shock wave first reaches the bottom of the ship, which causes localized deformation or even tearing. Simultaneously, the shock wave propagation creates a significant pressure differential among the bow, stern, and midship sections. It is accompanied by the expansion of the bubble, which leads to the ship's mid-arch deformation. As the bubble expands to the maximum, it commences a contraction. During this stage, the solid wall effect force (known as Bjerknes force) leads the bubble to move toward the ship and collapse on the side far from the structure. The collapse generates a high-speed water jet that strikes the deformed ship bottom, which results in local high-energy damage. The bubble pulsation causes a secondary response after the action of the shock wave. When the fundamental frequency of the bubble is close to the first- or secondorder vibration frequencies of the hull, the whipping effect will occur, which leads to buckling and strength damage of the hull girder (Keil, 1961). In extreme cases, this damage can even lead to catastrophic ship failure.

Given the prevalence and devastating nature of the overall damage, the navies of various countries have always focused on research concerning ship protection and attacks caused by UNDEX. Chertock (1970) proposed the hull girder method to study the principal vibration modes of the structure under UNDEX. Modal superposition theory has been used to study the whipping motion of the underwater cylindrical shell model. Since then, with improvements from Vernon (1986), Li et al. (2001a) considered bubble migration motion and energy loss to complete the elastic response test and theoretical analysis of the bubble to the overall elastic ship model.

Li et al. (2001b) and Zhang et al. (2011) used the hull girder model for testing. The results showed that the deformation of the hull girder caused by the action of the shock wave is small. However, during the bubble pulsation stage, the hull girder might be broken under the combined action of bubble pulsation, which bends the moment and highvelocity water jet. In some special cases, mainly rigid body motion occurs after the explosion, and the elastic–plastic deformation is not obvious. This result may be attributed to inadequate bubble performance (e.g., the bubbles broke on the free surface too early) or insufficient explosive quantity and power. Therefore, the effect of bubble pulsation on overall damage is greater than that of shock waves. Accordingly, bubble effects become the main object in the following research on overall damage. Notably, the effect of the bubble on the hull girder model includes not only overall damage but also rigid body movement. Longer beams sustain larger plastic deformations than shorter beams, but shorter beams undergo larger rigid body motion than longer beams (Zong, 2003; 2005). Subsequent studies have shown that the effect of bubbles on the hull girder is very large. First, given that the bubble pulsating frequency approaches the ship's low-order eigenfrequency, the loworder vertical mode of the warship is activated, and the ship presents a "whipping" motion (Zhang et al., 2008). Then, the cavitation zone is formed near the wall when the bubble contracts, which increases the strength and action time of the negative pressure of the bubble; it also results in the sagging failure of the hull girder (Huang et al., 2011). Finally, the hull girder is damaged in a longitudinal bending mode with a plastic hinge generated in the middle region (Gan et al., 2021). The overall damage is shown in Figure 14.

Figure  14  Overall damage of the simplified open floating slender structure subjected to the UNDEX bubble (Gan et al., 2021)

Download: Full-Size Img

The overall damage is also affected by the location of the explosive. The results showed that a bending deformation or an overall damage is more likely to occur when the UNDEX occurs directly below the midspan of the girder than when other explosions occur at different attack positions. Moreover, the structural damage is mainly concentrated in the middle of the 1/4 girder length region (Li et al., 2024). In the UNDEX hull girder test conducted by He et al. (2023) and Zhang et al. (2023c), when the charge is constant, a single peak is observed. A double peak relationship also exists between the structural damage and the explosion distance. The single peak means that only one explosion distance can lead to the most serious damage to the ship, while the double peak means two such distances exist. However, the tests' subjects and sizes of the two differ, and the correlation and occurrence conditions between the single and double peaks need to be further discussed.

For non-displacement ships, most or all of their hulls are perched above the free surface such as planning boats and hovercrafts. Thus, the damages they receive inflicted by UNDEX differ markedly from those of typical displacement ships. Given that the hulls are predominantly or entirely exposed above the water surface, little or no part is immersed in the water. Therefore, the excitations transmitted through water, such as shock wave loads, bubble pulsation loads, and excitation frequency caused by bubble pulsation, are far less harmful to non-displacement ships than displacement ships. Considering this unique scenario, violent disturbances on the free surface should be generated to achieve the goal of impacting the non-displacement ships. For example, a high-speed water jet generated by a UNDEX near the free surface can strike the bottom of the ship, which causes localized damage. Therefore, the damage of the disturbance on the free surface caused by UNDEX to the ship is worthy of further exploration.

4   Ship stability caused by UNDEX

The stability of a ship stands is a key concern for designers and users. This critical issue is related to many influencing factors, including natural factors like winds and waves (Figure 15), as well as the ship's internal factors, such as speed and navigation state. The presence of underwater weapons and other external threats adds an additional layer of complexity to ship stability. Early investigations into ship stability during navigation predominantly have focused on assessing the effect of these natural factors and the ship's internal factors on ship stability and predicting the resultant motion responses.

Figure  15  Marine explosion test on USS Gerald R. Ford (Gung, 2021)

Download: Full-Size Img

For displacement ships, higher wave height leads to a larger response amplitude, which causes the ship to easily lose stability at the same speed. With the same wave parameters, parametric rolling is more likely to occur at low speed, and the probability of parametric rolling can be decreased by increasing the speed suitably (Liang et al., 2010; Zhao, 2012).

For non-displacement ships, such as planing boats and hovercrafts, water provides less damping force than for displacement ships. As a result, external loads present a greater threat to the stability of these ships, which makes them more prone to instability. Scholars have studied the influence of natural factors (e. g., wind and waves) and ship's internal factors (e.g., speed) on the stability of nondisplacement ships. Research on the influence of wind load showed that the upwind is beneficial to the heading stability. The turning performance of the hovercraft differs under varying wind directions. Thus, relevant tests and controllers were designed by Fu et al. (2006) and Wang et al. (2008). Research on the influence of wave load showed that the wave affects the support condition of the non-displacement ship, which then influences the stability. For example, for hovercrafts, waves cause air cushion discharge, which affects their stability. In addition, different wave parameters, ship speeds, heading angles, air cushion heights, and ship centers of gravity affect the stability of non-displacement ships (Bhushan et al., 2011; Katayama and Habara, 2011; Wang, 2019; Shi et al., 2022; Yang et al., 2023).

Apart from natural factors and the ship's internal factors, human factors such as torpedoes and other underwater weapons can cause serious damage to the ship's structure during the early stage of the explosion. After a period of time, water plumes and waves are generated by explosions, which affect the stability of the ship during navigation. These effects are illustrated in Figure 16 and Figure 17.

Figure  16  Floating body affected by the water wave generated by an explosion (Luo, 2023)

Download: Full-Size Img

Figure  17  Ship affected by the water wave generated by an explosion (Liu et al., 2018b)

Download: Full-Size Img

Researchers have studied near-free-surface explosions, which can cause the water plume phenomena. The bubble breaks up on the free surface, which results in an obvious water plume phenomenon (Liang et al., 2006). The development process of a water plume can be divided into three stages: bubble out of water, water plume formation, and water plume fallback. According to the existing research, the boundary condition of the explosion and the ratio of the explosion depth to the bubble radius are important factors that affect the shape of the water plume. With the increase in the ratio, the interaction between the bubble and the free surface gradually weakens, the height of the water plume gradually decreases, and the width becomes larger (Wang et al., 2004; Zhi et al., 2009; Li et al., 2010; Zhang et al., 2016). However, a smaller explosion depth does not always lead to a stronger water plume. If the explosive is too close to the free surface, then the height of the water plume will be high, but the load will be low. A slight effect is exerted on ship navigation (Higdon, 2000; Qian and Yuan, 2001). In shallow water conditions, the development of the water plume is influenced by the free surface and the seabed boundary. The negative pressure generated by the free surface and the shock wave reflection from the seabed can affect the formation and motion of the bubble. Then, the bubble will affect the formation and shape of the water plume (Dong et al., 2018; Cheng et al., 2024).

Early studies have usually considered the water waves caused by large-charge nuclear explosions, which can reach the height of tens or even hundreds of meters. The height of water waves generated by the explosion of a certain charge explosive near the free surface can also reach the order of meters, which seriously affects the stability of ships (Blake and Gibson, 1981; Luo, 2023). The analysis of the time scale shows that water waves are caused by bubbles. The force of the water wave generated by the explosion on the floating body in the vertical direction is commensurate with its buoyancy, and the duration of the wave force in the vertical direction is roughly the same as the duration of the bubble pulsation (Li et al., 2010). Therefore, studying the influences of water waves generated by explosions on ships is important. However, the bubble model used is idealized. Specifically, it only considers the influence of bubbles on the free surface, while the influence of the free surface on bubbles is ignored. Consequently, the calculation results, although meaningful, cannot fully encapsulate the complexities of explosion wave effects on structures in proximity to the water's surface, particularly in near-free-surface explosion scenarios. Luo (2023) studied the influence of water waves generated by explosions in different array forms on ship motions. The results showed that heaving, swaying, and rolling are the most seriously affected motions by water waves generated by explosions. Compared with single-source explosions, the produced array explosions superimpose waves due to the interaction of multiple wavefronts. Consequently, the hull located in the middle of the explosion array experiences a combined action of superimposed waves, which has a greater effect on the hull motion response. In addition, when the sea waves are coupled with the water waves generated by the explosion, the wave parameters of the former greatly influence the latter.

Current studies have determined the generation mechanism of water plumes and waves generated by explosions. For some special types of ships, such as non-displacement ships, these phenomena may greatly affect their navigation stability. However, the majority of these works have been confined to numerical analyses, with experimental studies remaining scarce. Research on the interference mechanisms and capsizing modes of ships in their navigational state is scarce. In Section 3, under the action of an explosion, shorter ships (hull girders) are more prone to rigid body motion, while the longer ones are more prone to damage. Thus, whether the ship is damaged, experiences a rigid body motion, or both before the action of water plumes and waves generated by the explosion is unclear. Notably, exploring whether the different possible situations affect the action of water plumes or waves is important. Consequently, the aforementioned issues need further exploration and examination.

5   Conclusions

UNDEX is an important research direction in the field of naval architecture and ocean engineering. This study reviews the research on UNDEX from three aspects of loads, damage on structure, and ship stability to provide references for future investigations on the load characteristics of UNDEX and ship damage and stability under its action. While existing studies in this field have achieved remarkable progress, several challenges persist due to the nonlinearity of the UNDEX process and the intricate coupling phenomena involved. The following issues merit further exploration and refinement:

1) Studies on UNDEX loads serve as pivotal tools and foundations for works on the impacts of UNDEX on ships. Currently, compared with the explosion loads on water, most works in this domain have primarily focused on the underwater part of explosion loads and underwater impacts on ships. Although some research on water plumes is available, it primarily focuses on the shape and formation mechanism of water plumes and waves. The loads caused by these water plumes and waves and their effects on ships are less discussed and warrant further studies.

2) In research on ship damage caused by UNDEX, displacement ships and their simplified models, such as submarines and destroyers, are predominantly taken as the subjects, which provides insights into the mechanism of ship damage caused by shock waves and bubble pulsation. For non-displacement ships, such as planing boats and hovercrafts, few studies on the damage caused by UNDEX are available. Discussing how UNDEX affects and damages non-displacement ships is important.

3) Water plumes and waves generated by explosions may be formed by a large-charge deep-water explosion or a UNDEX near a free surface, which can significantly affect the navigation stability of adjacent ships. Several questions are still unanswered. The action process of water plumes and waves generated by explosions on ships is unclear, and the possible overturning modes of the ship are unknown. In addition, whether the ship is damaged, experiences a rigid body motion, or both before the action of water plumes and waves generated by the explosion is uncertain.