1   Introduction

Bubbles play significant roles in various fields, including ship engineering, geological exploration, biochemical treatment, and industrial design (Cole and Weller, 1948; Keller and Kolodner, 1956; Epstein and Keller, 1972; Schulze-Gettermann, 1972; De Graaf et al., 2014a; Dollet et al, 2019) (Figure 1). Underwater explosion shock waves and the violent flows induced by bubble dynamics can be destructive to marine structures (Zhang et al., 2023a; Zhang et al., 2023b; Du et al., 2022). Utilizing an air gun array, high-pressure bubbles can stimulate seismic waves to explore seabed resources (Chen et al., 2008; Liu et al., 2007). Ultrasound-induced cavitation bubbles exhibit intense oscillation and high-speed jets, enabling different applications, such as disintegrating stones, opening embolisms, achieving targeted drug delivery, and serving as a homeostatic and heat source during surgery (Dollet et al., 2019; Zhang et al., 2009; Yang et al., 2021; Coussios and Roy, 2008; Bailey et al., 2003). Cavitation generated by a highspeed rotating propeller will erode surfaces, reduce efficiency, induce noise, and cause vibration in ship appendages (Ju et al., 2012; Qi et al., 2022). Super-cavities are also employed to decrease frictional resistance by creating a gas gap between water and submersible vehicles. In essence, bubbles exert social and economic influences on modern life. Despite its strong connections with various specialized fields in fluid dynamics, such as hydrodynamics, acoustics, environmental science, marine mechanics, physics, and applied chemistry (De Graaf et al., 2014a; Duan et al., 2024; Behzadipour et al., 2023; Li et al., 2014; Naude and Ellis, 1960; Brennen, 2015), the motion of a bubble is highly affected by its surrounding environment, with fundamental mechanisms and physical laws exhibiting a high degree of similarity. Harnessing the beneficial effects of bubbles with in-depth investigations into bubble dynamics while mitigating undesirable consequences is crucial. Although several studies have examined cavitation in solid gaps (Chen et al., 1981; Pan et al., 2008), focusing more on materials, chemicals, and electronics, these investigations tend to lack strong fluid interactions, resulting in weak dynamics that are not extensively reviewed here.

Figure  1  Significant applications of bubbles in national defense and economic development

Download: Full-Size Img

Over recent decades, investigations into bubble-fluid interactions have explored fluid compressibility (Prosperetti and Lezzi, 1986; Gilmore, 1952; Lezzi and Prosperetti, 1987; Shima and Tomita, 1981), mass and heat transfer between bubbles and fluids (De Graaf et al., 2014b; Li et al., 2020; Jin et al., 2019), the influence of fluid field boundaries on bubbles (Soh, 1992; Wang et al., 1996a; Brujan et al., 2001; Klaseboer et al., 2005a; Zhang et al., 2013b; Li et al., 2023a), interaction between multiple bubbles and fluid fields (Laws et al., 1990; Bremond et al., 2006; Li et al., 2019; Liu et al., 2021), and gas evaporation and condensation inside bubbles (Zhong et al., 2020; Fujikawa and Akamatsu, 1980). These studies have employed various numerical and computational methods, such as finite difference method, finite volume method (FVM), boundary element method (BEM), particle tracking method, smoothed particle hydrodynamics (SPH), and discontinuous galerkin finite element method (DGFEM) (Li et al., 2021a; Sun et al., 2015; Huang et al., 2023; Zhang et al., 2015c; Zhang et al., 2013a; Zhang and Ni, 2013; Kim, 1994; Ge et al., 2019; Schmidmayer et al., 2020), leading to significant achievements in bubble dynamics. Simultaneously, a series of experimental studies focusing on the bubble dynamics under different environmental conditions accompanied by diverse modes of generation, such as electric spark bubbles (Fong et al., 2009; Chen et al., 2022), laser bubbles (Brujan et al., 2001; Rossell'o and Ohl, 2021), small equivalent explosion bubbles (Klaseboer et al., 2005a; Li et al., 2019), and actual vessel air gun bubbles (De Graaf and Brandner, 2014a; Wehner et al., 2019), have been conducted. Compared with theoretical studies and numerical simulations, experimental analyses are more reliable without limitations arising from the assumptions of models; however, some errors, which may cause difficulty in controlling variable analysis, are inevitably introduced. The mathematical relationship will also inevitably increase the experimental cost and safety risks. Generally, experiments are accompanied by theoretical or numerical studies; then, the experimental data can be used as a verification for the scientific validity of theoretical assumptions and numerical models. Numerical simulations provide a direct means of predicting bubble oscillation, and a series of review articles and books related to numerical studies of bubble dynamics that are suitable for the intuitive description and qualitative analysis of specific factors in bubble dynamics have been published. However, the development of theoretical studies predicting bubble motion in generality and resolvability remains relatively slow. In summary, theoretical studies of bubble dynamics need to be conducted to derive the universal laws.

In the development of bubble dynamics over a century, theoretical models have been influenced by numerous backgrounds and research directions. The assumptions and focuses of these theoretical models are various, and their relationships are not monotonically progressive. Hence, the theories of bubble dynamics need to be classified and discussed systematically. This paper aims to provide researchers in bubble dynamics and related fields with a clear, accessible overview of the development of the theory by reviewing significant literature and providing references for understanding current research. This paper is divided into two main sections, namely, the theoretical progress of bubble dynamics and practical marine applications of the bubble theory. The theoretical section covers investigations into free fields, near boundaries, clusters of bubbles, and the recently proposed unified equations of bubble dynamics, highlighting important theoretical models and related equations. The practical applications section discusses bubble dynamics induced by different sources, such as underwater explosions, marine cavitation, and seismic exploration.

2   Review of the bubble theory

2.1   Theory of bubble dynamics in incompressible fluid

Researchers began investigating bubble dynamics theory as early as the mid-19^th century, progressively realizing the close relationship between bubbles and physical phenomena, such as cavitation caused by high-speed propellers and the sound of water boiling. The theory evolved from the exclusive focus on cavitation bubbles, shaping the history of the study of bubble dynamics. The concept of computing the collapse time of a spherical cavity in an infinite incompressible fluid field was initially proposed by Besant (1859), who also made efforts to formulate it mathematically. Besant's assumption included an incompressible fluid field in space with constant pressure at infinity. The interior of the spherical cavity was deemed empty, and only the transformation of mechanical energy during the filling of the cavity with external fluid was considered to simplify the problem, which did not entail detailed bubble dynamics or represent a bubble model. Nevertheless, Parsons and Cook (1911; 1919) and Rayleigh (1917) were intrigued by Besant's idea and theoretical analysis, sparking their interest in cavitation research. Building upon Besant's theoretical model, Rayleigh (1917) derived the following equation to estimate the internal pressure p_g of a spherical cavity collapsing in an infinite incompressible free fluid field by combining Bohr's Law and the gas state:

where p_∞ is the pressure of the fluid field at infinity, p_g is the bubble internal pressure, R₀ is the radius of the spherical cavity at the moment, and R is the current radius of the spherical cavity after collapse. Lord Rayleigh's findings expanded upon Besant's mathematical formulation, differentiating a preliminary quantitative understanding of cavity collapse in a free fluid field. However, this conclusion relied on the assumption of constant pressure in the fluid field at infinity, making it challenging to address the complex bubble problem. Furthermore, extending and improving Equation (1) to characterize bubble behavior in a complex fluid environment proves difficult because it does not provide an intuitive relationship between cavity size and pressure. In other words, Equation (1) only correlates bubble radius and pressure at a specific moment; however, bubble radius and pressure are time-dependent during bubble oscillation, making it challenging to simulate, grasp, and predict the entire oscillation process.

Because of these limitations and assumptions, a fundamental equation that has a wider range of applicability and more potential for extensibility, which should be consistent with the basic principles of fluid dynamics, needs to be formulated. It was not until the 1940 s, drawing on Rayleigh's theory (Rayleigh, 1917) and the enhanced understanding of cavitation, that Plesset (1949) improved bubble dynamics by envisioning the bubble within a fluid field with rapidly variable internal pressure while the center of the bubble remained motionless. Expanding and refining Lord Rayleigh's theory, the relationship between bubble oscillation and fluid pressure in an incompressible fluid field was discovered, resulting in the distinguished Rayleigh-Plesset equation (R-P) for bubble dynamics:

where ρ is the density of the fluid field, p_b is the pressure on the bubble surface, p_∞ is the ambient pressure at infinity outside the bubble, R is the radius of the bubble with time, and $\dot{R}$ and $ \ddot{R}$ are the single-time and double-time derivations of R, which represent the oscillation velocity and acceleration of the interface of the bubble, respectively. If the fluid environment, fluid density, and pressure at infinity are defined, then the equation contains two unknowns, i.e., bubble radius and bubble surface pressure. For the case of a spherical cavity (vacuum) meeting the bubble surface with absolute pressure inside at 0, R-P equation is reduced to one unknown quantity, i. e., R. Under the given initial conditions, a special solution (Duclaux et al., 2007) of bubble oscillation velocity can be derived through the secondorder ordinary differential equation:

Based on this particular solution, the collapse time of Besant-Rayleigh problem can be simultaneously determined as follows:

where $T_{\mathrm{C}}^{\text {Rayleigh }} $ is the collapse time of Besant-Rayleigh problem. Meanwhile, the surface pressure of the cavitation bubble p_b expressed in Equation (2), which is generated by hydrodynamic fluid flow, such as behind high-speed propellers, has been precisely described by Plesset as follows:

where σ is the surface tension coefficient of the fluid and p_v is the saturated vapor pressure of the bubble. The pressure at the surface of the cavity expressed in Equation (5) does not account for the impact of internal gas because the cavity is assumed to be devoid of gas content. The bubble oscillation process can be simulated with p_∞ as a known term, first expressing the bubble surface pressure as a function of spherical bubble radius via Equation (5) and then generating closed equations by substituting Equation (2).

R-P equation provides a fundamental description of bubble oscillation in an incompressible fluid field. However, being a second-order ordinary differential equation, R-P equation cannot directly yield the expression of bubble radius, which leads to discrepancies in calculation accuracy among different numerical models, underscoring the necessity for a theoretical solution to compare and verify the scientific validity of numerical models. Addressing this, Kudryashov and Sinelshchikov (2014) analytically provided closed-form general solutions of R-P equation under the conditions of empty and gas-filled bubbles, establishing a reliable comparison basis for solutions derived from numerical iteration algorithms. For an empty bubble, the radius solution of the equation can be expressed as follows:

where R is the ambient bubble radius, ξ = 0.914 7 is also called the Rayleigh factor, and τ is the upper bound of the fixed integration of time:

where t is the time variable. For a gas-filled bubble, the solution can be articulated using the Weierstrass elliptic function (Kudryashov and Sinelshchikov, 2014), which exhibits different forms for noble and conventional gases.

Moreover, Plesset reanalyzed and extended Rayleigh's theoretical model, overcoming its limitation arising from the assumption of constant pressure in an infinite fluid field without providing a specific form of pressure. Drawing on the background of ultrasonic cavitation, Noltingk and Neppiras (1950) considered the effect of acoustic waves on ambient pressure in the fluid field expressed as follows:

where the ambient pressure p_∞(t) is a function of time, p_a is the static fluid pressure, p₀ is the pressure oscillation amplitude, and ω is the pressure oscillation frequency. Therefore, the bubble oscillation equation (Noltingk and Neppiras, 1950) of ultrasonic cavitation is expressed as follows:

which is based on the assumption that the gas distribution in the bubble is uniform, meaning that the pressure inside the bubble is the same as the pressure on the bubble surface.

Given that the gas density is significantly lower than the surrounding fluid, the mass of the bubble itself is no more than that of the fluid discharging the same volume. Thus, under the influence of the pressure gradient, the bubble exhibits buoyancy with evident migration characteristics. Incorporating Lagrange's description, Hicks (1970) integrated bubble migration behavior into the equation and modified R-P equation as follows:

where v is the bubble migration velocity, which can be obtained following Newton's Law to determine the acceleration and, thereby, the velocity for migration.

2.2   Theory of bubble dynamics in a compressible fluid

As cavitation bubble research advances, other research directions related to bubble dynamics have also progressed gradually. Herring (1941), Cole and Weller (1948), Trilling (1952), and Keller and Kolodner (1956) have examined the kinematic behavior of underwater explosion bubbles using R-P equation. The compressibility of the fluid field cannot be overlooked, given that underwater explosions produce powerful shock waves and the collapse velocity of the bubble is substantially higher, resulting in an elevated Mach number Ma > 0.3 during certain bubble oscillation processes. Consequently, significant disparities between theoretical and actual results arise. In addition, the incompressible fluid assumption overlooks shock wave radiation in the surrounding medium during bubble oscillation in underwater explosions, introducing errors between theoretically predicted and actual outcomes. In pursuit of deriving the spherical bubble oscillation equation for compressible fluid, Herring (1941) and Trilling (1952) assumed that pressure waves radiated in the fluid exhibit acoustic characteristics. When the bubble oscillation velocity is lower than the sound velocity, the bubble oscillation equation can be expressed as follows:

where C is the sound velocity in the fluid field, which satisfies C² = dp/dρ, and the density of the fluid is taken as that in the infinite space; hence, the compressibility effects are resolved using this equation.

The theoretical study of the bubble oscillation equation can be categorized according to the order of Mach number. For the zero-order approximation of Mach number, the bubble equation for a compressible fluid simplifies to R-P equation. For the first-order approximation of Mach number, Herring (1941) provided the bubble equation for a compressible fluid. Based on the assumption of Kirkwood– Bethe (John Gamble and Hans, 1942), Gilmore (1952) extended the compressible bubble equation to the secondorder approximation of Mach number, as follows:

where h is the thermodynamic enthalpy difference between the bubble surface pressure and the fluid pressure at infinity. For most liquids under the isentropic (adiabatic) condition, which can be expressed as follows:

where the coefficients n ≈ 7 and B ≈ 300 MPa (n and B are the constants which rely on the liquid property) for water. Fujikawa and Akamatsu (1980) and Prosperetti and Lezzi (1986) pointed out that if the coefficients n = 7.15 and B = 304.9 MPa, then the computational results will be consistent with the experimental results of the pressure-density relationship for water pressures below 1 × 10⁴ MPa.

In the investigations into compressible fluid bubbles, pressure waves are considered to possess acoustic properties that enable the radiative attenuation of the oscillation energy of bubbles. However, sound radiation is not reflected in the bubbles, indicating that the size and surface pressure of the bubble always have a linear relationship. To integrate the energy generated by the radiated pressure waves of the bubble with the reflected pressure radiation to the bubble itself, Keller and Kolodner (1956), Epstein and Keller (1972), Keller and Miksis (1980) described bubble oscillation in a compressible fluid through the combined solution of the wave and Bernoulli equations. Keller equation includes the nonlinear term of the interaction between bubble radius and surface pressure (Keller and Miksis, 1980), describing the forced oscillation of bubbles under acoustic radiation as follows:

Based on Keller's theory (Keller and Kolodner, 1956) of bubble oscillation in a compressible fluid considering the acoustic radiation effect, the computational results are significantly improved and consistent with the experimental data. The dynamic behavior of spherical cavitation bubbles described by Keller equation is compatible with the theoretical results of large-scale bubbles, such as underwater explosions, as presented in the research paper of Keller and Kolodner (1956). For small and medium-sized bubbles, such as cavitation bubbles, the results of Keller equation are consistent with those of Lauterborn (1976) based on R-P equation modified by Noltingk and Neppiras (1950). Consequently, Herring and Gilmore's theoretical model is extended to Keller's theoretical model, and Keller equation has become widely used as the primary equation for predicting bubble dynamics in a compressible fluid.

The theoretical development of spherical bubble dynamics (Flint and Suslick, 1991; Neppiras, 1980; Philipp and Lauterborn, 1998; Plesset and Chapman, 1971; Plesset and Zwick, 1994; Sun et al., 2020) has greatly benefited from the R-P and Keller equations, both serving as the primary representative equations of spherical bubble oscillation in incompressible and compressible fluid fields. Furthermore, Prosperetti and Lezzi (1986), and Lezzi and Prosperetti (1987) modified the higher-order quantities of Keller equation by introducing perturbation theory, thereby increasing the accuracy of the bubble equation for a compressible fluid field:

Although the theory accurately represents the equation, direct presentation of the differential computation of enthalpy dh/dt is infeasible as it involves a complex computational process. Hence, computation is performed using the internal/surface pressure of the bubble. Meanwhile, Prosperetti and Lezzi (1986) noted that Equation (15) is equivalent to Keller equation in the first-order accuracy of Mach number, but errors persist in Keller equation in the second-order accuracy of Mach number.

In addition to the compressibility of the free fluid field, numerous researchers have conducted theoretical studies of various aspects of bubble dynamics in the free field fluid, including the oscillation and migration of bubbles, the interaction between explosion shock waves and bubbles, and the heat and mass transfer between bubbles and the fluid field. For example, concerning the interaction between bubble oscillation and shock waves, Hicks (1970) based their work on the assumption of an incompressible fluid, whereas Geers and Hunter (2002) utilized the double asymptotic approximation (DAA) model to explore the bubble oscillation of underwater explosions, considering the effect of shock waves with the equation of state within a compressible free fluid field premise., and established both the bubble oscillation equation that does not consider migration and the bubble oscillation equation that incorporates both oscillation and migration. The DAA dilation equation derived from the aforementioned investigations is expressed as follows:

and the DAA bubble equation considering both oscillation and migration is expressed as follows:

where ζ is the acoustic impedance ratio of the bubble to the surrounding fluid, and ρ_b and C_b are the density of the bubble gas and the speed of sound, respectively, with φ₀ and φ₁ are the 0th and 1st order velocity potentials on the bubble surface, respectively, satisfying the following expressions:

where g is the gravity acceleration.

However, the bubble equations obtained by Geers and Hunter (2002) using the DAA method, which considers oscillation and migration, are not presented in an explicit format but rather in an iterative implicit format of parametric equations, necessitating a high degree of convergence in numerical solution computation. Moreover, known as the bubble DAA-consolidated equation, it unifies the firstorder internal and external double asymptotic approximations (IDAA1 and EDAA1) (Geers and Zhang, 1994). Figure 2 illustrates that the theoretical models of Geers and Hunter (2002) predicted more accurate bubble dynamics than those of Hicks (1970). The DAA bubble model of Geers and Hunter (2002) advanced the theoretical study of bubble dynamics by considering multiple factors and provided general motion equations, oscillation equations, and oscillation equations incorporating the migration of spherical bubbles, considering the wave effects of liquid and gas. However, the DAA model still has some issues, such as overprediction of maximum bubble radius and underprediction of bubble migration, which can only be rectified based on results obtained from at least three cycles of artificial correction.

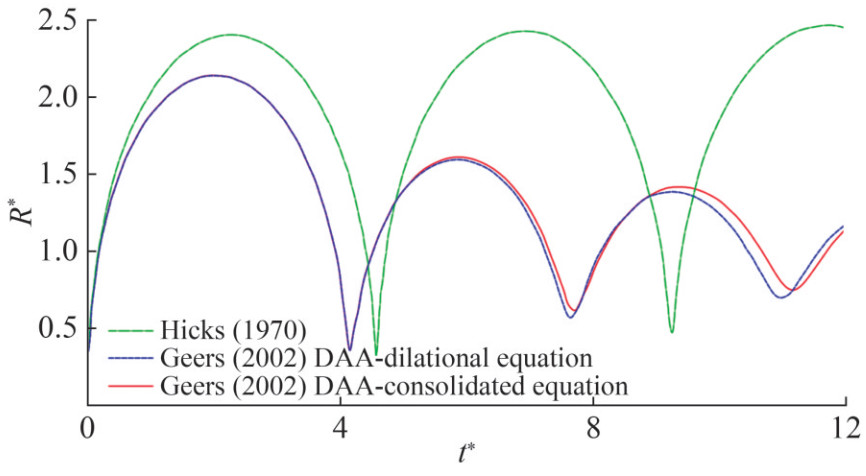Figure  2  Comparison of the predicted bubble dynamics based on the compressible fluid assumption by Geers and Hunter (2002) and the incompressible fluid assumption by Hicks (1970) theoretical models (R^* is the ratio of bubble radius to the adiabatic equilibrium radius, t^* is the corresponding dimensionless time)

Download: Full-Size Img

Regarding the heat transfer and temperature changes on the bubble surface during the collapse stage, Fujikawa and Akamatsu (1980) revised the bubble oscillation equation by considering the effects of fluid compressibility, viscosity, surface tension, surface heat conduction, and nonequilibrium condensation of fluid, based on the ideal gas equation, derived as follows:

and

In Equations (22) – (27), the source term $ \dot{m}$ is the net evaporation rate of fluid per unit area and per unit time at the bubble surface (where the condition $ \dot{m}$ > 0 indicates evaporation and the condition $ \dot{m}$ < 0 indicates condensation), and µ is the fluid viscosity coefficient. Yasui (1998) utilized the van der Waals gas equation for higher accuracy at high pressure instead of the ideal gas equation to analyze argon bubbles under the principle of single-bubble sonoluminescence conditions, accounting for the influence of chemical reactions. Fujikawa and Akamatsu (1980) and Yasui (1998) suggested that, apart from the thermal boundary layer near the bubble-fluid interface, the temperature distribution inside the bubble is spatially uniform. However, the rapid collapsing speed results in the gas-liquid interface undergoing a sharp boundary layer evolution (Szeri et al., 2003) during bubble collapse. To address this issue, Szeri et al. (2003) presented a computational method for the inner and outer thermal boundary layers and the mass boundary layer on the bubble surface. Zhong et al. (2020) constructed a laser bubble dynamics model by considering the evaporation and condensation effects between the bubble and fluid based on earlier studies, such as that of Yasui (1998), using the van der Waals gas equation. Their mathematical model is expressed as follows:

where a and b are the van der Waals correction coefficients, R_G is the universal gas constant, and T is the thermodynamic temperature of the gas. In addition, Soliman et al. (2010) revised R-P equation for laser cavitation to consider the effect of surface tension on the actual bubble form and the purity of the surrounding fluid, albeit at the expense of simplifying other components that Zhong et al. (2020) found to yield higher computational accuracy.

In conclusion, theoretical studies of single-bubble oscillation in a free fluid field are rooted in the concept of spherical bubbles, yet actual bubble dynamics often exhibit nonspherical features because of external environmental disturbances (Feng and Leal, 1997). This deviation is primarily attributed to the linear stability of spherical bubbles under infinitesimal shape perturbation, a concept initially explored by Longuet-Higgins (1989a; 1989b), which has inspired subsequent researchers to delve into nonlinear fluid-structure interaction problems. For instance, Pumphrey and Elmore (1990) investigated the effect of droplet impact on bubbles; Longuet-Higgins et al. (1991) examined the gas release characteristics of underwater nozzles; and Lauterborn and Kurz (2010) conducted characteristic studies of stability and acousto-optic energy radiation stemming from the nonlinear dynamics of bubbles. Generally, researchers have shifted focus toward estimating practical bubble dynamics, as elaborated in the subsequent subsections.

2.3   Theory of bubble dynamics in viscous/viscoelastic fluid

The core equations and theories of bubble dynamics presented in the previous subsection apply whether the fluid is compressible or not, but these are theoretical equations based on the ideal fluid background. In the case of large-scale bubbles, where the Reynolds number (Re = ρRṘ/2µ) can reach magnitudes of at least 10⁷, the viscosity around the bubble becomes negligible, and only the effect of fluid compressibility on bubble dynamics properties needs to be discussed. However, for specific cases of bubbles, viscosity can influence bubble oscillation behavior. Viscous fluids typically involve rotational flow, which cannot be analyzed solely using the velocity potential premise of potential flow. Consequently, directly studying bubble dynamics in viscous fluids using the Navier-Stokes equation poses significant challenges, resulting in a delayed start to the theory of bubble dynamics in viscous fluids.

Early studies trace back to the theories of bubble dynamics proposed by Plesset (1964), Yang and Yeh (1966), and Fogler (1969), focusing on incompressible purely viscous and Newtonian fluids. Among these, the study of Yang and Yeh (1966) began from the perspective of the NavierStokes equations, neglecting the body force of the bubble and providing the radial equations in the spherical coordinate system:

where u_r is the radial velocity at a point in the fluid field, p is the pressure at a point in the fluid field, τ is the viscous stress at a point in the fluid field, r is the radial variable of space. If the boundary layer theory is used to list the pressure equilibrium equation on the bubble surface, as shown in Figure 3, then it satisfies the following expression:

Figure  3  Boundary layer model of the bubble surface

Download: Full-Size Img

where µ is the tensile and compressive dynamic viscous coefficient of the fluid. Substituting the radial velocity (u_r = ṘR²/r²) in the equation and integrating into infinity from the bubble radius R yields:

In the case of a bubble in a Newtonian fluid, the viscous stress integral term is 0, meaning the effect of fluid viscosity on bubble dynamic behavior lies only in the boundary layer at the bubble surface corrected for pressure. In the subsequent theoretical development, Apfel (1981) introduced viscous effects to the equation by relating work and energy, where the work done by the pressure difference between the inside and outside of the bubble partially converts into the kinetic energy of additional fluid mass during bubble oscillation, with viscous dissipation consuming another portion of the converted energy. The final equation can be expressed as follows:

which further confirms the correctness and reasonability of the purely viscous fluid bubble equation proposed by Yang and Yeh (1966).

Considering the physical properties of fluids, besides Newtonian fluids, viscous fluids encompass a range of non-Newtonian fluids. Viscoelasticity plays a crucial role in characterizing the viscosity of non-Newtonian fluids. Theoretical investigations into bubbles within purely viscous fluids have typically overlooked non-Newtonian fluids and the influence of viscoelasticity. Hence, further research is necessary to explore and analyze the effects of viscoelasticity on bubble dynamics and fluid field characteristics. In such cases, the viscous stresses expressed in Equation (31) would no longer be negligible. Yang and Yeh (1966) provided the expressions for the integral term of viscous stress in their study, considering two non-Newtonian fluid models, namely, Bingham's plasticity model and the power law model.

1) Bingham's plasticity model fluid:

2) Power law model fluid:

where τ_s is the yield stress of the fluid, η is the shear dynamic viscous coefficient of the fluid, and α is the non-Newtonian index. The plural signs in Equations (33) and (34) are taken as positive during the bubble expansion phase and negative during the bubble collapse phase. Despite this integral result, expressing the viscoelastic term remains highly complex, posing significant limitations in terms of computation and application. Fogler and Goddard (1970) addressed this complexity in his theoretical study of bubbles in non-Newtonian fluids by expanding R-P equation into the following expression:

where τ_r is the viscoelastic radial stress, and its corresponding integral term can be expressed as a "memory" function N(t) of the viscoelastic coefficient, as follows:

where the "memory" function of the viscoelasticity coefficient is expressed as follows:

where δ(t) is the delta function, G₀ is the fluid elastic modulus, and λ₁ is the characteristic stress relaxation time. Building upon Fogler's theory of viscoelastic fluid bubbles, Ichihara et al. (2004) presented the bubble equation in a processed and intuitive form as follows:

Equation (38) illustrates that when the elastic term is neglected in Equation (37), Equation (32) is derived by organizing it alongside Equations (35) and (36), considering surface tension and the gas equation of state. However, Fogler's theory regards the inside of the bubble as a vacuum bubble, overlooking the thermodynamic properties of the gas inside. Tanasawa and Yang (1970) addressed this issue by combining the bubble equation of state and further modifying the equation as follows:

where λ₂ is the characteristic strain relaxation time, and the fluid shear dynamic viscous coefficient satisfies η = G₀λ₁. This equation describes the oscillation behavior of actively forming bubbles in non-Newtonian fluids.

Subsequent developments in the theory of spherical bubbles in viscous Newtonian fluids and viscoelastic non-Newtonian fluids have introduced various factors, including mass diffusion between bubbles and fluids and fluid compressibility. Regarding mass diffusion, Venerus et al. (1998) refined the bubble oscillation equations around the upper-convected Maxwell fluid (UCM) and Oldroyd-B fluid (ODB). For the UCM fluid, the bubble oscillation equation is expressed as follows:

For the ODB fluid, the bubble oscillation equation is expressed as follows:

Building upon this theory, Jiménez-Fernández and Crespo (2005) investigated the mechanism of the influence of fluid elasticity, shear-thinning viscosity, and tensile viscosity effects on bubble behavior by considering differentialtype eigen structure equations with interpolated time derivatives related to nonlinear acoustic oscillations of bubbles in viscoelastic fluids. Using the UCM fluid background, Naude and Mendez (2008) employed the modified R-P equation in combination with the wave effect in the fluid field proposed by Noltingk and Neppiras (1950) to investigate the degree of chaos of the Deborah number (De = ωλ₁, which represents the competition between relaxation and residence times of the fluid) on bubble oscillation behavior under different gas thermal conditions:

where $ S_{\mathrm{p}}^1+S_{\mathrm{p}}^2$ is the normal stress difference for non-Newtonian fluids, and the time derivatives of the two terms are satisfied as follows:

Notably, Cunha and Albernaz (2013) conducted a study of the effect of viscoelasticity on bubble oscillation in non-Newtonian fluids. Although their study yielded significant and representative conclusions regarding several characteristic parameters, such as the Reynolds, Weber, and Deborah numbers, the background fluid described in their study differed from the one described in the previous subsection, as it was a lower-convected Maxwell (LCM) fluid. The advantage of using LCM fluid instead of UCM fluid is that the bubble radius-time curve obtained in the LCM background exhibits better convergence and oscillation phenomena than that obtained in the UCM background.

The aforementioned theories regarding bubble dynamics concerning viscosity and viscoelasticity are based on the assumption of incompressible fluids. However, various aspects of the effect of fluid compressibility on bubbles have been investigated, as discussed in Section 2.2, including Keller equation, Prosperetti's perturbation theory, and the Geers-Hunter DAA model. Notably, these theories do not cover viscous fluids. To address this limitation, Shen et al. (2017) integrated previous models and theories on fluid compressibility and viscosity while simultaneously considering heat transfer effects, such as evaporation and condensation on the bubble surface, as illustrated in Figure 4, and proposed the bubble equation for a viscous compressible Newtonian fluid, as follows:

Figure  4  Boundary layer model with mass diffusion through heattransfer of the bubble surface

Download: Full-Size Img

where $ \dot{m}$ and $ \ddot{m}$ are the bubble gas diffusion rate and acceleration, respectively. For certain bubble dynamics problems, such as underwater explosion bubbles, where the evaporation and condensation effects of the gas inside the bubble are not considered, and based on the conclusion of Prosperetti (presented in Section 2.2) that the higher-order Mach number has only a slight effect on the actual bubble oscillation behavior, Equation (45) can be simplified as follows:

The simplified equation indicates that the viscous term only affects the pressure component at the right end of the equation when dealing with purely viscous Newtonian fluids. Consequently, the viscosity of Newtonian fluids can be viewed as a modification of the pressure term in the bubble equation. This simplification significantly streamlines subsequent studies of bubble dynamics theory. To explore the effects of other factors on bubble oscillation behavior in purely viscous fluids, obtaining equations through the potential flow assumption and making viscous corrections to the pressure term instead of starting from the complex Navier-Stokes equation to deduce the bubble in purely viscous Newtonian fluids suffices.

In this subsection, the theory of bubble dynamics in viscous and viscoelastic fluids is elaborated while staying true to the basic assumption of spherical bubbles. However, describing nonspherical bubbles elegantly in theoretical methods poses challenges, and the study of nonspherical bubbles is predominantly conducted through numerical computational methods. Nonetheless, scholars often prefer to simplify the description of nonspherical bubbles through theoretical methods. Hence, perturbation theory, commonly used to solve approximate analytical solutions in mathematical physics problems, is applied to the field of bubble dynamics. One of the early studies of bubbles in viscous fluids using perturbation theory can be found in the work of Prosperetti (1977). In this theoretical study, the bubble scale is no longer solely symbolized by the radius, and the following bubble surface equation is applied:

where ε is a small parameter satisfying 0 < ε « 1, A(t) is the amplitude of the perturbation term, and Y_n^m (n ≥ 2) is the spherical harmonic function. Notably, rotational flow typically accompanies viscous fluids, and Ω is used to characterize the rotation of a viscous fluid. Combined with the Stokes theory, Ω is considered source-less and can be expressed as the sum of two terms by introducing the poloidal-toroidal field theory in electromagnetism:

where Λ and Γ are the poloidal and toroidal vector fields, respectively, and Λ and Γ are the poloidal and toroidal scalars of Ω, respectively. Thus, Equation (32) is satisfied for R in Equation (47), and the first-order perturbation term satisfies the following expression:

Apart from this, a series of studies based on the perturbation method have also been conducted for Newtonian fluids by Hao and Prosperetti (1999) and non-Newtonian fluids by Allen and Roy (2000a; 2000b) to analyze and explore the effects of the Reynolds number, Deborah number, and other factors in the regimes. These studies are considered with a series of theories through the modified R-P equation.

2.4   Theory of bubble dynamics near boundaries

With the continuous improvement of bubble dynamics theory in the free fluid field, from a mathematical perspective, solving complex problems does not only require continuously complicating the control equation but also starting with reliable boundary and initial conditions. Then, computing and solving the control equation under the complex boundary and initial conditions becomes necessary. As a typical fluid-structure interaction dynamics problem, bubble dynamics studies must commence with the properties of the bubble itself and the surrounding fluid, considering the particular environmental conditions. Previous studies conducted by Rayleigh (1917), Plesset (1949), Gilmore (1952), Keller and Kolodner (1956), Fujikawa and Akamatsu (1980), Geers and Hunter (2002), and many others did not involve the computational method of bubble dynamics near the boundary of the fluid field. If bubble oscillation is stimulated near the boundary of the fluid field, then the presence of the boundary will significantly affect the dynamic behavior of the bubbles. Such a situation is mainly reflected in ship anti-explosion and corresponding structural damage (Zhang et al., 2023a; Zhang et al., 2013b), the influence of seismic air gun bodies on bubbles (Li et al., 2020), and the interaction between drug-targeted bubbles and blood vessel walls (Shi and Lin, 2009; Hong, 2020). Among them, rigid wall boundary conditions are needed for problems concerning ship anti-explosion and corresponding structural damage, as well as the impact of seismic air gun bodies on bubbles, whereas flexible surface boundary conditions are required for problems regarding the interaction between drug-targeted bubbles and blood vessel walls.

Quantifying and addressing the theoretical level of the bubble dynamics problem under rigid wall circumstances is challenging, and intuitively expressing the effect of the wall on the bubbles in the equations for bubble oscillations is difficult. Notably, the rigid wall condition ignores the slight structural deformation brought on by bubble oscillation. Based on this assumption, treating the wall as a mirror surface that reflects the oscillation effect of the bubbles in the form of a reaction force is possible. Cole and Weller (1948), Shima and Tomita (1981), Soh (1992), and many others primarily used the image-based method to investigate bubble oscillation near rigid boundaries and mapped corresponding point sources derived from images, also called image point sinks, using the wall boundaries as mirror surfaces for computation, as shown in Figure 5. The assumptions developed by Shima and Tomita (1981) while analyzing bubbles close to walls are as follows:

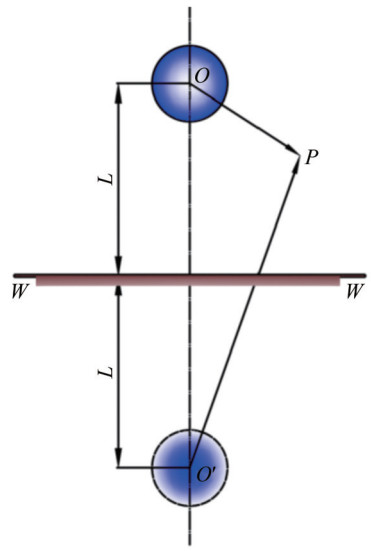Figure  5  Solution of the spherical bubble oscillation model near the rigid wall obtained by the image method (Shima and Tomita, 1981)

Download: Full-Size Img

1) The bubbles remain spherical during the entire oscillation process and will not migrate to the solid wall;

2) The inside of the bubbles is always uniform;

3) The effects of gravity, heat transfer, and gas diffusion are negligible; the bubble oscillation equation in the incompressible fluid is expressed as follows:

where L is the distance between the center of the spherical bubble and the solid wall. Although actual bubbles no longer meet the isotropy requirements, the theoretical model assumptions continue to treat the bubbles close to the solid wall boundary as spherical bubbles. As a result, the model has evident accuracy errors and is unsuitable for use in investigations into the dynamic behavior of the bubbles. However, such a theoretical model can be used to make preliminary predictions about the far-field properties of the fluid field.

In addition to the equivalent simulation of the effect of rigid walls on bubbles by the image method, Naude and Ellis (1960) provided the control equation and boundary conditions to describe the cavitation problem of non-hemispherical bubbles and wall-contacted collapse, assuming that the fluid is inviscid, irrotational, and incompressible, and neglected several factors, such as gravity, surface tension, and adhesion. Their control equation and boundary conditions are expressed as follows:

where φ is the fluid velocity potential, and the control equation is the Laplace equation. Equation (51) is based on the description of the spherical coordinate system, as established in Figure 6. According to the mathematical properties of Legendre polynomials in the spherical coordinate system, Naude and Ellis (1960) expressed the fluid velocity potential and bubble radius as follows:

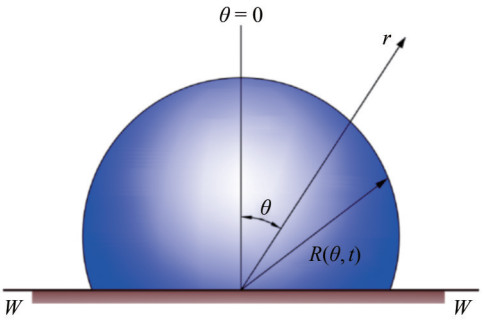Figure  6  Spherical coordinate system for theoretical modeling of nonhemispherical bubbles near the wall (Naude and Ellis, 1960)

Download: Full-Size Img

where P_2n(cosθ) is the Legendre polynomial of order 2n, and A₀, A_2n, R₀, and R_2n are time-dependent coefficients (their specific computational method is given by Naude and Ellis (1960)). Naude and Ellis (1961), Benjamin and Ellis (1966), Wu and Liang (2021), and many others have postulated that a cavitation bubble does not collapse while maintaining a spherical shape near the solid wall. This observation further confirms the idealistic assumptions proposed by Shima and Tomita (1981) and many others through the image method; however, it cannot describe the nonspherical characteristics of the bubble collapse stage.

The use of mathematical forms, such as Legendre polynomials, to describe bubble dynamic behavior near the wall requires solving a large number of time-related coefficients and cooperating with Legendre polynomials for computation. If more intuitive results are desired, then the computation at the theoretical level would be disastrous, necessitating the use of numerical methods that might improve computational efficiency and accuracy. Blake and Gibson (1987) investigated and defined the Kelvin impulse as follows:

where γ is the dimensionless distance parameter (ratio of the distance between bubble center and nearby rigid boundary to maximum bubble radius), T is the first oscillation period of the bubble (starting from bubble growth), and m is the equivalent source intensity of the rapid expansion of bubbles. Based on Kelvin impulse theory to quantitatively analyze the phenomenon of gravitational migration of bubbles near rigid walls, Blake and Gibson (1987) provided the distribution of Kelvin zero pulse lines as a criterion for the high-speed jet produced by bubbles in the collapse stage near the wall.

For flexible boundary conditions, flexible surfaces are typically regarded as linear elastic surfaces when the extent of the flexible boundary deformation magnitude caused by the bubble oscillation radiation pressure is smaller than that caused by bubble collapse. Soh (1992) derived the modified form of the Kelvin impulse combined with the energy equation based on the study of the bubble dynamic behavior near the flexible boundary surface conducted by Gibson and Blake (1980; 1982), expressed as follows:

where δ is the dimensionless buoyancy parameter, and r is the ratio of the instantaneous radius of the bubble to the maximum radius. The correction of the Kelvin impulse increased the judgment accuracy of the direction and intensity of high-speed jets generated near various types of boundaries. The modification advanced the theoretical study of bubble dynamics near flexible boundaries, such as free surfaces, and led to the conclusion that bubbles generated near flexible boundaries are more likely to be repelled away from the boundary, i.e., the jetting direction could be reversed. For situations where bubbles are between the free surface and the rigid wall at the bottom of the fluid field, according to the source-sink equivalence theory proposed by Blake (1988), the bubble expansion stage can be equivalent to a point source and the bubble collapse stage can be equivalent to a point sink, postulating that the rigid wall will cause the same effect as the original bubbles, whereas the free surface will affect the bubbles in reverse. Source-sink equivalence theory was used several times in Soh's model (Soh, 1992) to simulate the boundary conditions composed of multiple free surfaces and rigid walls, and their results predicted reliable bubble dynamics.

Another research direction of interest in the theory of bubbles near boundaries involves determining Besant-Rayleigh problem collapse time in an inviscid, irrotational, and incompressible free fluid field. However, for the nearboundary case, this particular collapse time result does not fit and needs to be corrected based on it. When the dimensionless distance parameter γ ≥ 1, Rattray (1951) solved the problem by adding a correction factor to the collapse time, as follows:

and the correction factor satisfies the following expression:

When surface tension is considered, the correction factor k in water is expressed as follows:

The shortcoming is that these corrections to the collapse time will no longer be satisfied at 0 < γ < 1, and it took half a century for this theoretical vacuum to be filled by Reuter et al. (2022). However, the correction factors under the 0 < γ < 1 condition are highly fitted by a seventh-order polynomial, as follows:

The root-mean-square error of fit for this equation is 0.006 8 (Reuter et al., 2022). Notably, in the study of Besant-Rayleigh problem, the effect of the boundary on cavity deformation needs to be neglected. The nonspherical deformation of the cavity is assumed to be weaker than that of the collapse effect.

In summary, it is challenging to use theoretical models based on spherical bubble assumptions for researching bubble collapse near boundaries. Near-boundary bubbles migrate to rigid walls under the influence of the Bjerknes force, showcasing complex migration behavior near flexible boundaries. Numerical approaches not only conduct highly accurate simulations of bubble formation but also significantly reduce computational time. Research on nearboundary bubble dynamics primarily relies on BEM, FVM, and SPH. Recent notable contributions include studies conducted by Wang et al. (1996a; 1996b), Liu et al. (2003), Klaseboer et al. (2005a; 2005b), Rambarzin et al. (2016), Li et al. (2020; 2018), Zhang et al.(2015a; 2015b), Shervani-Tabar et al. (2018), Wang et al. (2019), and Li et al. (2023a).

2.5   Theory of clustered bubble dynamics

Bubble dynamics problems extend beyond single bubbles to encompass bubble clusters in practical applications, such as air gun array bubbles for deep-sea exploration, ultrasonic cavitation bubble clusters, and underwater multiple weapon explosions. The interaction between multiple bubbles in clusters produces specific effects akin to the Bjerknes force effect provided by boundaries. Early theoretical studies of multi-bubble dynamics date back to the 1970 s, including works by Shima (1971), Morioka (1974), and Safar (1976). Before these studies, the majority of the research was devoted to examining and estimating the natural frequency of single-bubble oscillations (Minnaert, 1933; Neppiras and Noltingk, 1951; Hirose and Okuyama, 1957; Strasberg, 1953; Howkins, 1965; Shima, 1970) to solve cavitation-related problems, sidelining the study of bubble clusters. Shima (1971) pioneered natural frequency problems related to the interaction between two distinct bubbles, assuming that the distance between bubbles is larger than the bubble radius:

where R_i and R_j are the radii of the two bubbles, p_bi is the surface pressure of the bubble in the ith fraction, and r_ij is the distance between bubbles. Chahine (1984) theoretically analyzed pressure generated by bubble clusters in the context of cavitation-impacted erosion problems, postulating cavitation and erosion mechanisms through singular perturbation theory. Studies conducted by Bremond et al. (2006) and Nasibullaeva and Akhatov (2013) have explored theoretical aspects of clustered bubble dynamics, with bubble clusters as integral units made up of numerous individual bubbles with gas-liquid phase mixing (Figure 7). The following equations governing the bubble cluster and individual bubbles enable a comprehensive kinetic description of clustered bubble dynamics:

and

Figure  7  Classification model of bubbles in the bubble cluster(Nasibullaeva and Akhatov, 2013)

Download: Full-Size Img

where p_c indicates the liquid phase pressure inside the bubble cluster (according to the distance between the bubbles and the center of the bubble cluster, the bubbles in the cluster are graded), and p_bi is the surface pressure of bubbles in the ith fraction. The radius of the bubble cluster R and the bubbles in the ith fraction a_i satisfy the following relation:

where N_i is the number of bubbles in the ith fraction of the cluster and n is the total number of bubble fractions. Equation (64) enables the bubble cluster equation (Equation (62)) to be related to the individual bubble oscillation equation (Equation (63)) for the kinetic description of the clustered bubble.

Nevertheless, multi-bubble dynamics problems not only involve the interaction effect between bubbles but also, under specific conditions, the dynamics of the collapse phase of multi-bubbles and multi-bubbles near the free surface and surface of structures, which makes these problemsmore complicated. Similar to the study of single-bubble dynamics, various factors of a fluid environment need to be adequately considered. In terms of near-boundary multibubble dynamics problems, Tomita et al. (1984) experimentally investigated the double-bubble interaction mechanism at solid wall boundaries, which combined multi-bubble interaction dynamics with near-boundary bubble dynamics. Although these experimental observations provided intuitive bubble dynamics phenomena, some perspectives still require further investigations into the interaction mechanism and analysis of the bubble dynamics. Beylich and Gülhan (1990) fully considered thermodynamic effects, shock waves, and wave packets to analyze the dynamics of bubble clusters interacting with structures/rigid boundaries and free surfaces. However, the multifactorial and simultaneous complexity of the problem has made theoretical studies challenging. Consequently, most subsequent related studies have adopted a combination of theory and experiments accompanied by numerical computational methods, such as those conducted by Kodama et al. (1996), Betney et al. (2015), Han et al. (2022), Han et al. (2023), and many others.

The aggressive collapse phenomenon occurs within the bubble cluster, where Mach number may be larger under specific conditions, and the compressibility of the fluid field needs consideration. In terms of clustered bubble dynamics in a compressible fluid, Fujikawa and Takahira (1986) established a theoretical model based on the assumptions of spherical bubbles without migration and adiabatic gas without heat transfer, as shown in Figure 8, and combined wave theory with the potential flow theory approach to propose a bubble oscillation equation applicable to double bubbles, expressed as follows:

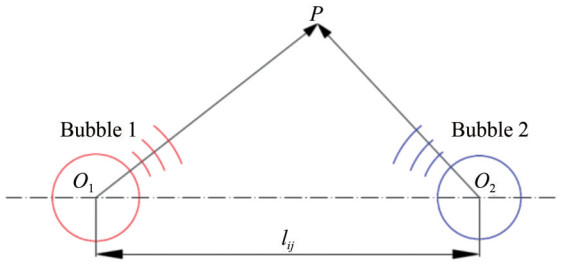Figure  8  Multibubble dynamics model for compressible fluid(Fujikawa and Takahira, 1986)

Download: Full-Size Img

where the physical quantities have the same meaning as that in Equation (61).

Equation (65) bears a high formal similarity to Equation (11) in the compressible fluid proposed by Herring (1941) and Trilling (1952); however, Equation (14) exhibits relatively better applicability in a compressible fluid. Wang et al. (2015) provided a multi-bubble interaction equation in acompressible fluid based on Keller equation, as follows:

where the physical quantities have the same meaning as that in Equation (63).

This set of clustered bubble oscillation equations expands as the number of bubbles within the bubble cluster increases, significantly increasing computational efforts. To address this, Wang et al. (2015) established the following assumptions:

1) The initial conditions are the same, and the gas is homogeneous for each bubble within the bubble cluster;

2) The acoustic radiation effects and any mass transfer can be neglected;

3) The bubbles always remain spherical during oscillation, and oscillations are nearly synchronized. Then, the bubble oscillation equation at a distance r₀ from the center of the bubble cluster is derived as follows:

and

where a₀ is the initial radius of the bubble, R₀ is the initial radius of the bubble cluster boundary surface, and N is the total number of bubbles in the cluster.

Similarly, for the clustered bubble dynamics problem, the interaction between bubbles challenges the spherical assumption. In problems involving bubbles near boundaries, Naude and Ellis (1960) used the Legendre polynomials method for analysis, which was extended to the study of clustered bubble problems. Figure 9 shows some representative examples, including studies conducted by Doinikov (2001) and Liang et al. (2012). These studies provide the velocity potential function in an inviscid, irrotational, and incompressible fluid with double bubbles as an example:

Figure  9  Spherical coordinate system for the theoretical modelingof bubbles (Liang et al., 2012)

Download: Full-Size Img

where n is the order of the Legendre polynomial, j = 1 and 2 denote Bubbles 1 and 2, respectively, and A and B are the influence coefficients of the bubble itself and the neighboring bubbles, respectively, which can be obtained from the study of Doinikov (2001). Then, the total velocity potential of the fluid can be written as a linear superposition of the velocity potentials of two bubbles, as follows:

In the form of Legendre polynomials, the radii of the two bubbles are determined using the following expressions:

where ε is the small perturbation parameter. For ε⁰, the equation obtained is identical to the form expressed in Equation (61), which has the advantage that the form of the equation corresponding to ε¹ can be obtained simultaneously.

The aforementioned overview essentially encompasses the main developments in the theoretical study of clustered bubble dynamics. With the continuous development of computational mechanics and numerical algorithms, more complex bubble cluster dynamics mechanisms have been mostly analyzed using numerical computational models, such as the coalescence, jetting, and splitting characteristics of bubbles involved in clustered bubble dynamics (Han et al. 2022; Rungsiyaphornrat et al. 2003; Han et al. 2019) and the properties of large-scale nonspherical bubbles (Liu et al. 2021).

2.6   Unified theory of bubble dynamics

The diverse research on bubble dynamics has yielded numerous theoretical achievements. However, these achievements need to be analyzed for specific problems and factors separately. At the practical level, the bubbles are not isolated from the fluid system (Zhang et al. 2023d); their dynamics are affected by multiple factors simultaneously. Previous theoretical studies of bubble dynamics have focused on the effects of fluid compressibility, boundary effects, and bubble interactions but have not incorporated the effects of bubble migration in a compressible fluid, the interaction between various forces on bubbles, and the effects of boundary conditions and bubble interactions on bubble migration into the research model. This situation poses a challenge for subsequent theoretical research with instructive and predictive properties.

To comprehensively address the aforementioned situation, Zhang et al. (2023c) simultaneously considered the effects of boundaries, multi-bubble interactions, ambient fluid field properties, gravity, bubble migration, fluid compressibility, viscosity, and surface tension. Their considerations led to their proposal of unified equations for bubbles, i. e., a theoretical model for bubble dynamics based on the wave equations using the method of moving singularity solution, also referred to as Zhang equation. This theory formally unifies different classical bubble equations, such as R-P, Gilmore, and Keller equations. Zhang equation is expressed as follows:

where dF/dt is the source term, which can be determined according to the physical problem under consideration, such as underwater explosions and ultrasonic cavitation. Zhang et al. (2023c) divided the complex kinetic behavior of bubbles into two major components, namely, oscillation and migration. For bubble oscillation, the source term is organized to obtain the bubble oscillation equation, expressed as follows:

where v is the bubble migration velocity, i.e., the reflection of bubble migration, which needs to be obtained from the bubble migrating equation, as follows:

where C_a and C_d are the additional mass and drag coefficients, respectively. Meanwhile, because multiple factors are considered in Zhang equation, a unified form for the pressure caused by the bubble oscillation radiation can be obtained as follows:

where r is the position vector of the bubble center and the prediction point in the fluid field. Because of the time delay effect caused by the compressibility of the fluid, the pressure of the fluid field at time t needs to be predicted based on the corresponding physical quantities at time t − (|r| − R) /C.

For Besant-Rayleigh problem near boundaries, under the premise of using the traditional theory of bubble dynamics, the given collapse time can only be corrected by introducing the empirical coefficient k based on the initial analytical solution of Besant-Rayleigh problem in the context of the free fluid field. Based on Zhang equation for bubbles, an analytical solution of the collapse time of Besant-Rayleigh problem near boundaries can be derived as follows:

The solutions shown in Equations (57) to (60) are more accurate but complex to calculate, and the equation of Besant-Rayleigh problem near boundaries is expressed as follows:

Based on the analytical results of Zhang equation for bubbles, combined with clustered bubble dynamics theory, such as that proposed by Bremond et al. (2006), the interaction between multibubbles is reflected in the correction of the pressure of the fluid field, and the form of the unified equations for the bubbles interaction in an incompressible fluid can be obtained as follows:

and

where v_i is the bubble migration velocity in the ith fraction, r_ij is the position vector from the bubble in the ith fraction to the jth fraction, and the rest of the physical quantities are the same as those in Equation (61). If the theoretical study of near-boundary clustered bubble dynamics is conducted, then, combined with the principle of the image method of near-boundary bubble dynamics, its equation can be uniformly expressed as follows:

and

In these equations, the bubble in the j′th fraction is the image of the jth fraction about the boundary, and the rest of the physical quantities are the same as those defined in the previous equations. The bubble behavior in the free fluid field can be simulated using Equations (76) and (77), the clustered bubble behavior can be simulated using Equations (81) and (82), and the clustered bubble behavior near boundaries can be simulated using Equations (83) and (84). The equations satisfied by the oscillation and migration of a single bubble near boundaries can also be obtained after simplification.

The results obtained are based on Zhang equation, as shown in Figure 10. The results obtained using Zhang equation are significantly improved compared with those obtained using Keller equation (Keller and Miksis, 1980) and the theoretical results of Geers and Hunter (2002) in terms of accuracy and applicability. In addition, the results of Zhang equation provide a comprehensive representation of the time delay effect of the pressure wave superposition caused by interfacial reflections. The theories are briefly summarized in Table 1. However, the drag and additional mass coefficients, which represent the viscous drag and nonstationary hydrodynamic force term, respectively, cannot be obtained directly. Xu et al. (2024) focused on the influence of these migration characteristic parameters on bubble dynamics and determined that the drag coefficient has stronger effects on bubble migration than the additional mass coefficient and should be determined through physical experiments under the explosion bubble conditions. Researchers have conducted studies of the dynamic properties of bubbles near the boundaries of complex structures and in the environment of complex fluids (Li et al. 2023a; Zhang et al., 2023d; Zhang et al., 2023e; Lv et al., 2023; Zhao et al., 2024) based on the unified theory to realize more in-depth mechanistic research in the field of bubble dynamics. Moreover, some numerical studies (Tang et al., 2023; Li et al., 2023b) have taken the unified equation as the standard to examine the correction of their numerical models.

Figure  10  Comparison of the theoretical results (Zhang equation, Keller equation, and Geers and Hunter (2002) model) and experimental data of bubble dynamics (Zhang et al., 2023c)

Download: Full-Size Img

3   Applications of bubble theory The development of the theory

The development of the theory of bubble dynamics cannot be isolated from actual production and daily life. On the one hand, the development of theoretical studies encourages the optimization of technology and production and life concepts. On the other hand, the advancement of theory is influenced by the emergence of new bubble dynamics problems in real-world development and life, which forces it to guide the cutting-edge theoretical development of bubble dynamics. In this section, we briefly discuss the current state of the application and the future development direction of the theory of bubble dynamics from the perspective of the main marine practical fields, such as underwater explosion, cavitation erosion, and seismic exploration, and focus on the issues that need to be resolved in these application fields.

3.1   Large-scale bubbles of underwater explosions

Underwater explosions serve as deterrents and deliver deadly strikes for the destruction of navy and battle equipment, making them a critical aspect of marine defense and naval vessels. Underwater explosions are always accompanied by high-frequency strong shock waves and low-frequency large-scale oscillating bubbles. The explosion emits strong shock waves that may cause local impact damage to structures, such as ship hulls. Large-scale oscillating bubbles disturb the surrounding fluid, which may resonate with ships and result in structural bending oscillations or instability of the entire ship, and the oscillation damage to the entire vessel is even more severe for marine facilities. Moreover, the high-speed jet with significant kinetic energy is a derivative of the underwater explosion bubble collapse. When the jet produced during an underwater explosion penetrates the bubble surface, it may cause a violent impact, cutting off or piercing through nearby ships. The theory of bubble dynamics in underwater explosion and ship damage holds tremendous research value because bubbles have a stronger and longer-lasting destructive force than shock waves.

At an earlier stage, the theory of bubble dynamics primarily focused on R-P equation, i. e., Equation (2), when the significance of studying bubble mechanisms in underwater explosions was realized (Cole and Weller, 1948; Herring, 1941). Furthermore, theoretical studies in the context of compressible fluid were primarily dominated by Herring (1941). As underwater explosion bubbles have large scales and more rapid oscillation velocities, the Reynolds number Re = (2ρRṘ) /µ in such a context is nearly up to the order of 106, which indicates that inertial force dominates in the oscillation of underwater explosion bubbles and the viscous influence is relatively small. Hence, the theoretical models and equations in such ideal fluid contexts represented by R-P equation in the early period can be utilized to achieve a decent degree of accuracy in the descriptions. The bubbles oscillate at a relatively lower velocity than the sound speed in the fluid for most of the first period that the bubbles remain spherical; thus, Mach number Ma = Ṙ/C is typically less than 0.3. Then, based on the assumptions of the incompressible fluid field, the largescale oscillation of bubbles can be reasonably analyzed. Notably, achieving equation closure by simply depending on the bubble oscillation equations, which contain two unknown quantities, namely, the radius of the oscillating bubble R and the pressure on the bubble surface p_b, is impossible from the perspective of the mathematical form of the physical problems. Given that the explosion is transient, the gas inside the bubble during oscillation can be assumed to be homogeneous and satisfies the adiabatic condition. Then, the state equation for pressure can be expressed as the adiabatic equation for gas (Cole and Weller, 1948), as follows:

where β is the gas adiabatic index, which is 1.25 for TNT. The starting pressure p₀ and the initial scale of the underwater explosion bubble R₀ must be estimated using empirical methods because the chemical reaction process of explosions is typically ignored, and the detonation process is considered infinitesimal on the time scale (Cole and Weller, 1948). Notably, the adiabatic equations are idealized in the description of the gas model, and the initial scales and pressures of the explosive gas products are given by an empirical model, which determines the gas equivalent of a solid explosive. A semiempirical theoretical model related to the material properties of solid explosives needs to be established if the shock waves and bubbles of underwater explosions need to be considered so that the pressure inside the bubbles is more reflective of the differences between solid explosives of different materials. Typically, the internal pressures provided by explosive sources, such as TNT, RDX, and hessonite, can be estimated to some extent using the Jones-Wilkins-Lee (JWL) equation (Wang et al., 2016) and corrected appropriately to consider the explosion shock wave. The JWL equation can be expressed as follows:

where K₁, K₂, K₃, k₁, and k₂ are empirical coefficients related to the type and purity of the explosive, ρ₀ is the charge density, and ρ is the fluid density. If the internal pressure of the bubble can be obtained from the adiabatic state, then, in combination with Equation (30), the bubble surface pressure can be obtained directly, which can then be substituted in the bubble equation for iterative computations.

In practice, underwater explosion bubbles produce significant jets during the collapse. If such jet impulses are considered in the theoretical model, then the bubble oscillation velocity will likely make Mach number greater than 0.3. Thus, the bubble equation considering fluid compressibility is more realistic and more convincing. Keller and Kolodner (1956) noticed that the influence of fluid compressibility on the underwater explosion problem is vital. The Laplace equation based on the potential flow theory has been expanded into the wave equation, and the bubble equation can be extrapolated as Equation (14). As the theoretical model has been continuously verified and become more generalizable in mathematical form, it can be simplified as R-P equation. Meanwhile, as the sound speed C → ∞ under the incompressible fluid assumption, fluid compressibility has been widely considered in underwater explosion bubbles and other related fields. Compared with the theoretical model of the incompressible fluid field, although fluid compressibility is considered in Keller equation, the radius of the bubble will gradually decay with periodical oscillations, as shown in Figure 11. From the physical perspective, fluid compressibility causes the bubble energy to radiate outward continuously; thus, the potential energy of the bubble decreases gradually. In the context of underwater explosions, this radiated energy acts in the form of secondary pressure waves to form further impacts on marine structures.

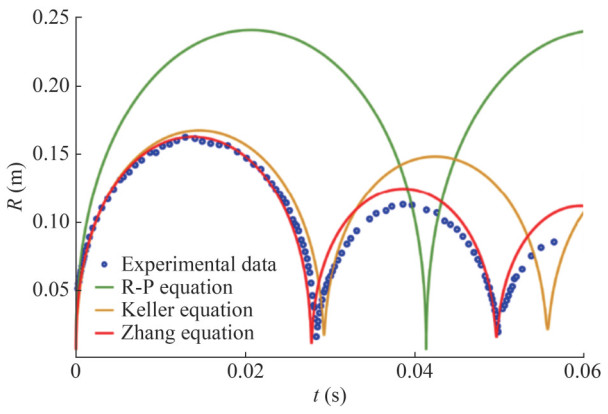Figure  11  Comparison of bubble radius during oscillation by considering fluid compressibility or not (Xu et al., 2024)

Download: Full-Size Img

Returning to the aim of underwater explosion studies, the dynamics of underwater explosion bubbles need to be explored to provide information about the design and assessment of the explosion-proof performance of the ship and the explosion performance of underwater weapons. This preliminary simulation of underwater explosion bubbles can be realized based on the bubble oscillation equation and the equation of state, taking Equations (50) and (86) as the examples, respectively. The vast majority of ship hull structures are relatively close to rigid wall conditions, and the free surface meets flexible boundary conditions. After developing and applying the theory of bubbles near boundaries to the analysis of the explosion resistance of the ship and the explosion mechanisms of underwater weapons, research has continued to progress for a variety of marine warship structures, including flat plate types (Epstein and Keller, 1972; Chahine et al., 1988; Liu, 2002; Li et al., 2001), cylindrical submarine structures in water (Epstein and Keller, 1972; Zhang et al., 2023b), and various combinations of forms with bubbles in underwater explosions (Li et al., 2019; Hicks, 1970; Geers and Hunter, 2002; Liu et al., 2003; Kodama et al., 1996; Chahine et al., 1988, Li et al., 2024).

Currently, with the declaration of the unified equations by Zhang et al. (2023c), the underwater explosion bubbles can be described and predicted more accurately. As the marine environment is more complex in reality, using Zhang equation for bubble dynamics that corresponds to Equation (75), the underwater explosion bubbles with various factors, such as gravity, fluid compressibility, weak viscosity, surface tension, and boundary effects, can be expressed sufficiently (Zhang et al., 2023a). Furthermore, the unified equations for bubble dynamics can guide production in marine facilities (Zhang et al., 2023a). Despite Zhang equation considering several fluid factors in the theoretical model, it is still limited by the assumption of a spherical bubble shape that is reflected by the bubble radius and a jet that is induced by bubble collapse. Some new phenomena that can hardly be predicted in previous models cannot possibly be described directly with radius. Some applications of bubble jets for underwater explosions can hardly realize more advancements as they only rely on the theory without any numerical simulations, such as the giant water curtain, to achieve the antimissile role (Higdon, 2000; Wang et al., 2014).

3.2   Cavitation on marine hydrodynamics

The theory of bubble dynamics can be viewed as a foundational element for understanding and developing ultrasonic or hydrodynamic cavitation problems. When the pressure decreases below the saturation pressure of the liquid, fluid microparticles lead to the formation of cavitation bubbles. Both hydrodynamics and ultrasonic cavitation result from local pressure reductions in the fluid field, although both are commonly referred to as hydrodynamic cavitation. Initial theoretical analyses of cavitation dynamics problems were conducted by Besant (1859) and Rayleigh (1917). Research on cavitation bubbles has been continuously advanced by many researchers. Cavitation phenomena have both beneficial and detrimental effects on society. For instance, they are advantageous in ultrasonic cleaning (Wang, 2002), the development of super-vacuum weapons (Chen, 2011), and the degradation of chemical wastewater (Wu et al., 2008; Wang, 2009), among other applications (Qian, 2004; Sun et al., 2023). However, cavitation bubbles can also induce vibration noise and damage propellers (Qi et al., 2022), leading to cavitation erosion of underwater structures (Naude and Ellis, 1960). This subsection mainly concentrates on the applications of the bubble theory of cavitation and erosion on marine structures.

In contrast to underwater explosion bubbles, cavitation bubbles are typically produced in association with the high-speed movement of complex structures through or in contact with the fluid, such as a marine propeller, and hydrodynamically produced bubbles form passively in low-pressure regions, which are vacuums sometimes. To measure whether the fluid pressure satisfies the conditions for cavitation to occur, Plesset (1949) used a cavitation parameter to determine it in their study of R-P equation, which is dimensionless:

where u is the fluid velocity at the point with pressure p that satisfies the Bernoulli equation:

When C_p < 0, the cavitation will be formed at this point. By substituting Equation (87) in Equation (88), the cavitation threshold (C_p = 0) fluid velocity can be further obtained:

The critical speed of a marine high-speed propeller can be further extrapolated by the generalized solution.

Notably, the size of the cavitation cannot reach a considerable magnitude similar to that of an underwater explosion bubble; thus, the viscous effects during bubble oscillation in the ocean need to be considered. Meanwhile, the effect of viscoelasticity is not considered because the ocean is a Newtonian fluid. In this case, the viscous bubble model by Apfel (1981), which is expressed in Equation (32), can be utilized. Then, the cavitation parameter p expressed in Equation (87) under the assumption that the ideal fluid will have errors in the estimation of cavitation needs to be modified as p_b because the pressure inside the cavitation is generally low, and there is no external power to supply high-pressure gas to the inside of the bubble. Instead, a structure moving at higher speeds will cause the internal pressure of the bubble to decrease. Therefore, the internal pressure of the cavitation can be simulated with the following ideal gas equation:

where the density of gas inside the bubble is obtained based on the mass and volume of vaporized fluid microparticles. Because the mass of the fluid microparticle is conserved before and after the vaporization-induced phase change, the densities of the gas and liquid phases differ, and the volume of cavitation bubbles due to the reduction of pressure in the high-speed flow is smaller than the space occupied by the fluid microparticle before cavitation, which is an intuitive reason why the cavitation bubbles have a smaller size than other types of bubbles. Naturally, in the theoretical model of bubbles, the volume of cavitation bubbles can be obtained using the spherical volume equation. When it is assumed that the cavitation bubble is a vacuum inside, the internal pressure p_g expressed in Equation (32) will become 0. If other factors are not considered, then the classic Rayleigh collapse phenomenon (Rayleigh, 1917) will occur.

Nevertheless, when these cavitation bubbles migrate to high-pressure regions, they implode aggressively because of pressure differences, resulting in shock waves and microjets as derivatives (Sagar et al., 2018; Sagar and Moctar, 2020). For the description of erosion induced by the blast of a cavitating jet, the preconditions of the spherical theory have limitations; thus, the problem of the erosion mechanism is mainly simulated and analyzed by applying numerical models. Philipp and Lauterborn (1998) and Sagar et al. (2018) focused on bubble cavitation and erosion and further investigated the characteristics of aluminum plates. Notably, these studies are more likely to prefer numerical simulations and experiments to establish the principles and still have many obstacles to revealing the essential mechanisms and universal properties. With the proposal of Zhang equation, many factors can be considered simultaneously, and computations to analyze the effect of cluster oscillations on the fluid pressure can be conducted. However, numerical models need to be combined with theoretical models to investigate the erosion of propellers in depth in future studies. In this way, a rapid understanding of the status of different models and factors in the cavitation process will be helpful, and the characteristic patterns can be expressed in an analytical form.

3.3   Seismic source exploration in deep sea and polar regions

With the rapid development of the world economy and industry, many coastal countries have shifted their focus to marine exploration to tap into the abundant resources contained within the ocean and establish marine development circles. Utilizing high-pressure air gun sources, which rapidly release gas into water, has become a preferred method because of its advantages of high precision, high resolution, and deep exploration capabilities. These high-pressure air-filled bubbles generated by air gun sources emit seismic waves toward the seabed, which are then reflected to the free surface through the seabed, enabling the extrapolation of resource distributions beneath the seabed (Jin, 2015). Although high-pressure air gun technology has been widely used in marine resource exploration, the main air guns, such as bolt, sleeve, and G guns (Chen et al., 2008), still cannot fully meet the requirements for ultradeep-sea exploration in terms of structural design. To be viable for ultra-deep-sea exploration, high-pressure air guns must possess certain characteristics, such as stronger low-frequency energy and longer pulse width within the frequency band (Li et al., 2022). Consequently, the development of new low-frequency air gun sources has become a focal point for current research in coastal countries and related technology enterprises (Li et al., 2021b).

Early research on air gun bubbles primarily focused on the growth process of bubbles. In contrast to simple cavitation bubbles, bubbles generated by air gun sources exhibit distinct physical behavior because of the high pressure they provide. Moreover, compared with underwater explosion bubbles, the mass and pressure gas transport between air guns and bubbles takes a certain amount of time because of certain factors, such as gas transport and heat transfer (De Graaf et al., 2014a; De Graaf et al., 2014c; Li et al., 2011). Therefore, air gun bubbles cannot be assumed to instantly reach high pressure like explosion bubbles, and their physical collapsing mechanism is not entirely consistent with underwater explosion bubbles. Air gun bubbles, as governed by gas state equations, follow either an ideal gas equation or the van der Waals gas equation, whereas underwater explosion bubbles adhere to an adiabatic equation of state. Because the air gun bubble is not adiabatic and mass is not conserved during air gun excitation, additional consideration of the mass transport process is needed on top of the equation of state. Initially, researchers employed the mass throttling model proposed by Landro and Sollie (1992) for gas transport, which considered that the mass throttling rate is constant during the air gun release period and is 0 during the bubble oscillation period. With more in depth theoretical research, DE Graaf et. al. (2014b), Li et al. (2020), and many others primarily adopted the more suitable mass throttling model (White and Xue, 2006) to investigate the air gun bubble characteristics, which assumed that the mass throttling rate between the air gun and the bubble is related to the ratio of the pressure inside them, i.e., it is dynamic and time-dependent:

where p_G, ρ_G, and S_G are the inside pressure, density, and port area of the air gun, respectively, and the ratio pg/pG has the minimum condition p_g/p_G ≥[2/(β+1)]^β/(β+1). Heat transfer can be typically described using the first law of thermodynamics:

where U is the internal energy of the bubble, H is the enthalpy of the transported gas, Q is the exothermic heat of the bubble to the fluid, and $\dot{m} $ is the mass throttling rate, which can be determined by the model. Some works have also introduced the influence of gun bodies on bubbles (Li et al., 2020) and the migrating effect of vessels on bubbles (Zhao et al., 2024) to realistically depict air gun bubble characteristics, employing various numerical methods in subsequent studies (Li et al., 2021a; Cox et al., 2004). The relationship between the bubble theory, ideal gas, and mass transfer models is satisfied, as shown in Figure 12.

Figure  12  Relationship between bubble, ideal gas, and mass throttling models in the air gun seismic source application for bubble theory

Download: Full-Size Img

The design of low-frequency air gun seismic sources primarily focuses on two aspects, namely, large-capacity air gun seismic sources and clustered air gun arrays. For large-capacity air gun sources, researchers have discovered that increasing air gun capacity and appropriately suppressing gas pressure can stimulate bubbles with longer oscillating periods and greater energy, thus enhancing the low-frequency components in seismic waves while reducing high-frequency components (Chelminski et al., 2019; Ronen and Chelmiinski, 2017), which has led to the proposal of a new tuned pulse source (TPS) (Ronen and Chelminski, 2017; Chelminski et al., 2021; Baeten et al., 2019; Zhang et al., 2019). As for clustered air gun arrays, researchers have combined the theoretical model of air gun bubble gas transport with the theory of clustered bubbles to conduct a series of studies (Laws et al., 1990; Safar, 1976; Zhang et al., 2019). Although current low-frequency clustered air gun array designs surpass those of single air gun sources, whether they can be optimized to surpass TPS remains uncertain.

In addition to serving as carriers for high-pressure air gun sources in marine resource exploration, bubbles can be harnessed as effective tools to aid in icebreaking activities in polar exploitation and ice disaster prevention. However, icebreaking relies more on the principle of bubbles accompanied by high-speed jets and less on bubble oscillation, wherein the bursting bubbles drive the surrounding fluid to create a trailing flow during oscillation and collapse, leading to ice surface damage (Cui et al., 2018). The jet can hardly be simulated by the theoretical models, whereas the oscillation behavior of bubbles interacting with elastic and brittle barriers, such as ice layers, reflects the challenges posed by fluid field boundaries, which are believed to be elastic and brittle compared with flexible boundaries, such as free surfaces, and rigid boundaries, such as solid structures. Early experiments on underwater explosion bubble icebreaking date back to the works of Kley (Van der Kley, 1965), Barash (1966), Nikolaev (1973), and many others. Building upon their research, Meller (1982) combined experimental data with theoretical insights to establish relationships between the icebreaking radius of explosion bubbles and the quantity and distance of explosions. In recent years, research on bubble icebreaking has delved deeper and diversified, as indicated in the studies conducted by Cui et al. (2018), Zhang et al. (2015d), Ni et al. (2020), and Du et al. (2021).

4   Conclusions and outlooks

Since the study of cavitation bubble dynamics began in the 19th century, numerous scholars have contributed to expanding the field with a wide range of potential applications. The journey of bubble dynamics theory started with Rayleigh in 1917, followed by distinguished scientists for a century, up to the unified equations for bubble dynamics proposed by Zhang in 2023. The theoretical research in bubble dynamics extends beyond free fluid field dynamics to encompass near-boundary bubbles and clustered bubble dynamics under complex boundary conditions. Factors such as compressibility, viscosity, viscoelasticity, surface tension, evaporation and condensation, heat conduction, and acoustic radiation have been thoroughly investigated. However, most of the present theories are still based on the assumption of spherical or spheroidal bubbles, and the description of realistic nonspherical bubbles cannot be entirely described by analytical methods. With further development of mathematical methods and a profound understanding of bubble properties, theoretical models are expected to be able to more accurately characterize bubble dynamics.

The application of bubble theory in underwater explosions, cavitation erosion, and seismic exploration has promising avenues for future development. However, challenges remain in leveraging bubble theory, such as optimizing underwater explosion bubbles for naval weaponry, designing air gun seismic sources for ultra-deep-sea exploration, developing marine propellers with strong cavitation resistance, and achieving efficient and cost-effective polar icebreaking. In conclusion, the theoretical development of bubble dynamics is ongoing, underscoring the importance for academic researchers and professionals to deeply understand the theory before applying their theoretical findings to real-world production and daily life.