Analysis of the Behavior of a Chemical Tanker in Extreme Waves
https://doi.org/10.1007/s11804-024-00508-0
-
Abstract
The behavior of a chemical tanker (CT) in extreme waves was discussed in detail, that is, in terms of rigid body heave and pitch motions, vertical bending moments (VBMs) amidships, green water, and slamming impacts through the analysis of the experimental data from model tests. Regular wave tests conducted for two wave steepness showed that the increase in wave steepness caused the increase in the asymmetry between hogging and sagging moments and the contribution of green water on deck to the decrease in vertical wave bending moments. Random uncertainty analysis of statistical values in irregular wave tests with various seeds revealed slight experimental uncertainties on motions and VBMs and slightly higher errors in slamming pressure peaks. With the increase in forward speed, experimental uncertainty on slamming pressures at the bow increased. Breather solutions of the nonlinear Schrödinger equation applied to generate tailored extreme waves of certain critical wavelengths showed a good performance in terms of ship response, and it was further verified for the CT.-
Keywords:
- Extreme wave events ·
- Wave-structure interaction ·
- Draupner wave ·
- Breather solutions ·
- Model tests
Article Highlights● Motions and loads on a chemical tanker subjected to extreme waves were analyzed via a series of model tests.● The contribution of the green water on deck to the decrease in vertical wave bending moments was further confirmed.● Breather solutions of the nonlinear Schrödinger equation were confirmed as good alternatives for modeling extreme waves.● Experimental random uncertainty on slamming pressures was relatively higher compared with those of motions and vertical bending moments. -
1 Introduction
Rogue or extreme storm waves reach a height more than twice the size of those around them. In November 2020, a freak wave lifted a single buoy off the coast of British Columbia 17.6 m high; the four-story wall of water has now been confirmed as the most extreme ever recorded (NBC News, 2023). Although that wave was not the tallest, its relative size compared with the waves around it was unprecedented. However, a recent study predicted that wave heights in the North Pacific will only increase with climate change, which means that the 2020 wave may not hold the record for long.
The increased severity of extreme weather events associated with global warming has resulted in the increased occurrence frequency of marine accidents in the last years, as reported by Kharif et al. (2009) and Pilatis et al. (2024). Extreme sea conditions that involve waves with large amplitude to abnormal waves have consistently been an area of interest for naval architects. However, knowledge of the behavior of seagoing vessels in these extreme conditions remains limited due to the unavailability of real data and the complexity involved with the reproduction of such a large deterministic wave profile in a wave tank. For the same reason, the validation of numerical codes in extreme sea conditions remains restricted.
Seakeeping analysis has been made possible by the development of numerical methods with various levels of complexity, which vary from linear strip theory solutions to complex computational fluid dynamics (CFD) codes (Parunov et al., 2022). Ship responses in extreme seas exhibit a high nonlinearity, which mainly originates from two sources, i.e., free surface and geometry of the ship. The classic linear methods, e.g., those proposed by Guedes Soares and Schellin (1998) and Clauss et al. (2010), cannot provide accurate predictions for responses of ships with large bow flare angles as reported by Fonseca and Guedes Soares (2004a, 2004b). The commonly known techniques for dealing with free surface nonlinearity include weakly and fully nonlinear numerical solutions. The partially nonlinear time domain method (Fonseca and Guedes Soares, 1998a, 1998b), where Froude–Krylov and hydrostatic-related forces are nonlinear, was validated for predictions of responses to abnormal waves (Guedes Soares et al., 2008; Fonseca et al., 2010). However, the sagging moment peaks in very large and steep waves are overestimated (Rajendran et al., 2011, 2012). Through the inclusion of body nonlinearities in radiation and diffraction forces, Rajendran et al. (2015) reported good predictions on vertical motions and loads of a cruise ship subject to large amplitude waves. Various nonlinear time-domain codes were compared by Watanabe and Guedes Soares (1999) to predict vertical bending moments (VBMs) in a containership. A good agreement was obtained among the computed values for low wave heights. However, high deviations were detected in the higher-wave region, where the elastic behavior of the hull played a crucial role. Holloway and Davis (2006) discussed high-speed strip theories, where the time-domain high-speed theory was recommended as a practical alternative to three-dimensional (3D) methods. Bhatia et al. (2023) conducted systematic comparative research on the investigation of the ship's pitch, heave, and roll movements in irregular waves using strip theory.
The 3D boundary element method (BEM), which uses either a Green's wave function (Zakaria, 2009; Sengupta et al., 2016; Datta and Guedes Soares, 2020; Negi et al., 2022) or a Rankine source (Yasukawa, 2003; Guo et al., 2013; Yao et al., 2019) is a good tool for the estimation of nonlinear ship responses in low to moderate seas. However, further investigations still need to be conducted to determine their capability to predict ship responses in extreme situations. CFD codes based on Navier–Stokes equations are considered the highest level of complexity method that can include most nonlinearities, including fluid compressibility, viscosity, and cavitation (Wang and Guedes Soares, 2020; Wang et al., 2021; Zhang et al., 2023). Various CFD solvers for the prediction of ship behavior in waves have been validated against experimental or other numerical solutions, e. g., those introduced by Oberhagemann et al. (2012), Simonsen et al. (2013), Chen and Chen (2014), Jiao et al. (2021), and Kudupudi et al. (2023). Phan and Sadat (2023) conducted CFD simulations of extreme ship responses by designing wave trails for a KRISO container ship (KCS) advancing at Fn = 0.26. The wave trails designed under the non-Gaussian process provided the desired response except for the heave response of 0.2 m.
However, in addition to high computational expenses, various uncertainties, such as the discretization error (Wang et al., 2022) or modeling uncertainty from the turbulence model (Xiao and Cinnella, 2019), affect the accuracy of numerical modeling. To ensure the accuracy of numerical solutions, scholars have focused on uncertainty quantification. Uncertainty analysis usually includes two steps, namely verification and validation (ITTC, 2008; ITTC, 2017). Verification refers to the process of determining whether a model implementation accurately represents the implemented algorithm and model solution. Validation indicates the determination process of the degree to which a model prediction adequately represents measured physical phenomena through their comparison with the findings observed in experiments.
Drummen and Holtmann (2014) presented a benchmark of uncertainties that relate to slamming and whipping analysis, and the results showed that uncertainties in wet frequencies may be lower compared with those relevant to dry modes. The damping coefficient affected the results considerably. Kim and Kim (2016) applied total difference in a benchmark study to assess the deviation of an individual numerical model against the means of all models of the predictions of motions and loads of a 6750-TEU containership. Abdelwahab et al. (2023) reported a new model of uncertainty measure for wave-induced motions and loads. Qiu et al. (2019) presented extensive experimental benchmark data and conducted a detailed uncertainty analysis of the findings of two-body interaction model tests. Quantification of uncertainties in model geometry, model mass properties, locations of models, and setup of the mooring system was performed. The uncertainties due to model geometry were negligible, but those resulting from the model mass properties may be crucial for roll motions. The uncertainty in the gap led to large uncertainties in all measured results. Parunov et al. (2020) presented an experimental benchmark and uncertainty assessment study organized by the MARSTRUCT Virtual Institute on global linear wave loads on a damaged ship; the study emphasized the unaccounted uncertainty in measurements. The review of Hirdaris et al. (2023) further confirmed the importance of uncertainties in the modeling and validation of wave loads for ship design development and assessment. The benchmark on the prediction of the whipping response of a warship model in regular waves (Parunov et al., 2024) revealed the similarity of uncertainty in rigid body response to that in previous analysis; however, whipping responses revealed considerable differences among approaches, which were mainly caused by slamming simulation. The differences arise not only from the models that calculate the elastic response of the structures but also from the models that quantify the slamming loads (Wang and Guedes Soares, 2017).
The ISSC-ITTC Joint Committee organized a benchmark study (Parunov et al., 2022) on global linear wave loads on a container ship with forward speed to assess uncertainties in linear transfer functions resulting from various seakeeping codes and consequences on long-term extreme vertical wave bending moments. The study confirmed the substantial differences between methods based on the same mathematical model and recommended the initiation of benchmark studies on various ship types to provide a basis for the quantification of uncertainties. To provide a database as the potential benchmark study, Klein et al. (2023) presented experimental data on the ship motions and wave- induced loads of an LNG carrier in extreme seas from the EU project EXTREME SEAS. This study aimed to provide a comprehensive discussion on the behavior of a chemical tanker (CT; from the same project) in extreme waves and provide additional information on benchmarks of various ship types.
2 Description of model tests
Model tests on the CT were conducted in the seakeeping basin of the Ocean Engineering Division of the Technical University Berlin. The basin measures 110 m in length, with a measurement range of 90 m, 8 m in width, and 1 m in water depth. One side is installed with an electrically driven piston-type wave generator. The wave generator is fully computer-controlled, and the implemented software enables the generation of transient wave packages, deterministic irregular sea states with definite characteristics, and tailored critical wave sequences. The opposite side is installed with a wave-damping slope to suppress wave reflection.
2.1 CT model
The investigated CT model comprised a fiberglass-reinforced plastic at a model scale of 1:70. Table 1 presents the main dimensions, and Figure 1 displays a side view sketch of the CT with the coordinate origin for all subsequent position specifications. Table A1 in Annex A provides the detailed mass distribution, including the moment of inertia and center of gravity of the individual mass.
Table 1 Main particulars of the CTItems Full scale Model scale Loa (m) 170.0 2.428 Lpp (m) 161.0 2.300 Breath (m) 28.0 0.400 Depth (m) 13.0 0.186 Draft (m) 9.0 0.129 Displacement (t) 30 666 0.894 Lcg (m) 82.466 3 1.178 09 Vcg (m) 6.151 6 0.087 88 Rxx (m) 9.31 0.133 Ryy (m) 32.9 0.47 Rzz (m) 33.53 0.479 2.2 Model equipment and test setup
The model tests were conducted to measure global ship motions, global and local loads, and the wave profile on the weather deck at the bow. For these purposes, the model was equipped with various sensors, hardware for data acquisition (a small computer, amplifier, analog-to-digital converter and measurement card) and power supply for self- sufficient tests, i. e., all sensor data from sensors on the ship were collected onboard. Thus, only one cable, which served as a trigger for time synchronization, was connected to the main control and measurement system. The main system was used to control the wave maker and measure surface elevation at various wave gauges and ship motions. The test setup comprised the suspension system that held the model in position during the tests, the tracking system that measured absolute motions, and the wave gauges that measured the encountering waves.
2.2.1 Pressure transducers
The model was instrumented with pressure transducers at various positions on the hull: on the bow, on deck at the forecastle area, and on the keel near the bow and at the stern. Figure 2 illustrates the pressure transducer locations at the bow (Figure 2(a)) and stern (Figure 2(b)). The model was used with a focus on the time series of pressure loads on the bow due to steep large waves. Therefore, a large area at the bow of the vessels was equipped with pressure transducers to obtain information on the local pressure distribution on the bow and the associated global effects on VBMs. Annex B provides a detailed discussion of the position of pressure transducers and their measurement characteristics and uncertainties.
2.2.2 Force transducers
The ship model was divided into two segments at Lpp/2 and connected to three force transducers for global load measurement, particularly the vertical wave bending moment. The deck of the ship model was mounted with two force transducers, with one being positioned underneath the keel. The force transducers, which had a nominal load of 200 kg and a protection class of IP68 (100 h at 1 m water column), registered the longitudinal forces from which vertical wave bending moments and longitudinal forces were calculated based on a given geometrical arrangement. On this basis, superimposed vertical wave bending moments, including the counteracting VBM caused by longitudinal forces with respect to selected vertical levels, were determined.
2.2.3 Green water gauges
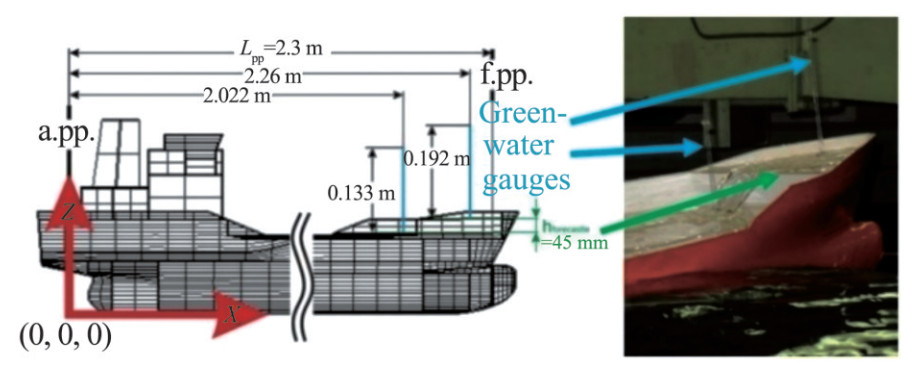
In addition to two pressure transducers (PT 37 and 38) mounted on the deck, two green water gauges (with absolute and measurable green water heights on the deck of 0.192 and 0.133 m) were installed at the same longitudinal positions. Figure 3 illustrates the positions and dimensions. The height of the forecastle level was approximately 45 mm.
2.2.4 Suspension system
The model tests involved fixing the model with an elastic suspension system using a triangular towing arrangement, which pulled the model without inducing a moment (Klein et al., 2023). A spring in front of the model and a counterweight behind it restricted the longitudinal motions. With this arrangement, heave and pitch motions and the measured forces and moments remained unrestrained.
2.2.5 Absolute motions
An optical tracking system recorded ship motions. The tracking system comprised a ceiling frame equipped with five infrared cameras, which were shifted parallel to the moving ship model. The system enabled high precision, contact-free motion tracking over large distances by following the trajectories of infrared light-emitting diodes mounted on the ship model.
2.2.6 Wave gauge positions
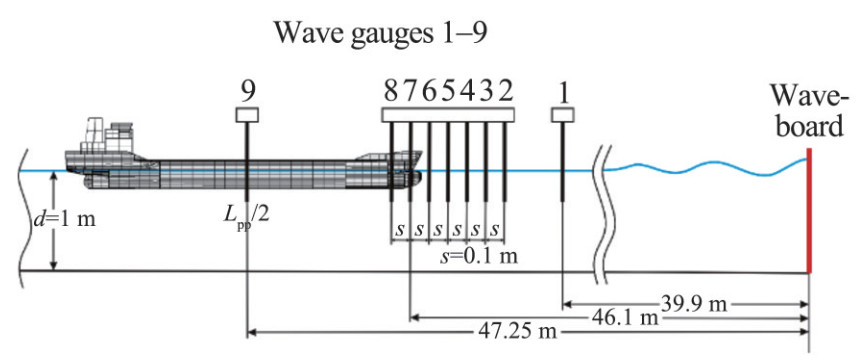
The number of wave probes varied based on the objective of the test campaign. Figure 4 illustrates the wave gauge positions in the model tests in stationary conditions. Altogether, nine wave gauges were installed, with the first one placed at 6.2 m in front of the model at xt1 = 39.9 m. A cluster of seven gauges, separated at s = 0.1 m intervals, was arranged around the target location to investigate the spatial evolution of waves at the bow.
Furthermore, one gauge was installed amidships. For the ship with a forward speed of Fn = 0.08, this setup was reduced to three wave gauges, with one placed at 6 m in front of the forward perpendicular (gauge No. 1 in Figure 4), one at the forward perpendicular (gauge No. 7 in Figure 4), and another amidships (gauge No. 9 in Figure 4) relative to the idle state of the model.
3 Experimental program and results
The experimental program focused on investigating the frequency and time domain. One goal of the model experiments was to determine behavior in the form of transfer functions. Therefore, the model was investigated via the transient wave packet (TWP) technique to obtain the response amplitude operator (RAO), and the results were evaluated via tests involving regular waves of various steepness. The model was also investigated in irregular waves, critical wave sequences, real extreme wave reproductions, and breather- type extreme waves. The following subsections present the various parts of the experimental program.
3.1 TWP
The TWP technique serves as an efficient method for the determination of the sea state behavior of ships and floating structures and the RAO in one test run (e. g., Clauss and Kühnlein, 1995, 1997; Clauss and Steinhagen, 1999; Clauss et al., 2010, 2014; Klein et al., 2021). TWPs comprise synthesized task-related wave spectra with tailor- made phase distribution, and they can be easily adapted to the relevant frequency range of interest.
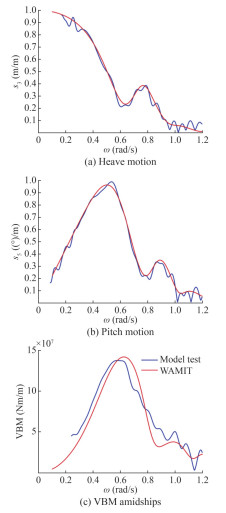
Figure 5 presents the test results on TWP measurements (blue curves) compared with numerical simulations (red curves). Numerical simulations were performed with the use of an established frequency domain program (Wave Analysis at Massachusetts Institute of Technology (WAMIT)) for comparison. WAMIT is a radiation/diffraction program that evaluates wave-structure interaction at zero speed in the frequency domain (Newman, 2018; WAMIT, 1994; Lee, 1995); this program is a widely accepted and validated numerical tool for hydrodynamic analysis and suitable for a multitude of applications.
For the VBM RAO, the agreement between experimental results and WAMIT was only sufficient as a distinct shift was identifiable. The detailed reason for the shift was indeterminable but is in line with the findings of other numerical tools (Ley and el Moctar, 2021; Guedes Soares et al., 2006).
3.2 High and steep regular waves
To identify the influence of wave height and steepness on the VBM, model tests on regular waves of various wavelengths and steepness were performed. Regarding the dependence of the ship length, different relative wavelengths (wavelength/ship length) with varied crest/trough asymmetries were selected to evaluate the influence of wave steepness on VBMs. The investigated discrete regular wave lengths (Lw) were selected to cover the complete range of interest in the frequency domain, i. e., from Lw/Lpp = 0.6 to Lw/Lpp = 2.2. For the evaluation of wave steepness influence, the test program was divided into two parts, with each part having the same wavelengths with varying wave steepness. Wave height and steepness were selected in such a manner to obtain wave profiles with various crest/trough asymmetries and evaluate the influence of unique wave profiles (asymmetries) on VBMs.
Figure 6 illustrates the regions of validity of wave theories on wave profiles and the selected wave steepness and wavelengths of the experimental program. The relative water depth and wave height were plotted on the abscissa and ordinate, respectively. The first part of the experimental program included regular waves with moderate amplitudes (0.002 ≤ H/(g·T2) ≤ 0.004), where the wave profile was within the Stokes Ⅱ domain (cf. Figure 6-red dots). The second part of the test campaign involved the generation of the same (regular) wavelengths but with increased relative wave heights (0.01 ≤ H/(g·T2) ≤ 0.012, where the wave profile was within Stokes Ⅲ domain (cf. Figure 6, blue dots).
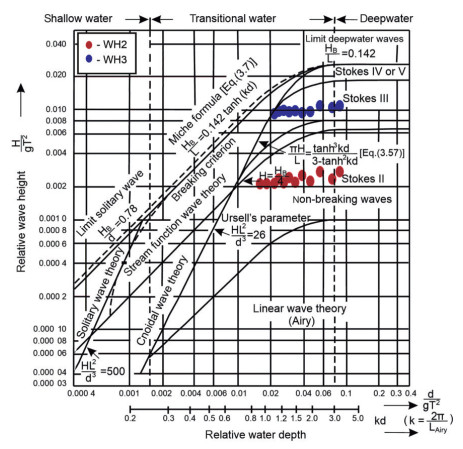 Figure 6 Breaking wave height and regions of validity of various theories on gravity water waves (Clauss et al., 1992)
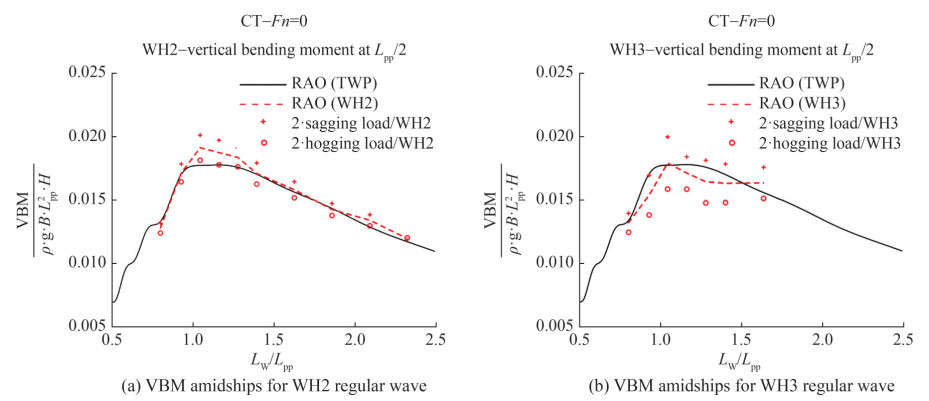
Figure 6 Breaking wave height and regions of validity of various theories on gravity water waves (Clauss et al., 1992)Figure 7 presents the test results on regular waves, including the respective RAOs (|sagging moment| + hogging moment-red dashed curves) compared with the TWP RAO (black curves). The sagging (red crosses- (2· |Msagging|/H)) and hogging moments (red circles- (2·Mhogging/H)) were additionally registered to evaluate the asymmetry of measured bending moments compared with the wave steepness. Msagging and Mhogging refer to the minimum and maximum vbm, respectively, i. e., the negative and positive amplitudes of the measured time series in different regular waves.
The results on RAOs obtained in regular waves (red dashed curves) and with the TWP (black curves) showed a generally good agreement. However, the increase in the asymmetry between hogging and sagging moments with the increase in wave steepness was identifiable and followed those of previous investigations (Fonseca and Guedes Soares, 2002; Clauss et al., 2010). In addition, the VBM trend for the WH3 regular wave results displayed a distinctive feature, which was unexpected at first glance: the overall VBM obtained with the WH3 regular waves (red dashed curve) was below the RAO acquired through the TWP technique. This finding does not denote shrinkage of the VBM shrunk. Instead, the RAO value decreased proportionally to the wave height. This effect can be attributed to the small freeboard height of the CT compared with the large wave height, with parts of large wave crests spilling over the deck in terms of green water instead of acting on the bow, which resulted in a smaller VBM-to-wave height ratio. Furthermore, additional effects due to the influence of the shipping of water on deck, which affect ship motions (Fonseca and Guedes Soares, 2005) and induce a counteracting moment due to the green water mass on deck (Clauss et al., 2010; Rajendran et al., 2011), may be considered.
3.3 Irregular sea states with random phases
Several irregular sea states were investigated in model tests representing design storms in accordance with existing probabilistic methods. These sea states, each lasting 30 min in real time, are presented in Table C1 in Annex C. Each characteristic sea state parameter set was used to generate up to six wave sequences having the same Tp, Hs, and ɣ but various random phase seeds for long-term statistical analysis. The phases were randomly generated and varied within each parameter set but were constantly plugged for each one. Parameter set No. 1 (Table C3), phase seed #1 had another random phase distribution than phase seed #2, #3, and so on of the same set but the same phase seed such as set No. 2, phase seed #1, set No. 3, phase seed #1, and so on. Altogether, 45 runs were conducted under stationary conditions (Fn = 0) and at forward speed (Fn = 0.08).
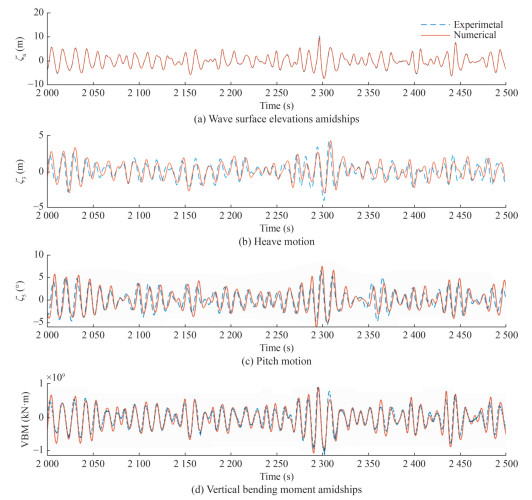
Figure 8 presents the comparison of the time series of the wave surface elevation at Lpp/2, heave, pitch, and VBM at Lpp/2 between experimental measurements and numerical predictions from the work of Rajendran et al. (2015) for the CT with zero forward speed. The sea state IRREGULAR20 with Tp = 12 s and Hs = 11.5 m with phase seed #1 was used. The wave surface elevation showed good agreement, which indicates that the numerical approach reproduced the wave surface sequences very well. The motion and loads agreed well, although the peaks exhibited slight deviations. The experimental results on heave and pitch motion transpired slightly earlier than numerical predictions. This phase shift was attributed to the suspension systems applied in the tests to maintain the model in position as the ship model generally shifted backward due to waves and oscillated around a new dynamic position. Another reason for the discrepancies was the assumption made in the numerical method, which disregarded the interaction between the incident wave field and the ship hull. Typically, this interaction resulted in a wave run-up as the waves encountered the hull, which led to further differences between experimental and numerical findings.
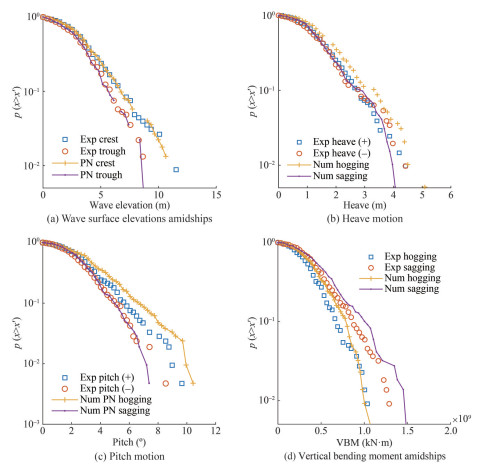
Figure 9 shows the comparison of the exceedance of probability of the maxima and minima of the wave elevation, motions and loads in the sea state IRREGULAR20 phase seed #1. Consistent with the time series, the peaks of wave surface elevation showed excellent agreement. For heave and pitch motions, the positive peaks from numerical predictions were slightly higher, and the negative peaks were in good agreement for small values but were slightly lower for extreme values. As for the VBMs at Lpp/2, the numerical approach overpredicted the hogging and sagging peaks in general, although the maximum values in hogging were a bit lower than the measurements. The comparisons between the numerical predictions and the measurements were similar to those for the LNG in the work of Klein et al. (2023).
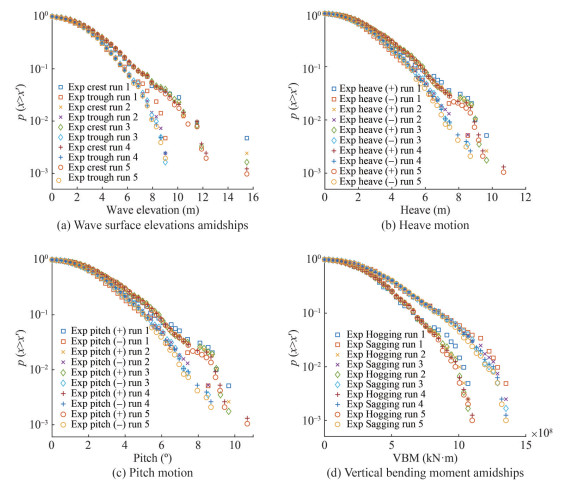
To study the experimental uncertainties in the model tests, we performed statistical analysis of the measurements in the same sea states but with various phase seeds. Figure 10 presents the exceedance of the probability of the peaks for the wave surface elevation, motions, and loads of the CT in IRREGULAR20 conditions from five repeated model tests with different phase seeds. When the values of peaks were small, the five tests provided almost the same exceedance probabilities, whereas slight deviations were observed for the calculations on higher peaks. In particular, the highest deviations were found in the peaks from run 1 (seed #1).
For quantification of experimental random uncertainties, the statistical values, e.g., the means of all the peaks, the 1/3 largest peaks, and the 1/10 largest peaks, were calculated for all the five runs, and random uncertainties were presented as percentages relative to the mean values of the five runs. Table D1 in Annex D lists all random uncertainties of wave surface elevation, heave, and pitch motions and VBM at Lpp. Except for the random uncertainty for the mean of the 1/10 largest peaks of the heave trough (1.8%), the uncertainties for all other metrics were lower than 1%, which is considered low.
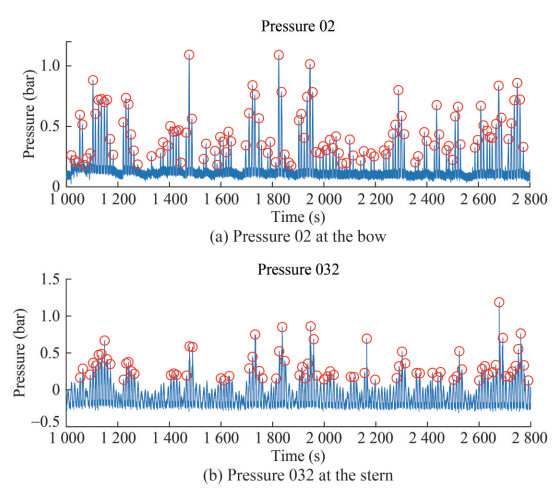
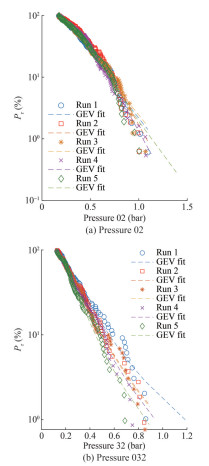
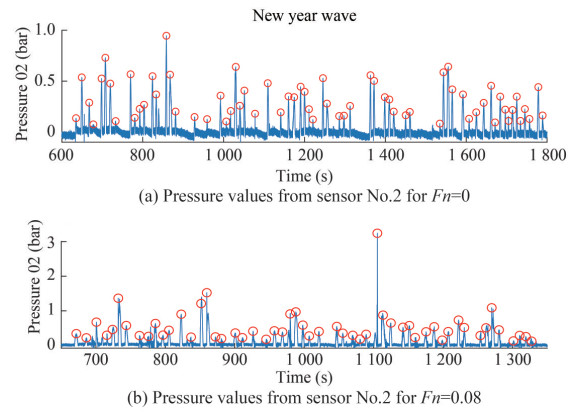
The wave-induced pressures at the bow and stern of the CT were also measured in the model tests. The comparison the numerical prediction and experimental data on the pressures can be found in Wang and Guedes Soares (2016a, 2016b). Figure 11 shows the part of the time series of pressures at the bow (Pressure transducer #02) and stern (Pressure transducer #32), together with the identified peaks. Given the small draft at the stern, the identified peaks were more than those at the bow. The probabilities of exceedance for the identified pressure peaks were compared (Figure 12) for the five phase-seeds when the ship's forward speed was zero. The deviations of pressure peaks between the five runs were larger than the motions and the VBM, in particular for those from pressure sensor #32.
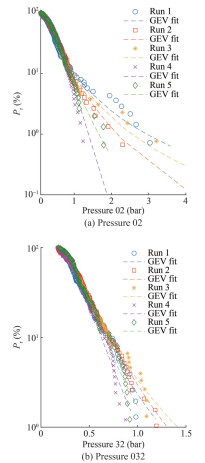
Figure 13 shows the probability of exceedance for the pressure peaks when Fn = 0.08. The deviation was lower compared with that when Fn = 0, in particular for the smaller peaks. To quantify the experimental random uncertainties for the pressures, we also calculated the statistical values for the five phase seeds. The random uncertainties are listed in Tables D2–D3 when Fn = 0 and Fn = 0.08, respectively, where the extreme values (probability equals 1%) were estimated using the generalized extreme value (GEV) analytical distribution model by fitting the identified peaks. The maximum uncertainty occurred at the extreme value for the case pressure No. 02 with Fn = 0. When Fn = 0.08, the maximum uncertainty was the largest at the mean value of the 1/10 largest peaks. These results are consistent with the values in Figures 12 and 13, where high deviations were observed at low probability. All uncertainties at pressures were lower than 10.5%, and the forward speed of the ship did not cause a considerable increase in the uncertainties on the pressure at the bow.
3.4 Extreme wave events
The investigation of extreme wave events is essential for the thorough assessment of ships. In addition to the statistical determination of extreme responses through investigations of irregular sea states with predefined design wave spectra and random phase distributions, the exploration of deterministic extreme wave sequences enables the deterministic evaluation of critical wave sequences and extreme responses. Specifically, experiments on deterministic extreme wave events enable the detailed analysis of the cause-and- reaction chain concerning specific research questions. This approach allows for the evaluation of whether such wave events are critical for the investigated structure, a dimension not covered by statistical analysis.
The investigations on extreme wave events encompass real measurements and the study of specific design extreme wave groups. The renowned Draupner wave, also known as the "New Year's wave" (NYW) (Slunyaev et al., 2005; Cherneva and Guedes Soares, 2008), was recreated in the seakeeping basin to provide a real-world replication. For the generation of extreme design wave groups, exact solutions of the nonlinear Schrödinger equation (NLS), known as breather solutions, were employed. These breather solutions exhibit quasimonochromatic waves that experience slight disturbances in time or space. The modulation instability leads to an escalated disturbance during development, which results in a considerable amplification of the original amplitude. Three types of breather solutions were utilized in total: the Kuznetsov–Ma (Kuznetsov, 1977; Ma, 1979), Akhmediev (Akhmediev et al., 1985; Akhmediev and Korneev, 1986; Akhmediev et al., 1987) and Peregrine breather (Peregrine, 1983). These breather solutions were assessed for their suitability in addressing research questions related to the effects of extreme waves.
The utilization of breather solutions for model tests offers several advantages. One notable aspect is their straightforward applicability in designing extreme waves. According to Klein et al. (2016), "The major benefits include the potential to generate abnormal waves of a certain frequency up to the physically possible wave height, the symmetrical shape of the extreme wave, and the availability of an analytical solution." This analytical solution facilitates the rapid and uncomplicated generation of wave maker control signals.
Notably, breather solutions, particularly the Peregrine breather, are considered a unique prototype of extreme waves (Shrira and Geogjaev, 2010). Wang et al. (2016) have demonstrated the applicability of the Peregrine breather for modeling extreme waves in realistic oceanic conditions. Such a result was achieved by embedding the Peregrine breather in complex sea states based on JONSWAP spectra. In alignment with this outcome, experimental findings by Klein et al. (2016) reveal the possibility of incorporating Peregrine breathers into irregular sea states to create tailored extreme wave sequences. Moreover, such designed extreme waves exhibit dynamics similar to the real-world Draupner wave.
Next, experiments on the Peregrine breather solution were presented exemplarily and compared with the results on the Draupner wave. Klein et al. (2023) reported the application of all three breather solutions in model tests in extreme waves. The Peregrine breather solution was used to generate a set of high, steep single waves of various discrete carrier wavelengths to cover the range of interest in the frequency domain covering the VBM. The initial steepness at the wave board was defined in such a manner as to guarantee that a single wave at the target location is as high as physically possible for the defined wavelengths.
3.4.1 Breather-type extreme waves—Peregrine breather
The Peregrine breather solution (Peregrine, 1983), also known as a rational solution, represents the limiting case of the time-periodic Kuznetzov–Ma breather and space- periodic Akhmediev breather. Specifically, this solution is neither temporally nor spatially periodic: it is a wave that "appears from nowhere and disappears without trace" (Akhmediev et al., 2009) and is considered a special prototype of freak waves (Shrira and Geogjaev, 2010).
The Peregrine breather solutions applied in the experiments represent an exact solution of the NLS equation:
$$ \frac{\partial A}{\partial x}+\frac{1}{C_g} \frac{\partial A}{\partial t}+i\left(\alpha^{\prime} \frac{\partial^2 A}{\partial t^2}+\beta^{\prime}|A|^2 A\right)=0 $$ (1) For the wave group evolution in the space of a time series, with
$$ \alpha^{\prime}=\frac{1}{8} \frac{\omega_c}{k_c^2} \frac{\alpha}{C_g^3} $$ (2) and
$$ \beta^{\prime}=\frac{1}{2} \omega_c k_c^2 \frac{\beta}{C_g} $$ (3) The coefficients and read for arbitrary water depth are as follows (Serio et al., 2005):
$$ \alpha=-v^2+2+8\left(k_c d\right)^2 \frac{\cosh \left(2 k_c d\right)}{\sinh ^2\left(2 k_c d\right)} $$ (4) $$ \begin{aligned} \beta= & \frac{\cosh \left(4 k_c d\right)+8-2 \tanh ^2\left(k_c d\right)}{8 \sinh ^4\left(k_c d\right)} \\ & -\frac{\left(2 \cosh ^2\left(k_c d\right)+0.5 v\right)^2}{\sinh ^2\left(2 k_c d\right)\left[\frac{k_c d}{\tanh \left(k_c d\right)}-\left(\frac{v}{2}\right)^2\right]} \end{aligned} $$ (5) where kc represents the carrier wave number, ωc denotes the corresponding angular frequency, Cg refers to the group velocity, and d is water depth. The correction for the group velocity in finite water depth is considered using the coefficient ν:
$$ v=1+2 \frac{k_c d}{\sinh \left(2 k_c d\right)} $$ (6) The analytical form of the Peregrine breather solution suitable for wave tank experiments is given in the following equation (Karjanto and van Groesen, 2007):
$$ A_B(x, t)=A_c(x)\left(\frac{4 \alpha^{\prime}\left(1-i 2 \beta^{\prime} a_c^2 x\right)}{\alpha^{\prime}+\alpha^{\prime}\left(2 \beta^{\prime} a_c^2 x\right)^2+2 \beta^{\prime} a_c^2 t^2}-1\right) $$ (7) with
$$ A_c(x)=a_c e^{\left(-i \beta^{\prime}\left(a_c\right)^2 x\right)} $$ (8) In general, full determination of the Peregrine solution in space and time requires predefined plane-wave amplitude ac and carrier frequency ωc (i.e., initial steepness).
3.4.2 Experimental results
The CT was investigated in the Peregrine breather solution introduced above to evaluate the effect of such a high, steep single wave. Initially, a series of high, steep single waves with various discrete carrier wavelengths was generated using the mentioned solution. These carrier wavelengths were selected to span the frequency domain of interest for the VBM in the range of Lw/Lpp = 0.8 to Lw/Lpp = 1.5. The initial steepness at the wave board was determined, and as a consequence, the high single wave at the target location reached the maximum wave height physically possible for the specified wavelengths.
The calculated waveboard surface elevation served as the basis for control signal generation. The theoretically predicted location of the extreme wave occurrence (input) and registrations/observations in the tank demonstrated satisfactory agreement. In most cases, the actual extreme wave event closely matched the given value. However, as wave-structure investigations necessitate the definition of target waves in the time domain at precise locations, the examined breather-type extreme waves presented here resulted from the adjustment of the first control signal to accurately achieve an extreme wave at the target location. For this adjustment process, up to three iteration steps were considered.
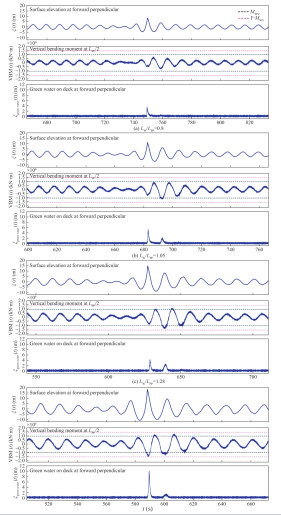
Figure 14 illustrates the outcomes of model tests conducted under stationary conditions (Fn = 0) in Peregrine breather extreme waves from the top (the shortest) to the bottom (the longest wavelength). The CT was investigated in four carrier wavelengths (Lw/Lpp = 0.8 to Lw/Lpp = 1.5). A trio of diagrams was used to present the findings for each carrier wavelength. The upper diagram displayed the surface elevation at the forward perpendicular, the middle diagram the VBM amidships, and the lower diagram the green water column height on the deck at the forward perpendicular. The design vertical wave bending moment following the IACS-Common Rules (IACS, 2015) was also presented to assess the measured VBM. During the dimensioning process of the transverse section, additional parameters, such as γR, cs, deck openings, etc., must be considered. The design vertical wave bending moment is represented by black dashed lines. The diagrams also show the ultimate design vertical wave bending moments, calculated based on the design VBM while considering safety factors.
The presented findings reveal that the distinct single wave was prominently visible at the forward perpendicular across all wavelength-to-ship-length ratios. The height of extreme waves shown increased proportionally with the carrier wavelength because all the presented waves were deliberately generated to achieve the highest physically possible wave height at the targeted location, which resembles a plunging breaker in proximity.
Similar to the outcomes noticed in regular waves, the resulting VBM was influenced by wavelength and attained maximum values at critical wavelengths corresponding to the wave height. However, the absolute values were notably elevated due to the influence of the highest physically possible wave height, which is in contrast to those of tests on regular waves featuring moderate wave steepness. The wave heights of the highest and steepest regular waves (WH3) were roughly 40% smaller compared with the Peregrine breather. A comparison of absolute VBM values indicates that the moments were at least 15% higher for hogging conditions and 30% higher for sagging conditions than those measured in regular waves. The maximum VBM, particularly in sagging moments, exceeded the design vertical wave bending moment and nearly reached the ultimate design wave bending moment. Although this excessive design vertical wave bending moment did not necessarily lead to an inevitable structural failure of the ship at full scale—given that additional parameters must be considered for transverse section dimensioning—it underscored the severity of the impact of Peregrine breather extreme waves, which constitutes a limiting case for the investigated ship.
This severity was further corroborated by the measured green water column heights at the forward perpendicular, which attained impressive values. A wavefront of 10 m in height, an elevation as tall as a single-family home, was detected spilling over the deck at the forward perpendicular.
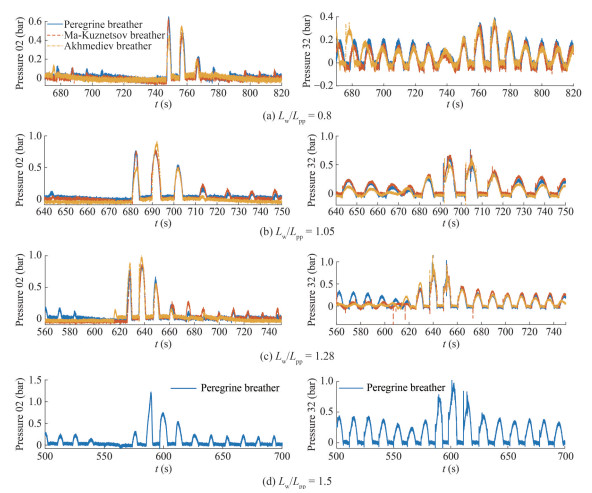
Parts of the time series of slamming pressures were compared with those of the model tests in breather-type extreme waves with Lw/Lpp = 0.8 to Lw/Lpp = 1.5 (Figure 15) with the results at the bow (pressure sensors No. 02) and stern (pressure sensors No. 32). Comparison with the time series of the wave surface elevation in Figure 14 indicated that for all presented pressure sensors, the maximum value occurred after the highest wave impacted the hull. The maximum pressure peaks from sensor No. 02 for Lw/Lpp = 0.8 (Figure 15(a)) were 0.65, 0.64, and 0.64 bar, for the Peregrine breather, Ma–Kuznetsov breather and the space-periodic Akhmediev breather extreme waves, respectively. The values were 0.78, 0.89, 0.92, 0.86, 0.87, and 1.07 bar for Lw/Lpp = 1.05 (Figure 15(b)) and 1.28 (Figure 15(c)). Thus, at a higher ratio of Lw/Lpp, the pressure peaks were larger. In general, the space-periodic Akhmediev breather extreme waves provided slighter higher pressure, but the deviations between the three types of waves were small.
As for the pressures at the stern (sensor No. 32), the maximum peaks were lower overall compared with those at the bow. However, when the ratio of Lw/Lpp increased, the differences became smaller. High slamming pressures were captured at the bow and the stern of the model for Lw/Lpp = 1.5. As displayed in Figure 15(d), the maximum pressures were 1.22 and 1.02 bar, respectively. Through the GEV distribution, the most probable extreme values of the peaks on pressure sensors No. 02 and No. 32 reached 1.02 and 0.74 bar for the case in sea state IRREGULAR20 with Hs = 11.5 m and Tp = 12 s and with zero forward speed. In particular, the peaks of the Peregrine breather Lw/Lpp = 1.5 case were 20%, 37% and 58% higher than the extreme values.
Altogether, the results indicate the Peregrine breather solution as a powerful tool for the generation of tailored extreme waves having certain critical wavelengths, which will enable the investigations of limiting cases on various subjects, e. g., local and global loads, green water effects, and air gap investigations (Klein et al., 2016).
3.4.3 Real-world extreme wave reproduction
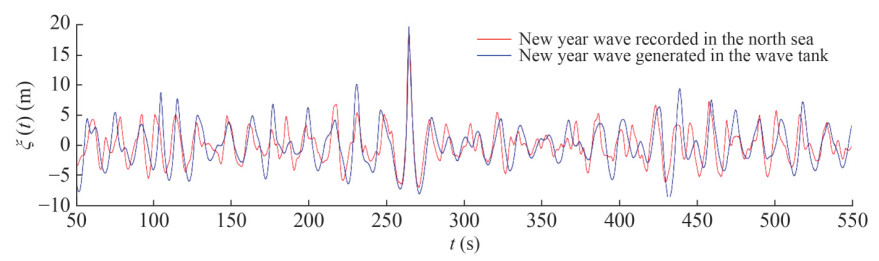
To assess the outcomes of the model tests utilizing the breather solutions, we subjected the CT to a real-world extreme wave replication—the famous Draupner wave. On January 1, 1995, the Draupner extreme wave was documented during a storm at the Draupner platform in the North Sea. A giant single wave (Hmax = 25.63 m) with a crest height of ζc = 18.5 m formed in a surrounding sea state, and it was characterized by a remarkable wave height of Hs = 11.92 m (Hmax/Hs = 2.15). The location had a water depth of d = 70 m. Figure 16 shows a comparison of the measured model wave train at the target position and the full-scale recorded sequence at the Draupner platform. The highest wave generated in the tank matched well with the real-world one. Given the complex reproduction of such steep wave groups due to strong nonlinearity, the NYW was reproduced in accordance with an optimization procedure (Clauss and Klein, 2011) that focused on the reproduction of the target wave as exactly as possible. As a result, the surrounding wave groups differed from real-world measurements.
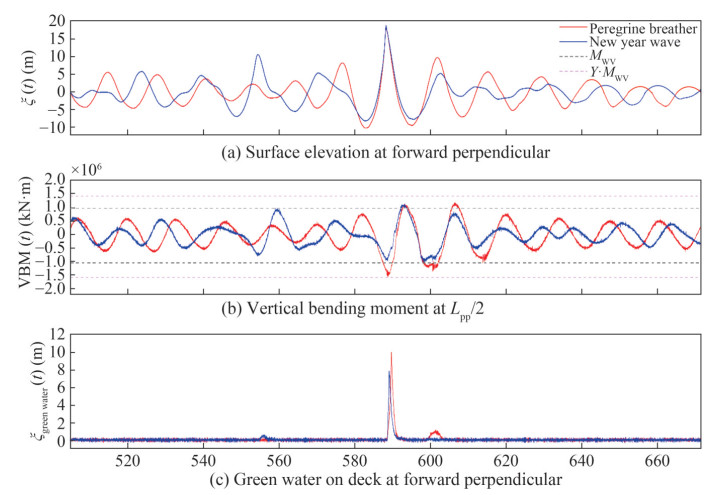
Figure 17 illustrates the outcomes for the CT under stationary conditions (Fn = 0) in the Draupner wave. Figure 17(a) presents the surface elevation at the forward perpendicular, Figure 17(b) depicts the corresponding VBM, and Figure 17(c) shows the green water on the deck at the forward perpendicular. The findings obtained in the Draupner wave (depicted by blue curves) were juxtaposed with those measured in the Peregrine breather (represented by red curves) with Lw/Lpp = 1.3 (Figure 14). The selection of this wave sequence was due to the nearly the same exceptionally high wave crest height of extreme waves at the target location. However, the Peregrine breather was also distinguished by deep preceding and following troughs and short up- and downcrossing wave periods. Thus, a high and steep Peregrine breather was observed.
Comparison of the recorded loads (Figure 17(b)) and the green water column on the deck (Figure 17(c)) showed that the Draupner wave and the Peregrine breather extreme wave pose substantially impacted the ship. In the case of the Draupner wave impact, the measured VBM reached the design vertical wave bending moment, and the green water column height on deck was notably impressive at approximately 8 m. However, the impact of the Peregrine breather was more severe, which resulted in higher hogging and sagging loads and a greater green water column height on deck.
This discrepancy was primarily attributed to the previously mentioned differences in wave height, steepness, and wavelength of the breather extreme wave, which made the investigation of CT more critical. This result did not diminish the value of real-world registrations reproduced in the wave tank for the evaluation of wave-structure interaction. These real-world events, in contrast to predefined breathers, represent abnormal wave occurrences at sea, and thus, they eliminate any doubts regarding discussions on the potential investigation of unrealistic, artificial wave sequences. However, breather solutions can serve as valuable tools for designing extreme wave events for specific wavelengths up to the maximum possible wave height. The techniqule aids in identifying critical wave sequences concerning wavelength, height, and steepness.
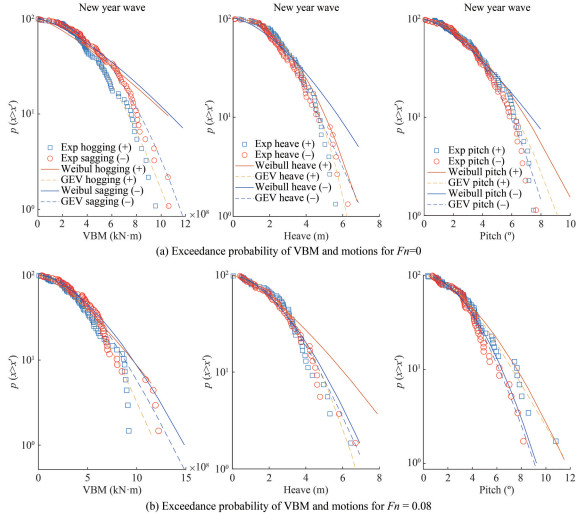
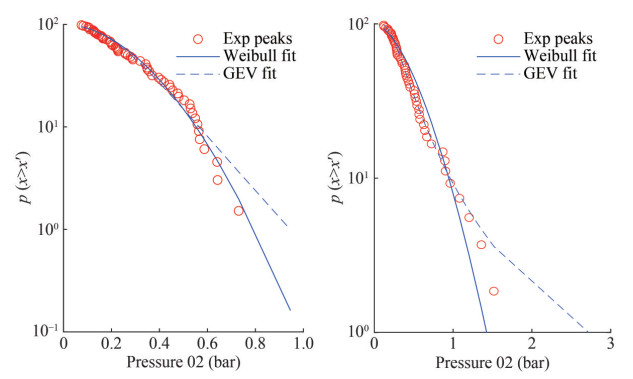
Figure 18 presents the probability of exceedance for the maxima and minima of VBM amidships, heave, and pitch motions for the CT subject to the Draupner wave, along with the fitted analytical models from Weibull and GEV distributions. Figure 18(a) shows the results for the model with zero forward speed, and Figure 18(b) displays those
for Fn = 0.08. For Fn = 0 and Fn = 0.08, the GEV model showed a better fit on the peak of motions and VBM, especially when Fn = 0, where significant deviations between the two distribution models were observed. Using the GEV distribution model, the most probable extreme values determined were 1.05×106 kN·m in hogging and 1.15×106 kN·m in sagging for VBM, 9.09° in positive and 8.21° in negative for the pitch and 6.15 m in positive and 6.90 m in negative for the heave. In the Peregrine breather solution (Lw/Lpp = 1.5) condition, the maximum values from the model tests were 1.129×106 and − 1.529 7×106 kN·m amidships, which are 7.5% and 33% higher than the extreme values from the Draupner wave tests. In the Peregrine breather solution (Lw/Lpp = 1.05) condition, the maximum value in hogging was 1.04×106 kN·m, which is almost the same as the extreme value, and the peak value in sagging was − 1.43× 106 kN·m, which is slightly high.
The time series of the pressures and identified peaks at the bow for the CT in the Draupner wave at Fn = 0 and Fn = 0.08 are presented in Figure 19, and the exceedance probability of pressure peaks are illustrated in Figure 20. The maximum peaks were 0.946 2 and 3.23 bar, respectively for the two cases. Using the Weibull and GEV distribution, the most probable extreme values were 0.73 and 0.83 bar for Fn = 0, with the Weibull model showing a better performance. In the Peregrin breather solution with Lw/Lpp = 1.28 and Lw/Lpp = 1.5, the maximum peak pressures were 0.86 and 1.22 bar at sensor No. 2 (Figures 15(c) and 15(d)), and these values are 18% and 67% higher than the extreme values estimated using Weibull model in the Draupner wave condition. In regard to the case of Peregrin breather solution with Lw/Lpp = 1.05, the maximum peak was 0.78 bar, which is in good agreement with the extreme pressure (0.73 bar from Weibull). The findings indicate breather solutions as desirable alternatives to real work abnormal waves, in consideration of the slamming load issue.
When Fn = 0.08, the most probable extreme values were 1.36 and 2.00 bar for Weibull and GEV distribution models, respectively. However, significant deviations were observed at the tails of the exceedance probability between the analytical distribution model and measured values. The Weibull model underestimated, and the other overestimated the extreme pressure peaks. In any case, the pressures increased with the increase in the forward speed of the model.
4 Conclusions
This study investigated the impact of extreme waves on the behavior of a CT. Experimental data from model tests in regular, irregular, and real-world extreme waves were analyzed in terms of the generated wave surface elevations, heave, pitch motions, vertical bending motions, slamming pressures, and green water. Some conclusions were drawn from the analysis:
1) Model tests conducted in high steep regular waves revealed that the asymmetry between hogging and sagging moments intensified as the wave steepness increased. Furthermore, green water on deck affected ship motions by inducing a counteracting moment.
2) Random uncertainty analysis of irregular wave test results indicated that uncertainties for motions and VBM were all below 1.8%, but they were considerably higher for slamming pressures (with a maximum of 10.5%). The forward speed of the ship did not result in substantially higher uncertainties on bow pressure but induced higher errors at the bow.
3) The GEV model provided better fits for the peaks of motions and VBM. Regarding pressure peaks, the Weibull model performed better for the bow, and the GEV model was more effective for the stern. Nevertheless, considerable deviations occurred at the tail of the exceedance probability curves for pressure peaks.
4) Statistical values of generated extreme waves, ship motions, VBM, and pressures with experiments were compared, and the results demonstrate that breather solutions are effective substitutes for real abnormal waves. The measured VBM attained the design vertical wave bending moment, with higher values observed for the Peregrine breather solution yielding. Regarding slamming pressures, peak values from breather solution extreme waves matched those from the Draupner extreme wave.
Breather solutions serve as powerful tools for the generation of tailored freak waves of critical wavelengths for wave/structure investigations on various ships. They are recommended to be applied in future research.
Appendix A Details on ship model mass distribution
A1 Detailed mass distribution, moments of inertia, and center of gravity (model scale)Items Center of gravity Moment of inertia Mass (kg) x (m) y (m) z (m) Jxx (kg·m2) Jyy (kg·m2) Jzz (kg·m2) Fore ship 23.640 1.579 0.000 0.095 0.512 4 2.621 5 2.925 5 Aft ship 18.660 0.640 0.000 0.121 0.566 8 2.437 3 2.725 1 Force transducer 2.000 1.150 0.168 0.201 0.081 7 0.027 2 0.057 7 Force transducer 2.000 1.150 −0.168 0.201 0.081 7 0.027 2 0.057 7 Force transducer 2.000 1.150 0.000 −0.016 0.021 6 0.023 2 0.001 6 Trim weight 1 4.980 0.651 0.000 0.030 0.012 1 0.012 1 0.023 7 Trim weight 2 3.835 0.868 0.074 0.064 0.012 1 0.012 1 0.023 7 Trim weight 3 3.835 0.868 0.074 0.064 0.005 9 0.010 0 0.010 3 Trim weight 4 3.835 1.018 −0.074 0.064 0.005 9 0.010 0 0.010 3 Trim weight 5 3.835 1.018 −0.074 0.064 0.005 9 0.010 0 0.010 3 Trim weight 6 9.820 1.624 0.000 0.064 0.005 9 0.010 0 0.010 3 Trim weight 7 10.040 1.442 0.000 0.064 0.031 4 0.022 4 0.030 3 Trim weight 8 0.340 1.167 0.000 0.225 1.160 0 0.038 1 0.000 0 Trim weight 9 0.057 1.780 0.000 0.309 0.000 0 0.000 0 0.000 0 Trim weight 10 0.057 0.333 0.186 0.445 0.000 0 0.000 0 0.000 0 Trim weight 11 0.057 0.333 −0.186 0.445 0.000 0 0.000 0 0.000 0 Equipped ship model 88.991 1.178 0.000 0.088 1.563 3 19.692 6 20.386 8 Appendix B Details on pressure transducers
Table B1 presents the positions of pressure transducers on the hull and the X and Z-coordinates, that is, the corresponding Y-positions resulting from the according hull geometry. The positions are given in meters in the model scale, with the origin located at the aft perpendicular at the keel level (Figure 1).
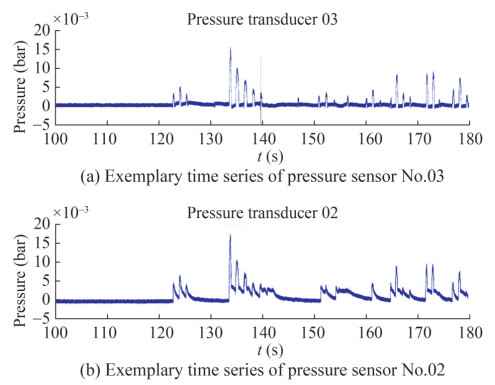
B1 Positions of pressure transducersNo. X (m) Z (m) Position No. X (m) Z (m) Position 1 2.320 0.210 C1 R1 18 2.200 0.140 C5 R4 2 2.320 0.185 C1 R2 19 2.170 0.210 C6 R1 3 2.290 0.210 C2 R1 20 2.170 0.185 C6 R2 4 2.290 0.185 C2 R2 21 2.170 0.163 C6 R3 5 2.290 0.163 C2 R3 22 2.170 0.140 C6 R4 6 2.290 0.140 C2 R4 23 2.140 0.210 C7 R1 7 2.260 0.210 C3 R1 24 2.140 0.185 C7 R2 8 2.260 0.185 C3 R2 25 2.140 0.163 C7 R3 9 2.260 0.163 C3 R3 26 2.140 0.140 C7 R4 10 2.260 0.140 C3 R4 31 0.000 0.149 stern 3 top 11 2.230 0.210 C4 R1 32 0.000 0.124 stern 3 middle 12 2.230 0.185 C4 R2 33 0.000 0.110 stern 3 bottom 13 2.230 0.163 C4 R3 34 0.030 0.124 stern 2 middle 14 2.230 0.140 C4 R4 35 0.060 0.124 stern 1 middle 15 2.200 0.210 C5 R1 36 2.140 0.000 C7 keel 16 2.200 0.185 C5 R2 37 2.260 0.231 C3 deck 17 2.200 0.163 C5 R3 38 2.022 0.186 ‒ deck For the model tests, the pressure transducer HKM375-1.7 Bar A from Kulite was installed. The signal amplifiers for the pressure transducers were custom-made, designed, and manufactured in-house. The motivation for the development of an in-house signal amplifier lay in the application area. The dynamic pressures were expected to be in an extremely small measurement range, and as a result, only a very low-noise amplifier can accurately detect the measured signals. Figure B1 presents time traces of two exemplary pressure transducers. The noise level is considerably lower compared with the measured values.
Nevertheless, experimental uncertainties were observed in the model tests, i. e., some of the pressure transducers showed unusual behavior during the model tests (cf. Figure B1(a)). This finding can be related to the different temperature compensation behavior of the sensors although all sensors should provide the same specifications, a circumstance that must be considered carefully for the interpretation of the measured results. The installed pressure transducers can be classified into three different types:
• Regular behavior: no shifting pressure offset (cf. Figure B1(a)).
• Disputable behavior: a fast shifting offset related to the reference pressure during each wave impact (cf. Figure B1(b)) and a slow decay of the original reference pressure after each impact.
• Acceptable behavior: a fast shifting offset related to the reference pressure at the first wave impact, with the constant offset through the entire test run regarded as a new reference pressure level, i.e., no decay of the original reference pressure.
Appendix C Details on investigated irregular sea states
C1 Investigated irregular sea statesNo. Synonym Hs (m) Tp (s) ϒ Steepness Phase seed 1 IRR.13 16.5 16.1 1 0.079 98 5 2 IRR.14 16.5 15.9 3.3 0.069 08 3 3 IRR.15 3 12 33 0.022 05 1 4 IRR.16 9.7 12 1 0.084 63 3 5 IRR.17 9.7 12 3.3 0.071 30 5 6 IRR.18 9.7 12 6 0.064 37 5 7 IRR.19 11.5 12 1 0.100 34 3 8 IRR.20 11.5 12 3.3 0.084 53 5 9 IRR.21 11.5 12 6 0.076 32 6 10 IRR.02 8.5 10.92 3.3 0.075 41 1 11 IRR.06 10.5 12.21 3.3 0.074 58 1 12 IRR.10 13.5 13.49 3.3 0.078 49 1 13 IRR.12 16.5 14.78 3.3 0.079 98 1 14 IRR.22 8.5 9.638 3.3 0.096 87 1 15 IRR.23 12.5 12.21 3.3 0.088 78 1 16 IRR.24 13.5 12.21 3.3 0.095 89 1 17 IRR.25 14.5 13.49 3.3 0.084 31 1 18 IRR.26 11 11.4 3.3 0.089 59 1 Appendix D Details on experimental uncertainty
D1 Random uncertainties regarding the motions and loads in irregular seas IRREGULAR20Items Run 1 Run 2 Run 3 Run 4 Run 5 Uncer. Percent 1/3 mean 8.75 8.74 8.75 8.68 8.55 0.04 0.444% Wave crest (m) 1/10 mean 6.24 6.37 6.36 6.37 6.31 0.03 0.403% Mean 3.68 3.78 3.76 3.77 3.74 0.02 0.489% 1/3 mean 7.07 6.90 6.97 6.91 6.87 0.04 0.519% Wave trough (m) 1/10 mean 5.38 5.32 5.36 5.33 5.32 0.01 0.230% Mean 3.19 3.26 3.26 3.23 3.24 0.01 0.389% 1/3 mean 3.49 3.34 3.30 3.34 3.35 0.03 0.979% Heave crest (m) 1/10 mean 2.57 2.59 2.56 2.60 2.59 0.01 0.244% Mean 1.56 1.63 1.61 1.63 1.60 0.01 0.835% 1/3 mean 3.62 3.45 3.44 3.47 3.45 0.03 0.970% Heave trough (m) 1/10 mean 2.55 2.57 2.61 2.64 2.65 0.02 0.753% Mean 1.48 1.57 1.61 1.63 1.64 0.03 1.845% 1/3 mean 7.16 7.08 7.07 7.03 6.95 0.03 0.483% Pitch crest (°) 1/10 mean 5.21 5.38 5.37 5.37 5.31 0.03 0.604% Mean 3.09 3.26 3.24 3.25 3.22 0.03 0.944% 1/3 mean 6.15 6.18 6.13 6.08 5.95 0.04 0.650% Pitch trough (°) 1/10 mean 4.56 4.74 4.66 4.69 4.61 0.03 0.645% Mean 2.74 2.88 2.83 2.85 2.81 0.02 0.861% 1/3 mean 8.40E+08 8.16E+08 8.10E+08 8.08E+08 8.02E+08 6.65E+06 0.816% VBM crest (kN·m) 1/10 mean 6.25E+08 6.27E+08 6.22E+08 6.25E+08 6.20E+08 1.28E+06 0.205% Mean 3.82E+08 3.86E+08 3.83E+08 3.85E+08 3.83E+08 8.62E+05 0.225% 1/3 mean 1.06E+09 1.05E+09 1.04E+09 1.03E+09 1.02E+09 7.40E+06 0.712% VBM trough (kN·m) 1/10 mean 7.82E+08 7.85E+08 7.74E+08 7.81E+08 7.74E+08 2.25E+06 0.289% Mean 4.74E+08 4.77E+08 4.71E+08 4.75E+08 4.72E+08 1.07E+06 0.226% D2 Random uncertainties regarding the pressures in irregular seas IRREGULAR20 for Fn = 0Items Run 1 Run 2 Run 3 Run 4 Run 5 Uncer. Percent Pressure 02 (bar) Extreme value 1% 1.02 1.16 1.20 1.14 1.16 0.01 0.8% 1/10 mean 0.85 0.85 0.88 0.83 0.84 0.01 1.0% 1/3 mean 0.66 0.68 0.67 0.64 0.66 0.01 1.0% Mean 0.43 0.45 0.43 0.43 0.43 0.00 1.0% Pressure32 (bar) Extreme value 1% 0.75 0.72 0.76 0.72 0.63 0.02 3.2% 1/10 mean 0.79 0.68 0.70 0.63 0.60 0.03 4.6% 1/3 mean 0.55 0.49 0.48 0.47 0.44 0.02 3.8% Mean 0.33 0.30 0.30 0.29 0.28 0.01 2.9% D3 Random uncertainties regarding the pressures in irregular seas IRREGULAR20for Fn = 0.08Items Run 1 Run 2 Run 3 Run 4 Run 5 Uncer. Percent Pressure 02 (bar) Extreme value 1% 0.84 1.58 1.20 1.44 1.55 0.14 10.4% 1/10 mean 1.91 1.47 1.73 1.08 1.22 0.15 6.00% 1/3 mean 1.05 0.95 0.99 0.81 0.85 0.04 4.30% Mean 0.55 0.54 0.57 0.51 0.51 0.01 2.40% Pressure32 (bar) Extreme value 1% 1.03 1.25 1.11 1.03 1.06 0.04 3.7% 1/10 mean 0.89 0.97 1.01 0.77 0.85 0.04 4.7% 1/3 mean 0.64 0.68 0.69 0.60 0.64 0.02 2.6% Mean 0.41 0.43 0.44 0.40 0.43 0.01 1.8% Competing interest C. Guedes Soares is one of Editors for the Journal of Marine Science and Application and was not involved in the editorial review, or the decision to publish this article. Shan Wang, Marco Klein and Sören Ehlers are editorial board members for the Journal of Marine Science and Application and were not involved in the editorial review, or the decision to publish this article. All authors declare that there are no other competing interests.Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyrightholder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. -
Figure 6 Breaking wave height and regions of validity of various theories on gravity water waves (Clauss et al., 1992)
Table 1 Main particulars of the CT
Items Full scale Model scale Loa (m) 170.0 2.428 Lpp (m) 161.0 2.300 Breath (m) 28.0 0.400 Depth (m) 13.0 0.186 Draft (m) 9.0 0.129 Displacement (t) 30 666 0.894 Lcg (m) 82.466 3 1.178 09 Vcg (m) 6.151 6 0.087 88 Rxx (m) 9.31 0.133 Ryy (m) 32.9 0.47 Rzz (m) 33.53 0.479 A1 Detailed mass distribution, moments of inertia, and center of gravity (model scale)
Items Center of gravity Moment of inertia Mass (kg) x (m) y (m) z (m) Jxx (kg·m2) Jyy (kg·m2) Jzz (kg·m2) Fore ship 23.640 1.579 0.000 0.095 0.512 4 2.621 5 2.925 5 Aft ship 18.660 0.640 0.000 0.121 0.566 8 2.437 3 2.725 1 Force transducer 2.000 1.150 0.168 0.201 0.081 7 0.027 2 0.057 7 Force transducer 2.000 1.150 −0.168 0.201 0.081 7 0.027 2 0.057 7 Force transducer 2.000 1.150 0.000 −0.016 0.021 6 0.023 2 0.001 6 Trim weight 1 4.980 0.651 0.000 0.030 0.012 1 0.012 1 0.023 7 Trim weight 2 3.835 0.868 0.074 0.064 0.012 1 0.012 1 0.023 7 Trim weight 3 3.835 0.868 0.074 0.064 0.005 9 0.010 0 0.010 3 Trim weight 4 3.835 1.018 −0.074 0.064 0.005 9 0.010 0 0.010 3 Trim weight 5 3.835 1.018 −0.074 0.064 0.005 9 0.010 0 0.010 3 Trim weight 6 9.820 1.624 0.000 0.064 0.005 9 0.010 0 0.010 3 Trim weight 7 10.040 1.442 0.000 0.064 0.031 4 0.022 4 0.030 3 Trim weight 8 0.340 1.167 0.000 0.225 1.160 0 0.038 1 0.000 0 Trim weight 9 0.057 1.780 0.000 0.309 0.000 0 0.000 0 0.000 0 Trim weight 10 0.057 0.333 0.186 0.445 0.000 0 0.000 0 0.000 0 Trim weight 11 0.057 0.333 −0.186 0.445 0.000 0 0.000 0 0.000 0 Equipped ship model 88.991 1.178 0.000 0.088 1.563 3 19.692 6 20.386 8 B1 Positions of pressure transducers
No. X (m) Z (m) Position No. X (m) Z (m) Position 1 2.320 0.210 C1 R1 18 2.200 0.140 C5 R4 2 2.320 0.185 C1 R2 19 2.170 0.210 C6 R1 3 2.290 0.210 C2 R1 20 2.170 0.185 C6 R2 4 2.290 0.185 C2 R2 21 2.170 0.163 C6 R3 5 2.290 0.163 C2 R3 22 2.170 0.140 C6 R4 6 2.290 0.140 C2 R4 23 2.140 0.210 C7 R1 7 2.260 0.210 C3 R1 24 2.140 0.185 C7 R2 8 2.260 0.185 C3 R2 25 2.140 0.163 C7 R3 9 2.260 0.163 C3 R3 26 2.140 0.140 C7 R4 10 2.260 0.140 C3 R4 31 0.000 0.149 stern 3 top 11 2.230 0.210 C4 R1 32 0.000 0.124 stern 3 middle 12 2.230 0.185 C4 R2 33 0.000 0.110 stern 3 bottom 13 2.230 0.163 C4 R3 34 0.030 0.124 stern 2 middle 14 2.230 0.140 C4 R4 35 0.060 0.124 stern 1 middle 15 2.200 0.210 C5 R1 36 2.140 0.000 C7 keel 16 2.200 0.185 C5 R2 37 2.260 0.231 C3 deck 17 2.200 0.163 C5 R3 38 2.022 0.186 ‒ deck C1 Investigated irregular sea states
No. Synonym Hs (m) Tp (s) ϒ Steepness Phase seed 1 IRR.13 16.5 16.1 1 0.079 98 5 2 IRR.14 16.5 15.9 3.3 0.069 08 3 3 IRR.15 3 12 33 0.022 05 1 4 IRR.16 9.7 12 1 0.084 63 3 5 IRR.17 9.7 12 3.3 0.071 30 5 6 IRR.18 9.7 12 6 0.064 37 5 7 IRR.19 11.5 12 1 0.100 34 3 8 IRR.20 11.5 12 3.3 0.084 53 5 9 IRR.21 11.5 12 6 0.076 32 6 10 IRR.02 8.5 10.92 3.3 0.075 41 1 11 IRR.06 10.5 12.21 3.3 0.074 58 1 12 IRR.10 13.5 13.49 3.3 0.078 49 1 13 IRR.12 16.5 14.78 3.3 0.079 98 1 14 IRR.22 8.5 9.638 3.3 0.096 87 1 15 IRR.23 12.5 12.21 3.3 0.088 78 1 16 IRR.24 13.5 12.21 3.3 0.095 89 1 17 IRR.25 14.5 13.49 3.3 0.084 31 1 18 IRR.26 11 11.4 3.3 0.089 59 1 D1 Random uncertainties regarding the motions and loads in irregular seas IRREGULAR20
Items Run 1 Run 2 Run 3 Run 4 Run 5 Uncer. Percent 1/3 mean 8.75 8.74 8.75 8.68 8.55 0.04 0.444% Wave crest (m) 1/10 mean 6.24 6.37 6.36 6.37 6.31 0.03 0.403% Mean 3.68 3.78 3.76 3.77 3.74 0.02 0.489% 1/3 mean 7.07 6.90 6.97 6.91 6.87 0.04 0.519% Wave trough (m) 1/10 mean 5.38 5.32 5.36 5.33 5.32 0.01 0.230% Mean 3.19 3.26 3.26 3.23 3.24 0.01 0.389% 1/3 mean 3.49 3.34 3.30 3.34 3.35 0.03 0.979% Heave crest (m) 1/10 mean 2.57 2.59 2.56 2.60 2.59 0.01 0.244% Mean 1.56 1.63 1.61 1.63 1.60 0.01 0.835% 1/3 mean 3.62 3.45 3.44 3.47 3.45 0.03 0.970% Heave trough (m) 1/10 mean 2.55 2.57 2.61 2.64 2.65 0.02 0.753% Mean 1.48 1.57 1.61 1.63 1.64 0.03 1.845% 1/3 mean 7.16 7.08 7.07 7.03 6.95 0.03 0.483% Pitch crest (°) 1/10 mean 5.21 5.38 5.37 5.37 5.31 0.03 0.604% Mean 3.09 3.26 3.24 3.25 3.22 0.03 0.944% 1/3 mean 6.15 6.18 6.13 6.08 5.95 0.04 0.650% Pitch trough (°) 1/10 mean 4.56 4.74 4.66 4.69 4.61 0.03 0.645% Mean 2.74 2.88 2.83 2.85 2.81 0.02 0.861% 1/3 mean 8.40E+08 8.16E+08 8.10E+08 8.08E+08 8.02E+08 6.65E+06 0.816% VBM crest (kN·m) 1/10 mean 6.25E+08 6.27E+08 6.22E+08 6.25E+08 6.20E+08 1.28E+06 0.205% Mean 3.82E+08 3.86E+08 3.83E+08 3.85E+08 3.83E+08 8.62E+05 0.225% 1/3 mean 1.06E+09 1.05E+09 1.04E+09 1.03E+09 1.02E+09 7.40E+06 0.712% VBM trough (kN·m) 1/10 mean 7.82E+08 7.85E+08 7.74E+08 7.81E+08 7.74E+08 2.25E+06 0.289% Mean 4.74E+08 4.77E+08 4.71E+08 4.75E+08 4.72E+08 1.07E+06 0.226% D2 Random uncertainties regarding the pressures in irregular seas IRREGULAR20 for Fn = 0
Items Run 1 Run 2 Run 3 Run 4 Run 5 Uncer. Percent Pressure 02 (bar) Extreme value 1% 1.02 1.16 1.20 1.14 1.16 0.01 0.8% 1/10 mean 0.85 0.85 0.88 0.83 0.84 0.01 1.0% 1/3 mean 0.66 0.68 0.67 0.64 0.66 0.01 1.0% Mean 0.43 0.45 0.43 0.43 0.43 0.00 1.0% Pressure32 (bar) Extreme value 1% 0.75 0.72 0.76 0.72 0.63 0.02 3.2% 1/10 mean 0.79 0.68 0.70 0.63 0.60 0.03 4.6% 1/3 mean 0.55 0.49 0.48 0.47 0.44 0.02 3.8% Mean 0.33 0.30 0.30 0.29 0.28 0.01 2.9% D3 Random uncertainties regarding the pressures in irregular seas IRREGULAR20for Fn = 0.08
Items Run 1 Run 2 Run 3 Run 4 Run 5 Uncer. Percent Pressure 02 (bar) Extreme value 1% 0.84 1.58 1.20 1.44 1.55 0.14 10.4% 1/10 mean 1.91 1.47 1.73 1.08 1.22 0.15 6.00% 1/3 mean 1.05 0.95 0.99 0.81 0.85 0.04 4.30% Mean 0.55 0.54 0.57 0.51 0.51 0.01 2.40% Pressure32 (bar) Extreme value 1% 1.03 1.25 1.11 1.03 1.06 0.04 3.7% 1/10 mean 0.89 0.97 1.01 0.77 0.85 0.04 4.7% 1/3 mean 0.64 0.68 0.69 0.60 0.64 0.02 2.6% Mean 0.41 0.43 0.44 0.40 0.43 0.01 1.8% -
Abdelwahab HS, Wang S, Parunov J, Guedes Soares C (2023) A new model uncertainty measure of wave-induced motions and loads on a container ship with forward speed. Journal of Marine Science and Engineering 11(5): 1042. https://doi.org/10.3390/jmse11051042 Akhmediev N, Eleonskii V, Kulagin N (1985) Generation of periodic trains of picosecond pulses in an optical ber: exact solutions. Sov. Phys. JETP 62(5): 894–899. https://doi.org/10.1016/j.optcom.2005.10.032 Akhmediev N, Eleonskii V, Kulagin N (1987) Exact first-order solutions of the nonlinear Schrödinger equation. Theoretical and Mathematical Physics 72(2): 809–818. https://doi.org/10.1007/BF01017105 Akhmediev N, Korneev V (1986) Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theoretical and Mathematical Physics 69(2): 1089–1093. https://doi.org/10.1007/BF01037866 Akhmediev N, Ankiewicz A, Taki M (2009) Waves that appear from nowhere and disappear without a trace. Physics Letters A 373(6): 675–678. https://doi.org/10.1016/j.physleta.2008.12.036 Bhatia M, Das N, Dutta P, Chattopadhyay H (2023) Numerical analysis on the seakeeping performances of a full-scale container ship hull using strip theory. Physics of Fluids 35(11): https://doi.org/10.1063/5.0172626 Chen CR, Chen HC (2014) CFD simulation of extreme slamming on a containership in random waves. In ISOPE International Ocean and Polar Engineering Conference (pp. ISOPE–I). ISOPE-I-14-415. https://doi.org/10.17736/ijope.2015.sh15 Cherneva Z, Guedes Soares C (2008) Non-linearity and non-stationarity of the new year abnormal wave. Applied Ocean Research 30(3): 215–220. https://doi.org/10.1016/j.apor.2008.08.003 Clauss G, Kühnlein W (1995) A new approach to seakeeping Tests of self-propelled models in oblique waves with transient wave packets. Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Kopenhagen, Denmark, 279. https://api.semanticscholar.org/CorpusID:107214377 Clauss G, Kühnlein W (1997) A new tool for seakeeping tests-nonlinear transient wave packets. Proceedings of the 8th Int. Conference on the Behaviour of Offshore Structures (BOSS), Delft, The Netherlands, 269–285. https://www.osti.gov/etdeweb/biblio/634779 Clauss G, Steinhagen U (1999) Numerical simulation of nonlinear transient waves and its validation by laboratory data. Proceedings of 9th International Offshore and Polar Engineering Conference (ISOPE), Vol. Ⅲ, Brest, France, 368–375. https://api.semanticscholar.org/CorpusID:126125536 Clauss G, Lehmann E, Östergaard C (1992) Offshore structures, Volume 1: Conceptual design and hydrodynamics. Springer Verlag London Clauss GF, Klein M, Dudek, M (2010) Influence of the bow shape on loads in high and steep waves. International Conference on Offshore Mechanics and Arctic Engineering, 49101: 159–170. https://doi.org/10.1115/OMAE2010-20142 Clauss G, Klein M (2011) The new year wave in a seakeeping basin: Generation, propagation, kinematics and dynamics. Ocean Engineering 38(14): 1624–1639. https://doi.org/10.1016/j.oceaneng.2011.07.022 Clauss GF, Stuppe S, Dudek M (2014) Transient wave packets: New application in CFD-Methods. International Conference on Offshore Mechanics and Arctic Engineering, Jun American Society of Mechanical Engineers 8(45516): V08BT06A035. https://doi.org/10.1115/OMAE2014-24104 Datta R, Guedes Soares C (2020) Analysis of the hydroelastic effect on a container vessel using coupled BEM-FEM method in the time domain. Ships & Offshore Structures 15(4): 393–402. https://doi.org/10.1080/17445302.2019.1625848 Drummen I, Holtmann M (2014) Benchmark study of slamming and whipping. Ocean Engineering 86: 3–10. https://doi.org/10.1016/j.oceaneng.2013.12.012 Fonseca N, Guedes Soares C (1998a) Time domain analysis of large amplitude vertical motions and wave loads. J. Ship Res. 42(2): 100–113. https://doi.org/10.5957/jsr.1998.42.2.139 Fonseca N, Guedes Soares C (1998b) Nonlinear wave induced responses of ships in irregular seas. Proceedings of the 12th International Conference on Offshore Mechanics and Arctic Engineering (OMAE'98), ASME Paper No. OMAE1998-0446. http://www.mar.ist.utl.pt/en/centec/publications.aspx?publicationid=139 Fonseca N, Guedes Soares C (2002) Comparison of numerical and experimental results of nonlinear wave-induced vertical ship motions and loads. Journal of Marine Science and Technology 6: 139–204. https://doi.org/10.1007/s007730200007 Fonseca N, Guedes Soares C (2004a). Experimental investigation of the nonlinear effects on the vertical motions and loads of a containership in regular waves. Journal of Ship Research 48(2): 118–147. DOI: 10.5957/jsr.2004.48.2.148 Fonseca N, Guedes Soares C (2004b) Experimental investigation of the nonlinear effects on the statistics of vertical motions and loads of a containership in irregular waves. Journal of Ship Research 48(2): 148–167. DOI: 10.5957/jsr.2004.48.2.148 Fonseca N, Guedes Soares C (2005) Experimental investigation of the shipping of water on the bow of a containership. Journal of Offshore Mechanics and Arctic Engineering 127(4): 322–330. https://doi.org/10.1115/1.2087527 Fonseca N, Pascoal R, Guedes Soares C, Clauss GF, Schmittner CE (2010) Numerical and experimental analysis of extreme wave induced vertical bending moments on a FPSO. Appl. Ocean Res. 32(4): 374–390. https://doi.org/10.1016/j.apor.2010.08.001 Guedes Soares C, Fonseca N, Pascoal R (2008) Abnormal wave induced load effects in ship structures. J. Ship Res. 52(1): 30–44. https://doi.org/10.5957/jsr.2008.52.1.30 Guedes Soares C, Schellin TE (1998) Nonlinear effects on long-term distributions of wave-induced loads for tankers. Journal of Offshore Mechanics and Arctic Engineering 120(2): 65–70. https://doi.org/10.1115/1.2829525 Guedes Soares C, Fonseca N, Pascoal R, Clauss GF, Schmittner CE, Hennig J (2006) Analysis of design wave loads on an FPSO accounting for abnormal waves. ASME. J. Offshore Mech. Arct. Eng 128(3): 241–247. https://doi.org/10.1115/1.2166656 Guo BJ, Bitner-Gregersen EM, Sun H, Helmers JB (2013) Prediction of ship response statistics in extreme seas using model test data and numerical simulation based on the Rankine panel Method. Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, OMAE 2013-10351. https://doi.org/10.1115/OMAE2013-10351 Hirdaris S, Parunov J, Qui W, Iijima K, Wang XL, Wang S, Brizzolara S, Guedes Soares C (2023) Review of the uncertainties associated to hull girder hydroelastic response and wave load predictions. Marine Structures 89: 103383. https://doi.org/10.1016/j.marstruc.2023.103383 Holloway DS, Davis MR (2006) Ship motion computations using a high Froude number time domain strip theory. J Ship Res 50: 15–30. https://doi.org/10.5957/jsr.2006.50.1.15 IACS (2015) Common structural rules for bulk carriers and tankers. Technical report ITTC (2008) Recommended Procedures and Guidelines. Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures. ITTC-7.5-03-01-01 (2008) ITTC (2017) Recommended Procedures and Guidelines. Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures. ITTC-7.5-03-01-01 (2017). Jiao J, Huang S, Wang S, Guedes Soares C (2021) A CFD-FEA twoway coupling method for predicting ship wave loads and hydroelastic responses. Applied Ocean Research 117: 102919. https://doi.org/10.1016/j.apor.2021.102919 Karjanto N, van Groesen E (2007) Derivation of the NLS breather solutions using displaced phase-amplitude variables. Proceedings of the 5th SEAMS-GMU International Conference on Mathematics and its Applications, Yogyakarta, 357–368. https://doi.org/10.48550/arXiv.1110.4704 Kharif C, Pelinovsky E, Slunyaev A (2009) Rogue Waves in the ocean. Springer-Verlag, Berlin, Heidelberg. https://link.springer.com/book/10.1007/978-3-540-88419-4 Kim Y, Kim JH (2016) Benchmark study on motions and loads of a 6750-TEU containership. Ocean Engineering 119: 262–273. https://doi.org/10.1016/j.oceaneng.2016.04.015 Klein M, Clauss GF, Rajendran S, Guedes Soares C, Onorato M (2016) Peregrine breathers as design waves for wave-structure interaction. Ocean Engineering 128: 199–212. https://doi.org/10.1016/j.oceaneng.2016.09.042 Klein M, Hartmann M, von Bock, Polach F (2021) Note on the application of transient wave packets for wave-ice interaction experiments. Water 13(12): 1699. https://doi.org/10.3390/w13121699 Klein M, Wang S, Clauss G, Guedes Soares C (2023) Experimental study on the effect of extreme waves on a LNG carrier. Journal of Marine Science and Application 22(1): 52–74. https://doi.org/10.1007/s11804-023-00321-1 Kudupudi RB, Datta R, Guedes Soares C (2023) Modelling green water loads on ships using coupled impulse response function and CFD solution. Ocean Engineering 281: 114918. https://doi.org/10.1016/j.oceaneng.2023.114918 Kuznetsov E (1977) Solitons in a parametrically unstable plasma. In Akademiia Nauk SSSR Doklady, Vol. 236: 575–577. https://api.semanticscholar.org/CorpusID:117469322 Lee C (1995) WAMIT theory manual. Technical report, Massachusetts Institute of Technology, Preliminary Copy Ley J, el Moctar O (2021) A comparative study of computational methods for wave-induced motions and loads. Journal of Marine Science and Engineering 9(1): 83. https://doi.org/10.3390/jmse9010083 Ma Y (1979) The perturbed plane-wave solutions of the cubic schrodinger equation. Studies in Applied Mathematics 60: 43–58. https://doi.org/10.1002/sapm197960143 NBC News (2023) Largest rogue wave ever observed swelled off the coast of British Columbia. Available from https://www.nbcnews.com/science/science-news/largest-rogue-wave-ever-observed-swelled-coast-british-columbia-rcna16218, [Accessed on 2023, January 29] Negi A, Ganesan TS, Sen D (2022) A 3D panel method for monohull ship motions and loads with moderate forward speed. In ISOPE International Ocean and Polar Engineering Conference (pp. ISOPE–I), Shanghai, China, ISOPE-I-22-308. https://onepetro.org/ISOPEIOPEC/proceedings-abstract/ISOPE22/All-ISOPE22/ISOPE-I-22-308/493932 Newman J (2018) Marine hydrodynamics. The MIT Press, Cambridge, Massachusetts Oberhagemann J, Shigunov V, Moctar OE (2012) Application of CFD in long-term extreme value analyses of wave loads. Ship Technology Research 59(3): 4–22. https://doi.org/10.1179/str.2012.59.3.001 Parunov J, Ćorak M, Guedes Soares C, Jafaryeganeh H, Kalske S, Lee YW, Liu S, Papanikolaou A, Prentice D, Prpiæ-Oršiæ J, Ruponen P, Vitali N (2020) Benchmark study and uncertainty assessment of numerical predictions of global wave loads on damaged ships. Ocean Engineering 197: 106876. https://doi.org/10.1016/j.oceaneng.2019.106876 Parunov J, Guedes Soares C, Hirdaris S, Wang XL (2022) Uncertainties in modelling the low-frequency wave-induced global loads in ships. Marine Structures 86: 103307. https://doi.org/10.1016/j.marstruc.2022.103307 Parunov J, Badalotti T, Feng QD, Gu XC, Iijima K, Ma N, Qiu W, Wang S, Wang XL, Yang P, Yoshida Y, Zhang Z, Guedes Soares C (2024) Benchmark on the prediction of whipping response of a warship model in regular waves. Marine Structures 94: 103549. https://doi.org/10.1016/j.marstruc.2023.103549 Peregrine D (1983) Water waves, nonlinear Schrödinger equations and their solutions. J. Austral. Math. Soc. Ser. B 25(1): 16–43. DOI:https://doi.org/ 10.1017/S0334270000003891 Phan KM, Sadat H (2023) CFD study of extreme ship responses using a designed wave trail. Ocean Engineering 268: 113178. https://doi.org/10.1016/j.oceaneng.2022.113178 Pilatis AN, Pagonis DN, Serris M, Peppa S, Kaltsas G (2024) A statistical analysis of ship accidents (1990–2020) focusing on collision, grounding, hull failure, and resulting hull damage. Journal of Marine Science and Engineering 12(1): 122. https://doi.org/10.3390/jmse12010122 Qiu W, Meng W, Peng H, Li J, Rousset JM, Rodriguez CA (2019) Benchmark data and comprehensive uncertainty analysis of twobody interaction model tests in a towing tank. Ocean Engineering 171: 663–676. https://doi.org/10.1016/j.oceaneng.2018.11.057 Rajendran S, Fonseca N, Guedes Soares C, Clauss GNF, Klein M (2011) Time domain comparison with experiments for ship motions and structural loads on a container ship in abnormal waves. In International Conference on Offshore Mechanics and Arctic Engineering, Vol. 44380, pp. 919–927. https://doi.org/10.1115/OMAE2011-50316 Rajendran S, Fonseca N, Guedes Soares C (2012) Experiment and time domain method comparison for the responses of a container ship induced by the three sisters abnormal waves. Marine Technology and Engineering, C. Guedes Soares, Y. Garbatov, S. Sutulo, and T. A. Santos, eds., Taylor & Francis, London, pp. 223–230. DOI: https://doi.org/10.1201/b12726-34 Rajendran S, Fonseca N, Guedes Soares C (2015) Simplified body nonlinear time domain calculation of vertical ship motions and wave loads in large amplitude waves. Ocean Engineering 107: 157–177. https://doi.org/10.1016/j.oceaneng.2015.07.050 Sengupta D, Datta R, Sen D (2016) A simplified approach for computation of nonlinear ship loads and motions using a 3D time-domain panel method. Ocean engineering 117: 99–113. https://doi.org/10.1016/j.oceaneng.2016.03.039 Serio M, Onorato M, Osborne A, Janssen P (2005) On the computation of the benjamin-feir index. Nuovo Cimento della Societa Italiana di Fisica C-Geophysics and Space Physics 28(6): 893–903. https://doi.org/10.1393/ncc/i2005-10134-1 Shrira V, Geogjaev V (2010) What makes the peregrine soliton so special as a prototype of freak waves? Journal of Engineering Mathematics 67(1): 11–22. https://doi.org/10.1007/s10665-009-9347-2 Simonsen CD, Otzen JF, Joncquez S, Stern F (2013) EFD and CFD for KCS heaving and pitching in regular head waves. Journal of Marine Science and Technology 18(4): 435–459. https://doi.org/10.1007/s00773-013-0219-0 Slunyaev A, Pelinovsky E, Guedes Soares C (2005) Modeling freak waves from the north sea. Applied Ocean Research 27(1): 12–22. https://doi.org/10.1016/j.apor.2005.04.002 WAMIT (1994) WAMIT Version 5.1-A Radiation-diffraction panel program for wave-body interactions. Technical report, userguide Wang S, Guedes Soares C (2016a) Experimental and numerical study of the slamming load on the bow of a chemical tanker in irregular waves. Ocean Engineering 111: 369–383. https://doi.org/10.1016/j.oceaneng.2015.11.012 Wang S, Guedes Soares C (2016b) Stern slamming of a chemical tanker in irregular head waves. Ocean Engineering 122: 322–332. https://doi.org/10.1016/j.oceaneng.2016.05.013 Wang S, Guedes Soares C (2017) Review of ship slamming loads and responses. Journal of Marine Science and Application 16(4): 427–445. https://doi.org/10.1007/s11804-017-1437-3 Wang S, Zhang HD, Guedes Soares C (2016) Slamming occurrence for a chemical tanker advancing in extreme waves modelled with the nonlinear Schrödinger equation. Ocean Engineering 119: 135–142. https://doi.org/10.1016/j.oceaneng.2016.04.017 Wang S, Guedes Soares C (2020) Effects of compressibility, three-dimensionality and air cavity on a free-falling wedge cylinder. Ocean Engineering 217: 107589. https://doi.org/10.1016/j.oceaneng.2020.107589 Wang S, Xiang G, Guedes Soares C (2021) Assessment of three-dimensional effects on slamming load predictions using OpenFoam. Applied Ocean Research 112: 102646. https://doi.org/10.1016/j.apor.2021.102646 Wang S, González-Cao J, Islam H, Gómez-Gesteira M, Guedes Soares C (2022) Uncertainty estimation of mesh-free and mesh-based simulations of the dynamics of floaters. Ocean Engineering 256: 111386. https://doi.org/10.1016/j.oceaneng.2022.111386 Watanabe I, Guedes Soares C (1999) Comparative study on time domain analysis of non-linear ship motions and loads. Marine Structures 12(3): 153–170. https://doi.org/10.1016/S0951-8339(99)00012-X Xiao H, Cinnella P (2019) Quantification of model uncertainty in RANS simulations: A review. Progress in Aerospace Sciences 108: 1–31. https://doi.org/10.1016/j.paerosci.2018.10.001 Yao, CB, Sun XS, Liu WM, Feng DK (2019) Seakeeping computation of two parallel ships with Rankine source panel method in frequency domain. Engineering Analysis with Boundary Elements 109: 70–80. https://doi.org/10.1016/j.enganabound.2019.09.012 Yasukawa H (2003) Application of a 3-D time domain panel method to ship seakeeping problems. In: Proceedings of 24th Symposium on Naval Hydrodynamics, Fukuoka, Japan, 376–392. https://nap.nationalacademies.org/read/10834/chapter/27 Zakaria NMG (2009) Effect of ship size, forward speed and wave direction on relative wave height of container ships in rough seas. Journal of the Institution of Engineers 72(3): 21–34. https://api.semanticscholar.org/CorpusID:161050012 Zhang A, Li SM, Cui P, Li S and Liu YL (2023) A unified theory for bubble dynamics. Physics of Fluids 35(3): 033323. https://doi.org/10.1063/5.0145415