1   Introduction

According to the new stringent regulations issued by the International Maritime Organization (IMO), several technologies have been suggested and developed to reduce the amount of power required to operate the ships (Mallouppas and Yfantis, 2021; Tadros et al., 2023) for instance, optimizing hull shape (Nazemian and Ghadimi, 2021), integration of air lubrication technologies (Hao, 2019), benefiting from wind energy (Seddiek and Ammar, 2021) and reduction of ship speed (Taskar et al., 2023). The selection of a suitable propulsion system during the preliminary stages of ship design is another concept and becomes an essential process (El-Gohary, 2013) to ensure the safety of the ship during the trip as well as the operation of the ship with the lowest amount of fuel onboard (Vettor et al., 2016; Zaccone et al., 2018; Moreira et al., 2021). This procedure directly affects the operation cost of the ship along the life span, which decreases the amount of fuel consumed and thus increases the percentage of the profit of the ship owner (Du et al., 2022). This procedure is not specific to marine diesel oil, which shows an increment in the fuel price nowadays, as shown in Figure 1, but also for the other new type of fuels (El Gohary and Ammar, 2016; Karatuğ et al., 2022), including those that will be available in the market shortly, such as hydrogen, biofuel, ammonia and methanol (El-Gohary et al., 2014; Chiong et al., 2021; Tadros et al., 2021b; Vedachalam et al., 2022).

Figure  1  Average price at top 20 bunker ports (Miller, 2022)

Download: Full-Size Img

The typical propulsion system of large ships is composed of the marine diesel engine coupled to a propeller through the propeller shaft and gearbox in the case of a four-stroke engine, and without a gearbox in the case of a two-stroke engine, thus various models are developed to be available to simulate their performance (Nahim et al., 2015; Altosole et al., 2017; Tadros et al., 2020a).

In addition to the engine, the different types of propellers (Zainol and Yaakob, 2016; Najafi and Pourmostafa, 2022) have been well designed due to the fast rapid technology that allows high-accuracy models during production and provides more control during different operational conditions.

Regarding the main source of power, the diesel engine, engines with high performance are already available in the market from different manufacturers to produce the required power supporting the ship's needs to achieve a certain speed. The efficiency of the new engines has been increased due to the control procedures applied on the different parts of the engine and thus achieving more than 50%, showing a good increment compared to the old engines (Wartsila, 2023). The new engines have been optimized to reduce the amount of brake-specific fuel consumption (BSFC) for each operating point (Tadros et al., 2019; Tadros et al., 2020b; Stoumpos and Theotokatos, 2020; Figari et al., 2022; Xiang et al., 2023). Thus, these types of procedures allow the engines to comply with the stringent regulations of international organizations towards mitigating climate change (Latarche, 2020).

These types of control are implemented in developing high-performance turbocharger(s) and intercoolers and providing control to the intake and exhaust valves (Wei et al., 2019; Wei et al., 2022), injection systems (Raeie et al., 2014; Tadros et al., 2020a) and exhaust gas recirculation (EGR) (Wang et al., 2021). The recuperation of the exhaust heat is seen in several solutions (Cherednichenko and Mitienkova, 2020; Cherednichenko and Serbin, 2018; Tadros et al., 2021c).

The main concept of implementing these types of controls is to increase the amount of intake air inside the cylinders accompanied by the perfect injection timing, which will reduce the amount of fuel consumption and the level of exhaust emissions (Zetterdahl et al., 2017; Tadros et al., 2020b; Fridell et al., 2021; Mocerino et al., 2021). Therefore, the development of several numerical models easily assists in the computation procedures to take the optimal decision and achieve highly accurate models, ensuring the sustainability of the propulsion systems (Benvenuto et al., 2021; Benvenuto and Campora, 2022; Trivyza et al., 2022). These models can vary from the look-up table to the complex computational fluid dynamics (CFD) depending on the required level of detail of the computed results.

Regarding the propulsor, several profiles of propellers have been developed to be used according to the application. The selection of an appropriate propeller(s) from the given series is important to ensure the generation of the required thrust to the ship. Also, it is crucial to take into consideration the criteria of cavitation, noise and strength (Carlton, 2012). For instance, Wageningen B-Series (Van Lammeren et al., 1969) has been widely used in commercial ships equipped with fixed-pitch propellers (FPP). However, by the increased demand for controllable-pitch propellers (CPP) to provide more control to the ship, Wageningen Propeller C- and D-Series have been developed and taking place to serve the market demands (Dang et al., 2013).

Recently, the Wageningen F-series (Huisman et al., 2021) has been designed to provide the highest efficiency and compliance with cavitation limits for the merchant's vessels. The propeller is usually designed at the maximum propeller efficiency (Hong et al., 2014), while the selection of a propeller at the engine operating point with minimum fuel consumption and power management can achieve a higher reduction in fuel consumption, either with a fixed pitch (Vesting and Bensow, 2018; Arapakopoulos et al., 2019; Tadros et al., 2021a), a controllable pitch propeller (Jaurola et al., 2020; Bacciaglia et al., 2021; Tadros et al., 2022b) or contra-rotating propeller (Nouri et al., 2018; Tadros et al., 2022c). In addition, applying several modifications to the propeller, such as the cupping percentage (Hwang et al., 1995; Tadros et al., 2022e), boss cap fins (Xiong et al., 2013) or installing energy devices before or after the propeller (Stark et al., 2022) will help to improve the wake flow and thus increase the propeller performance.

From the concept of design, designers need to select the optimal number of propulsion systems, including the number of engines and propellers. The single-screw propulsion has an advantage over twin-screw propulsion as it is simpler and consists of only one engine and one propeller. However, the engine and propeller can be bigger to produce the required power and thrust for the ship, therefore the loads on this system are larger than on the twin screw propulsion system. On the other hand, the twin screw is more complex, where the number of each part of the propulsion system is doubled, as well as the initial cost, in addition to the hull modification by adding a twin-skeg to support the propulsion system (Williams, 1975; Kim et al., 2014). However, the engine and propeller size are smaller than the single screw propulsion, and the loads are distributed along the two propulsion systems. Also, it shows an advantage in emergencies as the ship can operate with one of the two lines of the propulsion system until reaching the nearest safe port.

Usually, small ships with higher speeds require more than a single propulsion system due to the limitations of the stern part and stability computations to install a large engine with only one propeller and achieve the required speed. Therefore, the twin-screw propulsion system will be more effective than the single one. On the other hand, selecting the number of propulsion systems in large ships becomes more difficult as the ship can operate effectively using both systems (single and twin-screw).

However, due to international regulations and increments in fuel prices, it is beneficial to select the optimum propulsion system to ensure the lowest fuel consumption. To the authors' knowledge, the research works already published and mentioned in the literature review mainly focus on determining the amount of power required and the reduction of the installed engine loading ratio without comparing the amount of fuel consumed between the different configurations. This is due to the lack of fuel consumption information along the engine load diagram.

Therefore, this paper used the data of engine performance previously calculated using engine simulation software to present a comparative analysis between the single and twin-screw propulsion systems of a bulk carrier to evaluate the ship and propeller performance in terms of fuel consumption as well as discuss the cavitation and noise criteria. The computations are performed based on the propeller geometry of each case that is designed using optimization procedures and has been selected to minimize fuel consumption.

The remainder of this paper is organized as follows. The main characteristics of the bulk carrier are presented in Section 2. Next, the numerical model used to perform the simulation is described in section 3. The discussion of the computed results is presented in section 4. Finally, a summary of the main findings and future recommendations are presented in Section 5.

2   Main characteristics of the bulk carrier

This study considers the selection of a bulk carrier's single and twin screw propellers from B-series as an FPP depending on the number and rated power of the engine(s). The ship is 154 m in length and can sail at 14.5 kn. The ship is operated by a four-stroke marine diesel engine(s) from the series of MAN 32/44CR, where each cylinder's power is 510 kW, and the engine's total power differs according to the number of cylinders. The main characteristics of the ship and the engine are presented in Tables 1 and 2, respectively.

3   Numerical model

The computation of each case is performed using a developed optimization model coupling NavCad (HydroComp, 2018) and an optimizer implemented in Matlab to select the optimum propeller geometry and the operational point of the propeller inside the engine load diagram for a given ship speed (V_s) and the number of propeller blades (Z). This model allows operational research techniques to find the optimal values of the design variables of the propeller while minimizing the fuel consumption as the main objective of the model and complying with the limitations of several criteria as constraints, such as cavitation and noise. The design variables include propeller diameter (D), expanded area ratio (EAR), pitch diameter ratio (P/D) and gearbox ratio (GBR). Figure 2 shows a schematic diagram of the developed optimization model that is used in this study, coupling the different software components and showing the different variables and the output results of the optimization model.

Figure  2  Schematic diagram of the developed optimization model (Tadros et al., 2021d)

Download: Full-Size Img

In general, the optimization model based on the fmincon function can find the minimum of the problem specified by:

where f(x) is the objective of the optimization model, x is the optimization variables, c is the inequality constraints, c_eq is the equality constraints, A as a matrix and b as a vector are the linear inequality constraints, A_eq as a matrix and b_eq as a vector are the linear equality constraints, and lb and ub are the lower and upper bounds, respectively.

This model is slightly converted, where the objective and constraints are defined into one single function called the fitness function. This conversion is performed to reduce the time of simulation combining all the computed results into one equation and evaluated by the optimizer as in the following equation.

where R is a constant, g is the penalty function presenting the constraints, and j is the number of constraints.

The fuel consumption, FC, is computed using the following expression:

where P_B is the brake power.

The first step of the model is to compute the ship resistance by defining all the required variables into the software to be implemented into the numerical equations presented by Holtrop (1984) and Holtrop (1988) as the suggested method by NavCad, which comply with the ship type and dimensions. This method shows good computational accuracy in the estimation of the ship resistance for several ship speeds (Gaafary et al., 2011; Elkafas et al., 2019; Islam et al., 2022) and ship conditions (Islam and Guedes Soares, 2019). After defining all the ship parameters and operational speed, the total ship resistance is computed, as shown in Figure 3, as a summation of the bare-hull resistance and marginal resistance taking into account the roughness of a clean hull (Tadros et al., 2022d). The marginal resistance is used to predict an appropriate value of the resistance as a percentage of the bare-hull resistance. The value used in this study is 10% and corresponds to the feasibility estimation.

Figure  3  Total ship resistance for different ship speeds

Download: Full-Size Img

Once the resistance is computed, the simulation is then moved to compute the propulsion system as the second step. The method by Holtrop and Mennen (1982) is considered to compute the propulsive coefficient to evaluate the wake fraction (w), thrust deduction fraction (t) and relative rotative efficiency (η_RR), which differs from single and twin-screw. The main important parameters required in this step are the selection of propeller series, maximum propeller diameter, rated engine power and speed and the gearbox and propeller shaft efficiencies.

The value of these parameters differs for each case suggested in this study, and they will be presented in detail in section 4. After defining all the variables, the ship power, the propulsive coefficients, the operation of the engine(s) and propeller(s), as well as the cavitation and noise criteria are computed. The main characteristics of the propeller, such as the advance coefficient (J_A), thrust coefficient (K_T), torque coefficient (K_Q) and open water efficiency (η_o) are computed. The cavitation is evaluated by the method of Keller (1973) to compute the minimum EAR, Burrill and Emerson (1963) to compute the average loading pressure, Blount and Fox (1978) to calculate the average predicted back cavitation percentage and the minimum pitch as suggested by MacPherson (1991) to avoid face cavitation. The noise is computed based on the tip speed and the limits are provided in the manual of HydroComp (2018). More information about the methods and the limits of each criterion is presented in detail by Tadros et al. (2022a).

4   Results and discussion

In order to perform the comparison between the two cases, the simulation is performed twice, and the results are exported for each case. The first case concerns the simulation of the performance of a single-screw propulsion system, and in the second one, the performance of a twin-screw propulsion system is simulated. In both cases, the hull is assumed to be the same, and the total resistance is kept the same, as the difference between the two cases is the modification of the stern by adding another skeg in the second case, which can increase the wetted surface by a small amount than the first case. Therefore, it is preferable to keep the use of the same hull with the same resistance for comparison.

The engines from the same series MAN 32/44 CR are selected as they have the same performance along the engine load diagram, even if the number of cylinders is changed.

In the first case, the engine with fourteen cylinders is selected, providing 7 140 kW brake power and coupled with an FPP. In the second case, two engines with seven cylinders each are selected, each one able to produce 3 570 kW, and coupled as well to an FPP. The maximum diameter in each case is selected according to the shape of the stern. The maximum diameter in the first case is 60% of the ship draft, and the maximum diameter of each FPP in the second case is 50% of the ship draft. This maximum value is used to define the upper boundary of the optimization model, while the lower boundary is defined by 80% of the upper boundary.

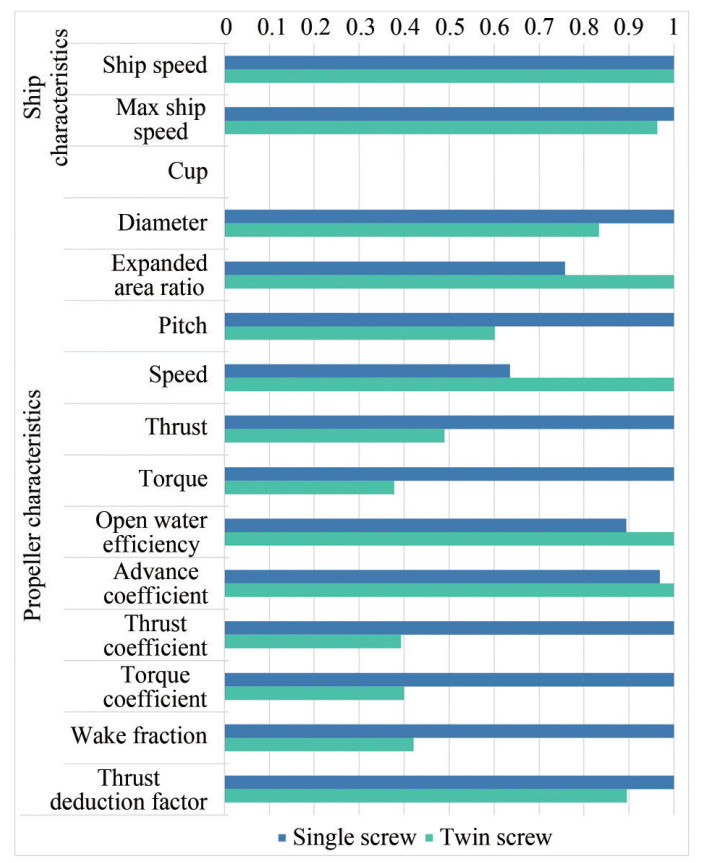
Once all the parameters are defined, the input data are processed into the optimization model and thus going through NavCad using the premium feature; then the results are computed and exported into Excel spreadsheet files, which have been collected to evaluate the fitness function to reduce the fuel consumption as in equation (3) and comply with all the limit values of the constraints defined. The numerical optimized results are presented in Table A1 for more information, while the results are normalized in Figures 4 to 6 to provide a clear comparison between the two cases.

Figure  4  Ship and propeller characteristics of each calculated case

Download: Full-Size Img

Figure  5  Cavitation and noise criteria of each calculated case

Download: Full-Size Img

Figure  6  Gearbox and engine characteristics as well as exhaust emissions of each calculated case

Download: Full-Size Img

Regarding the ship characteristics, as shown in Figure 4, it has been shown that the two propulsion systems can provide the required thrust to operate the ship smoothly at 14.5 kn as service speeds. However, the single screw can allow the ship to reach 16 kn with more than 5% in the case of the twin screw. This is due to the larger diameter that is installed in the first case compared to the second one. Otherwise, larger engines in the second case can replace the suggested ones to allow the ship to reach the same maximum speed as in the first case. Engines with eight cylinders can be selected to produce 4 080 kW to achieve the top speed, and thus the propeller can be designed to operate at lower loads and thus reduce fuel consumption.

Regarding the propeller characteristics, the propeller diameter is always selected at the upper boundary limits (6 m for the single screw and 5 m for the twin screw). This parameter shows its importance in increasing the propeller efficiency compared to the same propeller with lower diameter, and the propeller can produce the required thrust at lower engine loads. It has been shown that the propeller thrust in the twin screw is a little bit lower than half of the single screw to achieve the same ship speed due to the propulsive coefficient calculations, in particular, the thrust deduction factor, which shows a reduction in the twin screw case by almost 10% compared to the single screw case.

As the propeller diameter decreases in the second case, the EAR is higher than in the first case to provide the required thrust to propel the ship at the same speed. The EAR in the twin screw case is higher by 25% than in the single screw case. This increment leads to an increase in the blade area and thus reduces the amount of pressure on the blades, which affects the cavitation criteria as described in the next paragraphs. From the calculation, it has been shown that the pitch in the first case is higher by 40% than in the second case, this leads to achieve higher ship speed in the single screw than in the twin screw, also reducing the engine loading conditions and reducing the fuel consumption, and thus affects the gear between the engine and propeller. Furthermore, it has been affected by the minimum pitch value in the cavitation section to avoid face cavitation, where the single screw has a higher minimum pitch than the twin screw. Based on the pitch value, the propeller speed is reduced in the case of a higher pitch and increases in the case of a lower pitch.

Based on the overall propeller design, the open water efficiency is lower by 10% in the single screw case compared to the twin screw case. A slight difference in advance coefficient between the two cases is noticed and not exceeding 2%. However, the K_T and K_Q are in the twin screw are less by 60% compared to the single screw. Therefore, the thrust and torque are less in the second case than the first case by almost 50% to 60%. Based on the empirical formulas, the wake fraction in the twin screw case is lower by around 60% compared to the single screw case.

Regarding the cavitation criteria and due to the empirical equations to compute the propulsive coefficients, a change in thrust deduction factor is noticed between the two cases and, thus, a slight change in the total thrust of the two propellers by around 2% to achieve the design speed.

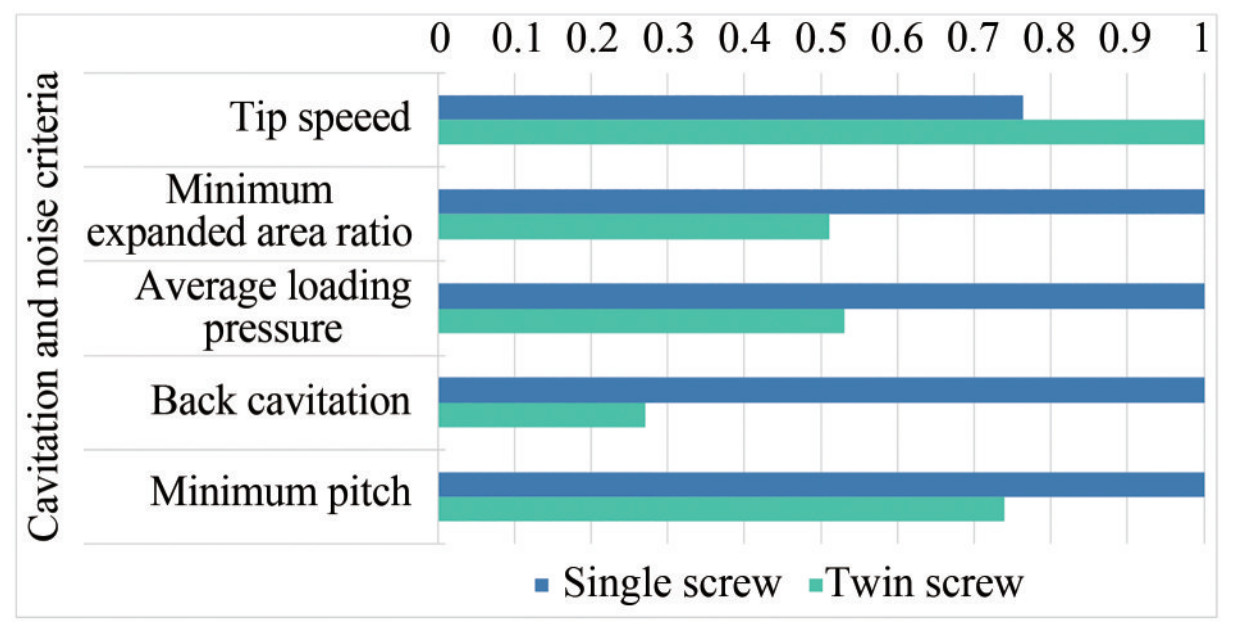
From Figure 5 and based on the propeller diameter and speed, the tip speed is reduced in the first case than in the second one, while both comply with the maximum tip speed to reduce the noise. The minimum EAR using the Keller method is higher in the first case than the second one and is equal to the selected EAR; however, the minimum EAR in the twin-screw propeller is reduced due to the split of the required thrust by the two propellers. The same behaviour is followed by the other cavitation criteria, where both the average loading pressure and the back cavitation are lower in the case of a twin screw than the single screw. As the propeller speed is lower in the first case than in the second one, the GBR is higher in the first case as the rated engine speed is the keeping same (750 r/min).

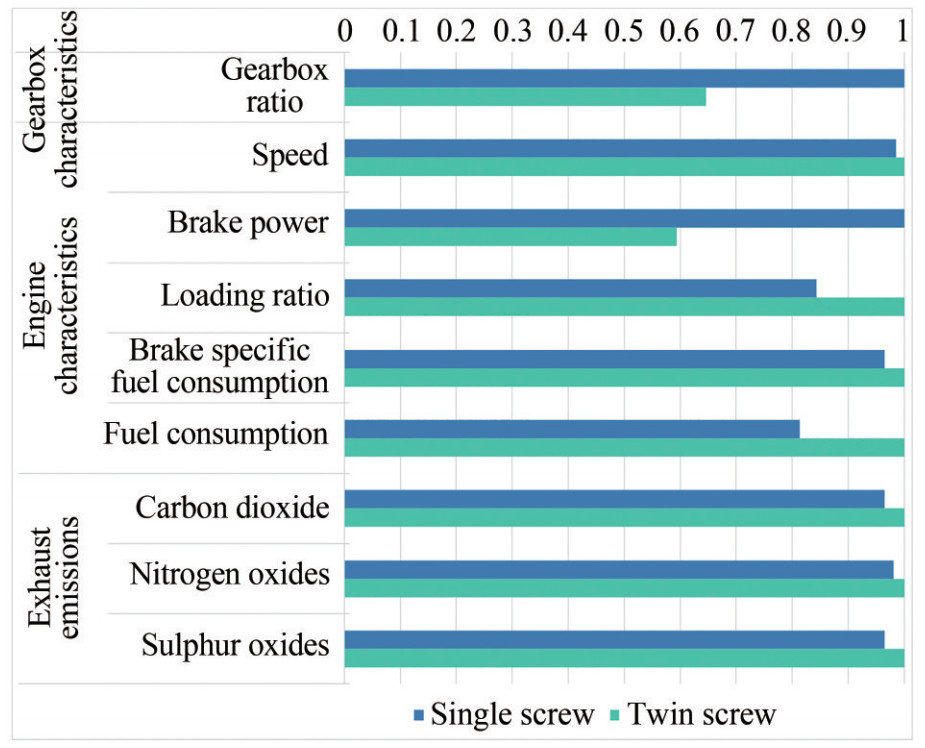
Regarding the engine performance in Figure 6, the single-screw propeller is selected at a lower loading ratio due to the large propeller diameter than the twin screw as it plays effectively to provide higher thrust at lower engine power. A big difference in the loading ratio between the two cases has been noticed, where the difference in brake power reaches 19% higher in the twin screw propeller for the two lines of the propulsion system compared to the single screw.

This increment in the brake power for each engine in the second case will increase the total amount of fuel consumed in the first case by around 19% to achieve the same speed. Thus, affects the total energy efficiency of the ship based on the values of the different exhaust emissions, including carbon dioxide (CO₂), nitrogen oxides (NO_x) and sulphur oxides (SO_x) that will increase according to the increment in fuel consumption.

5   Conclusions

This paper presents a comparative study between two types of propulsion systems for the concept of ship design of a bulk carrier, helping ship designers towards improving the energy efficiency of the ships. The first case is a single-screw propulsion system, and the second one is a twin-screw propulsion system. The engines in each case are selected from the same series due to the same behaviour along the engine load diagram. Based on the developed optimization model coupling NavCad and Matlab, the geometry of the propellers is optimized based on the selected B-series as an FPP as well as the gearbox ratio for each case. The hull of the ship is assumed to be the same, as the difference in the total resistance in both cases is small and can be negligible. From the computed results, it has been concluded that:

1) It is important to select an optimum propulsion system that is not complex and can operate at lower fuel consumption due to the higher fuel prices.

2) The computed results can be extended to reach any kind of engine operated with any type of fuel.

3) The optimization model can successfully find the optimum value of propeller geometry and operation for different configurations.

4) While the components of the single-screw propulsion system are larger than the twin-screw, the single-screw propulsion system shows advantages over the twin screw in terms of fuel consumption by around 19% and thus reducing the level of exhaust emissions.

5) The twin-screw propulsion system performs better in cavitation while evaluating the different cavitation criteria due to the pressure distribution over the two propellers.

The model can be extended to implement the prices of each part to provide an economic study of the capital expenditure (CAPEX) besides the operating expenses (OPEX) along a specific route. Also, hybrid propulsion systems combining dual-fuel engines and electrical components can be considered for further research.

Appendix