1   Introduction

Slamming is a commonly observed and important phenomenon in many areas of violent water impacts and water entry problems. Experiments have shown this in droplet impact with a rigid substrate as well as in solid impacts into water layers. Applications of slamming are widespread in engineering problems such as the landing of trans-media aerial underwater vehicles (Bi et al. 2022), hull slamming during the (re)entry of a ship into water (Kapsenberg 2011), wet-deck slamming in ships or offshore structures (Faltinsen 2005), fluid sloshing (Faltinsen and Timokha 2009), wave impacts on offshore rigs or wind turbine pillars (Tu et al. 2017), and wave impacts on harbors or sea walls (Bullock et al. 2007). Note that there are differences between water entry and wave impact problems. In wave impact problems, there are much more complex free surfaces, and even a simple formulation of the steep wave would make theoretical research more difficult.

A single impact of severe wave slamming can cause damage (Bitner-Gregersen and Gramstad 2015). An incident occurred in the North Sea in December 2015 when a large steep wave smashed into the COSL Innovator drilling rig, leading to the death of one staff, the injury of four people, and the disconnection of the rig from the well. The official report indicated that heavy wave slamming was the cause of the accident (Viste-Ollestad et al. 2016). Repeated mild slamming over a short duration can cause a whipping or ringing response, which induces high accelerations, and a significant high-frequency contribution, resulting in fatigue damage. The slamming loads can result in voluntary speed reduction for ship speed, high wave pressures, and run-up, which will increase the construction cost of boat landing and platform facilities.

Wave slamming on a cylinder can be characterized by the imposition of a high wave load on the cylinder over a relatively short duration. In this case, there is a high speed expansion of the contact region between the fluid and the body surface. Even at a moderate speed of the fluid motion, the resulting forces and overturning moments can cause highly localized slamming pressures. Besides, such an event can also cause a local or a global structural vibration or both modes together. Rather than direct impacts, steep waves can strike the cylinder with a curling jet (or entrapped gas pocket) which consequently forms escaping air bubbles. Air cushioning might also cause gas compression producing pressure oscillations (Chan et al. 1995).

Compared to 2D structures such as vertical or horizontal plates, slamming loads on vertical cylinders are much more complex. First, slamming loads on a cylinder have more prominent 3D characteristics, even in cases whereby 2D incident waves are used (Chan et al. 1995). A 3D cylinder can completely alter the shape of the wave surface near the impact area, while air entrapment can complicate this 3D phenomenon even more. Secondly, the influence of air pockets should be re-explored due to the air escape. Relevant studies include different plunging stages impacting a cylinder (Irschik and Oumeraci 2006; Kamath et al. 2016; Tai et al. 2019). Lastly, structural responses of the elongated cylinder are likely activated (Chaplin et al. 1997; de Ridder et al. 2011; Grue and Huseby 2002; Manjula and Sannasiraj 2019).

In recent years, several literature reviews have been conducted to describe the wave impact loads on cylinders from different perspectives of engineering applications, such as the nearshore breaking waves impacting piers of sea-crossing bridges (Wei et al. 2022) and offshore breaking waves on wind turbines (Chella 2012; Tu et al. 2017). However, these studies are mainly viewed from the perspective of the application of calculation methods. The present work presents a comprehensive review of the progress of wave slamming forces on a vertical cylinder based on the physical phenomena.

2   Analytical methods of wave impacting

One approach to calculating wave forces on a cylinder is based on the strip theory approach, which determines the sectional force and then integrates it over the interaction area, as in the famous Morison formula (Morison et al. 1950). However, the Morison formula ignores the Froude-Krylov action associated with the convective acceleration component, which is unsuitable for steep or breaking waves. To account for the impact forces induced by breaking waves, three approaches are used in structural design (Chella 2012). The first approach entails the application of the nonlinear wave kinematics in the Morison formula (Birkinshaw et al. 1988), the second approach entails modifying the drag term in the Morison formula to consider the effects of the wave impact (Chaplin et al. 1992), and the third method, also referred to as the impact-flow method, entails adding an extra term to include the impact force in the total wave force (Goda et al. 1966). Thus, the breaking wave force is composed of the impact load appearing on the upper part of the wave peak and the flow load of the wave below this part, as seen in Figure 1. In these approaches, an impact-flow method is the most effective method and has been adopted in many standards like DNV·GL (2019), IEC (2019), and ABS (2020).

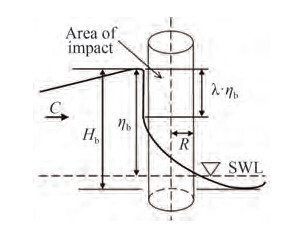Figure  1  Sketch of breaking wave impact force on a vertical cylinder (Wienke and Oumeraci 2005)

Download: Full-Size Img

The core of the impact-flow method for forces on a cylinder is the calculation of the impact term to calculate the impact forces F_s. The earliest model is proposed by Goda et al. (1966), which applied the 2D impact model of von Kármán (1929) multiplied by an assumed uniform impact area, written as:

where η_b is the breaking wave surface elevation; λη_b is the height of the impact area (seen in Figure 1) where the dimensionless parameter λ is called the curling factor; ρ is the mass density of water; V is the wave velocity; R is the radius of the cylinder; C_s is the slamming coefficient, and t is time.

2.1   2D impact models

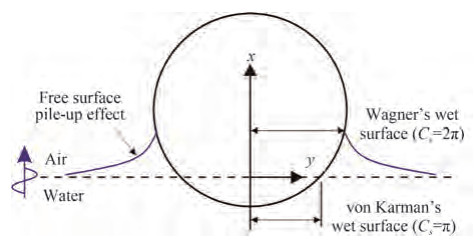
As far as the impact force calculation in Eq. (1) is concerned, either providing a more accurate 2D impact model to calculate the inline force per unit height or improving the distribution of the impact force would improve the impact force calculations. The first method of tackling the slamming problem is the momentum theory, although its classical publication dates from the study on the landing of seaplanes on the water by von Kármán (1929). In von Karman's model, the change in added mass of the wetted part of the floater (with an approximate method for fully submerged 2D sections) was used for calculation. This approach, which ignores free surface effects (also known as the pile-up effect), is equivalent to using an in fi nite frequency added mass calculation for a body at the free surface. Wagner (1932) completed another important work, pointing out the importance of the pile-up effect on impact forces, and also calculated the effect using potential flow theory. The maximum slamming coefficient C_s = 2π for the pile-up effect considered in the Wagner model is twice that found in the von Karman model. The difference in the wet surface on a circle-shaped section between the von Karman model and the Wagner model can be seen in Figure 2. Cointe and Armand (1987) also studied the problem of an impacting circular cylinder, using matched asymptotic expansions method to solve a boundary-value problem, and they found the same slamming coefficient as in the Wagner model.

Figure  2  Sketch of the pile-up effect

Download: Full-Size Img

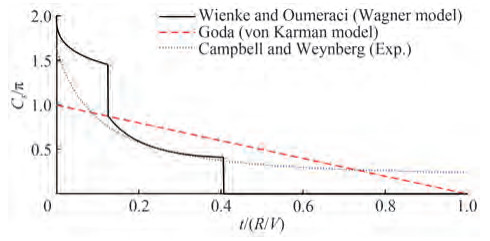
The measured pressures were found to be in good agreement with the calculated values. When employing the pressures in the calculation of total forces, strip theory was used as in Goda et al. (1966), while the curling factor λ was determined based on the measured total forces. Wienke-Oumerachi's method has been recommended in many standards, such as the DNV·GL (2019) and IEC (2019). However, though there are several calculation models for the slamming coefficients, as seen in Figure 3, their applications were found to vary with in-situ measurements (Hallowell et al. 2016). The discrepancies could be due to the many assumptions/simplifications adopted in these models and/or the in-situ measurements themselves.

Figure  3  Slamming coefficients of different studies

Download: Full-Size Img

Additionally, experiments are also used to determine the all/semi-empirical slamming coefficients. Campbell and Weynberg (1980) approximated the wave impact by forcing a horizontal cylinder with impact velocities through a still water surface, measuring the force and fitting the data for the slamming coefficient (seen in Eq. (2)). They checked with the integrated data of measured pressures. This experimental coefficient is widely used for slamming forces on slender structures and was adopted by DNV·GL (2019).

However, due to the inherent complexity of breaking waves, waves impacting a cylinder present a much more complex problem compared to a cylinder entering the still water. Wienke and Oumeraci (2005) conducted a large set of experiments on breaking waves impacting a large-scale cylinder, and the total forces, as well as pressures, were measured carefully. They introduced a polynomial stepwise function using Wagner's model to give a good approximation of the wetted surface, which is related to the pile-up effect, and thus derived the impact pressures and the sectional forces/slamming coefficient (seen in Eq. (3)).

where τ = Vt/R.

In addition to the 2D Wagner model, researchers have extended it to a three-dimensional Wagner model, such as the water-entry study of Scolan and Korobkin (2001). For wave impact, Tsaousis et al. (2020) considered the steep wave impact on a vertical circular cylinder and proposed a semi-analytical solution for this three-dimensional Wagner problem. Results showed that the actual 3D solution of Wagner fell between the simplified 2D von Karman and the 2D Wagner approximations. Other than that, a 3D Wagner model has not been found for calculating the wave impact on a cylinder. However, the development of 3D impact models could enhance the accuracy and robustness of the analytical model through wider consideration of breaking waves and 3D load distributions, which need further studies in future.

2.2   Distribution of impact forces

Since the sectional forces on a cylinder are calculated by the 2D impact models mentioned above, and only a few 3D impact models exist, modifying the vertical distribution of the impact forces is an improvement to the calculation method of Goda et al. (1966). Veić et al. (2019) found that the vertical load distribution was far more realistic than a rectangular shape, which is the distribution commonly applied in engineering practice. Dassanayake et al. (2021) found that different pressure distributions can cause different structure displacements while holding the pressure-integrated force unchanged. Although the triangular shape distribution has been considered in previous studies (Arntsen et al. 2011; Sawaragi and Nochino 1984), almost all distributions are obtained through assumptions or experiments, and no analytical solution for the impact distribution exists.

In practice, applying a wave impact model on a cylinder must be based on many assumptions hence a more accurate and practical wave impact model with a detailed analytical expression of the spatial distribution of impacts is needed in the future. Additionally, experiments have found air bubbles to have a great effect on wave impacts (Ha et al. 2020). As such, more studies of future wave impact models are needed to account for the influences of entrapped air or bubbles and air leakage, which are related to the wave-breaking type and the wave-breaking locations.

2.3   Pressure impulse theory

It is known that large variances can exist in pressure measurement or force peaks, even with nominally identical waves impacting the same structure; this might be due to the small environmental changes or the stochastic behavior of the slamming pressure. Bagnold (1939) found that the time integration of pressure throughout the impact, which gives the pressure impulse, was much more reproducible than the pressure measurement. Additionally, once the pressure impulse was determined, it was found that there were subtle differences in the overall dynamic structure response (Dassanayake et al. 2021). This finding shows that impact impulse acts as a simplified but much more stable approach to investigating breaking wave impacts on structures (Peregrine 2003). The definition of pressure impulse P can be written as:

where t_a and t_b are two representative times, respectively, before and after the wave slamming; p is pressure, and x is the position in a Cartesian reference system.

Cooker and Peregrine (1995) derived a two-dimensional pressure impulse theory for breaking wave impact on a vertical wall. Later this model was extended to three dimensions by Deborah and Peregrine (1998), and the case of trapped air was studied by Wood et al. (2000). Subsequently, this approach has been applied in more complicated configurations, including the breaking wave impact on a wall (Lobovský et al. 2014; Lugni et al. 2006), breaking wave impact on a permeable breakwater (Cooker 2013), wave impact on an oscillating wave energy converter (Renzi et al. 2018); and wave impact on a hydraulic structure with an overhang (Chen et al. 2019). Chen et al. (2019) also used impact impulses as the primary design variable to estimate the impulsive reaction force. Furthermore, Ghadirian and Bredmose (2019) derived a 3D pressure impulse model for a wave impact on a vertical circular cylinder and a good match of the pressure impulse fields relative to the numerical results, was found. Recently, this model was extended for directional waves by Ghadirian et al. (2023). However, like the wave impact model described in Subsection 2.1, the pressure impulse model for breaking waves on a cylinder needs further improvements to enable it to consider the influence of entrapped air or bubbles, the influence of wave breaking type and wave breaking locations.

3   Experiments to research wave impacting

Since the theoretical calculation of slamming wave forces on slender cylinders is highly complex and subject to several assumptions, laboratory experiments have contributed to a large extent to the knowledge of impact pressures/total loads and the associated flow features around them. However, a good wave slamming experiment requires well-controlled wave generation techniques and high-accuracy measuring instruments due to the high sensitivity of impact loads to the waves and the external phenomena and the short durations of these events.

3.1   Wave generation method

Depth-induced breaking through topography changes, such as what occurs on sloping beaches, might be the simplest approach to induce waves evolving into steep/breaking waves in a flume or basin. However, waves are usually limited to shallow water. The waves can be categorized by type as regular/irregular waves (Apelt and Piorewicz 1987; Goda et al. 1966), cnoidal waves (Ting and Kirby 1995), solitary waves (Mo et al. 2013) and so on. With the understanding of steep and rogue waves, many physical mechanisms have been used to generate steep/breaking waves. These mechanisms include wave-current interaction (Suastika et al. 2000), geometrical focusing (McAllister et al. 2019), dispersive focusing (Rapp and Melville 1990), and modulational instability (Deng et al. 2016). The most widely used of these mechanisms for breaking wave generation is the dispersive focusing method and its improved versions (Fernández et al. 2014; Niu et al. 2020); and it is most widely used because it can produce breaking waves at a pre-determined focal point/time and can be used in a wide range of water depths. It is worth noting that the wave group generated by focused waves propagates into calm water without consideration of the load history attributed to the previous waves, which is important to the dynamic response of structures. To consider a random background sea state, Taylor et al. (1997) introduced a Constrained NewWave method by constraining the NewWave group into an irregular background sea state with the same characteristic spectrum, which has been applied to generate waves on a fixed monopod platform by Pinna and Cassidy (2004). Under similar concepts, Zeng et al. (2022) embedded the expected freak wave in an irregular wave train to generate more realistic waves. Moreover, partially replacing oceanic wave conditions, Zhu et al. (2022) used irregular waves based on the JONSWAP spectrum to study wave slamming forces on a cylinder, and finally proposed a Gaussian distribution formula for use in describing the exceedance probability distribution of slamming forces. Recently, to produce more realistic waves, in-situ measured extreme waves were reconstructed in the laboratory with a new approach referred to as the time reversal (TR) method (Ducrozet et al. 2020; Ma et al. 2022). TR method was originally applied by Fink (1992) in ultrasonic fields, and can reconstruct target waves at almost any arbitrary position in a wave flume with reasonable accuracy. However, to the author's knowledge, this method has not been applied in any research on waves impacting a cylinder. The present study can contribute to statistical research and the cumulative effect of the wave impacts on the structural response under in-situ measured waves. These are required in future experimental investigations.

3.2   Total/sectional wave force measurement

Aside from the wave generation method, reliable measurement of impact loads is another important consideration. The total wave forces are usually the most commonly measured variable. Goda et al. (1966) used a cantilever-beam force transducer to measure total wave forces, which were then used to calculate the curling factor λ defined in Eq. (1); the maximum λ for a plunging breaker was found to be 0.4–0.5. However, Sarpkaya (1979) emphasized that the force experienced by the cylinder cannot be considered independently of the dynamic response of that cylinder since both λ and the slamming coefficients could be influenced by the dynamic response of the cylinder and its supports. Then, Sawaragi and Nochino (1984) devised a ring wave force transducer, which could accurately measure the sectional force on a vertical circular cylinder, as seen in Figure 4. With slightly dynamic responses of the cylinder in their measurements, Sawaragi and Nochino (1984) found that the vertical distribution of sectional forces simplified by Goda et al. (1966) through a uniform shape should be approximated by a triangular shape with its apex at about 70% of the wave crest above the still water level. The maximum curling factor λ without the influence of the dynamic response was found to be 0.9 for plunging breakers at a distance of 0.06L (L was the wavelength) shoreward from the breaking point. Arntsen et al. (2011) also used this type of ring wave force transducer and confirmed the triangularly distributed sectional forces along a vertical cylinder. The maximum impact loads were at 74% of the wave crest with a slamming coefficient C_s = 4.3 and the corresponding λ-value of 0.67. The curling factor was determined experimentally by Wienke and Oumeraci (2005) to produce the best agreement between the forces calculated by Eq. (3) and the measured total force, the maximum value of which was 0.46 in their experiments. All in all, the curling factor λ, partially reflecting the distribution of impact loads, varies according to different wave conditions and even the selected slamming coefficients hence the need for further studies on the curling factor along with the 3D impact force distribution.

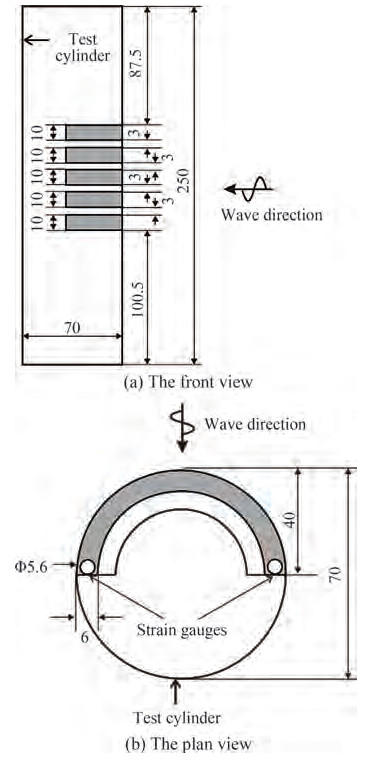Figure  4  Sketch of the half-ring wave force transducer (shaded area) in a cylinder (Unit: mm, not to scale) (Sawaragi and Nochino 1984)

Download: Full-Size Img

Except for the research on vertical distributions of total forces, the influences of the distance between the cylinder and the breaking point on total forces were investigated in both small and large-scale experiments (Tai et al. 2019; Wienke et al. 2000), and the plunging stage with a curling jet was found to induce the largest total impact forces on the vertical cylinder. Two main methods have been proposed to deal with the influences of the dynamic response of the cylinder on total forces. Irschik et al. (2002) suggested that measured forces consist of a quasi-static component and a dynamic component. While the former can be well approximated by the Morison equation, the latter is related to the response of a cylinder to slamming forces. Subsequently, to deal with the latter, the separation of dynamic components from the quasi-static components was attempted by an FFT band filter (de Ridder et al. 2011), the Empirical Mode Decomposition method (EMD) or EMD with an FFT low-pass filter (Irschik et al. 2002), the Ensemble Empirical Mode Decomposition method (Dassanayake et al. 2019; Tu et al. 2018), and the wavelet-based filter (Chen et al. 2019; Tai et al. 2019). The concept of quasi-static/dynamic forces is convenient for application, but of course, it will be influenced by empirical coefficients. Besides the concept of quasi-static/dynamic forces, another way of processing the structural responses of a cylinder is by extracting hydrodynamic forces from the measured forces and solving the equation of motion based on properties of the structure, including natural radian frequency and the damping ratio. Based on this concept, Paulsen et al. (2019) established a relation between the measured and the actual hydrodynamic force on a monopile wind turbine under the assumption of a linear stress-strain transfer function for the force transducers. In Ma et al. (2020), this approach was further developed by adding the relation between a cylinder's properties and surface elevations. Similar concepts, including the convolution between the input signal and the impulse response function to process structural responses, can be found in studies by Wienke and Oumeraci (2005), Tu (2018), and Antonini et al. (2021). It should be noted that while there is a theoretical basis to this concept, it still needs further improvement to be applicable in complex scenarios such as in structures with multiple vibration modes (de Ridder et al. 2011) or nonlinear elastic behavior. In addition to monopiles, total force measurements were also extended to more complex structures, such as square cylinders (Wei et al. 2022), an offshore wind turbine with a tripod structure (Hildebrandt 2013), and a jacket structure (Jose et al. 2017).

3.3   Pressure measurements

To gain more insight into impact loads, pressures are usually measured together with total forces. These measured data cannot only verify the implemented impact model as mentioned above (Campbell and Weynberg 1980; Wienke and Oumeraci 2005) but can also give both the vertical and azimuthal distributions of impact loads that are usually simplified in calculation methods. Zhou et al. (1991) measured pressure distributions on vertical cylinders during wave impact and found that the highest impact region was localized in space and time, and its pressures were subject to considerable variability due to the breaking and the entrapped air. Similar measurements were carried out by Chan et al. (1995), who found that for the cases where the wavefront directly impacts the cylinder, the impact zone spreads over an azimuthal range of about 22.5° on each half of the cylinder. Recently, Paulsen et al. (2019) assumed a 3D spatial distribution of the impact pressure by a pyramid-type shape centered at the wave crest in the vertical and at the centerline in the spanwise direction and first considered the 3D distribution of impact forces when calculating the total wave forces. However, the 3D distribution of impact pressures is also related to the breaking type and the positions of the breaking point (Chan et al. 1995). Thus, the 3D spatial distribution assumed by Paulsen et al. (2019) needs to be modified in the future. Additionally, the maximum impact pressures tend to occur at the plunging wave stage, where the wavefront is almost vertical (Wienke and Oumeraci 2005). This is different from the largest wave force stage, when a wave impacts the cylinder with a curling jet (Kamath et al. 2016; Tai et al. 2019; Wienke et al. 2000). The difference in breaking stages for maximum pressures and forces is also found in the numerical studies by Chella et al. (2019); the differences might be due to the various spatial/temporal distributions and concentrations of impact pressures for different breaking stages and breaking types, which should be studied further in the future.

3.4   Scale effects

Although experimental research is associated with many distinct advantages, its most notable drawback in physical hydraulic models is the scale effects (Hughes 1993). Scale effects arise from imperfect similitude, and a common scale effect under the Froude scaling law is viscous forces that are relatively larger in the scale model than in the prototype. Apelt and Piorewicz (1987) carried out experiments on breaking waves impacting a cylinder with the Froude scaling law. Two-cylinder diameters (102 mm and 153 mm) were adopted to study the scale effects in the experiments. Thirty-three comparable cases were found with an average scale effect coefficient C_se = 1 and a standard deviation σ = 0.13 (C_se is defined by Eq. (5)), indicating that no significant scale effect was detected.

where F_p is the prototype force, F_m is the measured model force, and L_r is the geometrical scale, set to 1.5 in Apelt and Piorewicz (1987).

Scale effect related to the impacts of breaking waves is very common in offshore and ocean engineering, e.g., waves impacting a vertical plate based on the Sloshel project and its follow-up studies (Guilcher et al. 2020; Kimmoun et al. 2010), the breaking wave-in-deck loads (Scharnke 2019) and so on. A new scaling law called the Bagnold– Mitsuyasu scaling law, which is quite different from the Froude scaling law, has been even proposed for pressure determination when a breaking wave impacts a flat plate with an air pocket (Bagnold 1939; Bredmose et al. 2015). The reasons why no significant scale effects of the total forces were seen in the study of Apelt and Piorewicz (1987) might be as follows: 1) breaking waves exhibit more local effects, to which the pressure might be much more sensitive than the total forces or integrated pressures; 2) the influence of air bubbles when waves impact a cylinder is smaller than the impact when waves impact a plate due to air leakage; 3) the choice of these two model scales by Apelt and Piorewicz (1987) is so close that the scale effects are small. All in all, the scale effect of breaking waves impacting a cylinder is still an open question, especially as regards the impact pressures.

4   Numerical simulations of wave impacting

Numerical simulations that are based on computational fluid calculations have been applied to wave impact problems for several decades, and two different primary approaches have been developed for solving these problems. One approach is the use of numerical methods to estimate the kinematics of breaking waves without the cylinder instead of using wave theories. Then, analytical models are applied to calculate impact forces. Marino et al. (2011) developed a higher-order boundary element method (HOBEM)-based code to simulate fully nonlinear breaking waves and then applied the calculated kinematics into impact models to compute the impulsive forces. This approach takes less time and has higher robustness, but it cannot consider more details, such as the density of wave breaking; hence, some coefficients in the impact models, such as the curling factor, are determined empirically.

The second approach is to directly simulate the interaction of breaking waves with the cylinder. This approach usually needs high CPU performance due to huge calculations, which have gradually become less important owing to the advancement of computational methods. In this approach, simulating models are mainly based on the Navier-Stokes equations together with the Volume of Fluid method (Choi et al. 2015) or the Level-set method (Kamath et al. 2016) to capture the water-air interface. Based on these methods, many models exist for solving the wave impact on cylinders, such as the open-source two-phase flow CFD models REEF3D (Kamath et al. 2016) and Open Field Operation and Manipulation (OpenFOAM^@) (Bredmose and Jacobsen 2010), and some business software Ansys CFX (Hildebrandt 2013) and Star-CCM⁺ (Zeng et al. 2021). Qu et al. (2021a) evaluated different RANS turbulence models through OpenFOAM^@; they found that the k−ω SST turbulence model presented a good agreement with the experimental free surface elevations and the breaking wave forces, although it over-predicted the turbulent kinetic energy. Besides these mesh-based numerical methods, meshless numerical methods such as the smoothed particle hydrodynamics (SPH) or incompressible SPH (ISPH) have advantages in processing large deformations, multiphase flow and moving boundaries due to its Lagrangian nature (Marrone et al. 2011; Zhang et al. 2017). Thus, with a natural fit for wave breaking and wave impact, the SPH/ISPH has been applied well in simulating water entry or exit (Meng et al. 2021), wet-deck slamming in ships or offshore structures (Sun et al. 2019) and wave slamming on cylinders (Lind et al. 2016). Note that the computational costs for SPH are higher compared to those of the finite volume methods due to the greater number of floating particles, especially for the 3D simulation of wave slamming on the cylinder, which generally requires optimized parallelization (Chow et al. 2019). All in all, numerical models for investigating breaking waves on a cylinder are universal, and many aspects associated with impact forces have been studied.

Using the dispersive focusing method, Bredmose and Jacobsen (2010) studied breaking wave loads on a monopile foundation using OpenFOAM^@ without a turbulence model, and the strongest wave loads were observed as the breakers hit the cylinder with a slightly curling jet, which was in qualitative agreement with the experimental results in Wienke et al. (2000) and Tai et al. (2019). The same finding was also made with depth-induced breaking waves. Kamath et al. (2016) simulated regular breaking waves over a submerged reef in shallow waters and the associated impacts on a cylinder. The numerical model was based on REEF3D with the RANS-LSM methods and the two-equation k-ω turbulence model. Their numerical results showed that the highest force occurred when the wave tongue hit the cylinder just below the wave crest level. Chella et al. (2019) also found that similar depth-induced breaking waves were adopted to investigate the vertical distribution of impacts under different breaking stages and breaking types through REEF3D. They found that the gradient of pressures in the vertical direction was much steeper than the corresponding velocity in the horizontal direction and was closely related to the location of the breaking point, while the breaking stage for maximum pressures or total force was variable for different wave impact conditions, even for the same breaking type. Using a GPU-based ISPH code by Chow et al. (2019), the local pressure increase was found to be directly related to the change in jet momentum in the normal direction. However, there is no common consensus on the relation between the pressures and the waves.

In their research, Chella et al. (2019) adopted shallow water waves that might be different from focused breaking wave packets. Veić et al. (2019) applied different wave generation techniques, including depth-induced breaking waves and focused breaking waves, to study the effect of breaking wave shape on the impact load on a monopile structure with OpenFOAM^@. In their simulations, breaking wave shapes were found to exhibit strong influence on the vertical load distribution, the curling factor, and the slamming coefficient; but the wave generation technique has not been found to have a clear relation with the impacts. This might be due to the limited number of simulation cases, which indicates a need for future studies. Likewise, as reported by Mo et al. (2013) and Chella et al. (2017), solitary plunging waves impacting a cylinder should also be included. Moreover, these numerical methods have been extended to study the wave impact on pile groups (Bihs et al. 2016; Cui et al. 2022), inclined piles (Choi et al. 2015), and inclined pile groups (Qu et al. 2021b).

Note that almost all cylinders in numerical simulations are regarded as rigid structures with no structural response. However, the structural response is universal in both experimental and full-scale conditions, which could amplify or attenuate the measured forces depending on the relation between the temporal distribution of the impact and the properties of the cylinder (Ma et al. 2020). To compare numerical results with the experimental results, Choi et al. (2015) applied the EMD and an FFT low-pass filter to remove the dynamic amplification caused by the vibration of the structure. However, these methods for processing measured forces have disadvantages, such as the choice of the empirical coefficient. The structural response induced by slamming, which is referred to as hydroelasticity, also influences local effects as it does global loads (Faltinsen 2005). Hydroelasticity theories for plates have been reviewed by Faltinsen (2000), while those for very large floating structures have been reviewed by Chen et al. (2006). Since published papers have not presented a consideration of the hydroelasticity in numerical models for waves impacting cylinders, this should be an area of study in the future.

5   Full-scale measurements

Considering the challenges and uncertainty of wave impact simulation, prototype measurements of wave impact loads and their statistics are always needed for both testing numerical models and improving engineering design. Compared to scaled experiments in the wave flume or basin, full-scale measurements have real-life details which can influence the impact phenomena as explained in Larroque et al. (2018): 1) Most flume experiments neglect the many 3D effects in nature for the sake of simplification; 2) affiliated facilities and some environmental variables such as wind are usually not considered; and 3) scale effects are non-existent during full-scale measurements. However, high-precision and repeatable instruments and measurement systems are common in laboratories but are very difficult to implement in the field.

Blackmore and Hewson (1984) summarized thirteen previous full-scale measurements of wave impact pressures on seawalls and breakwaters using spring dynamometers, and they found that these measurements could not capture the short-duration and high-intensity wave impact pressures. Meanwhile, they analyzed the in-situ measured pressures on the Ilfracombe seawall with modern recording techniques and found that the pressures were generally lower due to the high percentage of air entrained in the prevailing waves at this site. Drazen et al. (2012) fabricated an instrumented flat plate composed of three discrete modules and six pressure gauges for full-scale measurements, which were operated on a pile of the Scripps research pier in La Jolla, California. The threshold value for identifying slamming pressures was used in their study, and it was found that wave slamming occurred about every 12 seconds with a threshold value of 10.34 kPa. Recently, another in-situ measurement for impact pressures was carried out and a thorough analysis conducted. Larroque et al. (2018) gave a preliminary presentation of this measurement at the Artha breakwater in the Saint Jean de Luz Bay, southwest of France. d'Amico et al. (2020) described the procedures of pressure acquisition and post-processing. Finally, the relationship between the environmental variables on wave impact pressure in natural conditions was investigated by Poncet et al. (2022).

Figure  5  Phenomena where the full-scale measurements were carried out

Download: Full-Size Img

In-situ measurements of impacts on cylindrical structures such as offshore wind power foundations miss in published literature except for the offshore wind turbines (OWT) at Exposed Sites project described by Hallowell et al. (2016). The test structure of this project was a 2.0 MW OWT supported by a monopile installed in 8.0 m of mean water depth at the Blyth wind farm off the coast of England. The sea surface elevation and mudline overturning moment of the structure were monitored and recorded in the course of a 17-month campaign. In their analysis, the detection of breaking wave loads was based on the hypothesis that only breaking waves would cause the structure to oscillate in its second mode. The results showed that the measured wave overturning moments were quite different from values calculated by Goda's model and by Wienke and Oumeraci's model. The difference could be due to the imperfection of the breaking wave detection method, the dynamic and static conditions of the structure, such as wave slamming, and the variability in the kinematics of the breaking waves. Hence, in-situ measurements for wave impact on a cylinder need to include more details such as direct pressures, images, and wave velocities. Additionally, in-situ measurements, including shallow-, intermediate-and deep-water depths, are required to check the adaptability of these proposed impact models for coastal and offshore engineering.

Finally, considering high sampling frequencies and long-term monitoring of wave impact will require measurement of a lot of datasets, and a computer science-based approach is needed to process these big datasets rapidly. Recently, an artificial intelligence (AI) approach was adopted for big dataset processing in offshore engineering. Hoonhout et al. (2015) used structure support vector machines for the automatic extraction of beach widths and water lines from a coastal camera station. Stringari et al. (2019) applied machine learning procedures to track individual waves in the surf zone using data derived from nearshore imagery. Buscombe et al. (2020) used a deep convolutional neural network to estimate wave height and period from the imagery of waves in the surf zone. In experiments den Bieman et al. (2020) employed a convolutional neural network to measure surface elevations, wave run-up, and bed level development from video imagery. These AI approaches for images could also be used to process in-situ image data, such as the prediction of breaking wave characteristics and structural responses for waves impacting cylinders. In addition to image processing, a neural network method called Self Organizing Maps was used to classify the type of impacts on a breakwater according to in-situ wave impact pressures by d'Amico et al. (2020). In the future, similar use can be found in wave impact/non-impact segmentation, which can also be used in processing in-situ measured pressures/moments/total forces on a cylinder in the future.

6   Summary and discussions

This paper presents a review of the progress in studies conducted in the past decades on wave slamming forces on a vertical cylinder. Several ideas from both science and engineering perspectives are given as follows:

1) The spatial distribution of breaking wave impacts and their relation to impact conditions should be studied.

The spatial distribution of breaking wave impacts is obvious for waves impacting a cylinder, which is sensitive to impact conditions such as breaking wave types and breaking points. However, most analytical impact models have simplified the distribution of the wave impact like a rectangular distribution, which leads to overestimation or underestimation of impact loads in the application by the analytical impact models. An analytical model based on the 3D Wagner model or on more experiments/numerical simulations is required to construct a high-accuracy model with good robustness under various wave conditions and to provide a reasonable distribution law for the wave impacts.

2) Relationship between impact total forces and associated impact pressures.

Note that maximum impact pressures tend to occur at the plunging wave stage, where the wavefront is almost vertical (Wienke and Oumeraci 2005), as opposed to the stage where the largest wave force occurs (Kamath et al. 2016; Tai et al. 2019; Wienke et al. 2000). A similar finding is reported by Chella et al. (2019), and the reason must be highly related to the various spatial/temporal distribution and to the concentration of impact pressures for different breaking stages. The relationship between these total forces and associated impact pressures should be studied in the future.

3) Pressure impulse theory could be improved.

Pressure impulse is the integration of impact pressures, which preserves the features of wave impact but reduces uncertainty compared to impact pressures. (Integration is a smoothing process). Dassanayake et al. (2021) found subtle differences in the overall dynamic structure response once the pressure impulse was determined. Pressure impulse is suitable for engineering applications. However, there is a need for further improvement in the method to consider the influence of entrapped air or bubbles, the influence of the wave-breaking type and the wave-breaking locations.

4) The structural response should be considered in data-processing approaches or numerical models.

Wave slamming loads could excite structural reaction, while a structural response can induce fluid flow through a pressure field, adversely affecting the hydrodynamic loading. For a simple structure, it is possible to estimate the influence of this mutual fluid-structure interaction with current data-processing approaches. However, for realistic structures in engineering which have multiple vibration modes or nonlinear elastic behavior, these approaches need to be improved. Besides that, another way to research the influence of the structural response is to establish numerical models with the consideration of hydroelasticity.

5) Scale effects in breaking waves impacting a cylinder. At present, there are still no systematic studies of scaling laws for wave impacts on a cylinder. Though the experiments of Apelt and Piorewicz (1987) found the effects of the total forces to be of small scale based on two model scales, impact pressures that could reflect local features with more details may have scale effects due, for example, to the surface tension related to the trapped bubbles. Describing these phenomena, as done in the Sloshel project (Bogaert 2018; Lafeber et al. 2012), is the first step toward this goal.

6) Full-scale measurements of impacts of breaking waves on cylindrical structures.

To the authors' knowledge, few published papers exist for the full-scale measurement of the impacts of breaking waves on cylindrical structures, which is an urgent area of need for verification and modification of the various existing models for impact calculation. The associated processing methods for detecting and analyzing impact cases within structural dynamics, such as artificial intelligence for big data, are also needed.