1   Introduction

Electricity consumption in the world is mainly due to the growth of economic activity, industrialization and production techniques, increasing population, and welfare improvement. Morocco, like most countries in the word, is experiencing a significant growth in electricity consumption, with an average rate of 6.9% per year (Office National de l'Electricité. ONE 2010). This increase necessitates the exploitation of renewable and sustainable energy resources.

Nowadays, the energy sector in Morocco depends heavily on imports, about 90% of its energy needs are imported (Aparicio 2014). In this respect, the Moroccan government has put in place an ambitious energy plan, called the National Energy Strategy (NES) (Alhamwi et al. 2015). Its main objective is to increase the input of renewable energy resources into the national grid to 52% of electricity generated from renewable energy sources by 2030 (IRENA 2014; Alhamwi et al. 2015).

The NES has identified wind, hydro and solar as "high priority" resources to establish an ambitious renewable energy program. However, the presence of a coastline of 3 500 km, the country has a high potential of marine renewable energy (Alaoui 2019), which makes it a country with several sites for the exploitation of marine renewable energy (MRE).

Over the last few years, a big interest has been given to MRE (70% of the earth surface is covered by ocean). Among the potential sources of MRE, wave energy is considered as one of the energy sources with the greatest potential for development over the next few years (Iglesias et al. 2009). It may be seen as a condensed form of ocean wind energy (Akpinar et al. 2017). Wave energy development is suitable for countries or regions with extensive coastline and strong waves approaching the coast (Zhang et al. 2009).

According to (Sierra et al. 2016), the average wave power obtained along the Moroccan Atlantic coast is considerable (up to 30 kW/m, which is equivalent to annual wave energy of 262 MWh/m) and slightly lower than that of the neighboring Canary Islands. The spatial distribution of wave energy shows great variability, with a high energy stretch in the central part of this area (between latitudes 29.3° N and 34° N). The present work focuses on the anlysis of wave energy resource in the Casablanca-Mohammedia coast area (Moroccan Atlantic coast). The wave energy was characterized thoroughly in terms of wave directions, heights and periods based on numerical modeling, and using ECMWF (European Center for Medium range Weather Forecasts) ERA5 data-set.

Due to the advances in computer science, wave energy assessment uses numerical models capable of accounting for the physics of wave propagation in the deep and shallow waters. Within this context, spectral wave models such as Mike 21 (Vannucchi et al. 2012; Venugopa et al. 2017), SWAN (Simulating WAve Nearshore) (Bento et al. 2018; Carballo et al. 2014; Kamranzad et al. 2013; Amarouche et al. 2020), and WAVEWATCHIII (WWIII), WAM (WAve Model) (Rusu and Guedes Soares 2012; Zheng et al. 2013; Waters et al. 2009), and TOMAWAC (Dong et al. 2020; Guillou 2015), have been applied to assess and forecast global coastal wave resources at various locations.

To date, a very few studies explored the wave energy potential around the Moroccan waters.

As far as the authors know, the existing studies investigated the wave energy availability on a large scale using a deep water models (WAM and WAVEWATCHIII) (Bouhrim and El Marjani 2019; Sierra et al. 2016). The main novelty of this work is to study the wave energy on a local scale by the use of state-of-the-art coastal model SWAN. The studied area is the most important coastal stretch, in an economic view, and the most populated region of the kingdom. The main goal of the work is to prospect the most favorable areas (hotspots) for implementing wave energy farms.

To achieve this objective, the SWAN model was implemented to simulate the wave parameters during its propagation in the Casablanca-Mohammedia nearshore area. The SWAN model was previously used in many research studies in order to identify the wave energy hotspots sites (Iglesias and Carballo 2010; Lin et al. 2019; Majidi et al. 2020; Vannucchi and Cappietti 2016).

2   Wave models and data description

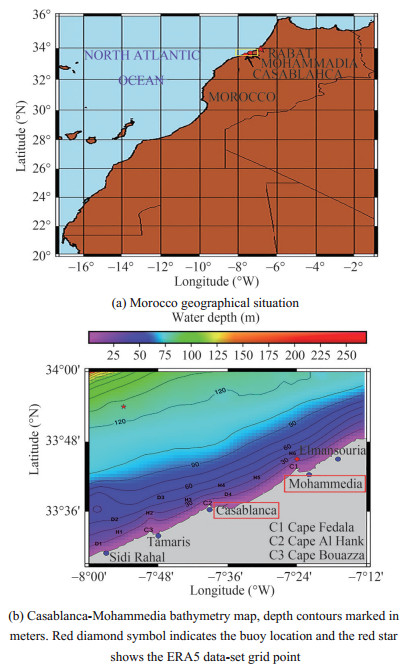
2.1   The study area

Morocco has an interesting geographical position. It is located at the crossroads between Africa and Europe (32°00'N 5°00'W). It is bordered by the Mediterranean and the Atlantic seas. The region concerned by the simulation includes the site of Casablanca-Mohammedia located at the northwest of Morocco on the Atlantic coastline. This coastal stretch has a NW-NE orientation, and is consequently exposed to waves coming from NW sector. The model zone extends longitudinally from 7° 2'W to 8° W, and at latitude from 33°45'N to 34°N. This area is characterized by a regular bathymetry showing a slope going down to the sea. The isobath is appreciably parallel to the coast, they vary from 5 m at the coast and 269 m offshore (Figure 1). This quasi-regular isobaths configuration is perturbed in the extreme south by the presence of submarine ridge extending about 11km from coastline. Moreover, we notice the presence of three very marked capes (Cap Dar Bouazza, cap Elhank, cap Fedala), these latter are elongated seawards by submarine ridges (D1, D2, D3 and D4). There exist also six shoals (H1, H2, H3, H4, H5, and H6) (Mouakkir et al. 2010) where water depth is nearly 28 m (Figure 1).

Figure  1  Study area location

Download: Full-Size Img

2.2   Modeling tools

2.2.1   SWAN model description

In order to force SWAN with a real wave boundary conditions, WWIII model was set up for the north atlantic area (Figure 2). It is a third-generation wave model developed at NOAA/NCEP (National Oceanic and Atmospheric Administration/National Centers for Environmental Prediction)(The WAVEWATCHIII DevelopmentGroup, 2019).

Figure  2  WAVEWATCHIII computational domain with ETOPO1 bathymetry used to force the model, water depths are in meter

Download: Full-Size Img

The analysis of the wave energy potential in the present study was developed based on the third generation wind-wave model SWAN version 41.20 (Booij et al. 1999; Mouhid et al. 2020; SWAN Team 2018). It is a numerical wave model that provides realistic estimates of wave parameters in open seas, coastal areas, lakes, and estuaries from given wind, bottom, and current conditions (Booij et al. 1999). The SWAN model computes the development of a sea states by means of the wave action density N(σ, ϴ), which is defined by the ratio of the spectral energy density E(σ, ϴ) to the intrinsic representative wave frequency σ. In SWAN model, the evolution of the wave spectrum is described by the spectral action balance expressed by the following equation:

where x and y are horizontal Cartesian coordinates, t is the time, θ is the propagation direction of each wave component, C_x, C_y, C_σ, and C_θ are the propagation velocity in x-space, y-space, σ-space, and θ-space respectively, and S_tot represents the energy source. The first term on the left-hand side of Equation (1) is the rate of change of action density in time, the second and third terms are the propagation of action in physical space. Term 4 represents the shifting of the relative frequency due to the variation of depth and current. Term (5) represents depth-induced and current-induced refraction.

The item S_tot on the right side of this equation includes dissipations, quadruplet interaction, and triad interaction caused by wind input, white-capping, bottom friction, and depth-induced wave breaking. Details of these processes can be found in the SWAN technical documentation manual (SWAN Team 2018).

2.2.2   Wave energy flux

The deformation of the surface water caused by wind and the transmitted water particles, give the swell a mechanical Energy. This energy is the sum of the potential and kinetic energy; it is considered as the total energy Contained in a wavelength per linear meter of Crest (Bonnefille 1992; Holthuijsen 2007). This energy is expressed by:

The wave power, flux of energy per unit crest, in terms of wave spectrum can be defined using the spectral output of the numerical wave model as energy flux per wave crest width unit in kW/m (Cornett et al. 2008; Sheng et al. 2017) as:

where x and y represent the problem coordinate system, C_x and C_y the propagation velocities of wave energy in the geographical space. The absolute value of energy transport (denoted also as wave power P_w) will be:

In deep water condition (d > 0.5 L), the Equation (2) becomes (Cornett et al. 2008; Randi et al. 2012):

The unit of wave power in Equation (6) is Kilowatts (kW) per meter (m) of wave front length as the significant wave height is given in meters and the wave period is in seconds. In this study, the Equation (6) is used to calculate the wave power.

ρ is the seawater density taken as 1 027 kg/m³, g is the acceleration of gravity, H_s is the significant wave height and T_e is the wave energy period. H_s and T_e are defined as:

The mean wave direction may be obtained from the directional wave energy spectrum through:

where E(ω, θ) is the variance density spectrum and ω is the absolute radian frequency equaling to the relative frequency σ when no ambient currents are present, it can be determined by the Doppler-shifted dispersion relation in the presence of the ambient current.

2.3   Forcing data and models setup

The model bathymetry is based on the ETOPO (www.ngdc.noaa.gov/mgg/global) global bathymetric data. ETOPO are the digital terrain elevation data released by the United States NGDC, including data about land elevation and sea bottom topography.

Figure 1 shows also the ETOPO bathymetry of the considered area. The wave climate in the general area of Casablanca–Mohammedia was drawn up using ECMWF (European Center for Medium range Weather Forecasts) ERA5 data-set (Hersbach et al. 2020). This global dataset provides an accurate and reliable time series describing the past wave climate and used in many studies for wave energy assessment on the global and regional scales (Amrutha et al. 2020; Mahmoodi et al. 2019; Rusu and Rusu 2021).

The wave time series spans twenty years and covers the period 2001-2020. The wave climate analysis was based on a standard wave parameter (significant wave height H_s, peak wave period T_e, and mean direction θ_m).

A Datawell buoy observations provided by Meteorological General Direction (MGD Morocco), were exploited to test the performance of SWAN model to simulate the propagation of waves in the nearshore area. The location of the buoy is indicated in the Figure 1 with a red diamond symbol.

In order to force SWAN with a real wave boundary conditions, WWIII model was set up for the north Atlantic area presented in the Figure 2. The source term physics package used in the present study is ST2 (Tolman and Chalikov 1996). Table 1 summarizes the main setting parameters of WWIII model. The weather forcing data of WWIII are extracted from ERA5 data-set with 0.25°×0.25° spatial resolution and 1 hour time step.

In this study, the SWAN cycle Ⅲ version 41.20 was used for wave simulations. The model was executed in both stationary and non-stationary modes. The spectral directions cover the full circle. The resolution in θ-space is 10° for the variable θ and 32 frequencies. The lowest frequency is fixed at 0.052 1 Hz and the highest at 1 Hz. The non-stationary application of SWAN was forced by winds retrieved from ERA5 database. While in the stationary mode, it was implemented without considering the effect of winds on the incident waves as in (El Mekadem et al. 2011) and (Hemdane et al. 2016). The SWAN physical processes during the wave simulation are wave generation, quadruplet nonlinear interaction, dissipation by friction on the bottom. The parameterization of the friction used for our simulations is that of Madsen. The simulations also take into account the effects of diffraction as well as wavewave interactions.

3   Wave climate and wave simulations

3.1   Offshore wave climate and wave energy

The study of data on the wave climate in the general area of Casablanca was drawn up using ECMWF (European Center for Medium range Weather Forecasts) ERA5 dataset. The wave climate analysis was based on a standard wave parameter (significant wave height, peak wave period, and mean wave direction) covering the period 2001-2020.

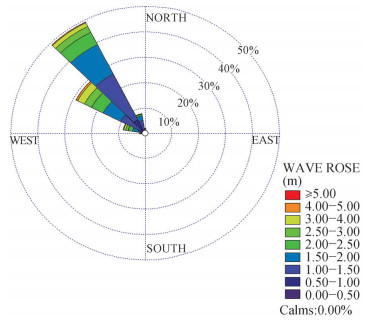
Figure 3 depicts the wave-rose off Casablanca-Mohammedia coast. The deep-water waves reaching the area of interest come mainly from NW and NNW directions. The dominant heights are in the interval [1.0-2.0 m] with about 62% of probability. As far as wave periods concerning, the most frequent are in the interval [12-15 s] with about 35% of frequency, followed by those in the intervals [10-12 s] and [8-10 s] respectively (frequencies 27% and 20%). Table 2 summarizes the yearly and seasonal mean wave parameters in the study area. Both observed mean significant wave height and wave energy period are significantly higher during winter months (H_s= 2.3 m, T_e= 11.8 s) than in summer period (H_s= 1.3 m, T_e= 8 s).

Figure  3  Wave-rose offshore the studied zone

Download: Full-Size Img

Based on the ERA5 wave data and using the Equation (6), the wave potential was calculated for the point (33.95° N8° W). The estimated wave energy potential in Casablanca provides a good resource for wave conversion with an estimated mean annual wave power of 22.4 kW/m with a maximum value of 37.1 kW/m in winter. The previous potential is characterized by a noticeable seasonal variability culminating at winter months (Table 2). The observed wave energy during winter months is five times higher than the quantity occurring during summer period. The corresponding theoretical annual wave energy is about 196 MWh/y. The results obtained in this study are in good agreement with those presented by Bouhrim and El Marjani (2019) and Sierra et al. (2016).

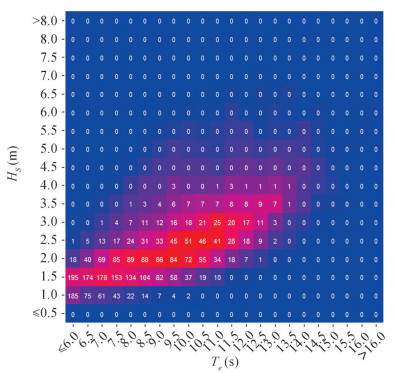
To design of a suitable WEC for a selected site, the so-called scatter diagram defined by wave height H_s and energy period T_e bins is a fundamental tool. Figure 4 illustrates the wave energy scatter diagram of Casablanca-Mohammedia coast. Wave height bins have 0.5 m width and energy period bins 0.5 s width. We note the fact that wave energy is concentrated in wave with H_s between 2.0 and 3.0 m, and T_e between 10.5 s and 12.0 s. The most energetic waves are those with 2.5 m of H_s and 11 s of T_e.

Figure  4  Wave energy Scatter diagram in terms of H_s and T_e for Casablanca-Mohammedia coast

Download: Full-Size Img

3.2   SWAN model simulations

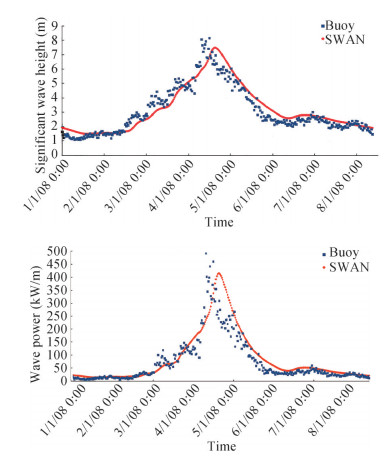
In order to evaluate the SWAN model, a wave buoy is installed in the study area (33° 44'81"N – 7° 23'2"W) (Figure 1). For this purpose, a simulation covering a period of 8 days period was conducted. The selected period spans from 01/01/2008 to 08/01/2008 and includes a heavy storm on 04/01/2008, with a significant wave height culminating at 8 m. The numerical models were forced by the ERA5 reanalyzed wind field corresponding to 10 m wind components (U10 and V10). A six-day period, starting from 26/12/2007, to spin-up the wave models was firstly performed.

The values of significant wave height computed by the SWAN model for the location of the buoy are compared with the actual buoy measurements in Figure 5. We notice that there is a good agreement between the model results and measurements throughout the simulation period, including the build-up of the storm, its peak (around noon of 04/01/2008). The correlation coefficient between the buoy and the model data is 0.94 for the wave height and 0.90 for the wave energy flux. The Figure 5 shows a comparison graphs depicting the model wave height, and energy versus observed data. The graphs demonstrate that, in general, the large wave event is well captured by the simulation. However, the peak of the episode was slightly underestimated by SWAN by less than 1m with three hours delay.

Figure  5  Significant wave height H_s and wave power P_w obtained with the SWAN model, and to buoy data observation from 01/01/08 at 0000GMT to 08/01/2008 at 0900GMT

Download: Full-Size Img

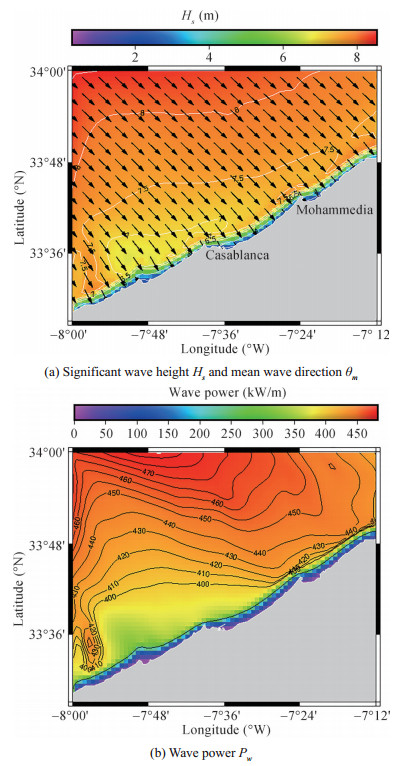
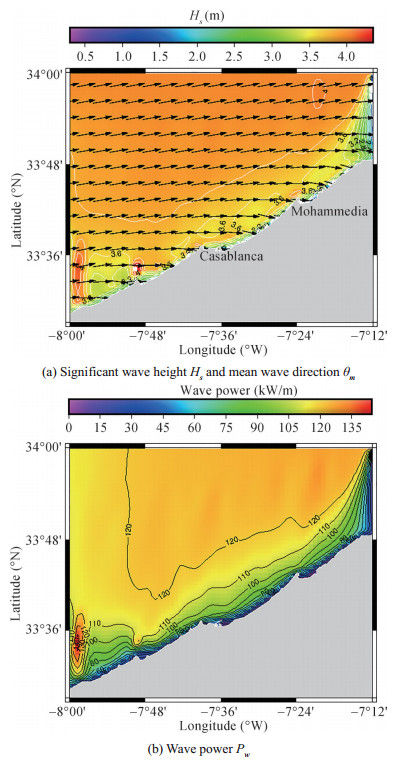
The modeled wave parameters (significant height, period, direction) and wave energy flux fields were provided at thirty minutes time step. The figure 6 illustrates the spatial distribution of the significant height wave energy flux relative to the conditions at 15:00 GMT, on 04/01/2008 i.e. the peak of a strong storm recorded during 2008. The forecasted wave heights are between 8.0-8.5 m offshore and in the range 6.5-7.5 m nearshore (Figure 6(a)). The observed waves come mainly from NW direction.

Figure  6  Spatial distribution of H_s and P_w simulated by SWAN on 04/01/08 at 1500UTC

Download: Full-Size Img

In term of wave energy flux (Figure 6(b)), the values are more pronounced in deep waters and decrease towards the shore. The maximum energy flux is around 480 kW/m in the northern edge of the studied domain. We note a nearshore high energy area situated north of Cap Fedala with values between 400-440 kW/m. South of Cap Fedala, the wave energy is generally low except in Sidi Rehal nearshore area, where wave energy arises locally and reaches 440 kW/m. This area, as mentioned in the section 2.1, contains a pronounced submarine ridge that probably led to a local wave energy concentration.

Having tested the coastal wave model in real conditions, it was applied to identify the location of the nearshore hotspots in the Casablanca-Mohammedia coast. For this purpose, the nearshore wave patterns were computed in three case studies. The first two are representative of a characteristic winter and summer situations, and the third, of a heavy storm conditions. These synthetic wave conditions were selected based on the wave climate analysis done in the section 3.1.

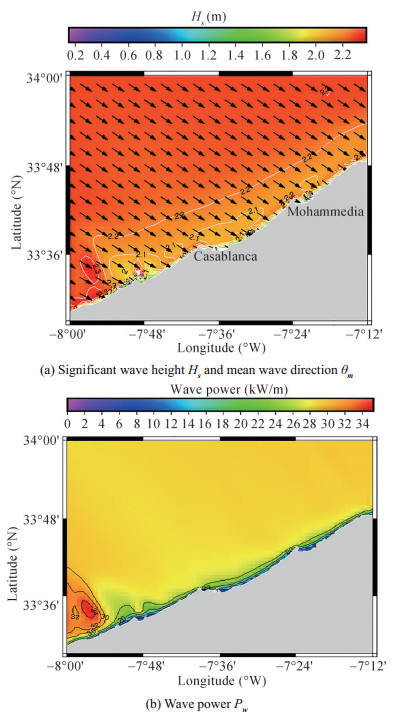
For the simulation results, the first case study I, represents a typical winter wave condition (H_s=2.3 m, T_e=12.4 s, θ₀=304°). The Figures 7(a) and 7(b), show the wave field, and wave energy flux simulated by SWAN in Mohammedia-Casablanca for this first case study. The wave heights are generally in the interval 2-2.2 m. In the extreme south, nearshore Sidi Rahal, significant height exceeds 2.3 m. As far as the wave energy flux, in the nearshore area, the values are in the range 20- 25 kW/m. We note a remarkable area of energy concentration located in the southern part of the coast in front of Sidi Rahal area, where wave energy rises significantly to 30-35 kW/m. This increase is equivalent to about 17% of the offshore wave energy.

Figure  7  Spatial distribution of Hs and Pw for the case study I (H_s =2.3 m, T_e=12.4 s, θ₀=304°)

Download: Full-Size Img

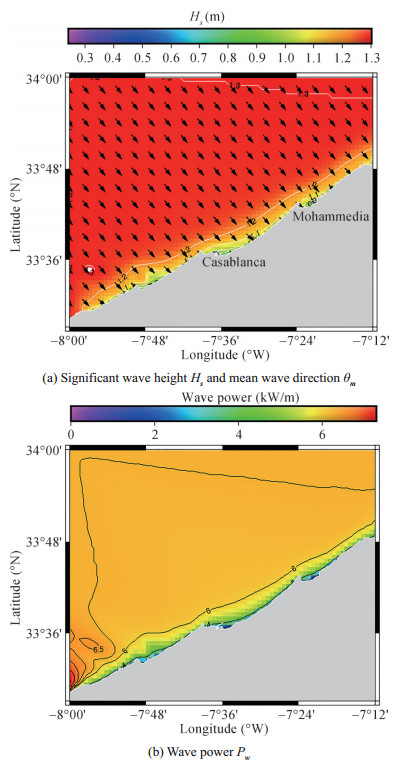
The second case study Ⅱ represents a typical summer wave condition (H_s =1.3 m, T_e =8.5 s, θ₀=321°). The wave height as well as wave flux in the nearshore region are significantly low (Figures 8(a) and 8(b)) with H_s between 1-1.2 m (4-6 kW/m), except in the southern extremity where H_s arises slightly above 1.2 m (about 7 kW/m).

Figure  8  Spatial distribution of H_s and P_w for the case study Ⅱ (H_s =1.3 m, T_e =8.5 s, θ₀=321°)

Download: Full-Size Img

Finally, the case study Ⅲ representing a typical storm waves (H_s =4.2 m, T_e =17 s, θ₀=259°) was considered. These conditions, extracted from ERA5 reanalysis, correspond to a real situation occurred on 28/02/18 at 15: 00 GMT. This situation is characterized by West-South Westerly (WSW) waves and was intentionally selected to study the WSW wave's transformation due to the local seabed. The simulation results of the last case study are given in Figures 9(a) and 9(b). The wave height, close to the shore, is between 3-3.6 m. We observe in the vicinity of the capes an increase of wave heights reaching 3.6-4 m. An area of wave accentuation is visible in the southernmost part of the coast.

Figure  9  Spatial distribution of H_s and P_w for the case study Ⅲ (H_s =4.2 m, T_e =17 s, θ₀=259°)

Download: Full-Size Img

The wave energy flux is mainly in the range 80-110 kW/m, except in the aforementioned area. In this zone, the wave potential amounts to 100-140 kW/m. This demonstrates that even WSW waves are affected by the submarine ridge D1. Thus, the wave transformation leads to wave energy concentration even in WSW wave condition.

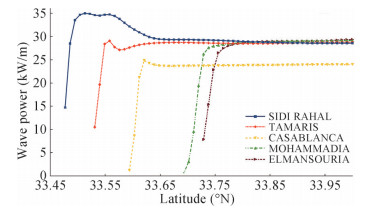
In conclusion, it is apparent that as the waves propagate from the sea to the coast, the wave height gradually decreases, however, this general trend is not verified in some coastal areas where the bathymetry leads to a concentration of wave energy and therefore an increase in wave height. This remark is observed in the vicinity of the Cape Dar Bouazza, precisely around the ridges D1 and D2 as well as the shoals H1 and H2. This observation is clearly visible on the longitudinal sections that pass through the three graphical capes, i.e., an increase in height as it moves from the open sea to the coast (Figure 10). (Idrissi et al. 2004) previously studied the evolution of wave in the studied region using a computer code developed by (Nicholas and Germain 1993). Based on this code, which considers the refraction of the waves, the wave orthogonals were drawn up in the coastal area. The study revealed that the convergence of the wave orthogonals, producing a concentration of wave energy, is observed behind the submarine ridges (D) and at the shoals (H). This finding may explain the remarkable increase of wave energy in the aforementioned hotspot located in front of Sidi Rehal due to the presence of the large submarine ridge (D2).

Figure  10  Wave power simulated by SWAN along five longitudinal sections for the first case study (winter)

Download: Full-Size Img

4   Conclusion

Currently, only 10% of energy needs in Morocco are satisfied by renewable energy, mainly hydraulic, wind and solar energy. However, with its geographical position, bordered by two seas: the Atlantic Ocean and the Mediterranean Sea, Morocco has a great potential in marine energy.

The present study presents an assessment of the potential wave energy resource in Casablanca-Mohammedia nearshore area (Moroccan Atlantic coast), considered as the most populated region of the country. The wave climate has been presented based on 20 years wave data provided by ECMWF. Afterwards, the SWAN model was used to compute the wave propagation and transformation in the studied area under three typical wave scenarios. The modeling tool was validated with a buoy data, indicating a good agreement between the measurements and the simulations with regard to significant wave heights and wave energy.

The spatial distribution of wave energy in the study area is examined under different conditions (winter, summer, and storm conditions). The results of this study shown in term of wave energy power analysis confirm the abundance of wave energy in the area with an annual mean potential of about 22 kW/m. Moreover, the study demonstrated a clear seasonal variability of the wave resource and that wave power levels are five times higher in winter than in summer. The application of SWAN demonstrated that the wave energy is unequally distributed within the studied area and presents areas with energy concentration.

In addition, an important hotspot site was identified to be taken in consideration when investigating WEC implementation. The hotspot site is located in the southern limit of Casablanca-Mohammedia coast, nearshore Sidi Rahal area.