1   Introduction

Large amounts of complex and labor-intensive works are carried out in winter when constructing hydraulic and transport structures on the ice of rivers and reservoirs. Such works include erection of bridges, overlapping of rivers, construction of bridge supports, installation of span structures, and laying of pipelines (Bychkovsky and Guryanov 2005). Since the 1930s, ice covers have been actively used as load carrying platforms for stationary facilities and equipment at winter polar stations and for equipment of ice aerodromes. However, there are difficulties in predicting the behavior of ice under various types of loading (static and dynamic). The destruction of ice from normal, inclined, and radial cracks was investigated in the works of scientists, such as Lu et al. (2015), Renshaw et al. (2017), and Tippmann et al. (2013).

Traditional methods of increasing the load bearing capacity of ice are ice freezing from above, ice freezing from below, and ice strengthening through a wooden copepod flooring (Common house needs, 1998). Practical experience shows that the physical and mechanical properties of ice covers are unreliable and changeable in time and strongly depend on various external factors. Therefore, ice covers should be strengthened through alternative methods. The introduction of various reinforcing materials into ice is quite promising. However, the amount of data on the stress–strain state of ice cover strengthening with reinforcing elements is limited.

Many works have been dedicated to the introduction of reinforcing elements in ice crossings. Yakimenko and Sirotyuk (Yakimenko and Sirotyuk 2014; 2015; Sirotyuk et al. 2016) performed an experimental research on the "surface reinforcement" of ice crossings using geosynthetic materials. Surface reinforcement by freezing steel meshes was proposed by Nikitin and Nikitina (2015). In another method, steel elements are frozen to increase the bearing capacity of ice covers (Kostenko et al. 2005; Kozin et al. 2003, 2011, 2018, 2019; Zemlyak et al. 2019). The surface reinforcement method, which introduces welded steel frames into relatively thin ice covers of 0.3–0.4 m thick, can actually be sufficiently promising.

The purpose of this study is to identify ice behavior on ice crossings under pure bending with various reinforcement materials. For this purpose, model experiments of reinforced samples were performed, and the results were compared with numerical calculations in an ANSYS PC. The authors investigated the dependence of the load on the deflection and stress–strain state of the reinforced ice samples.

2   Preparations for the Experimental and Numerical Research

In this paper, an experimental device for simulating the destruction of samples from pure bending is presented. A series of tests were carried out with a specified reinforcement scheme. The results of the model experiments were compared with numerical calculations in the ANSYS software package.

2.1   Data on the Experimental Research

In 1980, the International Association of Hydraulic Research (IAHR) Ice-Reinforced Issues Section provided recommendations for carrying out experimental simulations that take into account ice peculiarities. Researchers have proposed favorable ratios for the sizes of the experimental model when testing. Many studies have found that the best outcomes can reduce a scale effect. Thus, the geometrical dimensions of the samples influence the ice strength properties in case width B and height H of the beam are equal, and length L is approximately equal to (8–8.5) × H. The IAHR recommendations also indicate similar values: B = (1–2) × H; L = (7–10) × H.

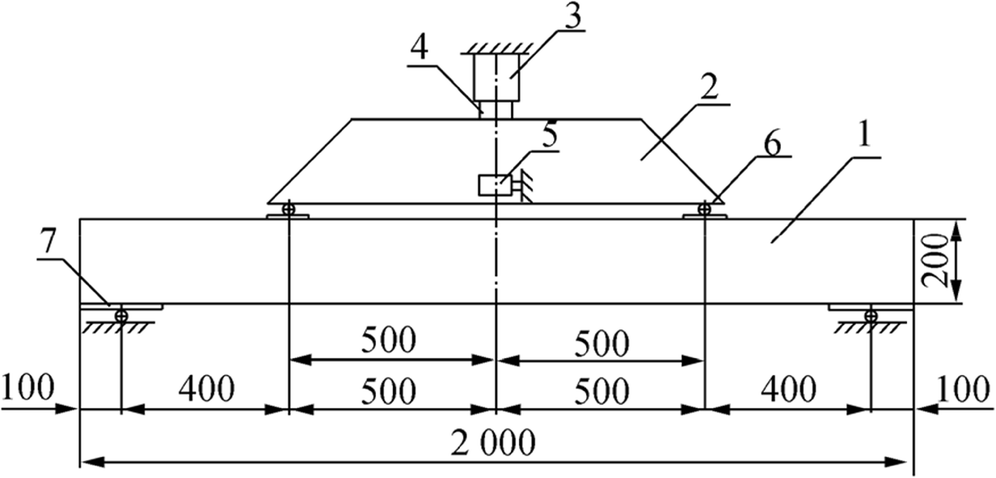
Simulation tests were performed on a multi-operated loading structure designed and assembled especially on that purpose (Figure 1).

Figure  1  Scheme for the experimental installation. (1) ice beam; (2) distribution beam; (3) hydraulic cylinder; (4) weighing indicator SH-20; (5) sensor of vertical displacements LAS-Z; (6) hinged supports of a distribution beam; (7) hinged supports of the ice beam

Download: Full-Size Img

The experimental unit has a load frame consisting of columns, racks, upper and lower beams, a loading unit, and a measurement module. The loading unit includes a hydraulic cylinder 4 with a PN of 9 atm and a distribution power beam of 5. The reinforcement from the loading unit is transmitted to the sample 7 through the pivot mounting 6. The loading system is designed so that it provides a pure bending in the mid-span deflection of the ice sample. The vertical displacements of the mid-span cross-section sample are measured using a noncontact laser LAS-Z by Way Con 3 (Germany) mounted on an independent column. The load influenced by the sample is fixed by a LPA-22t weight gauge with a SH-20 weighing indicator from TOKVES (Russian Federation) 2. The loading rate for all samples is 135 kPa/s.

To produce ice specimens with dimensions L × B × H = 2000 mm × 200 mm × 200 mm (L is length, B is width, and H is height), wooden formwork was constructed with 40-mm-thick boards. A 0.03-mm-thick two-layer polyfilm was placed in the formwork. The reinforcing frame was fixed in the formwork, which ensured its location inside the beam, excluding the reinforcement outcropping. Then, the formwork was filled with water. The liquid was exposed to low atmospheric temperatures (t < 0 ℃) until its complete congelation. Due to meteorological conditions, it took 5–7 days to prepare samples at an ambient temperature from 16 to 28 ℃ below zero. Berry et al. (2017) noted a strong effect of temperature below zero on the compressive and tensile properties of fragile materials. Obviously, this factor has a significant impact on the bearing capacity of ice beams.

The total number of experiments carried out was three. For each series, five samples were simultaneously prepared under the same conditions. The experimental data were averaged; the difference between the results did not exceed 15%. The researchers did not study the impact of temperature change on the sample mechanical characteristics.

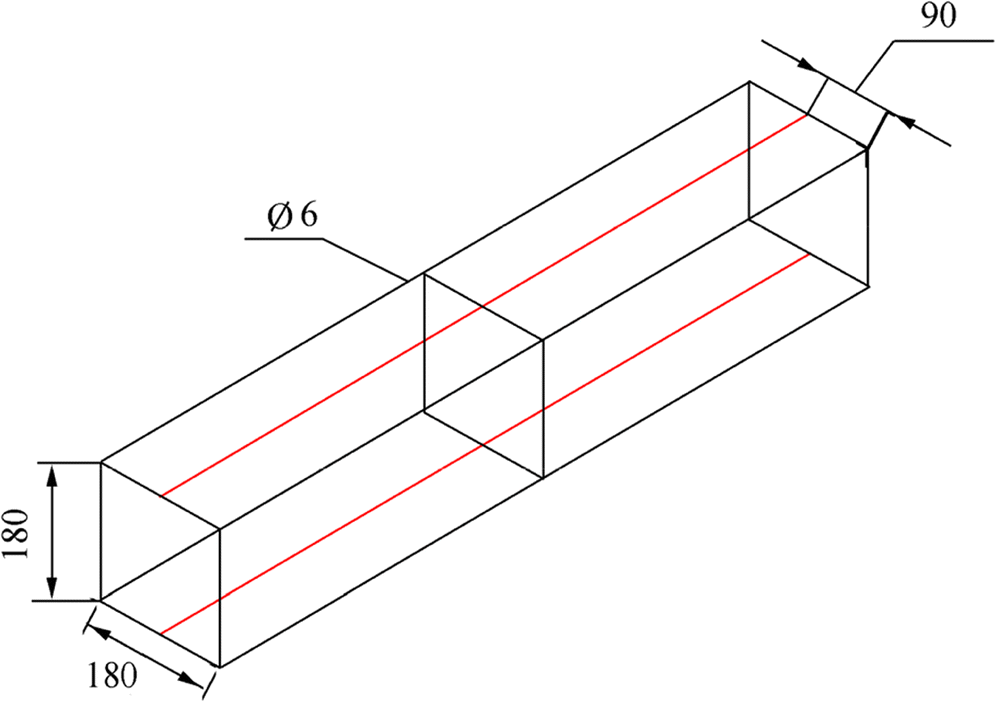
For the ice beam reinforcement, an all-welded reinforcing frame made of A400 steel reinforcement of a deformed section of 6 mm diameter (Figure 2) was used. A series of preliminary experiments on breaking down the ice samples reinforced by surface reinforcement showed that the most optimal thickness of the protective ice layer is 10 mm, which provided the combined action of ice and reinforcement when loading and the maximum bearing capacity. The temperature pattern inside the beam and heat growth coefficient effect that can weaken a bond between steel and ice have not been studied either.

Figure  2  Scheme of the ice beam reinforcement

Download: Full-Size Img

The experiments on the ice beams were carried out to evaluate the impact of the surface reinforcement of the stretched area strengthened with the reinforcing framework on the carrying capacity of the beams under pure flexure.

2.2   Data on the Numerical Research

Ice is expedient to represent both flexible and fragile materials in numerical research (Yu et al. 2007; Xu et al. 2010). The numerical calculation of the stress–strain state of ice samples was carried out in the ANSYS Workbench software system, with the use of the ANSYS Mechanical module. The model consists of 80 160 finite elements and 89 150 nodes. For ice, nonlinear finite element elements SOLID 65 in the form of a hexahedron were used to simulate elements that allowed cracking in tension and calculations based on Willam and Warnke (1974). User functions applying the deformation criterion of Bazant (Bazant and Cedolin 1980) were introduced to display the cracks.

The finite element BEAM188, which is a beam element with flexural rigidity, was used to simulate the work of the reinforcing materials.

The mechanical characteristics of the materials used to enhance ice in the numerical experiments are presented in Table 1: hot-rolled reinforcement А400 (sample No. 1), reinforcement fiberglass composite (sample No. 2), reinforcement carbon (sample No. 3), reinforcement aramid composite fiber (sample No. 4), and reinforcement combined with a combination of glass and basalt (sample No. 5).

On account of the multiplication of the standard characteristics Ϭ_bt and Ϭ_bc by the corresponding coefficients, the calculated mechanical characteristics of the used steel and composite reinforcement are shown in Table 1.

3   Results of the Experimental and Numerical Research

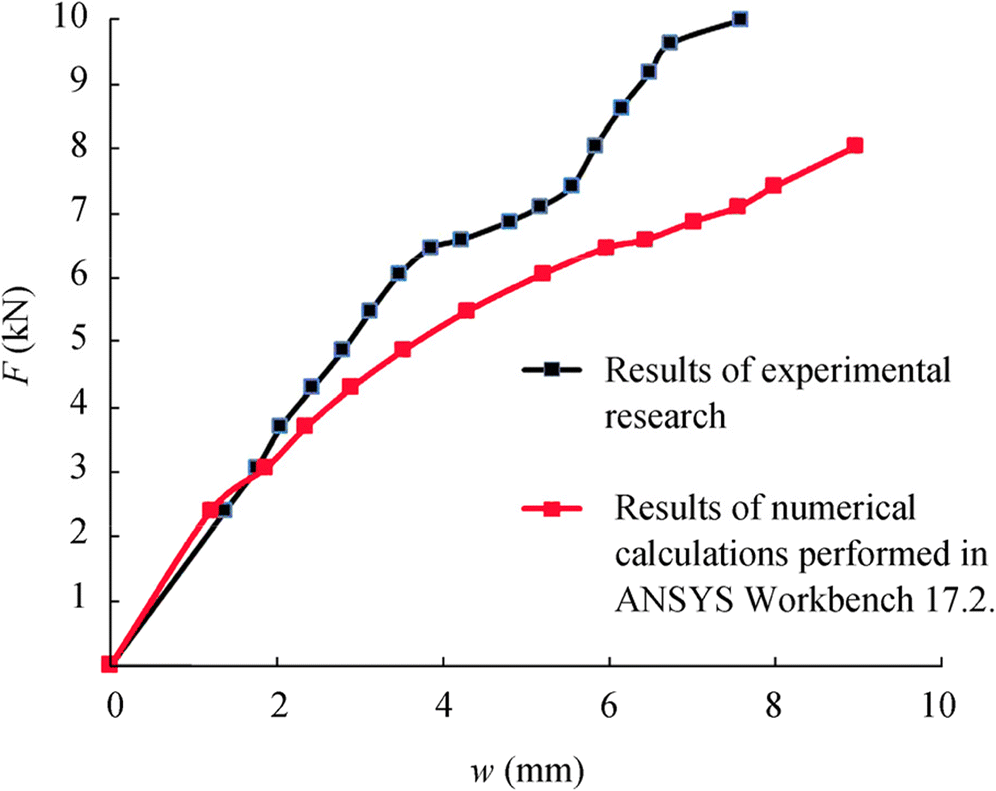
The physicomechanical properties of freshwater and sea ice were examined in the works of Qi et al. (2017), Goldstein and Osipenko (2015), Schulson (2015), Tsuchiya et al. (2013), Weiss and Dansereau (2015), and Kim and Keune (2007). A series of preliminary experiments on the loading of unreinforced ice beams were carried out to evaluate the impact of surface reinforcement on the ultimate load carrying capacity of samples. The experiment results determined the beam deflection caused by the load applied to the test sample. The main results of the experiments are shown in Figure 3. Ice had the following mechanical properties (Kozin et al. 2018): E = 700 MPa, uniaxial compression strength Rb = 0.55 MPa, uniaxial tensile strength Rbt = 0.4 MPa, density ρ = 930 kg/m³, and Poisson's ratio μ = 0.3.

Figure  3  Diagram of the dependence of the deflection of reinforced A400 samples from the load (black line indicates results of the experimental studies; red line indicates results of the numerical calculations performed in ANSYS Workbench 17.2.)

Download: Full-Size Img

3.1   Comparison of the Experimental and Numerical Research

Figure 3 presents the results of the model experiment with a reinforced A400 sample. The maximum load that the samples sustained in the experiment was approximately 10 kN, which significantly exceeded the maximum load that the unreinforced sample could withstand.

At this condition, the formation of through cracks in the tested samples occurred, and the maximum deflection reached 7.59 mm, after which the complete destruction of the beams occurred.

The outcome analysis of the simulation experiments and numerical calculations allowed the authors to conclude that the experimental values had good agreement in the elastic zone. A rapid growth in the sample strain caused by breaking down most part of its cross section and the loss of bearing capacity was taken as a failure criterion. However, the limit of stretching strain in the reinforcement was not reached. The structural failure occurred during the extensive ice cracking because of the moment of flection in the mid-span of the beam.

3.2   Results of the Numerical Research

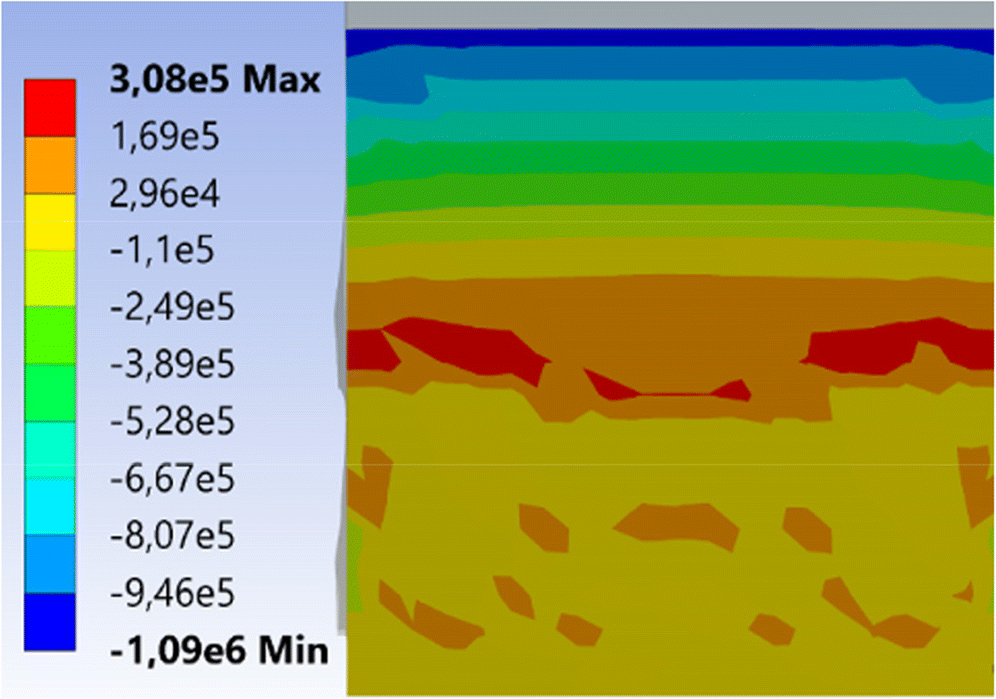
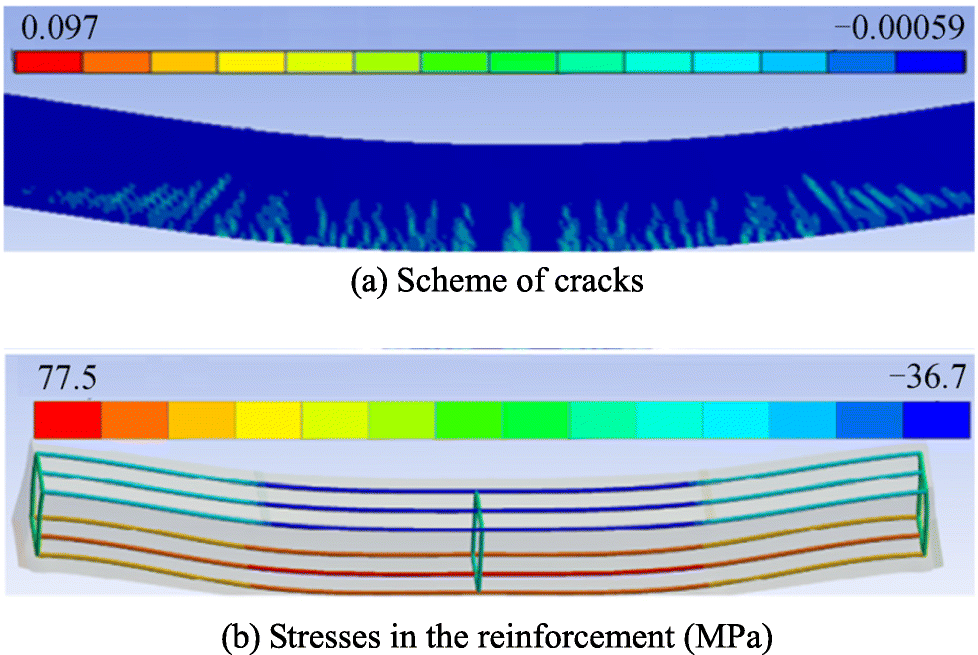
An example of calculating the stress–strain state of reinforced sample No. 1 with an A400 reinforcement in the ANSYS Workbench 17.2 software package is shown in Figures 4 and 5.

Figure  4  Normal stresses upon failure in median section of the ice beam sample No. 2

Download: Full-Size Img

Figure  5  Sample No. 2 during fracture

Download: Full-Size Img

Figure 4 shows the displacement of the neutral axis of the modeled sample (bottom section tensions are within zero) when the breaking load of approximately 6.88 kN.

The pattern of fractures according to Bazant criterion (Bazant and Cedolin 1980) from − 0.00059 to + 0.097 is shown in Figure 5a. Positive values of the criterion correspond to the occurrence and crack opening in the beam tensile region.

As shown in Figure 5b, the stresses in the reinforcement of the stretched part did not reach the yield point and were approximately 51 MPa.

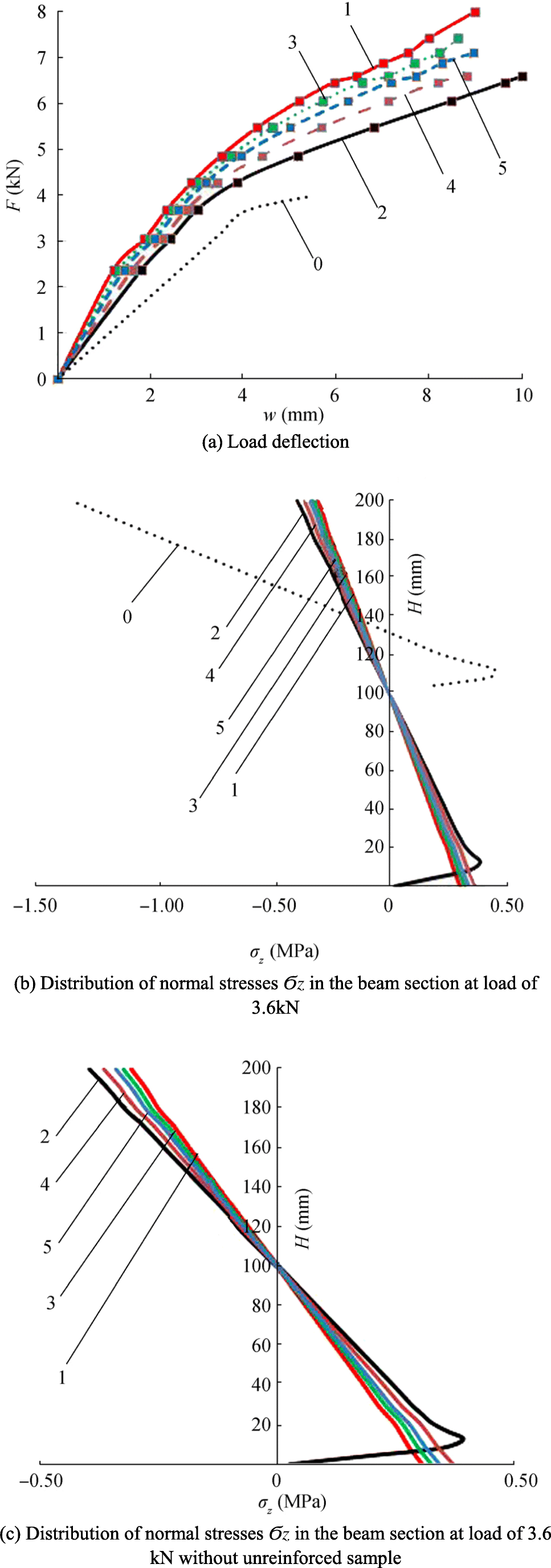
Figure 6a presents the main findings of the numerical calculations. It illustrates the dependences of the load on the kink for samples reinforced with various materials. Figure 6b and c show the stresses in the middle sections of each reinforced specimens caused by the breaking load for a non-reinforced specimen equal to 3.6 kN.

Figure  6  Results of the calculation

Download: Full-Size Img

The outcome analysis suggests that using reinforced frameworks made of composite materials causes great increase in the load carrying capacity of ice samples. The sample, reinforced with steel reinforcement A400, showed a greater load carrying capacity than the other samples. Samples reinforced with fiberglass and aramid composite reinforcement had the lowest bearing capacity.

The superior limits of stress under a load of 3.6 kN for sample Nos. 1–5 were respectively (in MPa) − 0.30, − 0.39, − 0.32, − 0.37, and − 0.34. The fastest growth of direct stress with increasing load was observed in sample No. 2 and the slowest in sample No. 1.

4   Conclusions

On the basis of the research results, the following conclusions can be drawn:

1) The efficiency validation using medites as reinforcing elements can increase the load carrying capacity of systems in the body of ice. The inclusion of various materials in the ice surface increased its strength by 65%–99% for the focused reinforcement scheme.

2) The breaking down of beam samples in all cases occurred due to extensive ice cracking and moment of flection influence in the mid-span. In this case, the yield stress is not reached in the reinforcement material.

3) The outcomes of the simulation experiments and calculations through the finite element approach agreed well within the elastic zone. The deviations between the compared data did not exceed 20% for sags and breaking strength for the samples reinforced with frameworks made of an A400 steel reinforcement.