1   Introduction

Noise pollution has been acknowledged as a serious issue for our safety, and the design of quiet systems has become one of the major concerns which have attracted a great deal of interest in ship cabin engineering (Ankit 2018; Kletschkowski 2012; Wszołek 2017). In many applications, an enclosure's interior noise is caused by external sound sources that transmit to the cavity through flexible plates such as rail carriages (Sadri and Younesian 2015), offices, and automobiles (Du and Zhang 2012). The noises generated by diesel, generator, and waves are more extreme for ship cabins, which dramatically reduces crew and passengers' work performance and comfort (Amromin 2018; Cheer and Elliott 2016; Kandouci and Adjal 2014). Fatigue and comfort for crew and passengers were given more priority during the design of modern ships (Kurt et al. 2016). The noise control of ships becomes an important subject in such a background (Naveen et al. 2014; Borelli et al. 2016; Zhang 2017). To make it easy to analyze the acoustics inside a ship cabin, it is usually simplified as a structural-acoustic coupling cavity, which has been investigated by many researchers. Snyder and Tanaka (1993) analyzed the feedforward control strategies to reduce the interior noise of an enclosure. Noise reduction was analyzed by Pan et al. (1990) and Pan and Hansen (1991) using a force actuator to control noise transmission to a cavity with various noise incident angles. Using both force and acoustic secondary sources, Kim and Brennan (2000) tried to reduce sound transmission into a cavity. Al-Bassyiouni and Balachandran (2005) then used a spherical wave as an incident sound to investigate the interactions between an external and enclosed field of sound. Tanaka and Kobayashi (2006) divided the coupling modes into four categories and handled them separately to effectively reduce the acoustic potential energy. Jin et al. (2009) and Cui and Chen (2012) researched a cavity having two opposite flexible panels and two adjoining flexible panels. The vibroacoustic response of a circular plate backed by a cylindrical enclosure was investigated by Hasheminejad and Shakeri (2017). The finite element method is also used to analyze the coupling mechanism in addition to the analytical method (Wang et al. 2014; Wang et al. 2015). Liang and Yu (2013) analyzed the impact on the cabin acoustic using the finite element of fireproof rock wools with different thicknesses. Xu et al. (2017) used finite element and boundary element methods to predict the ship cabin's sound response.

Most of the previous research, however, focused on coupling systems with one flexible plate on one side. A cavity with one flexible plate, consisting of multiple independently supported subplates, has not been thoroughly investigated, and these types of cavities are very common in ship cabins. For example, some ships cabins have several independently installed glasses, the acoustics inside them is more complicated than the previous analysis. Besides, the previous research optimized the secondary source positions to improve the noise reduction, resulting in a dispersive installation of secondary sources and being difficult to integrate into one control system device in the engineering. In this paper, the theoretical and numerical investigations were performed based on the research of Yang et al. (2017) to analyze the coupling mechanism for a system with multiple independently supported subplates by controlling one subplate each time and implementing closely distributed secondary sources to minimize the transmission of noise.

The rest of the paper is structured as follows: Section 2 introduces theoretical formulations of several self-supported subplate models. The maximum efficacy of the controller is derived from Section 3. Section 4 displays two different model simulations. The findings are presented in Section 5.

2   Analytical Models

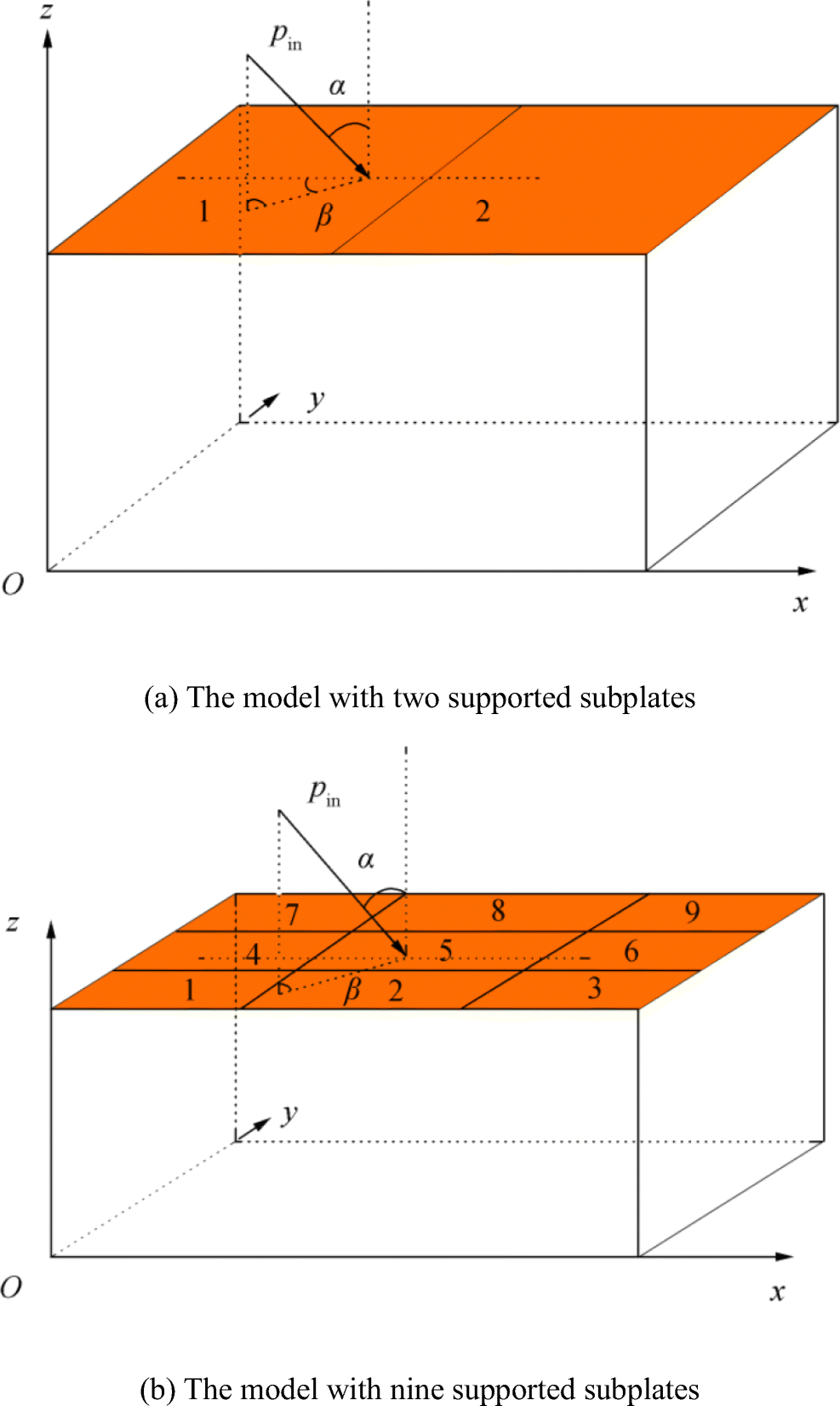
In this section, ship cabins are simplified as structural-acoustic coupling cavities and are investigated theoretically. Only the top plate is flexible and the other five plates are acoustically rigid. Assuming that the cavity has dimensions of L_x×L_y ×L_z. The incident sound simultaneously excites the top flexible plate consisting of different subplates. Figure 1 a and b show two different models, which consist of two and nine individually supported subplates, respectively.

Figure  1  Structural-acoustic coupling models

Download: Full-Size Img

Generally, assuming the top flexible plate consists of N_χ subplates and each subplate has the same size of (L_x/T_x)×(L_y/T_y), that is N_χ = T_x×T_y. The subplates are excited by an external sound p_ext, interior sound p, and N_f forces f_i from a control system simultaneously. Then, vibration of undamped subplate χ can be expressed as given in Eq. (1) (Hansen et al. 2012):

where L[·], ρ_s, h_s, and w_χ(r, t) are the self-adjoint differential operator, the density, thickness, and displacement of the subplate χ; r is the coordinate of interested area of the subplate χ.

If the vibration of subplate χ is expressed using a finite summation of N_s modes as ${w}_{\chi}\left(r,t\right)={\sum}_{i=1}^{N_s}{w}_{\chi, i}{\psi}_{\chi, i}(r)$ and each mode satisfies $L\left[{\psi}_{\chi, i}\right]-{\omega}_{s\chi, i}^2{\rho}_s{h}_s{\psi}_{\chi, i}=0$ (Fahy and Gardonio 2007), the ith structural modal amplitude is derived as:

where ξ_sχ is the damping of subplate χ, ω is the angular frequency of the incident sound, ψ_{χ, i}(r) is the ith structural mode shape function, and ω_{sχ, i} is the ith natural frequency. For a simply supported subplate, its mode shape is defined as ψ_{χ, i}(r) = sin (uπ(x − X_χ)/(L_x/T_x)) sin (vπ(y − Y_χ)/(L_y/T_y)), χ = 1, ⋯N_f, where X_χ and Y_χ are the coordinates of the nearest corner of the subplate χ to the origin in x and y directions, u and v are ith structural modal indices in x and y directions, and M_{χ, i} = ∫_Sρ_sh_sψ_{χ, i}(r)ψ_{χ, i}(r)dr. Since the interior pressure can be expressed as $p\left({r}_e\right)={\sum}_{j=1}^{N_c}{p}_j{\varphi}_j\left({r}_e\right),$ where mode shape function φ_j(σ) = cos (lπx/L_x) cos (mπy/L_y) cos (nπz/L_z), l, m, and n are jth acoustic modal indices in x, y, and z directions, the velocity modal amplitudes of the subplate χ can be written in vector form as:

where Λ_sχis a N_s × N_s diagonal matrix and is defined as ${\Lambda}_{s\chi}\left(i,i\right)=\mathrm{j}\omega /\left({M}_{\chi i}\left({\omega}_{s\chi, i}^2-{\omega}^2+\mathrm{j}2{\xi}_{s\chi}{\omega \omega}_{s\chi, i}\right)\right)$, F_χ is the control force vector defined as ${\boldsymbol{F}}_{\chi }=\left[{f}_{\chi, 1};{f}_{\chi, 2};\cdots; {f}_{\chi, {N}_f}\right]$ and the modal amplitudes of incident sound is ${\boldsymbol{P}}_{\mathrm{int}}=\left[{p}_1;{p}_2;\cdots; {p}_{N_c}\right]$, ${\boldsymbol{Z}}_{s\chi}=\left[{\psi}_{\chi, 1}\left({r}_1\right),\cdots, {\psi}_{\chi, 1}\left({r}_{N_f}\right),\cdots, {\psi}_{\chi, {N}_s}\left({r}_{N_f}\right)\right]$ denotes the structural impedance matrix input and is derived by substituting the coordinate of the excitation forces with the modal shape function of the subplate χ, ${\boldsymbol{G}}_{\chi }=\left[{g}_{\chi, 1};{g}_{\chi, 2};\cdots; {g}_{\chi, {N}_s}\right]$ is the modal amplitude vector of the subplate excited by the incident sound, and g_{χ, i} = ∫_Sp_ext(r, t)ψ_{χ, i}(r)dr. By defining the number coordinates of subplate χ as:

the generalized modal amplitude with a unit incident sound in τ direction can be obtained as:

where τ denotes the direction of x or y; a, n, and u are the length, the number coordinate, and the ith structural modal index of subplate χ in τ direction. The j in Eq. (5) is the imaginary unit and without a specific explanation, it denotes a number in other equations. According to the above analysis, the modal amplitude excited by the incident sound can be expressed as:

where u and v are ith structural modal indices in x and y directions.

B_χ(j, i) in Eq. (3) is the coupling matrix between the ith structural mode of subplate χ and jth acoustic mode of the cavity, which is defined as B_χ (j, i) = ∬_Sφ_j(r)ψ_{χ, i}(r)dr. By expressing the coupling relation between the ith structural mode of subplate χ and the jth acoustic mode of the cavity in τ direction as:

the following formulation can be derived:

The exact coupling matrix expressions are given in the Appendix for two-subplate and nine-subplate models. In compliance with Eq. (8), each subplate will affect the cavity's acoustic modes independently. Previous research divided the relationship of coupling between structural modes and acoustic modes into four categories, and only the modes in the same categories can be coupled with each other. However, the previous coupling relationships cannot hold in the multiple parallel-supported flexible subplates systems. For example, all structural modes will be coupled with the acoustic modes having an odd index in the x-axis.

The inhomogeneous sound equation inside the cavity is:

where N_q is the number of acoustic control sources inside the cavity. Similarly, the mode amplitude of the sound can be written as:

where ${A}_j={\iiint}_V{\varphi}_j^2(r)\mathrm{d}r$ and ξ_p are the damping of the air inside the cavity. The modal amplitudes of the sound can also be written in vector form as:

where Λ_c is a N_c × N_c diagonal matrix and ${\boldsymbol{\varLambda}}_c\left(j,j\right)=\mathrm{j}{\omega \rho}_0/\left({A}_j\left({k}_{p,j}^2-{k}^2+\mathrm{j}2{\xi}_p{kk}_{p,j}\right)\right)$, Z_c is an input acoustic impedance matrix and is defined as ${\boldsymbol{Z}}_c=\left[{\varphi}_1\left({\sigma}_1\right),\cdots, {\varphi}_1\left({\sigma}_{N_q}\right),\cdots, {\varphi}_{N_c}\left({\sigma}_{N_q}\right)\right]$, $\boldsymbol{Q}=\left[{q}_1;{q}_2;\cdots; {q}_{N_q}\right]$ is the acoustic control source strength vector, and N_χ represents the total number of subplates.

By combining Eqs. (3) and (11), the acoustic modal amplitude vector is rewritten as:

3   Minimization of Acoustic Potential Energy

It has been proven that the optimal cost function for controlling interior noise is acoustic potential energy, which is defined as ${E_p}\left( \omega \right) = \iiint {_V|p\left( {r,\omega } \right)2/\left( {4{\rho _0}c_0^2} \right){\rm{d}}r}$ and can be rewritten as (Nelson et al. 1987):

where Λ is a diagonal matrix and $\boldsymbol{\varLambda} \left(i,i\right)={A}_i/\left(4{\rho}_0{c}_0^2\right)$. By substituting Eq. (12) into Eq. (13), we can derive the following formulation:

where $\boldsymbol{G}=\left[{G}_1;\cdots; {G}_{N_{\chi }}\right]$, $\boldsymbol{Z}={\boldsymbol{\varLambda}}_c/\left({\boldsymbol{I}}_{N_c}+{\boldsymbol{\varLambda}}_c{\sum}_{\chi =1}^{N_{\chi }}{\boldsymbol{B}}_{\chi }{\boldsymbol{\varLambda}}_{s\chi}{\boldsymbol{B}}_{\chi}^{\mathrm{T}}\right)$, T = [B_χΛ_SχZ_Sχ, Z_cχ], and $\boldsymbol{C}=\left[{\boldsymbol{F}}_{N_{\chi }};\boldsymbol{Q}\right]$, χ denotes the subplate of being controlled, $\boldsymbol{X}=\left[{\boldsymbol{B}}_1{\boldsymbol{\varLambda}}_{S1},\cdots, {\boldsymbol{B}}_{N_{\chi }}{\boldsymbol{\varLambda}}_{SN_{\chi }}\right]$. By minimizing Eq. (14), the optimal output of the controller is derived as:

4   Simulation Results and Discussion

This section presents the results of the control mechanisms of the investigated multiple subplates and cavity coupling models, including the various control configurations, explored. All the following simulations were conducted based on the cabin coupling relationship and subplates analyzed using MATLAB in Sections 2 and 3. The models used here are a two-subplate model (cavity 1) shown in Figure 1a and a nine-subplate model (cavity 2) shown in Figure 1b. The basic parameters of the two cavities and incident angle (α, β) of unit noise are listed in Tables 1 and 2. The dimensions of two cavities are 2.34 m (L_x) ×0.9 m (L_y)×1.5 m (L_z) and 3.51 m (L_x)×2.7 m (L_y) ×1.5 m (L_z), respectively. The first ten modal frequencies of the subplate and two cavities are listed in Table 3.

4.1   Two-Subplate Model

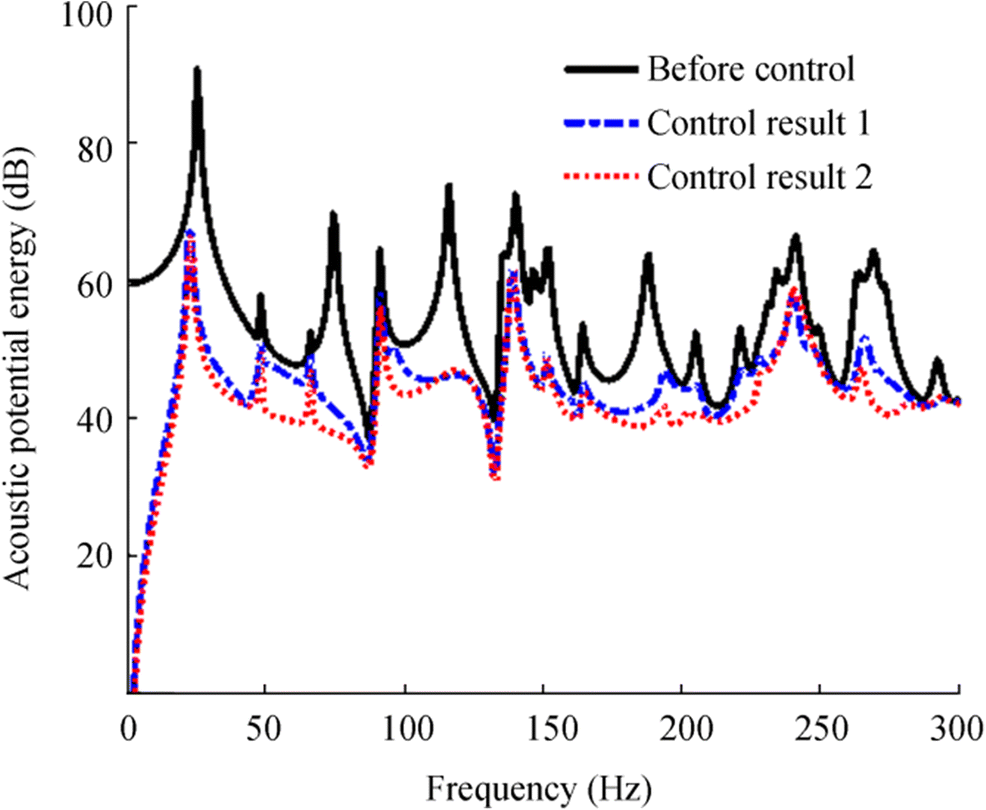
Two control strategies are introduced in this subsection to control the incident sound transmission into a cavity by two independently supported parallel subplates. One of the strategies uses one force and one speaker as actuators, and their installation positions were (0.195 × L_x, 0.205 × L_y, 1.5) and (0.195 × L_x, 0.205 × L_y, 1.35). The other strategy adopts three force actuators and their installation locations were (0.195 × L_x − 0.05, 0.205 × L_y − 0.05, 15), (0.195 × L_x + 0.05, 0.205 × L_y − 0.05, 1.5), and (0.195 × L_x, 0.205 × L_y + 0.05, 1.5). Due to the symmetry of the coupling system, only the subplate 1 is controlled and the acoustic potential energy is shown in Figure 2 with a reference energy of 10⁻¹² J.

Figure  2  The acoustic potential energy before and after control of cavity 1

Download: Full-Size Img

The control results of 1 and 2 in Figure 2 represent the outcomes of the two control strategies. The first includes the use of one force and one speaker, while the second involves the use of secondary sources of three force actuators. After the control, the residual acoustic potential energy of the two control strategies is dramatically reduced, and some cavity-dominated peaks such as at 74 Hz and 116 Hz disappeared. When the sound transmission is reduced by three force actuators, the acoustic potential energy reduction is more distinct both at the cavity and subplate dominated levels, which means that the force actuators can achieve substantial noise reduction without the use of acoustic secondary sources.

To investigate the control mechanism, the kinetic energy of each flexible subplate is defined as:

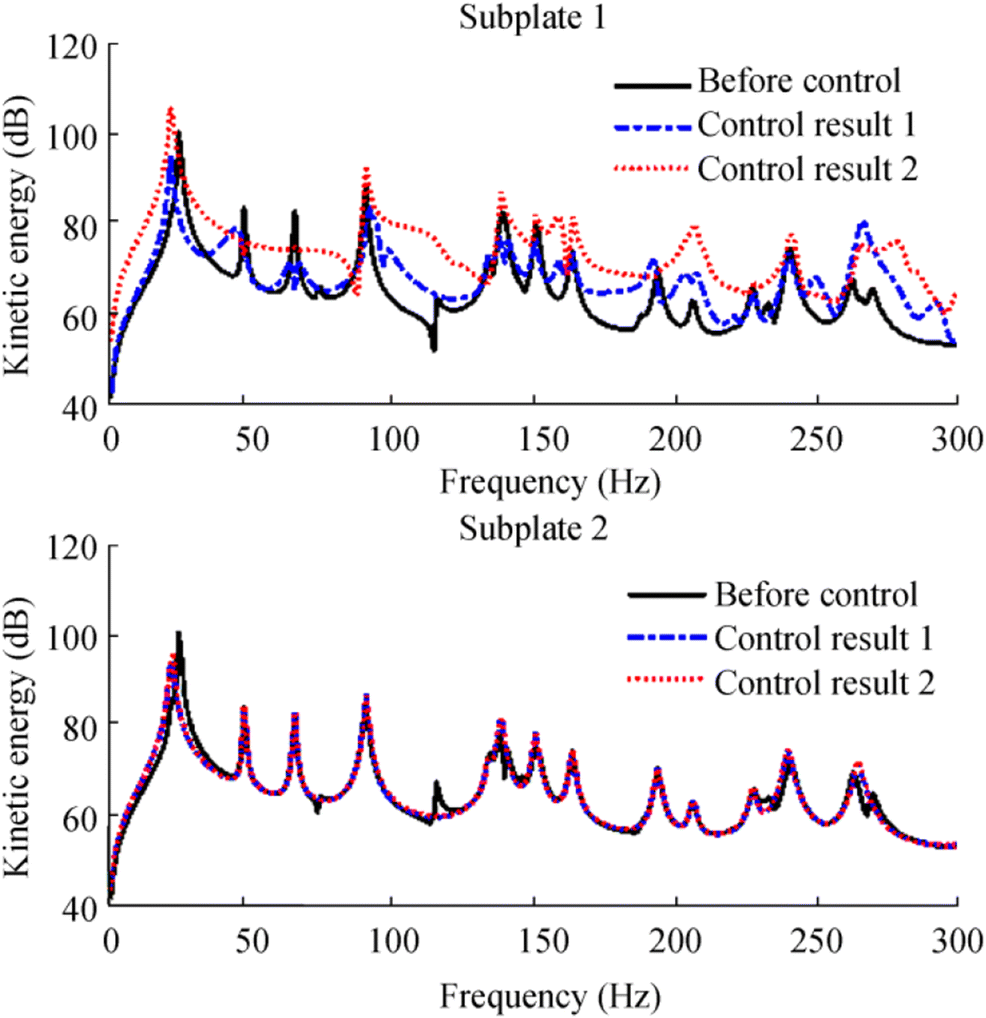
Before and after control, the kinetic energy of the two subplates is shown in Figure 3. Since the actuators were installed on the subplate 1, its kinetic energy increased after control, and the increased kinetic energy becomes more evident when three force actuators are used. Meanwhile, the kinetic energy of the second subplate changes slightly after control.

Figure  3  The kinetic energy of two subplates before and after control

Download: Full-Size Img

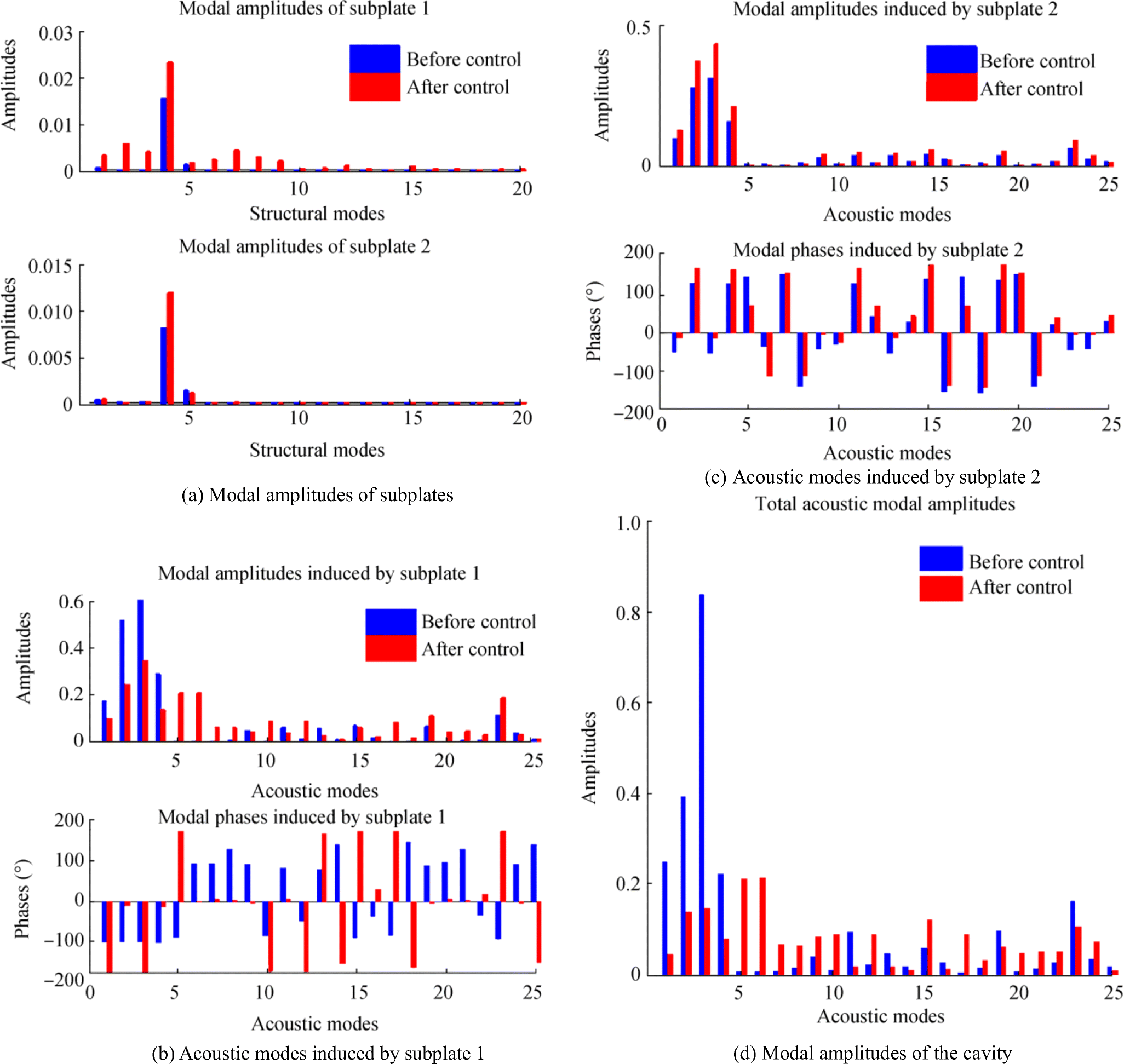
To further explore the control mechanism, the modal amplitudes of two subplates, the acoustic modal amplitudes of the cavity, the acoustic modal amplitudes, and phases induced by two subplates at 91 Hz of using three force actuators are presented in Figure 4, where the acoustic modal amplitudes induced by subplate χ is defined as:

Figure  4  The modal amplitudes and phases of cavity 1 at 91 Hz

Download: Full-Size Img

Figure 4 a shows the modal amplitudes of subplate 1 and subplate 2 with actuators placed on subplate 1. All the structural modal amplitudes of subplate 1 were increased after control and the fourth modal amplitude of subplate 2 was also increased. However, the acoustic modal amplitudes of the first four dominating modes due to the contribution of subplate 1 were reduced, while the acoustic modal amplitudes of the first four dominating modes from the contribution of subplate 2 were increased, which are shown in Figure 4 b and c. This phenomenon can be explained by checking the phases of two subplates shown in Figure 4 b and c. The phases of the acoustic modes induced by the two subplates were changed after the control, and the differences between them were about 180°, in particular, the first four modes. The first four modal amplitudes of the cavity were reduced by superimposing the contributions of two subplates, which is shown in Figure 4d. Therefore, the variation of the acoustic modal amplitudes induced by two subplates is to change their phases, and the control system's behavior in the multiple supported subplates is not to reduce the radiation of the controlled subplates themselves but to cancel the radiation of all subplates.

4.2   Nine-Subplate Model

Because force actuators can achieve satisfactory results, model 2 shown in Figure 1b uses only three force actuators to control noise transmission in this subsection. Because of the system's symmetry, only subplates 1, 2, and 5 were individually controlled. The actuators' positions on subplate 1 were (0.13 × L_x − 0.05, 0.0.137 × L_y − 0.05, 15), (0.13 × L_x + 0.05, 0.137 × L_y − 0.05, 1.5), and (0.13 × L_x, 0.137 × L_y + 0.05, 1.5). When the actuators are installed on subplates 2 or 5, the same relative positions were adopted.

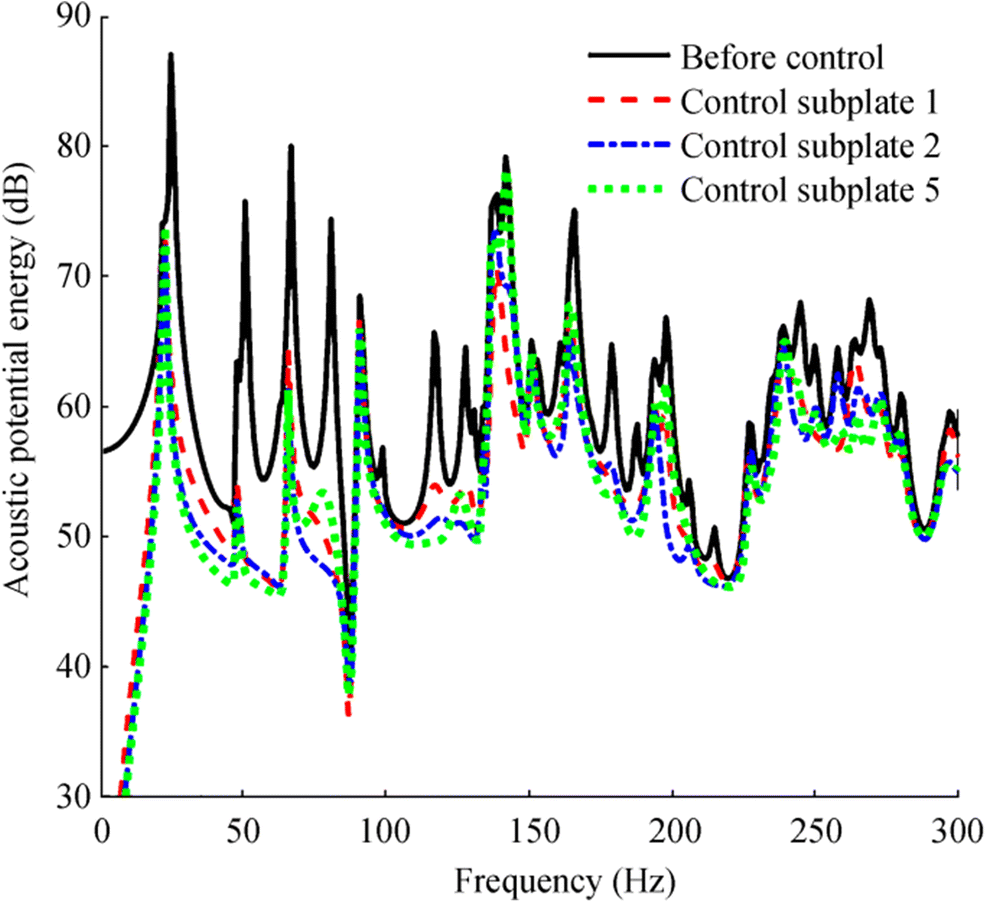
The acoustic potential energy curves obtained by controlling various subplates are shown in Figure 5. It can be seen that the control results are similar by controlling subplates 1, 2, and 5. All the internal noise is reduced particularly below 130 Hz. Among the three control results, most of the cavity-dominated peaks were reduced after control such as at 51 Hz, 87 Hz, 117 Hz, and 128 Hz, and various subplate-dominated peaks were also attenuated but not completely canceled. Also, after control, the frequencies corresponding to the subplate-dominated peaks were shifted back to the subplates' natural frequencies. For example, the first peak of acoustic potential energy occurs at 25 Hz before control. But, it is shifted to 23 Hz after control, which is the subplate's first natural frequency. It suggests that when we use force actuators to minimize the transmission of sound into a cavity, the control system mechanism aims to reduce the coupling between flexible subplates and the cavity, which explains why acoustic potential energy peaks controlled by the cavity can be totally canceled. Comparing Figure 5 with Figure 2, it can be observed that the results of the controls showed a deterioration as a result of the increase in subplates.

Figure  5  The acoustic potential energy of cavity 2 before and after control

Download: Full-Size Img

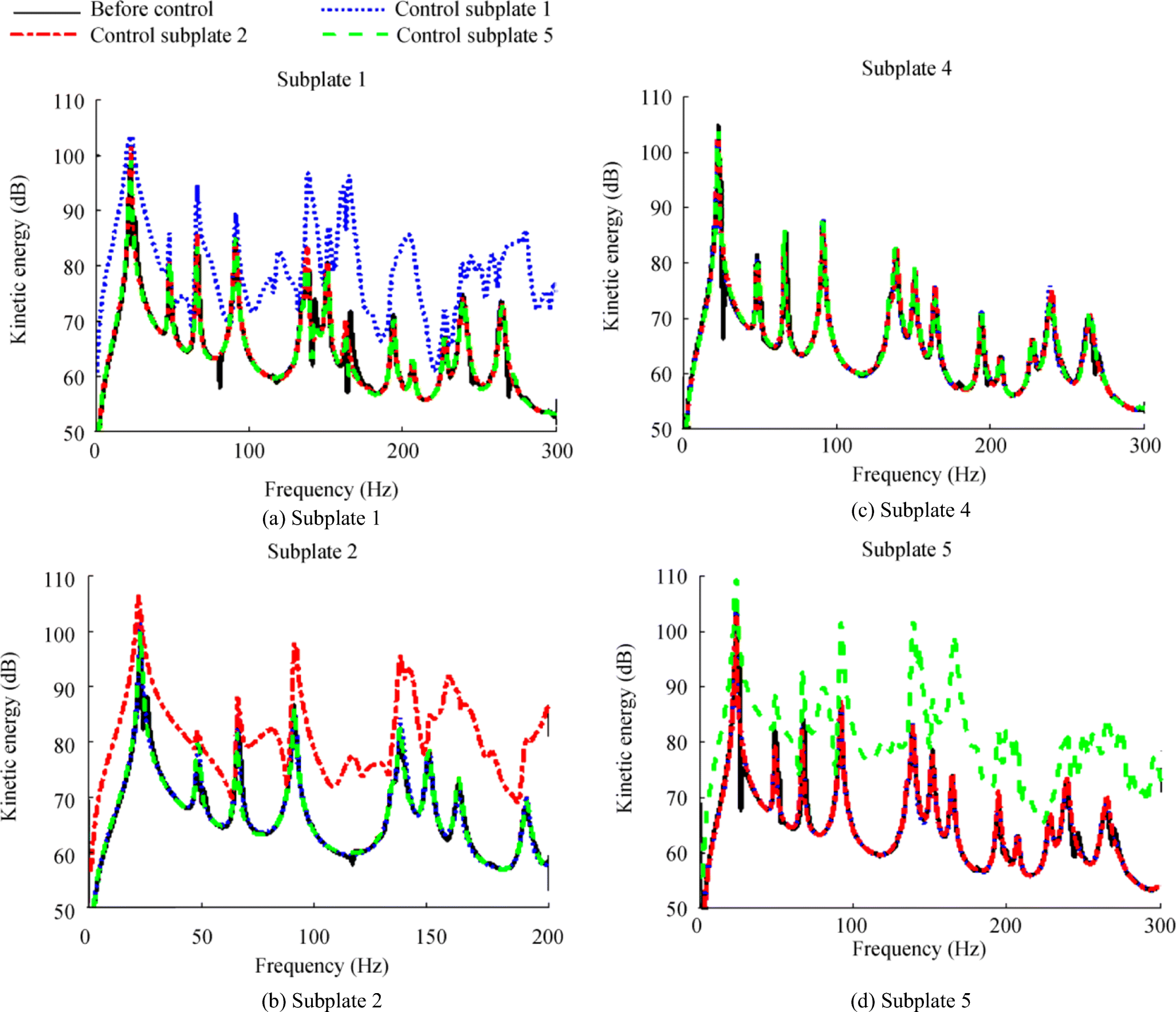
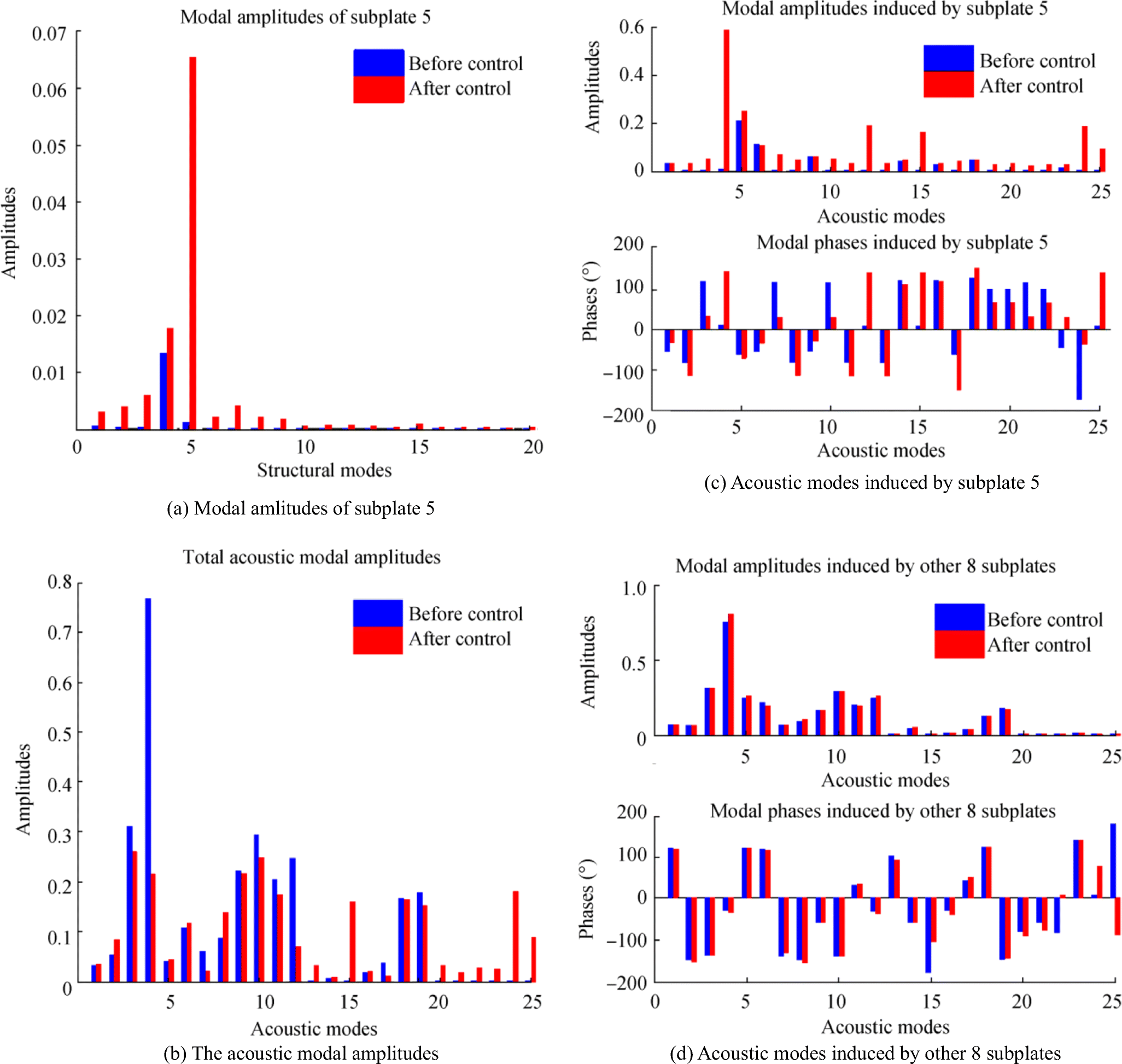
Model 2 subplates' kinetic energy is shown in Figure 6, and only four kinetic energy subplates are shown because of similarity. It can be seen that the kinetic energy of the controlled subplate is increased after control, and the increased energy is much greater than that of model 1, which means that the more subplate of a cavity, the more kinetic energy is increased for the controlled subplate. Notwithstanding, the uncontrolled subplates' kinetic energy remains at a similar level. The control of subplate 5 was taken as an example to investigate the control mechanism, and the modal vibration amplitudes of subplate 5, the acoustic modal amplitudes, the phases caused by subplate 5, and other subplates are shown in Figure 7.

Figure  6  The kinetic energy of four subplates of model 2 before and after control

Download: Full-Size Img

Figure  7  The modal amplitudes and phases of model 2 at 91 Hz

Download: Full-Size Img

Figure 7 a shows the structural modal amplitudes of subplate 5 before and after control at 91 Hz. Since the excitation frequency is near the fourth natural frequency of the subplate, the fourth modal amplitude is larger than others before the control. It can be observed from Figure 7b that the dominated acoustic mode of the cavity is the fourth mode. After the control, all subplate 5 modal amplitudes were increased, especially the fifth modal amplitude, which increases more than 60 times. And, there is also a significant increase in the fourth acoustic mode amplitude caused by subplate 5 and is shown in Figure 7c. The acoustic modal amplitudes from the contribution of the other 8 subplates are shown in Figure 7d.

To reduce this modal amplitude, since the dominated mode of the cavity is the fourth acoustic mode, an idealistic solution generates an acoustic modal amplitude of the same magnitude but opposite phase to the original one. Because the fourth modal acoustic amplitude induced by subplate 5 is very small before control, the vibration pattern of subplate 5 must be changed to increase the amplitude. Table 4 shows part of the subplate 5 and cavity coupling coefficients, where the numbers in the first column represent the subplate mode number and indicate the cavity's acoustic mode. It can be seen that the structural modes having a coupling relationship with the fourth acoustic mode are fifth and tenth structural modes. Since the excitation frequency is close to the subplate's fifth natural frequency, the fifth mode is easy to excite, which explains why subplate 5's fifth modal amplitude and subplate 5's fourth acoustic mode amplitude is significantly increased after control as shown in Figure 7 a and c. After superposition, radiations from subplate 5 and other 8 subplates canceled each other. So the dominating modal amplitudes of the cavity were reduced, which can be observed from Figure 7b.

5   Conclusions

In this paper, active control sound transmission through multiple independently supported flexible subplates in simplified ship cabins was studied, and the coupling relationships were formulated between each subplate and the cavity. To reduce the acoustic potential energy of the two-subplate and nine-subplate models, different control methods were introduced, and their control results were compared. The results of the simulation show that force actuators can achieve adequate noise reduction efficiency in modes controlled by both the subplate and the cavity without the use of secondary acoustic sources. The force actuators of the control system are effective in controlling the transmission of sound into a structural-acoustic coupling system by reducing the coupling between the flexible subplates and the cavity. In the future, the active noise control system could be integrated into one device with several force actuators and installed on the flexible subplates to reduce the transmission of noise.

Also, when actuators are used to attenuate noise transmission into a cavity via multiple subplates, the control results of the installation of actuators on the central subplate are relatively better, especially to reduce low-frequency noise. However, the results of noise reduction will deteriorate if there are more subplates in a cavity. Besides, the controlled subplate's vibration pattern is modified after regulation to improve the radiation of itself to cancel the radiation of the other subplates instead of the radiation of itself. At the same time, the controlled subplate's vibration increases, and the higher the subplates of a cavity, the greater the increase in kinetic energy. Therefore, for a cavity with many subplates, it is appropriate to control more than one subplates. And thus, the control efficiency could be improved, and the controlled subplate's kinetic energy increment could be relieved.

Appendix

The coupling matrixes between the two subplates and the cavity for model 1 are:

The coupling matrixes between the nine subplates and the cavity for model 2 are: