2. Department of Marin Tech., AmirKabir University of Tech, Tehran, Iran
1 Introduction
Added resistance in traditional ship design is accounted for using a rough proportional increase in calm water resistance of about 20%-40%. However, in modern ship design it is becoming increasingly important to accurately calculate the added resistance in waves, as this greatly affects the propulsion system selection and ship's performance. As an important part of ship design, consideration of added resistance is extremely important for both shipowners and operators, particularly in relation to economic implications.
The increase of resistance has long been recognized as being important, and many papers have studied associated problems using two main methods, far-field and near-field methods. In far-field methods, diffracted and radiated wave energy is considered by the total momentum change and leads to a steady added resistance force. In the near-field method, the added resistance force is obtained from direct integration of hydrodynamic, steady, and second-order pressure acting on the wetted ship's surface. The far-field method approach was first introduced by Maruo (1957), who then elaborated on it in subsequent years (1960, 1963). The radiated energy approach of Grritsma and Beukelman was introduced in 1972, and this basically follows Marou's approach. Strom-Tejson et al. (1973) then determined large discrepancies between numerical results from different theoretical approaches and experimental data. By applying Grritsma and Beukelman's method, but using the STF seakeeping strip theory, Salvesen (1974) obtained good results when investigating ship hull forms. Therefore, it is considered that if a more exacting calculation of ship motion is used, results of all the alternative approaches used for added resistance can be improved.
Iwashita and Ohkusu (1992) applied Maruo's method to improve the far-field formulation and the Kochin function using a 3D pulsating and traveling source Green function method; very good results were obtained for the added resistance of a fully submerged spheroid. Liu and Papanikolaou (2010) used the 3D panel method to solve a basic seakeeping problem; they calculated the first order potential and the linear ship responses, both of which are required in the added resistance calculation. The paper aimed to apply use of the B-spline based panel method to the 3D forward speed ship motion problem, which is based on the transient Green function.
The result of the radiation calculation has been applied to the exact calculation of added resistance. Hsin et al. (1994) developed a 2D higher order panel method based on B-splines, in which the geometry and singularity distribution were defined by the B-spline; Green's theorem then was applied at selected collocation points to solve unknown flow parameters. Maniar (1995) used B-splines to develop a higher order 3D panel method, where the potential and geometry of the body were allowed any degree of continuity. This developed method was then successfully applied to the zero-speed frequency-domain radiation-diffraction problem. Hsiung (2002) introduced a panel-free method and applied it to solve the radiation problem in the time domain; he then subsequently extended the method for the diffraction problem (Qiu et al., 2004). In this method, the body boundary was represented by a NURBS surface, and the integral equations (based on the source-strength distribution) were globally discretized over the body surface by Gaussian quadrature. In addition, due to the desingularization procedure adopted, it was not necessary to express the source strength and velocity potential using spline-representation. Gao et al. (2008) applied a NURBS-based high-order panel method for three-dimensional radiation and diffraction problems with forward speed.
As is evident from the above, a considerable amount of research has been focused on developing B-spline-based solution schemes to solve a variety of wave-structure and free-surface flow problems. In this paper, we firstly discuss the radiation problem in unbounded fluid and then calculate the added resistance using Kashiwagi's formula and the Kochin functions approach. Experimental and analytical results are then compared to validate the approach.
2 CalculationWhen a ship oscillates in relation to waves, it supplies energy to the surrounding water; this energy increases resistance (Fig. 1) that is primarily transmitted in waves radiating from the ship. The supplied energy is due to the damping of oscillatory motions. Hydrodynamic damping is dominant in heave and pitch motions, which are the biggest contributors to added resistance. Viscous damping can therefore be neglected, which means that added resistance can be considered as a non-viscous phenomenon and that potential theory can be used. In addition, the radiation and the reflection of incident waves, which are referred to as diffraction, cause added resistance.
|
| Figure 1 Radiating waves due to oscillation |
A Cartesian coordinate system, o-xyz, moving together with a body at a constant speed, U, along the positive x-axis is adopted. The origin is located on the undisturbed free surface, and the z-axis points upwards. The assumptions of linearity and the inviscid flow with irrotational motion allow the velocity potential Φ to be written in the form,
| $\Phi \left({x, y, z, t} \right) = - Ux + Re\left\{ {{{\rm{e}}^{ - {\rm{i}}\omega t}}\left[ {\mathop \sum \limits_{{\rm{j}} = 1}^6 {\eta _j}{\Phi _j}\left({x, y, z} \right) + \eta \left({{\Phi _0} + {\Phi _7}} \right)} \right]} \right\}$ | (1) |
where Øj=(j=1, 2, ..., 6) is the radiation potential corresponding to oscillations of the body in six degrees of freedom, ηj=(j=1, 2, ..., 6) is the corresponding motion amplitude, Ø0 is the potential of incoming waves, η0 is the incoming wave amplitude, Ø7 is the potential due to the diffracted waves of amplitude, and η7 and ω are the encounter frequencies. In an infinite depth water, Ø0 is given by
| ${\Phi _0} = \frac{{{\rm{i}}g}}{{{\omega _0}}}{{\rm{e}}^{[{K_0}z - {\rm{i}}{K_0}(x\cos \gamma + y\sin \gamma)]}}$ | (2) |
where K0=ω2/g is the wave number, ω0 is the natural frequency of the incoming wave, γ is the incident angel of the incoming wave, and g is gravitational acceleration.
For the radiation and diffraction problems of a body in unbounded fluid, the potential function satisfies the Laplace equation and the boundary condition as follows,
| $ {\nabla ^2}{\Phi _j} = 0\;\;\;j = 1, 2, \cdots, $ | (3) |
on the undisturbed free surface, SF (z=0),
| $ - {\omega ^2}{\Phi _j} - 2{\rm{i}}\omega U\frac{{\partial {\Phi _j}}}{{\partial x}} + {U^2}\frac{{{\partial ^2}{\Phi _j}}}{{\partial {x^2}}} + g\frac{{\partial {\Phi _j}}}{{\partial z}} = 0\;\;\;j = 1, 2, \cdots, 7$ | (4) |
on the body surface, SB
| $\frac{{\partial {\Phi _j}}}{{\partial n}} = \left\{ {\begin{array}{*{20}{c}} {{\rm{i}}\omega {n_j}j = 1, 2, \cdots, 6}\\ {\frac{{\partial {\Phi _0}}}{{\partial n}}j = 7} \end{array}} \right.$ | (5) |
where
| ${n_1}, {n_2}, {n_3}) = \boldsymbol{n}\left({{n_4}, {n_5}, {n_6}} \right) = \boldsymbol{X} \times {\boldsymbol{n}}$ | (6) |
and where X is the position vector over of a point on SB.Moreover, a radiation condition must be imposed at infinity,
| $ {\Phi _j} \to 0\;\;j = 0, 1, 2, \cdots, 7 $ |
where
and there are no waves generated by the unsteady flow far in front of the body.
Once the unknown potential, Øj, is solved, Øj can be used to calculate the complex function,
| $ H\left( {{k}_{j}},\theta \right)=\iint\limits_{{{S}_{B}}}{\left( \Phi \frac{\partial }{\partial n}-\frac{\partial \Phi }{\partial n} \right)}{{G}_{{{j}'}}}\left( \theta \right)\text{d}s $ | (7) |
where
| ${G_{j'}}\left(\theta \right) = \exp \left[ {{k_{j'}}\left(\theta \right)z + {\rm{i}}{k_{j'}}\left(\theta \right)\left({x{\rm{cos}}\theta y{\rm{sin}}\theta } \right)} \right]$ | (8) |
and
| ${k_{j'}}\left(\theta \right) = \frac{{{K_0}}}{2}\frac{{1 - 2\Omega {\rm{cos}}\theta {}_ - ^ + \sqrt {1 - 4\Omega {\rm{cos}}\theta } }}{{{\rm{co}}{{\rm{s}}^2}\theta }}\begin{array}{*{20}{c}} {}&{} \end{array}\left({\begin{array}{*{20}{c}} { + :j' = 1}\\ { - :j' = 1} \end{array}} \right)$ | (9) |
In the ab ove equation, θ is the angle of the elementary waves generated by the body, and Ω=
Following Maruo (1963), the added resistance may be expressed by the above Kochin function as
| $ \begin{align} &{{R}_{\text{aw}}}=\frac{\rho }{8\text{ }\!\!\pi\!\!\text{ }}\left\{ \int_{-\text{ }\!\!\pi\!\!\text{ }/2}^{-{{a}_{0}}}{+\int_{{{a}_{0}}}^{\text{ }\!\!\pi\!\!\text{ }/2}{-\int_{\text{ }\!\!\pi\!\!\text{ }/2}^{2\text{ }\!\!\pi\!\!\text{ }/2}{{}}}} \right\}{{\left| H\left({{k}_{1}}, \theta \right) \right|}^{2}}\frac{{{k}_{1}}\left({{k}_{1}}\text{cos}\theta -k\text{cos}\gamma \right)}{\sqrt{1-4\Omega \text{cos}\theta }}\text{d}\theta \\ &+\frac{\rho }{8\text{ }\!\!\pi\!\!\text{ }}\int_{{{a}_{0}}}^{2\text{ }\!\!\pi\!\!\text{ }-{{a}_{0}}}{{{\left| H\left({{k}_{2}}, \theta \right) \right|}^{2}}\frac{{{k}_{2}}\left({{k}_{2}}\text{cos}\theta -{{k}_{1}}\text{cos}\gamma \right)}{\sqrt{1-4\Omega \text{cos}\theta }}\text{d}\theta } \\ \end{align} $ | (10) |
where γ is the incident angle, ρ is density of sea water and α0 is the critical angle
| $ {{\alpha }_{0}}=\text{arc}\cos \left(\frac{1}{4\Omega } \right)\ \text{for}\ \Omega >\frac{1}{4}\ \text{and}\ {{\alpha }_{0}}=0\ \text{for}\ \Omega \le 1/4 $ |
From application of Green's function, the potential function can be represented over the body boundary surface as follows,
| $ \iint\limits_{S}{\left[ \Phi \left(q \right)\frac{\partial G\left(p;q \right)}{\partial {{n}_{q}}}-G\left(p;q \right)\frac{\partial \Phi \left(q \right)}{\partial {{n}_{q}}} \right]\text{d}S+2\text{ }\!\!\pi\!\!\text{ }\Phi \left(p \right)=0} $ | (11) |
This integral represents the potential at a field point, p, by distributing sources, q, on a surface, S, of the fluid domain. G here is the Green's function, which for the present problem can be taken as simple source.
Here we make reference to Landweber and Macagno (1969) to deal with the free-surface flow problems of surface ships, in which the method of images is used to automatically satisfy the linear boundary condition on the free surface and the radiation condition at infinite. Using the image method, the Green function can be written as
| $ G=\frac{1}{R}+\frac{1}{{{R}'}} $ | (12) |
If the source point is defined at
| $ 1/R=1/\sqrt{{{\left(x-{{x}_{1}} \right)}^{2}}+{{\left(y-{{y}_{1}} \right)}^{2}}+{{\left(z-{{z}_{1}} \right)}^{2}}} $ | (13) |
and R' is the image of R.
3 B-spline-based methodHere the body surface, SB, is divided into a number of large patches to solve the problem using the B-spline. Over each patch, Ø and
| $\boldsymbol{\bar X}\left( {{p_{\rm{B}}}} \right) = \mathop \sum \limits_{i = 1}^{n + 1} \mathop \sum \limits_{j = 1}^{m + 1} {A^{\bar x}}\left( {i,j} \right)N{\left( u \right)_{i,g}}M{\left( v \right)_{i,h}}$ | (14) |
in which N(u)i, g and M(v)i, h are open uniform B-spline basis functions of degrees g and h, respectively, Ax(i, j) is known as the control point, and (n + 1) and (m + 1) are the total number of the control points along the u and v parametric directions, respectively. Thus, the surface is described by (n + 1)×(m + 1) number of control points. The basis function should be firstly specified, then (n + 1)×(m + 1) number of equations are needed to solve finding the control points.
For i=n + 1 physical data points in the u parametric direction, the parameter value at the lth data point is
| $ u_{1}^{s}=0, \begin{matrix} {} \\ {} \\ \end{matrix}u_{i}^{s}=\frac{\mathop{\sum }_{g=2}^{i}\left| {{Q}_{g, s}}-{{Q}_{g-1, s}} \right|}{\mathop{\sum }_{g=2}^{r}\left| {{Q}_{g, s}}-{{Q}_{g-1, s}} \right|}, \begin{matrix} {} \\ {} \\ \end{matrix}i=2, n+1 $ | (15) |
| ${{u}_{i}}=\frac{1}{m+1}\underset{s=0}{\overset{m}{\mathop \sum }}\, u_{i}^{s}\begin{matrix} {}&{} \\ \end{matrix}i=1, \cdots, n+1$ |
Similarly, for j=m+1 physical data points in a υ parametric direction, the parameter value at the kth data point is
| $v_{1}^{r}=0, \begin{matrix} {} \\ {} \\ \end{matrix}v_{j}^{r}=\frac{\mathop{\sum }_{g=2}^{j}\left| {{Q}_{r, g}}-{{Q}_{r, g-1}} \right|}{\mathop{\sum }_{g=2}^{s}\left| {{Q}_{r, g}}-{{Q}_{r, g-1}} \right|}, \begin{matrix} {} \\ {} \\ \end{matrix}j=2, m+1 \\{{v}_{j}}=\frac{1}{n+1}\underset{r=0}{\overset{m}{\mathop \sum }}\, v_{j}^{r}\begin{matrix} {}&{} \\ \end{matrix}j=1, \cdots, m+1 $ | (16) |
Open uniform B-spline basis functions in the u parametric direction are defined as
| $ {{N}_{i, 0}}\left(u \right)=\left\{ \begin{matrix} 1&{{u}_{i}}<u<{{u}_{i+1}} \\ 0&\text{others} \\ \end{matrix} \right. $ |
| $ {{N}_{i, p}}\left(u \right)=\frac{u-{{u}_{i+1}}}{{{u}_{i+p}}-{{u}_{i}}}{{N}_{\text{i}, g-1}}\left(u \right)+\frac{{{u}_{i+p+1}}-u}{{{u}_{i+p+1}}-{{u}_{i+1}}}{{N}_{i+\text{1, }g-1}}$ | (17) |
Similarly in the v parametric direction, they are defined as
| $ {{M}_{i, \text{0}}}\left(v \right)=\left\{ \begin{matrix} 1&{{v}_{i}}<<{{v}_{i+1}} \\ 0&\text{others} \end{matrix} \right. $ |
| $ {{M}_{i, p}}\left(v \right)=\frac{v-{{v}_{i+1}}}{{{v}_{i+p}}-{{v}_{i}}}{{M}_{\text{i}, g-1}}\left(v \right)+\frac{{{v}_{i+p+\text{1}}}-v}{{{v}_{i+p\text{+1}}}-{{v}_{i+1}}}{{M}_{i+\text{1}, g-\text{1}}} $ | (18) |
Furthermore, the potential Ø and normal velocity Øn on the body surface are expressed by the same basis function,
| $\Phi =\underset{i=1}{\overset{n+1}{\mathop \sum }}\, \underset{j=1}{\overset{m+1}{\mathop \sum }}\, {{A}^{\Phi }}\left(i, j \right){{N}^{k}}{{\left(u \right)}_{i, g}}{{M}^{l}}{{\left(v \right)}_{i, h}}$ | (19) |
| ${{\Phi }_{n}}=\underset{i=1}{\overset{n+1}{\mathop \sum }}\, \underset{j=1}{\overset{m+1}{\mathop \sum }}\, {{A}^{{{\Phi }_{n}}}}\left(i, j \right){{N}^{k}}{{\left(u \right)}_{i, g}}{{M}^{l}}{{\left(v \right)}_{i, h}}$ | (20) |
To solve Equation 11 numerically, the boundary surface is subdivided into a number of panels and the integral over the panels is evaluated by applying the Gauss-Legendre quadrature. Here the source density distribution is replaced by discrete points called source points; the Gaussian points are used as the source points and the collocation points. Assuming that the body surface is subdivided into MB and NB panels in the u and υ directions, respectively, and KB, LB Gaussian points are used in the u, v directions on each panel, equation 11 can be written in the discretized form for u=uI and υ=υJ as (Zangeneh et al., 2012):
| $\begin{align} & 2\text{ }\!\!\pi\!\!\text{ }\left\{ \sum\limits_{i=1}^{n+1}{\sum\limits_{j=1}^{m+1}{{{A}^{\Phi }}}\left( r,i,j \right){{N}^{k}}{{\left( {{u}_{I}} \right)}_{i,g}}{{M}^{l}}{{\left( {{v}_{J}} \right)}_{i,h}}} \right\}+ \\ & \left\{ \sum\limits_{i=1}^{n+1}{\sum\limits_{j=1}^{m+1}{{{A}^{\Phi }}}\left( r,i,j \right)\int_{u=0}^{{{u}_{n=1}}}{\int_{w=0}^{{{w}_{m=}}_{1}}{{{N}^{k}}{{\left( {{u}_{I}} \right)}_{i,g}}{{M}^{l}}{{\left( {{v}_{J}} \right)}_{i,h}}\left| J \right|}}}\text{d}u\text{d}v \right\} \\ & =\sum\limits_{i=1}^{n+1}{\int_{u=0}^{{{u}_{n=1}}}{\int_{w=0}^{{{w}_{m=}}_{1}}{\left[ \sum\limits_{i=1}^{n+1}{\sum\limits_{j=1}^{m+1}{{{A}^{\Phi }}}\left( r,i,j \right){{N}^{k}}{{\left( {{u}_{I}} \right)}_{i,g}}{{M}^{l}}{{\left( {{v}_{J}} \right)}_{i,h}}} \right]G\left( {{u}_{I}}\text{,}{{v}_{J}}\text{,}{{u}_{i}}\text{,}{{v}_{j}} \right)\left| J \right|}}}\text{d}u\text{d}v \\ \end{align}$ | (21) |
for
| $n+1={{M}_{B}}\times {{K}_{B}}\begin{matrix} {}&{} \\ \end{matrix}m+1={{N}_{B}}\times {{L}_{B}}$ |
The normal n on the body surface is defined as follows,
| ${{\boldsymbol{X}}_{u}}=\underset{i=1}{\overset{n+1}{\mathop \sum }}\, \underset{j=1}{\overset{m+1}{\mathop \sum }}\, {{A}^{{\boldsymbol{x}}}}\left(i, j \right){N}'{{\left(u \right)}_{i, g}}M{{\left(v \right)}_{i, h}}$ | (22) |
| ${{\boldsymbol{X}}_{v}}=\underset{i=1}{\overset{n+1}{\mathop \sum }}\, \underset{j=1}{\overset{m+1}{\mathop \sum }}\, {{A}^{{\boldsymbol{x}}}}\left(i, j \right)N{{\left(u \right)}_{i, g}}{N}'{{\left(v \right)}_{i, h}}$ | (23) |
| $\boldsymbol{n}=\frac{{{{\boldsymbol{X}}}_{u}}\times {{{\boldsymbol{X}}}_{v}}}{\left| {{{\boldsymbol{X}}}_{u}}\times {{{\boldsymbol{X}}}_{v}} \right|}$ | (24) |
| $\left| \boldsymbol{J} \right|=\left| {{{\boldsymbol{X}}}_{u}}\times {{{\boldsymbol{X}}}_{v}} \right|$ | (25) |
All integrations are carried out using a 6×6 Gauss-Legendre quadrature,
| $ \begin{align} & 2\text{ }\!\!\pi\!\!\text{ }\left\{ \sum\limits_{i=1}^{n+1}{\sum\limits_{j=1}^{m+1}{{{A}^{\Phi }}}\left( r,i,j \right){{N}^{k}}{{\left( {{u}_{I}} \right)}_{i,g}}{{M}^{l}}{{\left( {{v}_{J}} \right)}_{i,h}}} \right\}+\sum\limits_{i=1}^{n+1}{\sum\limits_{j=1}^{m+1}{{{A}^{\Phi }}}\left( r,i,j \right)} \\ & \sum\limits_{{{m}_{0}}=1}^{{{M}_{B}}}{\sum\limits_{{{n}_{0}}=1}^{{{N}_{B}}}{\left\{ \sum\limits_{{{i}_{0}}=1}^{{{K}_{B}}}{\sum\limits_{{{j}_{0}}=1}^{{{L}_{B}}}{{{N}^{k}}{{\left( {{u}_{i}} \right)}_{i,g}}{{M}^{l}}{{\left( {{v}_{j}} \right)}_{i,h}}{{G}_{n}}\left( {{u}_{I}}\text{,}{{v}_{J}}\text{,}{{u}_{i}}\text{,}{{v}_{j}} \right)\left| J \right|\left( {{u}_{i}},{{v}_{i}} \right){{W}_{i}}{{W}_{j}}}} \right\}}} \\ & =\sum\limits_{{{m}_{0}}=1}^{{{M}_{B}}}{\sum\limits_{{{n}_{0}}=1}^{{{N}_{B}}}{{}}} \\ & \left\{ \sum\limits_{{{i}_{0}}=1}^{{{K}_{B}}}{\sum\limits_{{{j}_{0}}=1}^{{{L}_{B}}}{\left( \sum\limits_{i=1}^{n+1}{\sum\limits_{j=1}^{m+1}{{{A}^{{{\Phi }_{n}}}}}\left( r,i,j \right){{N}^{k}}{{\left( {{u}_{i}} \right)}_{i,g}}{{M}^{l}}{{\left( {{v}_{j}} \right)}_{i,h}}} \right)G\left( {{u}_{I}}\text{,}{{v}_{J}}\text{,}{{u}_{i}}\text{,}{{v}_{j}} \right)\left| J \right|\left( {{u}_{i}},{{v}_{i}} \right){{W}_{i}}{{W}_{j}}}} \right\} \\ & I=1,2,\cdots {{M}_{B}}\times {{K}_{B}}\ J=1,2,\cdots {{N}_{B}}\times {{L}_{B}}\ i=\left( {{m}_{0}}-1 \right){{K}_{B}}+{{i}_{0}} \\ & j=\left( {{n}_{0}}-1 \right){{l}_{B}}+{{j}_{0}}\ {{W}_{i}}=\frac{{{b}_{{{m}_{0}}}}-{{a}_{{{n}_{0}}}}}{2}{{w}_{1{{i}_{0}}}}\ {{W}_{i}}=\frac{{{c}_{{{m}_{0}}}}-{{d}_{{{n}_{0}}}}}{2}{{w}_{2{{j}_{0}}}} \\ \end{align} $ | (26) |
where
| $ \begin{align} & {{H}_{j}}\left( {{k}_{{{j}'}}},\theta \right)=\underset{u=0}{\overset{u={{u}_{\text{max}}}}{\mathop \int }}\,\underset{v=0}{\overset{v={{v}_{\text{max}}}}{\mathop \int }}\, \\ & \left\{ \left( \underset{i=1}{\overset{n+1}{\mathop \sum }}\,\underset{j=1}{\overset{m+1}{\mathop \sum }}\,{{A}^{{{\Phi }_{n}}}}\left( i,j \right){{N}^{k}}{{\left( u \right)}_{i,p}}{{M}^{l}}{{\left( v \right)}_{i,q}} \right){{G}_{n{j}'}}\left( \theta ;u,v \right)- \right. \\ & \left. \left( \underset{i=1}{\overset{n+1}{\mathop \sum }}\,\underset{j=1}{\overset{m+1}{\mathop \sum }}\,{{A}^{{{\Phi }_{n}}}}\left( i,j \right){{N}^{k}}{{\left( u \right)}_{i,p}}{{M}^{l}}{{\left( v \right)}_{i,q}} \right){{G}_{{{j}'}}}\left( \theta ;u,v \right) \right\} \\ \end{align} $ | (27) |
A FORTRAN-based computer code is been developed for the calculation and applied to the unbounded flow problem of a spheroid to verify the present method. The added resistance of a submerged and half-immersed spheroid is calculated and the numerical results are compared with the published analytical solution, as well as with experimental results. The method is used to solve the added resistance of different hull forms, and the results obtained are compared with analytical and experimental data.
4.1 Submerged spheroidIwashita and Ohkusu (1992) studied a submerged spheroid with length to breadth ratio L/B=5 and draught to breadth ratio d/B=0.75, where the draught, d, is measured from the free surface to body center. The proposed method is applied to calculate the added resistance of this spheroid with forward speed, U, in regular incoming wave of head seas. It is of note that the Froude number is defined as
| Ohkusu | B-spline method with different number of panels | ||||
| 4×4 | 6×4 | 8×4 | 10×4 | ||
| (Error %) | (Error %) | (Error %) | (Error %) | ||
| 0.63 | 0.2467 | 0.2432 | 0.2450 | 0.2463 | 0.2461 |
| (1.41) | (0.68) | (0.16) | (0.24) | ||
| 0.8 | 0.3456 | 0.3369 | 0.3412 | 0.3428 | 0.3428 |
| (1.73) | (1.22) | (0.81) | (0.81) | ||
| 1.0 | 0.2987 | 0.2950 | 0.2963 | 0.2985 | 0.2984 |
| (1.21) | (0.87) | (0.06) | (0.10) | ||
| 1.1 | 0.2489 | 0.2450 | 0.2463 | 0.2480 | 0.2495 |
| (1.55) | (1.04) | (0.36) | (0.24) | ||
| 1.2 | 0.2068 | 0.2022 | 0.2045 | 0.2061 | 0.2077 |
| (2.22) | (1.11) | (0.38) | (0.44) | ||
| 1.4 | 0.1009 | 0.1001 | 0.1004 | 0.1008 | 0.1008 |
| (0.79) | (0.49) | (0.007) | (0.007) | ||
| Ohkusu | B-spline method with different number of panels | ||||
| 4x4 | 6x4 | 8x4 | 10x4 | ||
| (Error %) | (Error %) | (Error %) | (Error %) | ||
| 0.63 | 0.2389 | 0.2341 | 0.2359 | 0.2382 | 0.2395 |
| (1.97) | (1.25) | (0.29) | (0.25) | ||
| 0.8 | 0.2745 | 0.2720 | 0.2736 | 0.2743 | 0.2743 |
| (0.91) | (0.32) | (0.07) | (0.07) | ||
| 1.0 | 0.2345 | 0.2314 | 0.2327 | 0.2336 | 0.2349 |
| (1.33) | (0.76) | (0.38) | (0.17) | ||
| 1.1 | 0.1784 | 0.1770 | 0.1781 | 0.1787 | 0.1790 |
| (0.78) | (0.16) | (0.16) | (0.20) | ||
| 1.2 | 0.1476 | 0.1452 | 0.1465 | 0.1673 | 0.1473 |
| (1.63) | (0.74) | (0.20) | (0.20) | ||
| 1.4 | 0.1109 | 0.1102 | 0.1004 | 0.1110 | 0.1111 |
| (0.63) | (0.18) | (0.009) | (0.18) | ||
The added resistance of a half-immersed (floating) spheroid with a length to beam L/B=5 is studied in Kashiwagi (1997). The present method is then used to calculate the added resistance of this spheroid, and is applied to calculate the added resistance of this floating spheroid at Fn=0.2. The panels from 0.5 ship lengths upstream to 1.5 ship lengths downstream cover the free surface domain. The transverse extension of the free surface is 1.5 that of the body width. A significant deviation between a variety of numerical results and experimental values is observed for this case, which is theoretically and practically a difficult benchmark case because of the complicated above still water level wetting the half-immersed spheroid. However, Kashiwagi presented good results for this case with his enhanced unified slender body theory.

|
| Figure 2 Added resistance of half-immersed spheroid at Fn=0.2 |
Journee' (1992) tested and reported a series of Wigley hulls. In this section the validation of Wigley-Ⅲ is presented and the hull surface is defined by the following expression
| $\frac{y}{b}=\left(1-{{\left(\frac{x}{l/2} \right)}^{2}} \right)\left(1-{{\left(\frac{z}{D} \right)}^{2}} \right)\left(1+0.2{{\left(\frac{x}{l/2} \right)}^{2}} \right)$ | (28) |
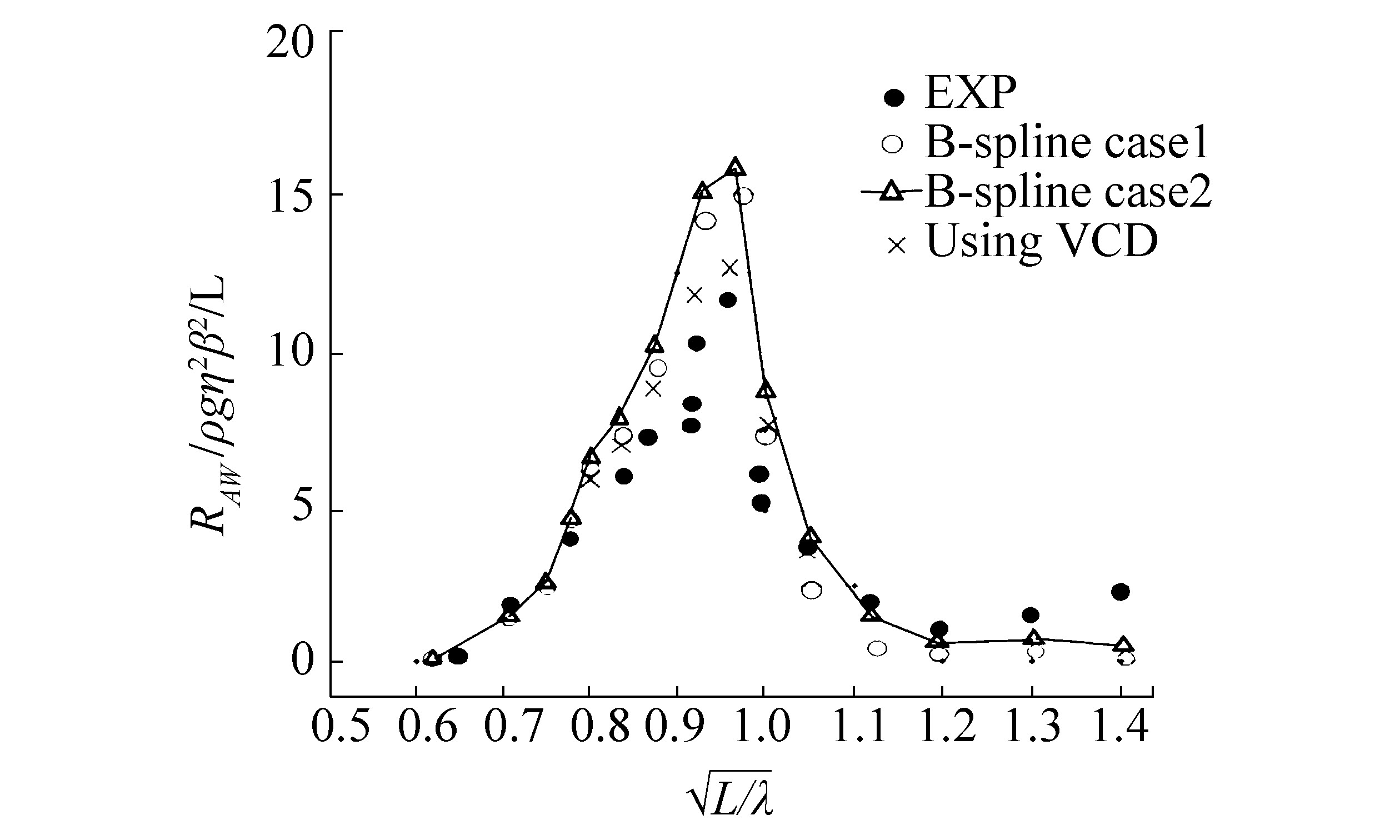
where 2b/l=0.1 and D/l=0.0625.8×4 panels on the body surface and 6×6 Gaussian points are used. Two cases of computations are performed. The results obtained for Fn=0.3 are shown in Fig. 3; in Case 1 only the radiation potential is used to compute the added resistance but in Case 2 both radiation and diffraction potentials are used. It is evident that the numerical values in Case 1 are underpredicting the added resistance in smaller wavelengths; this means that the diffraction potential induced resistance dominates for higher wave frequencies. In the short wave condition, the nonlinear effects increase because incident waves are fully reflected and the diffraction waves are mainly created close to the bow (Seo et al. 2014). In the present method, the nonlinear effects are neglected, and a considerable difference between numerical results and experimental data in shorts waves is observed. For example, in the region of resonance, the numerical values over-predict the added resistance. This is mainly due to the use of linear seakeeping methods based on potential theory, which under-estimate the damping coefficients, results in predictions of higher first-order motions in the vicinity of resonance. Another reason for the numerically predicted higher amplitude of motion and added resistance close to the resonance reign could be from the effects of nonlinearity above the still water level hull form; this is not considered in linear frequency domain methods. Papanikolaou et al. (2000) tried to overcome this problem by including additional viscous damping to potential theory terms. However, adding viscous damping effects to the first-order calculations for the Wigley hull results in a reduction of peak values for added resistance, which is much closer to results of the experimental measurements, as shown in Fig. 3.

|
| Figure 3 Added resistance of Wigley in head seas at Fn=0.3 |
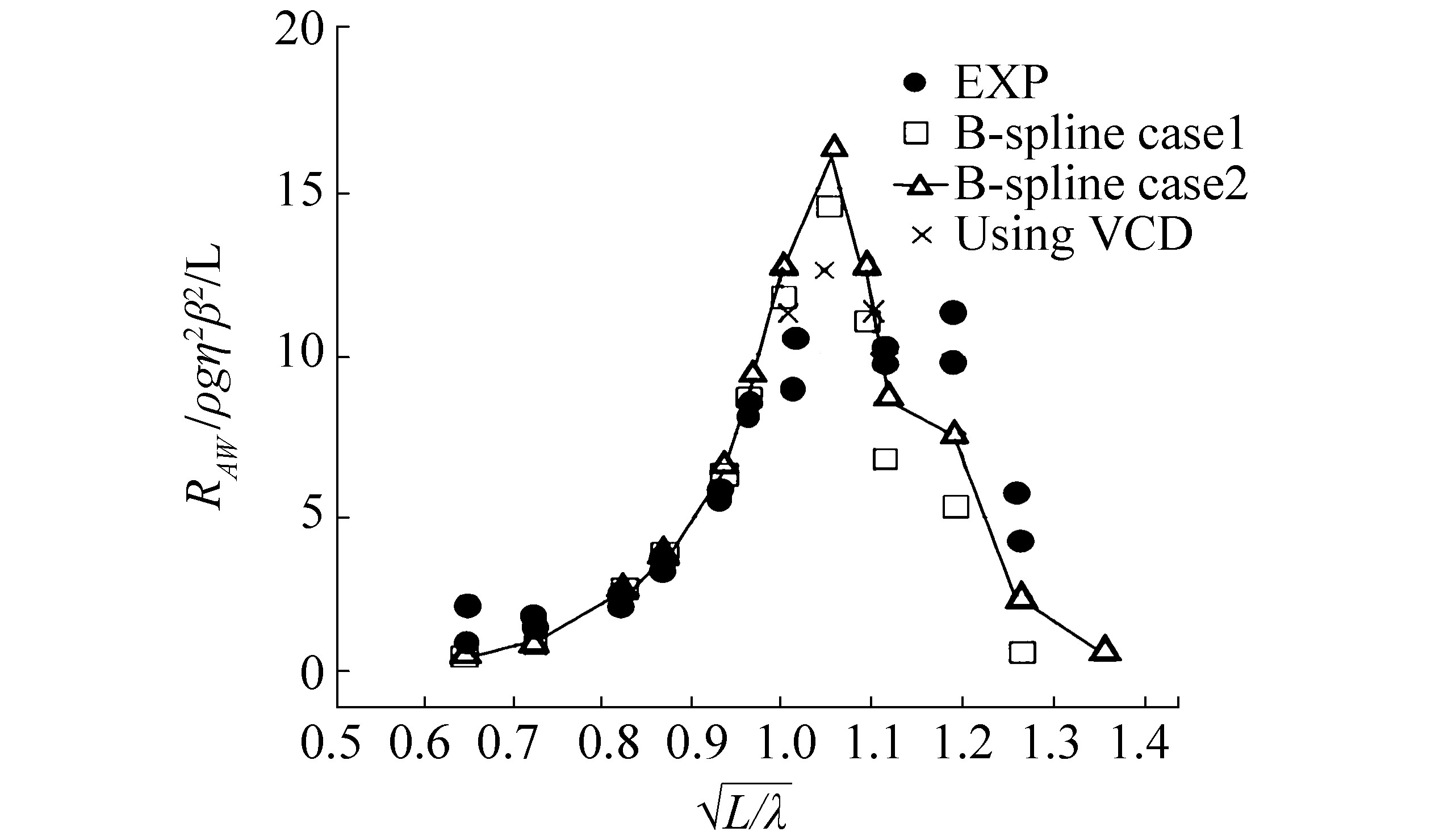
Calculations are conducted for a Series 60 hull with a block coefficient of 0.60; this has previously been studied by many researchers (e.g., StrØm-Tejsen et al. (1973)). The body surface is described by 1600 collocation points. The obtained results for Fn=0.266 and Fn=0.283 are presented in Figs. 4-5. In the low frequencies region, very good agreement between numerical results and experimental data is observed. Once again, as in the Wigley hull case, numerical results of Case 1 strongly under-predict the experimental measurements in the short wavelength. This means that neglecting the diffraction potential when calculating causes under-prediction of the amount of added resistance after the resonance region. Over prediction of peak values in the resonance region is due to using the potential theory based method. Once again, as in the Wigley hull case, numerical results without any viscous correction strongly over predict the experimental measurements. However, introduction of the viscous damping term in the first-order calculations results in a considerable reduction of the peak values of added resistance, which is much closer to results of experimental measurements.

|
| Figure 4 Added resistance on a S60 hull in head seas at Fn=0.266 |
|
| Figure 5 Added resistance on a S60 hull in head seas at Fn=0.283 |
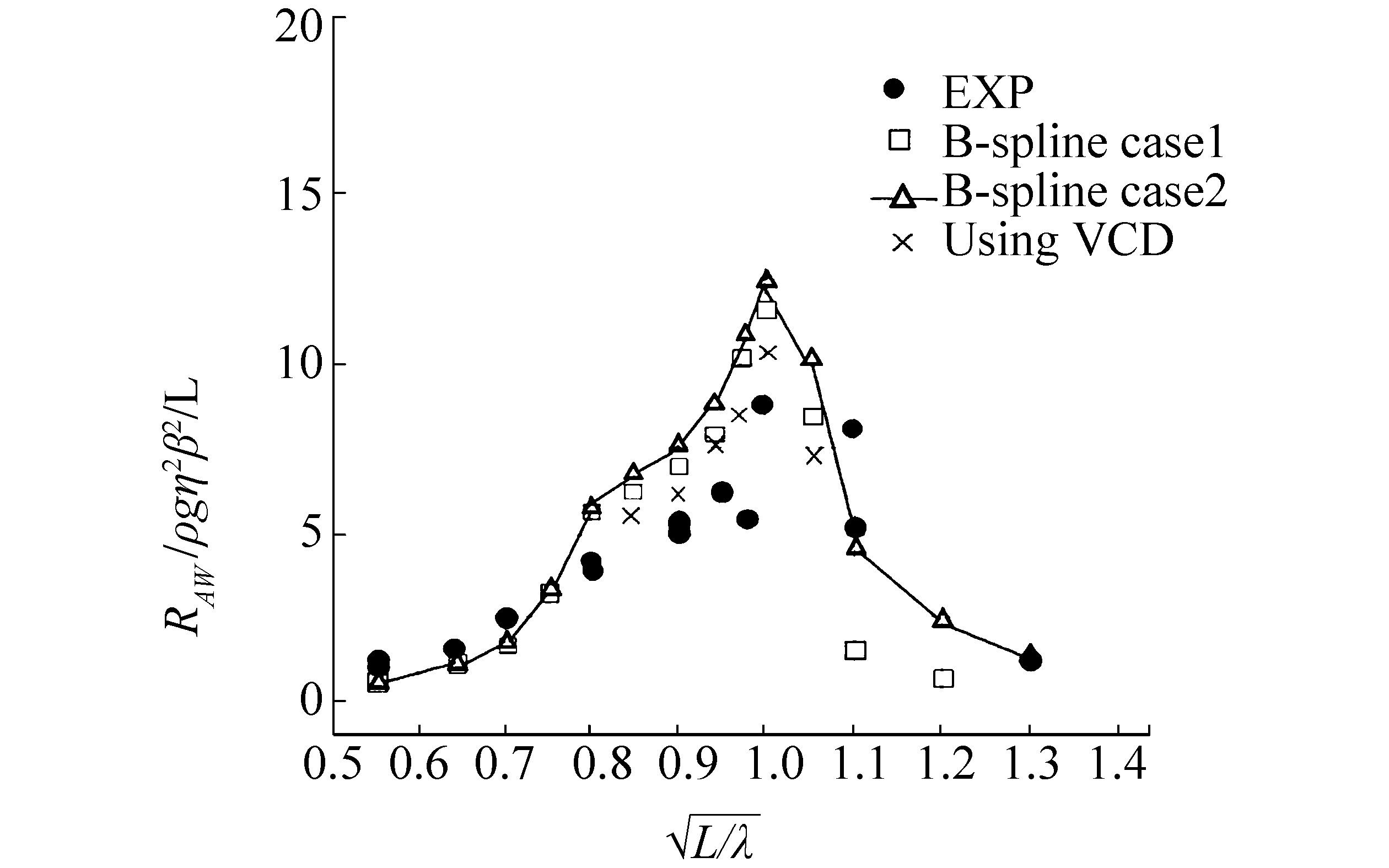
Calculations are then performed for Destroyer hull forms. A penalization consisting of 8×4 panels on the body are used for the calculations; added resistance results are shown in Figs. 6-7 for Fn=0.25 and Fn=0.35. Once again, by adding viscose damping to the first order calculations, the agreement between the current method and the experimental data improves dramatically.

|
| Figure 6 Added resistance on destroyer hull in head seas at Fn=0.25 |
|
| Figure 7 Added resistance on destroyer hull in head seas at Fn=0.35 |
The problem of added resistance of ships in waves is solved by following Maruo's theory and applying the NURBS technique. The main motivation behind this method is to use a panel method for 3D ship motion computations in a PC environment. The advantages of the NURBS technique are less computational time and memory in comparison to conventional panel methods. Initially, the NURBS technique is applied to accurately describe the body geometry, while the velocity potential distribution on the body surface is expressed by B-spline, so that the continuity of higher order derivatives of velocity potential on the body surface can be verified. A collocation method based on Gauss-Legendre quadrature is used for the numerical solution of the integral equation; this method is then applied to calculate Kochin functions, which are necessary for calculation of added resistance by Maruo's formula. Since the added resistance is due to both diffraction and the radiation potential, the effect of these on added resistance is studied separately. The results obtained are compared with those of other numerical and experimental data; reasonable agreement are observed, suggesting that the implemented procedure is a reliable method for the prediction of added resistance of a ship in waves.
| Gao Z, Zou Z, 2008. A NURBS-based high-order panel method for three-dimensional radiation and diffraction problems with forward speed. J. Ocean Eng., 35, 1271–1278. DOI:10.1016/j.oceaneng.2008.02.007 |
| Gerritsma J, Beukelman W, 1972. Analysis of the resistance increase in waves of a fast cargo ship. International Shipbuilding Proceeding. |
| Iwashita H, Ohkusu M, 1992. The Green function method for ship motions at forward speed. J. Ship Tech Research, 39(2), 3–21. |
| Hsin C. Y, Kerwin J. E, Newman J. N, 1994. A higher order panel method based on B-spline. In: Proceedings of the 6th International Conference on Numerical Ship Hydrodynamics, National Academy Press, Washington D. C. , 133-151. |
| Journee' J M J, 1992. Experiments and calculations on Wigley hull forms in head waves. DUT-SHLReport 0909. |
| Kashiwagi M, 1997. Numerical seakeeping calculations based on the slender ship theor. Ship Tech Research, 44. |
| Kashiwagi M, 2009. Impact of hull design on added resistance in waves-application of the enhanced unified theory. Proceedings of the 10th Int. Marine Design Conf., Trondheim, Norway, 521. |
| Liu S, Papanikolaou A, Zaraphonitis G, 2011. Prediction of added resistance in waves. J. Ocean Eng., 38, 641–650. DOI:10.1016/j.oceaneng.2010.12.007 |
| Maruo H, 1963. Resistance in waves. Soc. Nav. Arch. Japan 60t Anniv.Ser, 8, 67–102. |
| Maruo H, 1957. The excess resistance of a ship in rough seas. International Shipbuilding Progres, 4(35), 337–345. |
| Papanikolaou A, Zaraphonitis G, Maron A., Karayannis T, 2000. Nonlinear effects of vertical plane motions of ships with forward speed in waves. Proceedings of the Fourth Osaka Colloquium on Seakeeping Performance of Ships, Osaka, Japan, 459–468. |
| Qiu W, Hsiung CC, 2002. A panel-free method for time-domain analysis of the radiation problem. J.Ocean Eng., 29(12), 1555–1561. DOI:10.1016/j.oceaneng.2014.05.011 |
| Salvesen N, 1978. Added resistance of ships in waves. Journal of Hydronautics, 12(1), 24–34. DOI:10.2514/3.63110 |
| Seo MG, Yang KK, Park DM, Kim Y, 2014. Numerical analysis of added resistance on ships in short waves. Journal of Ocean Eng., 87, 97–110D. DOI:10.1016/j.oceaneng.2014.05.011 |
| Ström-Tejsen J, Hugh YH, Y eh, Moran D, 1973. Added resistance in waves. Society of Naval Arch and Marine Eng., 81, 109–143. |
| Washita H, Ohkusu M, 1992. The Green function method for ship motions at forward speed. J. Ship Tech Research, 39(2), 3–21. |
| Zangeneh R, Yan T, Ghiasi M, 2012. The exact calculation of added resistance in waves. Proceedings of ASME 2012 International Mechanical Engineering Congress and Exposition, Volume 12: Vibration, Acoustics and Wave Propagation. Houston, Texas, USA, November 9-15. |



