2. Welding and Offshore Engineering Department, Petroleum Training Institute, Effurun P.M.B. 20, Nigeria
The increase in demand and supply of Liquefied Natural Gas(LNG)in recent times, poses a threat to the maritime environment and the public, owing to its inevitable. This is because high risk hazards might occur, if not properly handled. The number of voyages per year has increased drastically, and it is likely that vessels will be changing routes more frequently because of “cross-trades” and “gas swaps”. As evidenced in various publications, the operation of LNG carriers is associated with hazards of various risk levels(Vanem et al., 2008; Nwaoha et al., 2011a; Bubbico et al., 2009; Moon et al., 2009; Pitblado et al., 2004). To maintain adequate safety standards in the LNG carrier industry, potentially high risk hazards must be proactively addressed with respect to where they fall on the spectrum from uncertainty to certainty. A proactive approach can be used to conduct a probabilistic and subjective risk assessment and develop maintenance models of LNG carrier operations(Nwaoha et al., 2011b, Zalewski, 2011; Nwaoha et al., 2013a; Elsayed, 2009; Nwaoha et al. 2013b; Nwaoha, 2014). High risk hazards are threats to LNG carrier operations, as their occurrence will result in a catastrophic or critical consequence if not detected in a timely manner. The hazards of LNG carrier operations can be investigated using risk analysis approaches, whereby the risks associated with hazards are prioritized such that effort can be concentrated on the highest risks for effective maintenance planning. The failure modes(basic events)of high risk LNG carrier systems can be identified using fault tree analysis.
In this study, we provide an overview of the maintenance of LNG carrier operations and various maintenance strategies are described in section 2 including preventive, reactive, proactive and predictive strategies. In section 3, we discuss novel modeling techniques and their application in the risk-based maintenance of LNG carrier operations, including Genetic Algorithms(GAs), fuzzy logic, and Evidential Reasoning(ER).
2 Overview of the maintenance of LNG carriersMaintenance is defined as a combination of all technical and administrative actions, including supervision of actions, intended to retain an entity in, or restore it to a state in which it can perform a required function(Pillay and Wang, 2003). The ultimate goal of maintenance is to ensure reliability in equipment, machines, or processes that meets the business needs of a company(Jones, 2009). Reliability is defined as the ability of a machine, components, or equipment to perform a required function under specified conditions and for a given period of time without failing(Jone, 2009; Wang and Trbojevic, 2007). The maintenance of LNG carrier systems is of upmost importance in the LNG industry to avoid the loss of the LNG and ensure the safety of the crew members onboard the vessel. Once a risk-based check is conducted, system maintenance is recommended as a preventive or mitigative measure for any identified hazard for which the consequence could be catastrophic, marginal, or critical. However, system maintenance must be prioritized based on the consequences of system failures and the manufacturers’instructions.
Various maintenance techniques have been developed, which industries have used on engineering systems and proved to be useful. Reliability Centred Maintenance(RCM)is a procedure for determining maintenance strategies based on reliability techniques, including Failure Mode Effect and Criticality Analysis(FMECA)(Pillay and Wang, 2003). RCM focuses on the maintenance of items that affect system reliability, thereby making this maintenance program inherently cost effective in the long run(Mokashi et al., 2002; Pillay and Wang, 2003). Maintenance involves conducting planned and unplanned activities to ensure that a system’s state of operation remains acceptable. The selection of a maintenance strategy will depend on one or a combination of criteria such as the maximization of reliability, minimization of downtime, and minimization of total maintenance costs(Savic et al., 1995; Wang and Trbojevic, 2007).
In the maritime industry, any selected maintenance strategy must consider cost, safety, and environmental and operational consequences. The prime objective of a maintenance program is to minimize costs, meet safety, environmental, and operational goals. A successful maintenance model in the maritime industry can be developed after the consideration of the specific problems associated with the maintenance of a ship and its systems and subsystems, as follows(Wang and Trbojevic, 2007):
· High cost incurred by a ship’s system being out of service.
· Strict safety and insurance conditions, which necessitate rigorous survey requirements.
· Using ships’ personnel as operators and maintainers.
· The frequency with which personnel join and leave ships, creating a need for continuity of ships’ maintenance plans.
· The high degree of isolation from repair and spare parts and equipment facilities.
· The high cost of the transport units(i.e., the ship).
· Varying costs, availability, and quality of labor and spare parts and equipment throughout the world.
The maintenance of the LNG carriers and their systems and subsystems can be conducted using any maintenance techniques, whether stand-alone or in combination with other maintenance techniques, to produce a sound maintenance regime in a cost-effective manner. Depending on the experience of LNG crew members, some maintenance activities can be conducted onboard the vessel. If the failures of the LNG carrier systems that affect the operations of the vessel cannot be addressed by the crew members, a tugboat must be used to tow the vessel to a nearby port for maintenance. The importance of maintenance is demonstrated by the fact that it is the only shipboard activity to which one whole International Safety Management(ISM)Code element is assigned(i.e., ISM code element 10). Experience has shown that, the most common types of maintenance performed are preventive, reactive, predictive and proactive.
· Preventive Maintenance(PM)is a maintenance strategy carried out on equipment before any failure occurs. PM is usually conducted on repairable systems to improve their overall reliability(Sun et al., 2009). PM can be defined as actions performed on a time-based schedule that detect, or mitigate the degradation of a component or system with the aim of sustaining or extending its useful life by controlling its degradation to an acceptable level.
· Reactive Maintenance(RM)is a maintenance strategy that involves reacting to equipment failures, as they occur and conduct maintenance as necessary to restore the equipment function. No actions are taken to maintain the equipment as originally designed or ensure that the design life of the equipment is reached. It could also be called break down, fix-when-fail, run-to-failure, or corrective maintenance. In an RM program, any procedures that could be used to influence equipment survivability are ignored, and the only actions taken on equipment are initiated when equipment breaks down(Samrout et al., 2009). When equipment failures are not critical, RM can be appropriate(Arunraj and Maiti, 2010). Equipment that can be reactively maintained without experiencing undesirable consequence must be non-critical and pose no serious hazards or affect the operation of the system as a whole(Pillay and Wang, 2003).
· Predictive maintenance is defined as routine measurements that detect the onset of a degradation mechanism, thereby allowing incipient failures, casual stressors to be eliminated or controlled prior to any significant deterioration or damage in the system. It can provide increased safety, quality, and availability of a system(Carnero, 2006). Predictive maintenance is also called Condition Monitoring(CM). A predictive maintenance program can be used to detect the need to conduct maintenance on a system, based on its operational state(Chu et al., 1998). The continuous analysis of equipment condition monitoring data allows for the planning and scheduling of maintenance or repairs in advance of any catastrophic and functional failure(Pillay and Wang, 2003).
Proactive maintenance is a strategy for determining the root causes of repeated failures. A root cause failure analysis is the determination of the mechanisms and causes of equipment faults and is a natural part of a proactive maintenance process(EPRI, 2001), wherein the fundamental causes of equipment failures can be identified and failure mechanisms corrected. Proactive maintenance improves overall maintenance outcomes through better design, installation, maintenance procedures, workmanship and scheduling(Pillay and Wang, 2003). This maintenance strategy is a daily process that complements the ongoing maintenance activity and predictive maintenance processes(EPRI, 2001). The techniques used in proactive maintenance to extend machinery life are proper installation and precision rebuilds, failed-part analysis, rebuild verification, age exploration, and recurrence control(Pillay and Wang, 2003).
3 Novel modeling techniques applicable in risk-based maintenance of LNG carrier operationsUses of advanced computational techniques for effective maintenance planning are overcoming the challenges associated with assessing risk in various modern complex LNG carriers. These techniques include GA, ER and fuzzy logic. The successes of the utilization of these methods with respect to LNG carriers have been recorded in various publications(Nwaoha et al., 2011b, Zalewski, 2011; Nwaoha et al., 2013a; Elsayed, 2009, Nwaoha et al. 2013b; Nwaoha, 2014).
In risk modeling of LNG carrier maintenance operations, GA is employed to minimize risk by ensuring a genetic diversity exists, thereby increasing the search space to produce the best optimal risk solution. In addition, GA can ensure that the search is probabilistic and not deterministic. Furthermore, the search is conducted in a generated population of points and not at a single point in each iteration, which improves efficiency and accuracy. GA can solve multi-objective problems effectively. However, GA does not always produce a global optimum, especially in situations where the overall solution involves various populations. The fuzzy operations risk modeling approach is employed in LNG carrier maintenance operations, when there is uncertainty due to lack of data and ambiguity. The advantages of fuzzy logic are the ability to model any complex or highly non-linear function to any arbitrary degree of accuracy; its tolerance to vague or imprecise data; its flexibility in dealing with different forms of uncertainty; and that it is easy to understand using “natural” mathematics and rules that can be specified with natural language. The disadvantages of fuzzy logic are that the estimation of the membership function is sometimes very difficult and that the user must be well informed, since there are many ways of interpreting fuzzy rules. The ER approach is adopted in risk modeling of LNG carrier maintenance operations for cases in which there exist an incomplete assessment of uncertainty. The advantage of ER is the use of a belief structure to represent an assessment as a distribution. Secondly, an ER mechanism can be used to combine bottom-to-top level criteria based on their Degree of Beliefs(DoBs). The ER algorithm can address both quantitative and qualitative criteria under uncertainty. The drawback of the ER algorithm is its mathematical complexity.
3.1 Genetic algorithmThe GA was developed by John Holland in the 1970s as an optimization technique that uses the principles of natural genetics. A GA maintains a population of candidate solutions, where each candidate solution is typically coded as a binary string called a chromosome(individuals)(Yen and Langari, 1999).The GA establishes a fitness function to facilitate the formation of an initial population. The fitness of the chromosomes that make up the initial population is assessed in order to select the best for the next generation. The chromosomes that are not selected by the selection operator for the next generation are replaced by the reproduced offspring. The offspring are reproduced by the parents(the selected chromosomes from the initial population)using the crossover operator. Premature convergence is overcome by the use of a mutation operator and a new population is formed, maintaining the population size of the initial population. The best chromosomes are retained using the elitism operator. This process continues until an optimal solution is found or until a fixed number of generations is reached. The application of a GA is facilitated using GA operators such as selection, crossover, mutation, and elitism.
3.1.1 SelectionThis operator chooses parents to be reproduced based on their fitness(Haupt and Haupt, 2004). It attempts to apply pressure upon the population in a manner similar to that of natural selection in biological systems(Colley, 1999). The selection operators use the fitness values in the current population to create a breeding pool for the next generation(Alim et al., 2007). A selection operator occurs at each iteration of the algorithm to allow the population of chromosomes to evolve over generations to include only fit chromosomes(members)as defined by the fitness(objective)function. The selection operators include a roulette wheel selection, stochastic universal sampling selection and tournament selection(Colley, 1999; Man et al., 1999, Mitchell, 1996; Haupt and Haupt, 2004).
3.1.2 CrossoverCrossover allowsgivensolutions to exchange information in a way similar to that used by a natural organism undergoing sexual reproduction(Colley, 1999). According to Haupt and Haupt(2004), crossover is an operator that forms a new chromosome from two parent chromosomes by combining partial information from each. The operator switches genes between two genotypes to generate offspring. The crossover operators include a single-point crossover(Colley, 1999; Mitchell, 1996; Haupt and Haupt, 2004), two-point crossover(Colley, 1999; Mitchell, 1996; Haupt and Haupt, 2004; Sakawa, 2002), and multipoint crossover(Colley, 1999; Man et al., 1999; Sakawa, 2002).
3.1.3 MutationMutation is a reproduction operator that randomly alters the values of genes in a parent chromosome(Haupt and Haupt, 2004). A mutation operator provides diversity in the population by making changes randomly in a selected genotype and the percentage of genes(bits)in a population that is mutated in each GA generation is lower than that of the crossover operator. In other words, mutation is applied with a lower probability than that of the crossover operator(Alim et al., 2007).
3.1.4 ElitismElitism is an operator that ensures that the GA retains the best chromosomes in each generation because sometimes a selection operator does not guarantee that the fittest chromosomes, as defined by the fitness function, are selected for the next generation. Without this operator, the likelihood of losing the best chromosomes is high during selection, crossover and mutation. In many applications, the search speed can be made more effective by not losing the best, or elite members.
There are different GA methods used to solve engineering problems. These include binary, continuous, steady-state, and multi-objective GAs:
· Binary GAs work with finite parameter space(Harikumar et al., 2004). The value of the chromosome(structure or potential solution)is represented using binary numbers(0 or 1).
· A continuous GA is an algorithm that uses real numbers to encode variables. It follows the same steps used in the binary GA, but while they share the same steps, there are significant differences between them. The difference in the continuous parameter GA occurs in the computation of the fitness function and in the crossover and mutation operators(Harikumar et al., 2004).
· The steady state GA is either a single or multi-objective GA with an ability to solve one or more objective function(s). It can be binary-based or continuity based, depending on the encoding of the constraints of the objective function(s)during the problem formulation. In steady-state selection, only a few chromosomes(individuals)are replaced in each generation. Usually a small number of the least fit chromosomes(individuals)are replaced by offspring resulting from the crossover and mutation of the fittest individuals(Mitchel, 1996). Steady-state GAs are used when evolving rule-based systems in which incremental learning(and retaining what has already been learned)is important and in which members of the population collectively(rather than individually)solve the problem at hand(Mitchel, 1996).
· Multi-objective GA involves more than one objective function. This solution solves problems simultaneously and helps to identify the effectiveness of minimizing the objective functions to benefit the constraint and vice versa. The comparison of two solutions with respect to several objectives can be achieved by introducing the concepts of Pareto optimality and dominance, which enable solutions to be compared and ranked without imposing any prior measure of the relative importance of individual objectives, either in the form of subjective weights or arbitrary constraints(Marseguera et al., 2004).
3.1.5 Application of GA in LNG carrier operationsNwaoha et al.(2011a)employed the GA in the risk-based maintenance of LNG carrier operations, primarily in order to estimate the cost of maintaining high risk LNG carrier systems such as containment and transfer arm systems. The authors considered various parameters, including hazard severity weighting, failure frequencies, and the time and cost of maintenance, and repair of the LNG carrier systems. These parameters were then used to develop an objective function. The objective function was then optimized using the GA in a MATLAB environment, and Probabilistic Risk Assessment(PRA)was used to reveal the total risk of the LNG carrier systems being investigated, based on available failure rates data, which facilitated the optimization exercise. The step-by-step GA methodology of this study is illustrated in Fig. 1.
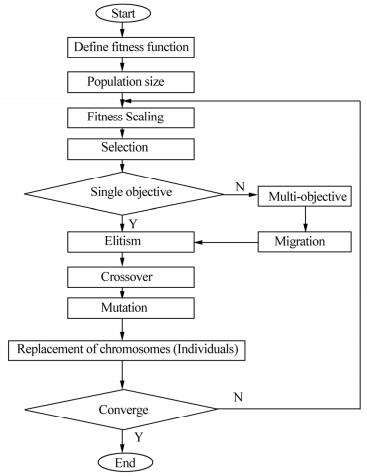
|
| Fig. 1 Flow chart of the GA methodology |
In the PRA exercise conducted by the authors, they identified LNG containment system’s basic failure events as fire and explosion, structural defects, corrosion effects, pressure relief system, installation defects and containment pressure with failure frequencies of 1.78e-006/hour, 2.31e-006/hour, 1.115e-006/hour, 2.12e-005/hour, 1.382e-005/hour and 0.01/hour respectively.
Nwaoha et al.(2011a) also identified the basic events associated with an LNG spill from a transfer arm to include manual release, auto release, application of ship motion, motion and controls, fire and explosion, material defects, pipe rupture and overpressure with failure frequencies of 0.024/hour, 0.03/hour, 0.000 66/hour, 1.382e-005/hour, 1.78e-06/hour, 11.15e-06/hour, 0.01/hour and 2.96e-010/ hour respectively. The hazard consequence, hazard probability and risk assessment matrix employed in that study are listed in Tables 1, 2, and 3, respectively. Finally, the GA methodology determined the cost of maintaining and repairing an LNG containment system and transfer arm, with respect to their risk levels and budgeted maintenance costs. Nwaoha et al.(2011a)determined that the costs of maintaining and repairing an LNG containment system and transfer arm were $729 087 and $570 913, respectively, with an overall budgeted maintenance cost of $1 300 000. The authors also recommended further research with respect to the uncertainty treatment of failure frequencies and the cost of maintenance and repair of LNG carrier systems. These issues are addressed in sub-section 3.2.1 by the use of fuzzy logic in combination with the GA.
| Category | Weight | Description | Equipment | Personnel |
| 1 | 1000 | Catastrophic | System loss | Death |
| 2 | 100 | Critical | Major system damage | Severe injury/Illness |
| 3 | 10 | Marginal | Minor system damage | Minor injury/Illness |
| 4 | 1 | Negligible | <Minor system damage | <Minor injury/Illness |
The Fuzzy Set Theory(FST)was first presented by Zadeh(1965). This theory is a mathematical formalization that enables the representation of degrees of membership by members in sets(Eleye-Datubo, 2006). Fuzzy logic is the term used for ad-hoc applications of rules based on a simplified FST(Eleye-Datubo, 2006). It is a versatile tool that is tolerant of imprecise, ambiguous, and vague data/information, and its reasoning builds understanding into a process. Fuzzy logic mainly uses the concept of linguistic variables, and provides a framework for systematically dealing with such variables.
| Level | Description | Frequency |
| A | Frequent | Likely to happen |
| B | Probable | Several times during lifetime |
| C | Occasional | Likely to happen once |
| D | Remote | Unlikely but possible during life time |
| Hazard severity | Weight | A(Frequent) | B(Probable) | C(Occasional) | D(remote) |
| 1. Catastrophic | 1 000 | A-1 | B-1 | C-1 | D-1 |
| 2. Critical | 100 | A-2 | B-2 | C-2 | D-2 |
| 3. Marginal | 10 | A-3 | B-3 | C-3 | D-3 |
| 4. Negligible | 1 | Negligible hazards No action required | |||
There are various fuzzy logic techniques such as discrete and continuous fuzzy sets, and the Fuzzy Rule Base(FRB), which have all been used in uncertainty treatments in the maritime industry(Shafiee, 2015; Yang and Wang, 2015; Pillay and Wang, 2002; Wang et al., 1995; Wang et al., 1996; Wang, 1997; Wang, 2000; Sii et al., 2001; Ung et al., 2006; Yang et al., 2005). Fuzzy logic can be used in linguistic approach application for a wide variety of problems.A fuzzy set is represented by a membership function on the universe of discourse or the universal set(X)(Zadeh, 1987). A membership rating ranging between 0 and 1 indicates the degree of membership. The shape of the fuzzy set depends on the way the data is represented. The membership is indicated on the vertical axis, ranging between 0 and 1, and the set domain is indicated along the horizontal axis. The fuzzy set shape defines the relationship between the domain and the membership values of a set. Different types of fuzzy membership functions are used when solving engineering problems. The particular membership function chosen for solving an engineering problem depends on the choice of the designer and the problem formulation. The most commonly used membership functions in engineering applications are triangular, trapezoidal, sigmoid-curve, generalized-bell- curve, and gaussian-curve membership functions. The features of the FSTmay be summarized as follows(Eleye-Datubo, 2006):
· It is conceptually easy to understand with “natural” mathematics.
· It is tolerant of vague or imprecise data. The use of FST is particularly adapted to the representation and manipulation of the imprecision and uncertainty of linguistic labels that define the criteria of the classes.
· It presents flexible ways of dealing with different forms of uncertainty. For example, there is a lot of freedom in choosing the membership functions of fuzzy sets.
· It is a more intuitive concept than is differential equation, and enables analysts and decision-makers to capture knowledge about how the system behaves in everyday linguistic terms(i.e. using natural language).
· Although it makes use of heuristics, the FST framework still offers a convenient way to express and capitalize on the experience of experts’ common sense knowledge.
· It has the ability to model any complex or highly non-linear function to any arbitrary degree of accuracy.
· It is based on rules(i.e., rule base logic)that can be specified with natural language. Basically, these laws are naturally broken down into individual IF-THEN statements that lend themselves to parallel processing.
3.2.1 Application of fuzzy logic in LNG carrier operationsNwaoha et al.(2013a) demonstrated an application of the FRB technique in combination with the GA for the uncertainty treatment of unit costs of maintenance of an LNG containment system and transfer arm to determine optimal maintenance. The authors used the hybridized algorithm mechanism to estimate the maintenance cost of high risk systems within a realm of uncertainty. The methodology of their research is illustrated in Fig. 2. In that study, the authors developed 125 FRB rules using the LNG Technical Consultancy Cost(LTCC), LNG Maintenance Duration(LMD)and LNG Spare Part Cost(LSPC)as the antecedents and the LNG Maintenance Cost(LMC)as the consequent.
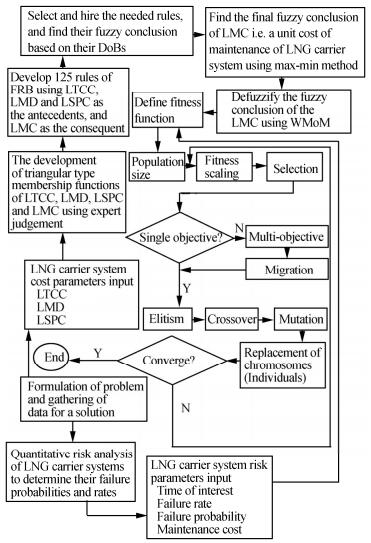
|
| Fig. 2 Flow chart of the fuzzy rule based genetic algorithm(FRB-GA)methodology |
The information presented in Tables 4, 5, 6 and 7 was used to develop these 125 rules. The FRB method is used to subdue the uncertainties associated with the maximum and minimum maintenance costs of each high risk LNG carrier system. The maintenance unit costs of LNG carrier systems are among the parameters in the risk model that are optimized using a continuous steady-state GA. Other parameters in the risk model include time of interest, failure probability, failure frequency and maintenance cost of the entire LNG carrier system.
| Category | Description of LTCC(Linguistic terms) | Level of damage onLNG carrier systems | Level of injury/Illness onLNG carrier personnel |
| 1 | Very low | <Minor system damage | <Minor injury/Illness |
| 2 | Low | Minor system damage | Minor injury/Illness |
| 3 | Moderate | Multiple system damage | Multiple injury/Illness |
| 4 | High | Major system damage | Severe injury/Illness |
| 5 | Very high | System loss | Death |
The information in Tables 1, 2 and 3 was also used to analyze the hazard consequence, hazard probability, and risk assessment matrix employed in the development of the risk model. In addition, the failure frequencies of basic events of the LNG containment system and transfer arm listed in sub-section 3.1.5 were utilized in this study. Lastly, using the aforementioned methodology, the optimal maintenance cost of each system was determined under uncertainty. These costs are $542 188 for the LNG containment system and $162 500 for the LNG transfer arm. Other applications of fuzzy logic in combination with ER are described below.
| Category | Description of LMD(Linguistic terms) | Level of damage onLNG carrier system | Level of Injury/Illness onLNG Carrier Personnel |
| 1 | Very short | <Minor system damage | <Minor injury/Illness |
| 2 | Short | Minor system damage | Minor injury/Illness |
| 3 | Medium | Multiple system damage | Multiple injury/Illness |
| 4 | Long | Major system damage | Severe injury/Illness |
| 5 | Very long | System loss | Death |
| Category | Description of LSPC(Linguistic terms) | Level of damage onLNG carrier system | Level of injury/Illness onLNG carrier personnel |
| 1 | Very cheap | <Minor system damage | <Minor injury/Illness |
| 2 | Cheap | Minor system damage | Minor injury/Illness |
| 3 | Average | Multiple system damage | Multiple injury/Illness |
| 4 | Costly | Major system damage | Severe injury/Illness |
| 5 | Very costly | System loss | Death |
| Category | Description of LMC(Linguistic terms) | Level of damage onLNG carrier system | Level of injury/Illness onLNG carrier personnel |
| 1 | Very cheap | < minor system damage | <Minor injury/Illness |
| 2 | Cheap | Minor system damage | Minor injury/Illness |
| 3 | Normal | Multiple system damage | Multiple injury/Illness |
| 4 | Expensive | Major system damage | Severe injury/Illness |
| 5 | Very expensive | System loss | Death |
ER was developed in the 1990s for addressing Multiple Criteria Decision Making(MCDM)problems, both quantitative and qualitative, under uncertainty. The ER algorithm is based on the decision theory and the Dempster-Shafer(D-S)theory of evidence, which is well suited for handling incomplete assessments of uncertainty(Yang, 2001; Yang and Singh, 1994). The D-S theory is a mathematical theory of evidence that can combine different pieces of evidence based on their DoBs. The ER differs from other conventional MCDM methods, such as the Analytical Hierarchy Processing(AHP)and additive utility function approaches because it uses a belief structure to represent an assessment as a distribution. The algorithm is used to aggregate bottom-to-top level criteria. In other words, once assessments of the conditions of the system components have been carried out, the ER algorithm can obtain an overall assessment of the entire system. As reported by various studies, the ER algorithm synthesizes the conditions of the components with respect to their evaluation grades in association with their DoBs(Ngan, 2015; Yang and Wang, 2015; Zhou et al., 2013).
Suppose a system has two subsystems and these subsystems each have components. To assess the safety/risk level of the system, the each component’s safety/risk levels can be synthesized using the ER approach. In the ER assessment framework, four synthesis axiomshave been proposed(Godaliyadde, 2008):
· If no subsystem has been assessed as to having a certain evaluation grade, then neither should the system be assessed at that grade.
· If all components have been precisely assessed at an individual grade, then the system should also be precisely assessed to that grade.
· If all components have been completely assessed as having a certain subset of grades, then the system should also be assessed as having that same subset.
· If any component assessment is incomplete, then the system assessment obtained by aggregating the incomplete and complete component assessments should also be considered to be incomplete, and the degree of incompleteness be properly assigned.
According to Sönmez et al.(2001) and Yang and Xu(2002), the properties of ER are:
· There is general recognition of the difficult of dealing with both quantitative and qualitative criteria under uncertainty, ER provides a systematic and consistent way of handling such information.
· The uncertainty and risk surrounding a problem can be represented using the concept of DoB.
· Both complete and incomplete information can be aggregated and modeled by using a belief structure.
· The ER algorithm has been integrated into a software package called the Intelligent Decision System(IDS), which is a graphically designed decision support tool. An IDS allows decision makers to build their own models and input their own data.
· An IDS software enables users to provide evaluation results in both tabular and graphical form.
Application of ER in LNG carrier operations
A practical application of the ER algorithm in LNG carrier operations is demonstrated in the work of Nwaoha et al.(2011b), in which the ER algorithm is used in combination with fuzzy logic in the risk analysis and control of LNG carrier operations. In the study, the authors used the ER algorithm to synthesize the safety/risk levels of the failure modes of the LNG carrier containment system and transfer arm. These failure modes were assessed and modeled using a fuzzy set, in order to identify the one of the top events and to select the best Risk Control Options(RCO)based on the safety principles of Formal Safety Assessment(FSA). Fig. 3 shows an FSA methodology flow chart, based on the Fuzzy Evidential Reasoning(FER)method in uncertainty environment, which is used to facilitate the identification of the best RCO.
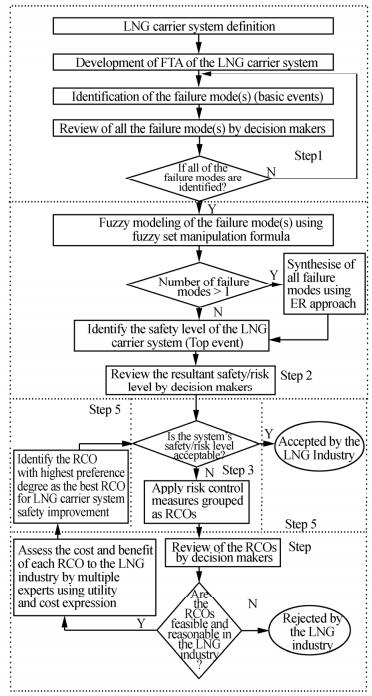
|
| Fig. 3 FSA methodology flow chart based on a FER method in an uncertainty environment |
The modeled failure modes of the LNG containment system are fire and explosion, structural defects, corrosion effects, containment pressure, pressure relief system failure, and installation defects. The safety/risk levels estimates of these seven failure modes, were determined using discrete fuzzy sets and information(i.e., membership values, categories, and linguistic variables/terms of failure likelihood(L), failure consequence probability(E), consequence severity(C)and safety expressions(S))provided in Tables 8, 9, 10 and 11 respectively.
| Linguistic variable | Scale | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Highly frequent | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
| Frequent | 0 | 0 | 0 | 0 | 0.75 | 1 | 0.25 |
| Reasonably frequent | 0 | 0 | 0 | 0.75 | 1 | 0.25 | 0 |
| Average | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 |
| Reasonably low | 0 | 0.25 | 1 | 0.75 | 0 | 0 | 0 |
| Low | 0.25 | 1 | 0.75 | 0 | 0 | 0 | 0 |
| Very low | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
| Linguistic variable | Scale | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Definite | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
| Highly likely | 0 | 0 | 0 | 0 | 0.75 | 1 | 0.25 |
| Reasonably likely | 0 | 0 | 0 | 0.75 | 1 | 0.25 | 0 |
| Likely | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 |
| Reasonably Unlikely | 0 | 0.25 | 1 | 0.75 | 0 | 0 | 0 |
| Unlikely | 0.25 | 1 | 0.75 | 0 | 0 | 0 | 0 |
| Highly Unlikely | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
| Linguistic variable | Scale | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Catastrophic | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
| Critical | 0 | 0 | 0 | 0.75 | 1 | 0.25 | 0 |
| Marginal | 0 | 0.25 | 1 | 0.75 | 0 | 0 | 0 |
| Negligible | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
| Linguistic variable | Scale | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1. Poor | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
| 2. Average | 0 | 0 | 0 | 0.5 | 1 | 0.25 | 0 |
| 3. Good | 0 | 0.25 | 1 | 0.5 | 0 | 0 | 0 |
| 4. Excellent | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
The estimated cost of preventing the failure of an LNG containment tank is determined using discrete fuzzy and ER approaches and the information provided in Tables 9, 10 and 11. Since the risk must be reduced using the most cost effective RCO, utility theory is employed to carry out this exercise. The RCOs for the LNG containment system include RCO1(regular inspection of the system per voyage), RCO2(training of crew members on new technology and change of operating procedures when loading LNG onto the system), and RCO3(effective maintenance of the system). A preference degree formula is used to estimate the utility of the RCOs for LNG containment system failure and to determine their respective values. The respective values of RCO1, RCO2, and RCO3 are 0.744, 0.782, and 0.903 7, with RCO3 being found to have the highest value. Therefore, RCO3 is chosen as the best RCO for improving the safety of the LNG containment system.
Nwaoha et al.(2013b) demonstrated another successful application of ER and fuzzy logic to LNG carrier operations in their comparative analysis of a risk matrix and combination of ER and fuzzy logic. In the study, the authors found that the hybridization of ER and fuzzy logic is more detailed than the risk matrix method in the risk assessment of LNG carrier operations, and can produce better and more reliable results. This research methodology is illustrated in Fig. 4. In their study, the authors used the risk matrix method to identify and assess twenty-six hazards associated with LNG carrier operations. The mechanisms of the method revealed that two hazards, including “spill from transfer arm” and “containment system failure” are associated with “very high” risk with the same score of 7, as determined using the information in Tables 14-17. This poses a problem in that the relative risk of these two hazards could not be determined with this method, and thus could not be used to guide decision makers in the management of the risks of these hazards in LNG carrier operations with respect to the appropriate allocation of available resources(Nwaoha et al., 2013b). However, a more detailed risk analysis of the two major hazards made possible by a combination of ER and fuzzy logic overcome this challenge and determine that, in fact, an LNG spill from the transfer arm is riskier than an LNG containment system failure, with utility values of 0.6126 and 0.620 5, respectively. The application of ER and fuzzy logic was facilitated by the use of the information provided in Tables 8-11 and the causes of the hazards were identified using the fault tree method.
| Linguistic variable | Scale | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Very high | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
| High | 0 | 0 | 0 | 0 | 0.75 | 1 | 0.25 |
| Moderately high | 0 | 0 | 0 | 0.5 | 1 | 0.25 | 0 |
| Average | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 |
| Moderately low | 0 | 0.25 | 1 | 0.5 | 0 | 0 | 0 |
| Low | 0.25 | 1 | 0.75 | 0 | 0 | 0 | 0 |
| Very low | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
| Linguistic variable | Scale | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1. Slightly preferred | 0 | 0 | 0 | 0 | 0 | 0.75 | 1 |
| 2. Moderately preferred | 0 | 0 | 0 | 0.5 | 1 | 0.25 | 0 |
| 3. Preferred | 0 | 0.25 | 1 | 0.5 | 0 | 0 | 0 |
| 4. Greatly preferred | 1 | 0.75 | 0 | 0 | 0 | 0 | 0 |
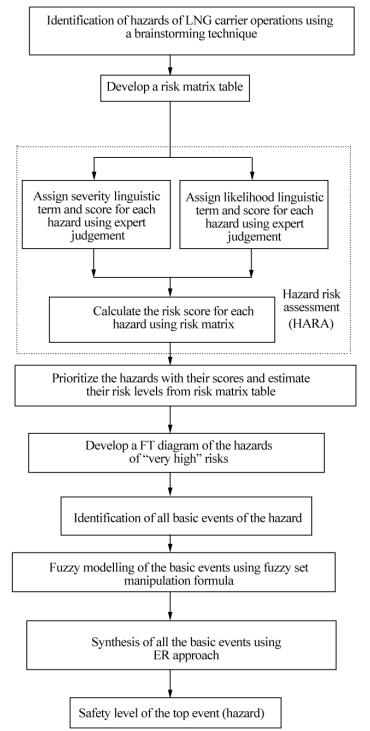
|
| Fig. 4 Methodology for estimating the risk/safety of hazards of LNG carrier operations |
| Linguistic term for consequence of a hazard | Description |
| Negligible | Less than minor system damage, less than minor injury/illness of personnel or negligible environmental damage |
| Marginal | Minor system damage, minor injury/illness of personnel or minor environmental damage |
| Critical | Major system damage, severe injury/illness of personnel or major environmental damage |
| Catastrophic | System loss, death of personnel or severe environmental damage |
| Linguistic term for occurrence likelihood of a hazard | Description |
| Remote | The hazard is unlikely to occur but possible on an LNG carrier operation at failure rate of <10−6/year |
| Occasional | The hazard can occur occasionally on an LNG carrier operation at failure rate of 10−3/year |
| Probable | The hazard is likely to happen from time to time on an LNG carrier operation at failure rate of 0.012 5/year |
| Frequent | The hazard is likely to happen repeated on an LNG carrier at failure rate of >0.025 |
| Consequence of a hazard | Occurrence likelihood of a hazard | |||
| 1. Remote | 2. Occasional | 3. Probable | 4. Frequent | |
| 1. Negligible | 2 | 3 | 4 | 5 |
| 2. Marginal | 3 | 4 | 5 | 6 |
| 3. Critical | 4 | 5 | 6 | 7 |
| 4. Catastrophic | 5 | 6 | 7 | 8 |
| Risk levels | Risk scores | Description of risk levels |
| Very high | 6, 7, 8 | Vessel operations have to be prohibited until the risk is reduced to an acceptable level. |
| High | 5 | Vessel operations can continue while risk reduction measures are being applied at an acceptable cost. |
| Moderate | 3, 4 | Vessel operations continue while efforts are being made to reduce the risk, but the cost of prevention should be carefully measured and limited. Risk reduction methods should be implemented within a defined time period. |
| Low | 2 | No actions are required on the vessel while in operation. |
The contribution of Nwaoha et al.(2014) to the optimal operation of LNG transfer arm under uncertainty was another welcome development. The LNG transfer arm is a system used in the loading and unloading of LNG in ocean going vessels and onshore tanks. The safety of this vital LNG system must not be comprised. As such, in this study, the authors identified safety improvement measures(SIMs)for the optimal and cost effective operation of an LNG transfer arms under uncertainty using the methodology illustrated in Fig. 5, thus benefitting an entire industry. They employed a hybrid algorithm comprised of ER and fuzzy logic in their study, in order to address the uncertainties associated with the costs of applying the SIMs. The ER algorithm mechanisms are used to facilitate the identification of an SIM group that can optimize the LNG transfer arm operations in a cost effective manner. The cost estimates of the SIM groups by various experts in fuzzy environment are combined using the ER algorithm in order to identify the one that is not only cost effective, but has the ability to ensure optimal operation of the LNG transfer arm. In the study, the authors determined that the cost of using SIM group 1 was less than those of SIM Groups 2 and 3 as evidenced by their respective utility values illustrated in Table 18.
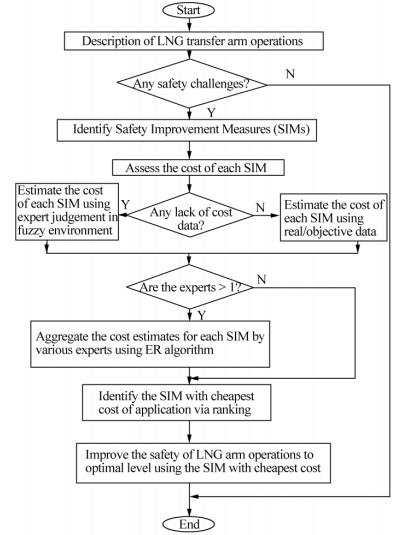
|
| Fig. 5 Flow chart of selection of SIM group for optimal operations of an LNG transfer arm |
| Name of SIM Group | Cost utility description | Preference degree value | Rank of SIM Group using its preference degree value |
| SIM Group 1 | {(0, “slightly preferred”), (0, “moderately preferred”), (0, “preferred”), (1, “greatly preferred”)} | 1.0 | 1 |
| SIM Group 2 | {(0.0250, “slightly preferred”), (0.9249, “moderately preferred”), (0.0269, “preferred”), (0.0232, “greatly preferred”)} | 0.490 6 | 3 |
| SIM Group 3 | {(0.0590, “slightly preferred”), (0.0754, “moderately preferred”), (0.8030, “preferred”), (0.0626, “greatly preferred”)} | 0.704 9 | 2 |
In this study, we described four maintenance strategies, including the preventive, reactive, predictive, and proactive methods. Analyses of various modeling techniques applicable to LNG carrier operations were also provided, along with illustrative examples. We highlighted algorithms such as fuzzy logic, GA and ER that can be used to solve risk assessment and maintenance modeling problems in the LNG industry and identified their advantages and disadvantages. We illustrated the relevance of these modeling techniques using five case studies/examples, with an emphasis on the proactive risk assessment of LNG carrier operations and maintenance modeling. These include the use of GA for standalone risk-based maintenance of LNG carrier operations; the combined use of GA and fuzzy logic to analyze the maintenance costs of LNG containment and transfer arm systems; the combined application of ER and fuzzy logic for the risk analysis and control of LNG carrier systems; the incorporation of a risk matrix and the combination of ER and fuzzy logic in hazard ranking of LNG carrier operations and finally, the use of a hybrid algorithm comprised of ER and fuzzy logic to achieve the optimal operation of an LNG transfer arm.
| Alim F, Ivanov K, Levine SH, 2007. New genetic algorithms to optimize PWR reactors. part 1: loading pattern and burnable poison placement optimization techniques for PWRs. Annals of Nuclear Energy, 35, 93-112. DOI: 10.1016/j.anucene.2007.05.007 |
| Arunraj NS, Maiti J, 2010. Risk-based maintenance policy selection using AHP and goal programming. Safety Science, 48(2), 238-247. DOI: 10.1016/j.ssci.2009.09.005 |
| Bubbico R, Cave SD, Mazzarotta B, 2009. Preliminary risk analysis for LNG tankers approaching a maritime terminal. Journal of Loss Prevention in the Process Industries, 22(5), 634-638. DOI: 10.1016/j.jlp.2009.02.007 |
| Carnero M, 2006. An evaluation system of the setting up of predictive maintenance programmes. Reliability Engineering and System Safety, 94(1), 44-52. DOI: 10.1016/j.ress.2005.09.003 |
| Chu C, Proth J, Wolff P, 1998. Predictive maintenance: the one-unit replacement model. International Journal of Production Economics, 54(3), 285-295. DOI: 10.1016/S0925-5273(98)00004-8 |
| Colley DA, 1999. An introduction to genetic algorithms for scientists and engineers. World Scientific Publishing, London, UK. |
| Eleye-Datubo AG, 2006. Integrated risk-based modelling to safety-critical marine and offshore applications. PhD thesis, Liverpool John Moores University, Liverpool, UK. |
| Elsayed T, 2009. Fuzzy inference system for the risk assessment of liquefied natural gas carriers during loading/offloading at terminals, Applied Ocean Research, 31, 179-185.DOI: 10.1016/j.apor.2009.08.004 |
| EPRI, 2001. Guideline on proactive maintenance. Electrical Power Research Institute, Report No. 1004015, USA. |
| Godaliyadde D, 2008. Application of formal safety assessment for ship hull vibration modelling. PhD thesis, Liverpool John Moores University, Liverpool, UK . |
| Harikumar R, Sukanesh R, Bharathi PA, 2004. Genetic algorithm optimization of fuzzy outputs for classification of epilepsy risk levels from EEG signals. TENCON, IEEE Region 10 Conference, Madurai, India, 588- 591. |
| Haupt RL, Haupt SE, 2004. Practical genetic algorithms. 2nd Edition, John Wiley and Sons Incorporated, Hoboken, USA. |
| Jones B, 2009. Maintenance modelling of manufacturing systems. PhD thesis, Liverpool John Moores University, Liverpool, UK. |
| Man KF, Tang KS, Kwong S, 1999. Genetic algorithms: Concept and design. Springer-Verlag, London, UK. |
| Marseguera M, Zio E, Podofillini L, 2004. Optimal reliability/ availability of uncertain systems via multi-objective genetic algorithms. IEEE Transactions on Reliability, 53(3), 424-435. DOI: 10.1109/TR.2004.833318 |
| Mitchell M, 1996. An introduction to genetic algorithms. MIT Press, Cambridge, USA. |
| Mokashi AJ, Wang J, Verma AK, 2002. A study of reliability centred maintenance in ship operations. Marine Policy, 26(5), 325-335.DOI: 10.1016/S0308-597X(02)00014-3 |
| Moon K, Song S, Ballesio J, Fitzgerald G, Knight G, 2009. Fire risk assessment of gas turbine propulsion system for LNG carriers. Journal of Loss Prevention in Process Industries, 22, 908-914. DOI: 10.1016/j.jlp.2008.11.008 |
| Ngan S, 2015. Evidential reasoning approach for multiple-criteria decision making: a simulation-based formulation. Expert Systems with Applications, 42(9), 4381-4396. DOI: 10.1016/j.eswa.2014.12.053 |
| Nwaoha TC, 2014. Inclusion of hybrid algorithm in optimal operations of LNG transfer arm under uncertainty. Ships and Offshore Structure, 9(5), 514-524. DOI: 10.1080/17445302.2014.887174 |
| Nwaoha TC, Yang Z, Wang J, 2011a. Application of genetic algorithm to risk-based maintenance operations of liquefied natural gas carrier systems. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 225(1), 40-52. DOI: 10.1243/09544089JPME336 |
| Nwaoha TC, Yang Z, Wang J, Bonsall S, 2011b. A new fuzzy evidential reasoning method for risk analysis and control of a liquefied natural gas carrier system. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 225(3), 206-225. DOI: 10.1177/1475090211411849 |
| Nwaoha TC, Yang Z, Wang J, Bonsall S, 2013a. A fuzzy genetic algorithm approach for analysing maintenance cost of high risk liquefied natural gas (LNG) carrier systems under uncertainty. Proceedings of IMarEST, Part A: Journal of Marine Engineering and Technology, 12(2), 57-73.DOI: 10.1080/20464177.2013.11020280 |
| Nwaoha TC, Yang Z, Wang J. Bonsall S, 2013b. Adoption of new advanced computational techniques to hazards ranking in LNG carrier operations. Ocean Engineering, 72(1), 31-44. DOI: 10.1016/j.oceaneng.2013.06.010 |
| Pillay A, Wang J, 2002. Risk assessment of fishing vessels using fuzzy set approaches. International Journal of Safety, Quality and Reliability, 9(2), 163-181. DOI: 10.1142/S0218539302000743 |
| Pillay A, Wang J, 2003. Technology and safety of marine system. Elsevier Science Ltd, Oxford, UK. |
| Pitblado RM, Baik J, Hughes GJ, Ferro C, Shaw SJ, 2004. Consequences of LNG marine accidents. Center for Chemical Process Safety (CCPS) Conference, Orlando, USA, 1-20. |
| Sakawa M, 2002. Genetic algorithms and fuzzy multiobjective optimization. Kluwer Academic Publishers, Massachusetts, USA. |
| Samrout M, Chatelet E, Kouta R, Chebbo N, 2009. Optimization of maintenance policy using the proportional hazard model. Reliability Engineering and System Safety, 94(1), 44-52.DOI: 10.1016/j.ress.2007.12.006 |
| Savic DA, Godfrey WA, Knezevic J, 1995. Optimal opportunistic maintenance policy using genetic algorithm, 1: formulation. Journal of Quality in Maintenance Engineering, 1(2), 34-49. DOI: 10.1108/13552519510089574 |
| Shafiee M, 2015. A fuzzy analytic network process model to mitigate the risks associated with offshore wind farms. Expert Systems with Applications, 42(4), 2143-2152.DOI: 10.1016/j.eswa.2014.10.019 |
| Sii HS, Ruxton T, Wang J, 2001. A fuzzy-logic-based approach to qualitative safety modeling for marine systems. Reliability Engineering and System Safety, 73, 19-34. DOI: 10.1016/S0951-8320(01)00023-0 |
| Sönmez M, Yang JB, Holt GD, 2001. Addressing the contractor selection problem using an evidential reasoning approach. Engineering, Construction and Architectural Management, 8(3), 198-210. DOI: 10.1046/j.1365-232X.2001.00199.x |
| Sun Y. Ma L, Mathew J, 2009. Failure analysis of engineering systems with preventive maintenance and failure interactions. Computers and Industrial Engineering, 57(2), 539-549. DOI: 10.1016/j.cie.2008.08.007 |
| Ung ST, Williams V, Chen HS, Bonsall S, Wang J, 2006. Human error assessment and management in port operations using fuzzy AHP. Marine Technology Society Journal, 40(1), 73-86. DOI: 10.4031/002533206787353583 |
| Vanem E, Antão P, Østvik I, De Comas FDC, 2008. Analysing the risk of LNG carrier operations. Reliability Engineering and System Safety, 93(9), 1328-1344. DOI: 10.1016/j.ress.2007.07.007 |
| Wang J, 1997. A subjective methodology for safety analysis of safety requirements specifications. IEEE Transactions on Fuzzy Systems, 5(3), 418-430. DOI: 10.1109/91.618277 |
| Wang J, 2000. A subjective modelling tool applied to formal ship safety assessment. Ocean Engineering, 27(10), 1019-1035.DOI: 10.1016/S0029-8018(99)00037-2 |
| Wang J, Trbojevic VM, 2007. Design for safety of marine and offshore systems. Institute of Marine Engineering, Science and Technology, London, UK, 1-403. |
| Wang J, Yang JB, Sen P, 1995. Safety analysis and synthesis using fuzzy set modeling and evidential reasoning. Reliability Engineering and System Safety, 47, 103-118. DOI: 10.1016/0951-8320(94)00053-Q |
| Wang J, Yang JB, Sen P, 1996. Multi-person and multi-attribute design evaluations evidential reasoning based on subjective safety and cost analyses. Reliability Engineering and System Safety, 52(2), 113-128. DOI: 10.1016/0951-8320(96)00003-8 |
| Yang JB, 2001. Rule and utility based evidential reasoning approach for multi-attribute decision analysis under uncertainties. European Journal of Operational Research, 131(1), 31-61. DOI: 10.1016/S0377-2217(99)00441-5 |
| Yang JB, Singh MG, 1994. An evidential reasoning approach for multiple attribute decision analysis with uncertainty. IEE Transactions on System, Man and Cybernetic, 24(1), 1-18. DOI: 10.1109/21.259681 |
| Yang JB, Xu DL, 2002. On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty. IEE Transactions on System, Man and Cybernetic-Part A: Systems and Humans, 32(3), 289-304. DOI: 10.1109/TSMCA.2002.802746 |
| Yang Z, Wang J, 2015. Use of fuzzy risk assessment in FMEA of offshore engineering systems. Ocean Engineering, 95, 195-204.DOI: 10.1016/j.oceaneng.2014.11.037 |
| Yang Z, Wang J, Bonsall S, Fang Q, Yang JB, 2005. A subjective risk analysis approach for container supply chains. International Journal of Automation and Computing, 2(1) 85-92. DOI: 10.1007/s11633-005-0085-2 |
| Yen J, Langari R, 1999. Fuzzy logic intelligence, control, and information. Prentice Hall Incorporated, USA. |
| Zadeh LA, 1965. Fuzzy set. Information and Control, 8, 338-353. DOI: 10.1016/S0019-9958(65)90241-X |
| Zadeh LA, 1987. Fuzzy sets and applications: Selected papers. John Wiley, New York, USA. |
| Zalewski P, 2011. Risk Assessment of LNG carrier systems failure using Fuzzy Logic. Scientific Journal of Maritime University of Szczecin, 25(95), 77-85 . |
| Zhou M, Liu X, Yang J, Fang C, 2013. Group evidential reasoning approach for MADA under fuzziness and uncertainties. International Journal of Computational Intelligence Systems, 6(3), 423-441. DOI: 10.1080/18756891.2013.780732 |



