2. Indonesian Hydrodynamic Laboratory, Surabaya 60111, Indonesia
1 Introduction
A number of studies on multihull ships have shown them to have better performance than monohull ships. The development of multihull shipsbegan with the catamaran, whichthenprogressed to the trimaran, quadramaran, and pentamaran. The multihull ship is one approachfor reducingship resistance. Studies of multihull ships have focused on their hull configurations, forms, and composition. Multihull ships are used as commercial and military ships, and differ in their speed and capacities.
In general, the multihull ship has the advantages of stability, payload, speed, and resistance. Seif and Amini (2004) confirmed the advantages of multihull ships in terms of their wider deck space, whichyields better stability compared to single-hull ships. Wave interferences may be divided into two types: constructive and destructive. Constructive interference can amplify the effects of a wave, and destructive negatively effects waves. Current multihull research efforts focus on identifying the configuration that createsthe lowest viscous resistance within a certain speed range.
Quadramarans with a diamond configuration are builton the basis of a similar concept to the trimaran, which has main and sidehulls. The trimaran has two sidehulls and one mainhull, and the diamond quadramaran has two sidehulls between two mainhulls. The trimaran concept has recently beeen claimed by Lindstrom et al. (1995) , Smith and Jones (2001) , and Mynard et al. (2008) to have significant advantages over monohulls and catamarans. Xu and Zou (2001) reported that the main and sidehulls may be arranged so that the ship generates destructive wave interference to produce smaller waves and thereby reduce the energy dissipated in overcoming wave-induced resistance. Yeung (2005) found that in specified hull configurations, trimarans are capable oflowering total ship resistance by about 25% at a speed of 12 m/s compared with monohulls. Yanuar et al. (2013; 2015) conducted studies on the effects of reducing the drag onvarious multihull vessels—including trimarans, tetramarans, and pentamarans—by changing the shape and configuration of their hulls.
The quadramaran is a multihull ship with four identical slender hulls (high ratio L/B) that are either parallel to each other or not. Most multihull ship research is based on thin-ship theory, wherein the focus is on minimizing wave-induced resistance. Fig. 1 shows a range of multihull ship models, as illustrated by Tuck and Lazaukas (1998) in their study of the wave resistance of some model configurations of the monohull, catamaran, trimaran, and quadramaran. Three configurations of the quadramaran have been tested by Tuck, including the tetra (TET), slice (SLI), and diamond (DIA). Three configurations of the Wigley quadramaran were numerically investigated by Peng (2001) . Quadramarans with tetra and slice configurations have been tested by Yanuar, which haveseparate stern and transom hulls. We continue this research, focusingon quadramarans with diamond configurations, and then compare the results with those from a previous experiment. The purpose of this study is to identify the possible effect and influence on ship resistance of a quadramaran with variousposition and hull spacing configurationsin which the dimension of each hull are L: 2 m, B: 0.21 m, and T: 0.07 m. The dimensions of the models used in this experiment are appropriate for the size of the towing tank. Towing test speeds varied at Fr values between 0.1-0.6.
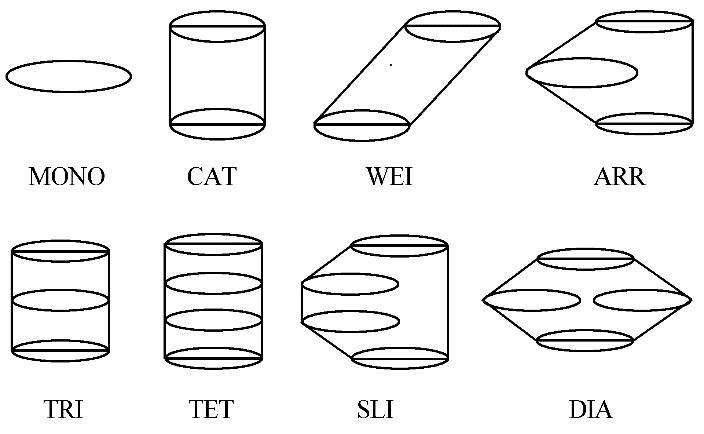
|
| Fig. 1 Ship models tested by Tuck and Lazauskas (1998) |
Our study was performed in a towing tank with calm water. Fig. 2 shows the experimental set-up in a towing tank 40m long, 10 m wide, and with water 2 m deep. The equipment consisted of a load cell transducer, the ship models, an electric motor, a data interface, and a computer. The ship modelswere pulled by an electric motor and maintained a constant speed, and we measured the pull force using a load cell transducer for each run at various velocities (U). The computer recorded, translated, and calculated the data from the load cell to obtain the total resistance (RT).
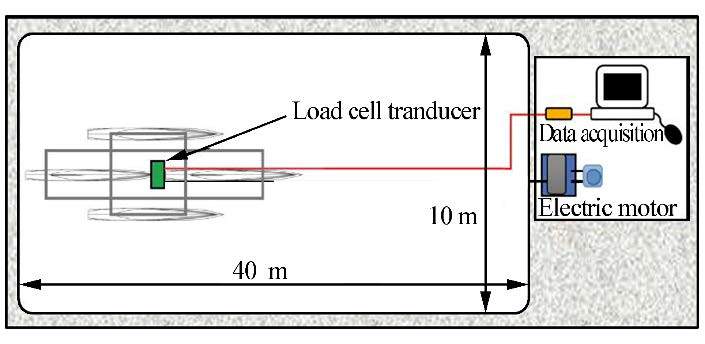
|
| Fig. 2 Experimental set-up in the towing tank |
Each quadramaran hull model was slender with an L/B=10, and the transom form and hull specificationsare shown in Table 1. The quadramaran in our experiment consisted of four identical hulls in a diamond configuration, with the model designs shown in Fig. 3, and a distance between the two central mainhulls of 0.1 m. We classified the ship model configurations into seven types and arranged each type by their transverse distance variations (hull separation, S/L) and longitudinal distance variations (staggered hull, R/L), as shown in Figs. 4 and 5.
| Dimension / Unit | Main hull | Side hull |
| Lm/ m | 2.0 | 2.0 |
| Lwlm/ m | 1.873 | 1.873 |
| Bm / m | 0.2 | 0.2 |
| Hm/ m | 0.205 | 0.205 |
| Tm / m | 0.045 | 0.045 |
| Cbm | 0.469 | 0.469 |
| Sm / m2 | 0.429 | 0.429 |
| Dispm/ kg | 12.5 | 12.5 |
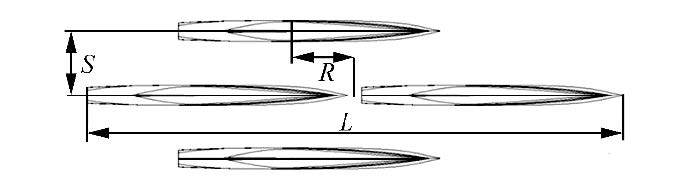
|
| Fig. 3 Design configurations of diamond quadramaran |

|
| Fig. 4 Diamond quadramaran configuration types |
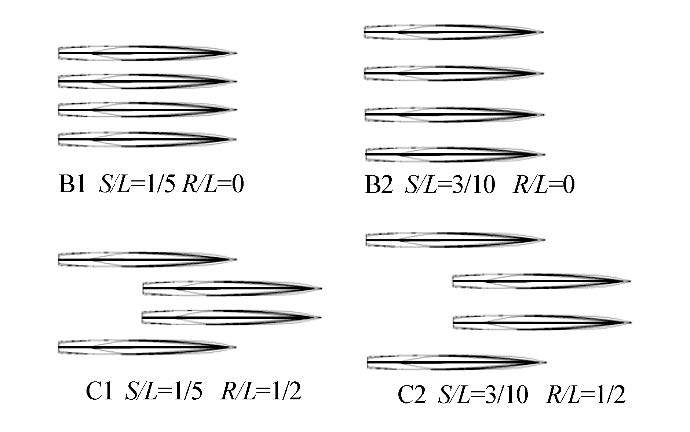
|
| Fig. 5 Tetra and slicequadramaran configuration types from Yanuar et al. [10] |
The International Towing Tank Conference (Recommended Procedure and Guidelines, 2002) classified ship resistance (RT) in calm water into two components: wave resistance (RW) and viscous resistance (RV). Wave resistance relates to the Froude number (inviscid flow) and viscous resistance relates to the Reynolds number (viscous pressure). There is an air resistance which can be ignored because the model testing does not include the superstructure. Total resistance can be defined as
\[{R_T} = {\rm{ }}{R_W} + {\rm{ }}{R_V}\]
(1)
The coefficient of total resistance can be written as
\[{C_T} = {\rm{ }}{C_W} + {\rm{ }}{C_V}\]
(2)
where CW is the coefficient of wake resistance and CV is the coefficient of viscous resistance.
The total resistance coefficient CTis calculated as
\[{C_T} = \frac{{{R_T}}}{{0.5\rho {\kern 1pt} {\kern 1pt} S\,{V^2}}}\]
(3)
The Froude number Fr and Reynolds number Re are defined as:
\[Fr = \frac{V}{{\sqrt {gL} }}\]
(4)
\[Re = \frac{{V \cdot L}}{\nu }\]
(5)
Prohaska defines the three-dimensional form factor k as follows:
\[k = \frac{{{C_V} - {C_F}}}{{{C_F}}} = \frac{{{C_V}}}{{{C_F}}} - 1\]
(6)
where CF is the coefficient of friction resistance. The friction resistance coefficient is calculated according to the ITTC-57 model-ship correlation line as
\[{C_F} = \frac{{0.075}}{{{{ (\lg Re - 2) }^2}}}\]
(7)
For multihull ships:
\[{C_T} = \tau {C_W} + (1 + \varphi k) \sigma {C_F}\]
(8)
where φis the interference factor of the form resistance (from pressure field changes), σ is the viscous resistance interference factor (from the increasing velocity stream around the multihull), and τis the wave resistance interference factor. According to Insel and Molland (1992) ;Molland et al. (1996) , it is difficult to separate the two factors σ and φ by experimental measurement. For practical purposes, therefore, we combined σ and φ into a viscous resistance interference factor β, inwhich (1+φk) σ = (1+βk).
To evaluate the hydrodynamic interference effects of individual design configurations, Hafez and El-Kot (2011) suggest that we can calculate the interference factor η as the difference in total resistance obtained when moving from four separate hulls into one bonded quadramaran. It is convenient to express this difference as a ratio of the non-interference total resistance, as in Eq. (9):
\[\eta = 1 - \frac{{{C_T}}}{{{C_{T - NI}}}}\]
(9)
where CT is the total resistance coefficient of a quadramaran model and CT-NI is the total resistance coefficient of a non-interference quadramaran or the summed individual resistances of the four hulls.
4 Results and discussionThe total resistance is dominated by the wave and viscous resistance components. According to Prohaska, the viscous resistance may be decomposed into the frictional resistance that is influenced by the form factor, and wave resistance can be divided into two components—wave-induced resistance and wave-breaking resistance. To explain further, the interference of waves on the quadraraman hull can generate a phenomenon called hump and hollow at various speeds. Constructive wave interference increaseswave resistance to form a hump, while destructive wave interference reduces the resistance and forms a hollow. The experimental results are shown on the graphs as a function of the Froude number, with the total resistance coefficient and the interference factor. An optimum configuration can be obtained from that with the smallest resistance value (CT).
Fig. 6 shows the total resistance coefficient ofquadramarans with a diamond configuration. The least ship resistance in this experiment was obtained in the DIA-A3 configuration, which utilizes ratios ofS/L=7/41 and R/L=3/82, particularly at high speeds, Fr>0.35. Longitudinal distance variationsthat are more to the front (smaller R/L ratio) and wider transversal distance variations (bigger S/L ratio) contribute to decreasesin ship resistance athigh Fr values, as well as reduced hump sizes.

|
| Fig. 6 Total resistance coefficient CT of diamond quadramaran configurations |
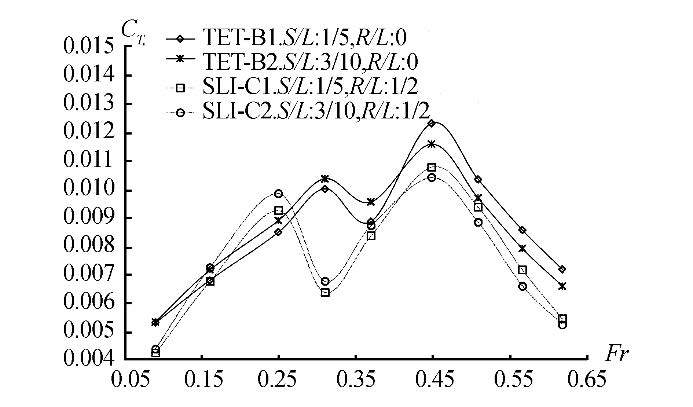
Fig. 7 shows the total resistance coefficients of quadramarans with tetra and slice configurations. The slice configuration has lower ship resistance than the tetra configuration overmost of the Fr range. Nevertheless, the ship resistance on the tetra configuration is more stable at low to medium speeds. The lowest ship resistance in this experiment was obtained by the SLI-C1 configuration, which utilizes ratiosof S/L=1/5 and R/L = 1/2, particularly on low to medium speedsofFr=0.9-0.4, and at high speeds ofFr>0.4. The least ship resistance was obtained on the SLI-C1 configuration at ratiosS/L=3/10 and R/L=1/2. Thus, a longitudinal distance variation of the ship’s main hull that is more to the front (bigger R/L ratio) and a wider transverse distance variation (bigger S/L ratio) contribute toa reduction in ship resistance at highFr values, as well as reducing the hump.
|
| Fig. 7 Total resistance coefficient CT of tetra and slice quadramaran configurations (Yanuar et al. 2015) |
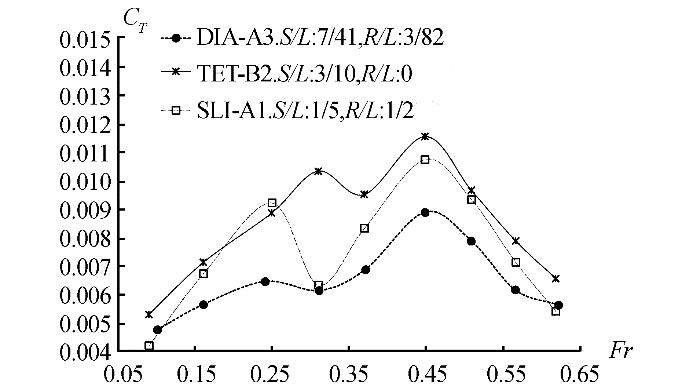
Fig. 8 shows the total resistance coefficient for each optimum quadramaran ship model. Of the three ship hull configurations, the lowest ship resistancesfor most of theFr range (0.1-0.6) was obtained by the diamond configurations. The reducing trend of ship resistance on the tetra configuration is greaterwith respect to the hump value, while in the diamond configuration, we see an increasing trend of the ship resistance value with speed in this experiment. Theseresults are similar to those obtained in experiments by Tuck (1998) , and by Peng (2001) with the Wigley ship hull.
|
| Fig. 8 Total resistance coefficient CT of each optimum quadramaran configuration |
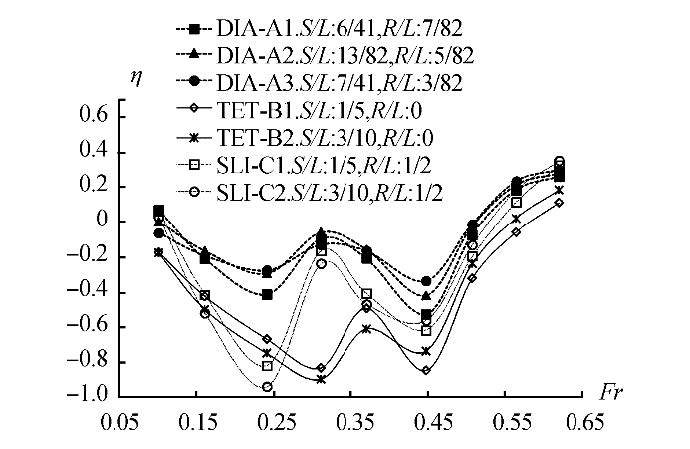
Fig. 9 shows the interference factor in each type of quadramaran configuration for the non-interference quadramaran. A positive interference factor indicates one that is beneficial, i.e., that the resistance of the diamond quadramaran configuration is less than the summed individual resistances of the four hulls, and negative values indicate a detrimental interference. The highest interference factor for this experiment was 0.35 at Fr = 0.62, obtained by the SLI-C2 configuration. For the diamond configuration, the greatest of interference value obtained was 0.3 at Fr = 0.62.
|
| Fig. 9 Interference factor ratio of each configuration |
This paper experimentally investigates the influence of different hull position configurations and side-hull spacing variations on the hydrodynamic interference of quadramaran ship models. Hull separations with greater S/L ratios have the least resistance in each configuration at high speeds (Fr>0.4), i.e., the configuration type A3 has lower resistance than A1 and A2, with similar results for the B and C configurations. The staggered hull generates the least resistance in each configuration, i.e., the configuration type A3 has lower resistance than A2 and A1, C1 is lower than B1, and C2 is lower than B2. The test resultsalso show that an effective interference factor of up to 0.35 can be achieved with the TET-C3 configuration (S/L=3/10, R/L=1/2).
Acknowledgement| Hafez K, El-Kot AR, 2011. Comparative analysis of the separation variation influence on the hydrodynamic performance of a high speed trimaran. Journal of Marine Science and Application, 10, 377-393. DOI: 10.1007/s11804-011-1083-0 |
| Insel M, Molland AF, 1992. An investigation into the resistance components of high speed displacement catamarans. Trans RINA, 134, 1-20. |
| Lindstorm J, Sirvio J, Yli-Rntala A, 1995. Super slender monohull with side hulls. FAST 1995 Conf., Lubeck-Travemunde, Germany, 295-308. |
| Smith RP, Jones JB, 2001. Design, construction and trials of the trident trimaran test craft. Jahrbuch Schiffbau Technische Gesellschaft, Berlin, 355-362. |
| Molland AF, Wellicome JF, Couser PR, 1996. Resistance experiments on a systematic series of high speed catamaran form:Variation of length-displacement ratio and breadth-draught ratio. Trans RINA, 138, 55-71. |
| Mynard T, Sahoo PK, Mikkelsen J, McGreer D, 2008. Numerical and experimental study of wave resistance for trimaran hull forms. The 6th International Conference on High-Performance Marine Vehicles, Naples, Italy, 117-127. |
| Peng HX, 2001. Numerical computation of multi-hull ship resistance and motion. Dalhousie University, Canada. |
| Recommended Procedure and Guidelines, 2002. Testing and extrapolation methods in resistance towing tank test, ITTC 7.5-02-02-02. |
| Seif MS, Amini E, 2004. Performance comparison between planing monohull and trimaran at high froude numbers. Iranian Journal of Science & Technology, Transaction B, 28(B4), 435-441. DOI:10.1.1.552.4761 |
| Tuck EO, Lazauskas L, 1998. Optimum spacing of a family of multihull. Ship Technology Research, 45, 180-195. |
| Xu H, Zou Z, 2001. Numerical prediction of wave-making resistance of a trimaran. Proc. 2nd Int. Workshop on Ship Hydrodynamic(IWSH'01), Wuhan, China, 105-109. |
| Yeung RW, 2005. interference resistance of multihull per thin ship theory. International Workshop on Water Waves & Floating Bodies, Longyearbyen, Spitsbergen, 1-4. |
| Yanuar, Gunawan, Talahatu MA, Indrawati RT, Jamaluddin A, 2013.Resistance analysis of unsymmetrical trimaran model with outboard side-hulls configuration. Journal of Marine Science and Application, 12(3), 293-297. DOI:10.1007/s11804-013-1193-y. |
| Yanuar, Gunawan, Kurniawan T, Waskito T, Jamaluddin A, 2015. Experimental study resistance of asymmetrical pentamaran model with separation and staggered hull variation of inner sidehulls. International Journal of Fluid Mechanics Research, 42(1), 82-94. DOI:10.1615/InterJFluidMechRes.v42.i1.60 |



