Performance of Marine Power Plant Given Generator, Main and Distribution Switchboard Failures
1 Introduction
Power supply without any interruption is the major necessity of every engineering/industrial plant. For continuous power supply, it is essential to identify exactly and accurately that which failures affect the availability/ reliability of the system.
In this area, a lot of research has been done to improve the reliability and production efficiency of various industrial plants(Ram, 2013). Arora and Kumar(1997)discussed the availability of a steam generating system, with three subsystems and a power generation system, consisting of four subsystems arranged in series. Kumar et al.(2006)developed a method for analyzing the fuzzy system reliability for a mixed configuration system using interval valued trapezoidal vague sets. Then with the help of that method analyzed fuzzy reliability of a marine power plant. Sannino et al.(2006)discussed the availability of large offshore wind parks for three different topologies of collection grid and investigated sensitivity and mean time to failure. Ben Elghali et al.(2007)reviewed marine tidal power fundamental concepts then reported on issues regarding electric generator topologies associated with tidal turbines. Eti et al.(2007)deliberated an applications of failure mode effect analysis, failure mode effects, criticality analysis, feedback, support system and risk analysis, in order to reduce the frequency of failures and maintenance costs.
As the failure of any component of a system leads to the failure of the system or degrades the system, fault diagnosis is important(Bhushan and Rengaswamy, 2002; Ram and Manglik, 2014)for the successful operation of any industry/system and for increasing reliability(Hu et al., 2009). In comparison to other production plants, like hydro power plants, Tavner et al.(2006)described an investigation of the reliability of generators and convertors, based on failure data collected in Germany and Denmark, and recommended how the designers and operators of wind turbines can increase their reliability by the choice of design concept and the operating regime. Ye et al.(2001)discussed reliability analysis of a hydro power station. Hosseini et al.(2005)proposed the technique to calculate the annual energy for a small hydro plant, for this, they developed two programs: one using Excel software and other Matlab software. With the help of these programs, the authors analyzed the most important economic indices of a small hydro power plant using sensitivity analysis methods and calculated the reliability indices for number of units for small hydro power plants using the Monte Carlo method. Kumar and Ram(2013)discussed the coal h and ling unit of a thermal power plant, and found some most important reliability measures for the same, using a probabilistic approach. Wang and Zhang(2007)discussed a repairable complex system, with the assumption that a repaired unit cannot work with the same efficiency as a new one, and determined an optimal replacement policy for the system in order to minimize long run expected cost.
2 System description
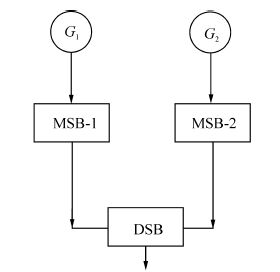
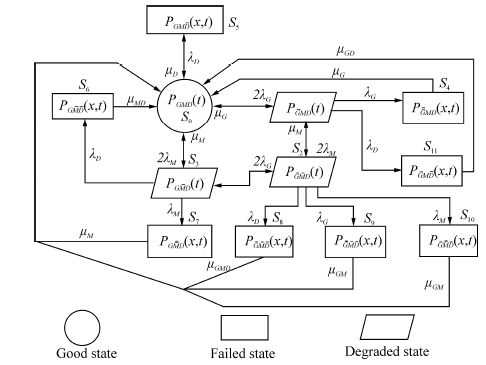
In the present paper, the authors have developed a mathematical model to find the reliability characteristics of an MPP. An MPP is a system which is responsible for power generation in a ship. The MPP consists of two generators, one at the stern and the other at the bow, two main switchboards(MSB) and one distribution switchboard(DSB). The two MSBs are interconnected by a cable(Srinath, 2008). The DSB gets power from the MSB for further distribution and the MSB gets power from the generators. The configuration and transition diagrams of the MPP are shown in Figs. 1 and 2, respectively.
Some assumptions are as follows:
1)Initially, the MPP system is working with full efficiency.
2)The MPP can also work at reduced capacity(i.e. in degraded state).
3)At every instant, sufficient repair facilities are available.
4)Failure rate of each unit is taken to be a constant.
5)No two units will fail simultaneously.
3 Mathematical formulation and solution of the problem
The set of intro-differential equations which governs the present mathematical model(on the basis of state transition diagram)is as follows:
|
$$\displaylines{
\left( {\frac{\partial }{{\partial t}} + 2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right){P_{GMD}}\left( t \right) = \cr
{\mu _G}{P_{\overline G MD}}\left( t \right) + {\mu _M}{P_{G\overline M D}}\left( t \right) + \cr
\int\limits_0^\infty {{\mu _D}{P_{GM\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _G}{P_{\overline {\overline G } MD}}\left( {x{\text{,}}t} \right)} {\text{d}}x\, + \cr
\,\int\limits_0^\infty {{\mu _{MD}}{P_{G\overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _M}{P_{G\overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \cr
\int\limits_0^\infty {{\mu _{GMD}}{P_{\overline G \overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GM}}{P_{\overline {\overline G } \overline M D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \cr
\,\int\limits_0^\infty {{\mu _{GM}}{P_{\overline G \overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GD}}{P_{\overline G M\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x\, \cr} $$
|
(1) |
|
$$\displaylines{
\left( {\frac{\partial }{{\partial t}} + {\lambda _G} + 2{\lambda _M} + {\lambda _D} + {\mu _G}} \right){P_{\overline G MD}}\left( t \right) = \cr
2{\lambda _G}{P_{GMD}}\left( t \right) + {\mu _M}{P_{\overline G \overline M D}}\left( t \right) \cr} $$
|
(2) |
|
$$\displaylines{
\left( {\frac{\partial }{{\partial t}} + {\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _G} + {\mu _M}} \right){P_{\overline G \overline M D}}\left( t \right) = \cr
2{\lambda _M}{P_{\overline G MD}}\left( t \right) + 2{\lambda _G}{P_{G\overline M D}}\left( t \right) \cr} $$
|
(3) |
|
$$\displaylines{
\left( {\frac{\partial }{{\partial t}} + 2{\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _M}} \right){P_{G\overline M D}}\left( t \right) = \cr
{\mu _G}{P_{\overline G \overline M D}}\left( t \right) + 2{\lambda _M}{P_{GMD}}\left( t \right) = \cr
{\mu _G}{P_{\overline G \overline M D}}\left( t \right) + 2{\lambda _M}{P_{GMD}}\left( t \right) \cr} $$
|
(4) |
|
$$\displaylines{
\left( {\frac{\partial }{{\partial x}} + \frac{\partial }{{\partial t}} + {\mu _i}} \right){P_j}\left( {x,t} \right) = 0 \cr
i = G,D,MD,M,GMD,GM,GM,GD \cr
j = \overline {\overline G } DM,GM\overline D ,G\overline M \overline D ,G\overline {\overline M } D,\overline G \overline M \overline D ,\overline {\overline G } \overline M D,\overline G \overline {\overline M } D,\overline G M\overline D \cr} $$
|
(5) |
Boundary conditions:
|
$$\displaylines{
{P_i}\left( {0,t} \right) = {\lambda _j}{P_k}\left( t \right) \cr
i = \overline {\overline G } MD,GM\overline D ,G\overline M \overline D ,G\overline {\overline M } D,\overline G \overline M \overline D ,\overline {\overline G } \overline M D,\overline G \overline {\overline M } D,\overline G M\overline D \cr
j = G,D,D,M,D,G,M,D \cr
k = \overline G MD,GMD,G\overline M D,G\overline M D,\overline G \overline M D,\overline G \overline M D,\overline G \overline M D,\overline G MD \cr} $$
|
(6) |
Initial condition:
|
$${P_{GMD}}\left( 0 \right) = 1$$
|
(7) |
and all other state probabilities are zero at t=0.
Taking Laplace transform from the Eqs.(1)-(6), one gets
|
$$\displaylines{
\left( {s + 2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right){\overline P _{GMD}}\left( s \right) = \cr
1 + {\mu _G}{\overline P _{\overline G MD}}\left( s \right) + {\mu _M}{\overline P _{G\overline M D}}\left( s \right) + \cr
\int\limits_0^\infty {{\mu _D}{{\overline P }_{GM\overline D }}\left( {x,s} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _G}{{\overline P }_{\overline {\overline G } MD}}\left( {x,s} \right)} {\text{d}}x + \cr
\,\,\int\limits_0^\infty {{\mu _{MD}}{{\overline P }_{G\overline M \overline D }}\left( {x,s} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _M}{{\overline P }_{G\overline {\overline M } D}}\left( {x,s} \right)} {\text{d}}x + \cr
\int\limits_0^\infty {{\mu _{GMD}}{{\overline P }_{\overline G \overline M \overline D }}\left( {x,s} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GM}}{{\overline P }_{\overline {\overline G } \overline M D}}\left( {x,s} \right)} {\text{d}}x + \cr
\,\int\limits_0^\infty {{\mu _{GM}}{{\overline P }_{\overline G \overline {\overline M } D}}\left( {x,s} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GD}}{{\overline P }_{\overline G M\overline D }}\left( {x,s} \right)} {\text{d}}x \cr} $$
|
(8) |
|
$$\displaylines{
\left( {s + {\lambda _G} + 2{\lambda _M} + {\lambda _D} + {\mu _G}} \right){\overline P _{\overline G MD}}\left( s \right) = \cr
2{\lambda _G}{\overline P _{GMD}}\left( s \right) + {\mu _M}{\overline P _{\overline G \overline M D}}\left( s \right) \cr} $$
|
(9) |
|
$$\displaylines{
\left( {s + {\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _G} + {\mu _M}} \right){\overline P _{\overline G \overline M D}}\left( s \right) = \cr
2{\lambda _M}{\overline P _{\overline G MD}}\left( s \right) + 2{\lambda _G}{\overline P _{G\overline M D}}\left( s \right) \cr} $$
|
(10) |
|
$$\displaylines{
\left( {s + 2{\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _M}} \right){\overline P _{G\overline M D}}\left( s \right) = \cr
{\mu _G}{\overline P _{\overline G \overline M D}}\left( s \right) + 2{\lambda _M}{\overline P _{GMD}}\left( s \right) \cr} $$
|
(11) |
|
$$\displaylines{
\left( {\frac{\partial }{{\partial x}} + s + {\mu _i}} \right){\overline P _j}\left( {x{\text{,}}s} \right) = 0 \cr
i = G,D,MD,M,GMD,GM,GM,GD \cr
j = \overline {\overline G } DM,GM\overline D ,G\overline M \overline D ,G\overline {\overline M } D,\overline G \overline M \overline D ,\overline {\overline G } \overline M D,\overline G \overline {\overline M } D,\overline G M\overline D \cr} $$
|
(12) |
|
$$\displaylines{
{\overline P _i}\left( {0{\text{,}}s} \right) = {\lambda _j}{\overline P _k}\left( s \right) \cr
i = \overline {\overline G } MD,GM\overline D ,G\overline M \overline D ,G\overline {\overline M } D,\overline G \overline M \overline D ,\overline {\overline G } \overline M D,\overline G \overline {\overline M } D,\overline G M\overline D \cr
j = G,D,D,M,D,G,M,D \cr
k = \overline G MD,GMD,G\overline M D,G\overline M D,\overline G \overline M D,\overline G \overline M D,\overline G \overline M D,\overline G MD \cr} $$
|
(13) |
Solving the above set of equations with the help of initial and boundary conditions, the operative transition state probabilities are given as:
|
$$\displaylines{
{\overline P _{GMD}}\left( s \right) = 1/{\text{[}}s + 2{\lambda _G} + 2{\lambda _M} + {\lambda _D} - \frac{{{\lambda _D}{\mu _D}}}{{\left( {s + {\mu _D}} \right)}} - {H_6} - {H_7} - \cr
\left( {\frac{{\left\{ {{\mu _G} + \frac{{{\lambda _G}{\mu _G}}}{{\left( {s + {\mu _G}} \right)}} + \frac{{{\lambda _D}{\mu _{GD}}}}{{\left( {s + {\mu _{GD}}} \right)}}} \right\}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right){\text{]}}\, \cr} $$
|
(14) |
|
$${\overline P _{\overline G MD}}\left( s \right) = {\overline P _{GMD}}\left( s \right)\left\{ {\frac{{2{\lambda _G} + {\mu _M}{H_4}}}{{{H_1} - {\mu _M}{H_5}}}} \right\}\,$$
|
(15) |
|
$${\overline P _{\overline G \overline M D}}\left( s \right) = {\overline P _{GMD}}\left( s \right)\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\}\,$$
|
(16) |
|
$${\overline P _{G\overline M D}}\left( s \right) = {\overline P _{GMD}}\left( s \right)\left[ {\frac{{{\mu _G}}}{{{H_3}}}\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\} + \frac{{2{\lambda _M}}}{{{H_3}}}} \right]\,$$
|
(17) |
|
$${\overline P _{\overline {\overline G } MD}}\left( s \right) = \frac{{{\lambda _G}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _D}} \right)}}\left\{ {\frac{{2{\lambda _G} + {\mu _M}{H_4}}}{{{H_1} - {\mu _M}{H_5}}}} \right\}$$
|
(18) |
|
$${\overline P _{GM\overline D }}\left( s \right) = \frac{{{\lambda _D}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _D}} \right)}}$$
|
(19) |
|
$$\displaylines{
{\overline P _{G\overline M \overline D }}\left( s \right) = \cr
\frac{{{\lambda _D}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _{MD}}} \right)}}\left[ {\frac{{{\mu _G}}}{{{H_3}}}\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\} + \frac{{2{\lambda _M}}}{{{H_3}}}} \right] \cr} $$
|
(20) |
|
$$\displaylines{
{\overline P _{G\overline {\overline M } D}}\left( s \right) = \cr
\frac{{{\lambda _M}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _M}} \right)}}\left[ {\frac{{{\mu _G}}}{{{H_3}}}\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\} + \frac{{2{\lambda _M}}}{{{H_3}}}} \right] \cr} $$
|
(21) |
|
$${\overline P _{\overline G \overline M \overline D }}\left( s \right) = \frac{{{\lambda _D}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _{GMD}}} \right)}}\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\}$$
|
(22) |
|
$${\overline P _{\overline {\overline G } \overline M D}}\left( s \right) = \frac{{{\lambda _G}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _{GM}}} \right)}}\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\}$$
|
(23) |
|
$${\overline P _{\overline G \overline {\overline M } D}}\left( s \right) = \frac{{{\lambda _M}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _{GM}}} \right)}}\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\}$$
|
(24) |
|
$${\overline P _{\overline G M\overline D }}\left( s \right) = \frac{{{\lambda _D}{{\overline P }_{GMD}}\left( s \right)}}{{\left( {s + {\mu _{GD}}} \right)}}\left\{ {\frac{{2{\lambda _G} + {\mu _M}{H_4}}}{{{H_1} - {\mu _M}{H_5}}}} \right\}$$
|
(25) |
where:
$${H_1} = \left( {s + {\lambda _G} + 2{\lambda _M} + {\lambda _D} + {\mu _G}} \right)$$
$${H_2} = \left( {s + {\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _G} + {\mu _M}} \right)$$
$${H_3} = \left( {s + 2{\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _M}} \right)$$
$${H_4} = \frac{{\frac{{4{\lambda _G}{\lambda _M}}}{{{H_2}{H_3}}}}}{{\left\{ {1 - \frac{{2{\lambda _G}{\lambda _M}}}{{{H_2}{H_3}}}} \right\}}}{\text{, }}{H_5} = \frac{{\frac{{2{\lambda _M}}}{{{H_2}}}}}{{\left\{ {1 - \frac{{2{\lambda _G}{\lambda _M}}}{{{H_2}{H_3}}}} \right\}}}$$
$$\displaylines{
{H_6} = \left\{ {{\mu _M} + \frac{{{\lambda _D}{\mu _{MD}}}}{{\left( {s + {\mu _{MD}}} \right)}} + \frac{{{\lambda _M}{\mu _M}}}{{\left( {s + {\mu _M}} \right)}}} \right\} \times \cr
\,\left[ {\frac{{{\mu _G}}}{{{H_3}}}\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\} + \frac{{2{\lambda _M}}}{{{H_3}}}} \right] \cr} $$
$$\displaylines{
{H_7} = \left\{ {\frac{{{\lambda _D}{\mu _{GMD}}}}{{\left( {s + {\mu _{GMD}}} \right)}} + \frac{{{\lambda _G}{\mu _{GM}}}}{{\left( {s + {\mu _{GM}}} \right)}} + \frac{{{\lambda _M}{\mu _{GM}}}}{{\left( {s + {\mu _{GM}}} \right)}}} \right\} \times \cr
\,\left\{ {{H_4} + \frac{{{H_5}\left( {2{\lambda _G} + {\mu _M}{H_4}} \right)}}{{\left( {{H_1} - {\mu _M}{H_5}} \right)}}} \right\} \cr} $$
From the transition state diagram, the probability that the system is up(i.e. in good or degraded state) and down(failed state)state at any time is given as:
|
$${\overline P _{{\text{up}}}}\left( s \right) = {\overline P _{GMD}}\left( s \right) + {\overline P _{\overline G MD}}\left( s \right) + {\overline P _{G\overline M D}}\left( s \right) + {\overline P _{\overline G \overline M D}}\left( s \right)$$
|
(26) |
|
$$\displaylines{
{\overline P _{{\text{down}}}}\left( s \right) = \cr
{\overline P _{\overline {\overline G } MD}}\left( {x,s} \right) + {\overline P _{G\overline {\overline M } D}}\left( {x,s} \right) + {\overline P _{GM\overline D }}\left( {x,s} \right) + {\overline P _{\overline {\overline G } \overline M D}}\left( {x,s} \right) + \cr
{\overline P _{\overline G \overline {\overline M } D}}\left( {x,s} \right) + {\overline P _{\overline G \overline M \overline D }}\left( {x,s} \right) + {\overline P _{G\overline M \overline D }}\left( s \right) + {\overline P _{\overline G M\overline D }}\left( {x,s} \right) \cr} $$
|
(27) |
4 Assessment of various reliability measures 4.1 Availability assessment
For computing the availability of MPP, setting the values of different failure rates as${\lambda _G} = 0.003{\text{,}}$${\lambda _M} = 0.011{\text{,}}$${\lambda _D} = 0.111$(Kumar et al., 2006) and repair rates as$\,{\mu _G} = \,{\mu _M} = \,{\mu _D} = \,{\mu _{MD}} = {\mu _{GMD}} = {\mu _{GM}} = {\mu _{GD}} = 1$(Ram and Kumar, 2014; Manglik and Ram, 2015)in Eq.(26)then taking the inverse Laplace transform, one can gets the availability of the system as:
|
$$\eqalign{
& {P_{{\text{up}}}}\left( t \right) = 0.122{\kern 1pt} {\kern 1pt} 351{\kern 1pt} {\kern 1pt} 756{\kern 1pt} {\kern 1pt} 2\,\,{{\text{e}}^{ - 1.117{\kern 1pt} 696{\kern 1pt} 201\,t}}{\text{cos}}\left( {0.014{\kern 1pt} {\kern 1pt} 822{\kern 1pt} {\kern 1pt} 852{\kern 1pt} {\kern 1pt} 41\,t} \right) + \cr
& 0.909{\kern 1pt} {\kern 1pt} 991{\kern 1pt} {\kern 1pt} 071{\kern 1pt} {\kern 1pt} 4\,{{\text{e}}^{ - 0.014{\kern 1pt} {\kern 1pt} 146{\kern 1pt} {\kern 1pt} 023{\kern 1pt} {\kern 1pt} 77\,t}} - 0.017{\kern 1pt} {\kern 1pt} 757{\kern 1pt} {\kern 1pt} 395{\kern 1pt} {\kern 1pt} 3\,{{\text{e}}^{ - 1.123{\kern 1pt} {\kern 1pt} 157{\kern 1pt} {\kern 1pt} 403\,t}} + \cr
& 0.147{\kern 1pt} {\kern 1pt} 736{\kern 1pt} {\kern 1pt} 705{\kern 1pt} {\kern 1pt} 3\,{{\text{e}}^{ - 1.117{\kern 1pt} {\kern 1pt} 696{\kern 1pt} {\kern 1pt} 201\,t}}{\text{sin}}\left( {0.014{\kern 1pt} {\kern 1pt} 822{\kern 1pt} {\kern 1pt} 852{\kern 1pt} {\kern 1pt} 41\,t} \right) - \cr
& 0.014{\kern 1pt} {\kern 1pt} 584{\kern 1pt} {\kern 1pt} 521{\kern 1pt} {\kern 1pt} 97\,{{\text{e}}^{ - 1.130{\kern 1pt} {\kern 1pt} 558{\kern 1pt} {\kern 1pt} 144\,t}} - 0.955{\kern 1pt} {\kern 1pt} 100{\kern 1pt} {\kern 1pt} 3\,{10^{ - 6}}{{\text{e}}^{ - 2.152{\kern 1pt} {\kern 1pt} 746{\kern 1pt} {\kern 1pt} 028\,t}} \cr} $$
|
(28) |
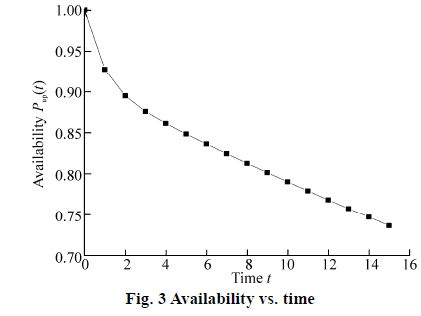
Now varying time unit t in Eq.(28), one gets Table 1 and corresponding Fig. 3, as given below, for availability of MPP.
Table 1 Availability of MPP
| Time t | Availability Pup(t) | Time t | Availability Pup(t) |
| 0 | 1 | 8 | 0.812 636 |
| 1 | 0.927 449 | 9 | 0.801 212 |
| 2 | 0.894 755 | 10 | 0.789 955 |
| 3 | 0.875 583 | 11 | 0.778 858 |
| 4 | 0.861 069 | 12 | 0.767 917 |
| 5 | 0.848 232 | 13 | 0.757 131 |
| 6 | 0.836 069 | 14 | 0.746 496 |
| 7 | 0.824 242 | 15 | 0.736 010 |
4.2 Reliability assessment
For computing the reliability of the MPP setting the values of different failure rates as ${\lambda _G} = 0.003{\text{,}}{\lambda _M} = 0.011{\text{,}}{\lambda _D} = 0.111$(Kumar et al., 2006)repair rates as $\,{\mu _G} = \,{\mu _M} = \,{\mu _D} = \,{\mu _{MD}} = {\mu _{GMD}} = {\mu _{GM}} = {\mu _{GD}} = 0$(Ram and Kumar, 2015)in Eq.(26)then taking the inverse Laplace transform, one gets the reliability of the MPP as:
|
$$\displaylines{
R\left( t \right) = 5\,{{\text{e}}^{ - 0.139\,t}} + 4\,{{\text{e}}^{ - 0.137{\kern 1pt} 5\,t}}{\text{sinh}}\left( {0.001{\kern 1pt} {\kern 1pt} 5{\kern 1pt} \,t} \right) - 4\,{{\text{e}}^{ - 0.136\,t}} + \cr
4\,{{\text{e}}^{ - 0.133{\kern 1pt} 5\,t}}{\text{sinh}}\left( {0.005{\kern 1pt} {\kern 1pt} 5\,t} \right) + 4\,{{\text{e}}^{ - 0.125\,t}} - 4\,{{\text{e}}^{ - 0.128\,t}} \cr} $$
|
(29) |
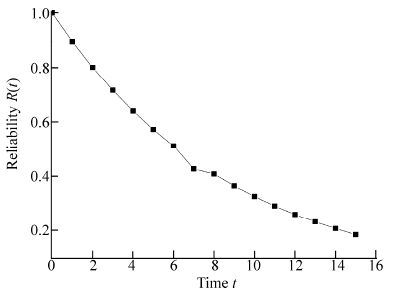
Now vary the time unit t from 0 to 15 in Eq.(29), one gets Table 2 and corresponding Fig. 4, as given below, for reliability of MPP.
Table 2 Reliability of MPP
| Time t | Reliability R(t) | Time t | Reliability R(t) |
| 0 | 1 | 8 | 0.408 328 |
| 1 | 0.894 823 | 9 | 0.364 716 |
| 2 | 0.800 507 | 10 | 0.325 698 |
| 3 | 0.715 957 | 11 | 0.290 797 |
| 4 | 0.640 185 | 12 | 0.259 587 |
| 5 | 0.572 301 | 13 | 0.231 684 |
| 6 | 0.511 500 | 14 | 0.206 743 |
| 7 | 0.427 060 | 15 | 0.184 455 |
4.3 Mean time to failure assessment
For computing the MTTF of MPP, taking all repairs equal to zero for exponential distribution in Eq.(26) and taking as s tends to zero, one can obtain the MTTF of MPP as:
|
$$\displaylines{
{\text{MTTF}} = \frac{1}{{\left( {2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right)}} + \cr
\frac{{2{\lambda _G}}}{{\left( {2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right)\left( {{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right)}} + \cr
\frac{{2{\lambda _M}}}{{\left( {2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right)\left( {2{\lambda _G} + {\lambda _M} + {\lambda _D}} \right)}} + \cr
\frac{{4{\lambda _G}{\lambda _M}}}{{\left( {{\lambda _G} + {\lambda _M} + {\lambda _D}} \right){{\left( {2{\lambda _G} + {\lambda _M} + {\lambda _D}} \right)}^2}}} + \cr
\frac{{4{\lambda _G}{\lambda _M}}}{{\left( {{\lambda _G} + {\lambda _M} + {\lambda _D}} \right)\left( {{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right)\left( {2{\lambda _G} + {\lambda _M} + {\lambda _D}} \right)}} \cr} $$
|
(30) |
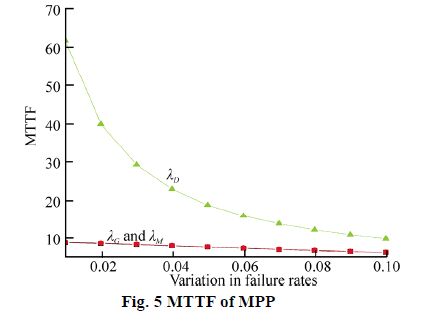
Setting failure rates as${\lambda _G} = 0.003{\text{,}}{\lambda _M} = 0.011{\text{,}}{\lambda _D} = 0.111$(Kumar et al., 2006) and varying failure rates from 0.01 to 0.10(with a time interval of 0.01)one by one in Eq.(30), we get the MTTF of the MPP as tabulated in Table 3 and Fig. 5.
Table 3 MTTF of MPP
| Variations in ${\lambda _G}\,{\text{,}}\,{\lambda _M}{\text{,}}{\lambda _D}$ | MTTF with respect to failure rates |
| ${\lambda _G}\,$ | ${\lambda _M}\,$ | $$\,{\lambda _D}$$ |
| 0.01 | 8.768 456 | 8.883 929 | 61.765 524 |
| 0.02 | 8.531 786 | 8.634 619 | 39.981 893 |
| 0.03 | 8.238 186 | 8.327 800 | 29.233 642 |
| 0.04 | 7.924 509 | 8.002 036 | 22.923 006 |
| 0.05 | 7.609 688 | 7.676 696 | 18.803 099 |
| 0.06 | 7.303 434 | 7.361 471 | 15.914 252 |
| 0.07 | 7.010 532 | 7.060 978 | 13.781 991 |
| 0.08 | 6.733 079 | 6.777 110 | 12.146 275 |
| 0.09 | 6.471 686 | 6.510 289 | 10.853 221 |
| 0.10 | 6.226 140 | 6.260 146 | 9.806 202 |
4.4 Sensitivity assessment
4.4.1 Sensitivity with respect to MTTF
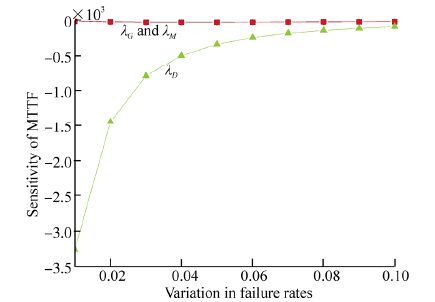
For sensitivity analysis of MPP with respect to MTTF, differentiating the Eq.(30)with respect to failure rates, then putting the values of various failure rates as ${\lambda _G} = 0.003{\text{,}}{\lambda _M} = 0.011{\text{,}}{\lambda _D} = 0.111$(Kumar et al., 2006; Wang and Zhang, 2007), we get the values of ${\partial \left( \text{MTTF} \right)}/{\partial {{\lambda }_{G}}}\;\,\text{,}\,{\partial \left( \text{MTTF} \right)}/{\partial {{\lambda }_{M}}}\;\text{, }{\partial \left( \text{MTTF} \right)}/{\partial {{\lambda }_{D}}}\;$ ${\partial \left( \text{MTTF} \right)}/{\partial {{\lambda }_{M}}}\;\text{, }{\partial \left( \text{MTTF} \right)}/{\partial {{\lambda }_{D}}}\;$. Now varying the failure rates one by one respectively as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10 in the partial derivatives of MTTF with respect to different failure rates, one can obtain Table 4 and corresponding Fig. 6 as given below.
Table 4 Sensitivity of MTTF
| Variations in ${\lambda _G}\,{\text{,}}\,{\lambda _M}{\text{,}}\,{\lambda _D}$ | $\,\frac{{\partial \left( {{\text{MTTF}}} \right)}}{{\partial {\lambda _G}}}$ | $\,\frac{{\partial \left( {{\text{MTTF}}} \right)}}{{\partial {\lambda _M}}}$ | $\,\frac{{\partial \left( {{\text{MTTF}}} \right)}}{{\partial {\lambda _D}}}$ |
| 0.01 | ‒18.828 004 | ‒19.937 357 | ‒3 260.827 933 |
| 0.02 | ‒27.345 142 | ‒28.684 763 | ‒1 445.660 690 |
| 0.03 | ‒30.788 850 | ‒32.067 973 | ‒796.836 785 |
| 0.04 | ‒31.644 330 | ‒32.776 529 | ‒499.058 284 |
| 0.05 | ‒31.164 750 | ‒32.137 029 | ‒339.838 967 |
| 0.06 | ‒30.009 906 | ‒30.834 707 | ‒245.450 799 |
| 0.07 | ‒28.537 386 | ‒29.234 359 | ‒185.174 359 |
| 0.08 | ‒26.944 078 | ‒27.533 202 | ‒144.459 072 |
| 0.09 | ‒25.338 557 | ‒25.837 752 | ‒115.724 449 |
| 0.10 | ‒23.779 663 | ‒24.204 187 | ‒94.719 457 |
4.4.2 Sensitivity with respect to reliability
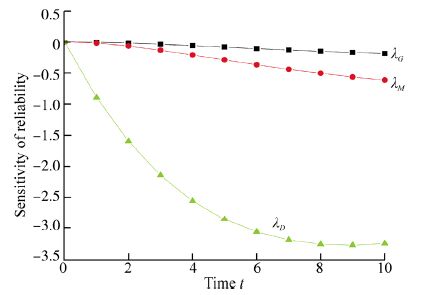
The sensitivity analysis of reliability is carried out by differentiating the reliability expression with respect to various failure rates, and then setting(Kumar et al., 2006), we get the values ofNow, taking time unit t from 0 to 10 in the partial derivatives of reliability with respect to different failure rates, one can obtain Table 5 and corresponding Fig. 7.
Table 5 Sensitivity of reliability
| Time t | $\frac{{\partial R\left( t \right)}}{{\partial {\lambda _G}}}$ | $\frac{{\partial R\left( t \right)}}{{\partial {\lambda _M}}}$ | $\frac{{\partial R\left( t \right)}}{{\partial {\lambda _D}}}$ |
| 0 | 0 | 0 | 0 |
| 1 | ‒0.005 344 | ‒0.019 366 | ‒0.894 823 |
| 2 | ‒0.019 040 | ‒0.068 191 | ‒1.601 014 |
| 3 | ‒0.038 146 | ‒0.135 061 | ‒2.147 872 |
| 4 | ‒0.060 370 | ‒0.211 361 | ‒2.560 742 |
| 5 | ‒0.083 954 | ‒0.290 708 | ‒2.861 506 |
| 6 | ‒0.107 576 | ‒0.368 494 | ‒3.069 005 |
| 7 | ‒0.130 267 | ‒0.441 499 | ‒3.199 423 |
| 8 | ‒0.151 342 | ‒0.507 595 | ‒3.266 625 |
| 9 | ‒0.170 343 | ‒0.565 488 | ‒3.282 451 |
| 10 | ‒0.186 990 | ‒0.614 520 | ‒3.256 983 |
4.5 Expected profit from MPP
The profit function(Ram and Kumar, 2014)for the MPP in time interval [0, t)is given as:
|
$${E_P}\left( t \right) = {K_1}\int_0^t {{P_{{\text{up}}}}\left( t \right){\text{d}}t - t{K_2}} $$
|
(31) |
Using Eq.(28)in Eq.(31), one obtains the profit function as given below:
|
$$\displaylines{
{E_p}\left( t \right)\, = \, \cr
{K_1}{\text{[}} - 0.111{\kern 1pt} 201{\kern 1pt} {\kern 1pt} 215{\kern 1pt} 3{\kern 1pt} {\kern 1pt} {{\text{e}}^{ - {\text{1}}{\text{.117696201 }}t}}{\text{cos}}\left( {0.014{\kern 1pt} 822{\kern 1pt} {\kern 1pt} 852{\kern 1pt} 41\,t} \right) - \cr
0.130{\kern 1pt} {\kern 1pt} 704{\kern 1pt} 9142\,{{\text{e}}^{ - 1.117{\kern 1pt} 696{\kern 1pt} 201\,t}}{\text{sin}}\left( {0.014{\kern 1pt} {\kern 1pt} 822{\kern 1pt} 852{\kern 1pt} {\kern 1pt} 41\,t} \right) - \cr
64.328{\kern 1pt} {\kern 1pt} 399{\kern 1pt} 71\,{{\text{e}}^{ - {\text{0}}{\text{.014}}{\kern 1pt} {\text{146}}{\kern 1pt} {\kern 1pt} {\text{023}}{\kern 1pt} {\text{77}}\,t}} + \cr
0.443{\kern 1pt} {\kern 1pt} 666{\kern 1pt} 037{\kern 1pt} {\kern 1pt} 5 \times {10^{ - 6}}\,{{\text{e}}^{ - 2.152{\kern 1pt} 746{\kern 1pt} 028\,t}} + \cr
0.012{\kern 1pt} {\kern 1pt} 900{\kern 1pt} 284{\kern 1pt} {\kern 1pt} 74\,{{\text{e}}^{ - 1.130{\kern 1pt} {\kern 1pt} 558{\kern 1pt} 144\,t}} - \cr
0.015{\kern 1pt} {\kern 1pt} 810{\kern 1pt} 246{\kern 1pt} {\kern 1pt} 41\,{{\text{e}}^{ - 1.123{\kern 1pt} {\kern 1pt} 157{\kern 1pt} 403\,t}} + 64.410{\kern 1pt} 889{\kern 1pt} 96{\text{]}} - t{K_2} \cr} $$
|
(32) |
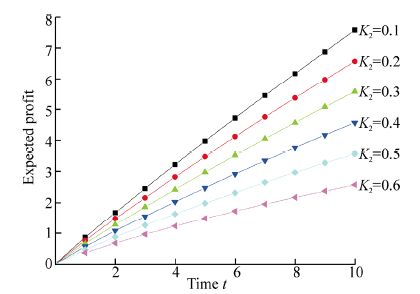
Setting revenue K1=1 and service cost as K2=0.1, 0.2, 0.3, 0.4, 0.5 and 0.6 respectively then varying time scale t in Eq.(32), one gets Table 6 and correspondingly Fig. 8 for expected profit of an MPP as follows.
Table 6 Expected profit of MPP
| Time t | Expected profit Ep(t) |
| K2= 0.1 | K2= 0.2 | K2= 0.3 | K2= 0.4 | K2= 0.5 | K2= 0.6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0.858 | 0.758 | 0.658 | 0.558 | 0.458 | 0.358 |
| 2 | 1.667 | 1.467 | 1.267 | 1.067 | 0.867 | 0.667 |
| 3 | 2.452 | 2.152 | 1.852 | 1.552 | 1.252 | 0.952 |
| 4 | 3.220 | 2.820 | 2.420 | 2.020 | 1.620 | 1.220 |
| 5 | 3.974 | 3.474 | 2.974 | 2.474 | 1.974 | 1.474 |
| 6 | 4.717 | 4.117 | 3.517 | 2.917 | 2.317 | 1.717 |
| 7 | 5.447 | 4.747 | 4.047 | 3.347 | 2.647 | 1.947 |
| 8 | 6.165 | 5.365 | 4.565 | 3.765 | 2.965 | 2.165 |
| 9 | 6.872 | 5.972 | 5.072 | 4.172 | 3.272 | 2.372 |
| 10 | 7.568 | 6.568 | 5.568 | 4.568 | 3.568 | 2.568 |
5 Results and discussion
In the present paper, the authors have developed a mathematical model to find the reliability characteristics of an MPP. The graph between availability and time shown in Fig. 3 reveals that the availability of an MPP decreases smoothly as time passes. The reliability of an MPP with respect to the time scale t is shown in Fig. 4. It can be seen from the figure that the reliability of an MPP decreases faster than availability as time passes. This reflects the importance of repair policy. Fig. 5 shows the graph between MTTF of an MPP and variation in failure rates. From the graph it is observed that the MTTF of a marine power plant decreases with respect to all types of failure rates. It is highest with failure rates of the distribution switchboard i.e. MTTF of an MPP is greatly affected by the failure rate of distribution switchboards. The sensitivity of MTTF for an MPP is shown in Fig. 6. It shows that the MTTF is equally sensitive to the failure rates of generators and main switchboards. Also, it is very sensitive to the failure rate of the distribution switchboard. From this one can say that we have to focus more on the failure rate of distribution switchboards to enhance reliability of an MPP. Fig. 7 shows the sensitivity analysis of reliability of an MPP with respect to different failure rates, and shows the reliability of an MPP is most sensitive to the failure rate of the distribution switchboards. Further, in order to make the system reliability less sensitive, one has to control the failure rate of distribution switchboards. Keeping the revenue per unit time fixed at 1 and varying service cost as 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6, Fig. 8 is obtained. It is very clear from the graph that the profit decreases as the service cost increases with the passage of time. So, in order to optimize the profit function one has to control service cost as well as various failure rates of an MPP.
6 Conclusion
On the basis of the calculation and discussion above for marine power plants, it is noticeable that the system is highly sensitive to failure rate of distribution switchboards. So in order to make marine power plants more reliable, one has to especially control failure rate of the distribution switchboards. Also, we see that it is equally sensitive to failure rates of generators and main switchboards. The difference between the graph of availability and reliability shows the importance of repairs. Hence it is observed that good maintenance is the major requirement for the successful functioning of any system. It is asserted that the findings of this paper are highly beneficial for the management of marine power plants.
Nomenclatures
The following notations have been used throughout the MPP model:
| $${P_{GMD}}\left( t \right)$$ | The probability that at time t, the MPP is working with full efficiency. |
| $${P_{\overline G MD}}\left( t \right)$$ | The probability that at time t, the MPP is operational in the degraded state with one failed generator. |
| $${P_{G\overline M D}}\left( t \right)$$ | The probability that at time t, the MPP is operational in the degraded state with one failed MSB. |
| $${P_{\overline G \overline M D}}\left( t \right)$$ | The probability that at time t, the MPP is operational in the degraded state with one failed generator and one failed MSB. |
| $${P_{\overline {\overline G } MD}}\left( {x,t} \right)$$ | The probability that at time t, the MPP has failed due to the failure of both the generators. |
| $${P_{G\overline {\overline M } D}}\left( {x,t} \right)$$ | The probability that at time t, the MPP has failed due to the failure of both the MSB. |
| $${P_{GM\overline D }}\left( {x,t} \right)$$ | The probability that at time t, the MPP has failed due to the failure of DSB. |
| $${P_{\overline {\overline G } \overline M D}}\left( {x,t} \right)$$ | The probability that at time t, the MPP has failed due to the failure of both generators and one MSB. |
| $${P_{\overline G \overline {\overline M } D}}\left( {x,t} \right)$$ | The probability that at time t, the MPP has failed due to the failure of one generator and both the MSB. |
| $${P_{\overline G M\overline D }}\left( {x,t} \right)$$ | The probability that at time t, the MPP has failed due to the failure of one generator and DSB. |
| $${P_{G\overline M \overline D }}\left( {x,t} \right)$$ | The probability that at time t, the MPP has failed due to the failure of one MSB and DSB. |
| $${\lambda _G}/{\lambda _M}/{\lambda _D}$$ | The probability that at time t, the MPP has failed due to the failure of one generator, one MSB and complete failure of DSB. |
| $${\mu _G}/{\mu _M}/{\mu _D}$$ | The failure rate of generator/MSB/DSB. |
| $${\mu _{GM}}/{\mu _{GD}}$$ | The repair rate of generator/MSB/DSB. |
| $${\mu _{MD}}/{\mu _{GMD}}$$ | Simultaneous repair rate of the generator and MSB/generator and DSB/MSB and DSB/generator, MSB and DSB. |
| $${K_1}/{K_2}$$ | The revenue/service cost from the MPP. |
| t/s | Time scale variable in years/Laplace transform variable. |
Appendix A
At any time t, if the system is in state Si, then the probability of the system to be in that state is defined as: Probability that the system is in state Si at time t and remains there in interval $\left( {t{\text{, }}t + {\text{Δ }}t} \right)$ or/ and if it is in some other state at time t then it should transit to the state Si in the interval $\left( {t{\text{, }}t + {\text{Δ }}t} \right)$ provided transition exist between the states and ${\text{Δ }}t \to 0.$
Accordingly the equations are interpreted as: the probability of the system to be in state S0 in the interval $\left( {t{\text{, }}t + {\text{Δ }}t} \right)$ is given by
$${P_{GMD}}\left( {t + {\text{Δ }}t} \right) = \left( {1 - 2{\lambda _G}{\text{Δ }}t} \right)\left( {1 - 2{\lambda _M}{\text{Δ }}t} \right)\left( {1 - {\lambda _D}{\text{Δ }}t} \right){P_{GMD}}\left( t \right) + $$
$${\mu _G}{P_{\overline G MD}}\left( t \right){\text{Δ }}t + {\mu _M}{P_{G\overline M D}}\left( t \right){\text{Δ }}t + \int\limits_0^\infty {{\mu _D}{P_{GM\overline D }}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _G}{P_{\overline {\overline G } MD}}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x + \int\limits_0^\infty {{\mu _{MD}}{P_{G\overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _M}{P_{G\overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x + \int\limits_0^\infty {{\mu _{GMD}}{P_{\overline G \overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _{GM}}{P_{\overline {\overline G } \overline M D}}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x + \int\limits_0^\infty {{\mu _{GM}}{P_{\overline G \overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _{GD}}{P_{\overline G M\overline D }}\left( {x{\text{,}}t} \right)} {\text{Δ }}t{\text{d}}x \Rightarrow $$
$$\frac{{{P_{GMD}}\left( {t + {\text{Δ }}t} \right) - {P_{GMD}}\left( t \right)}}{{{\text{Δ }}t}} + \left( {2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right){P_{GMD}}\left( t \right) = $$
$${\mu _G}{P_{\overline G MD}}\left( t \right) + {\mu _M}{P_{G\overline M D}}\left( t \right) + \int\limits_0^\infty {{\mu _D}{P_{GM\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _G}{P_{\overline {\overline G } MD}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{MD}}{P_{G\overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _M}{P_{G\overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _{GMD}}{P_{\overline G \overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GM}}{P_{\overline {\overline G } \overline M D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _{GM}}{P_{\overline G \overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GD}}{P_{\overline G M\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x$$
Now taking, one gets:
$$ \Rightarrow \mathop {{\text{lim}}\,}\limits_{{\text{Δ }}t \to 0} \frac{{{P_{GMD}}\left( {t + {\text{Δ }}t} \right) - {P_{GMD}}\left( t \right)}}{{{\text{Δ }}t}} + \left( {2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right){P_{GMD}}\left( t \right) = $$
$${\mu _G}{P_{\overline G MD}}\left( t \right) + {\mu _M}{P_{G\overline M D}}\left( t \right) + \int\limits_0^\infty {{\mu _D}{P_{GM\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _G}{P_{\overline {\overline G } MD}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{MD}}{P_{G\overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _M}{P_{G\overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _{GMD}}{P_{\overline G \overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GM}}{P_{\overline {\overline G } \overline M D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _{GM}}{P_{\overline G \overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GD}}{P_{\overline G M\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x$$
$$ \Rightarrow \left[ {\frac{\partial }{{\partial t}} + 2{\lambda _G} + 2{\lambda _M} + {\lambda _D}} \right]{P_{GMD}}\left( t \right) = {\mu _G}{P_{\overline G MD}}\left( t \right) + {\mu _M}{P_{G\overline M D}}\left( t \right) + $$
$$\int\limits_0^\infty {{\mu _D}{P_{GM\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _G}{P_{\overline {\overline G } MD}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{MD}}{P_{G\overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
$$\int\limits_0^\infty {{\mu _M}{P_{G\overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + + \int\limits_0^\infty {{\mu _{GMD}}{P_{\overline G \overline M \overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GM}}{P_{\overline {\overline G } \overline M D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + $$
|
$$\int\limits_0^\infty {{\mu _{GM}}{P_{\overline G \overline {\overline M } D}}\left( {x{\text{,}}t} \right)} {\text{d}}x + \int\limits_0^\infty {{\mu _{GD}}{P_{\overline G M\overline D }}\left( {x{\text{,}}t} \right)} {\text{d}}x$$
|
(A1) |
For state ${S_1}$,
$$\displaylines{
{P_{\overline G MD}}\left( {t + {\text{Δ }}t} \right) = \cr
\left( {1 - {\lambda _G}{\text{Δ }}t} \right)\left( {1 - 2{\lambda _M}{\text{Δ }}t} \right)\left( {1 - {\lambda _D}{\text{Δ }}t} \right)\left( {1 - {\mu _G}{\text{Δ }}t} \right){P_{\overline G MD}}\left( t \right) + \cr} $$
$$2{\lambda _G}{\text{Δ }}t{P_{GMD}}\left( t \right) + {\mu _M}{\text{Δ }}t{P_{\overline G \overline M D}}\left( t \right) \Rightarrow $$
$$\frac{{{P_{\overline G MD}}\left( {t + {\text{Δ }}t} \right) - {P_{\overline G MD}}\left( t \right)}}{{{\text{Δ }}t}} + \left( {{\lambda _G} + 2{\lambda _M} + {\lambda _D} + {\mu _G}} \right){P_{\overline G MD}}\left( t \right) = $$
$$2{\lambda _G}{P_{GMD}}\left( t \right) + {\mu _M}{P_{\overline G \overline M D}}\left( t \right)$$
Now taking, one gets:
|
$$\displaylines{
\Rightarrow \mathop {{\text{lim}}}\limits_{{\text{Δ }}t \to 0} \frac{{{P_{\overline G MD}}\left( {t + {\text{Δ }}t} \right) - {P_{\overline G MD}}\left( t \right)}}{{{\text{Δ }}t}} + \cr
\left( {{\lambda _G} + 2{\lambda _M} + {\lambda _D} + {\mu _G}} \right){P_{\overline G MD}}\left( t \right) = \cr
2{\lambda _G}{P_{GMD}}\left( t \right) + {\mu _M}{P_{\overline G \overline M D}}\left( t \right) \Rightarrow \cr
\left[ {\frac{\partial }{{\partial t}} + {\lambda _G} + 2{\lambda _M} + {\lambda _D} + {\mu _G}} \right]{P_{\overline G MD}}\left( t \right) = \cr
2{\lambda _G}{P_{GMD}}\left( t \right) + {\mu _M}{P_{\overline G \overline M D}}\left( t \right) \cr} $$
|
(A2) |
For state ${S_2}$,
$$\displaylines{
{P_{\overline G \overline M D}}\left( {t + {\text{Δ }}t} \right) = \cr
\left( {1 - {\lambda _G}{\text{Δ }}t} \right)\left( {1 - {\lambda _M}{\text{Δ }}t} \right)\left( {1 - {\lambda _D}{\text{Δ }}t} \right)\left( {1 - {\mu _G}{\text{Δ }}t} \right)\left( {1 - {\mu _M}{\text{Δ }}t} \right){P_{\overline G \overline M D}}\left( t \right) + \cr} $$
$$2{\lambda _G}{\text{Δ }}t{P_{G\overline M D}}\left( t \right) + 2{\lambda _M}{\text{Δ }}t{P_{\overline G MD}}\left( t \right) \Rightarrow $$
$$\displaylines{
\frac{{{P_{\overline G \overline M D}}\left( {t + {\text{Δ }}t} \right) - {P_{\overline G \overline M D}}\left( t \right)}}{{{\text{Δ }}t}} + \cr
\left( {{\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _G} + {\mu _M}} \right){P_{\overline G \overline M D}}\left( t \right) = \cr} $$
$$2{\lambda _G}{P_{G\overline M D}}\left( t \right) + 2{\lambda _M}{P_{\overline G MD}}\left( t \right)$$
Now taking, one gets:
|
$$\displaylines{
\Rightarrow \mathop {{\text{lim}}}\limits_{{\text{Δ }}t \to 0} \frac{{{P_{\overline G \overline M D}}\left( {t + {\text{Δ }}t} \right) - {P_{\overline G \overline M D}}\left( t \right)}}{{{\text{Δ }}t}} + \cr
\left( {{\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _G} + {\mu _M}} \right){P_{\overline G \overline M D}}\left( t \right) = \cr
2{\lambda _G}{P_{G\overline M D}}\left( t \right) + 2{\lambda _M}{P_{\overline G MD}}\left( t \right) \Rightarrow \cr
\left[ {\frac{\partial }{{\partial t}} + {\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _G} + {\mu _M}} \right]{P_{\overline G \overline M D}}\left( t \right) = \cr
2{\lambda _M}{P_{\overline G MD}}\left( t \right) + 2{\lambda _G}{P_{G\overline M D}}\left( t \right) \cr} $$
|
(A3) |
For state ${S_3}$,
$$\displaylines{
{P_{G\overline M D}}\left( {t + {\text{Δ }}t} \right) = \cr
\left( {1 - {\lambda _M}{\text{Δ }}t} \right)\left( {1 - {\lambda _D}{\text{Δ }}t} \right)\left( {1 - 2{\lambda _G}{\text{Δ }}t} \right)\left( {1 - {\mu _M}{\text{Δ }}t} \right){P_{G\overline M D}}\left( t \right) + \cr
{\mu _G}{\text{Δ }}t{P_{\overline G \overline M D}}\left( t \right) + 2{\lambda _M}{\text{Δ }}t{P_{GMD}}\left( t \right) \Rightarrow \cr} $$
$$\frac{{{P_{G\overline M D}}\left( {t + {\text{Δ }}t} \right) - {P_{G\overline M D}}\left( t \right)}}{{{\text{Δ }}t}} + \left( {{\lambda _M} + {\lambda _D} + 2{\lambda _G} + {\mu _M}} \right){P_{G\overline M D}}\left( t \right) = $$
$${\mu _G}{P_{\overline G \overline M D}}\left( t \right) + 2{\lambda _M}{P_{GMD}}\left( t \right)$$
Now taking, one gets:
|
$$\displaylines{
\Rightarrow \mathop {{\text{lim}}}\limits_{{\text{Δ }}t \to 0} \frac{{{P_{G\overline M D}}\left( {t + {\text{Δ }}t} \right) - {P_{G\overline M D}}\left( t \right)}}{{{\text{Δ }}t}} + \cr
\left( {{\lambda _M} + {\lambda _D} + 2{\lambda _G} + {\mu _M}} \right){P_{G\overline M D}}\left( t \right) = \cr
{\mu _G}{P_{\overline G \overline M D}}\left( t \right) + 2{\lambda _M}{P_{GMD}}\left( t \right) \Rightarrow \cr
\left[ {\frac{\partial }{{\partial t}} + 2{\lambda _G} + {\lambda _M} + {\lambda _D} + {\mu _M}} \right]{P_{G\overline M D}}\left( t \right) = \cr
{\mu _G}{P_{\overline G \overline M D}}\left( t \right) + 2{\lambda _M}{P_{GMD}}\left( t \right) \cr} $$
|
(A4) |
For state ${S_4}$,
|
$\begin{matrix}
{{P}_{\overline{\overline{G}}MD}}\left( x+\text{ }\!\!\Delta\!\!\text{ }x,t+\text{ }\!\!\Delta\!\!\text{ }t \right)=\left\{ 1-{{\mu }_{G}}\text{ }\!\!\Delta\!\!\text{ }t \right\}{{P}_{\overline{\overline{G}}MD}}\left( x,t \right)\Rightarrow \\
\underset{\begin{smallmatrix}
\text{ }\!\!\Delta\!\!\text{ }x\to 0 \\
\text{ }\!\!\Delta\!\!\text{ }t\to 0
\end{smallmatrix}}{\mathop{\text{lim}}}\,\frac{{{P}_{\overline{\overline{G}}MD}}\left( x+\text{ }\!\!\Delta\!\!\text{ }x,t+\text{ }\!\!\Delta\!\!\text{ }t \right)-{{P}_{\overline{\overline{G}}MD}}\left( x,t \right)}{\text{ }\!\!\Delta\!\!\text{ }t}+{{\mu }_{G}}{{P}_{\overline{\overline{G}}MD}}\left( x,t \right)=0\Rightarrow \\
\left[ \frac{\partial }{\partial t}+\frac{\partial }{\partial x}+{{\mu }_{G}} \right]{{P}_{\overline{\overline{G}}MD}}\left( x,t \right)=0 \\
\end{matrix}$
|
(A5) |
For state ${S_5}$,
|
$$\displaylines{
{P_{GM\overline D }}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) = \left\{ {1 - {\mu _D}{\text{Δ }}t} \right\}{P_{GM\overline D }}\left( {x,t} \right) \Rightarrow \cr
\mathop {{\text{lim}}}\limits_{\scriptstyle {\text{Δ }}x \to 0 \atop
\scriptstyle {\text{Δ }}t \to 0} \frac{{{P_{GM\overline D }}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) - {P_{GM\overline D }}\left( {x,t} \right)}}{{{\text{Δ }}t}} + {\mu _D}{P_{GM\overline D }}\left( {x,t} \right) = 0 \Rightarrow \cr
\left[ {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}} + {\mu _D}} \right]{P_{GM\overline D }}\left( {x,t} \right) = 0 \cr} $$
|
(A6) |
For state ${S_6}$,
$$\displaylines{
{P_{G\overline M \overline D }}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) = \left\{ {1 - {\mu _{MD}}{\text{Δ }}t} \right\}{P_{G\overline M \overline D }}\left( {x,t} \right) \Rightarrow \cr
\frac{{{P_{G\overline M \overline D }}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) - {P_{G\overline M \overline D }}\left( {x,t} \right)}}{{{\text{Δ }}t}} + {\mu _{MD}}{P_{G\overline M \overline D }}\left( {x,t} \right) = 0 \cr} $$
Taking $\underset{\begin{smallmatrix}
\text{ }\!\!\Delta\!\!\text{ }x\to 0 \\
\text{ }\!\!\Delta\!\!\text{ }t\to 0
\end{smallmatrix}}{\mathop{\text{lim}}}\, $, one gets:
|
$$ \Rightarrow \left[ {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}} + {\mu _{MD}}} \right]{P_{G\overline M \overline D }}\left( {x,t} \right) = 0$$
|
(A7) |
For state ${S_7}$,
$${P_{G\overline {\overline M } D}}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) = \left\{ {1 - {\mu _M}{\text{Δ }}t} \right\}{P_{G\overline {\overline M } D}}\left( {x,t} \right) \Rightarrow $$
$$\underset{\begin{smallmatrix}
\text{ }\!\!\Delta\!\!\text{ }x\to 0 \\
\text{ }\!\!\Delta\!\!\text{ }t\to 0
\end{smallmatrix}}{\mathop{\text{lim}}}\,\frac{{{P}_{G\overline{\overline{M}}D}}\left( x+\text{ }\!\!\Delta\!\!\text{ }x,t+\text{ }\!\!\Delta\!\!\text{ }t \right)-{{P}_{G\overline{\overline{M}}D}}\left( x,t \right)}{\text{ }\!\!\Delta\!\!\text{ }t}+{{\mu }_{M}}{{P}_{G\overline{\overline{M}}D}}\left( x,t \right)=0\Rightarrow $$
|
$$\left[ {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}} + {\mu _M}} \right]{P_{G\overline {\overline M } D}}\left( {x,t} \right) = 0$$
|
(A8) |
For state ${S_8}$,
$${P_{\overline G \overline M \overline D }}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) = \left\{ {1 - {\mu _{GMD}}{\text{Δ }}t} \right\}{P_{\overline G \overline M \overline D }}\left( {x,t} \right) \Rightarrow $$
$$\underset{\begin{smallmatrix}
\text{ }\!\!\Delta\!\!\text{ }x\to 0 \\
\text{ }\!\!\Delta\!\!\text{ }t\to 0
\end{smallmatrix}}{\mathop{\text{lim}}}\,\frac{{{P}_{\overline{G}\overline{M}\overline{D}}}\left( x+\text{ }\!\!\Delta\!\!\text{ }x,t+\text{ }\!\!\Delta\!\!\text{ }t \right)-{{P}_{\overline{G}\overline{M}\overline{D}}}\left( x,t \right)}{\text{ }\!\!\Delta\!\!\text{ }t}+{{\mu }_{GMD}}{{P}_{\overline{G}\overline{M}\overline{D}}}\left( x,t \right)=0\Rightarrow $$
|
$$\left[ {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}} + {\mu _{GMD}}} \right]{P_{\overline G \overline M \overline D }}\left( {x,t} \right) = 0$$
|
(A9) |
For state ${S_9}$,
$${P_{\overline {\overline G } \overline M D}}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) = \left\{ {1 - {\mu _{GM}}{\text{Δ }}t} \right\}{P_{\overline {\overline G } \overline M D}}\left( {x,t} \right) \Rightarrow $$
$$\underset{\begin{smallmatrix}
\text{ }\!\!\Delta\!\!\text{ }x\to 0 \\
\text{ }\!\!\Delta\!\!\text{ }t\to 0
\end{smallmatrix}}{\mathop{\text{lim}}}\,\frac{{{P}_{\overline{\overline{G}}\overline{M}D}}\left( x+\text{ }\!\!\Delta\!\!\text{ }x,t+\text{ }\!\!\Delta\!\!\text{ }t \right)-{{P}_{\overline{\overline{G}}\overline{M}D}}\left( x,t \right)}{\text{ }\!\!\Delta\!\!\text{ }t}+{{\mu }_{GM}}{{P}_{\overline{\overline{G}}\overline{M}D}}\left( x,t \right)=0\Rightarrow $$
|
$$\left[ {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}} + {\mu _{GM}}} \right]{P_{\overline {\overline G } \overline M D}}\left( {x,t} \right) = 0$$
|
(A10) |
For state ${S_10}$,
$${P_{\overline G \overline {\overline M } D}}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) = \left\{ {1 - {\mu _{GM}}{\text{Δ }}t} \right\}{P_{\overline G \overline {\overline M } D}}\left( {x,t} \right) \Rightarrow $$
$$\underset{\begin{smallmatrix}
\text{ }\!\!\Delta\!\!\text{ }x\to 0 \\
\text{ }\!\!\Delta\!\!\text{ }t\to 0
\end{smallmatrix}}{\mathop{\text{lim}}}\,\frac{{{P}_{\overline{G}\overline{\overline{M}}D}}\left( x+\text{ }\!\!\Delta\!\!\text{ }x,t+\text{ }\!\!\Delta\!\!\text{ }t \right)-{{P}_{\overline{G}\overline{\overline{M}}D}}\left( x,t \right)}{\text{ }\!\!\Delta\!\!\text{ }t}+{{\mu }_{GM}}{{P}_{\overline{G}\overline{\overline{M}}D}}\left( x,t \right)=0\Rightarrow $$
|
$$\left[ {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}} + {\mu _{GM}}} \right]{P_{\overline G \overline {\overline M } D}}\left( {x,t} \right) = 0$$
|
(A11) |
For state ${S_11}$,
$${P_{\overline G M\overline D }}\left( {x + {\text{Δ }}x,t + {\text{Δ }}t} \right) = \left\{ {1 - {\mu _{GM}}{\text{Δ }}t} \right\}{P_{\overline G M\overline D }}\left( {x,t} \right) \Rightarrow $$
$$\underset{\begin{smallmatrix}
\text{ }\!\!\Delta\!\!\text{ }x\to 0 \\
\text{ }\!\!\Delta\!\!\text{ }t\to 0
\end{smallmatrix}}{\mathop{\text{lim}}}\,\frac{{{P}_{\overline{G}M\overline{D}}}\left( x+\text{ }\!\!\Delta\!\!\text{ }x,t+\text{ }\!\!\Delta\!\!\text{ }t \right)-{{P}_{\overline{G}M\overline{D}}}\left( x,t \right)}{\text{ }\!\!\Delta\!\!\text{ }t}+{{\mu }_{GD}}{{P}_{\overline{G}M\overline{D}}}\left( x,t \right)=0\Rightarrow $$
|
$$\left[ {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}} + {\mu _{GD}}} \right]{P_{\overline G M\overline D }}\left( {x,t} \right) = 0$$
|
(A12) |
Appendix B
Boundary conditions of the system are obtained corresponding to transitions between the states where transition from a state with and without elapsed repair time exists, with elapsed repair times x and 0. Hence we have the following boundary conditions:
Boundary conditions
$${P_i}\left( {0,t} \right) = {\lambda _j}{P_k}\left( t \right)$$
|
$$\displaylines{
i = \overline {\overline G } MD,GM\overline D ,G\overline M \overline D ,G\overline {\overline M } D,\overline G \overline M \overline D ,\overline {\overline G } \overline M D,\overline G \overline {\overline M } D,\overline G M\overline D \cr
j = G,D,D,M,D,G,M,D \cr
k = \overline G MD,GMD,G\overline M D,G\overline M D,\overline G \overline M D,\overline G \overline M D,\overline G \overline M D,\overline G MD \cr} $$
|
(B1) |
When the system is in perfectly good state i.e. in initial state ${S_0}$, then
|
$${P_0}\left( 0 \right) = 1$$
|
(B2) |
and all other state probabilities are zero at t = 0.
Appendix C
System description:
| $${S_0}$$ | The MPP is working with full efficiency. |
| $${S_1}$$ | The MPP is operational in the degraded state with one failed generator. |
| $${S_2}$$ | The MPP is operational in the degraded state with one failed generator and one failed MSB. |
| $${S_3}$$ | The MPP is operational in the degraded state with one failed MSB. |
| $${S_4}$$ | The MPP has failed due to the failure of both the generators. |
| $${S_5}$$ | The MPP has failed due to the failure of DSB. |
| $${S_6}$$ | The MPP has failed due to the failure of one MSB and DSB. |
| $${S_7}$$ | The MPP has failed due to the failure of both the MSB. |
| $${S_8}$$ | The MPP has failed due to the failure of one generator, one MSB and complete failure of DSB. |
| $${S_9}$$ | The MPP has failed due to the failure of both generators and one MSB. |
| $${S_10}$$ | The MPP has failed due to the failure of one generator and both the MSB. |
| $${S_11}$$ | The MPP has failed due to the failure of one generators and DSB. |