1 Introduction
The problem of water wave scattering by a horizontal circular cylinder fully submerged in deep water with a free surface is well studied in the literature. Dean(1948)first investigated this problem by using complex variable theory. Shortly afterwards, Ursell(1950)studied the same problem using the method of multipoles. Both of them obtained the remarkable result that no reflection occurs for a normally incident wave train. Ogilvie(1963)considered some more general situations including Ursell’s case by using a similar mathematical technique. However, for oblique incidence of the wave train the cylinder does experience reflection as well as transmission as has been shown by Levine(1965)using an integral equation formulation. Later Mandal and Banerjea(1994)considered wave scattering by a nearly circular cylinder submerged in infinitely deep water. A simplified perturbation technique was used to h and le the problem upto first order and Green’s integral theorem was employed to solve the boundary value problems for potential functions upto first order. When the submerged cylinder is of arbitrary cross-section, generally it experiences reflection. Porter(2002)solved the problem by reducing it to a first kind integral equation for an unknown function related to the tangential velocity of the fluid around the cylinder by applying Green’s function technique.
All the aforesaid problems were studied for water with a free surface. When the water is covered with a thin ice sheet, modelled as a thin elastic plate, the corresponding water wave problems are also of some interest to ocean engineers. These have applications in ocean related industries in cold regions, such as the Arctic region. Das and M and al(2006; 2008)studied wave scattering by a horizontal circular cylinder, submerged beneath an ice-cover for normal as well as oblique incidences. They found that, there is reflection for obliquely incident wave but in case of normal incidence no reflection occurs as was in the case for water with a free surface. It may be mentioned here that the problem of a horizontal cylinder submerged below an ice-cover arose in connection with the plan to construct an underwater pipe bridge across one of the Norwegian fjords(Friis et al., 1991). In winter a fjord is covered by a layer of ice so that we have a model of a cylindrical pipe bridge submerged below an ice-cover and its interaction with a wave field is important to study. The present problem arises if the cross-section of the cylindrical pipe bridge is not perfectly circular, but nearly circular. Also we assume the ice-cover to be thin so that it can be modeled as a thin elastic plate floating on water.
In the present paper, the problem of water wave scattering by a nearly circular cylinder submerged beneath an ice-cover floating in infinitely deep water has been investigated. To solve the problem, a simplified perturbation expansion for the velocity potential describing the motion in the fluid and the reflection and transmission coefficients is employed in terms of δ, where δ is a measure of small departure of cylinder cross-section from its circularity.
This reduces the given problem into two independent boundary value problems up to the first order of δ. The first problem corresponds to the problem of water wave scattering by a circular cylinder in deep water with an ice cover, which has already been studied by Das and Mandal(2008) and the first order correction to the reflection and transmission coefficients are obtained by solving the second boundary value problem. These corrections are obtained by assuming a general Fourier expansion of the shape function.
Das and Mandal(2008)employed Green’s integral theorem to solve the first boundary value problem involving water wave scattering by a horizontal circular cylinder submerged beneath an ice-cover and obtained the corresponding reflection and transmission coefficients(zero order here). To find the first order correction to the reflection(R1) and transmission(T1)coefficients, Green’s integral theorem is employed to the zero-order and first-order potential functions in the fluid region. R1 and T1 are obtained in terms of integrals involving the zero-order potential and the shape function. These integrals are evaluated for some appropriate choice of the shape function. For some form of the shape function R1 vanishes so that there is no reflection up to first order. For this form of the shape function, the phase of the transmission coefficient is depicted graphically against the wave number in a number of figures for various values of the flexural rigidity of the ice cover and the other parameters. When the ice-cover parameters D/a4, ε/a a and δ(all defined below)are chosen to be very small, it is seen that the curves for the phase of the transmission coefficient almost coincide with the curves drawn by Ogilvie(1963)for a circular cylinder submerged in deep water with a free surface. This provides a check on the correctness of the numerical results obtained. Also, it is checked that the absolute value of the transmission coefficient for each data point is unity as it should be due to the energy identity since there is no reflection.
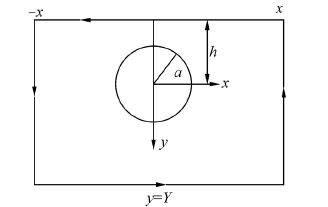
2 Mathematical formulationA two-dimensional rectangular Cartesian co-ordinate system is chosen in which the y-axis is taken vertically downwards, and the origin lies on the axis of an infinitely long nearly circular cylinder submerged in infinitely deep water with its generators parallel to the z-axis and h is the depth of the axis of the cylinder below the mean position of the thin ice-cover(cf. Fig. 1). The cross-section of the nearly circular cylinder is represented by
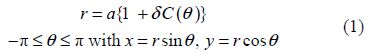
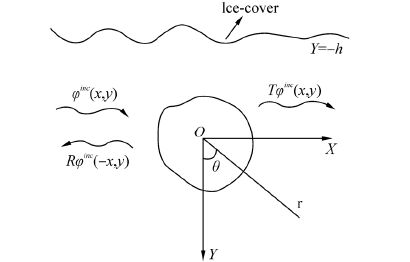
|
| Fig.1 Trace of the nearly circular cylinder |
The motion is assumed to be irrotational and water is considered to be an incompressible and homogeneous liquid. The incident field is described by the velocity potential function Re{ϕ inc(x, y)e−iσ t}. Here. σ denotes the angular frequency, and
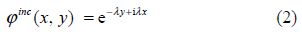
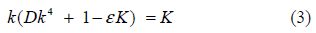
Now the velocity potential describing the fluid motion is $\text{Re}\{\varphi (x,\text{ }y){{\text{e}}^{-\text{i}\sigma t}}\}$, where φ satisfies

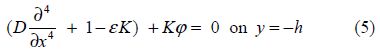

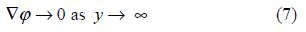
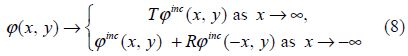
The condition(6)can be approximated to the first order of δ(cf. Mandal and Banerjea, 1994)as
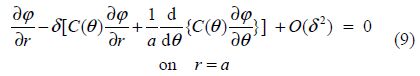
This suggests that one can assume the following perturbation expansion for ϕ (x, y), R and T in terms of δ as

Substituting(10)into(4)to(9), we find that ${{\varphi }_{0}}(x,\text{ }y)$ and ${{\varphi }_{1}}(x,\text{ }y)$ satisfy the following two independent boundary value problems.
1)BVP-I.
${{\varphi }_{0}}(x,\text{ }y)$ satisfies
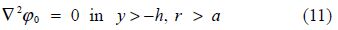
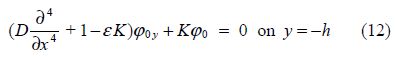
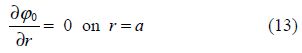
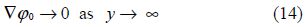
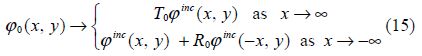
2)BVP-II.
${{\varphi }_{1}}(x,\text{ }y)$ satisfies
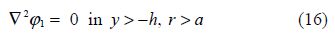
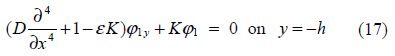
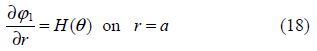
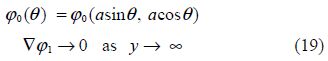
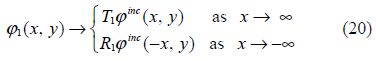
The BVP-I corresponds to the two-dimensional problem of water wave scattering by an infinitely long horizontal circular cylinder submerged in deep water with an ice cover. As stated in the introduction, this has already been studied earlier by Das and Mandal(2008).
The BVP-II corresponds to the problem of water wave radiation by an infinitely long horizontal circular cylinder submerged beneath an ice-cover. This BVP involves the first-order corrections to the reflection(R1) and transmission coefficients(T1)as amplitudes at large distance from either sides of the cylinder. From this BVP, R1 and T1 can be obtained byappropriate uses of Green’s integral theorem. However knowledge of ${{\varphi }_{0}}(\theta )$ is necessary to find these.
Now ${{\varphi }_{0}}(\theta )$ can be expressed as(cf. Das and Mandal, 2008)
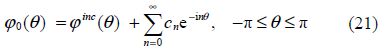
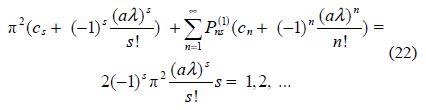
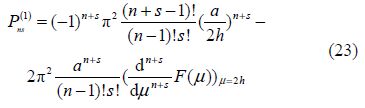
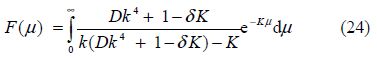
the contour being indented below the pole k=>λ. It is also known that(cf. Das and Mandal, 2008)

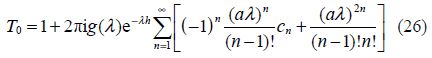
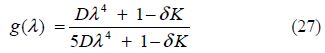
These results are independent of ${{c}_{0}}$ . Once ${{{c}'}_{n}}s$ (n=1, 2, …)are determined approximately by truncating the linear system(22), ${{T}_{0}}$ and can ${{\varphi }_{0}}(\theta )$ be obtained.
Now in order to obtain, we apply Green’s integral theorem to the harmonic functions ${{\varphi }_{1}}(x,y)$ and ${{\varphi }_{0}}(x,y)$ in the region bounded by the lines y=h, -X≤x≤X; x=X, -h≤y≤Y; y=Y, -X≤x≤X; x=-X, -h≤y≤Y and the circle r=a and make X, Y→∞(cf. Fig. 2), and obtain
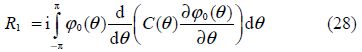
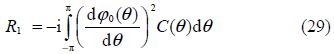
|
| Fig.2 Contour of integration |
Again, to find T1, we also apply Green’s integral theorem to the functions ${{\varphi }_{1}}(x,\text{ }y)$ and ${{\varphi }_{0}}(-x,\text{ }y)$ in the same region mentioned above and make $X,\text{ }Y\to \infty$, and obtain
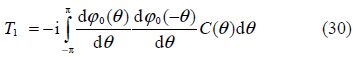
Now we assume a general Fourier expansion of C(θ)as
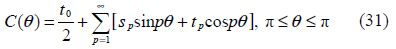
Substituting(21) and (31)into(29) and in(30), we obtain respectively

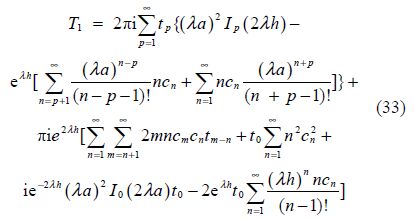
The unknown constants cn(n=1, 2, ...)are obtained from the solution of the linear system(22)after truncating the linear system at n=25. From(32), R1 is independent of t0, t1 and s1, while T1 given by(33), is independent of all sp(p=1, 2, ...). Thus it can be inferred that a nearly circular cylinder submerged in water with an ice cover does not experience any reflection up to first order if it has a shape function of the form
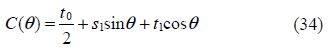
For numerical calculation of T1, we choose t1=0.1 and s1 to be arbitrary since R1 and T1 are independent of s1. Thus in this case, R1 becomes zero and R0 is also zero, so that the wave is totally transmitted, i.e., |T|≡1, up to first order. This first-order transmission coefficient |T1| is depicted against Ka for various values of and fixed values of in Fig. 3.

|
| Fig.3 |T1| against Ka |
Ogilvie(1963)investigated water wave scattering by a circular cylinder submerged in infinitely deep water with a free surface and he plotted the phase of T against 2Kh for different values of Ka in Fig. 9 of his paper. To check the correctness of our present results, the phase of $T(T=\frac{180}{\text{ }\!\!\pi\!\!\text{ }}\text{arctan}(\frac{\text{Im}T}{\text{Re}T}\text{ }),T={{T}_{0}}\text{ }+\delta {{T}_{1}})$ is depicted against 2Kh in Fig. 4 here for very small values of ${D}/{{{a}^{4}}}\;({D}/{{{a}^{4}}}\;=0.1\times {{10}^{-5}})$, ${\varepsilon }/{a}\;({\varepsilon }/{a}\;=0.1\times {{10}^{-4}})$ and δ $(\delta =0.1\times {{10}^{-5}})$so that the cylinder becomes almost a circular one and submerged in water with a free surface. It is seen that the curves in Fig. 4 drawn for Ka=0.5, 1.0, 2.0 and 4.0 as taken in Ogilvie(1963)are almost similar to the curves given in Fig. 9 of his paper.

|
| Fig.4 Phase of T against 2Kh |
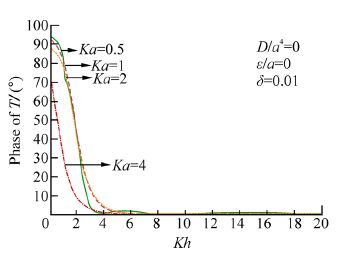
The phase of the transmission coefficient for Ka=0.5, 1, 2, 4 is depicted in Fig. 5 against Kh choosing =0, =0, δ=0.01. The curves in this Fig. 5 correspond to case of a free surface. The phase is also depicted in Fig. 6(a), 6(b), 6(c) and 6(d)against Kh taking and =0.001, δ=0.01. From each of these figures, it is observed that the phase of the transmission coefficient decreases with the increase of and the maximum value of the phase increases as Ka increases. The values of are chosen here somewhat arbitrarily to show the effect of the phase of the transmission coefficient on the flexural rigidity However, these values are somewhat comparable to the values of chosen by Maiti and Mandal(2008)in connection with the study of wave scattering by bottom undulation in an ice-covered two-layer ocean.
|
| Fig.5 Phase of T against Kh |
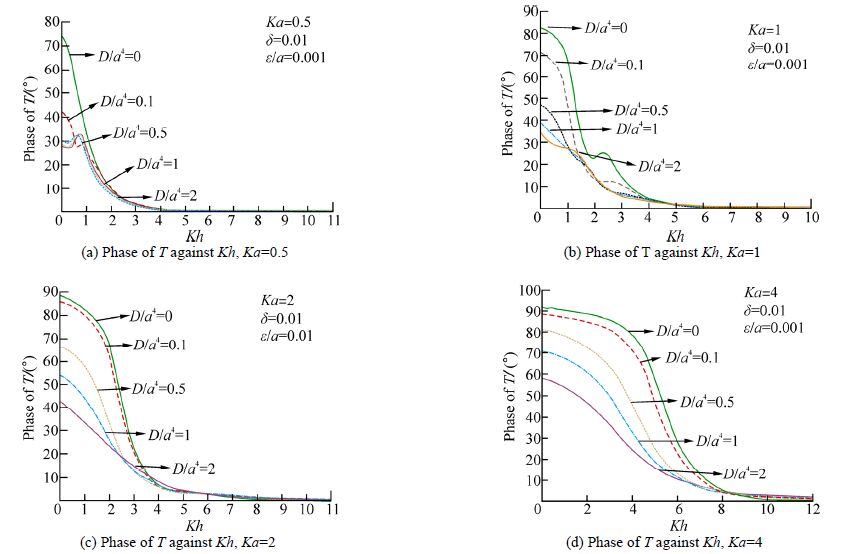
|
| Fig.6 Phase of T against different Kh and Ka |
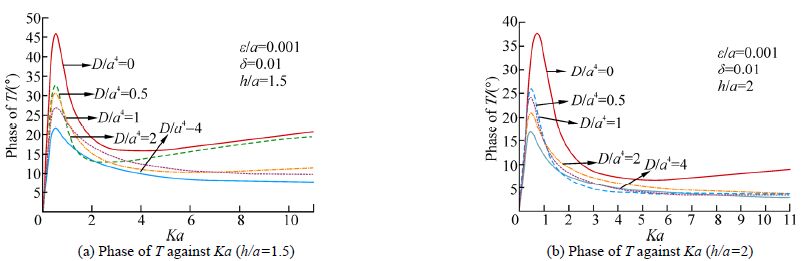
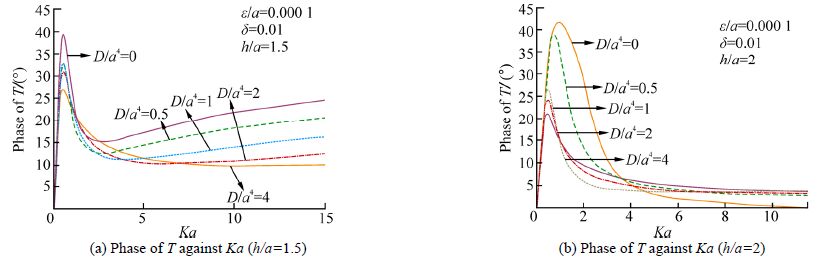
To observe the effect of the depth of submergence of the cylinder below the ice-cover, the phase of is depicted in Fig. 7(a) and Fig. 7(b)against Ka for =1.5 and 2 respectively for four different values of =0.0001, 0.5, 1, 2, 4 and fixed values 0.001 of and 0.01 of δ. From these figures it is observed that as the depth of the cylinder from upper surface increases, the phase of T decreases. To see the effect of the mass parameter on the phase of T, the curves in Fig. 8(a) and Fig. 8(b) are drawn for =0.000 1 keeping all other parameters to be the same as in Fig. 7(a) and Fig. 7(b) respectively. It is observed from these figures that the maximum amplitude of the phase increases with the decrease of . Lastly in all the cases the energy identity is always satisfied numerically.
|
| Fig.7 Phase of T against Ka(ε/a=0.001) |
|
| Fig.8 Phase of T against Ka(ε/a=0.000 1) |
The problem of water wave scattering by a long horizontal nearly circular cylinder submerged in deep water beneath a free surface is extended here when the free surface is replaced by an ice-cover modelled as a thin elastic plate floating on water. This problem has application in the plan to construct underwater pipe bridge across Norwegian fjords when during the winter season a fjords is generally covered by a layer of ice. If this layer is thin then it can be modelled as a thin elastic plate floating on water so that the ice-cover condition when linearised replaces the usual free surface condition involving first order derivatives which appears to be interesting mathematically. If the cross-section of nearly circular cylinder is represented by(1), then the condition of no flow normal to the cylinder can be approximated by(9), and this provides a clue to tackle the mathematical problem approximately by invoking a simple perturbation analysis in terms of δ, a small parameter describing the measure of departure of the cross-section of the cylinder from circularity. Up to the order of δ, two boundary value problems are obtained. The first one corresponding to the problem of wave scattering by a circular cylinder submerged beneath an ice-cover while the second one corresponds to a radiation problem involving the same circular cylinder. Appropriate uses of Green’s integral theorem produce the first-order correction to the reflection and transmission coefficients. As a circular cylinder is transparent to normally incident wave train, our interest here is to find if there is any other shape of the cross-section of the cylinder for which there is no reflection. For the shape function given by(34), it is found that there is no reflection up to first order. For this shape function, the first order transmission coefficient is |T1 | depicted graphically against Ka for various values of different parameters. Also, the phase of the transmission coefficient is depicted graphically in a number of figures to visualize the effect of the presence of the ice-cover, and appropriate conclusions are made.
AcknowledgementThe authors thank three anonymous reviewers for their comments and suggestions to improve the paper considerably. The first author acknowledges the financial support from CTS Visitors Program, Indian Institute of Technology, Kharagpur during the tenure of which the revision of the paper has been made.
| Das D, Mandal BN (2006). Oblique wave scattering by a circular cylinder submerged beneath an ice-cover. International Journal of Engineering Science, 44(3-4), 166-179. DOI: 10.1016/j.ijengsci.2006.01.001 |
| Das D, Mandal BN (2008). Water wave scattering by a circular cylinder submerged in water with an ice cover. Indian Journal of Pure and Applied Mathematics, 39(4), 299-315. |
| Dean WR (1948). On the reflexion of surface waves by a submerged circular cylinder. Mathematical Proceedings of the Cambridge Philosophical Society, 44(4), 957-983. DOI: 10.1017/S0305004100024506 |
| Friis A, Grue J, Palm E (1991). Application of Fourier transform to the second order 2D wave diffraction problem. In: Miloh T. (ed.), M. P. Tulin’s Festschrift: Mathematical Approaches in Hydrodynamics. SIAM, Philadelphia, USA, 209-227. |
| Fox C, Squire VA (1994). On the oblique reflection and transmission of ocean waves at shore fast sea ice. Proceedings of the Royal Society of London Series A, 347, 185-218. |
| Levine H (1965). Scattering of surface waves by a submerged circular cylinder. Journal of Mathematical Physics, 6(8), 1231-1243. DOI: 10.1063/1.1704765 |
| Mandal BN, Banerjea S (1994). Scattering of water waves by a submerged nearly circular cylinder. J. Austral. Math. Soc. Ser. B, 36(3), 372-380. DOI: 10.1017/S0334270000010481 |
| Maiti P, Mandal BN (2008). Water wave scattering by bottom undulations in an ice-covered two-layer fluid. Applied Ocean Research, 30(4), 264-272. DOI: 10.1016/j.apor.2008.11.004 |
| Ogilvie TP (1963). First and second order forces on a cylinder submerged under a free surface. Journal of Fluid Mechanics, 16(3), 451-472. DOI: http://dx.doi.org/10.1017/S0022112063000896 |
| Porter R (2002). Surface wave scattering by submerged cylinders of arbitrary cross-section. Proceedings of the Royal Society A, 458(2019), 581-606. DOI: 10.1098/rspa.2001.0885 |
| Ursell F (1950). Surface wave on deep water in the presence of submerged circular cylinder I and II. Mathematical Proceedings of the Cambridge Philosophical Society, 46(1), 141-155. DOI: 10.1017/S0305004100025561 |



