1 Introduction
Composite laminated plates, which are widely applied in aerospace and marine engineering, possess higher strengths, greater stiffness, better wear resistance and corrosion-resisting performance than ordinary steel. The free vibration analytical expressions of laminated plates under various boundary conditions are of great significance to underst and ing the relationship between geometric parameter and vibration performance. Additionally, the fundamental frequency of the structure has great attraction in applications. It’s important to make sure that excitation frequency is not close to lower frequencies of the structure, otherwise the destructive resonance will occur. Therefore, in preliminary design stage of composite structures, it’s reasonable to consider the lower frequencies, especially the fundamental frequency.
The analytical solution of the vibration characteristics of the specialty orthotropic laminates under various boundary conditions has been worked out as well as symmetric and antisymmetric angle-ply laminated plates. The variational equations of free vibration of arbitrarily laminated plates based on Hamilton’s principle and classical lamination theory was deduced by Shi et al.(1997). Yang and Peng(2001)studied the vibration characteristics of orthogonal laminated rectangular thin plate in hybrid constraint boundary conditions based on domain decomposition technology. The effect of in-plane loading was also taken into account. Someone put forward free vibration analytical solution of symmetric cross-ply laminated plates in various boundary conditions based on the first-order shear laminated plate theory(Xia and Wen, 1991; Huang et al., 2001). Zhang et al.(1993; 1994; 1995; 1996a; 1996b)proposed a new high-order displacement mode considering normal stress and strain. They analyzed the free vibration of cross-ply laminates in fully simply supported and clamped boundary conditions using Rayleigh-Ritz method. They also discussed the influence of orthogonal anisotropy ratio, number of layers, width-thickness ratio and length-width ratio on fundamental frequency. Dong and Sheng(2005)put forward free vibration analytical solution of orthotropic laminated plates with opposite sides free and simply supported from basic equations of three-dimensional elastic mechanics. It had advantages in dealing with free boundary conditions. Whitncy and Pagano(1970)discussed shear deformation in heterogenous anisotropic. Sheng(2012)studied free vibration of composite structures with interleaved viscoelastic damping layer. Ye et al.(2013; 2014)gave the modified Fourier solution for vibration analysis of moderately thick laminates with general boundary restraints, elastic boundaries and internal line supports.
This paper presents, a calculation method of fundamental frequency of laminated plates(N > 8-10)with arbitrary orientation under various boundary conditions from the perspective of coupling through example analysis. It provides a new thought in the analytical solution of laminated plates of arbitrary orientation under various boundary conditions.
2 Theoretical formulations 2.1 The differential equations of vibration of laminated platesThe force diagram in micro-block of the middle plane of laminated plates is shown in Fig. 1. The differential equations of vibration of laminated plates are derived by analyzing Fig. 1.
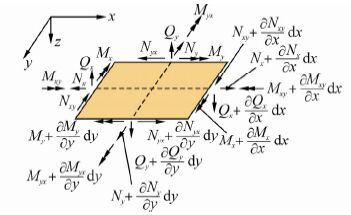
|
| Fig. 1 Micro-block diagram of the middle plane of laminated plates |
The Eq.(1)is obtained as the resultant force in x-direction is zero.

The Eq.(2)is obtained as the resultant force in y-direction is zero.

Considering inertia force caused by transverse vibration as well as the zero resultant force in z-direction, the Eq.(3)is gained.
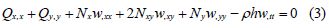
The zero resultant moment of all forces on the y-axis yields Eq.(4).
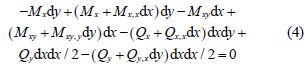
By neglecting the third-order terms of Eq.(4), it can be rewritten as

Similarly, the zero resultant moment of all forces on the x-axis yields
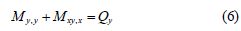
Substituting the Eqs.(5) and (6)into Eq.(4), yielding
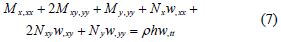
Hence, the differential equations of vibration can be written in the following pattern:
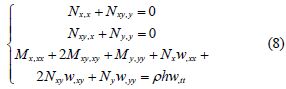
According to the constitutive relations of laminated plates, the stress-strain relations of a laminate among layers can be expressed by Shen and Hu(2006):
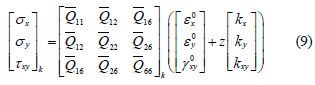
Internal forces-stress relations can be written as follows:
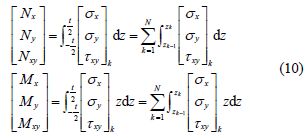
Internal forces-strain relations are gained by applying Eq.(9)to Eq.(10).
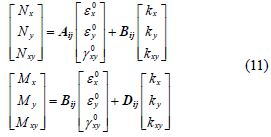
where
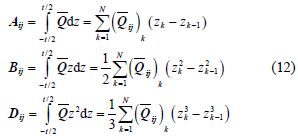
Based on the classical laminated theory, the strain-displacement relationship can be written as
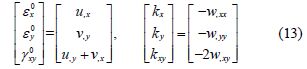
Substituting the Eqs.(11) and (13)into Eq.(8), the differential equations of vibration of laminated plates can be expressed as:
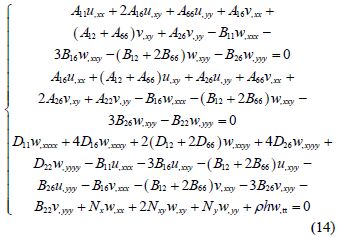
where, Bij is the coupling stiffness between tension and bending, A16 and A26 are the coupling stiffness between tension and shear, while D16 and D26 are the coupling stiffness between bending and torsion(Jones, 1998).
2.2 Analytical solution of specialty orthotropic laminatesFor specially orthotropic laminates, all the coupling stiffness are zero, viz.,
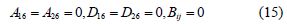
The following equilibrium’s differential equation of vibration is obtained by applying Eq.(15)to(14).
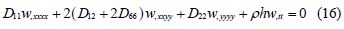
By separating variables of time and space, the expression of w can be assumed as
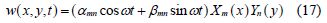
where Xm and Yn must meet certain boundary conditions.
By substituting the Eq.(17)in Eq.(16), the frequencies and modes under various boundary conditions can be obtained on the condition that nontrivial solution exists. The calculation formulas of frequencies of specially orthotropic laminates are given by Cao(1989)in the cases of fully simply supported(SSSS), fully clamped(CCCC), two opposite edges simply supported while the others clamped(SSCC), one edge clamped while the others simply supported(SSSC) and one edge simply supported while the others clamped(SCCC).
Take the boundary condition of fully simply supported, which meets the following expressions, as an example to explain the process.
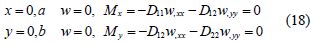
The expression of w, which satisfies Eq.(18), can be presumed as
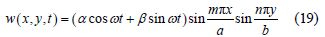
Substituting the Eq.(19)into Eq.(16), Eq.(20)can be derived from the existence of nontrivial solution.
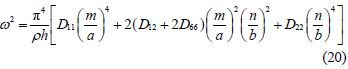
For antisymmetric angle-ply laminated plates, the coupling stiffness are given by
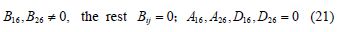
The differential equation of vibration of antisymmetric angle-ply laminated plates is obtained when zero coupling stiffness are omitted.
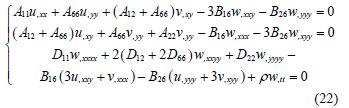
The displacements and internal forces must meet the following expressions according to the third simply supported boundary condition(un=0, Nnt=0).
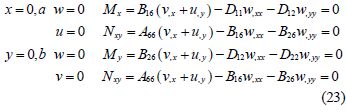
The displacements of the plate are given as
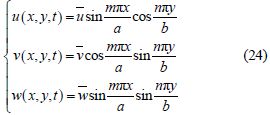
The condition for the existence of nontrivial solutions of Eq.(22)is
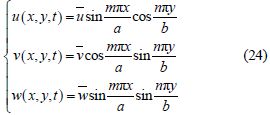
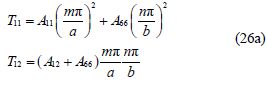
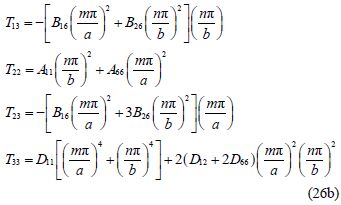
Example 1: The total length and breadth of laminated plate with specially orthotropic cross-ply(90°/0°/0°/90°)configuration are a = 0.3 m and b = 0.3 m, the thickness of a laminate is t = 0.125 mm. The material properties of a laminate are E11 = 1.35×1011 Pa, E22=8.8×109 Pa, G12= 4.8×109 Pa, ν12=0.33 and ρ =1 380 kg/m3. Compared with the ANSYS results, the first five nature frequencies are calculated in SSSS, CCCC, SSCC, SSSC and SCCC as presented in Table 1 and Fig. 2.
| Boundary conditions | Results | Order | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| SSSS | Present/Hz | 27.95 | 53.24 | 97.00 | 103.96 | 111.80 |
| ANSYS/Hz | 27.89 | 53.11 | 96.63 | 103.70 | 111.26 | |
| Relative error/% | 0.21 | 0.23 | 0.38 | 0.25 | 0.48 | |
| CCCC | Present/Hz | 59.43 | 87.73 | 144.24 | 150.24 | 166.01 |
| ANSYS/Hz | 59.78 | 88.90 | 145.68 | 149.65 | 167.51 | |
| Relative error/% | 0.58 | 1.34 | 1.00 | −0.39 | 0.90 | |
| SSCC | Present/Hz | 55.13 | 70.80 | 113.37 | 148.37 | 157.21 |
| ANSYS/Hz | 55.39 | 72.06 | 115.16 | 147.64 | 158.29 | |
| Relative error/% | 0.47 | 1.78 | 1.58 | −0.49 | 0.69 | |
| SSSC | Present/Hz | 39.30 | 59.16 | 106.36 | 120.73 | 131.18 |
| ANSYS/Hz | 39.83 | 60.69 | 108.16 | 120.75 | 133.17 | |
| Relative error/% | 1.33 | 2.51 | 1.66 | 0.02 | 1.49 | |
| SCCC | Present/Hz | 45.12 | 78.61 | 121.97 | 138.77 | 141.55 |
| ANSYS/Hz | 45.71 | 79.89 | 123.15 | 140.10 | 143.83 | |
| Relative error/% | 1.28 | 1.60 | 0.96 | 0.95 | 1.59 | |
|
| Fig. 2 Comparison of frequencies of specialty orthotropic laminates between present and ANSYS |
As shown in Table 1 and Fig. 2, the reliability of the analytical solution of frequencies of specialty orthotropic laminates is verified.
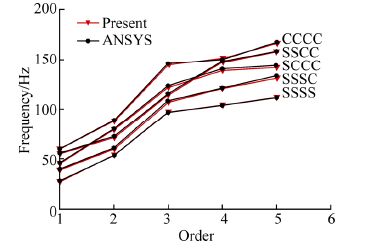
3.2 Results of antisymmetric laminated platesThe fundamental frequencies of antisymmetric angle-ply laminated plates with changing numbers of layers and angles are shown in Fig. 3(Jones et al, 1973).
|
| Fig. 3 Fundamental vibration frequencies of square antisymmetric angle-ply laminated plates |
As shown in Fig. 3, the greater the angle, mean the smaller the effect of coupling and the higher the frequency. For a certain thickness of plates there are more layers, which mean the smaller the effect of coupling and the higher the frequency. When the number of layers is infinite, the frequency tends to be the case of zero coupling. Additionally, the effect of coupling reduces faster than the rate of increase in the number of layers, leading to smaller frequency gaps between adjacent layers. In general, for certain material properties of a laminate and thickness of plates, higher frequency corresponds to lower coupling, and the coupling stiffness influence on the antisymmetric laminated plates with constant thickness decays rapidly with the increase of layers. Generally speaking, for any antisymmetric laminated plate, when the number of layers N > 8-10, the coupling influence on fundamental frequency can be negligible, viz., when the number of layers is large, the orthotropic laminates with the same thickness can be used specifically to calculate the frequencies, which also hold true for symmetric angle-ply laminated plates.
The fundamental frequency of antisymmetric angle-ply laminates with 10 layers in the angle of 30° is simulated by specialty orthotropic laminates with 10 layers to verify the above idea.
Example 2: The antisymmetric angle-ply plate(−30°/30°/−30°/30°/−30°/30°/−30°/30°/−30°/30°)holds the same material properties as Example 1. The frequencies are calculated in SSSS, CCCC, SSCC, SSSC and SCCC as listed in Table 2.
| Boundary conditions | Results | Order | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| SSSS | Present/Hz | 75.32 | 165.19 | 234.36 | 283.46 | 336.93 |
| ANSYS/Hz | 69.73 | 173.17 | 214.56 | 278.18 | 364.29 | |
| Relative error/% | −7.42 | 4.61 | −8.45 | −1.86 | 7.51 | |
| CCCC | Present/Hz | 144.91 | 237.82 | 340.33 | 380.90 | 455.84 |
| ANSYS/Hz | 149.51 | 277.57 | 335.62 | 419.00 | 499.57 | |
| Relative error/% | 3.17 | 14.32 | −1.38 | 10.00 | 8.75 | |
| SSCC | Present/Hz | 100.89 | 203.92 | 245.30 | 341.79 | 415.88 |
| ANSYS/Hz | 106.67 | 230.34 | 255.87 | 338.00 | 474.45 | |
| Relative error/% | 5.73 | 11.47 | 4.31 | −1.11 | 12.34 | |
| SSSC | Present/Hz | 91.61 | 183.22 | 239.31 | 311.99 | 362.12 |
| ANSYS/Hz | 84.78 | 211.90 | 220.63 | 304.97 | 423.22 | |
| Relative error/% | −7.45 | 13.53 | −7.81 | −2.25 | 14.44 | |
| SCCC | Present/Hz | 138.33 | 217.28 | 336.00 | 350.30 | 431.77 |
| ANSYS/Hz | 134.70 | 237.49 | 328.93 | 392.47 | 437.60 | |
| Relative error/% | −2.62 | 8.51 | −2.10 | 12.04 | 1.33 | |
It can be seen that the frequencies of antisymmetric angle-ply plates with a relatively large number of layers are approximately equal to those of specialty orthotropic laminates with the same thickness and number of layers, so the above idea is correct. However, larger number of layers requires more time to calculate, which is common for antisymmetric laminated plates in practice. So it is necessary to suppose: for any antisymmetric laminated plate, when N >8-10, the coupling influence on fundamental frequency can be negligible, its frequencies can be simulated by specialty orthotropic laminates with the same thickness but smaller number of layers.
Frequencies of antisymmetric laminated plates with 10 layers are gained by calculating frequencies of specialty orthotropic laminates with 4 layers in SSSS to verify the above assumption.
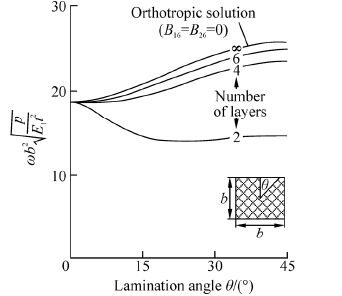
Example 3: The antisymmetric laminated plate(90°/0°/30°/90°/45°/−45°/0°/−30°/90°/0°)holds the same material properties as Example 1. The frequencies shown in Table 3 and Fig. 4 are calculated in SSSS.
| Order | Present/Hz /Hz 1 | ANSYS/Hz2 | Relative error/% |
| 1 | 72.10 | 69.88 | 3.09 |
| 2 | 182.53 | 133.09 | 27.09 |
| 3 | 208.53 | 242.51 | −16.30 |
| 4 | 286.01 | 259.91 | 9.13 |
| 5 | 383.54 | 279.50 | 27.13 |
|
| Fig. 4 Comparison of frequencies of antisymmetric plates between present and ANSYS |
It is observed from Fig. 4 that the relative errors of frequencies are small in the first order, while large in higher orders, namely, the assumption is only applicable to fundamental frequency. Therefore, the assumption should be revised as follows: for any antisymmetric angle-ply plate, when N > 8-10, its fundamental frequency can be simulated by specialty orthotropic laminates with the same thickness but smaller number of layers.
Fundamental frequency of antisymmetric laminates with 10 layers is gained by calculating those of specialty orthotropic laminates with 4 layers to verify the revised assumption.
Example 4: The fundamental frequencies of antisymmetric laminate plates are calculated in five boundary conditions as listed in Table 4. All the relative errors are within 10%, especially for SSSS and CCCC. It illustrates the correctness of the revised assumption.
| Boundary conditions | Present/Hz | ANSYS/Hz | Relative error/% |
| SSSS | 69.88 | 72.10 | 3.09 |
| CCCC | 148.59 | 148.74 | 0.10 |
| SSCC | 134.83 | 122.12 | −9.43 |
| SSSC | 98.26 | 93.19 | −5.16 |
| SCCC | 116.81 | 125.97 | 7.27 |
To get the analytical solution of fundamental frequency of arbitrary laminates under various boundary conditions, the final assumption is gained: for any laminated plates, when the number of layers N > 8-10, it’s reasonable to use the specially orthotropic laminates with the same thickness but less layers to calculate the corresponding fundamental frequency.
Fundamental frequency of arbitrary laminated plates with 10 layers is gained by calculating frequencies of specialty orthotropic laminates with 4 layers to verify the reliability of the final assumption.
Example 5: The composite laminates(80°/10°/75°/20°/ 45°/−45°/0°/−85°/15°/90°)hold the same material properties as Example 1. Compared with the ANSYS results, the fundamental frequencies are calculated in SSSS, CCCC, SSCC, SSSC and SCCC, as presented in Table 5.
| Boundary conditions | Present/Hz | ANSYS/Hz | Relative error/% |
| SSSS | 69.88 | 70.00 | −0.17 |
| CCCC | 148.59 | 145.91 | 1.80 |
| SSCC | 135.83 | 122.83 | 9.57 |
| SSSC | 98.26 | 92.36 | 6.01 |
| SCCC | 112.81 | 121.33 | −7.02 |
As shown in Table 5, all relative errors are within 10% and within only 2% in fully simply supported and clamped. It proves that final assumption is correct.
The influence of the number of layers of specialty orthotropic laminates on relative errors will be discussed below, taking the example of arbitrary laminates with 20 layers.
Example 6: The laminated plate(80°/10°/75°/20°/45°/ −45°/0°/−85°/15°/90°/0°/70°/15°/60°/45°/−45°/0°/−25°/90°/0°)holds the same material properties as Example 1. Compared with the ANSYS result, the fundamental frequencies are calculated in SSSS, CCCC, SSCC, SSSC and SCCC.
The relative errors are presented in Fig. 5. The relative errors can be limited within 15 percent by using the final assumption. They become smaller and gentler under all above boundary conditions as the number of the layers increases. Relative errors that are less than 6% keep steady even with a small number of layers fully supported and clamped. Those of other boundary conditions are greatly influenced by the number of layers, increasing the number of layers guarantees higher accuracy.
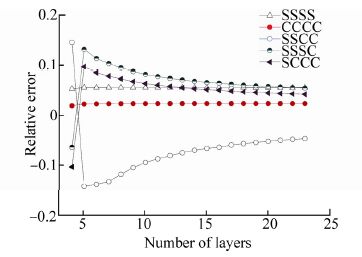
|
| Fig. 5 Relative errors of the fundamental frequency under various boundary conditions |
From the above discussion, it is obvious that the proper number of layers should be chosen when calculating fundamental frequency of arbitrary laminates by final assumption. The accuracy and complexity are determined by the number of layers. This paper suggests using the same thickness of special orthotropic laminates with 4 layers to simulate the fundamental frequency in fully simply supported and clamped condition and increasing number of layers for other boundary conditions.
4 ConclusionsFor fixed material parameters of a laminate and thickness of plates, the smaller the coupling, the greater the frequency. It is conclusion that for any laminated plate, when the number of layers N > 8-10, which is common in engineering, the coupling influence on fundamental frequency can be neglected. It’s reasonable to use especially the orthotropic laminates with the same thickness but less layers to calculate the corresponding fundamental frequency.
The relative errors of the fundamental frequency of arbitrary laminated plates fully supported and clamped, which are most common when the application is approximately 5%. It means that the conclusion in this paper has great value in engineering. Additionally, this conclusion can play a guiding role in frequency optimization. When a certain composite plate has a large number of layers, the fundamental frequency that is concerned most will not vary much with the change of angles, so it does not make sense to optimize the frequency by changing the angles of laminated plates.
| Cao Zhiyuan (1989). Vibration theory of plate and shell. China Railway Publishing House, Beijing, China, 88-103. (in Chinese) |
| Dong Chaowen, Sheng Hongyu (2005). Analytical solution of free vibration of composite laminates with free edges. Journal of Applied Mechanics, 22(3), 470-474, 512. (in Chinese) |
| Huang Yan, Tang Yuzhang, Xu Xiaoli (2001). A general analytical solution of free vibration of orthotropic rectangular thin plates. Engineering Mechanics, 18(3), 45-52. (in Chinese) |
| Jones RM (1998). Mechanics of composite materials. Mcgraw-Hill Company, Washington, DC, USA, 239-284. |
| Jones RM, Harold SM, James MW (1973). Buckling and vibration of antisymmetrically laminated angle-ply rectangular plates. J. Appl. Mech., 40(4), 1143-1144. |
| Shen Guanlin, Hu Gengkai (2006). Mechanics of composite materials. Tsinghua University Press, Beijing, China, 88-103. (in Chinese) |
| Sheng Jia (2012). Free vibration of composite structures with interleaved viscoelastic damping layer. PhD thesis, School of Aircraft Engineering, Nanchang Hangkong University, 10-23. (in Chinese) |
| Shi Junping, Liu Xiehui, Zhao Jucai (1997). Free vibration of any the composite laminated plates. Journal of Xi'an University of Technology, 9(2), 146-151. (in Chinese) |
| Whitncy JM, Pagano NJ (1970). Shear deformation in heterogenous anisotropic. Journal of Applied Mechanics, 37(4), 1931-1036. |
| Xia Chuanyou, Wen Lizhou (1991). Analytical method of free vibration of symmetric orthogonal composite laminated plates with various boundary conditions. Acta Materiae Compositae Sinica, 8(4), 89-99. (in Chinese) |
| Yang Jie, Peng Jianshe (2001). Vibration analysis of composite laminated plates with mixed edge boundary constraints and under in-plane loading. Structure & Environment Engineering, 13(1), 26-31. (in Chinese) |
| Ye Tiangui, Jin Guoyong, Chen Yuehua, Ma Xianglong, Su Zhu (2013). Free vibration analysis of laminated composite shallow shells with general elastic boundaries. Composite Structures 106, 470-490. DOI: 10.1016/j.compstruct.2013.07.005 |
| Ye Tiangui, Jin Guoyong, Su Zhu, Chen Yuehua (2014). A modified Fourier solution for vibration analysis of moderately thick laminated plates with general boundary restraints and internal line supports. International Journal of Mechanical Sciences, 80, 29-46. DOI: 10.1016/j.ijmecsci.2014.01.001 |
| Zhang Genquan, Lei Jianping, Tian Xiaoying, Jie Chiwen (1995). The influence of boundary conditions on composite laminates and transverse shearing. The Fourth National Conference on Structure Engineering, Quanzhou, China, 302-306. |
| Zhang Genquan, Ren Yongsheng, Lei Jianping, Wang Junkui (1996b). Effects of normal stress and normal strain on the fundamental frequencies of free vibration of composite laminated plates. Acta Materiae Compositae Sinica, 13(2), 105-109. (in Chinese) |
| Zhang Genquan, Sun Luyuan, Wang Mingsheng, Dang Quanyong (1993). Free vibration of angle-ply thick laminates using Rayleigh-Ritz method. The Second National Conference on Structure Engineering, Changsha, China, 664-669 . |
| Zhang Genquan, Tan Xuemin, Zhao Yonggang, Tian Xiaoying (1996a). Free vibration of thick composite laminates with clamped edges using characteristic orthogonal polynomials in Rayleigh-Ritz method. Acta Materiae Compositae Sinica, 13(1), 118-122. (in Chinese) |
| Zhang Genquan, Zhang Jinwen, Wang Junkui (1994). Free vibration of angle-ply thick laminates of bimodulus composite materials. Acta Materiae Compositae Sinica, 11(3), 91-96. (in Chinese) |



