0 引　言

船舶在海洋中航行，时刻遭受着复杂多变的海况影响，其中升沉运动尤为显著。这种垂直方向上的起伏，对船舶航行安全构成直接威胁，在货物运输方面，升沉运动致使货物重心频繁改变，容易造成货物位移、损坏，降低运输效率与质量。对于船舶上搭载的各类精密设备，如通信、导航以及科研探测设备，升沉运动产生的持续颠簸会干扰其正常运行，降低测量精度，影响数据准确性^[1]。

传统应对船舶升沉运动的方法，像被动式减摇鳍，虽能在一定程度上削减摇荡幅度，但受限于自身结构与工作原理，其减摇效果依赖于船舶航速与海浪条件，在低速航行或面对不规则海浪时，作用大打折扣。主动控制技术虽具有更强的针对性，可主动调节控制装置来对抗升沉运动，存在响应速度慢、能耗高以及对复杂海况适应性欠佳等问题，难以满足船舶在各种恶劣海况下安全、高效运行的需求^[2]。

王允峰^[3]基于切片理论，成功建立起大型水面船的六自由度运动微分方程。该方程综合考量船舶在海浪作用下的各种受力情况，为后续深入开展船舶摇荡运动仿真研究提供了极为精确的数学模型。预测方法研究方面，刘东等^[4]对不同恶劣海况下的船舶运动情况进行分析，通过建立模型的方式来对高海况下的船舶运动统计特征值进行预报。山东大学海洋工程装备技术研究团队在波浪升沉补偿系统等领域深入钻研，部分学者提出基于模糊控制的升沉补偿方法。该方法依据船舶升沉运动状态与设定目标的偏差，利用模糊规则动态调整控制量，对船舶升沉运动进行有效抑制。还有学者提出滑模控制的升沉补偿方法，通过设计合适的滑模面与控制律，使船舶升沉运动能够快速趋近并保持在期望状态，相关仿真与实验结果均验证了这些方法在一定程度上能够显著降低船舶升沉运动幅度^{[5 − 6]}。

尽管国内外在船舶升沉运动研究上已取得众多成果，但现有模型难以快速、准确地根据海况的急剧变化调整预测策略，导致预测精度大幅下降。在控制策略的鲁棒性方面，当船舶遭遇复杂多变且具有强干扰性的海况时，已有的控制策略容易受到干扰影响，无法稳定、有效地抑制船舶升沉运动，保障船舶安全稳定运行^[7]。

自回归（AR）模型作为时间序列分析领域的重要工具，凭借其独特优势，在船舶运动预测研究中崭露头角。该模型能够深度挖掘升沉运动历史数据中的潜在规律与特征，通过建立数学模型，实现对船舶未来升沉运动状态的精准预判。

1 AR时间序列模型构建 1.1 模型原理与自回归模型

AR的核心原理是通过历史观测值的线性组合来预测当前值，其数学表达式为：

$ {y}_{t}={\varphi }_{1}{y}_{t-1}+{\varphi }_{2}{y}_{t-2}+\dots +{\varphi }_{p}{y}_{t-p}+{\varepsilon}_{t} 。$

(1)

式中：$ {y_t} $为t时刻的船舶升沉位移观测值；$ {\phi _1},{\phi _2}, \cdots ,{\phi _p} $为自回归系数，表征历史值对当前值的影响权重；p为模型阶数，代表参与预测的历史数据长度；$ {\varepsilon}_{t} $为服从正态分布的白噪声序列。

模型假设条件如下：

1）平稳性：序列的均值、方差和自协方差不随时间变化，即船舶升沉运动的统计特性在观测期内保持稳定。这一假设确保模型参数具有时不变性，是AR模型应用的前提（非平稳序列需先通过差分等方法转化为平稳序列）。

2）零均值：序列的均值为0，即$ E\left( {{y_t}} \right){\text{ }} = {\text{ }}0 $。若实际数据均值非零，需先进行去均值处理。

3）同方差：序列的方差在各时刻保持一致，即$ {\text{Var}}({y_t}) = {\sigma ^2} $，避免因方差波动导致模型预测偏差。

4）无自相关噪声：噪声项$ {\varepsilon}_{t} $不存在自相关性，即$ E\left(\varepsilon_{t} \varepsilon_{s}\right)=0 $，确保模型残差中不包含可利用的预测信息。

1.2 自适应AR模型的构建

船舶升沉运动本质上是非平稳随机过程，尤其在复杂海况下（如台风、涌浪），其统计特性（均值、方差）会随时间显著变化。传统AR模型在海况突变时会出现预测偏差，无法满足预防控制需求。

为了应对这一情况，提出一种自适应AR模型预测方法，核心思路是通过动态参数更新，进而实现实时数据驱动模型参数自适应调整，通过引入遗忘因子λ（0.95≤λ≤1），对历史数据赋予递减权重，使模型能实时更新参数以适应时变特性。

1）模型动态更新流程初始化：设定初始参数$ {\hat \phi _0} = 0 $，初始协方差矩阵$ {{\boldsymbol{P}}_0} = \alpha I $，$ \alpha = {10^6} $，表征初始估计的不确定性。

2）实时递推：每获取一组新的升沉数据$ \left( {{y_t},{\text{ }}{Y_{t - 1}}} \right) $，计算增益矩阵K_t，确定新数据对参数的修正幅度，其表达式为：

$ {{\boldsymbol{K}}_t} = {P_{t - 1}}{Y_{t - 1}}{(Y_{t - 1}^{\text{T}}{P_{t - 1}}{Y_{t - 1}} + \lambda )^{ - 1}} 。$

(2)

基于预测误差$ {e_t} = {y_t} - Y_{t - 1}^{\text{T}}{\hat \phi _{t - 1}} $修正参数估计值$ {\hat \phi _t} $，其表达式为：

$ {\hat \phi _t} = {\hat \phi _{t - 1}} + {{\boldsymbol{K}}_t}({y_t} - Y_{t - 1}^{\text{T}}{\hat \phi _{t - 1}}) 。$

(3)

最后更新协方差矩阵P_t，反映参数估计的最新不确定性。

$ {{\boldsymbol{P}}_{\boldsymbol{t}}} = \frac{1}{\lambda }(I - {{\boldsymbol{K}}_t}Y_{t - 1}^{\text{T}}){P_{t - 1}} 。$

(4)

式中：$ {Y_{t - 1}} = {[{y_{t - 1}},{y_{t - 2}}, \ldots ,{y_{t - p}}]^{\text{T}}} $为历史升沉数据向量；P_t为表征参数估计的不确定性。

λ反映模型对历史数据的记忆强度，在船舶升沉预测中可理解为海况稳定性系数。当λ=1时，模型等价于传统OLS估计，适用于平稳海况；当λ<1时，模型对新数据更敏感，λ=0.98时，模型能在3个采样周期（约1.5 s）内响应升沉运动的均值突变，这对船舶穿越波峰波谷时的预测至关重要。

1.3 带外部输入的自回归模型

自适应AR模型通过动态更新算法实现了参数的时变更新，但本质上仍属于“黑箱”预测，仅利用升沉运动的历史数据，未考虑海浪这一核心激励源的影响。在前述AR模型基础上，引入海浪预报数据作为外部输入，即构建带外部输入的自回归模型（AutoRegressive with eXogenous input，ARX）模型，其数学表达式为：

${ {y}_{t}={\varphi }_{1}{y}_{t-1}+\dots +{\varphi }_{p}{y}_{t-p}+{\theta }_{1}{u}_{t-d}+\dots +{\theta }_{q}{u}_{t-d-q+1}+{\varepsilon}_{t} 。} $

(5)

式中：u_t为海浪参数向量，通常包括有效波高H_s、平均周期T_p；($ {\theta _1}, \cdots ,{\theta _q} $)为输入参数权重，反映海浪参数对升沉的影响强度；d为输入延迟，表征海浪从生成到影响船舶升沉的时间滞后。

$ d = {d_0} + \frac{{L \cdot \cos \alpha }}{{{v_w} + {v_s} \cdot \cos \beta }} 。$

(6)

式中：d₀为初始滞后；L为船长；α为浪向与船体中纵剖面夹角；v_w为波速；v_s为航速；β为航向来向角。

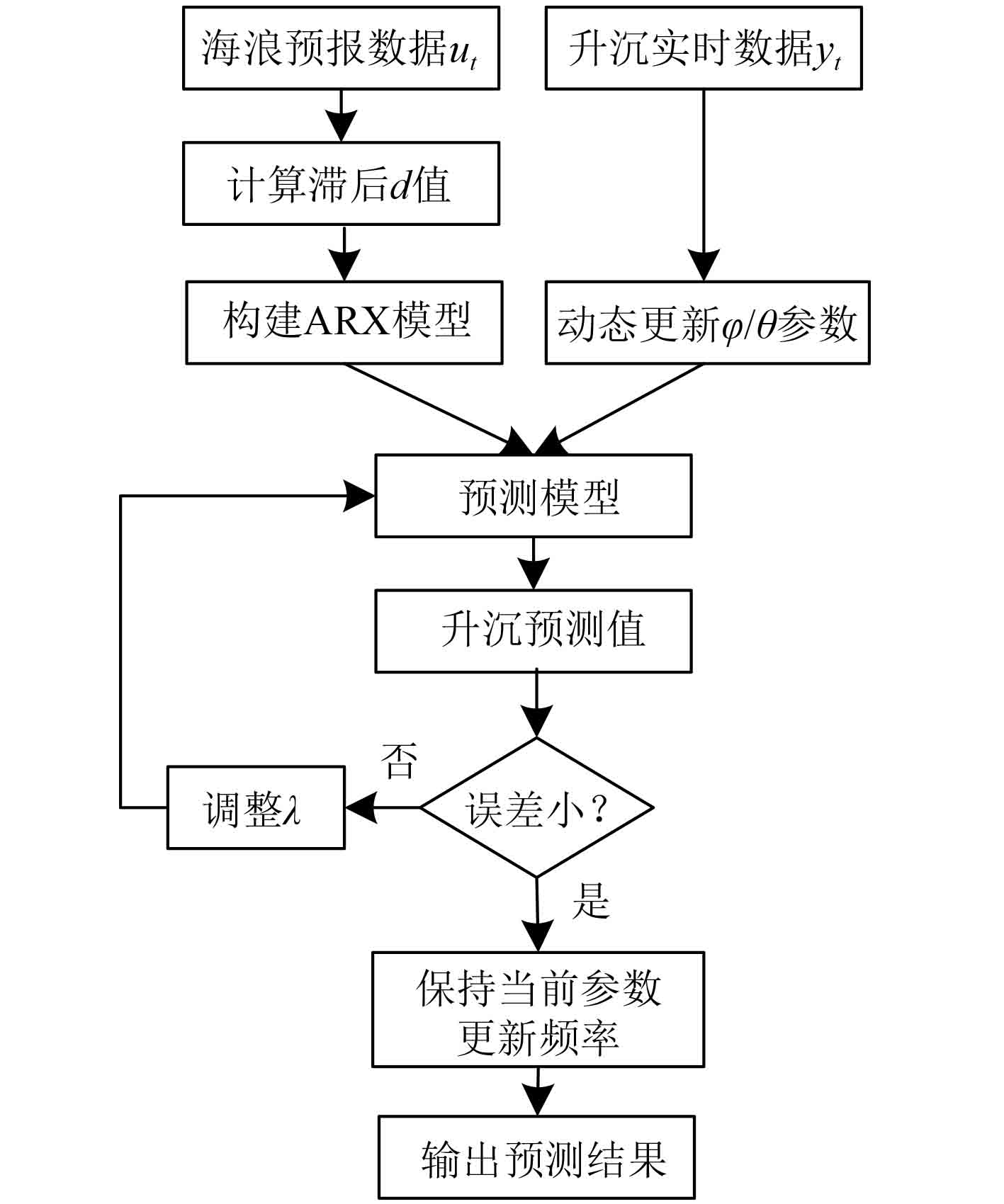
图1为ARX模型与自适应机制的协同流程，首先，输入海浪预报数据u_t和升沉实时数据y_t，对海浪数据计算滞后时间d并构建ARX模型，同时利用升沉数据通过动态更新机制迭代优化模型的自回归系数φ和输入系数θ。两者共同输入预测模型生成升沉预测值，随后通过误差判断模块：若预测误差较小，保持当前参数更新频率以维持模型稳定性；若误差较大，则调整遗忘因子λ，实现对船舶升沉运动的时变预测，既利用海浪预报的因果性提升物理可解释性，又通过误差反馈机制优化模型参数，确保在复杂海况下的预测精度，最终输出可靠的升沉预测结果，为船舶升沉运动的预防控制提供关键输入。

2 基于AR时间序列模型的船舶升沉预报仿真

仿真条件设定：采用某集装箱船在特定海况下的实测升沉数据，采样频率为2 Hz，共200个时间步长，同时结合同步的海浪预报数据（包含波高H_s、周期T_p，更新频率1 min）。对于模型，AR模型阶数设为p=5，遗忘因子λ处于0.95～0.98动态调整。

ARX模型引入海浪参数H_s、T_p作为外部输入，设定输入延迟d=2 s，采用升沉位移作为验证指标。对比自适应AR、ARX模型的预测性能，其中自适应AR模型利用算法结合遗忘因子动态调整参数以适应时变特性，ARX模型则在自适应AR模型基础上融合海浪数据构建，通过多源融合与自适应机制的协同逻辑进行预测，以探究不同模型在船舶升沉运动预测中的表现及优势。

表1为不同模型升沉运动预测对比，可以发现：传统AR模型由于参数时不变的特性，在复杂海况下预测性能较差，其均方根误差（RMSE）高达0.78 m，对海况突变的响应时间超过10 s，难以满足船舶升沉运动实时预测需求，且存在0.45 s的相位延迟，导致预测结果滞后于实际运动。而自适应AR模型引入遗忘因子和动态参数更新机制后，预测精度显著提升，RMSE降至0.32 m，对海况突变的响应时间大幅缩短至1.5 s，相位延迟也减少至0.15 s，能够更及时、准确地跟踪升沉运动变化。在此基础上构建的ARX模型，通过融合海浪预报数据作为外部输入，进一步优化了预测效果，RMSE低至0.28 m，海况突变响应时间缩短至1.2 s，相位延迟仅0.10 s，在三者中预测性能最优。

表2为不同模型升沉运动预测误差统计，从平均绝对误差看，ARX模型较自适应AR模型降低16%，较传统AR模型降低66.1%，表明其对升沉位移的整体预测偏差更小。最大误差指标中，ARX模型的0.76 m远低于传统AR模型的1.85 m，在极端海况下的预测稳定性更优，能有效避免因大幅预测偏差导致的控制策略失效。误差标准差（SED）反映预测误差的离散程度，ARX模型的0.03 m仅为传统AR模型的25%，说明其预测结果的一致性更强。

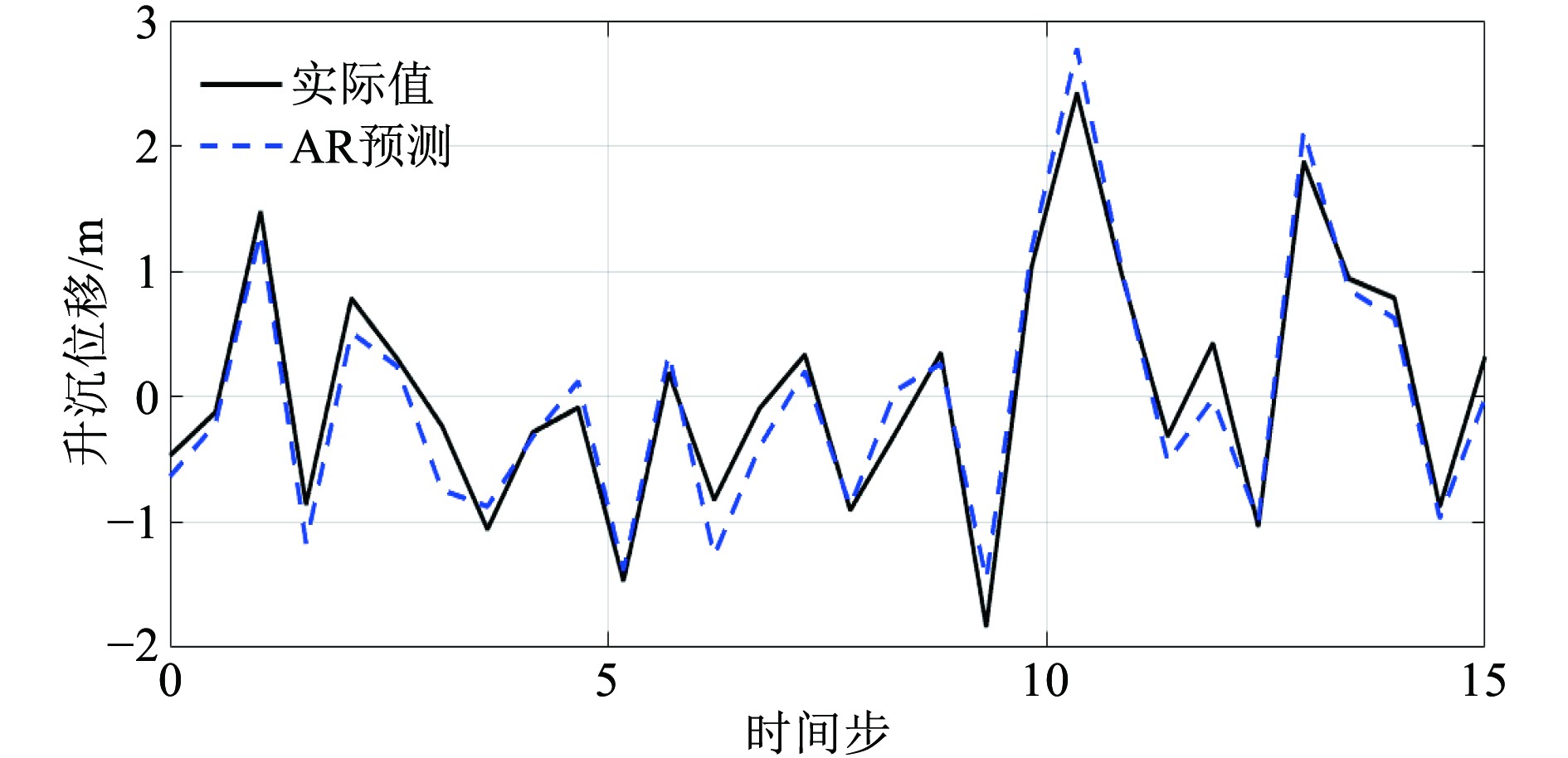
图2为自适应AR模型升沉位移预测仿真结果，横坐标代表时间步数，对应一定时长的时间序列，纵坐标为升沉位移，范围在−2～3 m。曲线的波动情况反映了模型对船舶升沉运动的预测。可以看到曲线较好地贴合了实际升沉的时变特性，该模型通过遗忘因子的动态调整，有效提升了对海况突变的响应能力，体现出其在处理非平稳海况下船舶升沉运动预测的优势，能够较为准确地跟踪升沉运动的动态变化。

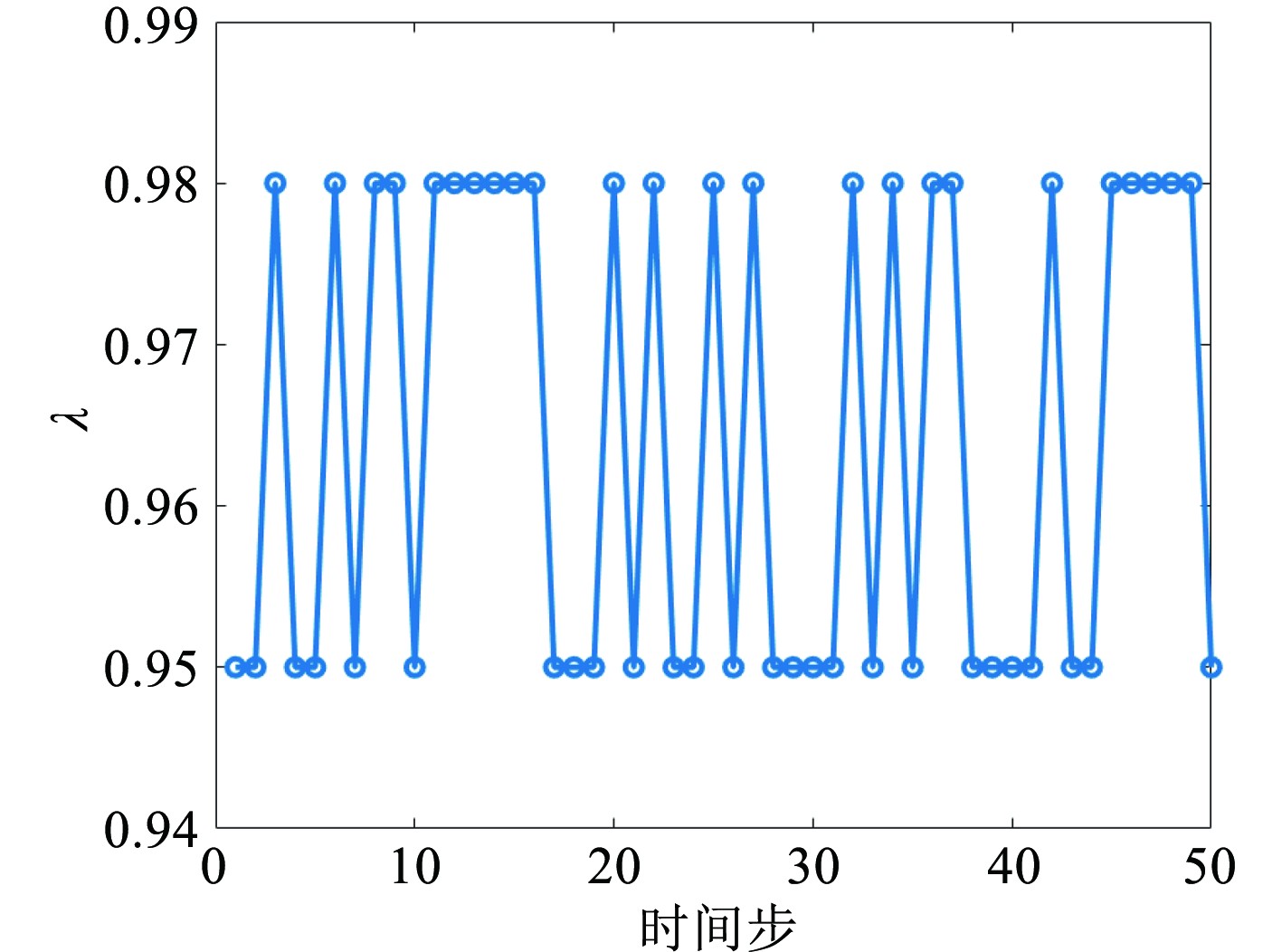
图3为误差驱动的遗忘因子调整，取值范围在0.95～0.98。从图中可以看出遗忘因子λ随着时间和预测误差呈现动态变化。当船舶升沉幅值出现骤升等海况突变情况时，λ会迅速下降，使模型能够快速更新参数以适应变化；当误差减小、海况相对平稳时，λ又会上升，维持模型参数的稳定性，避免过度拟合。这种误差驱动的遗忘因子调整机制，使模型在不同海况条件下都能保持较好的预测性能，根据实际情况动态平衡模型对历史数据的记忆强度和对新数据的敏感度，确保了模型在复杂海况下预测的鲁棒性。

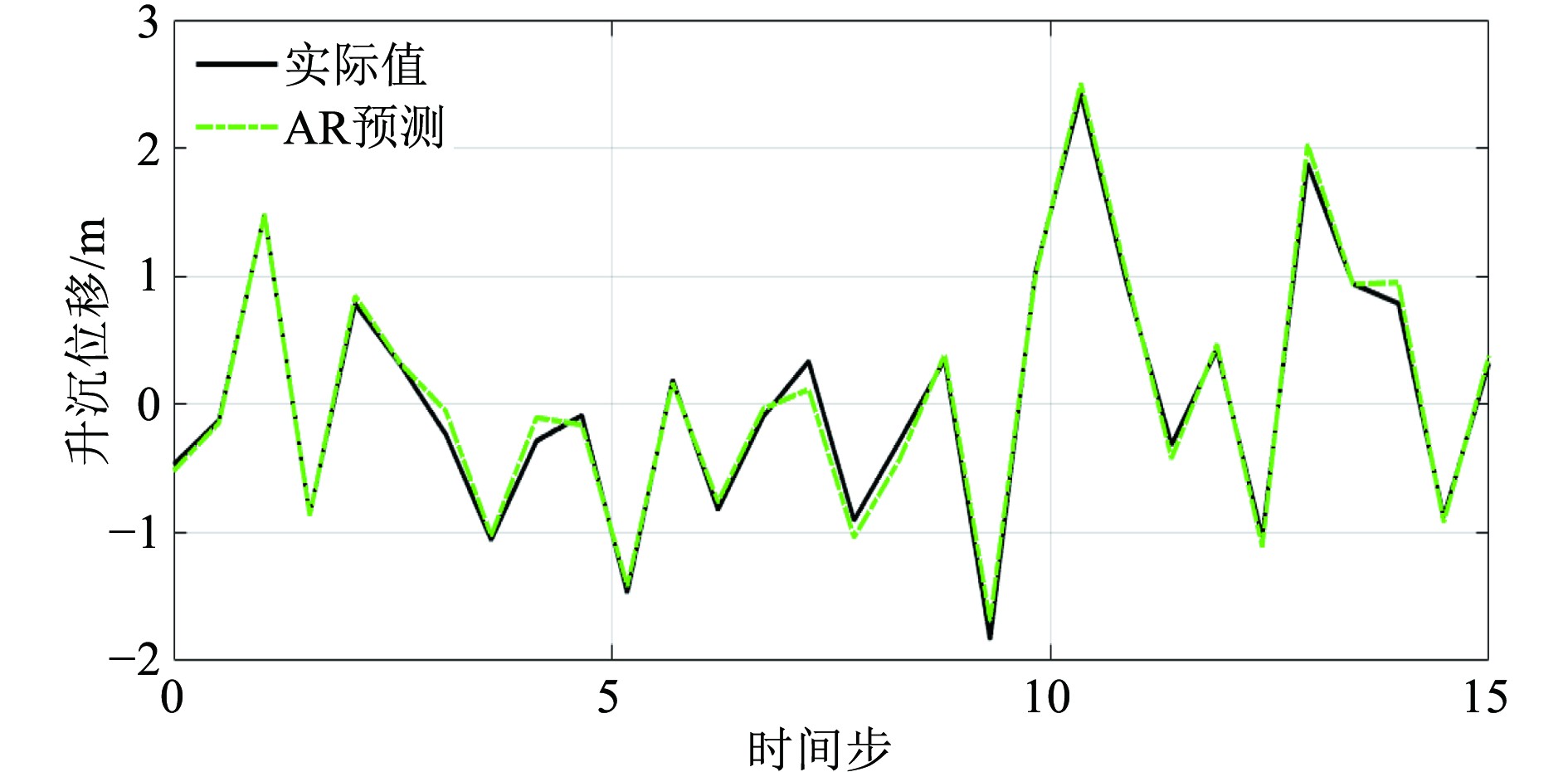
图4为ARX模型位移预测仿真结果，由于引入了海浪预报数据作为外部输入，相比自适应AR模型，ARX模型在幅值和频率的预测上更为准确，能更好地体现海浪对船舶升沉运动的影响。在特定时间步长内，峰值的预测更接近实际情况，波动的密集程度也更贴合海浪周期。

3 结　语

船舶升沉运动的准确预测对保障船舶安全与作业稳定性具有重要意义，在船舶航行、海上作业等场景中有着广泛的应用背景。通过研究基于AR时间序列模型的船舶升沉运动预测方法，得出以下结论：

自适应AR模型通过引入遗忘因子λ，相较于传统AR模型，其均方根误差（RMSE）从0.78 m大幅降低至0.32 m，对海况突变的响应时间从超过10 s缩短至1.5 s，相位延迟由0.45 s减少至0.15 s，能精准捕捉升沉运动的动态变化趋势，显著提升了模型在非平稳海况下的预测能力与实时性。

ARX模型在自适应AR模型基础上，创新性引入海浪向量u_t作为外部输入，并通过精确计算输入延迟d构建耦合预测机制。在同一仿真环境下，ARX模型将RMSE进一步优化至0.28 m，较自适应AR模型提升12.5%，突变响应时间缩短至1.2 s，相位延迟低至0.10 s。