2. 武汉理工大学 绿色智能江海直达船舶与邮轮游艇研究中心,湖北 武汉 430063
2. Research Center for Green and Intelligent River-Sea Direct Ship and Cruise Yachts, Wuhan University of Technology, Wuhan 430063, China
机舱是船舶最重要的舱室之一,其结构完整性对全船安全具有重要影响。与传统舱室不同,本文研究舱室由内壁、外壁及内外壁之间的密集加筋组成,之间形成大量细小的密闭空间。工作中由于突发事故内部设备可能发生损管破坏,形成热源并释放大量热量,导致舱室内壁温度迅速升高,并将热量传递至周围结构。一方面,高温环境会严重削弱钢结构的力学性能;另一方面,复杂舱室的迅速升温导致相邻构件温度分布不均,温差变形使局部构件产生热应力,进一步降低了结构的承载能力。因此,研究此类舱室的热载荷参数特性对保障其安全性能具有重要的实际意义。
国内外学者针对热载荷作用下板和加筋板的温度场分布和热力学响应进行了大量研究。Krzysztof[1]综述了热载荷对船舶结构性能影响的研究进展。板和加筋板作为船体结构的基本组成单元,研究其热力学性能可以为分析整船结构奠定基础。魏子阳[2]开展了加筋板热力耦合方法研究,发现高温载荷会显著削弱加筋板的极限承载能力。杨逸飞等[3]建立一种带隔热层加筋板结构的热力响应分析方法,发现内壁角点的应力大于外壁面对应点及内壁中点。郝军凯等[4]计算了甲板板架在火灾热载荷作用下的动态热力响应。
相较于加筋板,船舶舱室的温度场分布和力学性能变化更加复杂。袁敏杰[5]、汪金辉[6]、滕晓青等[7]通过FDS软件对热载荷作用下船舶舱室的温度场进行分析,将计算得到的边界热通量值导入Abaqus等力学分析软件,实现结构热耦合计算以获得结构的热力学响应。刘云山等[8]开展了火灾场景下船舶舱室结构动态热力响应研究,其采用的大涡模拟算法能够考虑实际环境温度时变、非均匀的特性。
除了数值分析方法,试验是揭示结构热载荷特性最直接最准确的手段。由于船用舱室尺度大、结构复杂,通过实船结构进行试验成本高且难于实施。因此,一般通过设计缩比模型的方法开展试验研究。朱小俊等[9]设计了一个方舱缩比模型开展钢制舱壁升温的试验,发现舱室整体温升呈对称分布,对称中心点为热源上方的舱顶位置。王进军等[10]运用相似理论对标准燃烧室建立了1∶10的模型试验箱,并证明了小尺度模型预测全尺寸舱室温度场的合理性。Wang等[11]开展了小尺度封闭机舱模型的火灾试验,分析了封闭空间结构的温度分布。
以上试验对象均为单舱壁简单舱室结构,本文针对的舱室结构具有多层舱壁,舱壁间贯穿大量密加筋,形成众多细小封闭空间。其结构形式与传统单层舱室存在较大差异,这必将导致其热传导方式和温度场分布规律明显不同。因此,本文以双层复杂舱室结构为研究对象,运用相似理论设计结构缩比模型,通过试验和仿真相结合的方法研究其温度场分布和热载荷特性。
1 模型相似设计在热载荷相似性设计中,模型和原型遵循同一热传导模型,现实中难以满足热传导方程中的所有同名特征数相等。因此,一般认为只要保证某些重要的特征数保持一致即可。本文舱室内部的热量主要依靠空气的流动进行传递,而空气的运动过程主要受到重力的作用,Froude数作为表征流体惯性力和重力相对大小的一个参数,在模型设计中是最重要的特征数。因此本文通过保证Froude模型的相似性来建立一个小尺寸的缩比模型。
1.1 相似条件在建立缩尺比模型时,首先要保证几何形状的相似。由于热源温度经由内部壁面向外部舱室传递,而舱室板厚远小于其长和宽,因此主要考虑模型特征长度的相似性。板厚对温度传导影响较小,可以近似视为一个二维的平面传热模型。考虑到模型加工精度问题,保证板的等效厚度比例一致即可。
| $ {\lambda _l} = \frac{{{l_m}}}{{{l_p}}} 。$ | (1) |
式中:λ为模型与原型的比例;l为特征长度;m和p分别为模型和原型。
为了保证模型和原型的Froude数相等,根据公式
| $ {\lambda _V} = \lambda _l^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} 。$ | (2) |
根据几何相似关系和速度相似关系,可以推导出时间相似关系为:
| $ {\lambda _t} = \frac{{{{{l_m}} \mathord{\left/ {\vphantom {{{l_m}} {{V_m}}}} \right. } {{V_m}}}}}{{{{{l_p}} \mathord{\left/ {\vphantom {{{l_p}} {{V_p}}}} \right. } {{V_p}}}}} = \lambda _l^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} 。$ | (3) |
模型与原型在相同位置的空气温度相同,因此温度相似关系为:
| $ {\lambda _T} = 1。$ | (4) |
舱壁之间通过热传导进行热量传递,因此模型与原型在边界必须满足换热相似:
| $ \frac{{{{\left( {k\rho c} \right)}_{w,m}}}}{{{{\left( {k\rho c} \right)}_{w,p}}}} = \lambda _l^{0.9} 。$ | (5) |
式中:k为热传导系数;ρ为壁面材料密度;c为比热容;w为壁面。
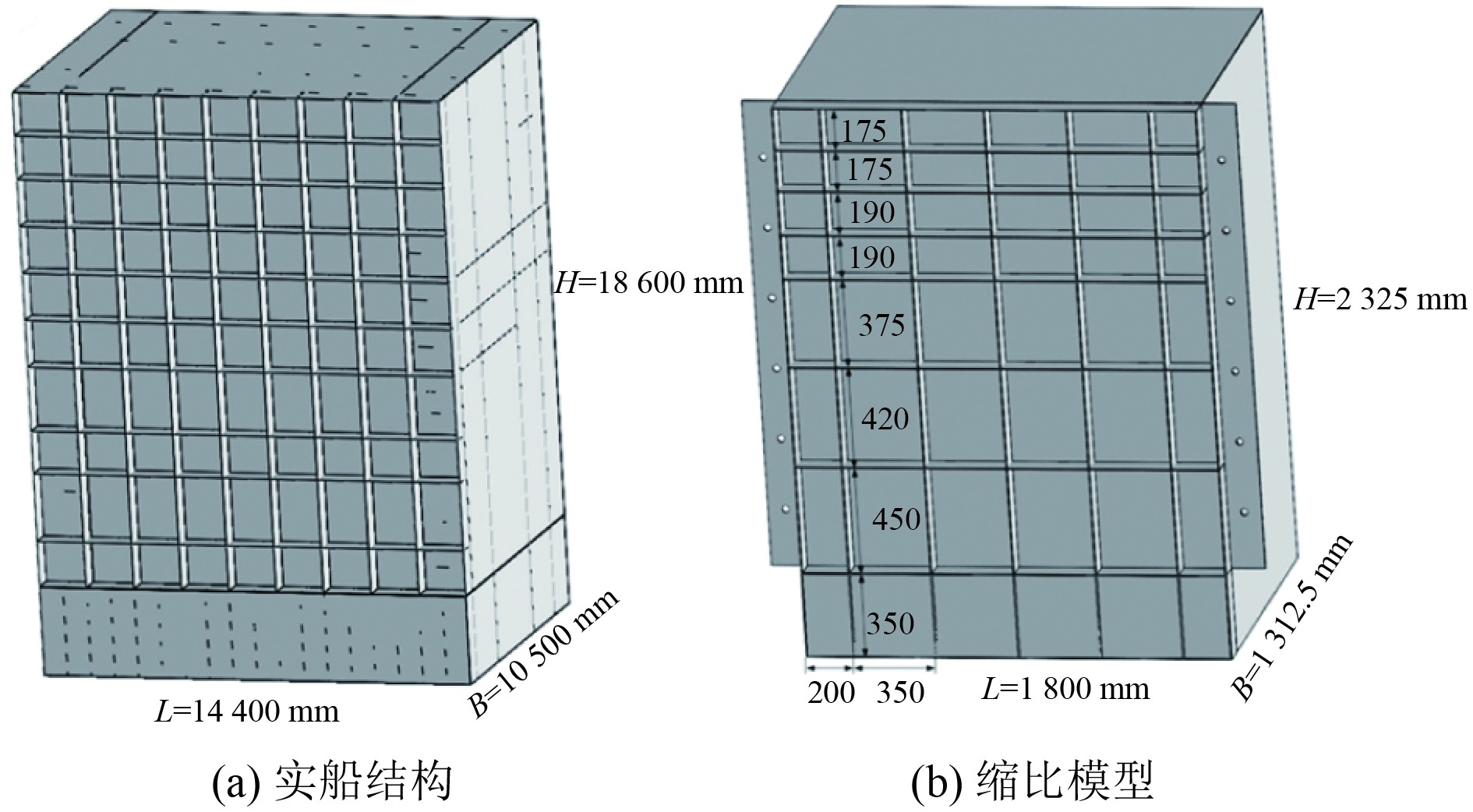
1.2 模型设计实船舱室结构主尺度长为
|
图 1 模型设计 Fig. 1 Model design |
本文中考虑的舱室模型与传统舱室不同,为密加筋结构。内外舱壁之间的加筋一部分为贯穿内外舱壁,即与内外壁板同时相连;一部分为非贯穿加筋,即只与内壁板相连,并不与外壁板接触。在热量由内壁板传递到外壁板的过程中,贯穿加筋在热传导中起到主要作用。由于实船结构加筋数量过多,按照实际布置缩比会导致各加筋尺寸及间距过小无法加工,且会产生较大的焊接变形。因此,本文进行缩比模型设计时对舱壁间的加强筋进行简化处理,只保留了贯穿加筋,非贯穿加筋则通过等效板厚的形式计入贯穿加筋中。缩比模型加筋厚度并非简单按照缩尺比进行调整,而是综合考虑了模型加工难度和实船密加筋热传递贡献度进行等效替代设计。通过缩比前后壁面加筋剖面面积一致,保证缩比模型与实船模型的热传导特性基本一致,加筋间距控制在100 mm以上,如图1(b)所示。为了方便调整热源位置以及布置传感器测量装置,将舱室靠近船中的舱壁设计为可拆卸式,并通过螺栓连接。
2 缩比模型有限元分析 2.1 有限元模型本节采用有限元方法(软件为Ansys Fluent 2023 R1)研究舱室结构整体的温度分布并验证该方法的准确性,为之后对实船结构的模拟做准备。
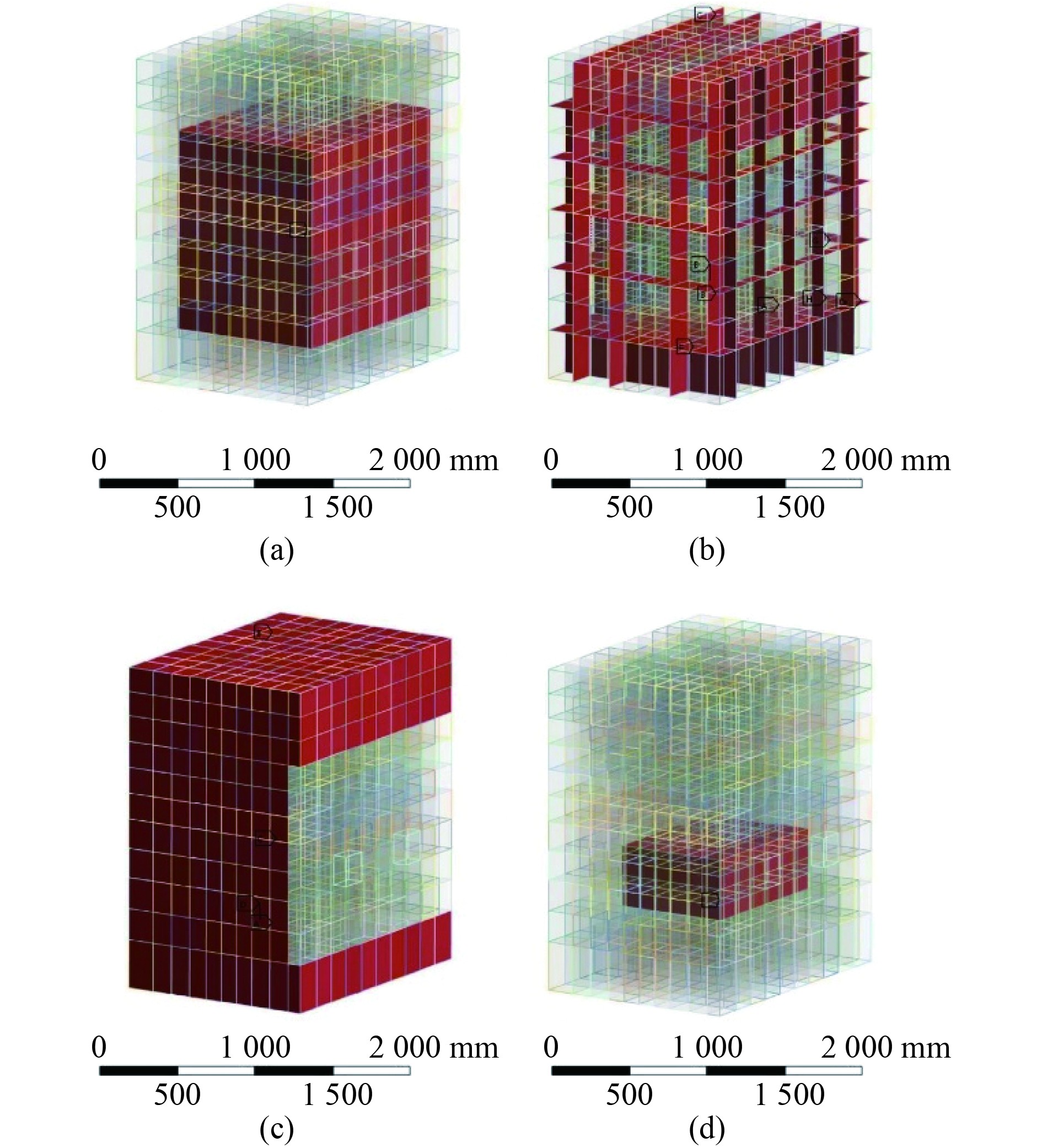
有限元模型如图2所示,整体三维模型按照试验模型建立。内部热源依照试验情况,选取底部2层网格,分别与四周间隔一层网格。热源大小为
|
图 2 有限元模型 Fig. 2 Finite element model |
为了保证有限元分析的准确性,需要使边界条件和工况与缩比试验保持一致。边界条件为内部与外部存在热交换,并模拟舱室静置在固定位置,对舱室的角节点进行完全固定。仿真过程中考虑了舱室对外热辐射导致的热量散失,不考虑外部空气温度变化的影响,外界空气温度设置为室温状态。仿真中的热源采用等效的长方体进行模拟,并保证体积、高度、质心位置与实验中的热源一致。所用的结构钢参数与内部空气参数见表1和表2。内部舱室仅包含空气一种流体,并对空气Air用理想气体进行模拟。在建立几何模型时采用命名面的方式设置壁面,主要参数包括壁面材料与厚度。传热相关边界条件设置为对流,来流温度与缩比试验时空气温度保持一致,为26.85 ℃。计算工况则与试验热源保持一致,即将热源温度设置为300 ℃。
|
|
表 1 结构钢参数 Tab.1 Structural steel parameters |
|
|
表 2 空气参数 Tab.2 Air parameters |
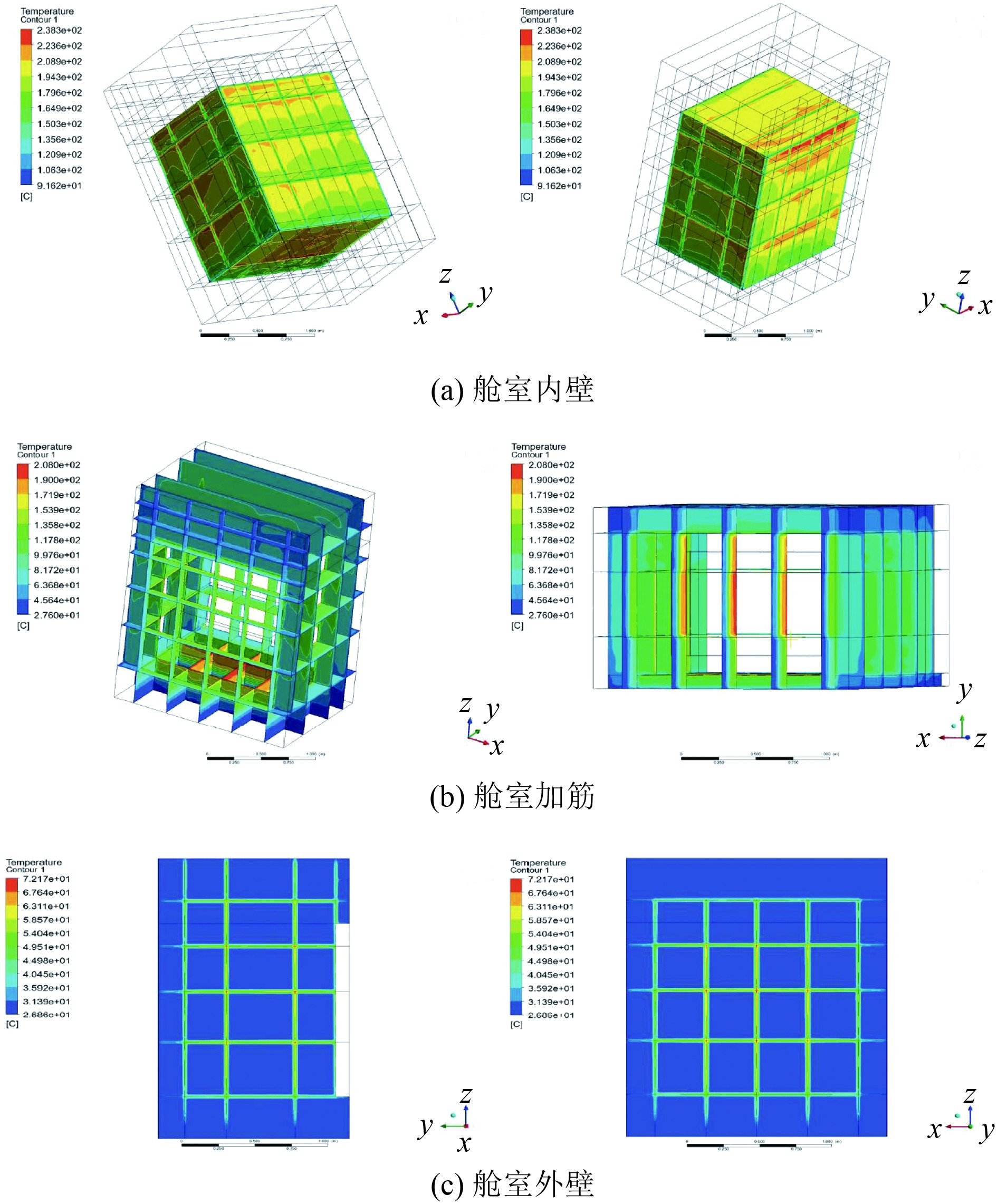
在确定边界条件及计算工况后,对模型进行计算分析,计算结果如图3所示。根据计算结果可以发现,内部舱壁大部分温度处于100 ℃~200 ℃,局部范围温度可以达到近240 ℃。由于空气加热后向上流动,因此舱室顶板的温度会明显高于底板温度。内外壁间由密加筋组成的方舱内也同样存在该现象,同时由于加筋的影响,这些垂直的舱壁上有明显的分层现象。内壁温度最低处主要是在底部舱壁的角隅处,因为其空气流动性差,换热较难。
|
图 3 双层舱室外壁温度云图 Fig. 3 Temperature cloud map of the outer wall of the double-layer compartment |
加筋温度分布则主要依靠内壁对外的热传导,因此板上有明显的温度梯度分布。底部和顶部结构由于加筋高度较大,相比四侧的加筋温度梯度分布更为显著。外壁温度则主要靠加筋结构对其的热传导,因此可以明显看出仅在外壁与加筋连接处有明显的局部温度升高。
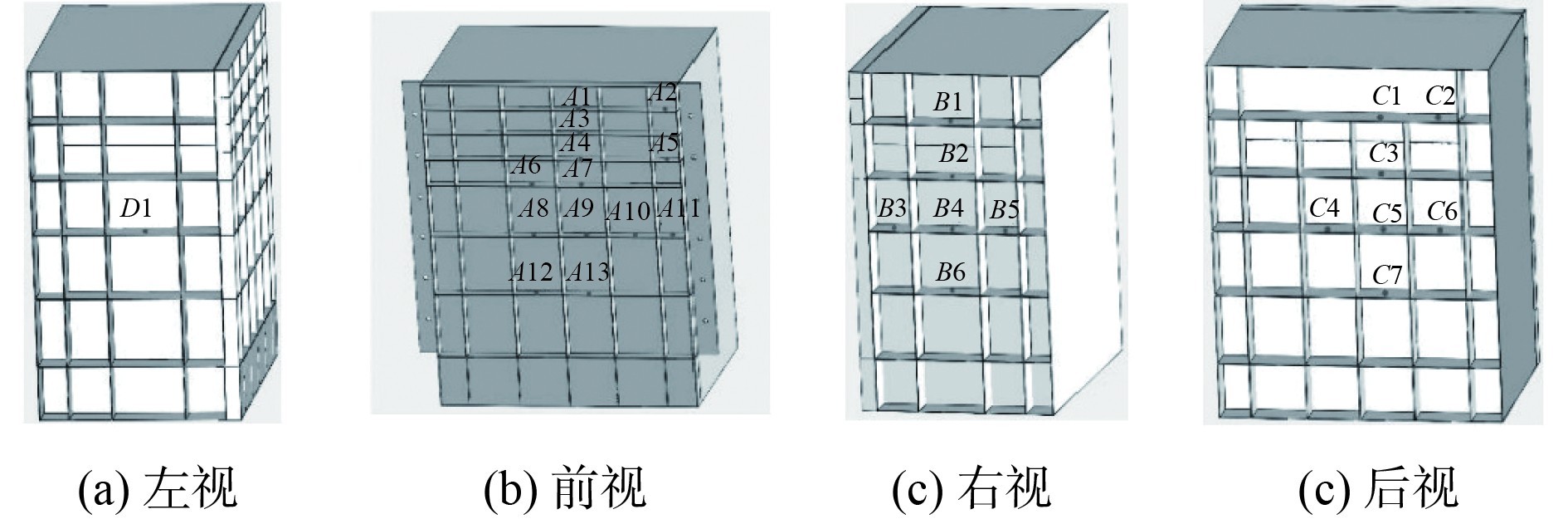
3 双层舱室结构热载荷试验研究 3.1 热源与材料系统实验采用30 kW风道加热芯作为试验热源,通过控制箱监测热源温度并进行控制。当热源达到目标温度后,控制箱会间歇式断电保证热源在目标温度值附近上下浮动。由于本实验模型为对称模型,因此将热源放置在舱壁内部中心,且离舱室内底板距离为10 mm。由于接触式测温系统简单且在气体温度测量方面较为成熟,因此本试验选用接触式测温方式中的热电偶测温方法。考虑到本实验的温度较低,选取K型铠装式热电偶,测温范围为−200 ℃ ~ +
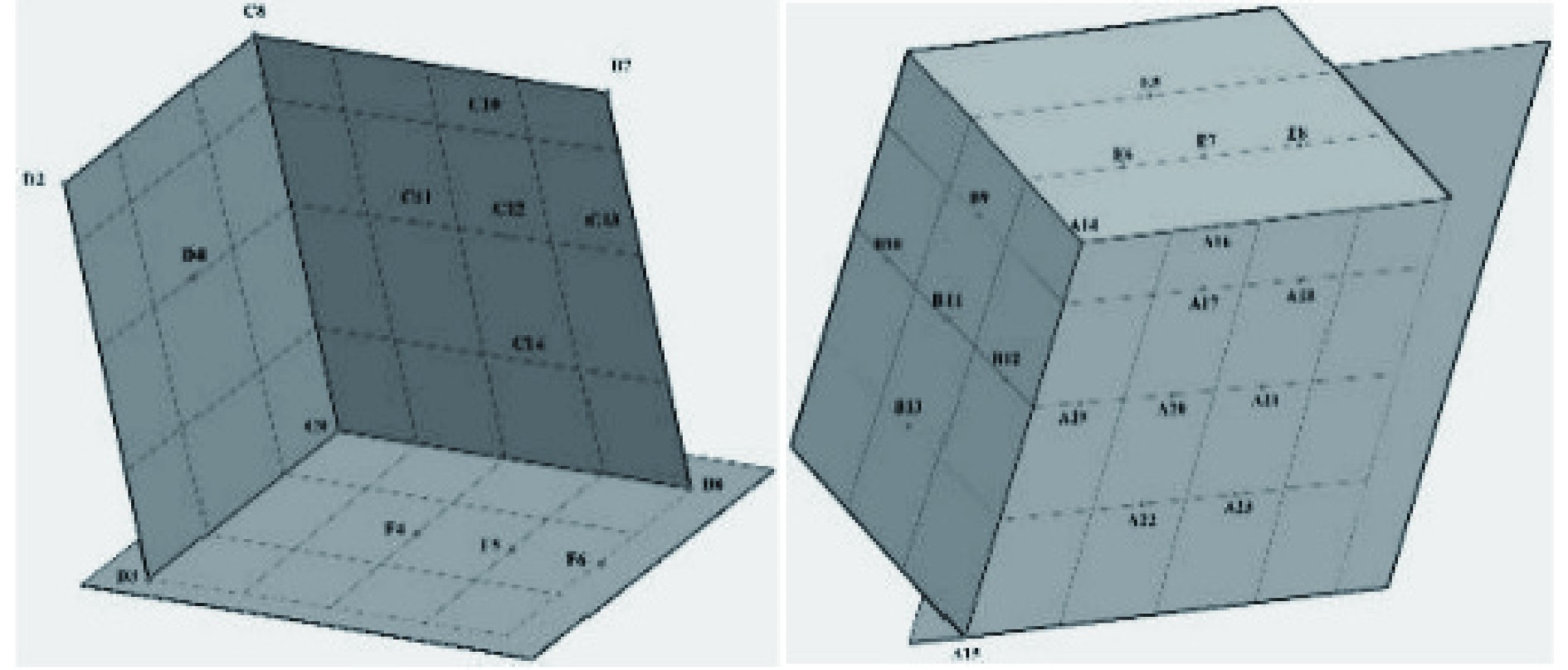
图4为双层舱室结构内壁温度测点布置示意图,图5为外壁温度测点布置示意图,图6为内外壁间加强筋的温度测点布置图。由于同一视图内测点编号前缀相同且各视图之间测点命名不同,为方便表述,后文将前视命名为A视图,右视命名为B视图,后视命名为C视图,左视命名为D视图,俯视命名为E视图,仰视命名为F视图。
|
图 4 双层舱室内壁温度测点布置示意图 Fig. 4 Schematic diagram of temperature measurement points arrangement on the inner wall of the double-layer compartment |
|
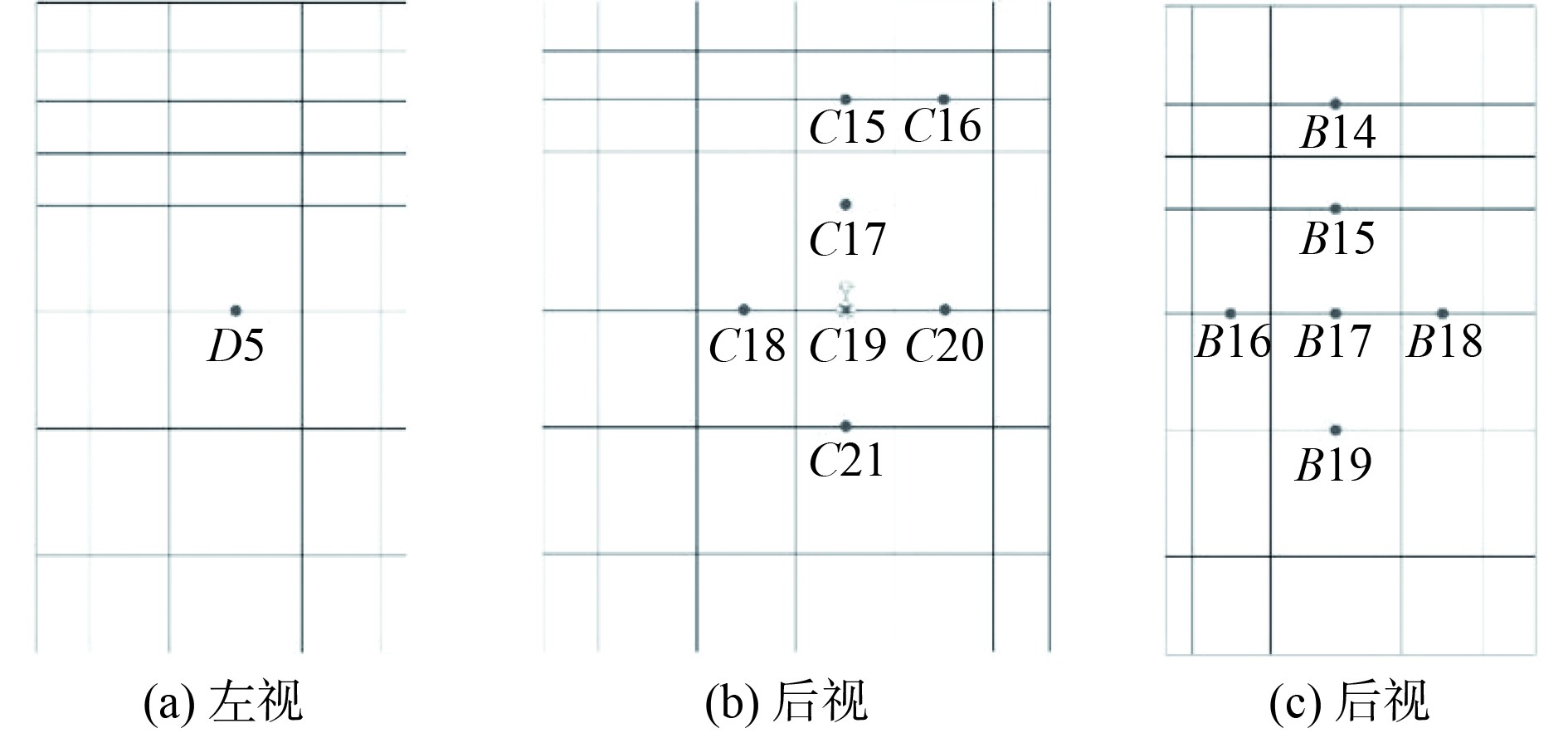
图 5 双层舱室外壁温度测点布置示意图 Fig. 5 Schematic diagram of temperature measurement points arrangement on the outer wall of the double-layer compartment |
|
图 6 双层舱室内外壁加筋处温度测点布置示意图 Fig. 6 Schematic diagram of temperature measurement point layout at the reinforced inner and outer walls of the double-layer cabin |
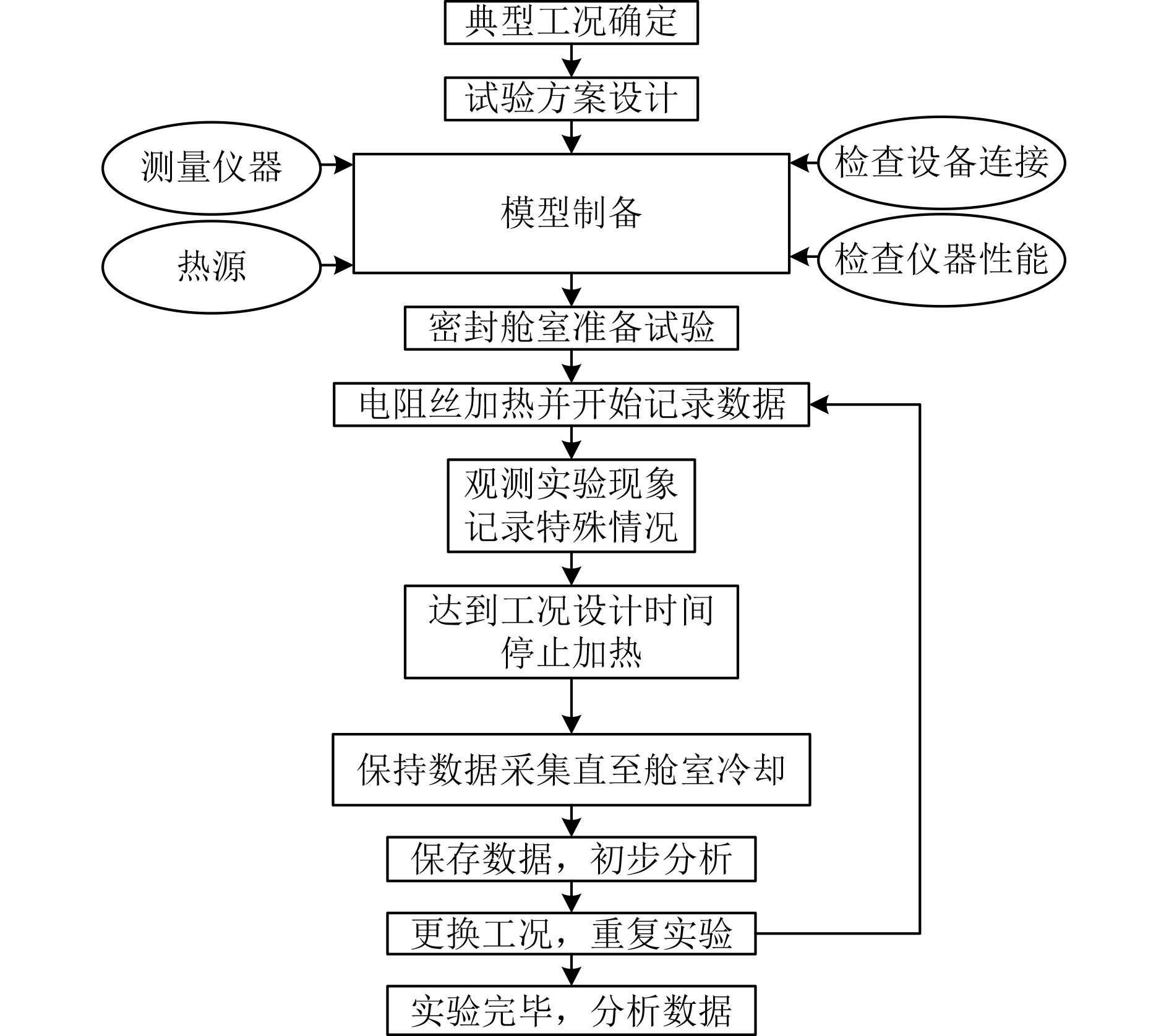
试验具体流程如图7所示。在正式试验开始前先进行3次预试验,试验工况分别为常温、热源恒温50 ℃、热源恒温100 ℃,以检查试验模型的封闭性能和隔热能力,检验数据采集系统的工作性能和精度。
|
图 7 舱室结构热载荷参数试验步骤流程图 Fig. 7 Flow chart of thermal load parameter test steps for cabin structure |
正式开始实验,将热源连接380 V高压电源,通过控制器设置温度上限300 ℃,启动温度和应力测量系统开始记录实时动态数据。
试验初期,随着热源温度快速上升,舱室结构内壁温度迅速升高。相比之下,加筋和外壁测点温度上升较缓。试验进行一段时间后,内壁温度上升趋势变缓,加筋和外壁测点温度稳步上升。试验后期,内外壁和加筋处温度都趋于稳定,测点温度处于平衡位置。在达到稳态平衡后继续记录10 min,随后关闭热源,继续采集数据1 h后停止采集并保持数据。
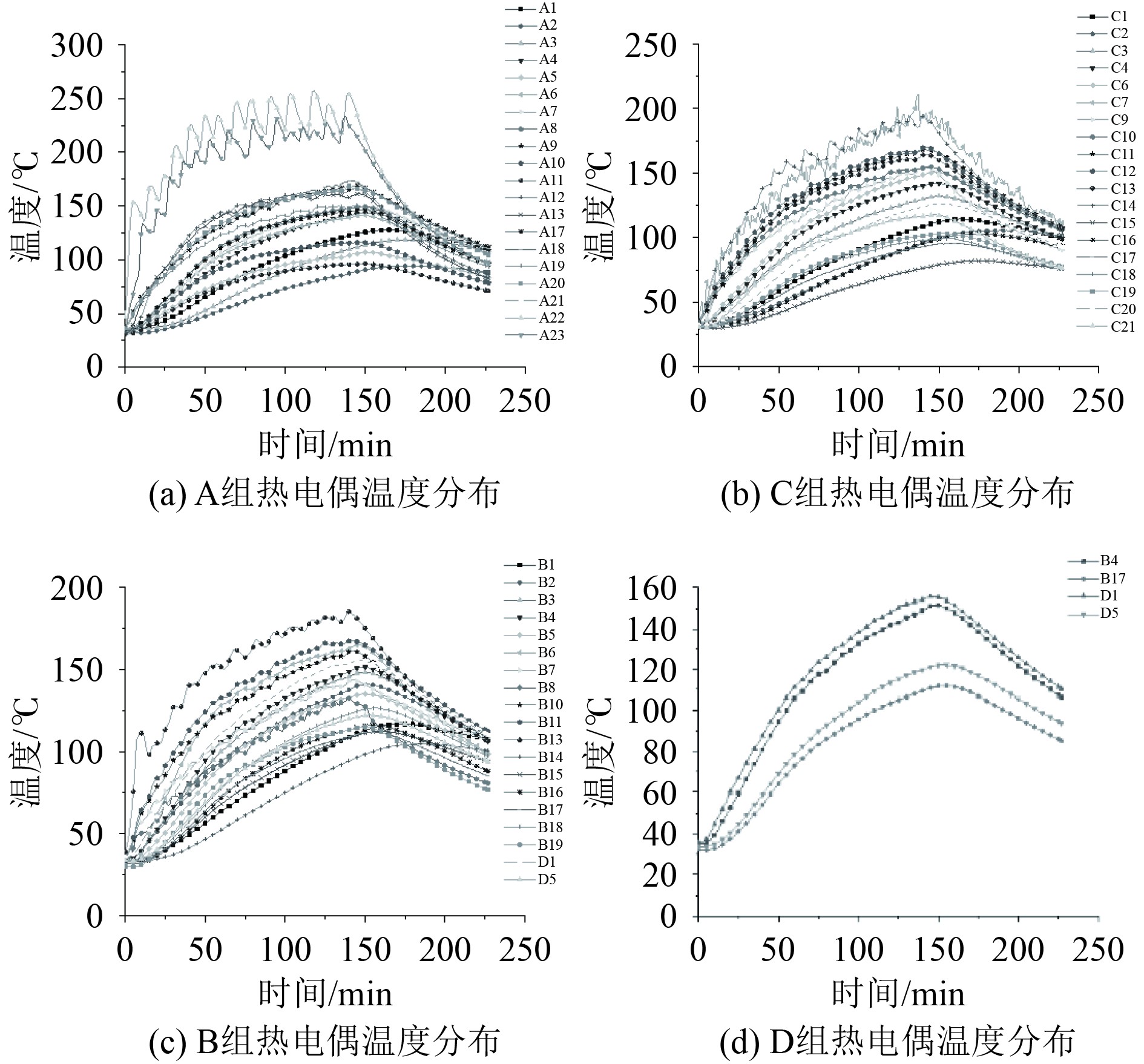
3.3 试验结果分析图8(a)和图8(b)分布为整个实验进程中舱室A视图测点升温图(A组热电偶)和C视图测点升温图(C组热电偶)。由于A22和A23最靠近热源,受热源影响最明显,温度上升速度明显高于其余测点。在加热过程中,热源温度不是恒定值,而是在目标值附近上下波动,这就导致A22和A23测点温度不是平稳上升而是波浪式上升。而其余测点由于温度相对较低,因此其温度上升过程大致呈平稳上升趋势,波动并不明显。由于A组热电偶这一侧为单层舱壁结构,保温性能较差,因此除A22和A23这2个最靠近热源的测点外,其余测点的热量容易向外界散失,因此温度较低。
|
图 8 A组-D组热电偶对称测点温度对比 Fig. 8 Comparison of temperature at symmetrical measurement points of thermocouples in group A to D |
而C组热电偶与A组热电偶最大的不同在于C组热电偶没有明显高于其余测点的数据,主要是因为C组热电偶处为双层舱壁,因此保温效果更好。温度最高的测点为C7和C14,分析认为C14温度最高主要是热源处于底部,因此热空气对该处测点的影响较为明显,而C7温度较高则是因为本研究采用钢材料,而钢材料是热的良导体,因此内壁与外壁加筋间的温度主要依靠内壁向外壁的热传导。且实验模型2层舱壁间距离较近,因此C7测点温度与C14测点温度近似相等。
图8(c)和图8(d)为整个实验进程中舱室B视图和D视图测点升温图(B组和D组热电偶)。与A组热电偶的分布类似,B组热电偶同样存在越靠近舱室内部升温越高的特点。由于本实验模型为对称模型,因此D组主要起验证对称性和温度分布是否可信的作用。根据图8(d)可以对比发现D1和B4测点温度趋势与极值近似相等,而D5和B17测点温度趋势近似相等,而温度极值则存在一定差异,主要是因为D5和B14测点位于外壁,试验时由于外界干扰导致。说明本实验模型内部温度分布均匀且对称性良好。此外,尽管B8测点位于整个舱室的底部,但其位于底部的角隅处,这就导致热空气难以流动至该位置,因此其温度较低。
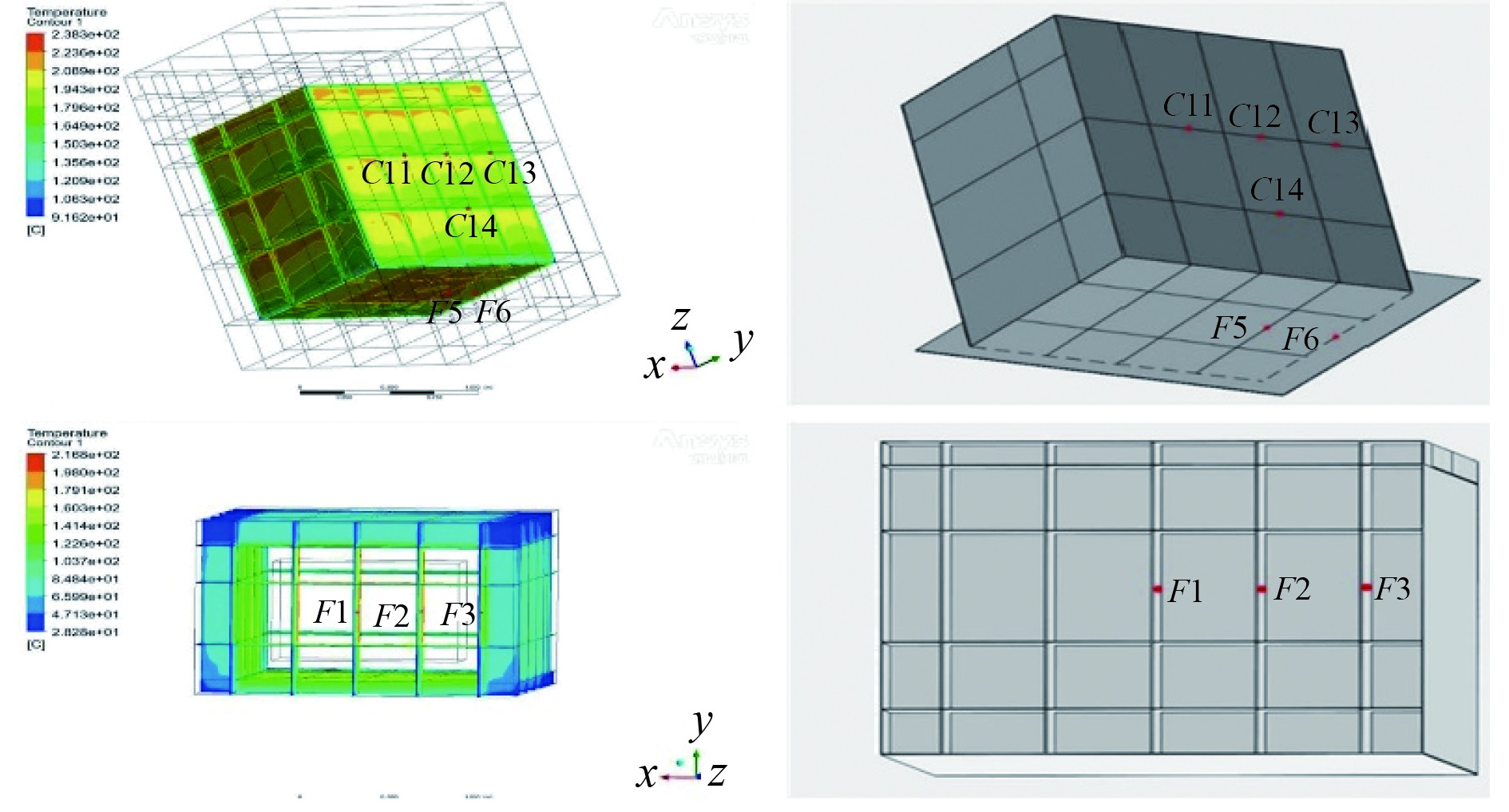
3.4 温度分布对比计算后得到恒温热源下双层舱室结构内壁温度分布,图9为温度对比点示意图,表3为试验和仿真方法的典型测点最高温度对比。可知,位于内舱壁高处的温度测点与实验数据差距较大,均大于15%,且最大误差为16.4%;而在位置低的地方,仿真结果与试验所测数据较为接近,均小于10%,且最小误差为1.8%。主要是因为舱室热源位于底部,垂直方向的较高位置空间更为宽广,空气流动的自由程度较高,导致该处测点的随机性更大。分析加筋的温度对比,可以发现最靠近外壁的加筋板中心测点对比差异最大,为15.4%,这主要是因为加筋的温度升高主要是由于内壁到加筋的温度热传导,且设计的缩比模型结构在内外壁之间纵横交错的加强筋组成了多个空腔,对热量交换和流动产生重要影响导致的。总体而言仿真结果与试验结果拟合良好,验证了数值仿真方法的准确性。
|
图 9 双层舱室温度对比点 Fig. 9 Temperature comparison points of double layered cabin |
|
|
表 3 双层舱室典型测点最高温度对比 Tab.3 Comparison of maximum temperatures at typical measurement points in double layered cabin |
本文分析试验数据研究模型的升温规律和温度场分布。通过数值仿真分析船舶动力结构热载荷分布情况。主要结论如下:
1)本文设计了双层舱室的缩比模型和一套研究温度分布特性的试验方法,然后将试验结果与仿真数据进行对比,验证了有限元方法的准确性,并通过有限元方法研究了缩比模型整体的温度分布变化。
2)试验过程中内壁上的最高温度约为240 ℃,外壁上的最高温度约为71 ℃。最高温度出现在舱壁的顶部,最低温度出现在底部角隅处。这主要与舱室的结构有关,舱壁底部靠近热源,热源加热空气后,空气流动将热量传递到最近的温度测点。而底部角隅处温度最低主要是因为空气受热后向上进行流动,无法流动到角隅处,而热空气上升至顶部后温度下降并沿着舱壁下沉,但当空气快下沉至底部时,会由于空气的流动特性脱离舱壁然后向热源处流动,这就导致角隅处存在一个小的环形回流,难以参与热量交换,因此温度最低。
3)与传统舱室相比,本文研究的舱室存在独特的密加筋结构,这就导致双层舱壁间有多个小空腔。内壁温度也会在加筋的对应位置出现温度的局部升高,然后通过加筋结构有效传递到外壁上,舱室结构温度分布复杂。同时,由于内外壁的热传导效应,加筋结构存在明显的温度梯度分布。
| [1] |
KRZYSZTOF W. Impact of thermal loading into the structural performance of ships: A review[J]. Ocean Engineering, 2022, 243: 110238. |
| [2] |
魏子阳. 高温下船体结构热力响应与损伤特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
| [3] |
杨逸飞, 袁昱超, 唐文勇. 高温载荷下带隔热层加筋板结构热力响应研究[J]. 船舶工程, 2023, 45(9): 152-159. YANG Y F, YUAN Y C, TANG W Y. Research on thermal response of reinforced plate structure with insulation layer under high temperature load[J]. Ship Engineering, 2023, 45(9): 152-159. |
| [4] |
郝军凯. 船舶甲板板架结构在高温火灾环境下的热力响应与极限强度研究[D]. 上海: 上海交通大学, 2020.
|
| [5] |
袁敏杰. 船舶舱室火灾载荷特性及结构响应分析[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [6] |
汪金辉. 顶部开口船舱火灾下结构热力耦合方法研究[J]. 中国舰船研究, 2021, 16(3): 74-85. WANG J H. Research on structural thermal coupling method under top open cabin fire[J]. China Shipbuilding Research, 2021, 16(3): 74-85. |
| [7] |
滕晓青, 顾永宁. 单壳双底货船舱段结构瞬态温度场和热应力[J]. 船舶力学, 2003, 7(2): 51-60. DOI:10.3969/j.issn.1007-7294.2003.02.007 |
| [8] |
刘云山, 薛鸿祥, 周佳, 等. 火灾场景下船舶舱室结构动态热力响应分析研究[J]. 中国造船, 2018, 59(4): 161-169. DOI:10.3969/j.issn.1000-4882.2018.04.018 |
| [9] |
朱小俊, 仲晨华, 杨志青, 等. 船舶火灾防火设计中舱室及舱壁温度分布试验模拟研究[J]. 中国造船, 2012, 53(4): 59−67.
|
| [10] |
王进军, 涂然, 曾怡, 等. 火灾标准燃烧室相似模型试验箱设计及有效性研究[J]. 安全与环境学报, 2011, 11(6): 181-184. DOI:10.3969/j.issn.1009-6094.2011.06.042 |
| [11] |
WANG J H, JIAO Y, SHI L. An experimental and non-dimensional study on the vertical temperature distribution of a sealed ship engine room fire[J]. Ocean Engineering, 2018: 22−33.
|
 2025, Vol. 47
2025, Vol. 47
