0 引　言

目前，ROV等机器人常用于各类水下作业^[1]，母船通过脐带缆为ROV提供动力、通信及控制信号，并确保其回收过程安全可靠，但脐带缆也给ROV带来极大隐患^[2]。复杂海况下，母船产生升沉摆动，同时导致相连的ROV也将产生升沉运动。极端条件下，脐带缆或因长期承受高幅应力交变冲击导致自身断裂，造成ROV丢失。因此，实施有效的补偿技术，降低脐带缆的张力波动与ROV升沉幅度，对保障作业平稳、延长缆绳寿命及提升作业安全性与效率至关重要。

主动式升沉补偿系统是一种实时监测并主动调整负载位置，以抵消母船因海浪引起的升沉运动，保障负载稳定的系统。然而实际过程中系统受非线性与时滞性因素影响，传统PID控制及模型预测控制对模型依赖程度高，难以实时应对扰动^[3]。

自抗扰控制以无模型依赖性和强自抗扰能力被广泛用于船舶、海洋电动绞车、海上起重机等平台的升沉补偿系统^{[4 − 6]}。为解决自抗扰控制参数复杂等问题，高志强^[7]提出线性自抗扰控制（Linear Active Disturbance Rejection Control, LADRC），简化控制结构实现性能优化，但在参数优化方面仍存在较大难度。崔文清等^[8]提出基于被控对象阶跃响应曲线的二阶LADRC调参法，该方法在扰动抑制方面性能良好。Humaidi等^[9]利用粒子群优化（PSO）调整LADRC参数，旨在提升被控系统动态响应性能，但其存在明显超调。

针对系统特点及问题，本文提出基于黑翅鸢算法^[10]（Black-winged Kite Algorithm, BKA）优化的LADRC控制策略，用于主动升沉补偿系统来进行仿真实验。该策略融合BKA全局寻优能力与LADRC参数优化需求，旨在快速锁定LADRC最优参数，提升控制器性能。

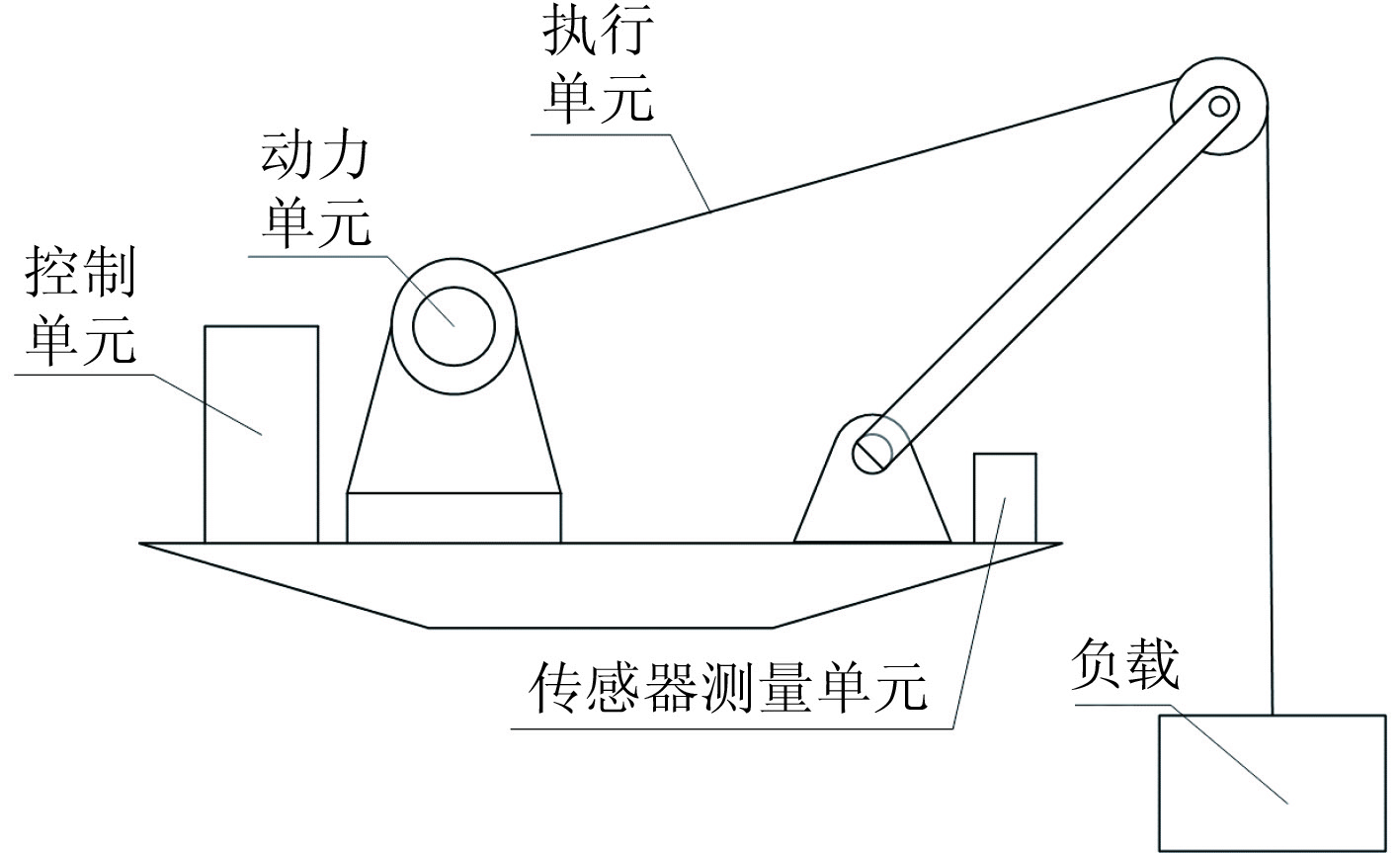
1 升沉补偿系统模型建立 1.1 系统组成

潜水器吊放系统包括动力、控制、传感器测量、执行单元，并常具备升沉补偿系统保证作业平稳完成，如图1所示。系统采用电绞车为执行单元，潜水器为负载。首先传感器测量单元实时获取位移、张力等关键参数，随之将其传至控制单元。控制单元向电机发送指令动态调整绞车转速，控制缆绳收放长度，旨在持续保持负载相对海底位置的稳定，实现升沉补偿目标，确保负载作业过程平稳安全。主动升沉补偿系统按补偿策略分为位移型、速度型和张力型。鉴于位移型以负载实时升沉位移为核心控制信号，能提供更精确的控制效果，故采取位移补偿策略。

1.2 系统动力学模型分析 1.2.1 缆绳-负载系统动力学模型

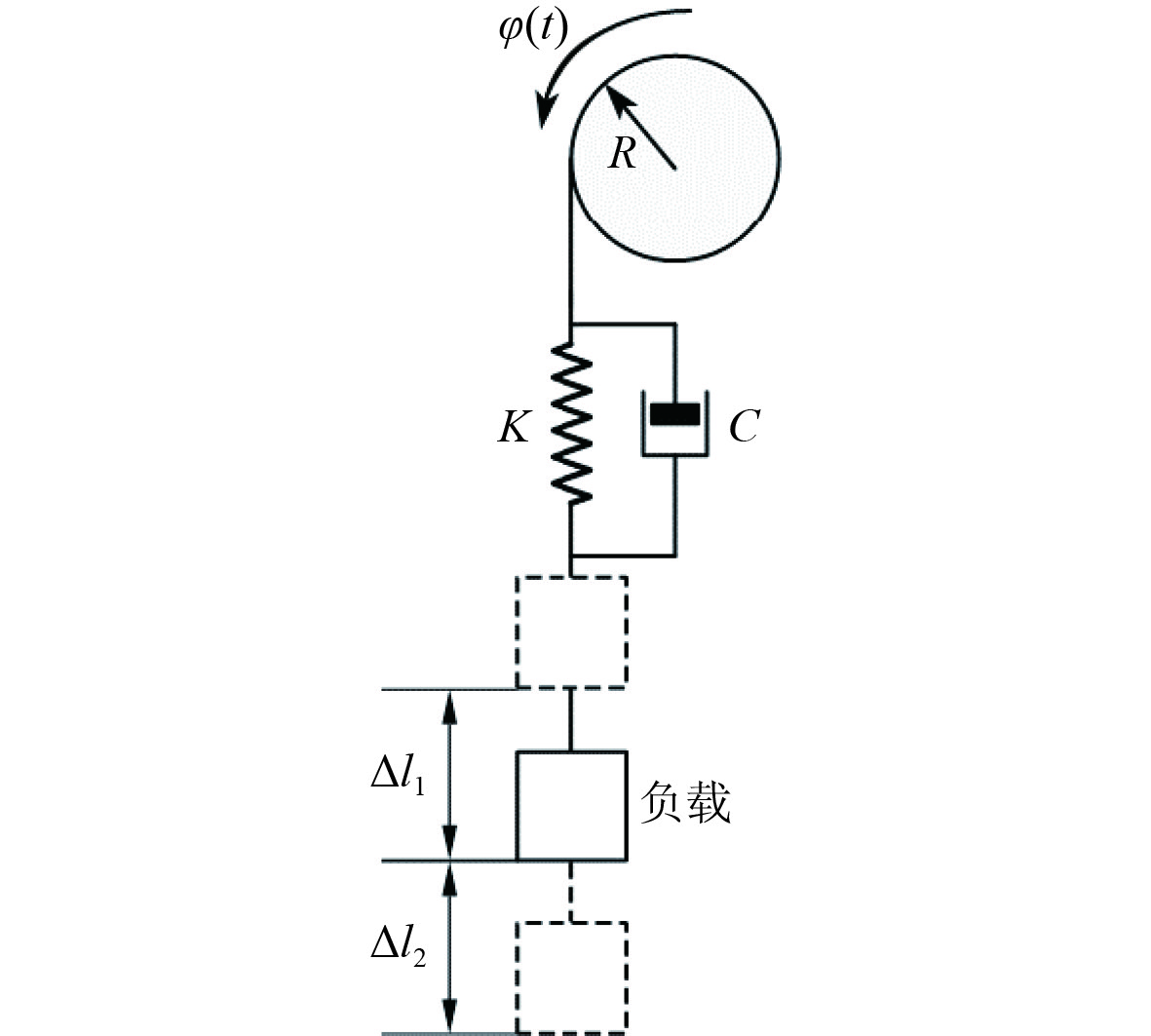
如图2所示，缆绳-负载系统简化为“弹簧-质量-阻尼”系统，$ \Delta {l}_{1}、\Delta {l}_{2} $分别为缆绳静、动伸长量；K、C分别为缆绳刚度、阻尼系数；$\varphi (t)$为卷筒转动角度；$R$为卷筒半径。

负载在垂直平面内的运动方程如下^[11]：

$ \left\{ \begin{gathered} {y_l} = \Delta l(t) + {y_m} + \varphi R ，\\ m{{\ddot y}_l} = - {F_t} - {F_z} - {F_l}。\\ \end{gathered} \right. $

(1)

式中：${y_l}$为负载位移；$\Delta l(t)$为缆绳弹性伸长量；${y_m}$为母船位移；$m$为系统等效质量；$ {F}_{t}、{F}_{z} $分别为缆绳受到的动弹簧力、阻尼力；${F_l}$为负载受到的流体阻力。

静态受力平衡情况下，假设负载位置恒定，缆绳静伸长量可视为常数，缆绳弹性伸长量等于动伸长量，即$\Delta l(t) = \Delta {l_2}(t)$。

由动伸长量$\Delta {l_2}(t)$可求得缆绳受到的动弹簧力${F_t}$、阻尼力${F_z}$和负载受到的流体阻力${F_l}$：

$ \left\{ \begin{gathered} {F_t} = K\Delta {l_2} ，\\ {F_z} = C\Delta {{\dot l}_2} ，\\ {F_l} = \frac{1}{2}\rho {C_z}A{{\dot y}_l}\left| {{{\dot y}_l}} \right|。\\ \end{gathered} \right. $

(2)

式中：$\rho $为海水密度；${C_z}$为海水阻尼系数；$A$为负载在垂直运动方向上的横截面积。

综上可知，式(1)可变为：

$ m{\ddot y_l} = K({y_m} + \varphi R - {y_l}) + C({\ddot y_m} + \dot \varphi R - {\dot y_l}) - \frac{1}{2}\rho {C_z}A{\dot y_l}\left| {{{\dot y}_l}} \right| 。$

(3)

1.2.2 电动绞车动力学模型

电动绞车仿真原理图如图3所示。

$ \left\{ \begin{gathered} 6T - {T_e} = J\frac{{\text{π}} }{{30}}\frac{{{\mathrm{d}}n}}{{{\mathrm{d}}t}} ，\\ J = \frac{{{G_s}D_s^2 + \displaystyle\frac{{{G_b}D_b^2 + {G_t}D_t^2}}{{{i^2}}}}}{{4g}} ，\\ {T_e} = ({G_n} + mr\frac{{{{\mathrm{d}}^2}\theta }}{{{\mathrm{d}}{t^2}}})ri。\\ \end{gathered} \right. $

(4)

式中：$T$为电机转矩；${T_e}$为负载阻力矩；$J$为系统转动惯量；$n$为电机转速；$ {G}_{s}、{G}_{b} $分别为小、大齿轮重量；$ {D}_{s}、{D}_{b} $分别为小、大齿轮直径；$ {G}_{t}、{D}_{t} $分别为卷筒的重量、直径；$i$为传动比；$g$为重力加速度；${G_n}$为系统静载荷；$ r、\theta $分别为卷筒的半径、转角；$m$为负载等效质量。

电机转矩$T$为：

$ T=\displaystyle\frac{3pU^2\displaystyle\frac{R_2}{S}}{2{\text{π}} f\left[(R_1+\displaystyle\frac{R_2}{S})^2+(X_1+X_2)^2\right]}。$

(5)

式中：$p$为电机极对数；$U$为输入电压；$S$为转差率；$ {R}_{1}、{R}_{2} $分别为定子、转子绕组相电阻；$ {X}_{1}、{X}_{2} $分别为定子、转子每相绕组漏电抗。

2 主动升沉补偿系统LADRC设计 2.1 LADRC设计

自抗扰控制技术核心思想在于“提取+消除扰动信号”，通过扩张状态观测器估算系统内外总扰动，然后利用非线性组合控制律给予补偿，消除干扰影响^{[12 - 14]}。

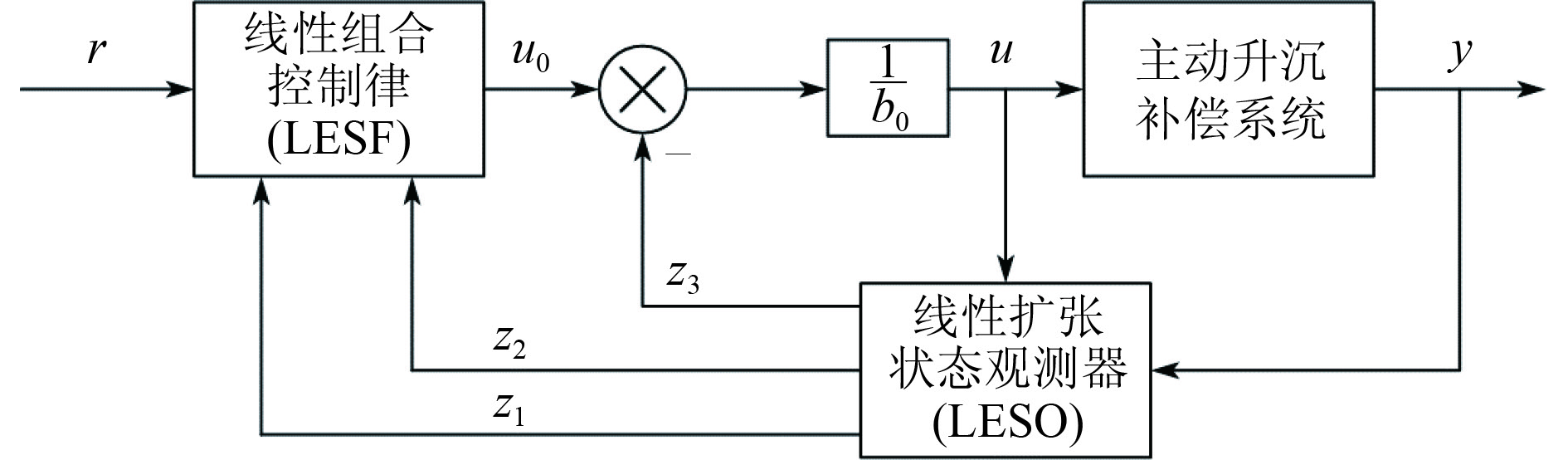
LADRC聚焦于扩张状态观测器和非线性组合控制律的线性简化，基本结构如图4所示。

图中：$r$为系统理想升沉位移阈值，$y$为绞车缆绳收放长度，${z_1}、{z_2}、{z_3}$均为LESO输出，${u_0}$为LESF输出，${b_0}$为控制器参数，$u$为控制量。

由式(1)可知，升沉补偿系统可表示为：

$ \ddot y = f(\dot y,y,\omega ) + {b_0}u 。$

(6)

式中：$ f(\dot y,y,\omega ) $为海浪外扰与控制器内扰的总扰动。

根据式(6)选取状态空间变量：${z_1} = y，{z_2} = \dot y，{z_3} = f$，构建连续扩张状态空间方程：

$ \left\{ \begin{gathered} \dot z = {\boldsymbol{A}}z + {\boldsymbol{B}}u + {\boldsymbol{E}}\dot f ，\\ y = {\boldsymbol{C}}z。\\ \end{gathered} \right. $

(7)

式中：

${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \\ 0&0&0 \end{array}} \right],{\boldsymbol{B}} = \left[ \begin{gathered} 0 \\ {b_0} \\ 0 \\ \end{gathered} \right]{\boldsymbol{,E}} = \left[ \begin{gathered} 0 \\ 0 \\ 1 \\ \end{gathered} \right],{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right],z = \left[ \begin{gathered} y \\ {\dot y} \\ f \\ \end{gathered} \right]。$

可得系统LESO方程：

$ \left\{ \begin{gathered} \dot z = Az + Bu + {\boldsymbol{L}}(y - \hat y)，\\ \hat y = Cz。\\ \end{gathered} \right. $

(8)

式中：L=$ {\left[ {\begin{array}{*{20}{c}} {{\beta _1}}&{{\beta _2}}&{{\beta _3}} \end{array}} \right]^{\mathrm{T}}}$为观测器增益矩阵；${\beta _1}、{\beta _2}、{\beta _3}$均为观测器增益。

联立式(7)和式(8)，可得：

$ \left[ \begin{gathered} {{\dot z}_1} \\ {{\dot z}_2} \\ {{\dot z}_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} { - {\beta _1}}&1&0 \\ { - {\beta _2}}&0&1 \\ { - {\beta _3}}&0&0 \end{array}} \right]\left[ \begin{gathered} {z_1} \\ {z_2} \\ {z_3} \\ \end{gathered} \right] + \left[ \begin{gathered} 0 \\ {b_0} \\ 0 \\ \end{gathered} \right]u + \left[ \begin{gathered} {\beta _1} \\ {\beta _2} \\ {\beta _3} \\ \end{gathered} \right]y 。$

(9)

通过参数化将极点配置在同一位置，得$L = \left[ {\begin{array}{*{20}{c}} {3{\omega _0}}&{3\omega _0^2}&{\omega _0^3} \end{array}} \right]，{\omega _0}$为观测器带宽。

系统的LESF设计为：

$ {u_0} = {k_p}(r - {z_1}) + {k_d}(r - {z_2}) 。$

(10)

可使系统等效为无零点的二阶系统：

$ G = \frac{{{k_p}}}{{{s^2} + {k_d}s + {k_p}}} 。$

(11)

式中：${k_p}、{k_d}$均为控制器增益矩阵$ {\boldsymbol{K}} = {\left[ {\begin{array}{*{20}{c}} {{k_p}}&{{k_d}} \end{array}} \right]^{\mathrm{T}}}$参数，经参数化得：

$ {k_p} = \omega _c^2,{k_d} = 2{\omega _c}。$

式中：${\omega _c}$为控制器带宽。

2.2 基于混合策略改进的黑翅鸢算法

针对LADRC的带宽参数调优难题，采用IBKA优化LADRC参数，旨在实现精确与高效的调参过程。

2.2.1 原始黑翅鸢算法（BKA）

BKA是通过模拟黑翅鸢在不同阶段的行为，实现全局优化搜索，并逐步逼近最优解的算法。每个种群均视为一个潜在解，并通过模拟攻击与迁徙行为来迭代更新位置。主要分为3个阶段：

1）初始化

采用随机初始化种群位置为初始解：

$ {x_m} = {U_{{b_{m,n}}}} + rand({U_{{b_{m,n}}}} - {L_{{b_{m,n}}}})。$

(12)

式中：${x_m}$为第$m$个种群；$ {U_{{b_{m,n}}}}、{L_{{b_{m,n}}}} $分别为第$m$个种群第$n$维的上、下界。

2）攻击行为

包含针对全局搜索的不同行为，模型为：

$ x_{m,n}^{t+1}=\left\{\begin{aligned} & x_{m,n}^t+0.05\times e^{-2\left(\frac{t}{T}\right)^2}\times \\ & \ \ \ \ \ \ \ \ \ (1+\mathrm{sin}(r))x_{m,n}^t\text{，if }\ 0.9 < {\mathrm{rand}}(0,1)，\\ & x_{m,n}^t+0.05\times e^{-2\left(\frac{t}{T}\right)^2}(2r-1)x_{m,n}^t\text{，else}。\end{aligned}\right. $

(13)

式中：$ {x}_{m,n}^{t}、{x}_{m,n}^{t+1} $分别为第$ t、t+1 $次迭代时第$m$个种群第$n$维的位置；$ t、T $分别为当前迭代次数、总迭代次数。

3）迁徙行为

基于鸟类迁徙行为假设，若当前种群适应度值低于随机种群，则领导者加入迁徙种群；反之继续。该策略可动态选择优秀种群，模型为：

$x_{m,n}^{t + 1} = \left\{\begin{aligned} & x_{m,n}^t + C(0,1) \times (x_{m,n}^t - P_m^t)，\text{if}\ f(i) < f({\mathrm{rand}})，\\ & x_{m,n}^t + C(0,1)\times \\ & \ \left(P_m^t-2\times\mathrm{sin}\left({\mathrm{rand}}\left(0,1\right)+\frac{{\text{π}}}{2}\right)x_{m,n}^t\right)\text{，else}。\end{aligned}\right. $

(14)

式中：$P_m^t$为第t次迭代时全局最优位置；$ f(i)、f({\mathrm{rand}}) $分别为当前种群、随机种群适应度值。

但BKA因固有特性，使得在优化过程中展现出局限性，如采用随机初始化策略易致搜索过程不稳定、种群多样性过高时易陷入局部最优等。因此采用IBKA自适应调整 LADRC参数，融合多种策略，旨在克服BKA不足，提升全局搜索能力与收敛效率。

2.2.2 改进策略

1）Logistic-tent混沌映射融合反向学习策略

BKA因采用随机初始化策略易致个体分布不均、多样性变差，阻碍算法快速收敛。混沌映射可改善初始化过程，提升全局搜索能力。结合Tent和Logistic混沌模型特点，引入反向学习策略，优化种群初始化过程。

Logistic-Tent映射表达式：

$ x_{n+1} = \left\{\begin{aligned} & \left[rx_n(1-x_n)+\frac{(4-r)}{2}x_n\right]{\mathrm{mod}}1\text{，} x_n < 0.5，\\ & \left[rx_n(1 - x_n) + \frac{(4 - r)(1 - x_n)}{2}\right]{\mathrm{mod}}1\text{，} x_n \geqslant 0.5。\end{aligned}\right. $

(15)

式中：$r$为控制参数，$ x\in [0,1]，r\in (0,4) $。

计算初始化种群${x_{m,n}}$经反向学习得到的反向种群$x_{m,n}^*$：

$ x_{m,n}^* = {U_{{b_{m,n}}}} + {L_{{b_{m,n}}}} - {x_{m,n}}。$

(16)

最终通过比较$ {x}_{m,n}、{x}_{m,n}^{*} $的适应度值，选择优秀种群为初始解。

2）黄金正弦引导策略

黄金正弦算法（Gold-SA）由Tanyildizi提出^[15]，Gold-SA在位置更新机制中引入黄金分割系数，对潜在可行解区域进行深度搜索，加速算法收敛进程，提高整体优化效率。位置更新公式为：

$ x_m^{t + 1} = x_m^t \cdot \left| {\sin ({r_1})} \right| - {r_2} \cdot \sin ({r_1}) \cdot \left| {{c_1}P_m^t - {c_2}x_m^t} \right|。$

(17)

$ \left\{ \begin{gathered} {c_1} = a\gamma + b(1 - \gamma )，\\ {c_2} = a(1 - \gamma ) + b\gamma 。\\ \end{gathered} \right. $

(18)

式中：$ {r}_{1}、{r}_{2} $分属于$ [0,{\text{π}} ]、[0,2{\text{π}} ] $的随机数；$ {c}_{1}、{c}_{2} $均为黄金分割系数；$ a、b $初始值分别为$ {\text{π}} 和-{\text{π}} $；$\gamma $为黄金分割数，即$\gamma = (\sqrt 5 - 1)/2$。

经BKA迭代，以全局最优位置$P_m^t$为基础，使用Gold-SA二次更新$P_m^t$，若更新后种群适应度值更优，则替换原$P_m^t$：

$ \left\{\begin{aligned} & x_m^{t+1}=x_m^t\cdot\left|\mathrm{sin}(r_1)\right|-r_2\cdot\mathrm{sin}(r_1)\cdot\left|c_1P_m^t-c_2x_m^t\right|\text{，} \\ & \qquad \;\;\; {\mathrm{if}}\text{ }f(x_m^{t+1}) > f(P_m^t)。\\ & \text{ }P_m^t\text{ }\text{，else}。\end{aligned}\right. $

(19)

式中：$ \text{ }f({x}_{m}^{t+1})、f({P}_{m}^{t}) $分别为$ {x}_{m}^{t+1}、{P}_{m}^{t} $适应度值。

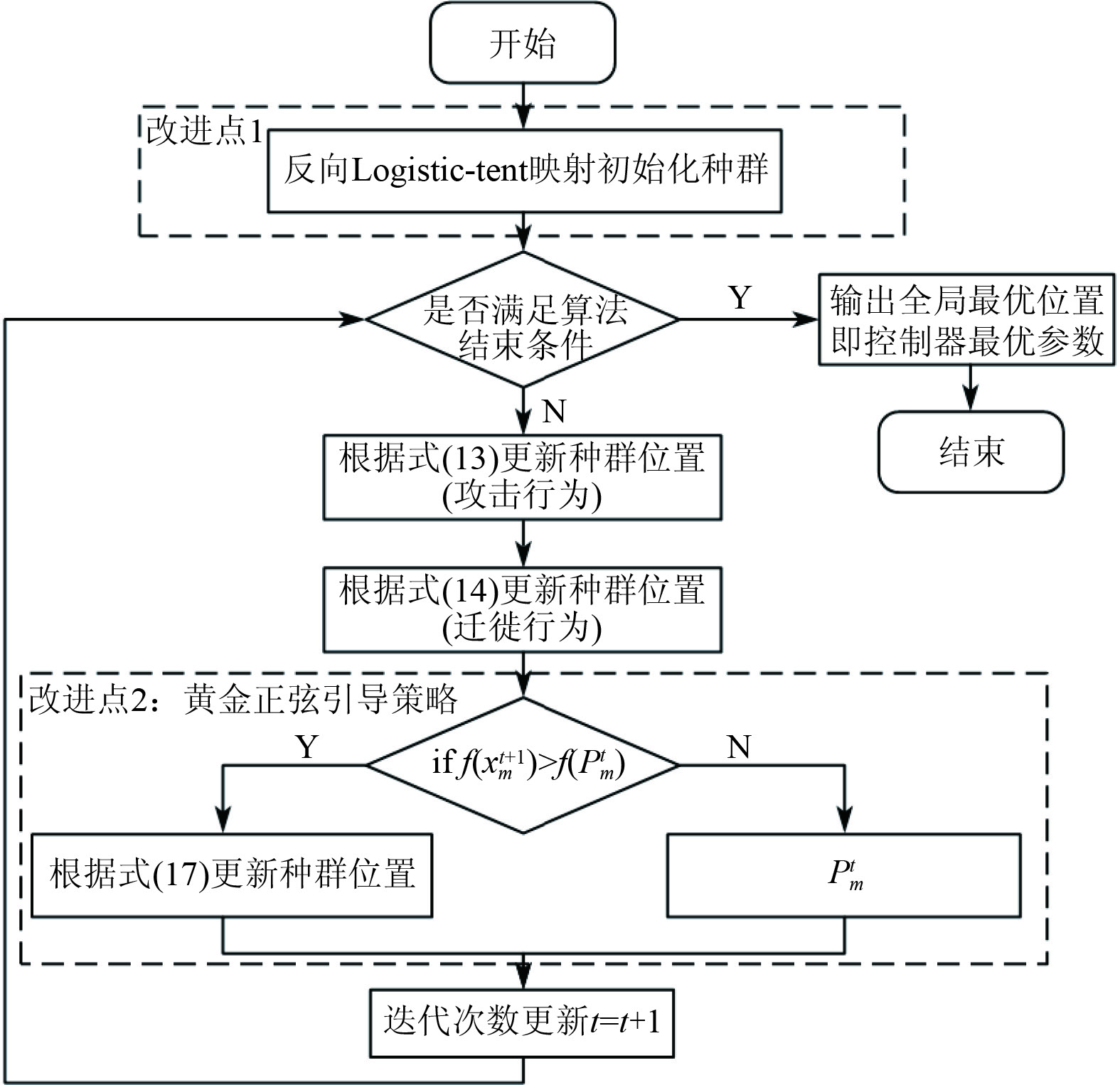
改进后算法流程图如图5所示。

2.3 IBKA整定LADRC控制器参数

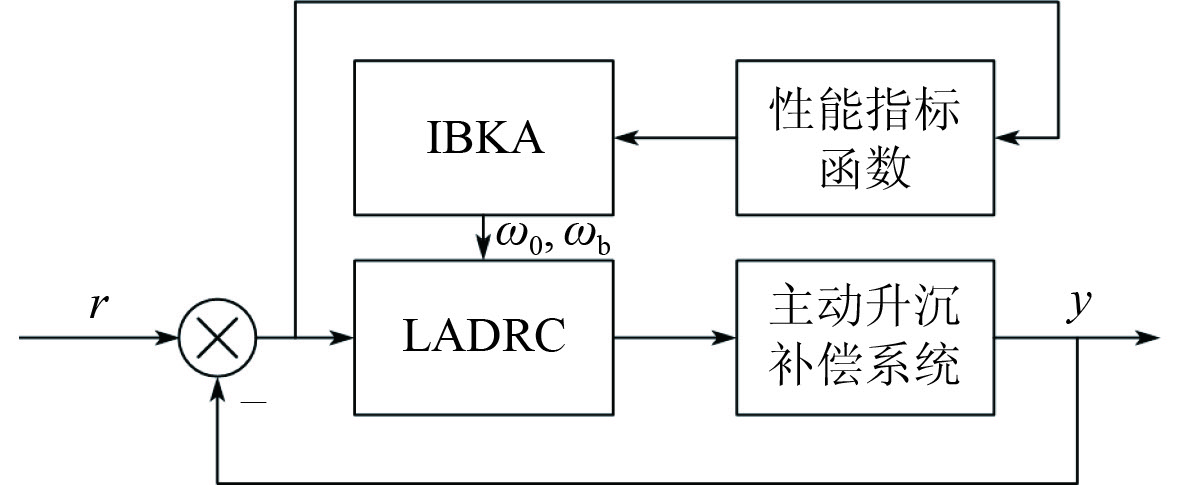
图6为IBKA整定LADRC控制器框图，首先设定理想升沉位移阈值$r$，然后持续迭代调整控制器参数，旨在最小化性能指标函数值，直至找到能够实现稳定升沉补偿的LADRC控制器参数配置，进而动态控制缆绳收放长度$y$。

3 仿真结果分析 3.1 实验1：无干扰系统的控制信号跟踪实验

在无干扰工况下模拟升沉补偿系统，评估粒子群算法（PSO-LADRC）、黑翅鸢算法（BKA-LADRC）、混合策略改进的黑翅鸢算法（IBKA-LADRC）对系统控制信号跟踪性能和时滞消除能力。

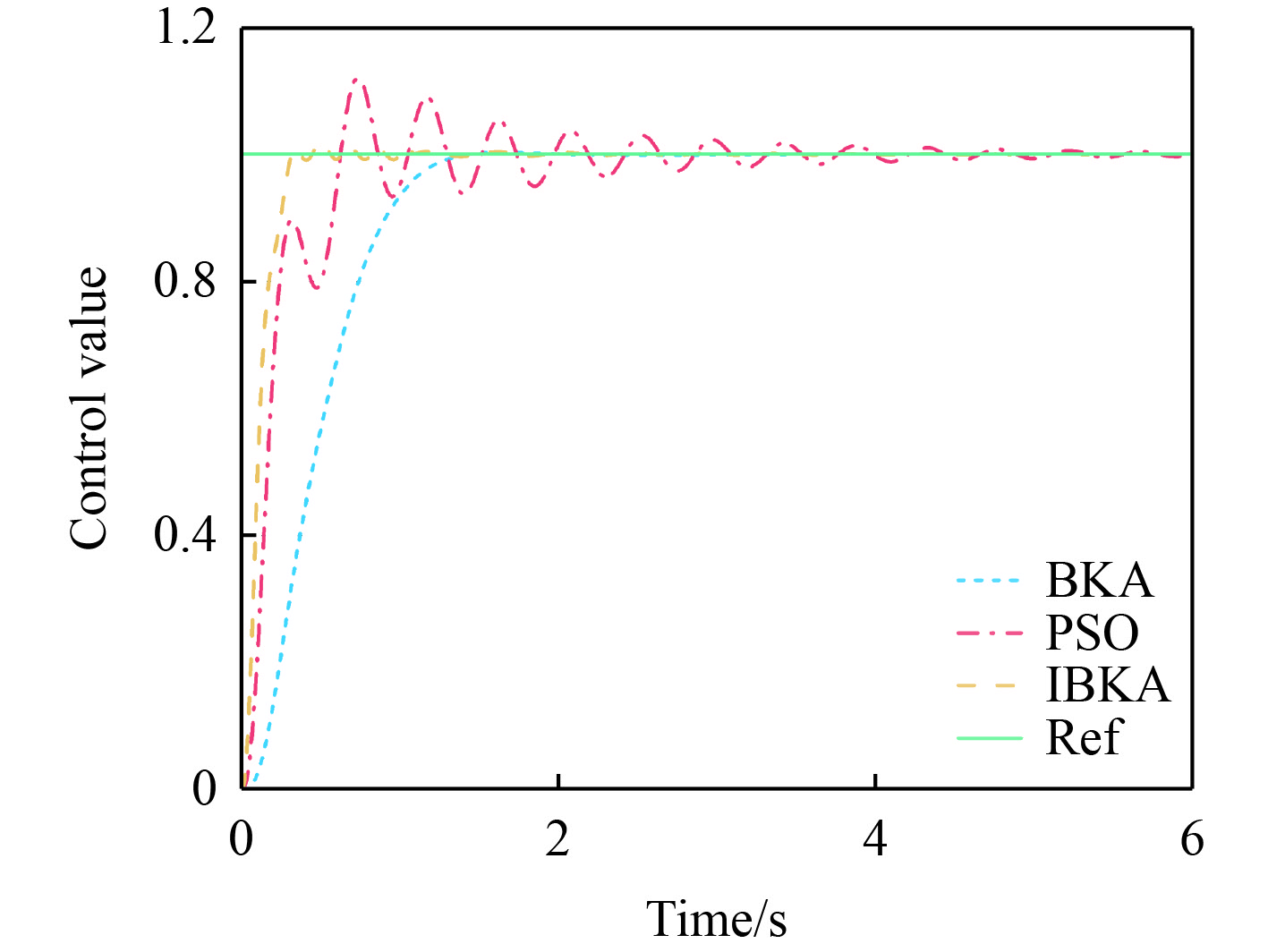
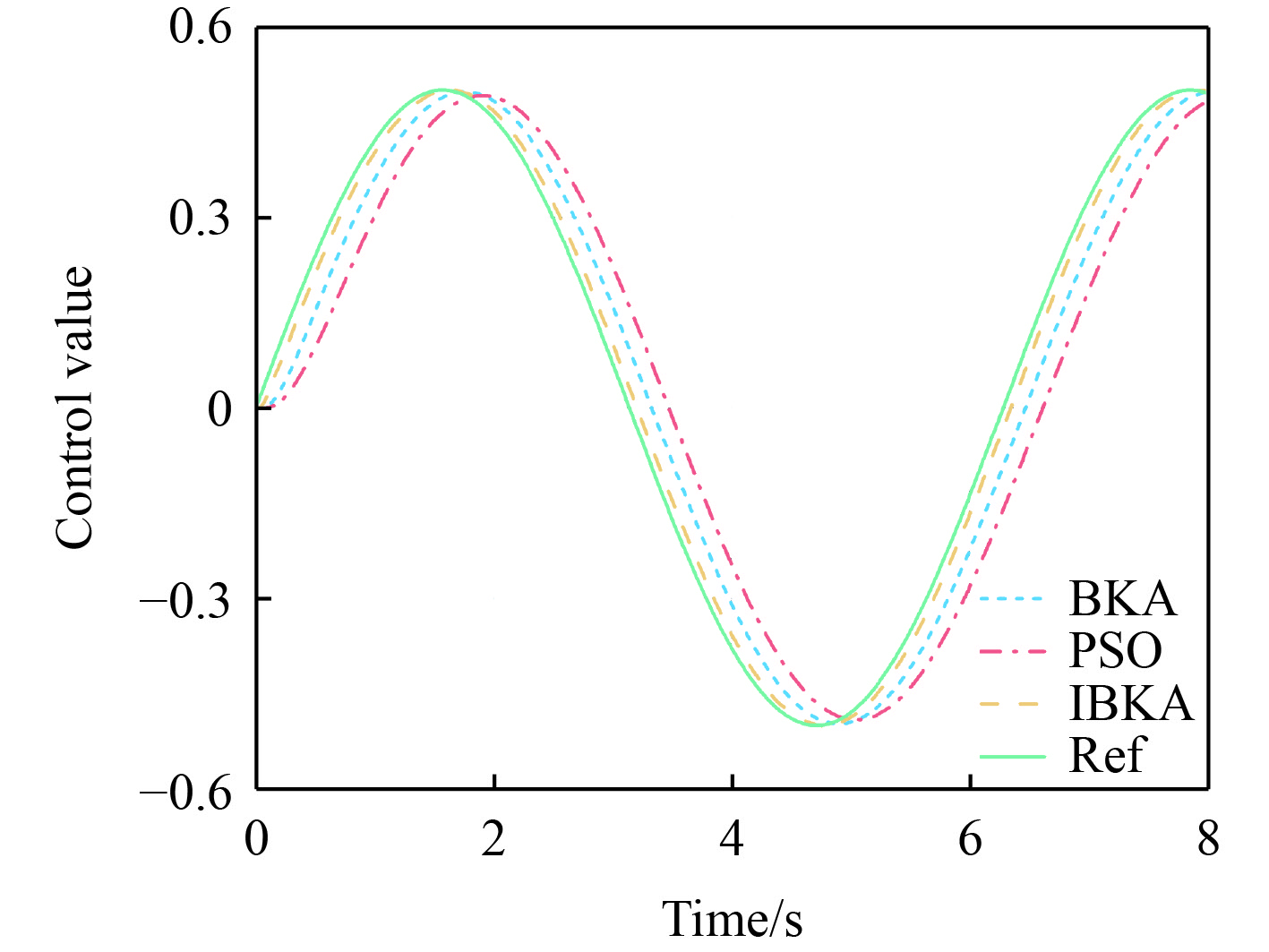
如图7所示，单位阶跃信号输入下，PSO-LADRC算法因对解空间的高敏感性，导致搜索效率相对较弱，引发严重信号波动。BKA-LADRC、IBKA-LADRC算法展现差异化的搜索行为，有效减小了信号波动。结合表1，虽然IBKA-LADRC的超调量略高于BKA-LADRC，但得益于IBKA-LADRC引入的创新种群初始化策略及优化参数的搜索机制，显著提升了收敛速度，降低了调节时间，使系统更快到达稳态。如图8所示，输入信号为$ y = 0.5\sin (2{\text{π}} t)$, IBKA-LADRC最快消除了系统时滞效果，实现最佳跟踪性能；BAK-LADRC次之；而PSO-LADRC则相对较差。

综上，在无干扰的模拟环境下，IBKA-LADRC控制器凭借更快的收敛速度及卓越的控制性能，为升沉补偿系统的优化控制提供了一种有效的解决方案。

3.2 实验2：带干扰系统的升沉补偿控制实验

基于实验1，将系统理想升沉阈值（输入信号）设为0，并添加$y = 0.5\sin (2{\text{π}} t)$的正弦干扰信号，模拟系统受到正弦干扰后控制效果的变化。

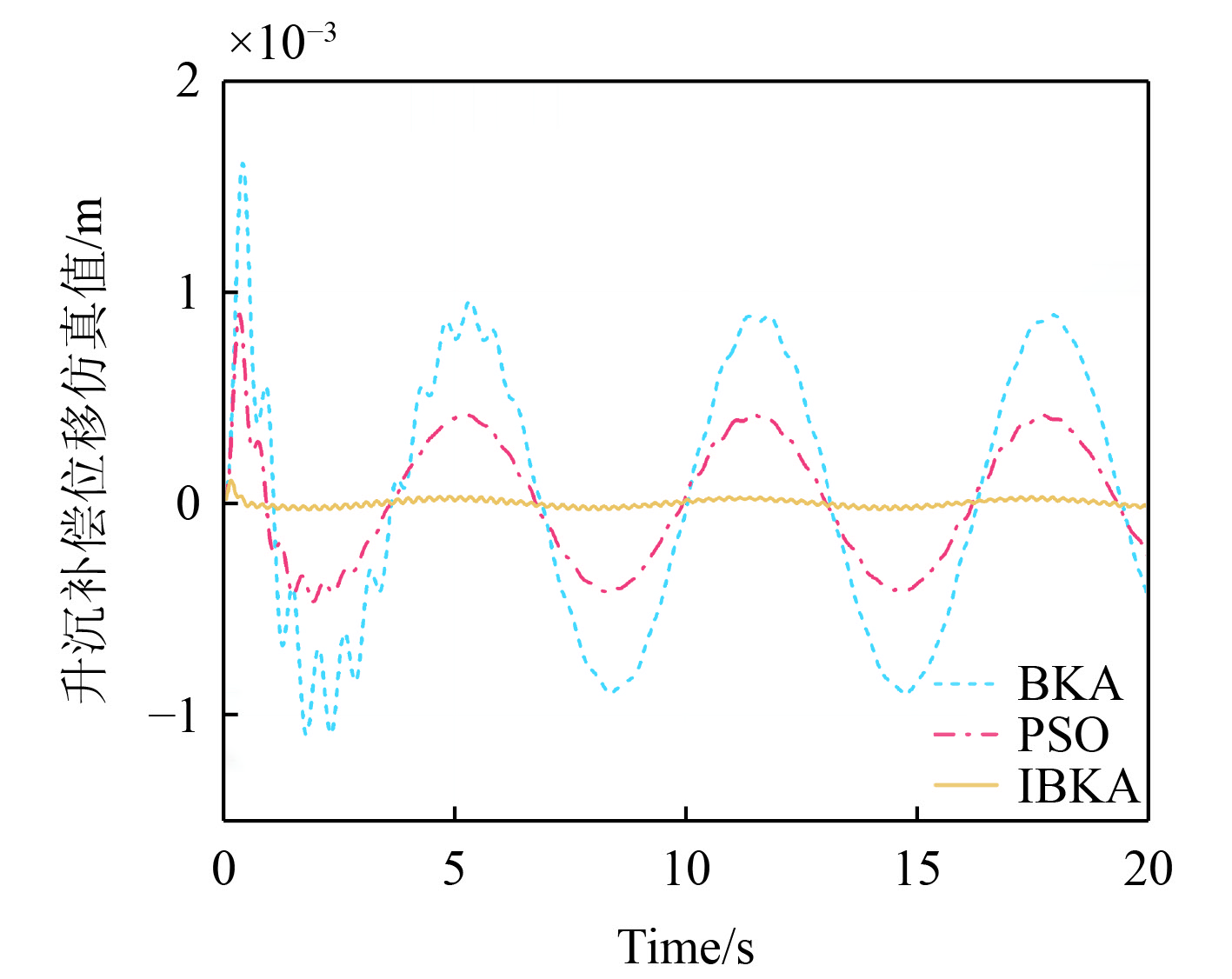
由图9及表2知，补偿算法的引入显著降低了负载的升沉运动幅度。BKA-LADRC、PSO-LADRC、IBKA-LADRC算法分别将负载最大升沉位移补偿至$1.6 \times {10^{ - 3}}$、$8.0 \times {10^{ - 4}}$、$1.0 \times {10^{ - 4}}$，补偿后各算法均实现了负载位移幅值在较小范围内的稳定波动，从而有效提升了系统的稳定性与控制性能。

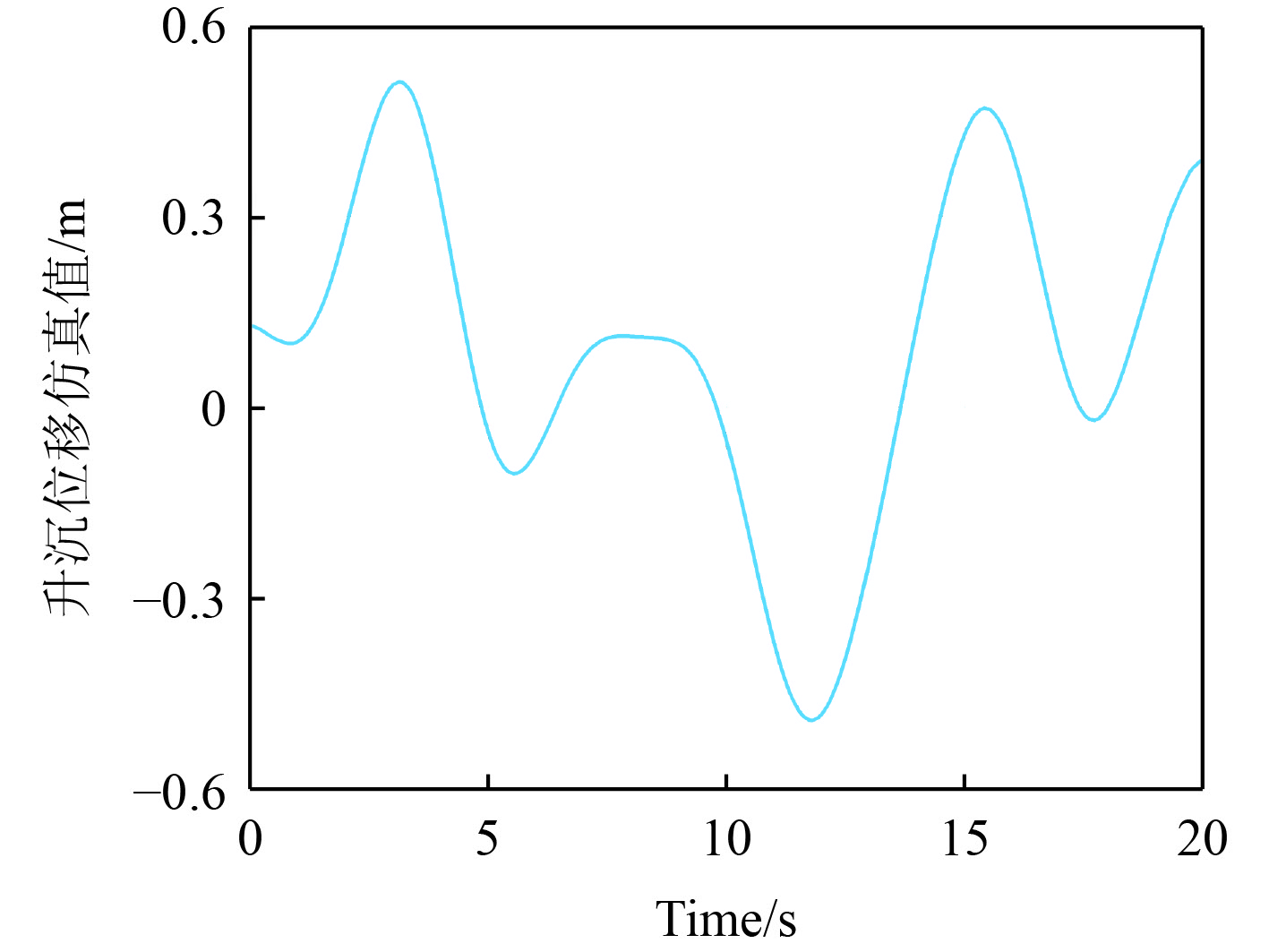
将正弦扰动替换为由PM谱生成的模拟波浪波形并计算母船重心处升沉位移^[16]，如图10所示。

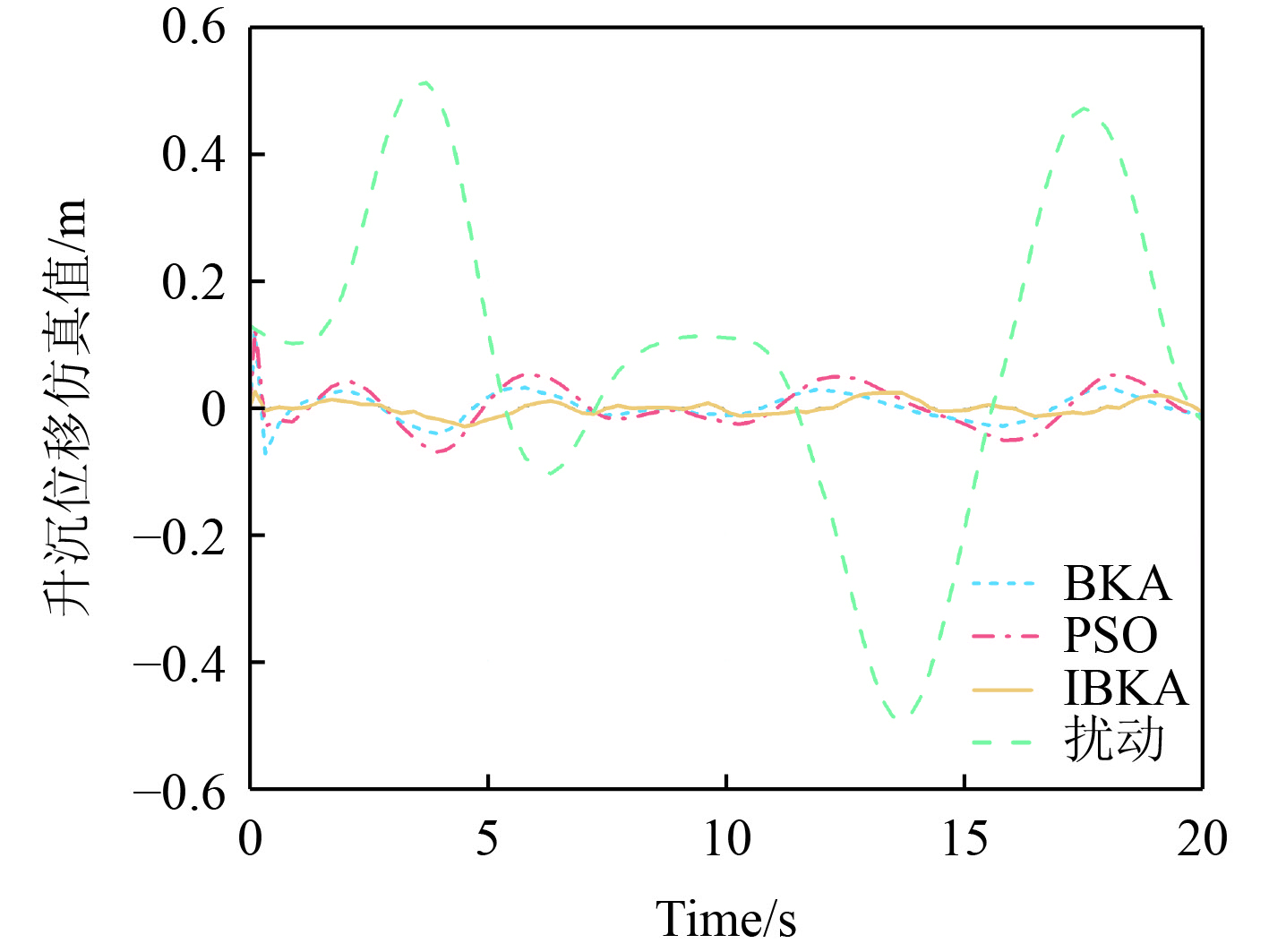
如图11及表3所示，无补偿时负载最大升沉位移达到0.523 m，BKA-LADRC、PSO-LADRC、IBKA-LADRC分别将其减至0.119、0.124、0.035 m，衰减了77.2%、76.2%、93.3%。这不仅显示算法在减少负载升沉运动方面的有效性，还进一步体现了算法间的性能差异。

实验2表明，面对正弦干扰或模拟海浪扰动时，IBKA-LADRC算法凭借Gold-SA策略二次快速搜索最优解空间，极大缩短了响应时间，使系统在面对外界干扰时能迅速做出调整，增强了系统抑制干扰能力，提高了补偿精度，避免过冲。但PSO-LADRC与BKA-LADRC未采用Gold-SA策略且在随机初始化过程中导致解空间分布不均，影响控制器无法及时有效抑制干扰，因此其负载位移幅值波动较大。

综上，仿真实验验证了IBKA-LADRC算法在各模拟工况下的卓越补偿效果，大幅降低负载升沉位移，确保了负载的稳定运行。这不仅验证了算法的有效性及良好的控制效果，也为提升升沉补偿系统的整体性能提供有力支持。

4 结　语

针对复杂海况下母船升沉运动影响负载水下作业的情况，本文基于原始BKA优化算法并融合混沌映射反向学习策略、黄金正弦策略，提出IBKA优化算法并应用于主动升沉补偿自抗扰控制系统。通过实验，验证了IBKA-LADRC在不同工况下均具有优良的控制性能。与PSO-LADRC、BKA-LADRC相比，在模拟海况下最大升沉位移衰减率分别提升17.1%、16.1%，验证了IBKA-LADRC具有较高的控制精度与优良的抗干扰性能。然而，IBKA目前仅在Matlab环境中验证，仍需进一步通过实物实验全面评估性能。