0 引　言

随着全球航运业的快速发展以及对船舶性能要求的不断提高，船型船体结构的优化设计成为提升船舶效率、降低能耗和减少环境影响的关键^[1]。传统船体设计方法主要依赖经验公式和实验测试，存在设计周期长、成本高且难以全面考虑多目标优化问题的局限性。此外，传统方法在应对复杂海洋环境和多样化任务需求时，往往难以实现性能与成本的平衡^[2]。因此，研究船型船体结构优化设计方法，不仅能够显著提高船舶的综合性能，还能为船舶设计提供科学、高效的技术支持，对推动船舶工业的可持续发展具有重要意义。

当前船型船体结构优化设计方法的研究已取得显著进展，丁健亮等^[3]考虑船体受到的复合载荷，将最大化扭转极限强度、弯曲极限强度和最小化质量作为优化目标，同时，设计还需要满足强度、稳性、频率等一系列设计约束条件，最后采用智能优化算法实现船体结构优化设计。但该方法对船体在复杂载荷作用下的局部变形控制考虑不足，可能导致某些区域变形过大，影响结构整体性能。Ferreira等^[4]通过基于分区方法的优化方法对流体结构展开模拟分析，结合有限元与边界元法实现结构优化，分区方法需要将大的计算区域分解成若干个子区域，这些子区域之间的边界处理变得尤为复杂。边界上的条件需要从相邻区域的解中获得，因此在每一时间步都需要在边界上交换数据，这增加了计算的复杂性和开销。如果边界处理不当，可能会导致数值不稳定或计算结果的误差增大。Kang等^[5]通过支持向量机、径向基函数神经网络与BP神经网络结合SMOTE过采样算法获取船体结构的极限状态，设定可靠性、结构等约束条件，通过模拟退火算法实现船体的轻量化结构优化，在使用SMOTE过采样算法处理不平衡数据时，可能会引入一些噪声或导致过拟合，影响最终的优化效果。许博方等^[6]利用Abaqus软件建立了船体有限元模型，通过非线性有限元方法展开碰撞运动学分析，根据分析结果实现船体结构优化，在碰撞运动学分析中，接触算法的选择对分析结果具有重要影响。选择了不合适的接触算法，可能会导致分析结果的不准确或不稳定，从而影响船体结构优化的有效性。

为了解决上述方法存在的问题，提出基于有限元分析的船型船体结构优化设计方法。

1 船型船体结构优化设计 1.1 基于有限元分析的船型船体结构网格划分

利用船舶设计软件MAXSURF建立船体有限元模型，首先建立船体钢结构的几何曲面，将其设置为IGES格式并存入HyperWorks内，在HyperWorks单元库内选择PSHELL单元对船体面元素（舷侧外板、甲板等）展开网格划分。PSHELL单元通常情况下由材料属性、节点、弹性地基刚度与厚度定义，PSHELL单元上可以施加法向与切向荷载。选取PBEAM单元对片体舷侧纵梁，甲板横梁、纵梁以及桥舷横梁、侧纵梁等线元素展开网格划分。

通过下述过程完成网格划分：

1）定义单元属性。通过PBEAM单元与PSHELL壳单元对船体单元展开网格划分^{[7 − 8]}。

2）设定网格尺寸。根据照肋矩对船体网格尺寸展开控制，分别将船体U型梁与船宽的网格设置为0.275 m、0.5 m，建模过程中，在应力集中以及角隅处设定较小的网格尺寸。

3）网格划分。将船体划分为33590个单元，16635个节点，根据设定好的网格尺寸，通过PBEAM单元与PSHELL壳单元实现船体网格划分。

在流水的作用下船体会产生振动，采用湿模态分析方法展开船体结构耦合振动分析^{[9 − 10]}，为后续结构优化设计提供依据。

1.2 船体耦合振动分析

通过1.1节构建的有限元模型能够准确描述船体的结构特征和边界条件，基于该模型，评估船体在复杂载荷作用下的动态响应，揭示其振动特性及潜在的结构问题，确保优化后的船体结构在满足强度要求的同时，具备良好的振动性能。

在理想流体状态下，建立下述平衡方程：

$ \nabla p + \eta \dot v + {\rho _f}\ddot v = 0 。$

(1)

式中：$ \eta $为体积常数；$ \dot v $为流体粒子对应的速度；$ {\rho _f} $为流体对应的密度；$ \ddot v $为流体粒子对应的加速度；$ p $为流体动压力，其计算公式为：

$ p = - {L_f}\nabla \cdot v。$

(2)

式中：$ {L_f} $为弹性模量；$ v $为流体体积。

结合上述公式，建立流体运动方程：

$ \frac{{\ddot p}}{{{L_f}}} + \frac{{\eta \ddot p}}{{{\rho _f}{L_f}}} - \frac{{{\nabla ^2}p}}{{{\rho _f}}} = 0 。$

(3)

设$ {{\boldsymbol{M}}_s} $为结构质量矩阵，对上式展开离散化处理，获得计算公式为：

$ {{\boldsymbol{M}}_s}\ddot d + {{\boldsymbol{C}}_s}\dot d + {{\boldsymbol{L}}_s}d = {F_s} 。$

(4)

式中：$ {{\boldsymbol{L}}_s} $为结构刚度矩阵；$ d $为流固耦合交界面位移矢量；$ {{\boldsymbol{C}}_s} $为结构阻尼矩阵；$ {F_s} $为流体力。

设$ {\gamma _i} $为第$ i $项对应的振型矢量，通过下式确定位移矢量$ d $：

$ d = \sum\limits_{i = 1}^n {{\gamma _i}{z_i}}。$

(5)

式中：$ {z_i} $为第$ i $项的模态坐标。

由于式(4)中的刚度矩阵与质量矩阵都表现出一定的正交性，因此可利用$ i $个独立的微分方程为^{[11 − 12]}：

$ {\ddot z_i} + 2{\xi _i}{\psi _i}{\dot z_i} + \xi _i^2{z_i} = {f_i}。$

(6)

式中：$ {\xi _i} $为第$ i $项对应的固有频率；$ {\psi _i} $为第$ i $项对应的阻尼系数；$ {f_i} $为流体力。

1.3 船型船体结构优化

根据1.2的耦合振动分析结果对船体结构展开优化，将船体静态结构刚度最大化作为优化目标，船体刚度最大化是在载荷不变的情况下获取最小静态变形能，通过上述分析可知，可将求解最大结构刚度问题转变为最小挠度问题：

$ \left\{ \begin{gathered} {u_c} = \mathrm{min}f({\iota _i}) ，\\ {\mathrm{s.t}}.0 \lt {\iota _i} \leqslant 1，\\ V \leqslant {V_0} - {V^*}。\\ \end{gathered} \right. $

(7)

式中：$ {\iota _i} $为船体每个有限单元$ i $的内部伪密度，$ {\iota _i} $在区间[0,1]内取值，当$ {\iota _i} $=0时，表明需要移除材料，当$ {\iota _i} $=1时，表明需要保留材料；$ V $为船体的总体积；$ {V_i} $为第$ i $个单元的体积；$ i = 1,2, \cdots ,N $，$ N $为船体有限元模型的单元数量；$ {u_c} $为柔顺性；$ f() $为目标函数；$ {V_0} $为船体原始体积；$ {V^*} $为去除的体积。

在多载荷条件下，建立船体最大刚度目标函数：

$ \mathrm{min}f(u_C^1,u_C^2,\cdots,u_C^K)=\sum\limits_{i=1}^kf_iu_C^i。$

(8)

式中：$ u_C^i $为第$ i $种载况下对应的柔顺性。

采用人工鱼群算法^{[13 − 14]}求解船体结构的最大刚度，以此实现船型船体结构优化设计，在求解过程中，每一条鱼对应的位置即为式(8)的一个可行解，求解的具体过程如下：

1）根据最大刚度目标函数对人工鱼算法的相关参数展开初始化处理，用$ {X_i} $表示人工鱼的位置。

2）计算人工鱼在函数求解过程中的适应度值$ {Y_i} = f({X_i}) $，确定当前种群中具有最高适应度的人工鱼，将其作为当前目标函数的最优解，并记录在公告牌中。

3）通过觅食行为、聚群行为以及追尾行为对人工鱼的位置展开更新。

觅食行为：已知人工鱼的当前位置$ {X_i} $以及对应的适应度$ {Y_i} $，随机在人工鱼的视野范围选择一个位置$ {X_j} $，如果该位置处对应的适应度$ {Y_j} $>$ {Y_i} $，通过下式更新人工鱼的位置：

$ X_{\mathrm{next}}=X_i+\frac{X_j-X_i}{||X_j-X_i||}\times S_t\times\mathrm{rand}(0,1) 。$

(9)

式中：$ {S_t} $为移动步长；$ \mathrm{rand}(0,1) $为随机正数，在区间[0,1]内取值。

如果$ {Y_j} \lt {Y_i} $，通过下式更新人工鱼位置：

$ X_{\mathrm{next}}=X_i+S_t\times\mathrm{rand}(0,1) 。$

(10)

聚群行为：如果以$ {X_i} $为中心的视野范围内存在$ {m_f} $个人工鱼，当$ {m_f} \geqslant 1 $时，通过下式确定人工鱼中心位置$ {X_c} $：

$ {X_c} = \frac{{\displaystyle\sum\limits_{j = 1}^{{m_f}} {{X_j}} }}{{{m_f}}} 。$

(11)

设$ {Y_c} $为$ {X_c} $的适应度值，$ \delta $为拥挤度因子；当$ {Y_c}/ {m_f} \gt \delta {Y_i} $时，表明鱼群的拥挤度较低，通过下式更新人工鱼位置：

$ X\mathrm{_{next}}=X_i+\frac{X_c-X_i}{||X_c-X_i||}\times S_t\times\mathrm{rand}(0,1)。$

(12)

追尾行为：在当前人工鱼视野方位内确定最大适应度的位置$ {X_{\max }} $，该位置对应的适应度为$ {Y_{\max }} $，当$ {Y_{\max }} \gt {Y_i} $时，将$ {X_{\max }} $作为中心点，在相应的视野范围内对人工鱼展开搜索，如果$ {Y_{\max }}/{m_f} \gt \delta {Y_i} $，表明$ {X_{\max }} $的拥挤度较低，通过下式更新人工鱼位置：

$ X\mathrm{_{next}}=X_i+\frac{X_{\max}-X_i}{||X_{\max}-X_i||}\times S_t\times\mathrm{rand}(0,1) 。$

(13)

4）完成位置更新后，重新对人工鱼的适应度展开计算，将更新后的适应度值与公告板中的最优解展开对比，若更新后的适应度值较高，则更新公告牌。

5）判断人工鱼的求解目标函数的次数是否达到最大值，如果达到，输出公告板中的最优解，获得船体结构的最大刚度，实现结构优化。

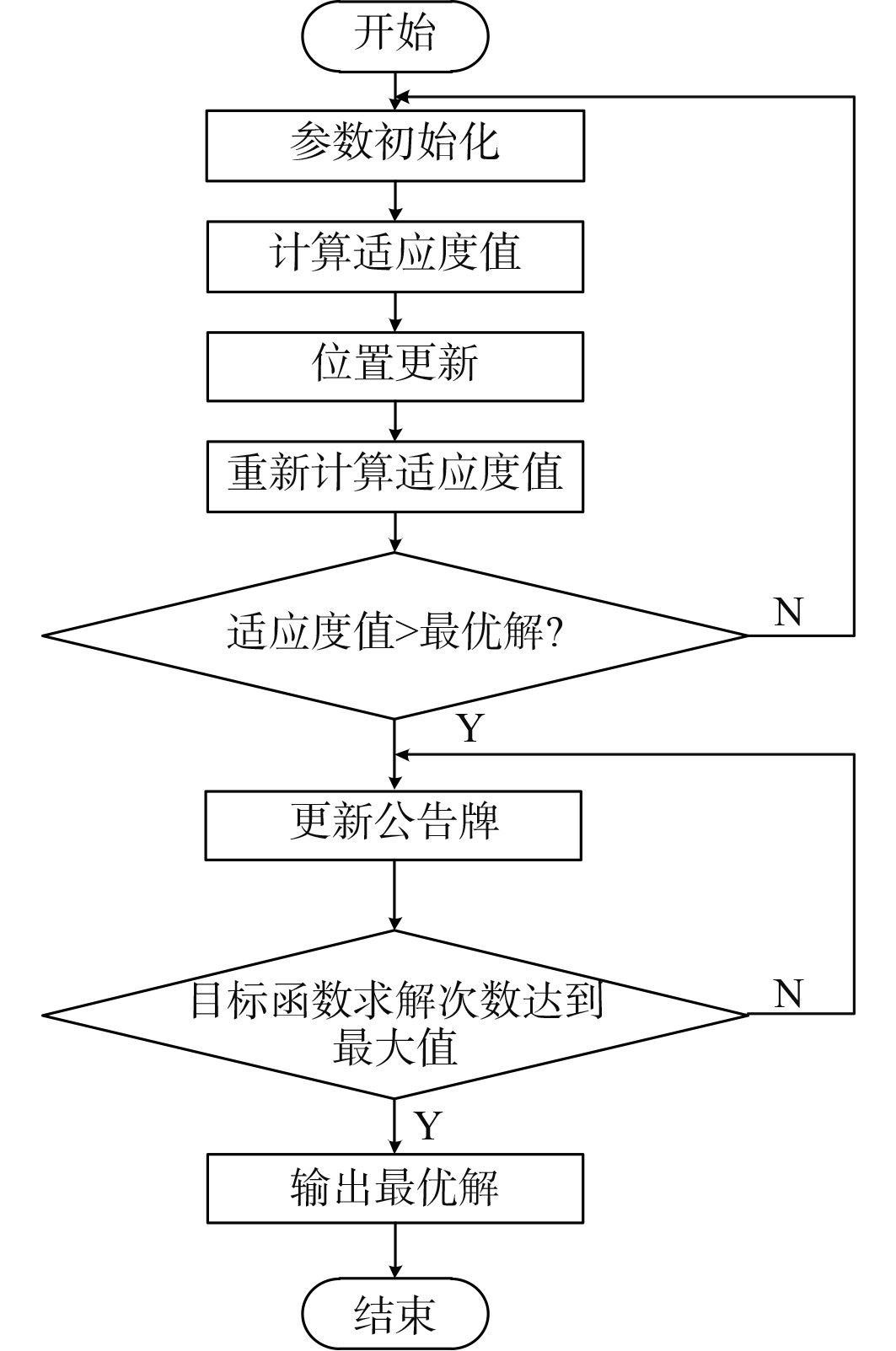
船型船体结构优化流程如图1所示。

2 实验与分析

本次实验旨在验证基于有限元分析的船型船体结构优化设计研究方法的整体有效性。通过与基于智能优化算法的优化方法和基于Abaqus的优化方法对比，评估其在极限弯矩和最大变形量方面的优化效果。本次测试优化目标参数如表1所示。

在波浪载荷工况下展开实验，因为波浪载荷是船舶在航行过程中面临的主要动态载荷之一，对船体结构的强度、刚度和疲劳寿命具有重要影响。船舶在海上航行时，波浪冲击会导致船体产生周期性振动和局部应力集中，严重时可能引发结构破坏或疲劳失效。因此，研究船体在波浪载荷下的响应是评估其结构性能和安全性的关键。在波浪载荷工况下，实验模拟了中等海况下的波浪冲击，波高为5 m，波长为100 m，波速为10 m。通过分析船体在波浪载荷下的变形情况和极限弯矩，实验能够全面评估船体结构的抗波浪冲击能力，为优化设计提供重要依据。

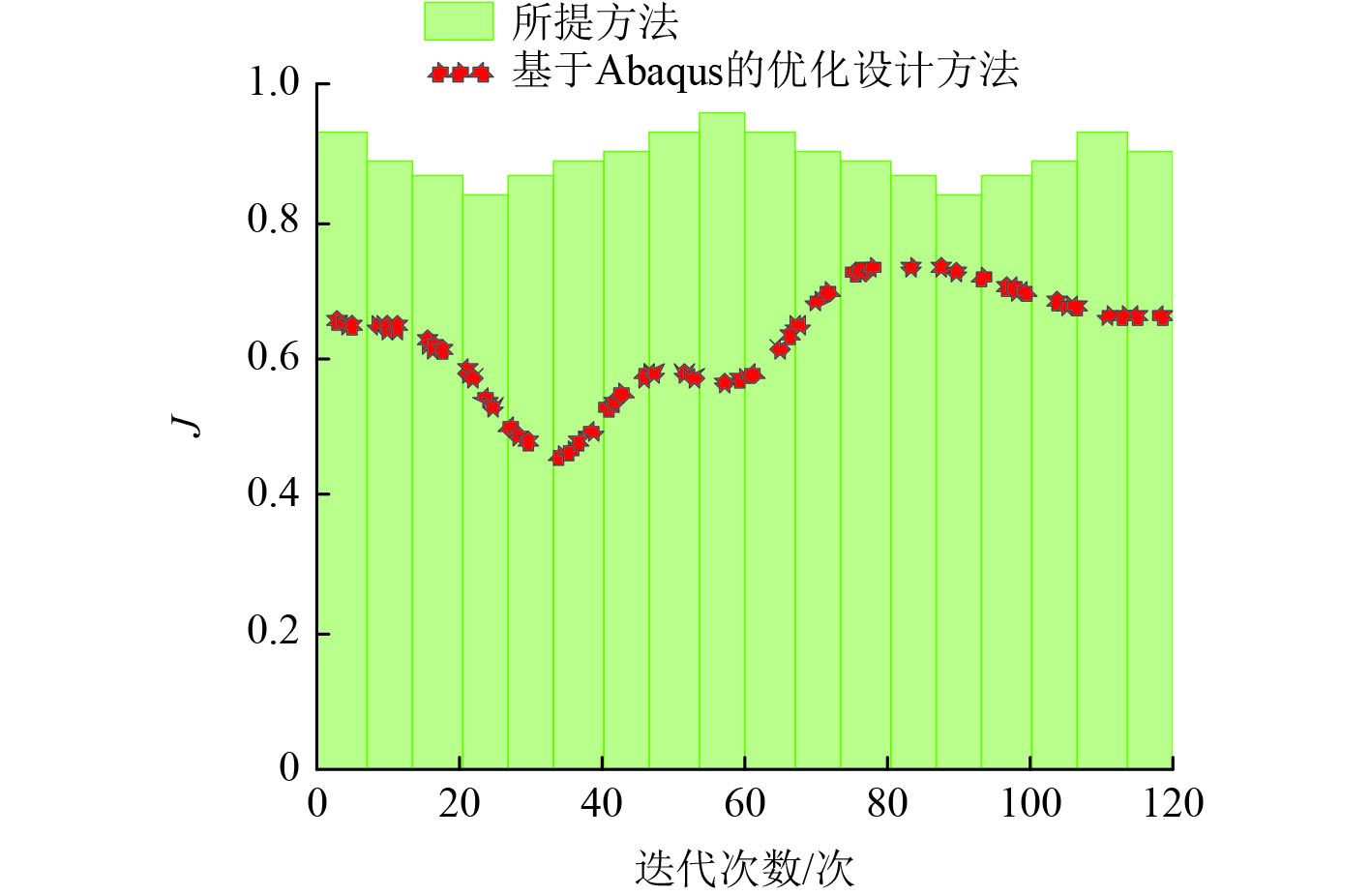
基于有限元分析的船型船体结构优化设计研究方法和基于Abaqus的优化设计方法均是通过建立船体有限元模型展开结构优化设计的，有限元模型的精度直接决定了结构优化效果，雅克比率可有效评估有限元网格单元的形状质量，雅克比率$ J $的公式为：

$ J = \frac{{\min ||\det ({J_i})||}}{{\max ||\det ({J_i})||}}。$

(14)

式中：$ \det ({J_i}) $为第$ i $个网格单元的雅克比矩阵的行列式；$ \min ||\det ({J_i})|| $、$ \max ||\det ({J_i})|| $分别为$ \det ({J_i}) $的绝对值最小值与最大值。

雅克比率$ J $越接近1表明网格形状质量越高，建立的有限元模型精度越高。

分析图2可知，在多次迭代过程中，所提方法的雅克比率$ J $始终稳定在0.8以上，显著高于基于Abaqus的优化设计方法。这一结果表明，所提方法在网格生成过程中能够有效控制单元形状的规则性和均匀性，从而确保了较高的网格质量。高质量的网格不仅能够更精确地模拟船体结构的几何特征和材料属性，还能减少数值计算中的误差，提高有限元分析的可靠性。此外，高精度的有限元模型为后续的结构优化设计奠定了坚实基础，降低了因网格畸变导致的收敛困难或计算失效的风险。

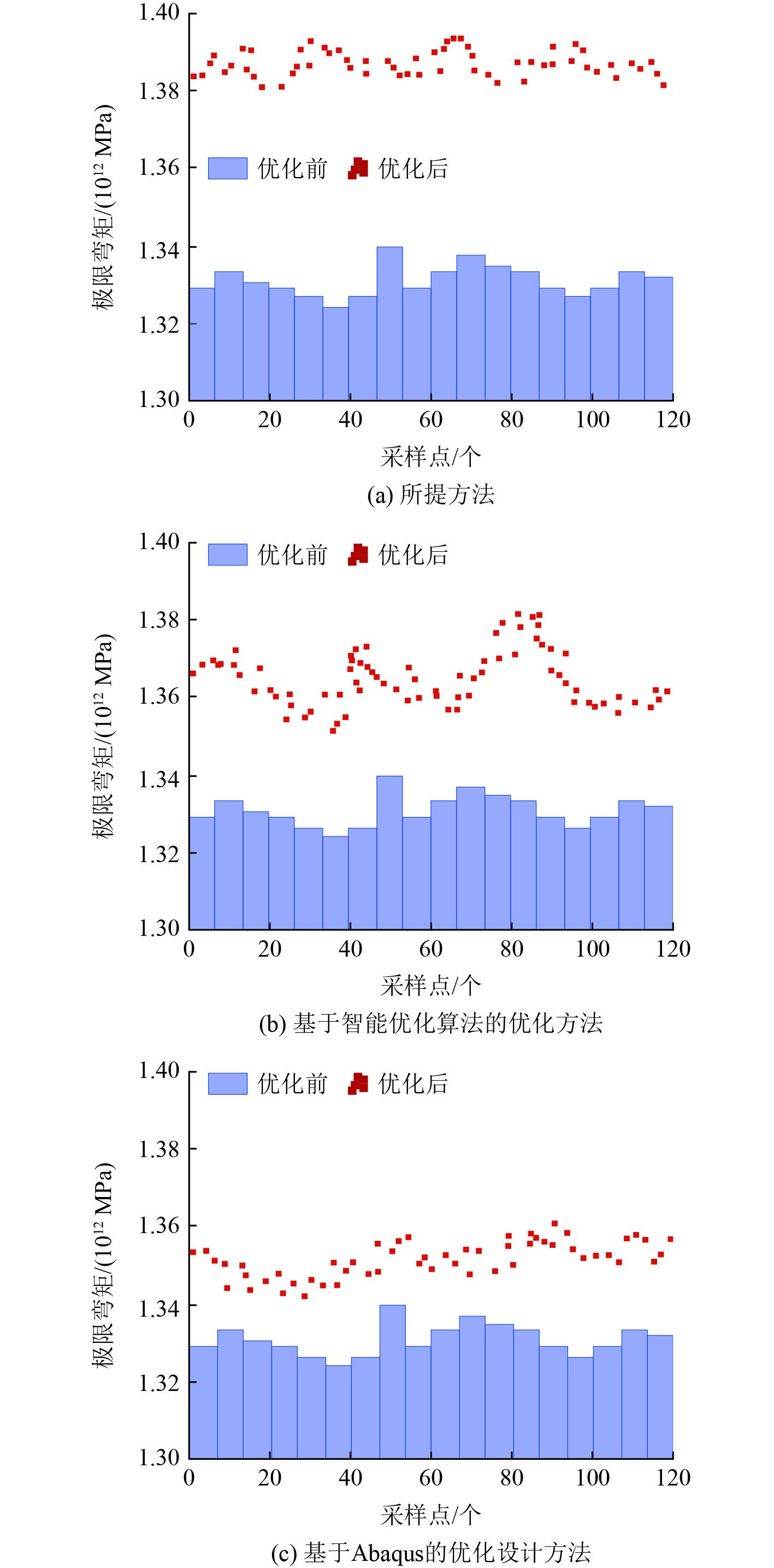
采用基于有限元分析的船型船体结构优化设计研究方法、基于智能优化算法的优化方法与基于Abaqus的优化方法展开结构优化测试，通过船体的极限弯矩与最大变形量测试上述方法的优化效果。极限弯矩是衡量结构抵抗弯曲变形能力的重要指标，其值越大，说明结构在受到外力作用时越不易发生破坏，即结构的刚度越强。结果如图3所示。

分析可知，相较于未经优化的原始结构，3种优化方法均显著提升了船体结构的极限弯矩，表明这些方法在增强结构承载能力方面均取得了积极效果。具体而言，所提方法引入了智能优化算法和精细化有限元分析，不仅实现了极限弯矩的最大化提升，还确保了优化结果的全局最优性和工程适用性。此外，所提方法在优化过程中充分考虑了复杂载荷条件和结构变形约束，使得优化后的船体结构在实际应用中表现出更高的可靠性和稳定性。

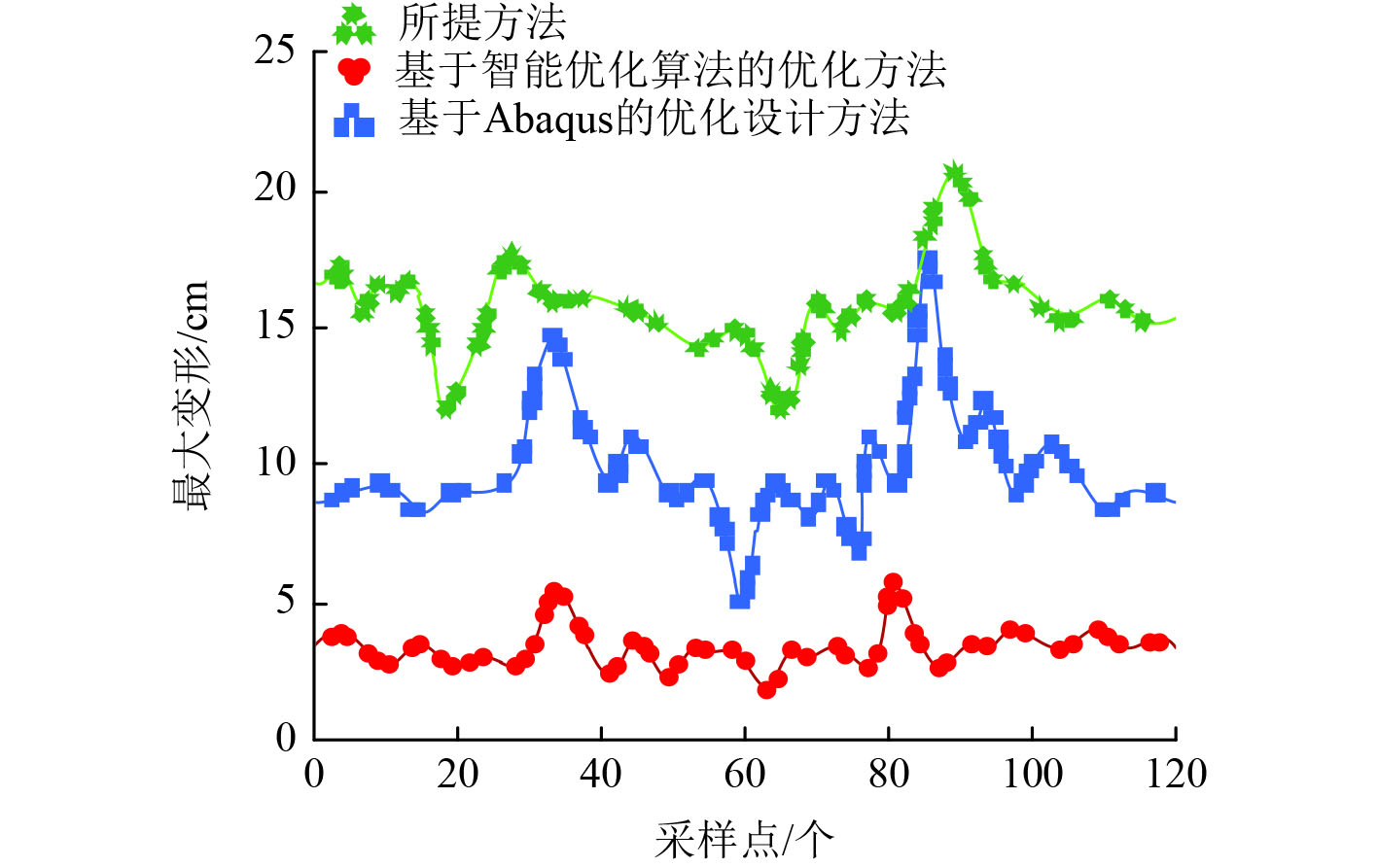
图4揭示了不同优化方法下船体结构的最大变形情况。最大变形越小，说明结构的稳定性和抗变形能力越强。

图中数据表明，所提出的方法最大变形值远低于其他2种方法。这一发现进一步强化了所提方法在优化船体结构性能方面的优势，因为它不仅增强了结构的刚度，还有效控制了结构在受力时的形变。

3 结　语

本文提出基于有限元分析的船型船体结构优化设计研究方法，根据有限元分析结果建立了结构优化目标函数，结合人工鱼群算法实现结构优化。实验结果表明，所提方法在网格质量、极限弯矩和最大变形量方面均表现出显著优势。网格质量始终稳定在0.8以上，所提方法实现了极限弯矩的最大化，展现了其全局最优性和工程适用性。此外，所提方法有效控制了船体结构的形变，进一步验证了其在增强结构刚度和抗变形能力方面的优越性。综上所述，所提方法通过为复杂船体结构的优化设计提供了更高效、更可靠的技术支持。