2. 船舶振动噪声重点实验室,江苏 无锡 214082
2. National Key Laboratory on Ship Vibration and Noise, Wuxi 214082, China
舰艇航行时有三大噪声源,包括机械噪声、螺旋桨噪声和水动力噪声,其中机械噪声源是慢速时最主要的噪声,由舰艇上各种机械设备产生的振动引起。应对机械噪声的重要技术手段之一是使用隔振系统,即在机械设备下使用筏架和隔振器大幅减小动力机械的振动和噪声。筏架作为中间质量块其惯性力可以平衡部分设备的激励力,并且能够降低系统的固有频率、吸收振动能量,从而加强系统的隔振效果。目前浮筏隔振系统已经在舰船上普遍使用并有较好的隔振效果,但是随着隔振系统复杂化集成化的演变趋势,虽然大质量的筏架可以增强系统的隔振效果,但是筏架增加的质量会削减舰艇的有效承载质量,工程要求保证隔振效果的同时尽量削减筏架的质量,传统的经验设计不足,需要更为方便科学的优化方法对浮筏进行优化。
近年来,对于隔振系统的优化主要有2个方面。一方面是对筏架的结构形式进行优化,Cui等[1]、李旸等[2]、满思伟等[3]使用了拓扑优化方法,基于变密度法对筏架本身进行结构优化,在减重的同时提升了隔振效果,并进行了试验验证。Zhao等[4]研究了基于拓扑优化的隔振与结构支撑一体化耦合设计,分别对具有横向对称约束和双对称约束的子结构进行拓扑设计,从数值结果的Pareto前沿得到了具有不同机理带隙的拓扑优化结构,为筏架拓扑优化提供了重要的优化方法。
另一方面是对系统中的关键参数进行优化,康秀丹[5]使用了一种岛屿遗传优化算法对隔振系统进行优化,王修成等[6]结合多岛遗传算法和序列二次规划算法对隔振器参数进行组合寻优分析,优化后的浮筏隔振系统隔振性能得到改善,为船用浮筏隔振系统设计提供指导。Liu等[7]通过频率分析、静力分析、频率响应、隔振果和总质量分析,对5个模块进行约束限制,通过遗传算法得到优化结果。邹涛[8]利用对遗传算法代码进行改进,并使用改进后算法对浮筏隔振器参数和筏架结构参数进行了优化。徐匡迪等[9]基于APDL语言零阶优化方法对浮筏进行结构优化,在总体积基本不变的前提下提升了各阶固有频率。Zou等[10]采用伪并行改进遗传算法(PPIGA)对浮筏隔振系统的质量和刚度进行优化,结果证明PPIGA算法在参数优化中具有较好的效果。徐明成等[11]基于改进的RBF-PSO算法,调整权重参数对浮筏隔振系统进行轻量化优化设计。
本文基于Abaqus仿真软件和Isight集成软件,以筏架的形状、结构尺寸作为设计变量,输入到基座的加速度为目标函数,基对浮筏系统中的筏架进行拓扑优化和尺寸优化,通过灵敏度分析和近似模型方法,结合遗传算法,在满足约束条件的情况下得到最优的结果,从而使得隔振系统在隔振效果变动较小的同时降低筏架质量。
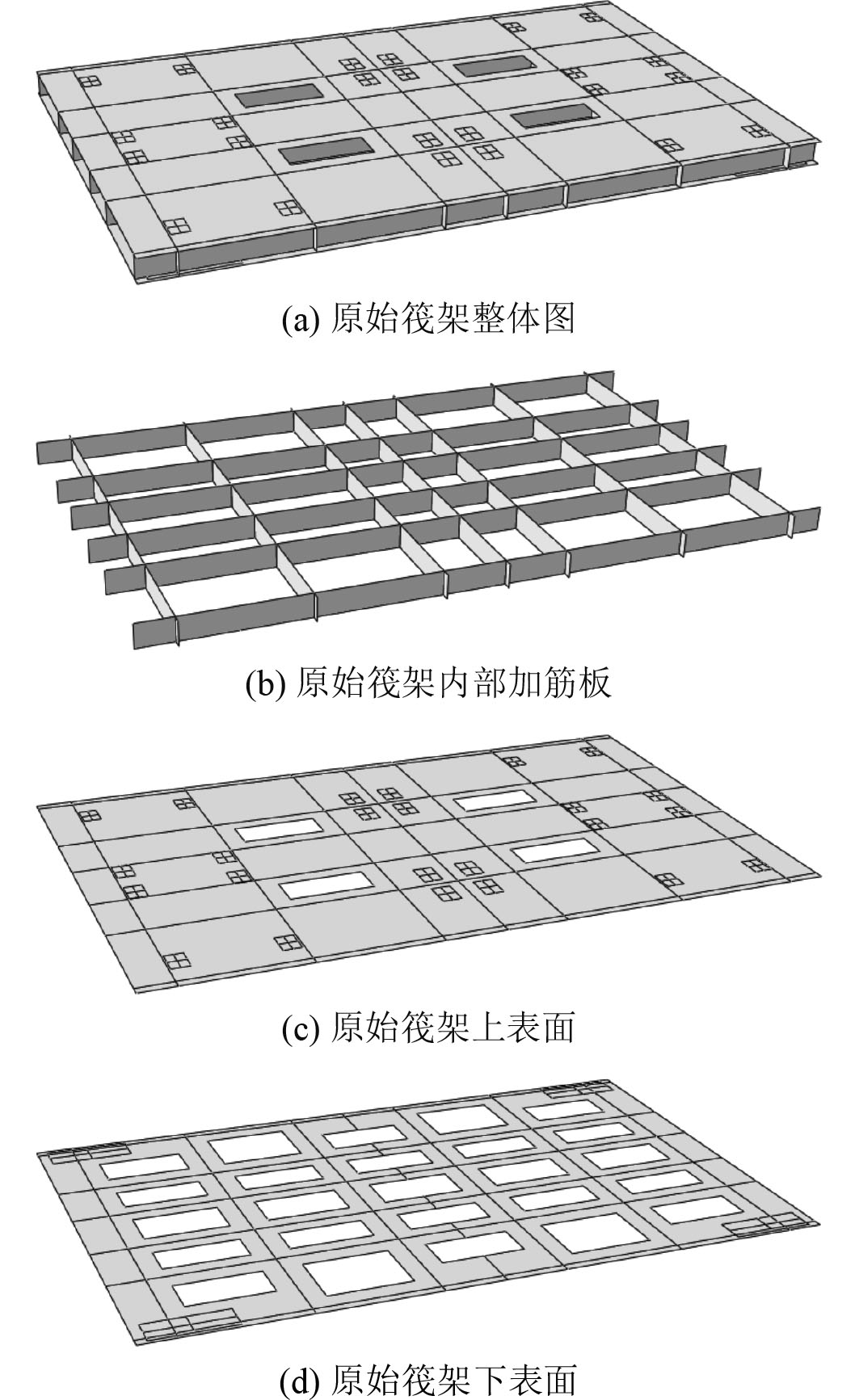
1 隔振系统的设计及仿真计算 1.1 参数化仿真建模本文主要针对板式筏架的优化进行研究,为了应对不同尺寸的板式筏架,在Abaqus软件中采用了参数化建模。选择的具体案例如图1所示,该筏架主要分为上面板、下面板、横向加筋板、纵向加筋板、上层隔振器基座和下层隔振器基座。
|
图 1 原始筏架模型 Fig. 1 The original raft model |
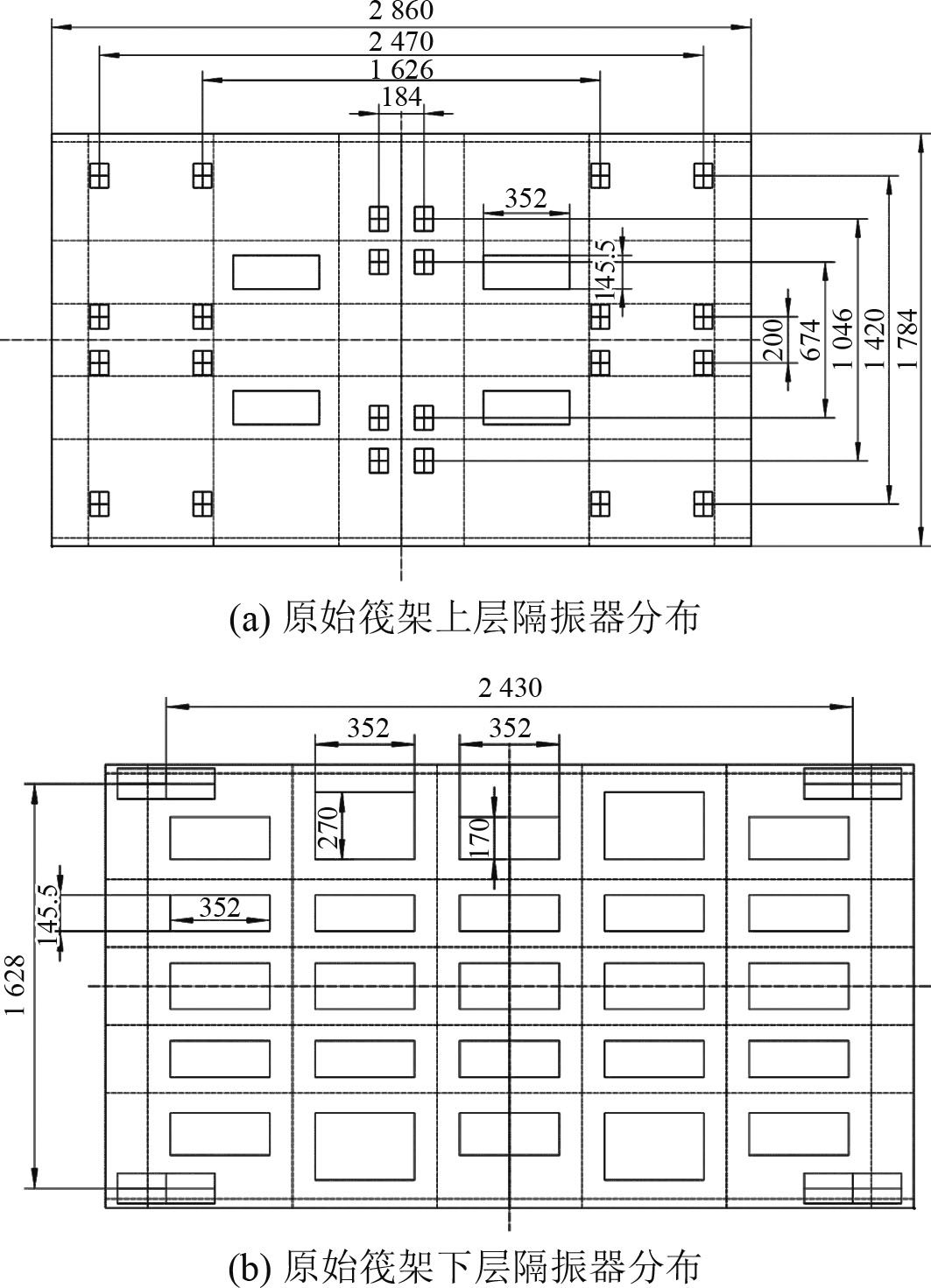
各部分的原始尺寸数据如图2和表1所示。该筏架上装有6台设备,其中同型号的激振机、泵体和齿轮箱各2台,激振机和齿轮箱的质量为112 kg,泵的质量为126 kg。在有限元仿真中将6台设备简化为6个惯性质量点,点位置在设备实际重心位置。6台设备都通过上层隔振器与筏架相连,每台设备的下层配有4个隔振器。筏架通过4个下层隔振器与基座相连,隔振器型号参数与对应位置如表2所示。
|
图 2 原始筏架尺寸 Fig. 2 Original raft size |
|
|
表 1 各部分原始厚度 Tab.1 Original thickness of each part |
|
|
表 2 隔振器参数 Tab.2 Vibration isolator parameters |
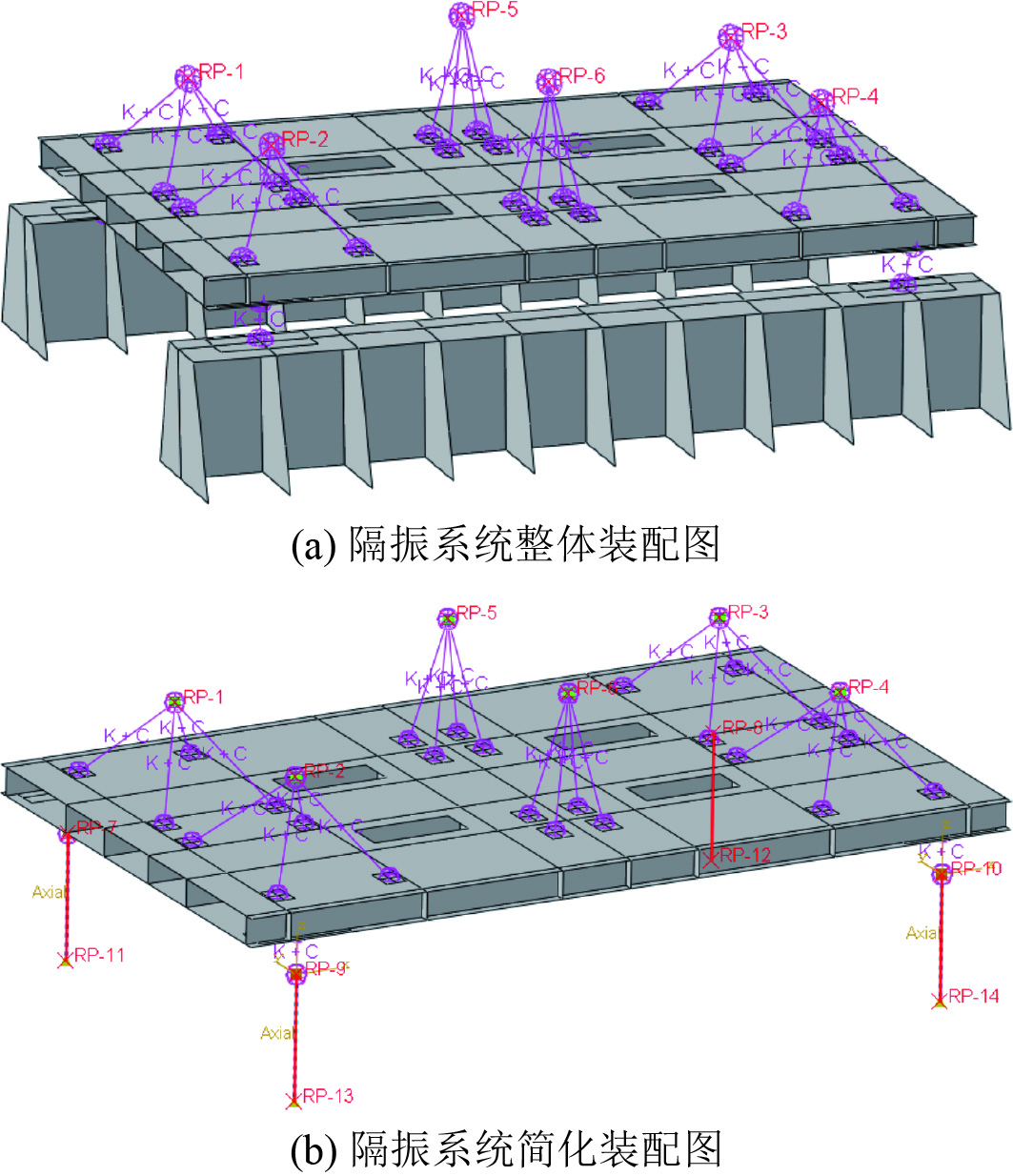
隔振系统中基座与舱段固定在一起,舱段的下半部分浸入水体中,整体装配图如图 3所示。由于仿真模型中涉及到设备、筏架、基座、舱段以及水体,所以计算时间较长,本文将基座、舱段及水体简化为弹簧单元,弹簧刚度
|
图 3 装配图 Fig. 3 Assembly drawing |
| $ K_f=\text{i}\omega\mathit{Z}_f。$ | (1) |
式中:
本文采用Abaqus仿真软件对浮筏隔振系统的隔振性能进行有限元仿真计算。通过谐响应分析计算浮筏隔振系统的加速度频率响应,每个设备处的输入选用实际激励数据,在基座底部施加简支约束,谐响应分析方法采用完全法,计算频率范围为10~250 Hz,激励力的步长为1 Hz。经过仿真计算,得到各点的加速度响应。
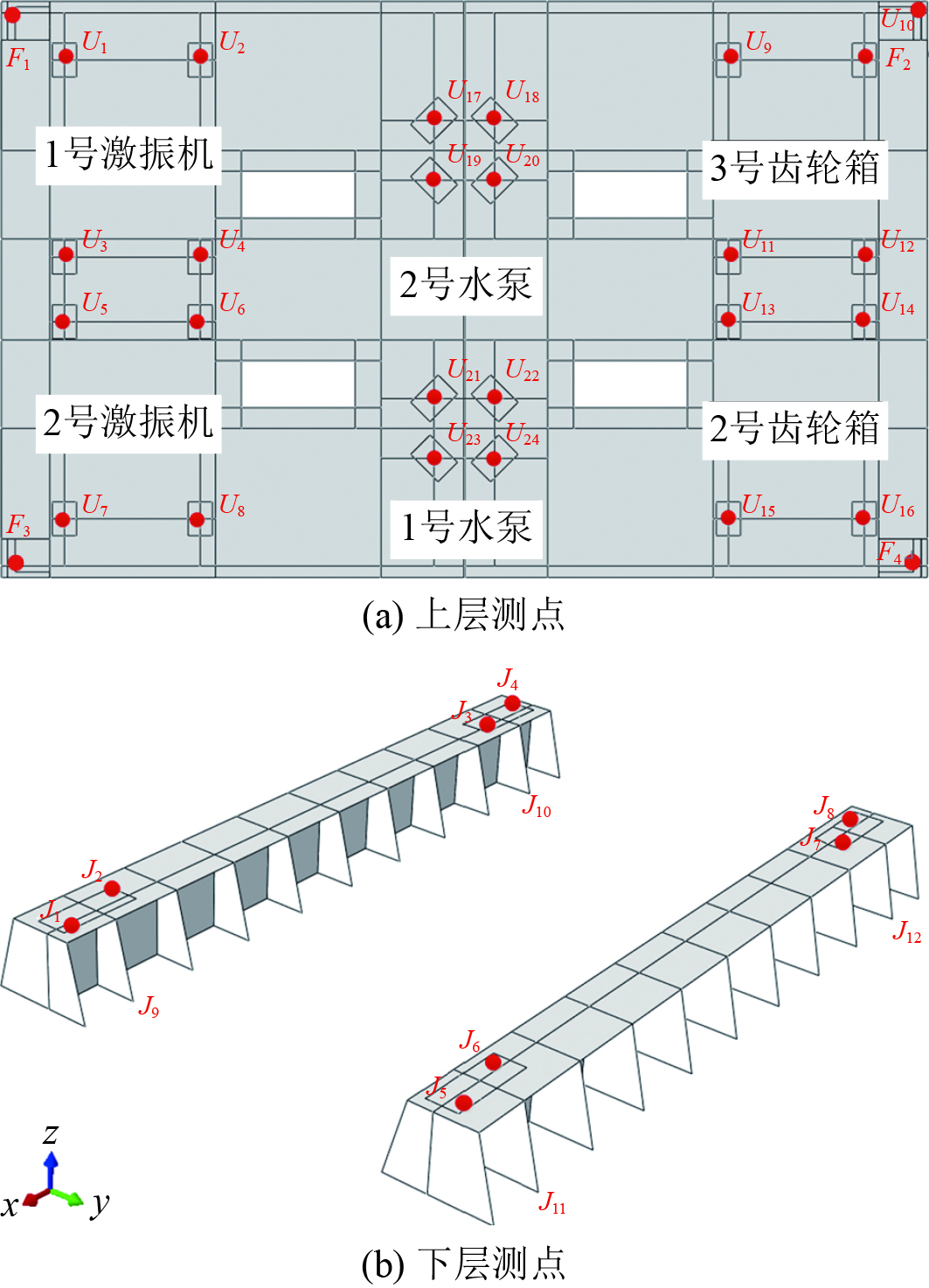
1.3 试验验证有限元方法试验在模拟舱段内进行,基座搭建在舱段内,等比制作的原始筏架通过4个sh750型隔振器连接在基座上。筏架上分别搭载有6台设备,包括2台激振机、2台泵和2台齿轮箱,主要工况为6台设备全开的情况,设备的激励频率为30 Hz及50 Hz。布置64个加速度测点,测点图如图4所示,其中D为设备基座测点,编号与机脚测点U对应,如U1对应D1位置。F1~F4为浮筏测点,反向安装。根据仿真输入对设备进行调试,通过加速度传感器测得布点的加速度。对比软件仿真结果和试验结果的加速度振级落差。
|
图 4 测点图 Fig. 4 Point chart |
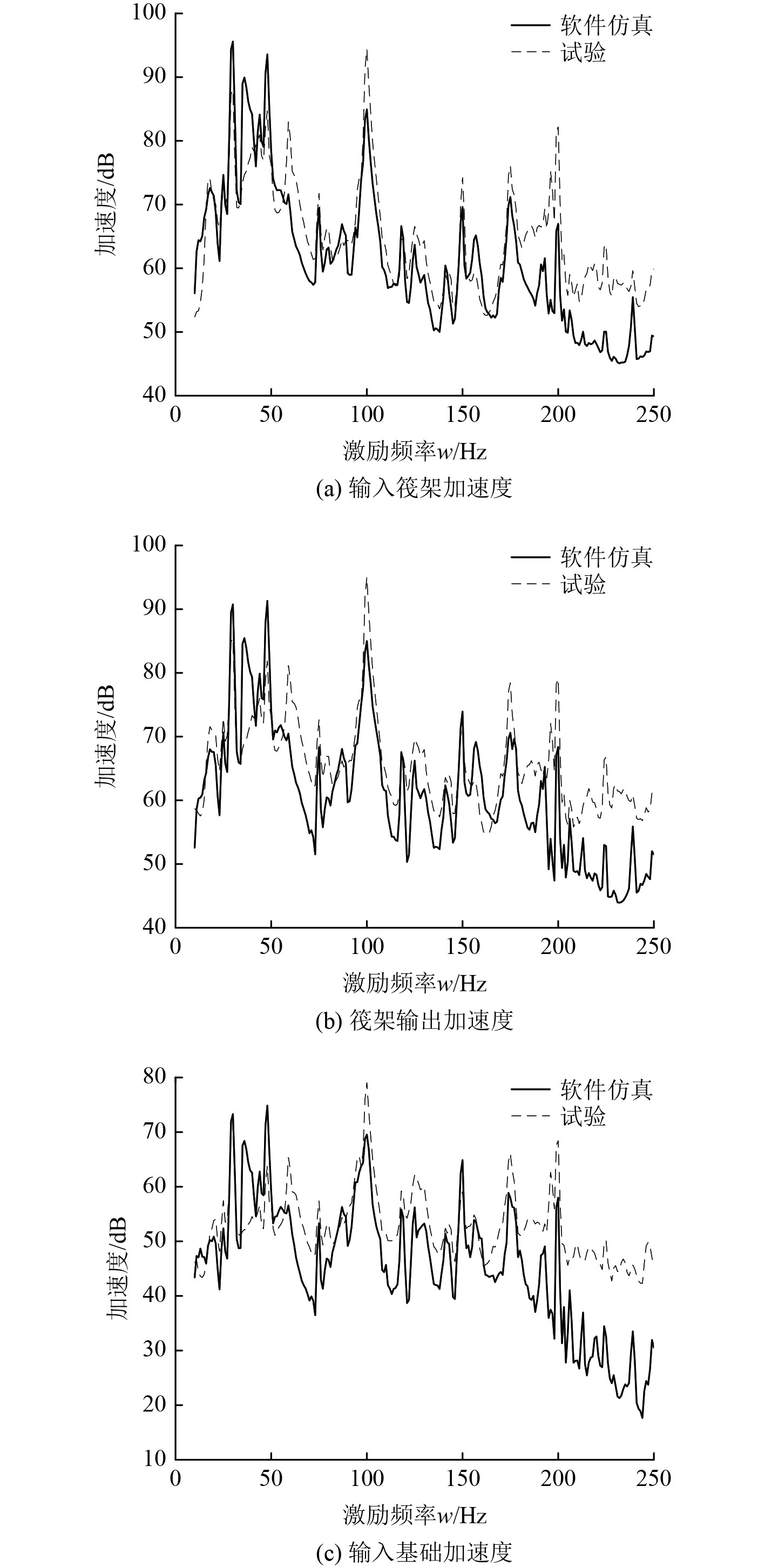
试验结果与仿真结果比较如图5所示,主要比较上层隔振器与筏架连接处(即输入筏架加速度)、下层隔振器与筏架连接处(即筏架输出加速度)和下层隔振器与基座连接处(即输入基础加速度)3个位置的加速度。在150 Hz内吻合效果最佳。仿真结果比试验结果多了一个峰值,这是因为低频阻抗大难激励,试验依靠宽频激励没有激励出此频率的峰值。
|
图 5 软件仿真结果与试验结果对比图 Fig. 5 Comparison between software simulation results and test results |
变密度法是结构拓扑优化中的一种常用方法,通过在设计空间内变化材料的密度来寻找最优的材料分布。这种方法因其形式简单、方便实行而被广泛应用于工程中结构优化设计。该方法的设计变量通常是材料的密度,这些密度值被定义在网格的每个单元内或每个节点上。通过变换这些设计变量的数值来模拟结构中材料的实际分布,进而找到更优的分布方案从而优化结构的性能。变密度法的一个关键特点是在优化过程中结构拓扑变化灵敏,大大增加了其在实际工程优化中的实用性。同时为了尽可能减少中间密度单元的数目,使结构单元密度尽量趋于端点值即0或1(其中0代表完全无材料,1代表材料完全)。本文采用固体各向同行材料惩罚法(以下简称SIMP法)。SIMP方法通过引入惩罚因子来模拟材料的各向同性行为,进而避免出现中间密度的单元[2]。
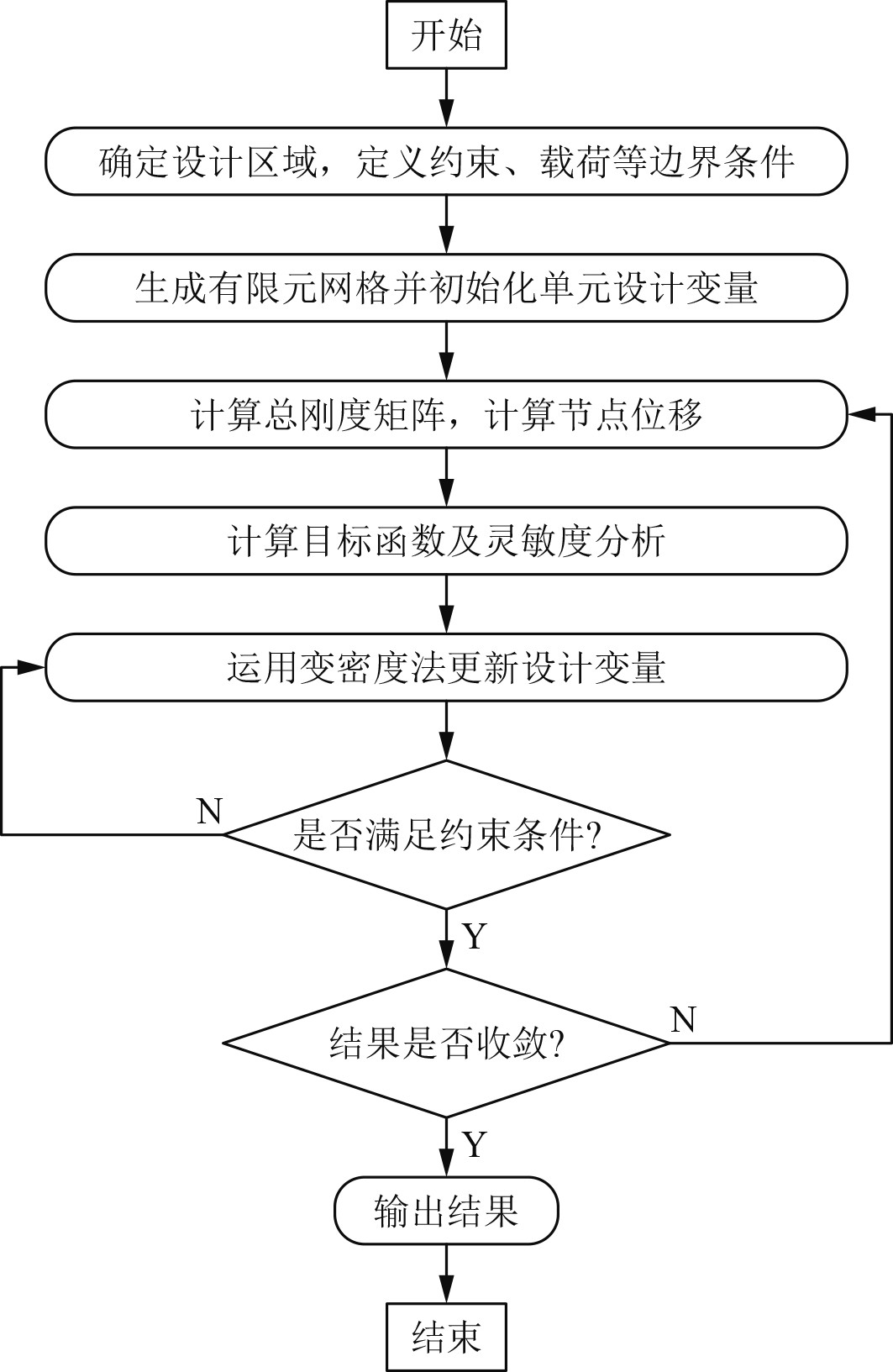
拓扑优化的基本步骤如图6所示。首先将结构域离散成有限元网格,计算每个单元初始的相对密度值,设定目标函数和边界条件后进行灵敏度分析确定哪些单元对结构性能的贡献更大,根据分析的结果,更新每个单元的密度,增加对结构性能贡献大的单元的密度,减少贡献小的单元的密度。
|
图 6 拓扑优化计算流程图 Fig. 6 Topology optimization calculation flow chart |
SIMP方法的优点:计算效率高,适用于复杂的几何形状和广泛的设计域。能够处理多种载荷情况和多类边界条件。通过惩罚因子和过滤技术,可以有效地避免灰色区域,得到清晰的拓扑边界。
由于在拓扑优化中进行频率响应分析困难,而主要的优化频率在设备的激励频率,所以研究在定频下讨论,可以把振动当成是单频的简谐振动,隔振效果的评价用位移代替加速度是可行的[12]。
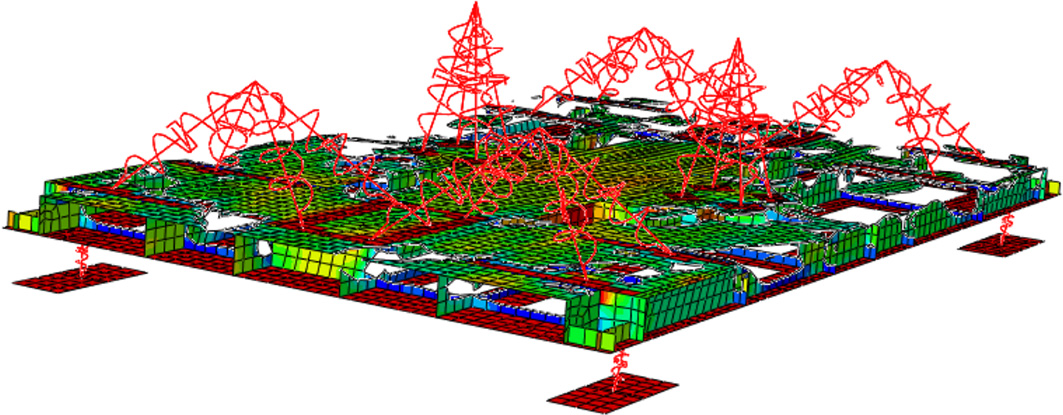
2.2 拓扑优化结果将设备的激励频率下的输入力作为拓扑优化的输入,以系统中的隔振器连接点的最大位移作为约束,以输入基座的位移最小作为目标函数进行拓扑优化,优化结果如图7所示。
|
图 7 拓扑优化密度分布图 Fig. 7 Topology optimization density distribution map |
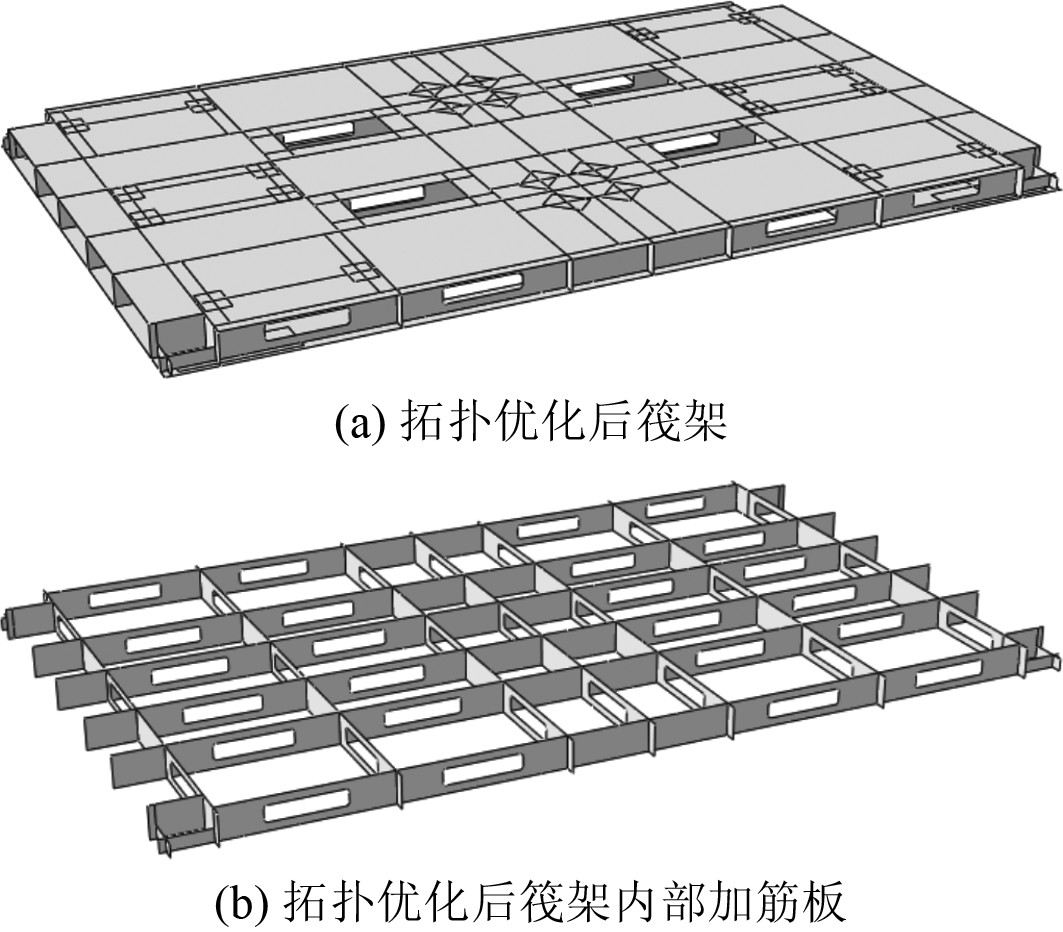
从图中可以发现,上下面板保留部分主要是隔振器与筏架连接的平台部分,而纵向的加筋板和横向的加筋板主要保留边界,这是因为能量在传递过程中主要在这些位置流动。因为筏架上方安装有多个设备,为了方便实际工程中安装设备和管理,不对筏架上表面进行修改。而筏架下表面在设计过程中已经进行了减重设计,所以根据拓扑优化的密度云图结果,结合工程实际重新设计筏架内部的加筋板,优化结果如图8所示,纵向和横向加筋板的开孔参数见表3。拓扑优化后筏架质量由862 kg减少至828 kg。
|
图 8 拓扑优化后筏架模型 Fig. 8 Raft model after topology optimization |
|
|
表 3 加筋板开孔参数 Tab.3 Stiffened plate opening parameters |
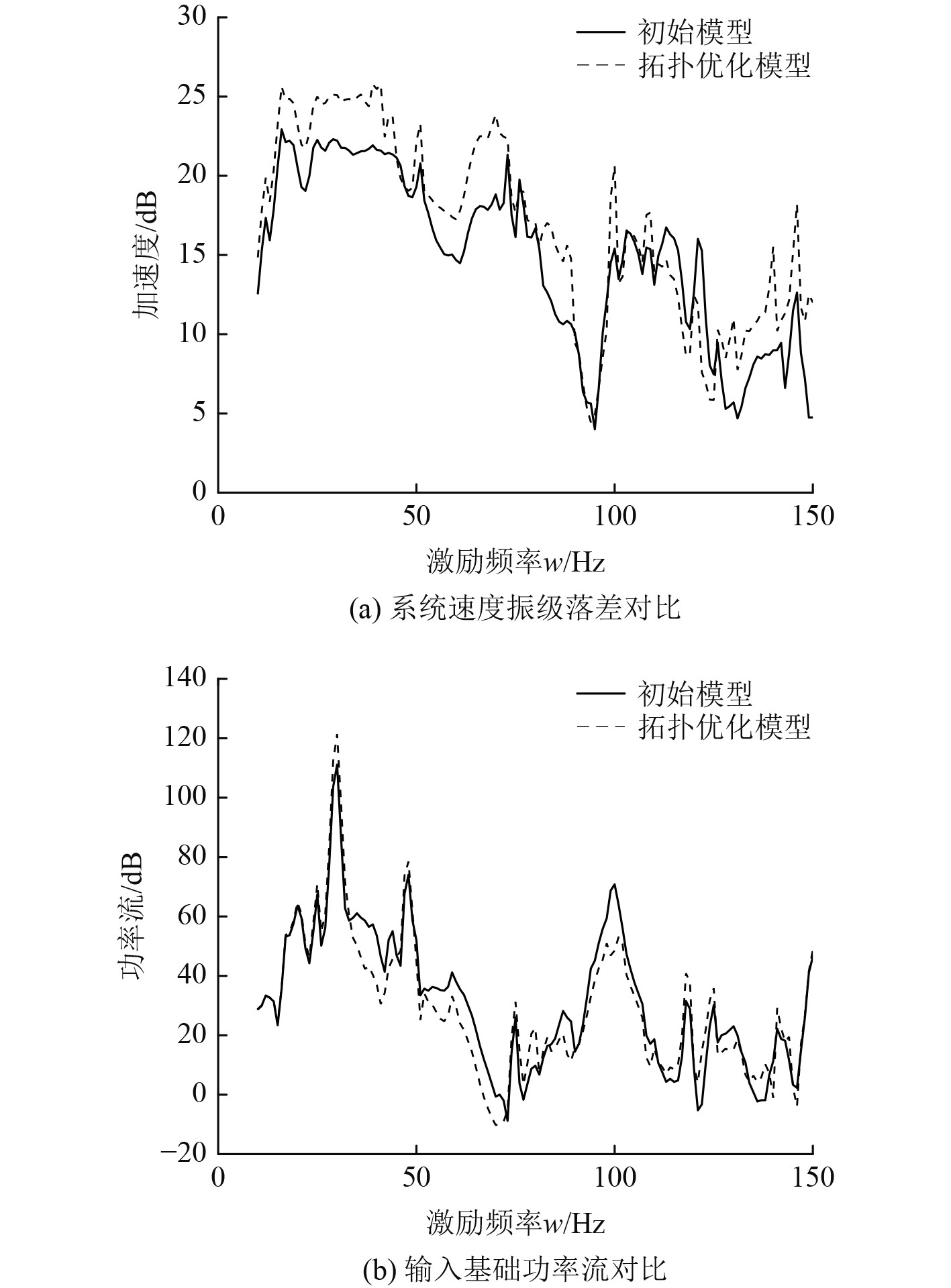
对比拓扑优化模型与初始模型的仿真结果,从图9可以发现,虽然系统的加速度振级落差相比初始模型增加,但是输入到基础的功率流在30 Hz和50 Hz处也增加,说明筏架本身消耗的能量相比初始模型减少,输入到筏架的加速度增加,导致更多的能量流入基座,需要进一步优化板厚尺寸降低最终功率流的输出。
|
图 9 拓扑优化结果对比 Fig. 9 Comparison of topology optimization results |
工程中最常用的隔振效果评价标准就是加速度振级,计算公式如下:
| $ {L_A} = 20\log \bar A 。$ | (2) |
式中:
| $ \bar A = \sqrt {\frac{{\sum\limits_{k = 1}^n {A_k^2} }}{n}}。$ | (3) |
因为筏架上搭载的设备较多,仅仅以加速度体现隔振效果比较片面。在隔振效果方面,目前功率流因为其同时涉及力和速度2个重要指标逐渐被重视,严济宽[13]推导了振动功率流的一般表达式,伍先俊等[14 − 16]在Ansys和Isight平台上针对隔振系统功率流进行优化,许树浩等[17]通过有限元计算证明采用功率流来评价隔振系统隔振效果的优劣更加接近实际效果。
对于振动结构来说,时间平均的功率流更为重要,将速度和力分别写为:
| $ F\left( t \right) = {{{R}}_{{e}}}\left\{ {\tilde F \cdot {e^{{\text{i}}\omega t}}} \right\} ,$ | (4) |
| $ V\left( t \right) = {{{R}}_{{e}}}\left\{ {\tilde V \cdot {e^{{\text{i}}\omega t}}} \right\} 。$ | (5) |
则输入功率P的计算式如下[13]:
| $ P = \frac{1}{T}\int_0^T {{{{R}}_{{e}}}\left\{ {\tilde F \cdot {e^{{\text{i}}\omega t}}} \right\} \cdot {{{R}}_{{e}}}\left\{ {\tilde V \cdot {e^{{\text{i}}\omega t}}} \right\}{\text{d}}t}。$ | (6) |
式中:
若令:
| $ \tilde F = F' + {\text{i}}F'',\tilde V = V' + {\text{i}}V'' ,$ | (7) |
| $ {\tilde F^ * } = F' - {\text{i}}F'',{\tilde V^ * } = V' - {\text{i}}V''。$ | (8) |
式中:
| $ \begin{aligned} P = & \frac{1}{T}\int_0^T {\left[ {F'\cos \omega t - F''\sin \omega t} \right] \cdot \left[ {V'\cos \omega t - V''\sin \omega t} \right]{\text{d}}t}= \\ & \frac{1}{2}\left( {F'V' + F''V''} \right) = \frac{1}{2} \cdot {{{R}}_{{e}}}\left\{ {\tilde F \cdot {{\tilde V}^ * }} \right\}。\end{aligned} $ | (9) |
由于验证试验测得的是输入点的加速度,上式可以转化为通过加速度及加速度阻抗计算功率流,且速度
| $ \tilde Z = \frac{{\tilde F}}{{\tilde V}},$ | (10) |
| $ \tilde A = \frac{{\tilde Z}}{{{\text{i}}\omega }},$ | (11) |
| $ \tilde V = \frac{{\tilde a}}{{{\text{i}}\omega }}。$ | (12) |
将式 (8)~式(10)代入式(7)得:
| $ P = \frac{1}{{2\omega }} \cdot {\left| {\tilde a} \right|^2} \cdot {{\text{I}}_{\text{m}}}\left\{ {\frac{{\tilde Z}}{{{\text{i}}\omega }}} \right\} 。$ | (13) |
式(13)就是计算试验与仿真结果功率流的表达式。
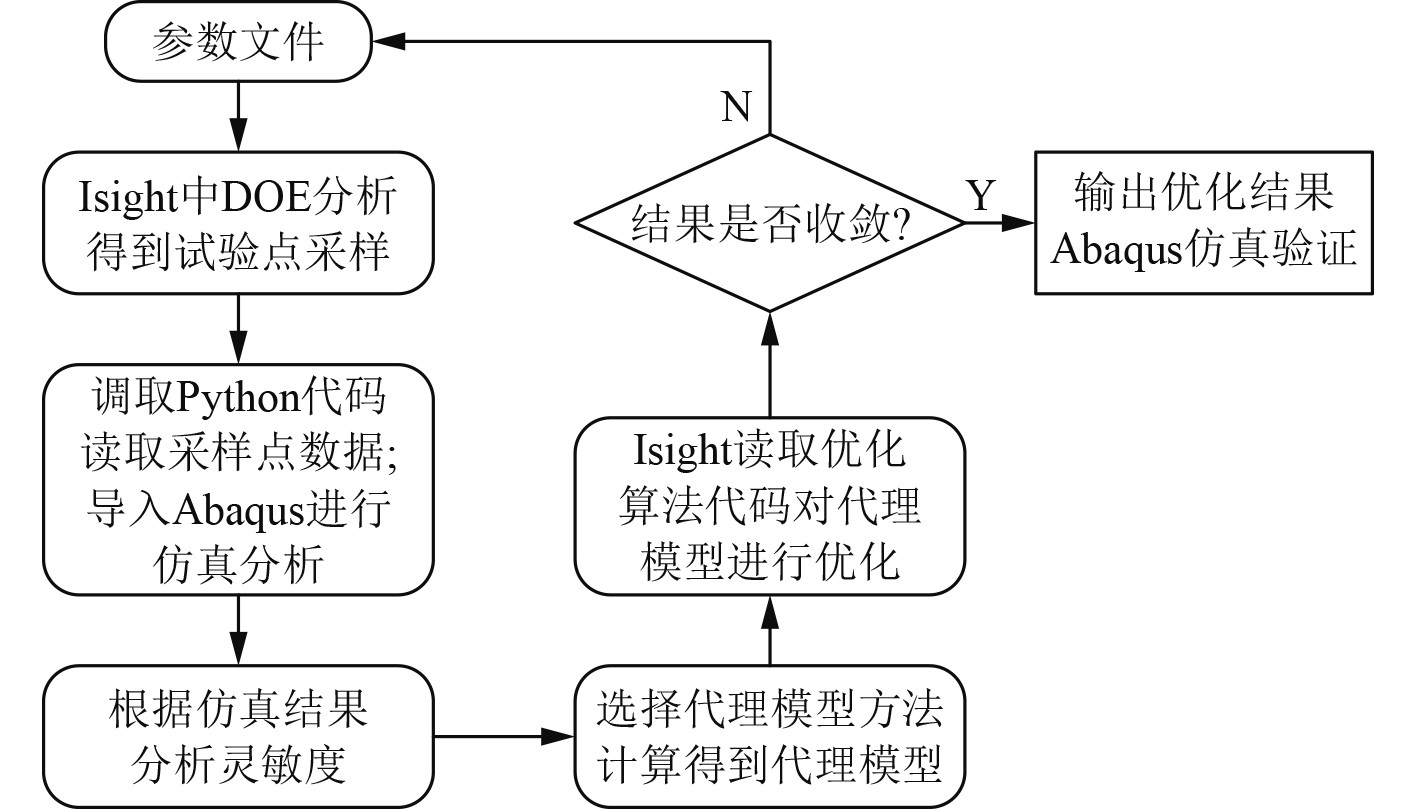
3.2 优化流程Isight参数优化平台具有广泛的CAE\CAD的集成接口,并且可以加入自编程序。通过快速拖拽功能模块搭建优化流程,优化流程见图10。选择筏架的上面板厚度tup,下面板厚度tdown,纵向加筋板厚度ty,横向加筋板厚度tx,上隔振器底座厚度tisoup,下隔振器底座厚度tisodown作为设计变量。由于系统激励不变,浮筏隔振系统得到隔振效果可以转化为输入基座的加速度振级和功率流,选该2个变量作为目标函数。设计变量的变化范围见表 4。
|
图 10 基于Isight平台的优化流程图 Fig. 10 Optimization flow chart based on Isight |
|
|
表 4 设计变量变化范围 Tab.4 Design variable variation range |
确认优化设计的三要素之后,由于实际工程中隔振系统振动传递复杂,所以需要借助试验设计方法(DOE模块)选择合适的代理模型进行优化计算。
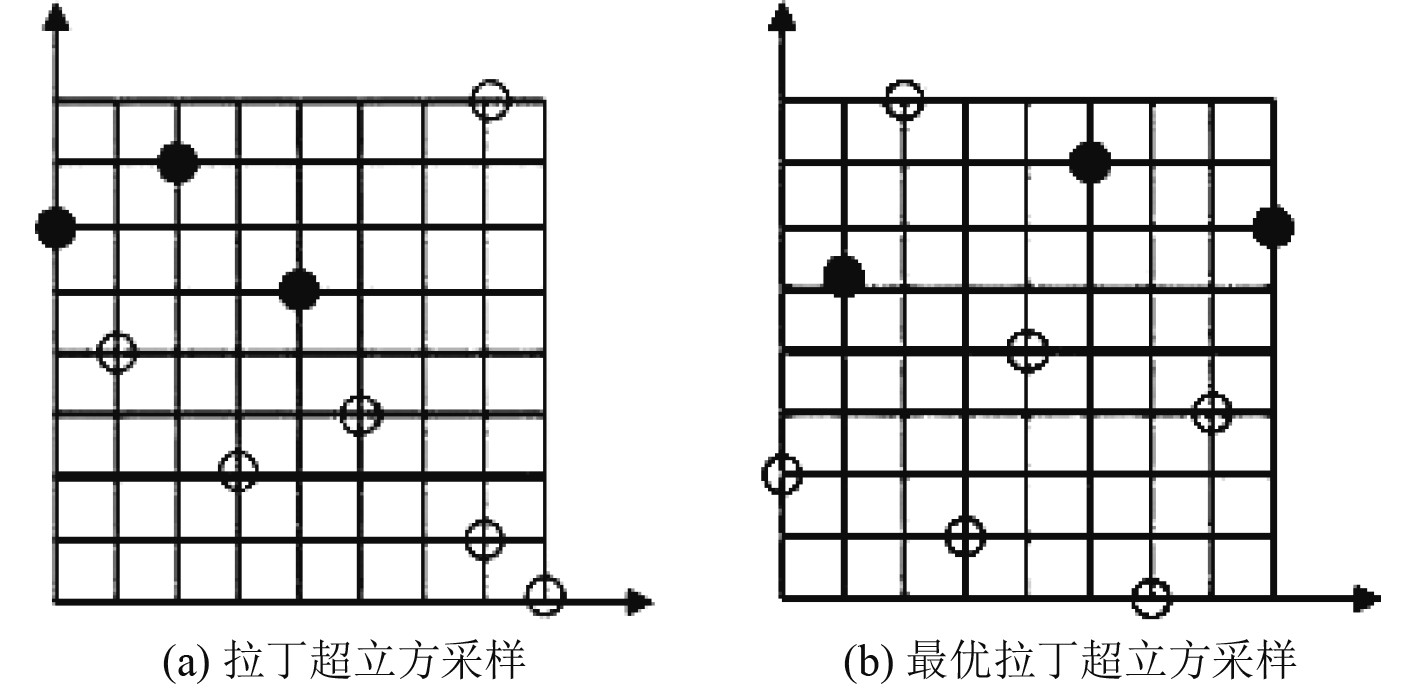
试验设计方法选择最优拉丁超立方设计(Optimal Latin Hypercube Design),该方法在兼顾随机拉丁超立方设计方法空间填补能力强、非线性拟合效果强的优点同时改进了原设计方法的均匀性,使得因子和响应的拟合更均匀分布在给定区间中。图11为2种方法生成试验点的分布。
|
图 11 试验点采样分布图 Fig. 11 Sample distribution map of the test site |
根据生成的试验点在Abaqus中进行仿真得到响应结果,该过程中由于将Abaqus直接加入模块会使得计算变得缓慢,所以采用了Python编程将试验点结果导入Abaqus后自动生成作业完成计算,再将结果汇总重新导入DOE模块中。该处理方式比原处理计算时间较少60%。
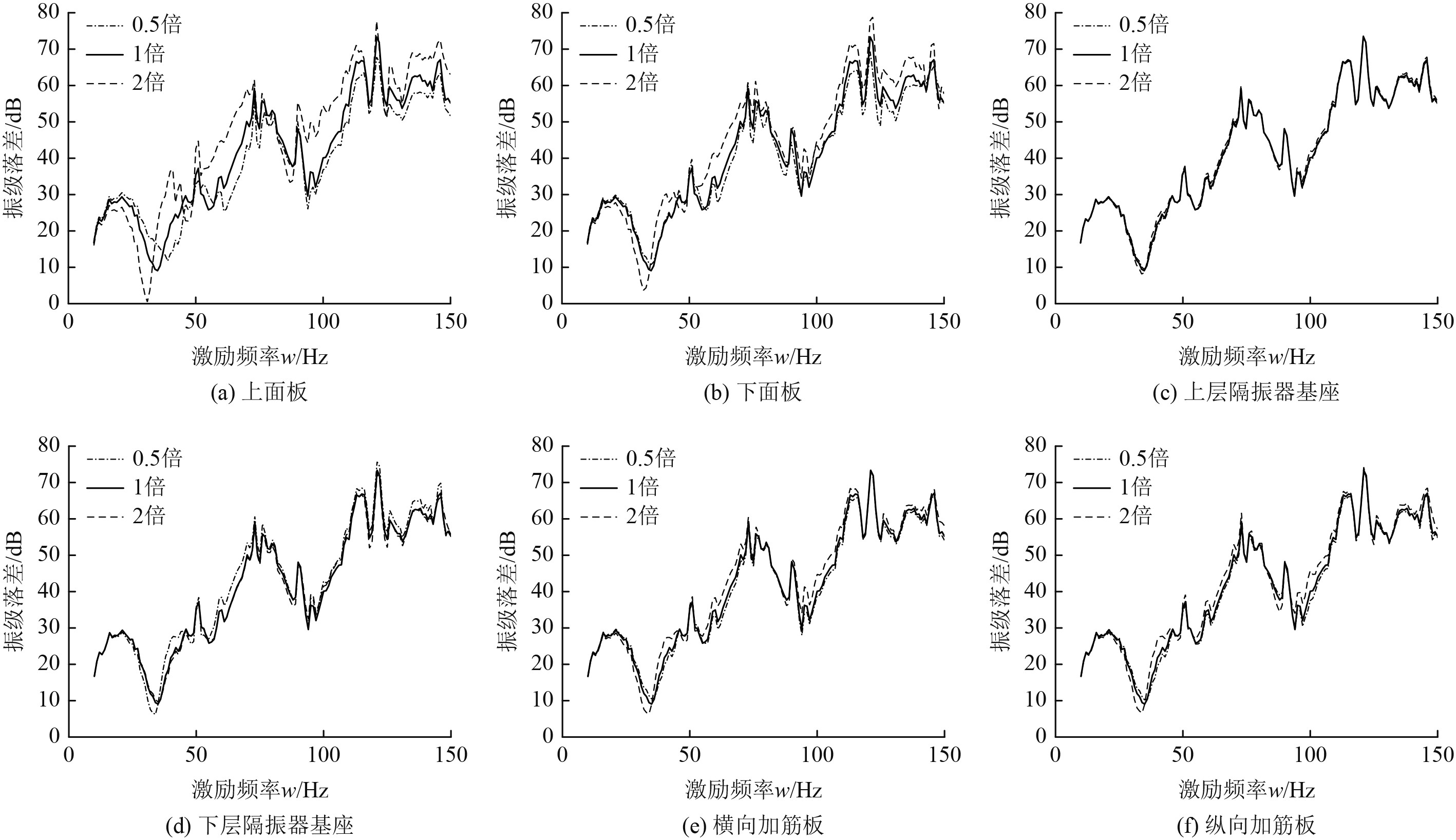
根据试验分析结果,得到筏架6个主要参数对隔振效果的影响如图12所示。其中上下面板、上层隔振器基座以及加筋板的影响类似,随着板厚的增加,系统功率流振级落差整体呈现增长趋势,但30 Hz附近呈现低谷且随着板厚增加最小值更接近30 Hz。上下面板厚度的变化对系统功率流影响最为明显,上层隔振器基座的影响最小。下层隔振器基座对系统功率流影响则相反,随着基座厚度的增加输入基座的功率流增加,在30 Hz附近的谷值向低频移动。所以为了保证筏架维持原隔振效果的同时减少质量,应在适当减少上下面板厚度的同时增加纵横加筋板的厚度。
|
图 12 参数对系统功率流振级落差的影响 Fig. 12 The influence of parameters on the power flow level drop of the system |
代理模型选择神经网络模型,该模型有快速的学习能力,逼近复杂非线性函数能力强,不需要数学假设,所以具有极好的泛化性能。对Isight中计算代理模型得到的结果进行误差分析,R2为
根据加工的实际情况对优化结果取整,优化结果如表5所示。
|
|
表 5 优化结果 Tab.5 Optimization result |
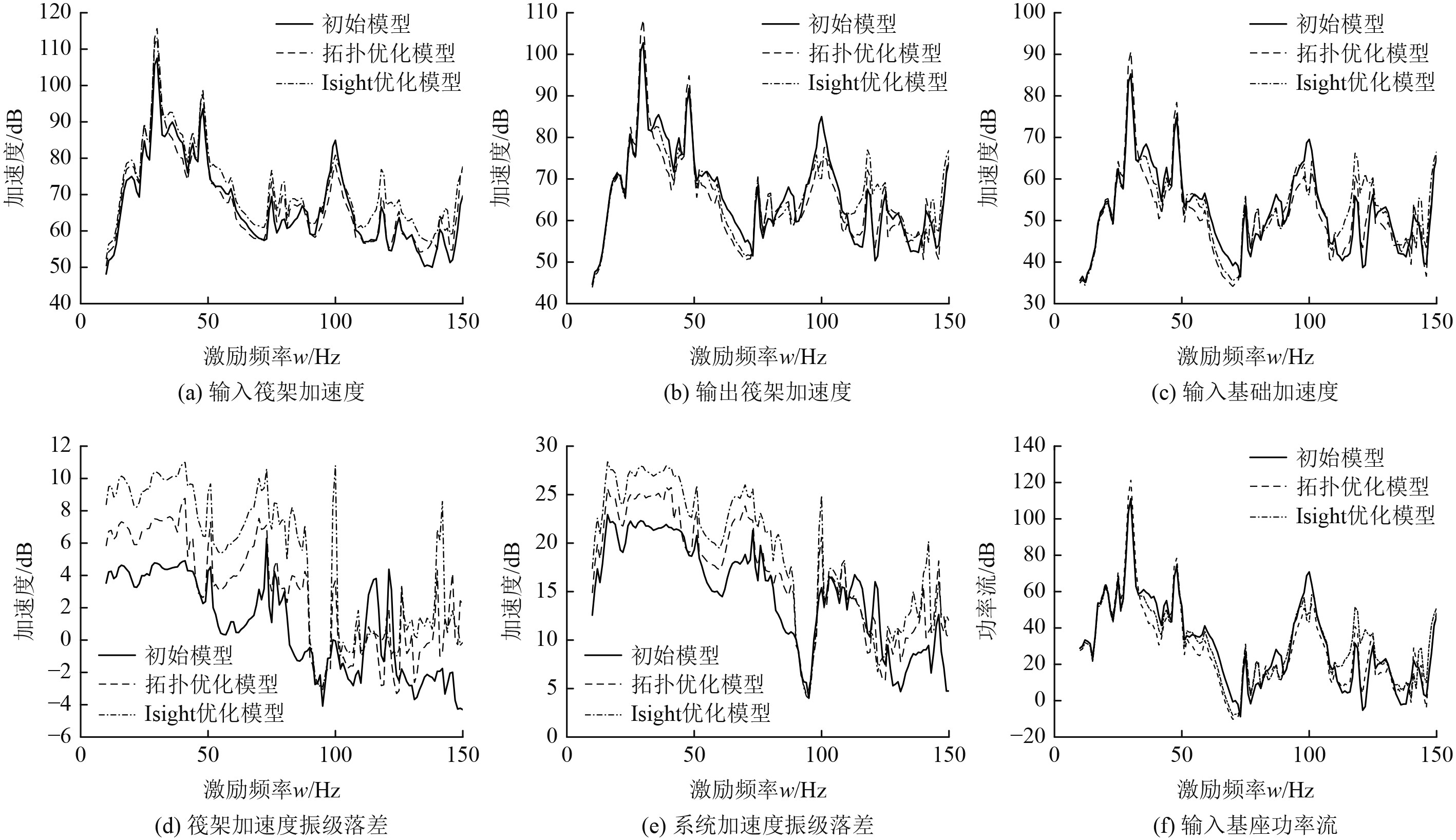
因为上下层隔振器基座的厚度对系统隔振效果影响很小,为了适应加工需要,将上下层隔振器基座统一改为12 mm与原模型基座实际厚度保持一致,根据优化结果重新在Abaqus中进行仿真运算,得到各级的输入、输出加速度以及输入基座的功率流。2次优化结果与原始结果进行对比,对比结果如图13所示。由于系统的输入功率流一定,所以系统的功率流落差只需对比输入基座的功率流大小。
|
图 13 优化前后频率响应曲线对比 Fig. 13 Comparison of frequency response curves before and after optimization |
从结果可以看到最终优化结果在加速度和功率流上与原始筏架差别不大,在30 Hz处,原始筏架加速度为111 dB,而优化结果为110 dB,差距仅为1%,50 Hz处均为48 dB。但是优化后筏架质量由862 kg减少至540 kg,质量减少了37.4%。说明本文优化方法对原始筏架进行了轻量化设计。
4 结 语本文以板架式浮筏隔振系统为研究对象,基于有限元法对隔振系统进行仿真分析,基于各向同性材料惩罚法对筏架进行拓扑优化,通过优拉丁超立方法进行试验设计,分析参数灵敏度。使用神经网络模型得到代理模型,通过NSGA-II完成筏架参数优化设计。最终确定本文对浮筏隔振系统进行拓扑优化以及多目标优化设计,在保证了输入基础加速度及功率流与原始模型差距在1%的同时,质量降低了37.4%,证明该方法可有效地应用在板架式浮筏隔振系统的优化设计中。通过分析最终优化结果,在板架式浮筏隔振系统减重优化中,根据功率流流动方向应优先增加纵横加筋板的厚度,减少上下面板的厚度。纵横加筋板主要起到增加筏架刚度、传递能量的作用,应布置在隔振器基座的下方区域并在能量集中的位置适当增加厚度。
| [1] |
CUI H, ZHU H. Topology optimization research and vibration characteristics analysis of the floating raft isolation system[J]. Zhendong Ceshi Yu Zhenduan/Journal of Vibration, Measurement and Diagnosis, 2021, 41(1): 120-125. |
| [2] |
李旸, 魏博, 路彤, 等. 泵类设备浮筏结构轻量化设计研究[J]. 科学技术创新, 2023(10): 56-59. LI Y, WEI B, LU T, et al. Research on lightweight design of floating raft structure of pump equipment[J]. Scientific and Technological Innovation Information, 2023(10): 56-59. DOI:10.3969/j.issn.1673-1328.2023.10.015 |
| [3] |
满思伟, 张保成, 马翠贞, 等. 双层底结构优化及减振效果分析[J]. 噪声与振动控制, 2024, 44(1): 86−91. MAN S W, ZHANG B C, MA C Z , et al. Optimization and vibration reduction effect analysis of double bottom structures[J]. Noise and Vibration Control, 2024, 44(1): 86−91. |
| [4] |
ZHAO H, FENG Y, LI W, et al. Numerical study and topology optimization of vibration isolation support structures[J]. International Journal of Mechanical Sciences, 2022, 228: 107507. DOI:10.1016/j.ijmecsci.2022.107507 |
| [5] |
康秀丹. 发动机悬置系统隔振性能仿真与优化设计[D]. 哈尔滨: 哈尔滨理工大学, 2020.
|
| [6] |
王修成, 崔洪宇, 孙继彬. 基于isight优化平台的浮筏隔振系统参数集成优化[C]//第十八届船舶水下噪声学术讨论会论文集, 2021.
|
| [7] |
LIU W, WU W, YIN X. Optimal design of a floating raft vibration isolation system with multiple constraints[C]//OKADA T, SUZUKI K, KAWAMURA Y. Practical Design of Ships and Other Floating Structures. Singapore: Springer, 2021: 198−208.
|
| [8] |
邹涛. 浮筏隔振系统优化设计与隔振特性研究[D]. 大连: 大连理工大学, 2022.
|
| [9] |
徐匡迪, 游彩霞, 何雪松. 基于APDL的潜艇浮筏结构优化设计与分析[J]. 农业装备与车辆工程, 2023, 61(10): 83−87. XU K D, YOU C X, HE X S. Optimal design and analysis of submarine floating raft structure based on APDL[J]. Agricultural Equipment & Vehicle Engineering, 2023, 61(10): 83−87. |
| [10] |
ZOU X, WU G, JIANG G. Characteristics analysis for floating raft isolation system based on FEM and PPIGA[C]//2023 International Conference on Mechatronics, IoT and Industrial Informatics (ICMIII). 2023: 54−57[2023−10−20].
|
| [11] |
徐明成, 肖邵予, 王汝夯, 等. 基于RBF-PSO算法的浮筏隔振系统性能优化及轻量化设计[J]. 中国舰船研究, 2024, 19(X): 1-9. XU M C, XIAO S Y, WANG R H, et al. Performance optimization and lightweight design of floating raft vibration isolation system based on RBF-PSO algorithm[J]. Chinese Journal of Ship Research, 2024, 19(X): 1-9. |
| [12] |
余林波. 浮筏隔振系统隔振特性与筏体拓扑优化研究[D]. 武汉: 华中科技大学, 2007.
|
| [13] |
严济宽. 振动功率流的一般表达式及其测量方法[J]. 噪声与振动控制, 1987(1): 24−29. YAN J K. The general expression of vibration power flow and its measurement method[J]. Noise and Vibration Control, 1987(1): 24−29. |
| [14] |
伍先俊, 朱石坚. 基于有限元的功率流计算及隔振系统优化设计技术研究[J]. 船舶力学, 2005(4): 138−145. WU X J, ZHU S J, Calculation technique of vibration power flow based on finite element analysis and its application in the isolation system optimization[J]. Journal of Ship Mechanics, 2005(4): 138−145. |
| [15] |
伍先俊, 程广利, 朱石坚. 最小振动功率流隔振系统Ansys优化设计[J]. 武汉理工大学学报(交通科学与工程版), 2005(2): 186−189. WU X J, CHENG G L, ZHU S J. Isolation system optimization by Ansys for minimizing vibration power flow[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering) , 2005(2): 186−189. |
| [16] |
伍先俊, 朱石坚. 组件功率流计算法和iSIGHT环境下隔振系统优化设计[J]. 船舶力学, 2006(2): 138-145. WU X J, ZHU S J. Vibr ation power flow calculation based on component modal technique and isolation system optimization using Isight[J]. Journal of Ship Mechanics, 2006(2): 138-145. DOI:10.3969/j.issn.1007-7294.2006.02.018 |
| [17] |
许树浩, 桂洪斌. 浮筏系统隔振性能的功率流评价指标[J]. 船舶力学, 2012, 16(5): 567-572. XU S H, GUI H B. Power flow estimation of float raft isolation system[J]. Journal of Ship Mechanics, 2012, 16(5): 567-572. DOI:10.3969/j.issn.1007-7294.2012.05.014 |
| [18] |
MARANO G C, QUARANTA G, GRECO R. Multi-objective optimization by genetic algorithm of structural systems subject to random vibrations[J]. Structural and Multidisciplinary Optimization, 2009, 39(4): 385-399. DOI:10.1007/s00158-008-0330-8 |
 2025, Vol. 47
2025, Vol. 47
