在极地地区,矿产资源极其丰富,且其军事价值和航运价值正不断地被各国重视。传统解决极地地区海上作业破冰由具备破冰能力的破冰船进行,但由于冰层较厚破冰船作业涉及较多局限性,利用破冰船携带气泡发生装置进行水下爆炸气泡破冰,在破冰船之前破坏冰层,加大破冰船破冰的最大厚度。故水下爆炸破冰的研究具有很高的学术价值以及现实意义[1]。
冰材料具有对温度敏感性、各向异性、对应变率敏感、不均匀性等特性[2 - 3]。王莹等[3]采用试验和数值仿真相结合,冲击波载荷是冰层损伤主要毁伤要素,气泡载荷影响毁伤区域破坏形态。曲艳东等[4]利用Ls-dyna模拟爆炸冲击波压力的作用特征和传播规律,对比了冰体覆盖和常规水下爆炸两者水中压力变化的差异性,得到相同的集中炸药爆距的影响是比较明显的。Cui等[5]实验研究得出冰破裂的模式与冰的厚度和气泡-冰的距离有关,冰裂缝从冰板顶部开始发展,界面处冲击波反射引起的张力所致。可见冲击波载荷在爆炸初期对冰层产生的毁坏是瞬时且主要的。Wang等[6]通过改变炸药类型、形状和圆柱装药长径比,研究冰盖在水下和空气接触爆炸载荷作用下的损伤特性,冲击波和气泡载荷的共同作用,水下爆炸破冰方式优于空气接触爆炸。张忠和等[7]模拟了炸药在水下不同深度处的爆破破冰效果,药包位于冰下约1.5 m破冰效果较好,当水深较小时药包的最佳深度相应增加。吴瑞波等[8]采用2#岩石乳化炸药布置成集中药包型式,炸药量分别为8、10、12 kg,得出炸药重量和入水深度在最优化组合参数下,爆炸物才能得到充分的利用。
以上成果大多数通过改变爆距、炸药类型、药量、冰厚等因素,得到最优的排列组合,分析在爆炸载荷下冰层的破坏效果,少有关注冲击波载荷和气泡脉动载荷联合作用下冰层的破坏特性。本文将通过实验和数值模拟对比验证,研究在水下爆炸产生的冲击波载荷和气泡脉动载荷的联合作用下,通过改变爆距、炸药量对不同冰层的破坏特性。
1 计算理论运用Abaqus/Explicit求解器中的CEL算法开展水下爆炸数值仿真,对水下爆炸模型采用1/4整体建模,包括空气、水、炸药和层冰,空气、水、炸药采用欧拉域建模,具体材料模型描述如下:
水采用Mie-Gruneisen状态方程进行定义,炸药状态方程为JWL(Jones-Wilkins-Leej),爆震产物采用JWL状态方程压力是密度和内能的函数[9]。表1为水、炸药的参数[3-10]。空气使用理想气体方程可以表示为[9]:
|
|
表 1 水介质及TNT参数 Tab.1 Water medium and TNT parameters |
| $ p + {p_A} = \rho R(\theta - {\theta _Z}) 。$ |
式中:
冰材料具有复杂特性在不同的载荷作用下会产生不一样的损伤过程,表现为弹性、韧性、脆性和弹塑性等多种变化模式[6]。冰选用各向同性的弹塑性材料模型进行模拟[11],研究冰材料在爆炸载荷下的破坏特性,并参考文献[12]屈服应力的速率效应可以用Cowper-Symonds应变速率模型来模拟,其中冰材料的
|
|
表 2 冰材料参数 Tab.2 Ice material parameters |
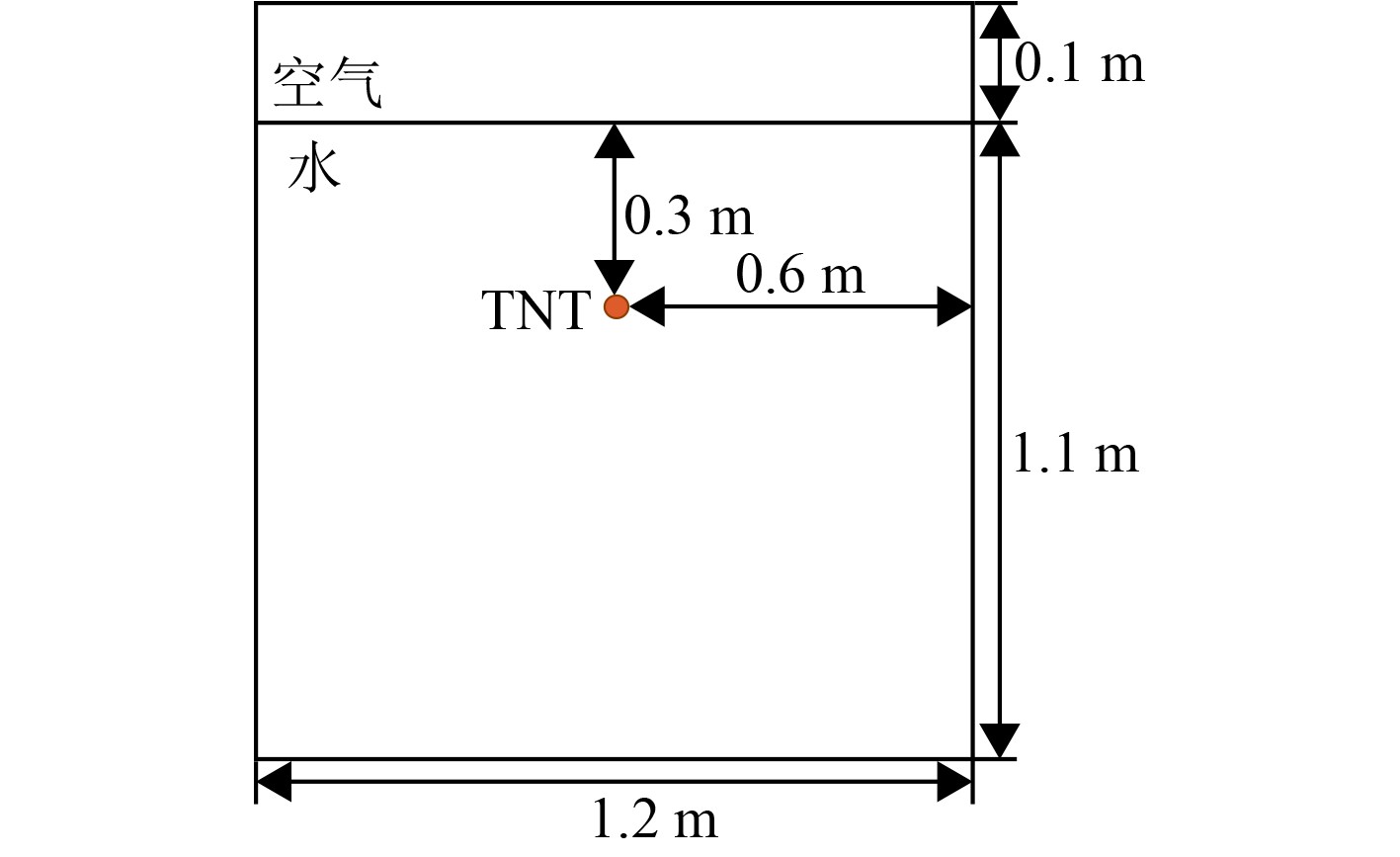
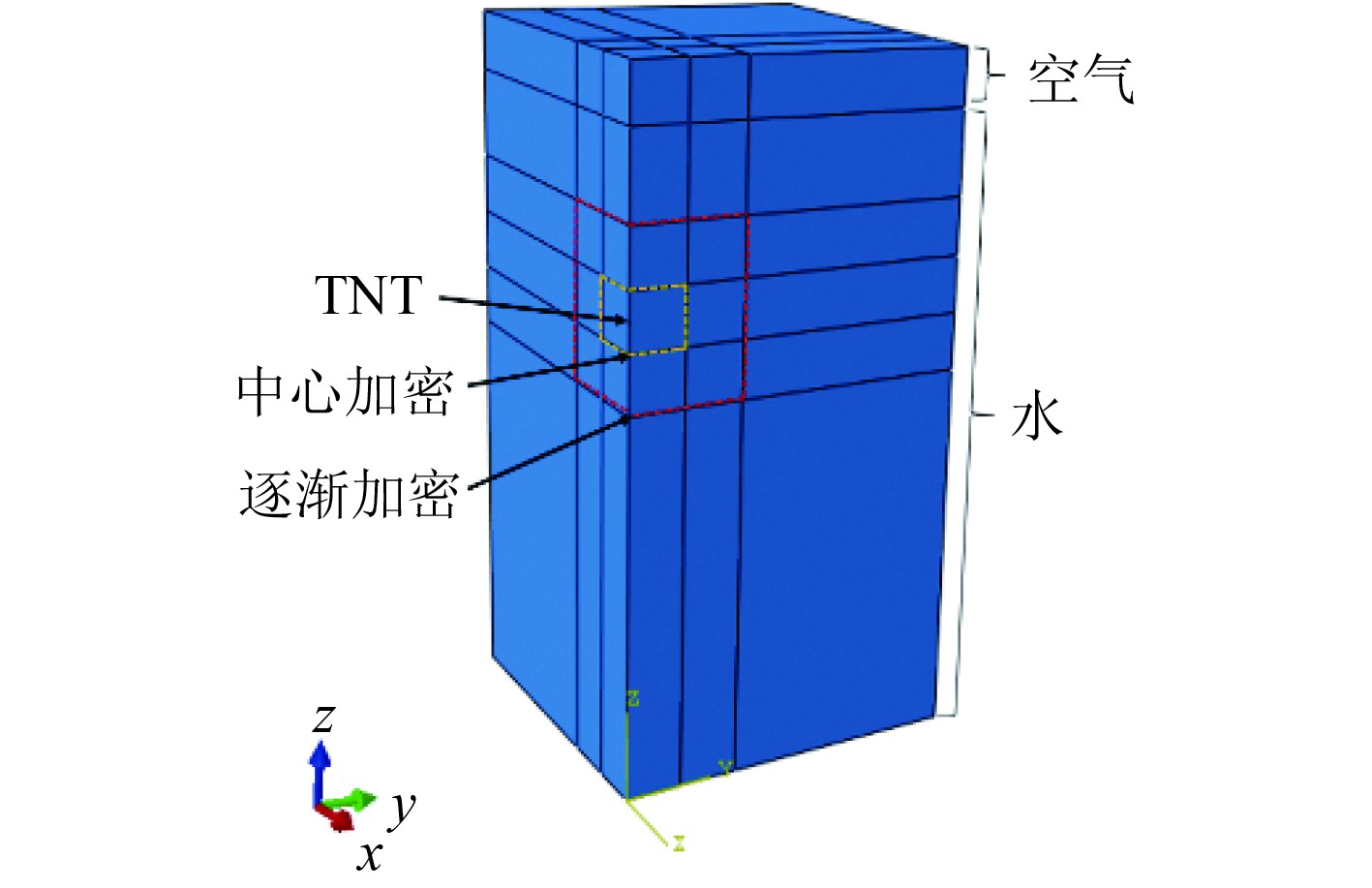
利用CEL分析水下爆炸后气泡的形态演变过程,基于有限元软件建立水下爆炸模型整体的1/4建模,包括空气、水、炸药,模拟自由场环境下气泡的脉动形态,建立的欧拉域尺寸为1.2 m×1.2 m×1.2 m,球形炸药的爆距距离水面0.3 m,炸药量为110 mg,初始气泡半径尺寸为2.5 mm,球形炸药的球心坐标位置为(0, 0, 0.8),如图1所示。模型采用离散场填充方式设置重力场和地应力条件,边界设置流出无反射条件,防止材料自由流出和减少冲击波反射的影响,侧面和底面设置垂向无速度边界,内侧2个对称面设置对称边界。欧拉域设置逐渐加密的单元网格,如图2所示,最小的网格尺寸为2 mm的正六面体[10],最外侧网格为8 mm,欧拉域网格的总数量为
|
图 1 自由场水下爆炸仿真模型正视图 Fig. 1 Front view of the free-field underwater explosion simulation model |
|
图 2 仿真模型3D装配及网格划分示意图 Fig. 2 Schematic diagram of 3D assembly and meshing of the simulation model |
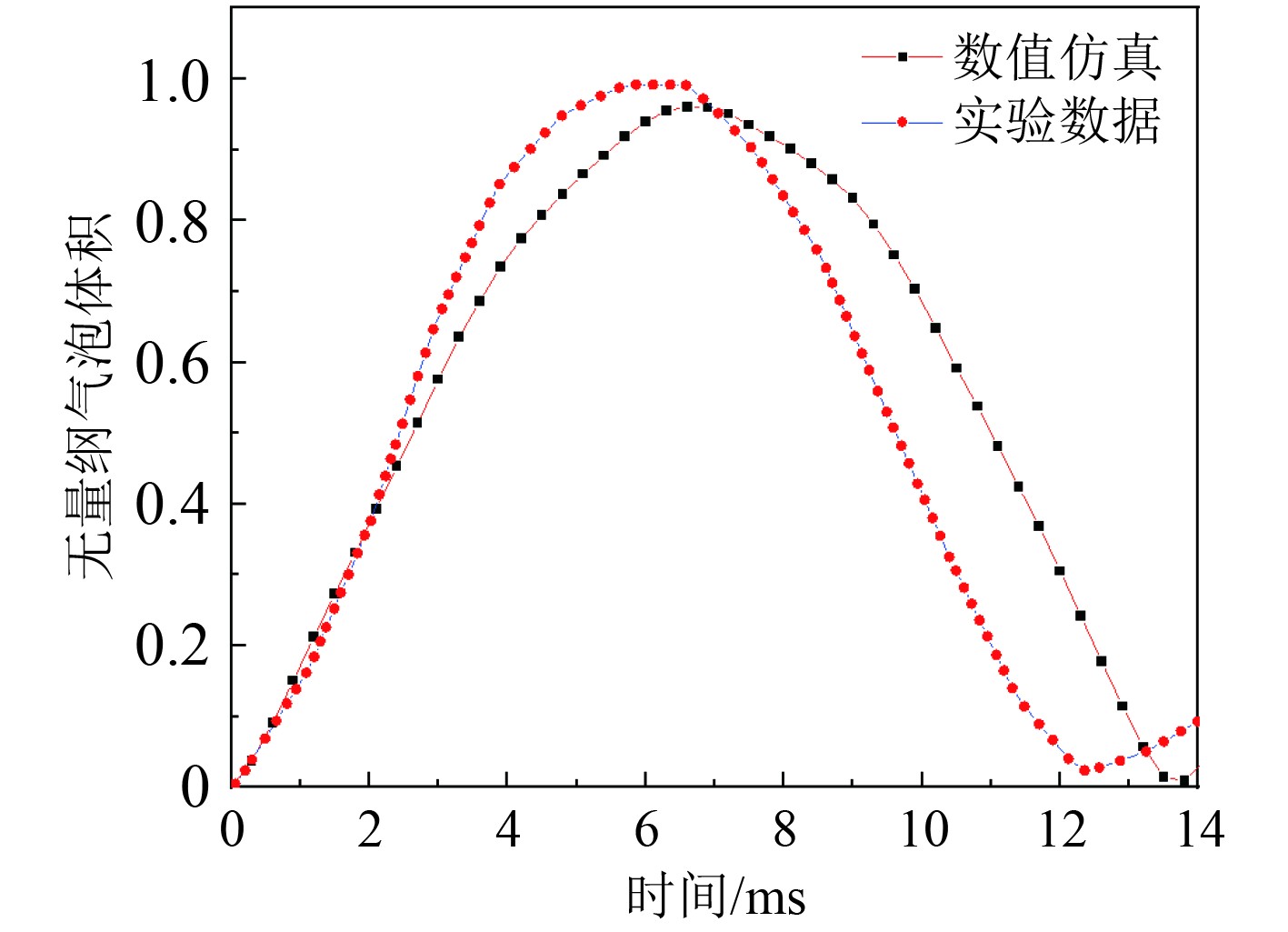
图3为高速摄像机记录的气泡膨胀、收缩、溃灭的脉动过程,图4为基于CEL的气泡脉动仿真结果。实验结果中在t=6.2 ms气泡膨胀到最大气泡半径

|
图 3 气泡脉动实验结果图 Fig. 3 Bubble pulsation test results |

|
图 4 气泡脉动仿真结果图 Fig. 4 Bubble pulsation simulation results |
|
图 5 自由场气泡体积时间历程曲线 Fig. 5 The time history curve of the free-field bubble volume |
基于数值仿真模拟验证理论,建立欧拉域为0.3 m×0.3 m×0.3 m、空气域为0.3 m×0.3 m×0.07 m、水域为0.3 m×0.3 m×0.23 m的数值仿真模型,TNT设置在水下2.6 cm处,距离四周15 cm,气泡最大半径尺寸
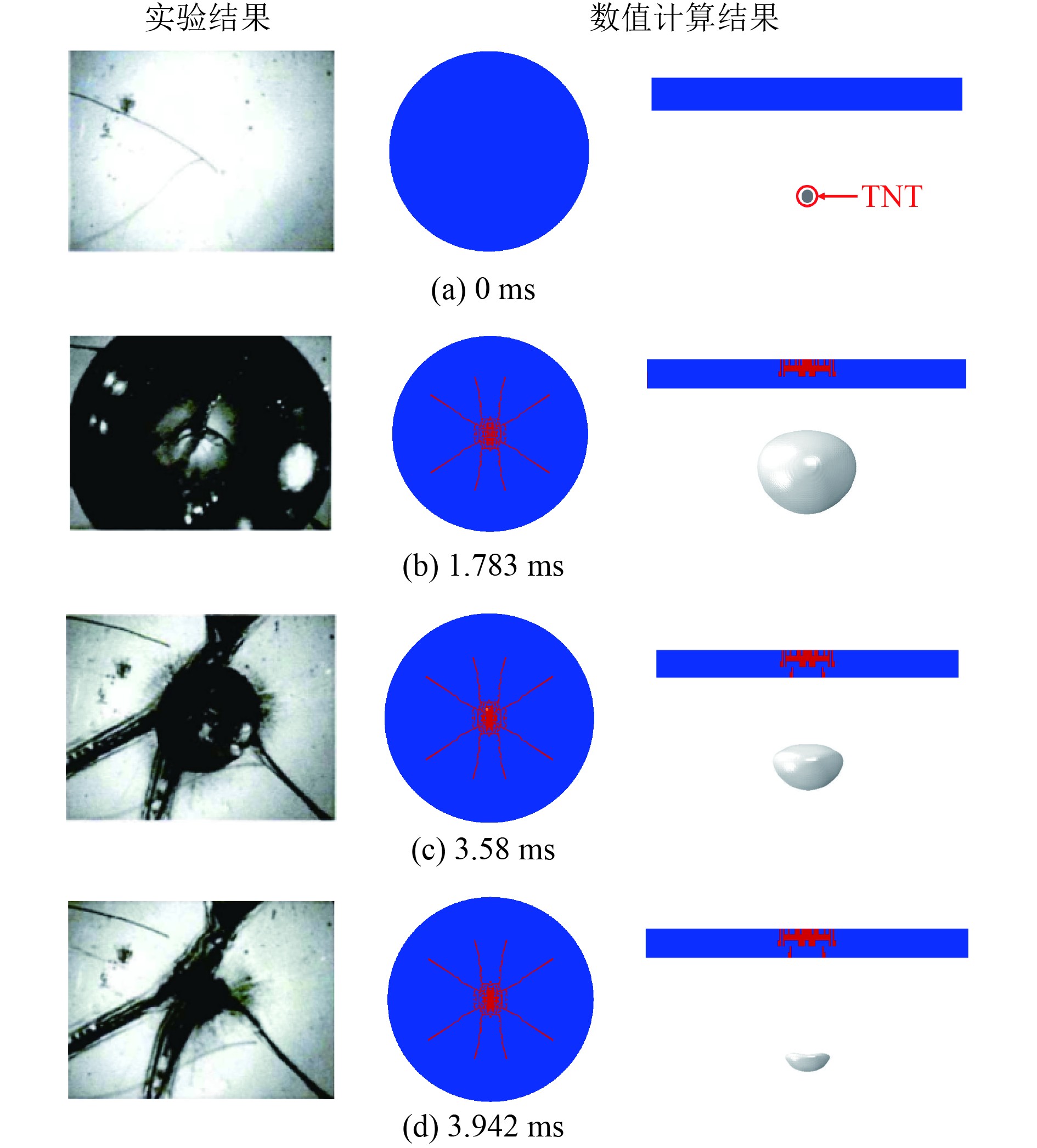
图6为气泡与冰板相互作用的实验结果和仿真结果。左列为实验结果图,中间列为数值模拟俯视图,右列为数值模拟纵剖面图(数值模拟建立的1/4模型均匀对称,故裂纹的产生较规则且对称),展现了气泡膨胀、收缩、溃灭的整个周期过程,t=0.08 ms时的4条裂纹演变成8条裂纹,t=1.783 ms时气泡体积最大,最大半径尺寸为0.0163 m,与实验结果对比误差为9.4%,两者的相似度较好。载荷直接作用于层冰下表面,裂纹首先出现在上表面,因层冰四周完全固定,下表面承受气泡载荷发生位移,层冰承受中拱弯曲力矩,使上边面受拉下表面受压,且冰的抗拉强度小于抗压强度,因此层冰上表面在高压气泡作用下先产生了裂纹损伤;气泡受到冰层影响开始收缩,t=3.58 ms时层冰下表面开始出现了较小的裂纹,层冰位移向反方向移动。以上气泡载荷对层冰的破坏分析为研究不同参数影响下冰层破坏特性奠定了较好的基础。
|
图 6 气泡-层冰相互作用实验结果与仿真结果比较 Fig. 6 Comparison of the experimental results of bubble-ice interaction with the simulation results |
不同参数对气泡与冰结构流固耦合特性影响不同。水下爆炸载荷包括冲击波和气泡载荷。冲击波产生的频率高、峰值压力高、且具有瞬时性,作用时会导致结构的局部变形;气泡脉动载荷具有低频特征,通常对结构的纵向强度产生影响。不同的参数对冰结构特性产生不同的影响。本节主要研究爆炸距离对层冰的动态破坏特性,合理选择初始气泡相对层冰的爆炸距离是有效运用气泡能量的重要因素之一。保证装药量和冰层参数及厚度不变,将冰层简化为半径为5 m、厚度为0.25 m的圆盘,气泡最大等效半径为0.585 m,圆盘边缘刚性固定且进行网格加密划分,如图7(a)所示,冰层网格最小尺寸为0.02 m,单元数量为
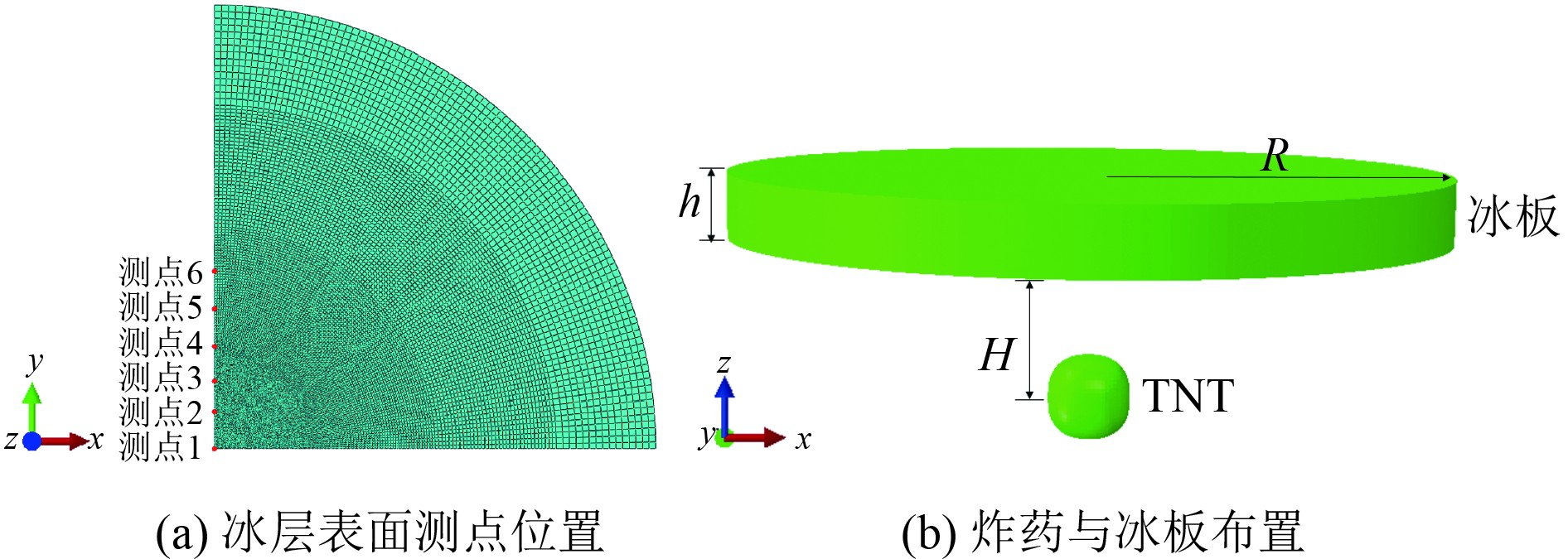
|
图 7 冰层表面测点位置及炸药与冰板布置示意图 Fig. 7 Schematic diagram of the location of the ice surface measurement point and the arrangement of explosives and ice plates |
|
|
表 3 不同的爆炸距离和药量工况参数表 Tab.3 Parameters of different explosion distances and charge conditions |
图8为工况1、工况3、工况5的冰层与炸药相互作用下层冰的破坏位移情况,展现层冰在不同的爆距下垂直方向上的位移云图变化,为了更好地观察裂纹,将冰板倾斜30°角进行观察。
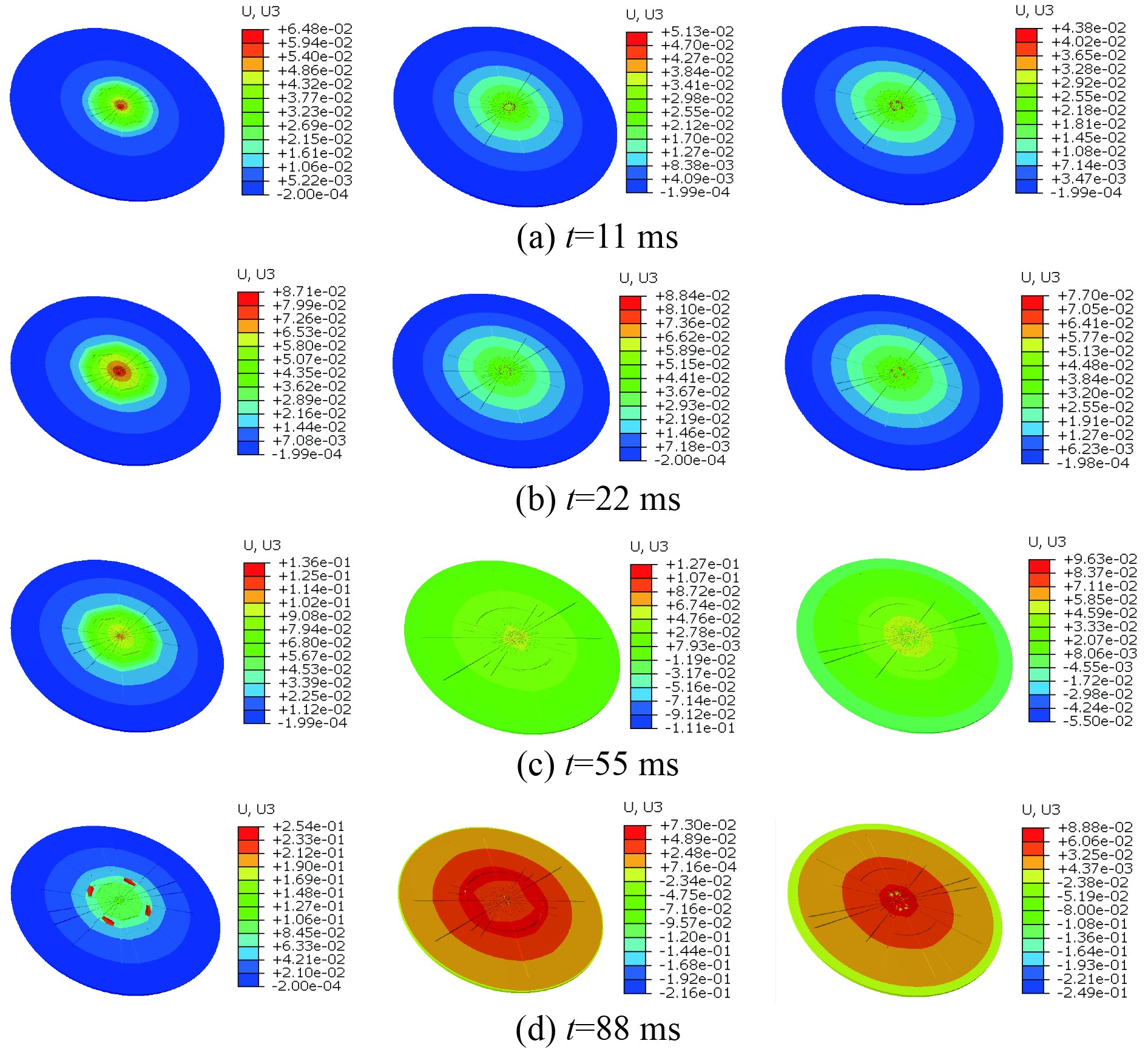
|
图 8 不同爆距下冰层的破坏位移 Fig. 8 Failure displacement of ice at different blast distances |
冰的抗压强度远远大于抗拉强度,中心上凸使背爆面出现径向裂纹。图8(a)~图8(b)冰层在冲击波载荷和气泡载荷作用初期,层冰中心出现小范围的挤压破坏,工况1垂向位移最大且出现了环向裂纹,工况3、工况5并没有产生,爆距增加使产生裂纹的时间延后;55 ms时气泡在气压作用下收缩,层冰受损区域在气泡的吸附作用下进一步发生断裂,3种工况的背爆面都出现了环向裂纹,工况3和工况5比较中,爆距增大使得冲击波载荷影响面积增大,环向裂纹离中心的半径也增大,但垂向位移变化较小。
爆距增加气泡膨胀体积越来越接近理论值,无量纲参数接近于1时气泡膨胀、收缩、溃灭的过程是完整的,如图9所示。对比于图8爆距增加环向裂纹的产生时间也随之推迟。工况3的测点位移如图10(b),因气泡完整收缩使层冰垂向位移向负方向移动,测点5和测点6距离冰板中心较远所受影响不明显,测点2、测点3、测点4位移较大,因此测点之间产生交点,当无量纲爆距
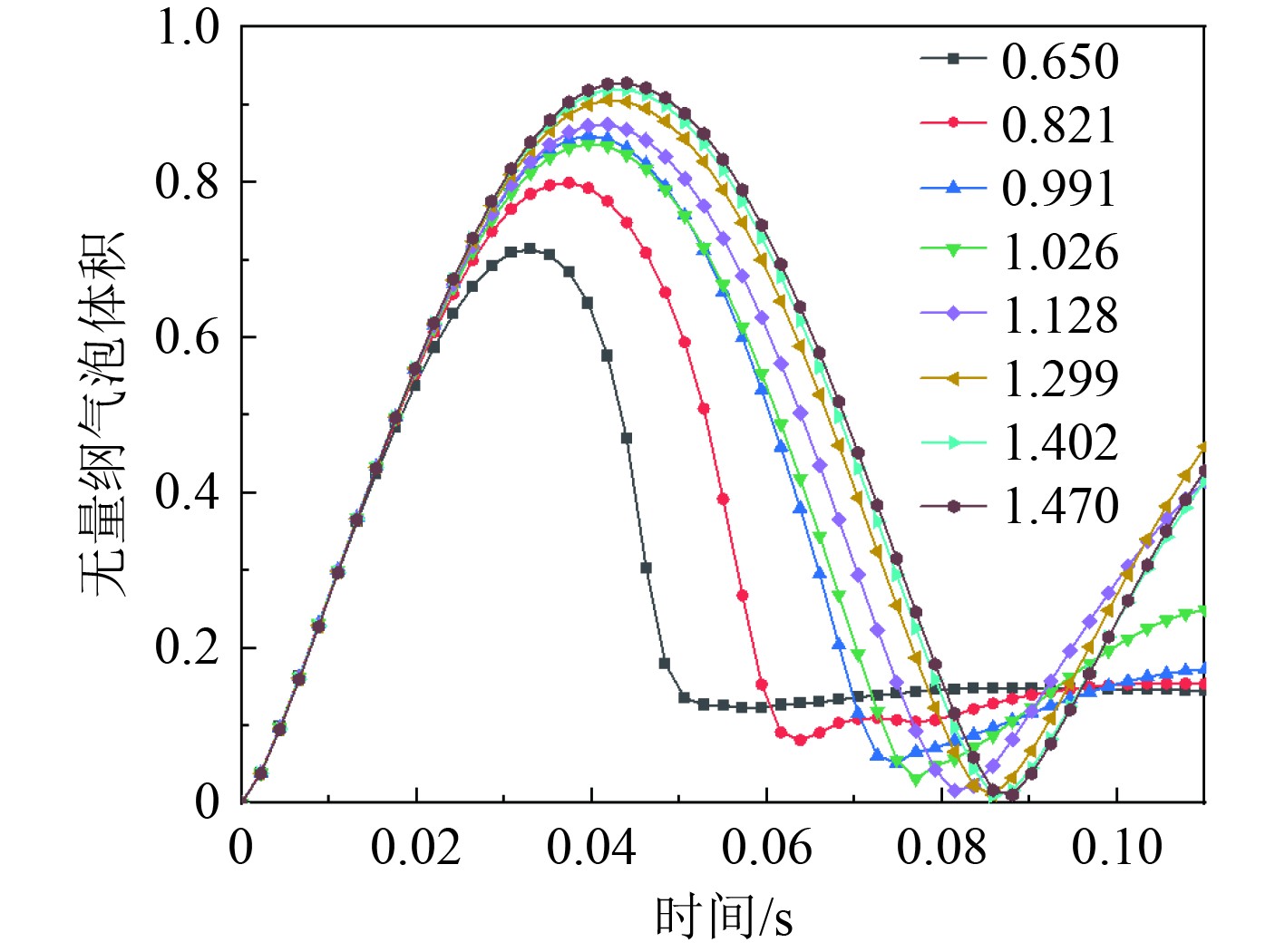
|
图 9 不同爆距下无量纲气泡体积变化 Fig. 9 Variation of dimensionless bubble volume at different burst distances |
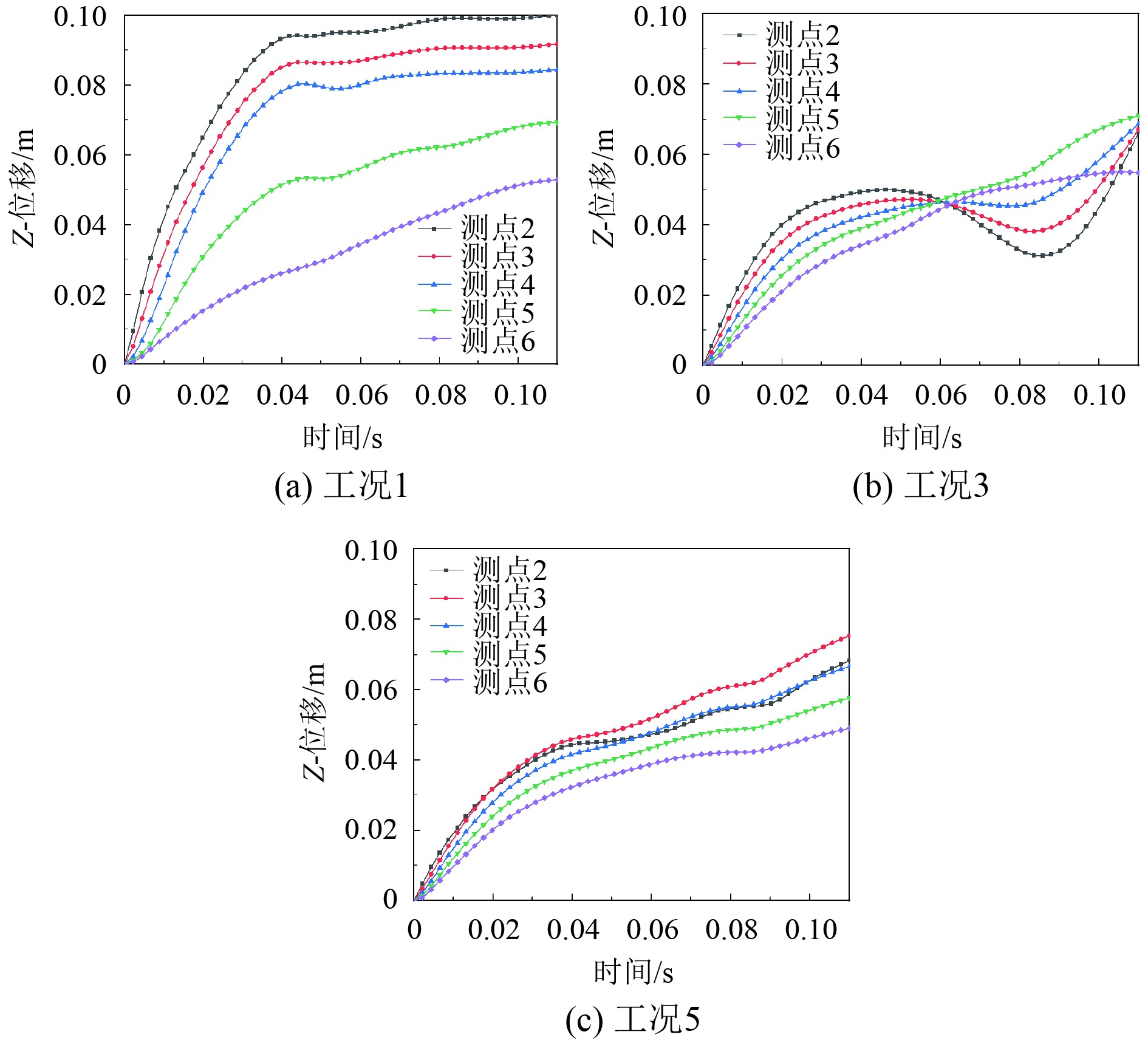
|
图 10 冰层测点的时间-位移曲线 Fig. 10 Time-displacement curves of ice measurement points |
本节主要研究装药量对冰层产生的破坏影响。气泡最大半径
图11为不同炸药量产生的气泡最大半径
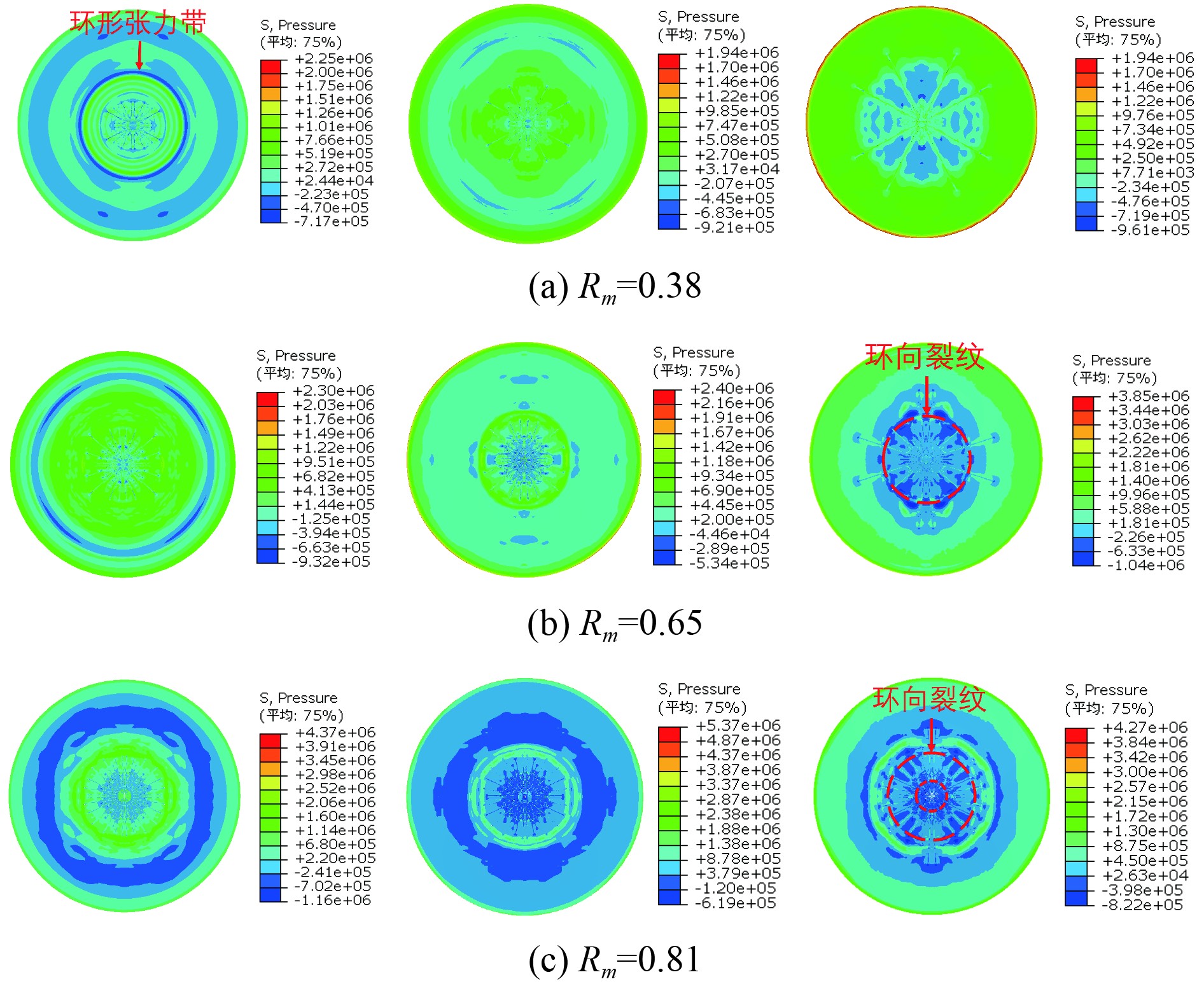
|
图 11 不同装药量下冰层的破坏 Fig. 11 Destruction of ice at different charges |
本节研究在装药量和爆距保持不变的情况下,通过改变冰层厚度观察裂纹以及破坏情况。气泡最大半径取
| $ \lambda = \frac{T}{{{R_m}}}。$ |
式中:
图12为3种典型工况结果图,
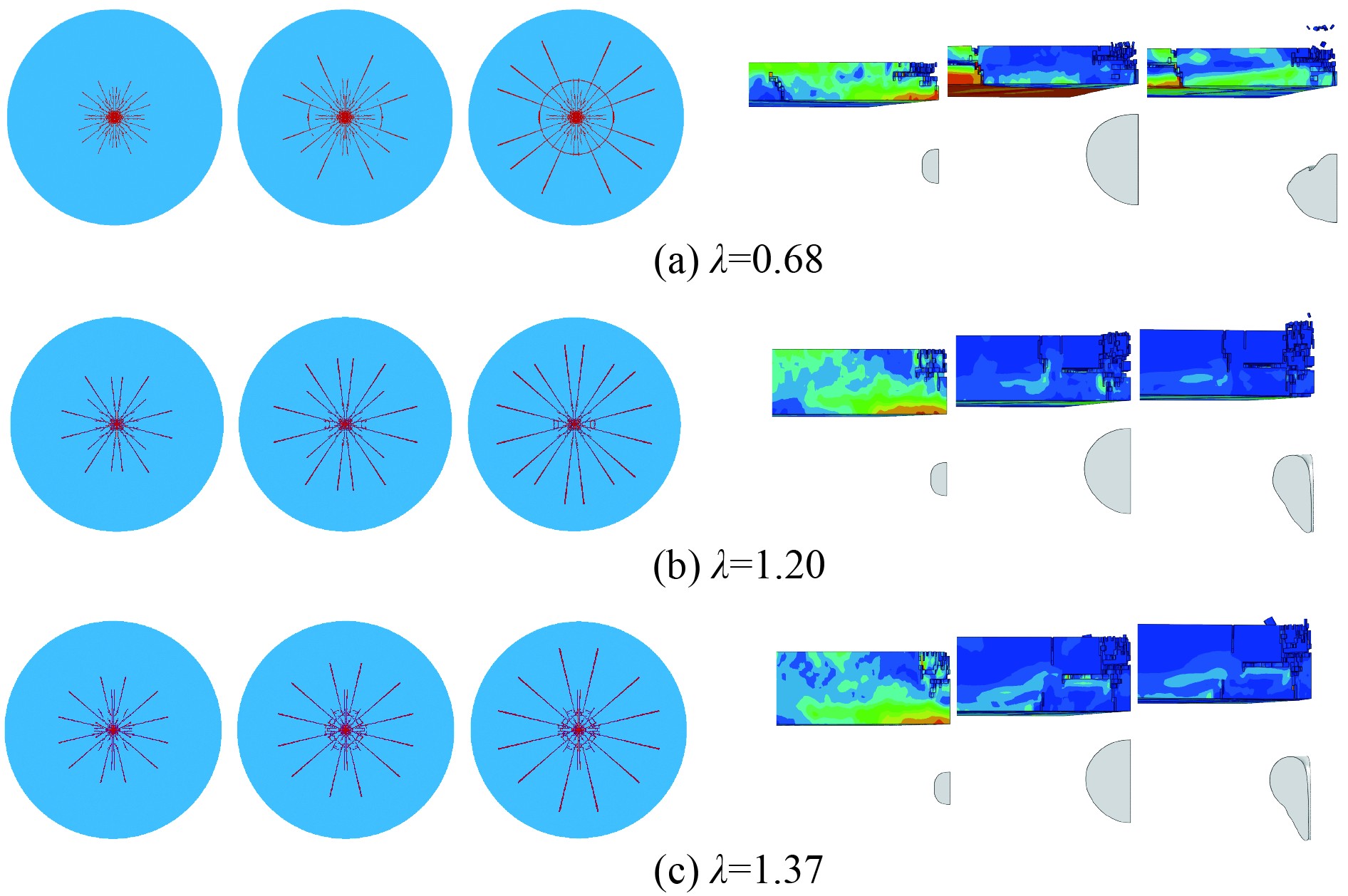
|
图 12 不同冰层厚度下冰层的破坏 Fig. 12 Ice destruction at different ice thicknesses |
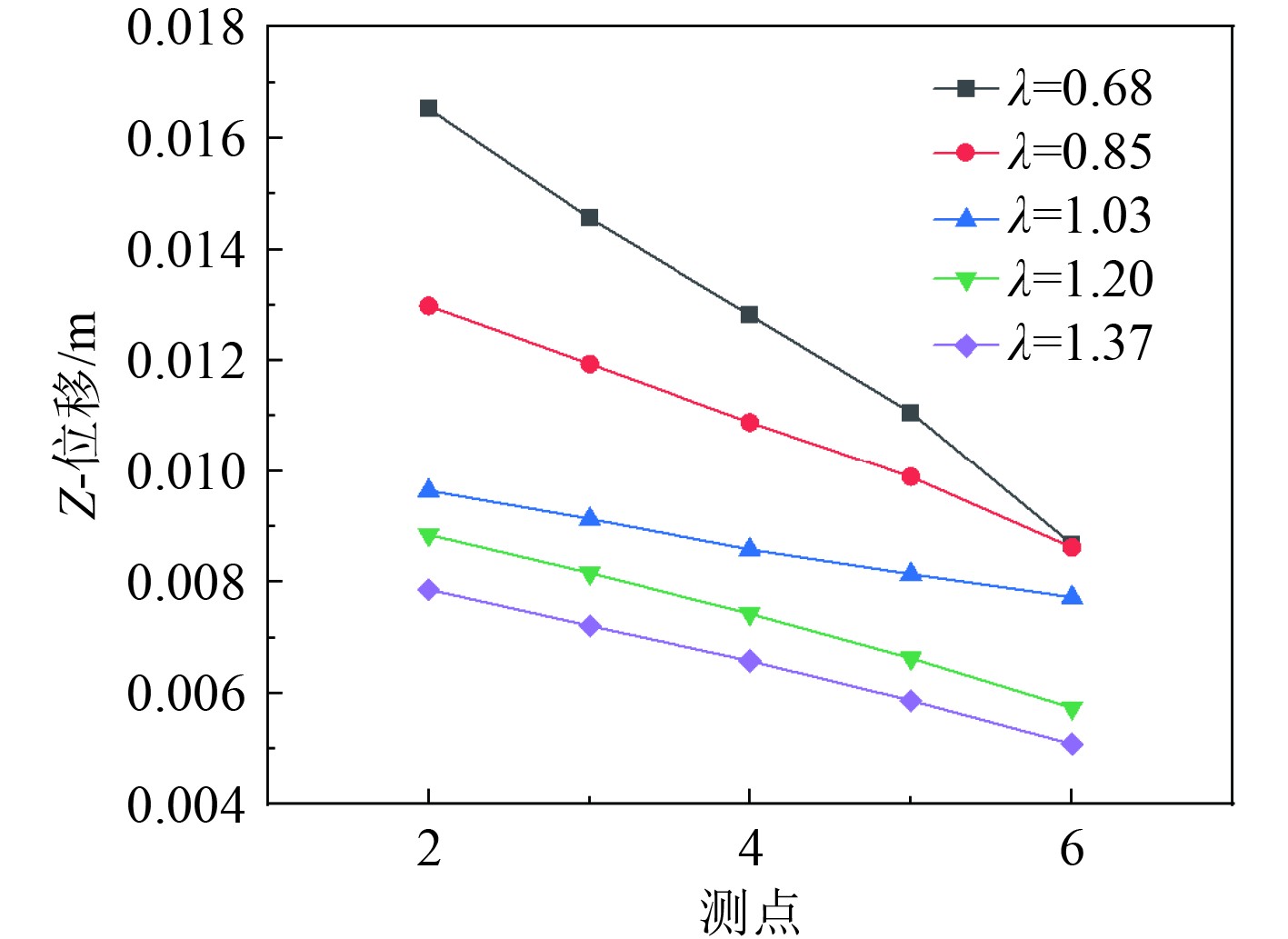
|
图 13 不同冰层厚度中测点的位移变化 Fig. 13 Displacement changes of measurement points in different ice thicknesses |
本文通过CEL法研究水下爆炸冲击波和气泡载荷对冰层的破坏特性,通过十字交叉法改变爆炸距离、装药量(气泡半径尺寸)、冰层厚度3个方面,使爆炸载荷最大化作用在冰层结构。研究发现:
1)CEL方法结算结果与模型试验相互间有效验证,表明CEL法在解决水下爆炸、气泡脉冲、冰层破坏等问题方面的可行性与准确性。本文研究的层冰破坏取决于气泡与层冰之间的爆距大小、装药量及冰层厚度,其中爆距是决定层冰裂纹产生的关键因素。
2)水下爆炸载荷包括冲击波和气泡载荷,冰的背爆面先产生了挤压破坏的径向裂纹,迎爆面产生环向裂纹,爆距的增大使得冲击波的影响面积增大,环向裂纹半径增大,但破坏程度减小,爆距的增加出现环向裂纹的时间延后。
3)改变装药量时,装药量较小在膨胀与坍塌时对层冰产生局部影响,冰的背爆面无环向裂纹产生;装药量较大产生的影响区域较宽,作用时间长,产生裂纹更多且有环向裂纹产生,应选择合适的药量使气泡破冰的效率最大化。当冰厚无量纲参数
| [1] |
郭文琦. 近场水下爆炸气泡与多形状浮冰相互作用实验研究[D]. 威海: 山东交通学院, 2024.
|
| [2] |
王思强. 碎冰和层冰下航行体出水破冰动力学特性试验研究[D]. 哈尔滨: 哈尔滨工程大学, 2023.
|
| [3] |
王莹, 秦业志, 王志凯, 等. 不同类型炸药水下爆炸时冰层损伤特性研究[J]. 振动与冲击, 2022, 41(9): 189-198. |
| [4] |
曲艳东, 刘万里, 翟诚, 等. 水下爆破破冰爆炸冲击波传播规律数值分析[J]. 爆破, 2017, 34(2): 100-104. DOI:10.3963/j.issn.1001-487X.2017.02.019 |
| [5] |
PU C, MAN A Z, SHI PING W, et al. Ice breaking by a collapsing bubble[J]. Journal of Fluid Mechanics, 2018, 841(3): 287-309. |
| [6] |
YING W , XIONG L Y , YE Z Q. Investigation on influence factors about damage characteristics of ice sheet subjected to explosion loads: Underwater explosion and air contact explosion[J]. Ocean Engineering, 2022, 260.
|
| [7] |
张忠和, 梁向前, 徐溦, 等. 装药位置对爆破破冰效果影响的数值分析[J]. 爆破, 2015, 32(4): 118-122+127. |
| [8] |
吴瑞波, 郝明盛, 武彩岗, 等. 水中爆破破冰参数的优化实验[J]. 工程爆破, 2014, 20(6): 25-28. |
| [9] |
SIMULIA D. Abaqus version 2016 documentation[Z]. USA: Dassault Systems Simulia Corp, 2012.
|
| [10] |
孙成. 近场水下爆炸载荷作用下结构防护数值模拟研究[D]. 哈尔滨: 哈尔滨理工大学, 2023.
|
| [11] |
ANGHILERI M , CASTELLETTI L M L , INVERNIZZI F, et al. A survey of numerical models for hail impact analysis using explicit finite element codes[J]. International Journal of Impact Engineering, 2005, 31(8): 929−944.
|
| [12] |
ZAMANKHAN P. Simulations of collision of ice particles[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 15(6): 1538−1552.
|
| [13] |
WANG Y , QIN Y , YAO X. A combined experimental and numerical investigation on damage characteristics of ice sheet subjected to underwater explosion load[J]. Applied Ocean Research, 2020, 103(4): 102347.
|
| [14] |
阚兴玉. 水中高压气泡与弹/脆性边界流固耦合特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2022.
|
 2025, Vol. 47
2025, Vol. 47
