2. 直流输电装备与海底电缆安全运行联合实验室,广东 广州 510000;
3. 集美大学 轮机工程学院,福建 厦门 361021
2. Joint Laboratory of HVDC Equipment and Submarine Cable Safety Operation, Guangzhou510000, China;
3. College of Marine Engineering, Jimei University, Xiamen 361021, China
船舶在高速航行中,由于波浪载荷的冲击,导致其耐波性不佳,严重时无法保证安装设备的正常工作[1]。为了提高船舶的耐波性,常规方法主要集中在增加船舶附体方面,通过提高船体的纵摇、横摇以及垂荡阻尼系数,达到降低运动幅值的效果。本文借助于汽车悬架系统理念,设计一款弹簧或者液压支撑形式的动态悬架系统,并将传统船体结构拆分为上下2个部分,其中上船体作为各种设备、人员的搭载平台,下船体与水面接触随浪运动,上下船体间通过悬架系统进行连接。该悬架系统能够吸收和分散来自于下船体的能量,从而实现下船体随浪剧烈运动的情况下大幅度降低上船体的运动幅值,减少各种设备和人员受到的振动和冲击。
对于类似的提高船舶耐波性的措施,国内外开展了一系列研究。其中,美国海军高级研发中心在2005 年研发了一种波浪自适应船舶[2 − 3],该船舶主体与浮筒之间设置了由弹簧及阻尼器组成的被动式悬架系统,使浮筒可相对于船舶主体进行独立运动,并通过系列试验获得了最优弹簧种类,配合油液阻尼器,使整船在遭遇波浪冲击时能获得良好缓冲。澳大利亚 Nauti-Craft 公司开发了一种悬架技术[4],主要采用被动式液压悬架系统,这种由气缸、连接杆及滑块组成的机构能够有效降低波浪的冲击,可将10g的波浪冲击力降低到约1.5g。日本东京大学的Jialin Han等[5 − 6],通过试验方法对一款配备弹簧悬架系统的主动式悬架系统进行研究,通过强制振动试验,验证了其由电机控制垂向运动的可行性。
而国内也开展了类似的研究工作,其中王默等[7]提出一种新型主动式液压互联悬架系统。该悬架系统充分利用互联的液压回路,削弱波浪对救助船舶本体造成的冲击和振动,并能主动调节船体姿态,以提高救助船舶对波浪的适应能力。该研究基于AMESIM平台,搭建液压悬架系统的动力学模型,并对模型进行联合仿真,分析不同海况下悬架的动态特性。研究结果表明,与传统被动式弹簧阻尼悬架相比,主动式液压互联悬架系统的波浪自适应能力较好,能提高救助船舶在极端海况下的安全性。白雪松[8]通过搭建动力学模型,在ADAMS软件中多次仿真发现横浪冲击及大幅垂荡2种工况对减振器的安全工作影响不大,且刚度系数及阻尼系数取值较小,对缓冲吸振的效果有更大帮助。
对于悬架系统的方法研究,国内外研究学者多采用ADAMS对悬架系统进行仿真分析和优化。彭婧等[9]基于ADAMS设计了液压支架刚柔耦合模型,对其运动过程进行仿真分析,且得到的运动学仿真结果满足预期,可作为液压支架及相关设备设计与改进的参考。刘成武等 [10 − 11]利用ADAMS对汽车悬架系统进行了仿真优化,并通过进一步进行悬架优化设计,使得汽车的操纵稳定性得到提高。陈华等[12]基于ADAMS与Ansys环境建立了光学检测平台刚柔耦合动力学仿真模型,通过该模型进行了动力学仿真求解,计算出两者结构薄弱位置的应变值,校核了负载平台和导轨刚度,并通过实物实验验证了仿真分析结果。本文利用ADAMS在动力学仿真方面的计算方法,建立悬架系统模型并添加约束与工况,从液压缸和弹簧构件形式对悬架系统减震效率的影响入手,实现最佳悬架系统的设计优化,并拓展至双体船构型实现波浪同步和异步状态下的运动模拟。
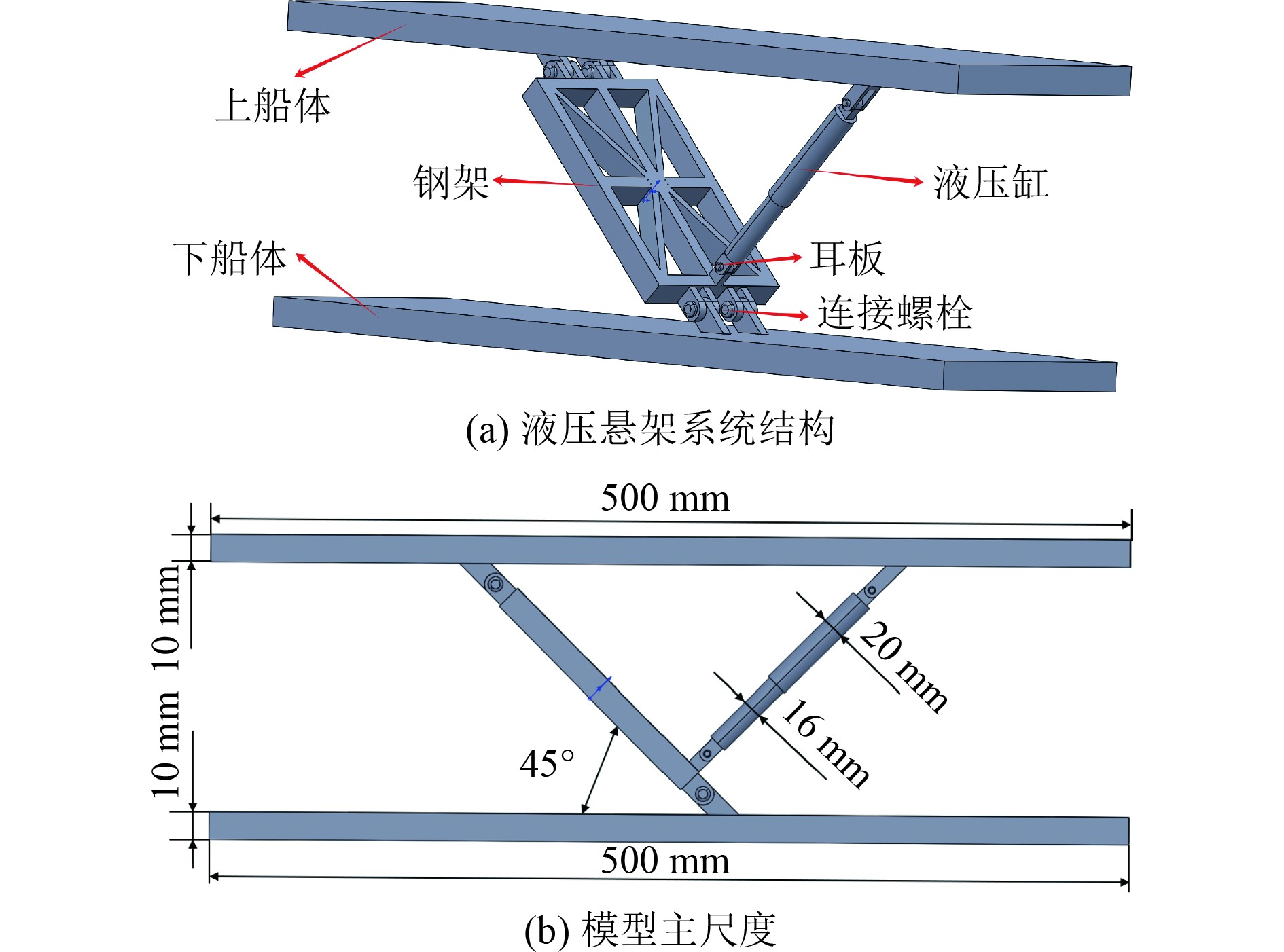
1 模型及数值理论 1.1 模型简介本文首先建立了悬架系统结构,并通过2组平板结构模拟上下船体,使用液压或弹簧等支撑形式进行减振连接,如图1所示。该单船体构型主要包含船架、上船体、下船体、液压筒式减振器、连接螺栓、耳板等部分,其中构件采用钢材,密度为7.8 g/cm3,杨氏模量为2.07×105 N/mm2。液压缸通过其两端的耳片,分别和上船体与船架上的耳片通过连接螺栓连接在一起,船架再通过耳片和连接螺栓与上船体和下船体连接在一起,形成一个简易连接。主尺度如表1所示。
|
图 1 液压悬架系统计算模型 Fig. 1 Hydraulic suspension system calculation model |
|
|
表 1 计算模型参数 Tab.1 Calculation model parameters |
本文所开展的研究类似于传统机械运动,由非自由质点系表示。将非自由质点系的动力学普遍方程用广义坐标表示,即拉格朗日方程。在拉格朗日方程的基础上用拉格朗日乘子法处理带多余自由度的完整约束方程(位置约束)和非完整约束方程(运动约束),从而得到一般机械系统的运动微分方程[13–14]如下:
| $ \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial\dot{q}_i}\right)-\frac{\partial L}{\partial q_i}+p\Phi(q,t)+\mu\theta\left(q,\dot{q},t\right)=Q。$ | (1) |
式中:
令
| $ \left\{ \begin{aligned} &F(q,u,\dot u,\lambda ,t) = 0,\\ &\Phi (q,t) = 0 ,\\ &G(u,\dot q) = \mu - \dot q = 0 。\\ \end{aligned} \right. $ | (2) |
式中:
定义系统的状态向量
| $ {{g}}({{y}},{{\dot y}},t) = 0 。$ | (3) |
模型对上下船体的纵摇运动通过驱动
| $ {\text{STEP}}(x,{x_0},{h_0},{x_1},{h_1}) 。$ | (4) |
式中:
使用
| $ {{h}} = \sin ({\text{π}} \cdot t) 。$ | (5) |
减震效率
| $ \eta=\frac{k_1-k_2}{k_1}。$ | (6) |
式中:
为模拟船舶在海面上航行受到的波浪作用,本文在下船体重心处添加点驱动,用于模拟船舶受波浪力作用而产生的六自由度运动,驱动力的纵摇运动角度为15°,升沉运动幅值为40 mm,减振结构采用活塞式液压缸,主要参数如表2所示。为了探究垂向和纵摇运动的减振特性,释放六自由度运动中垂向和纵摇2个自由度,在此基础上,分别在上船体和下船体的首尾处设立4个测量点,并分别检测升沉、加速度以及纵摇变化,同时测量液压杆处的位移以及液压杆的轴向力。
|
|
表 2 弹簧液压系统参数 Tab.2 Parameters of spring hydraulic system |
针对悬架系统的支撑结构形式,为了明确液压支撑结构和弹簧支撑结构对减振效果的作用效果,首先对单液压悬架系统进行计算分析,在阻尼系数为40 N·s/m时对不同液压支撑力的各运动幅值及上下船体间通过悬架系统的减振效率进行计算。
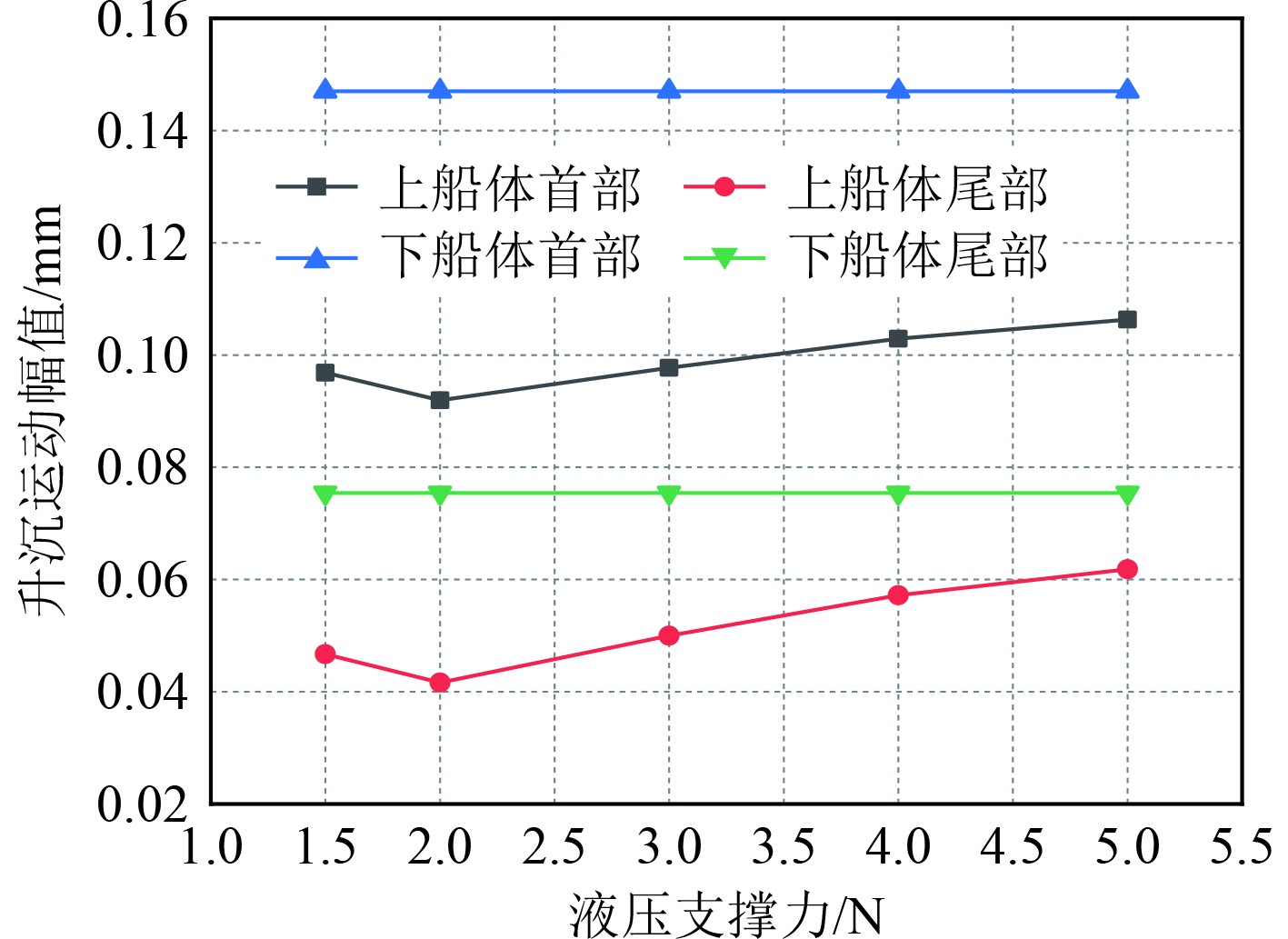
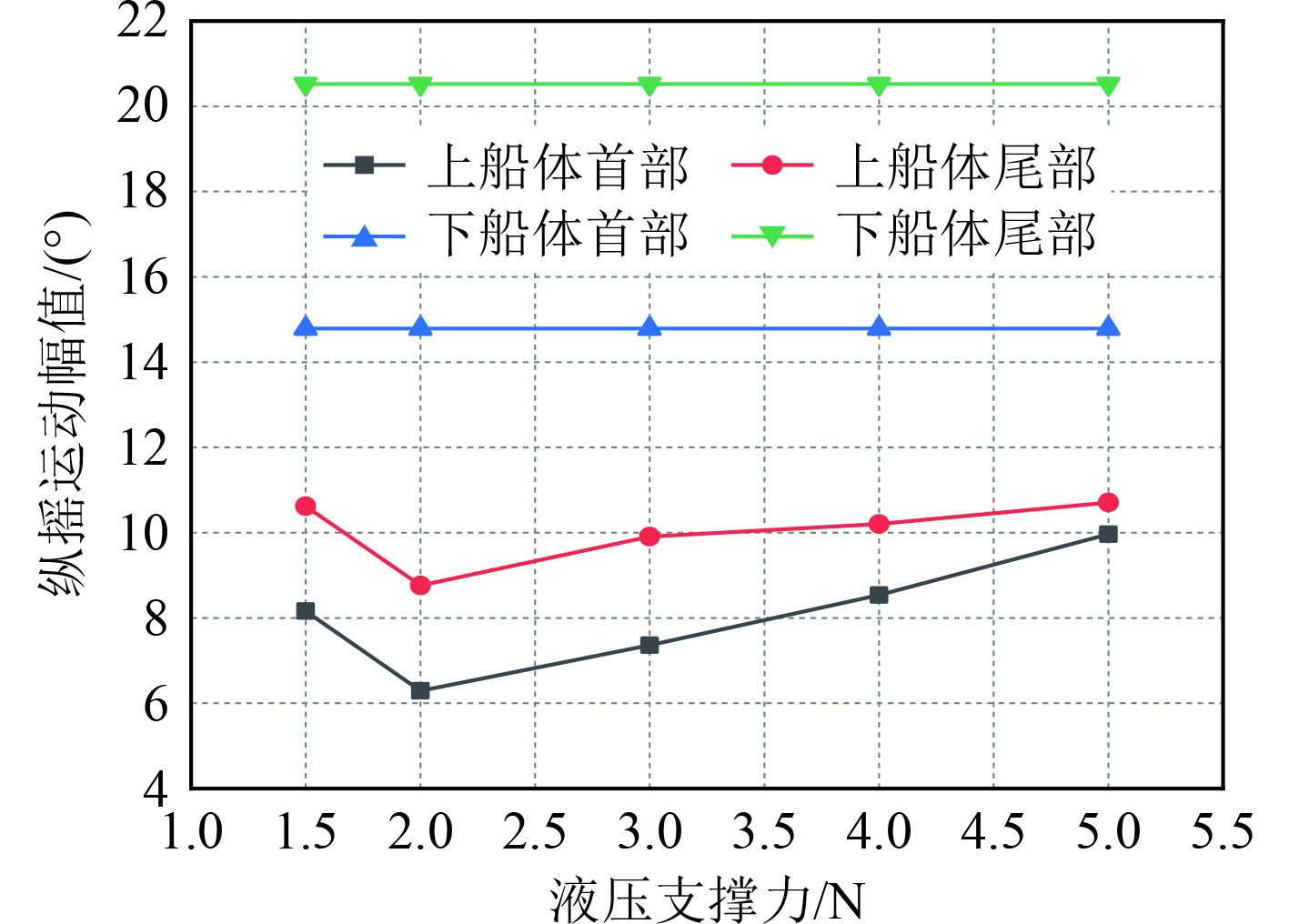
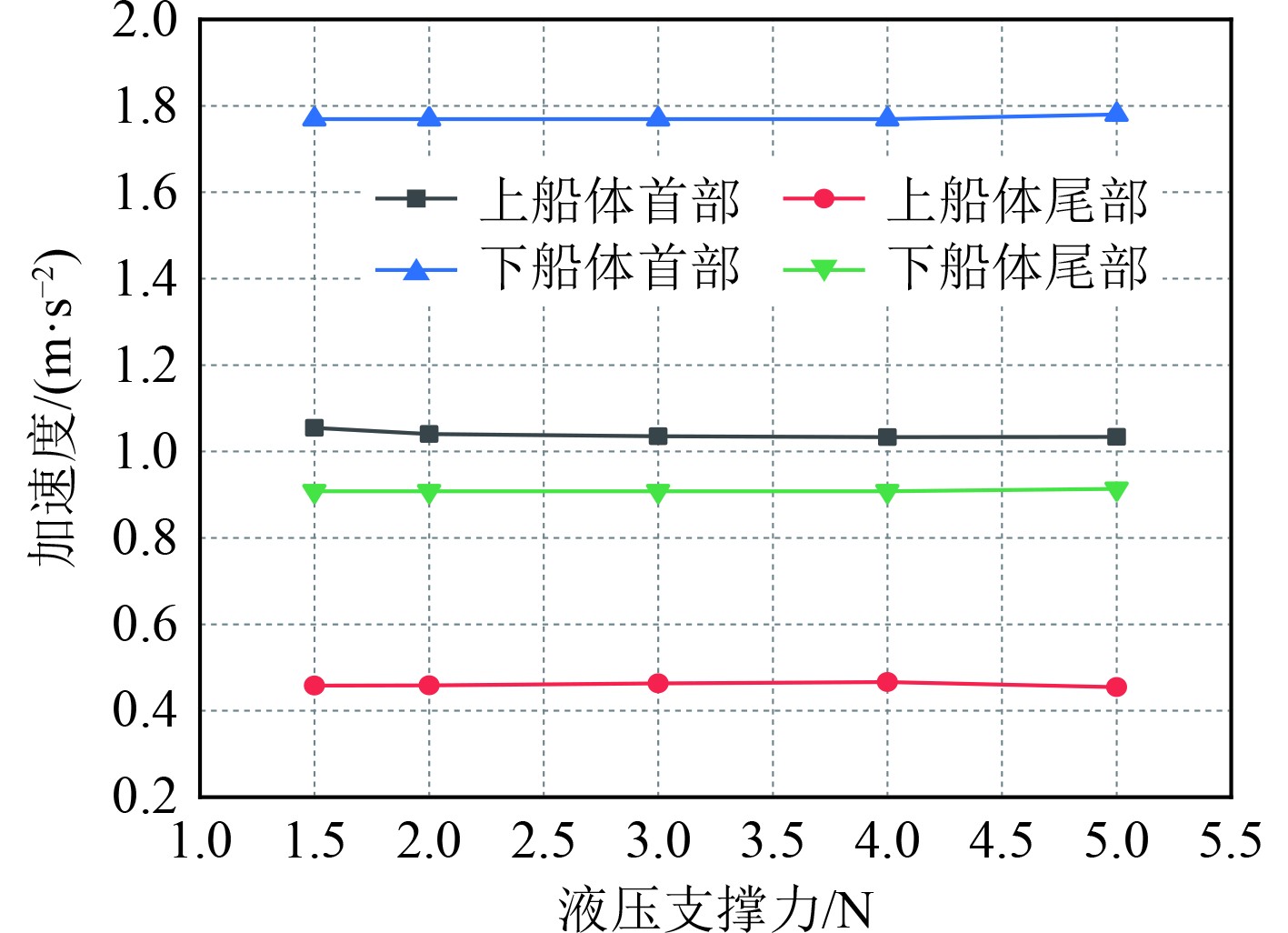
由图2~图4可知,下船体在强制驱动力作用下,不同液压支撑力的各运动幅值基本一致,无论是在船体首部还是在船体尾部;对于上船体来说,无论是船体首部还是尾部,升沉和纵摇运动幅值在液压支撑力为2 N时出现谷值,且随着液压支撑力的增大运动幅值有加大趋势,但加速度响应在各不同液压支撑力下变化不大;对于上下船体首尾部的情况来看,升沉和加速度在船首部的运动幅值要大于船尾部,而纵摇运动相反。这主要原因为液压支撑力的作用点在上船体首部,下船体的运动力可以直接传递到上船体首部,导致上船体首部的升沉和加速度运动相较于上船体尾部纵摇更为显著,可见单液压支撑结构虽能有效减弱来自波浪的冲击,但对于前后支撑力的平衡仍有改进的空间。
|
图 2 不同液压支撑力时船体各部分升沉运动幅值 Fig. 2 Heave motion amplitude of each part of hull under different hydraulic support forces |
|
图 3 不同液压支撑力时船体各部分纵摇运动幅值 Fig. 3 Pitch motion amplitude of each part of hull under different hydraulic support forces |
|
图 4 不同液压支撑力时船体各部分加速度响应 Fig. 4 The acceleration response of each part of the hull under different hydraulic support forces |
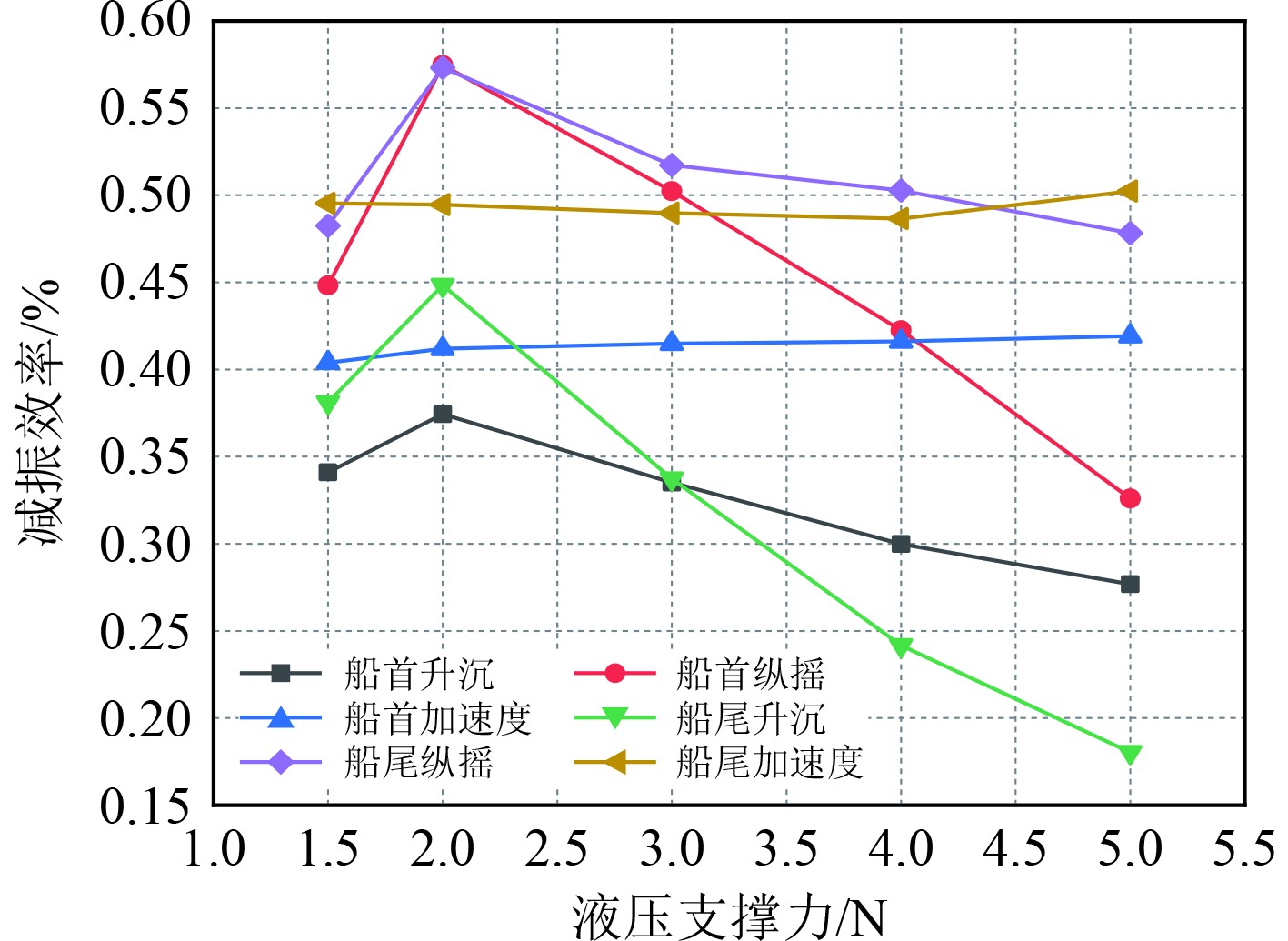
由图5可知,经过悬架系统减振,各运动幅值均有不同程度的降低。其中加速度运动幅值在各支撑力时减振效率变化不大,首部减振效率在42%左右,尾部减振效率在50%左右。升沉和纵摇运动减振效率变化规律相似,均在支撑力为2 N时达到最大,随后有不同程度的降低,其中首部升沉和纵摇的最大减振效率均为57%左右,而尾部升沉最大减振效率为45%左右,纵摇为36%左右。
|
图 5 不同液压支撑力时各运动减振效率 Fig. 5 Vibration reduction efficiency of each motion under different hydraulic support forces |
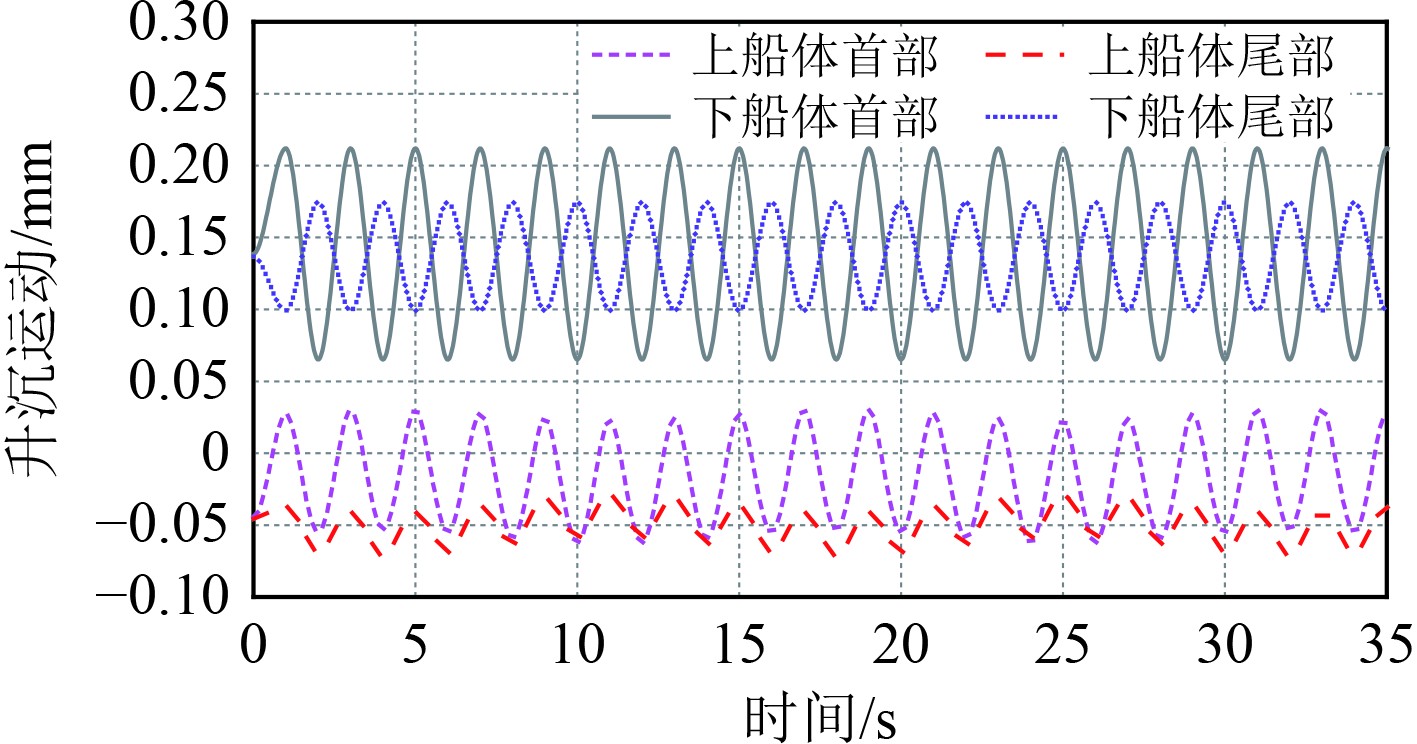
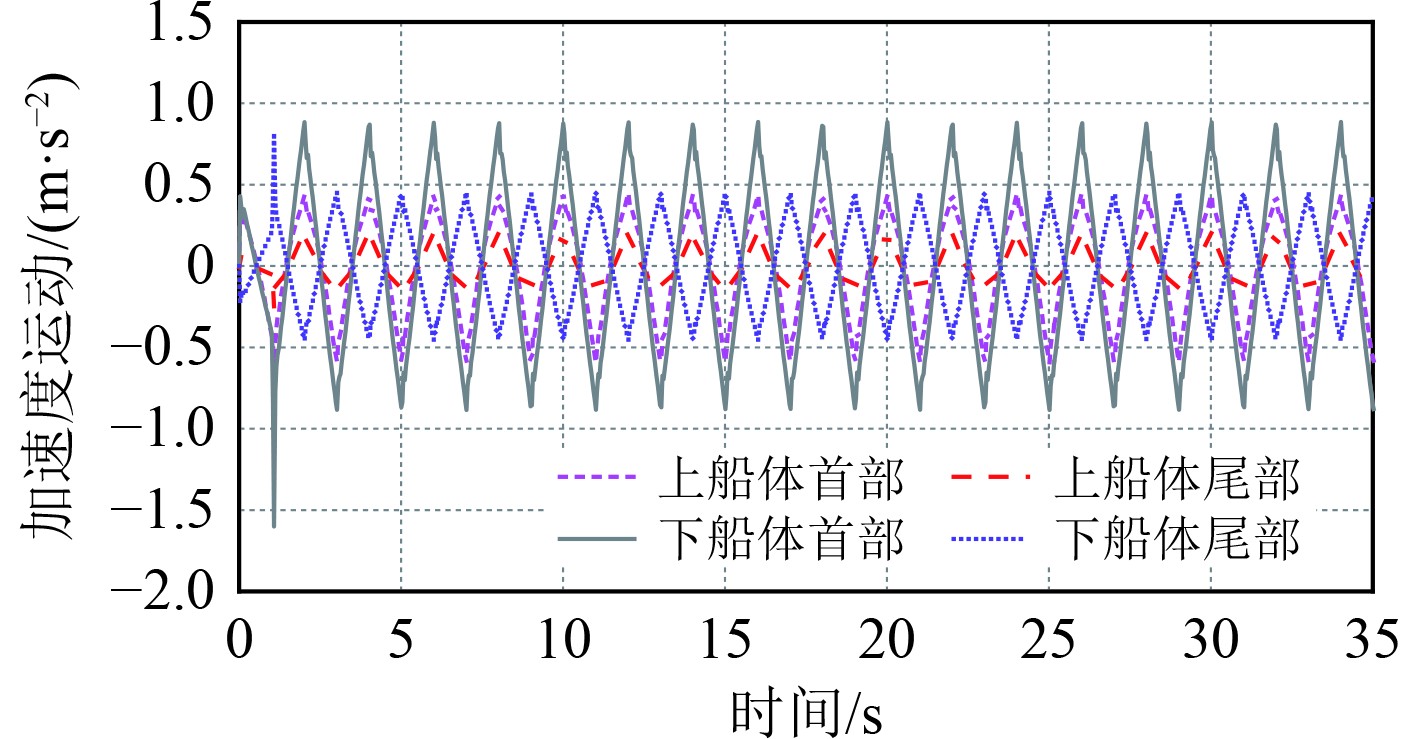
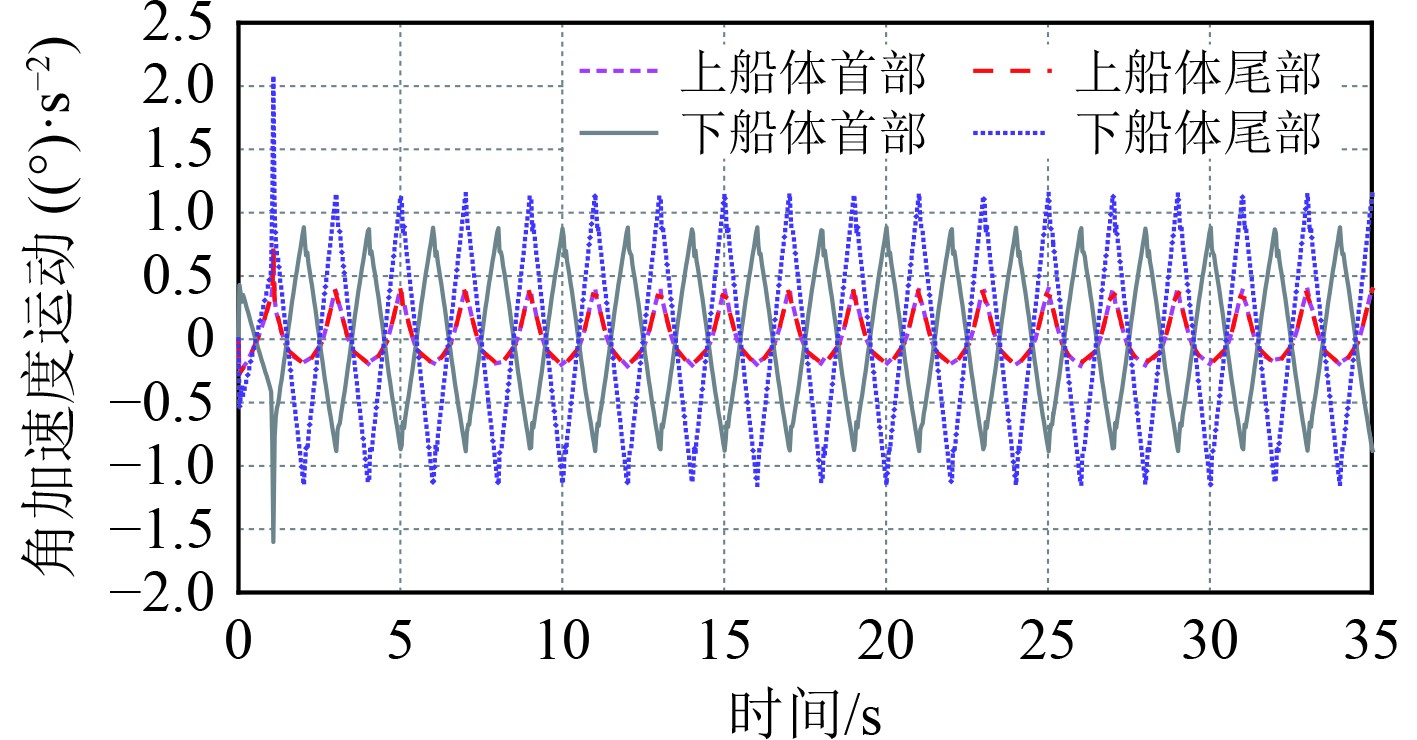
由图6~图8可知,上船体经过单支撑液压系统减振后的规律与图2~图4所得到的结果基本一致,且无论是升沉还是纵摇等运动参数,各个计算值在强制驱动力作用下均呈现规律性的正弦震荡曲线。由图6可知,下船体船首处的升沉运动与船尾刚好相差一个相位,此时上船体的首尾部升沉运动与下船体船尾在同一个相位内,这种特性与加速度历时曲线相似(见图7)。在角加速度的历时曲线中,虽下船体的首尾处仍相差一个相位,但上船体的运动与下船体的船尾在同一个相位内。
|
图 6 单液压支升沉运动历时曲线 Fig. 6 Duration curve of lift movement of single hydraulic support |
|
图 7 单液压支撑加速度历时曲线 Fig. 7 Acceleration duration curve of single hydraulic support |
|
图 8 单液压支撑角加速度历时曲线 Fig. 8 Single hydraulic support angular acceleration duration curve |
对于单液压支撑形式,实际情况下船舶采用单个支撑点很难在复杂海况下保持良好的稳定性,因此这里在单液压支撑的基础上,在船尾增加了一个弹簧支撑,用于模拟液压和弹簧双支撑悬架系统的减振特性。其三维模型如图9所示。这里液压支撑力设置为减振效率最优点,为2 N,其他参数与表2保持一致。弹簧的特性主要与刚度系数和阻尼系数有关,这里将阻尼系数设置为变量,其他参数设置为定量,与液压支撑的参数一致。其中阻尼系数分别为30、40、50和60 N·s/m。

|
图 9 弹簧液压支撑结构形式 Fig. 9 Structure of spring hydraulic support |
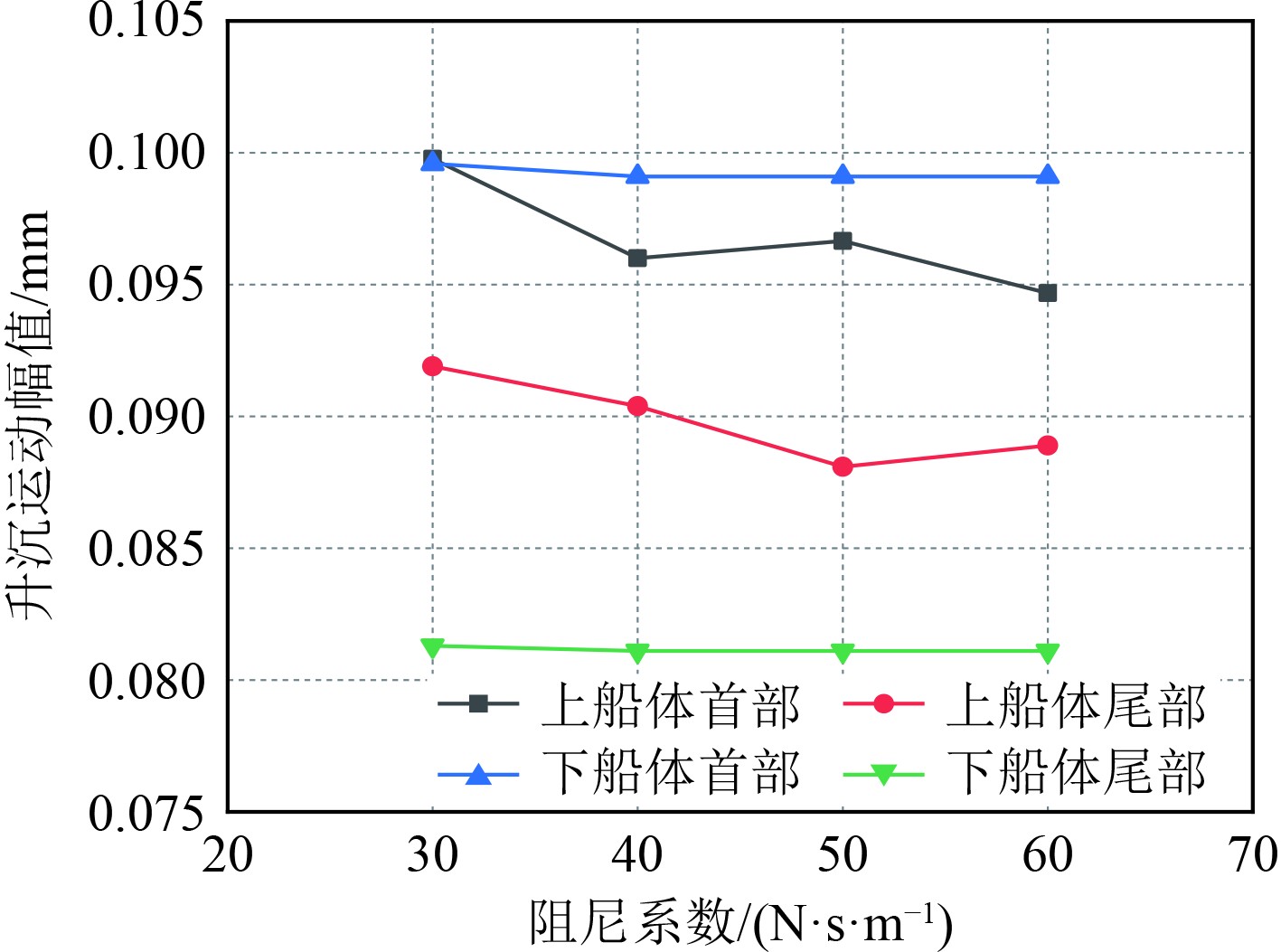
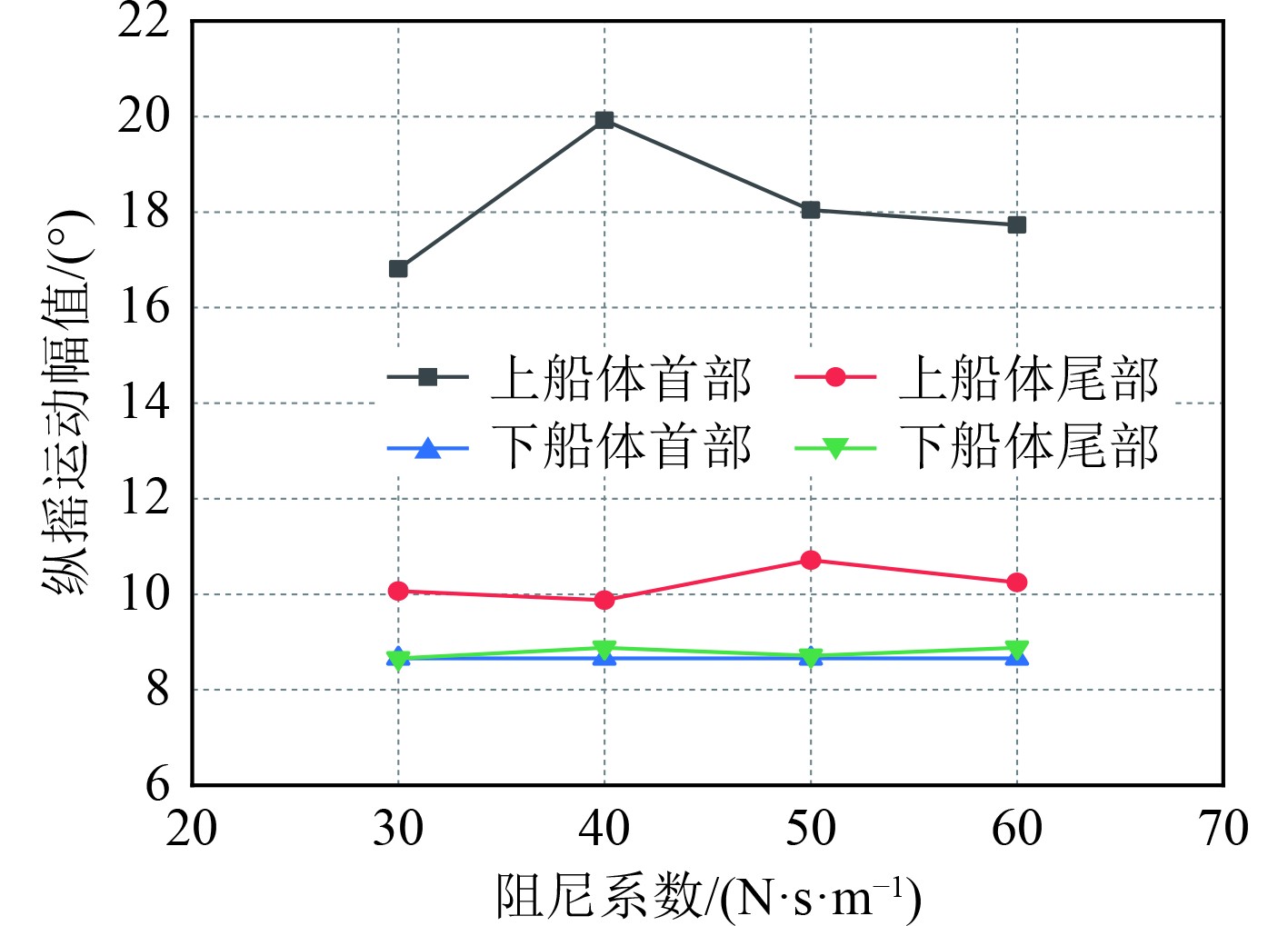
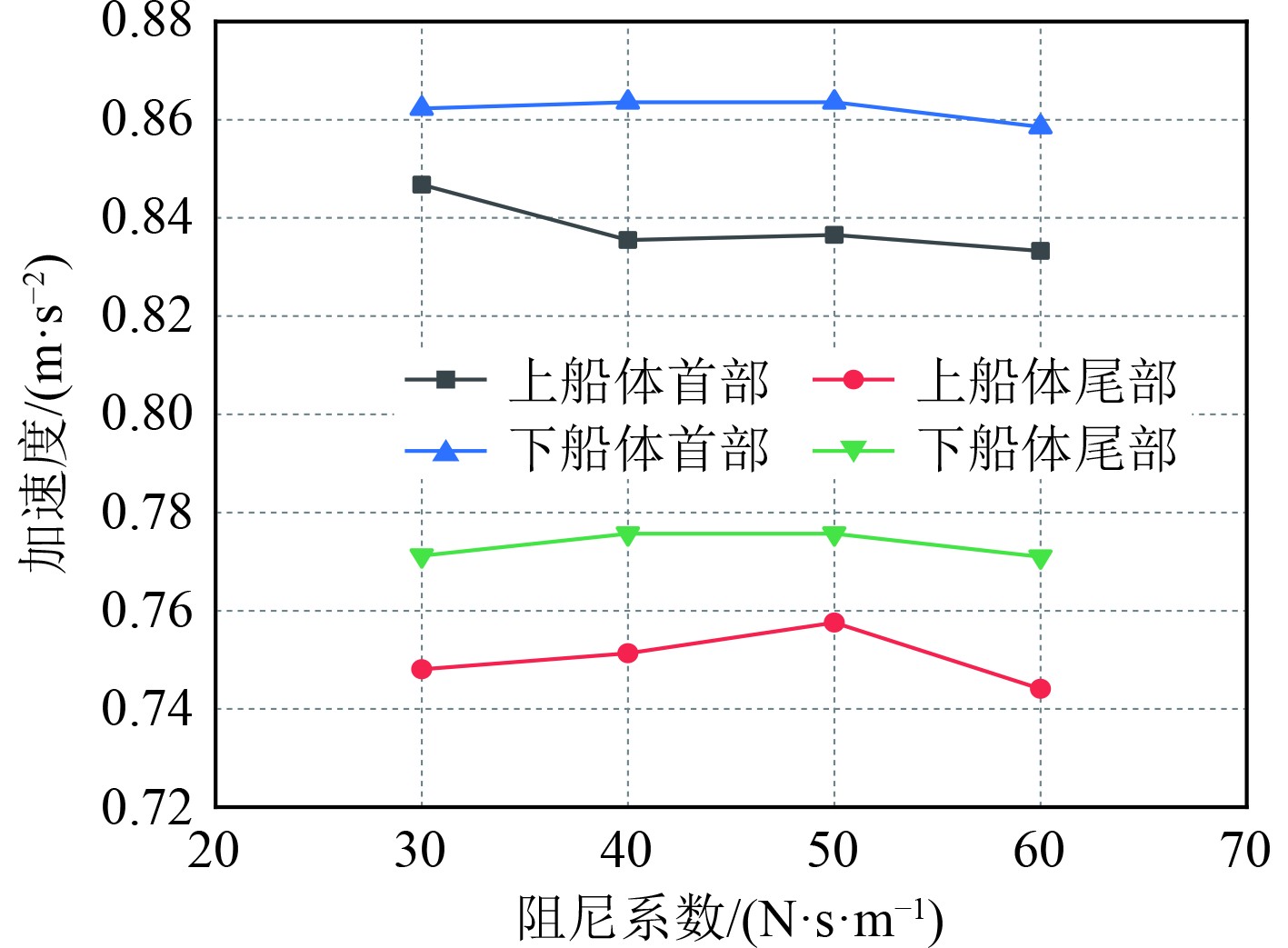
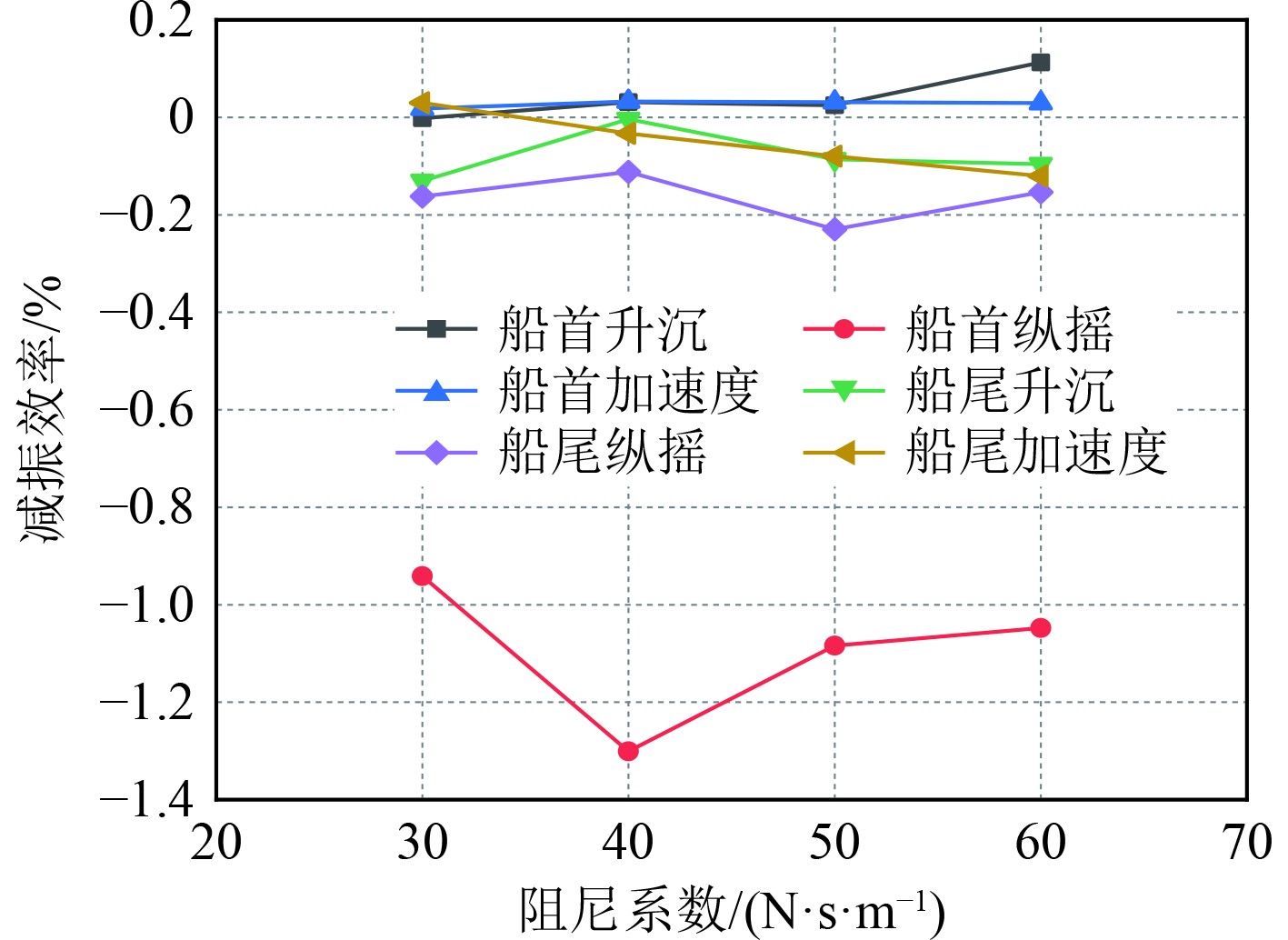
由图10可知,下船体的运动幅值首部为0.99 mm左右,尾部为0.81 mm左右,而上船体经悬架系统减振后,首部运动幅值平均为0.97 mm,尾部为0.89 mm,相比于下船体未有明显的减振效果,相反尾部运动幅值还有所增大。该规律在纵摇运动中更为明显,即上船体的运动幅值比上船体更大(见图11)。图12所示的加速度运动上船体同一位置处的数值均小于上船体,其中上船体首部的加速度值平均在0.836 m/s2,而下船体首部加速度值平均为0.862 m/s2。因此可以看出,弹簧+液压支撑形式的悬架系统并未有效地实现对上船体的减振处理,仅对纵摇运动有抑制作用。造成该结果的原因一方面是弹簧和液压系统本身无法做到一致的响应,另一方面也可能与悬架系统钢架本身设计有所不足。图13为不同位置处各运动参数的减振效率,可以非常直观地看出弹簧+液压的悬架支撑形式仅对垂向加速度运动有正向的减振效果,且减振效率在5%左右,也极其有限。对升沉和纵摇运动并未有良好的抑制作用,相反却加剧了上船体的运动幅值。此外,这种减振效率的变化规律没有因弹簧阻尼系数的改变而带来明显变化,说明在30~60 N·s/m的弹簧阻尼系数范围内,弹簧属性不是影响减振效率的关键因素。
|
图 10 不同弹簧阻尼系数时船体各部分升沉运动幅值 Fig. 10 Heave motion amplitude of each part of hull with |
|
图 11 不同弹簧阻尼系数时船体各部分纵摇运动幅值 Fig. 11 Pitch motion amplitude of each part of hull with different spring damping coefficients |
|
图 12 不同弹簧阻尼系数时船体各部分加速度运动幅值 Fig. 12 Acceleration motion amplitude of each part of hull with different spring damping coefficients |
|
图 13 不同弹簧阻尼时各运动减振效率 Fig. 13 Damping efficiency of each motion under different spring damping |
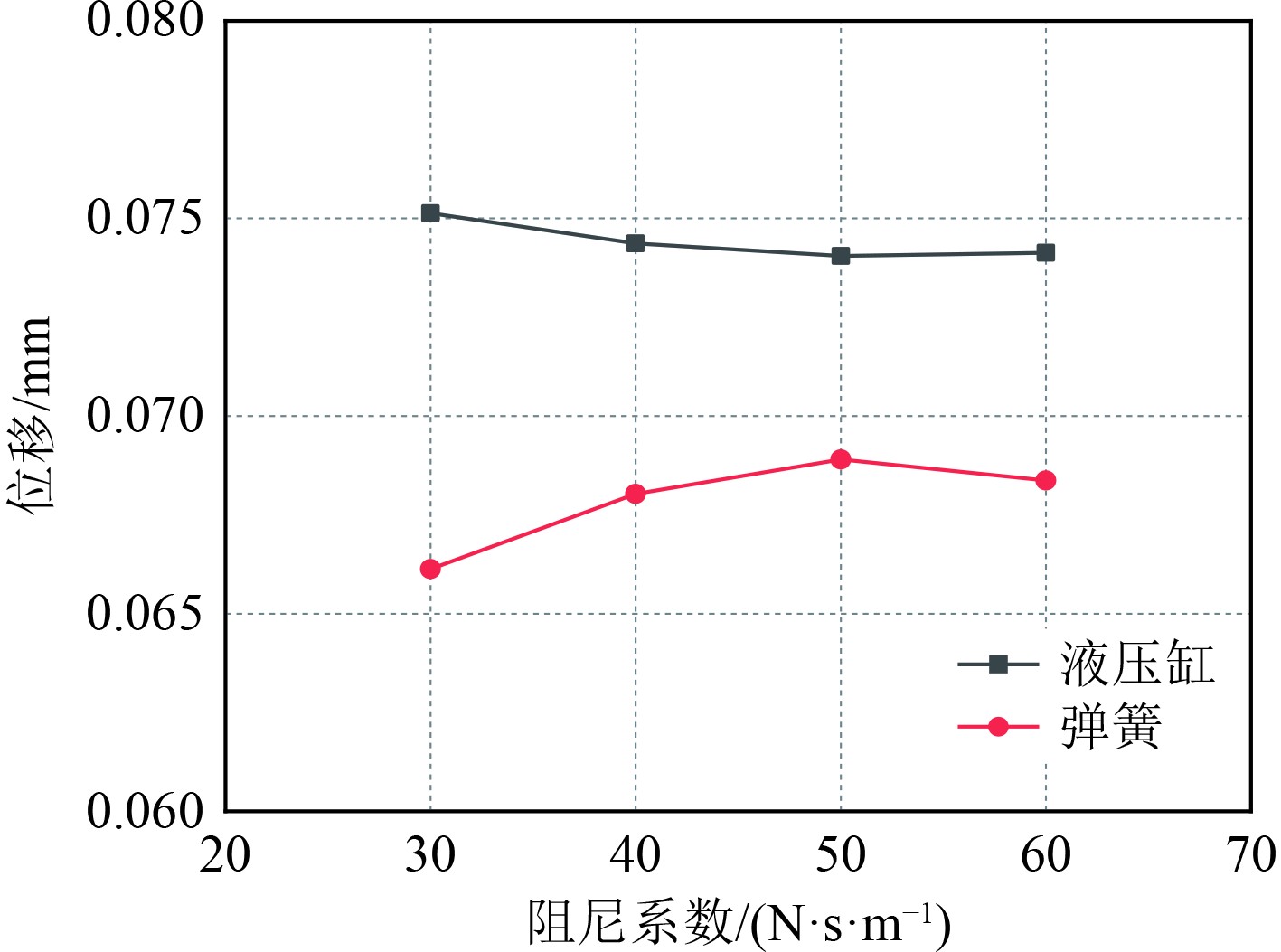
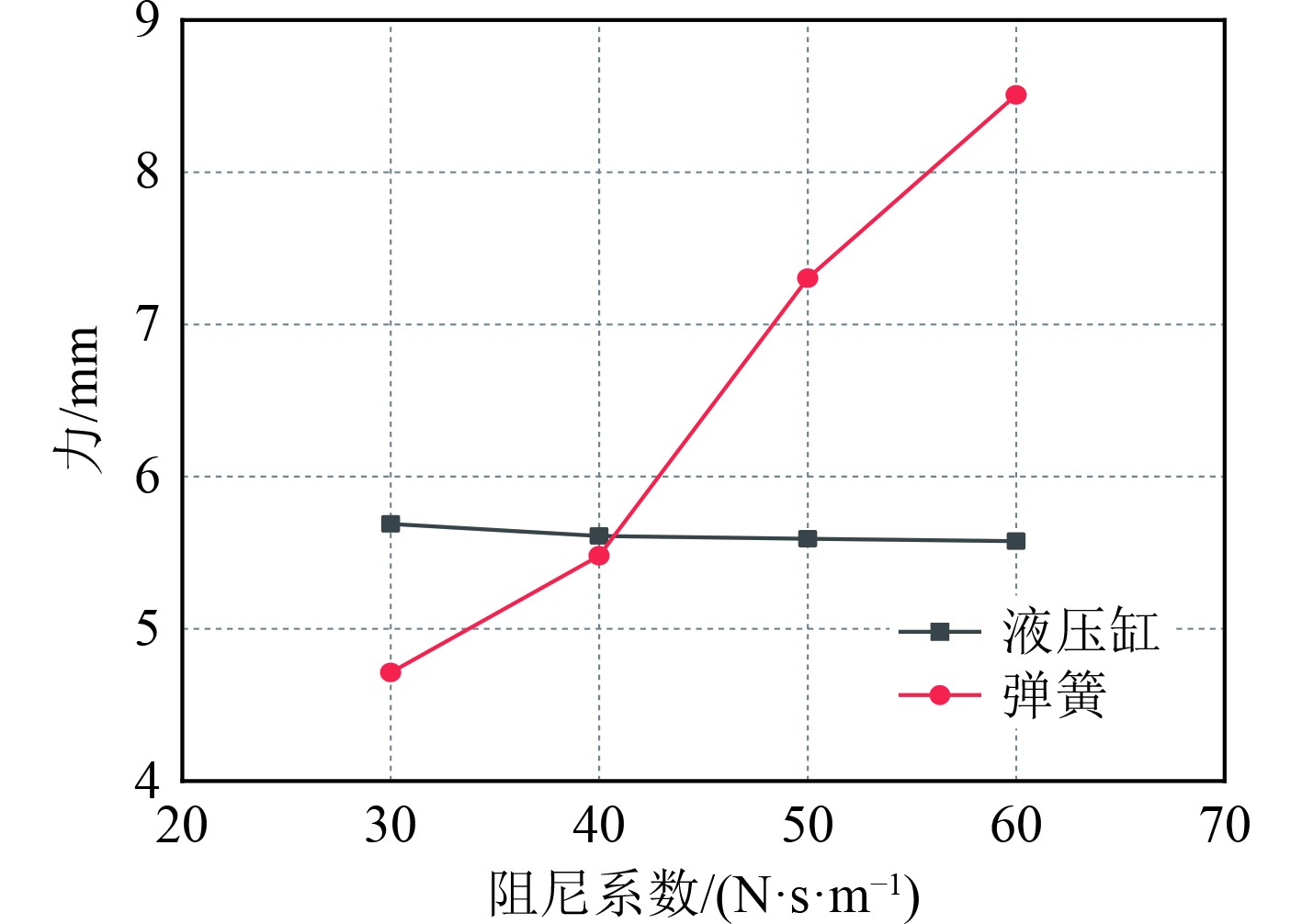
由图14~图15可知,受到力的作用,弹簧和液压缸均产生了不同程度的位移,其中液压缸的平均位移在0.074 mm左右,弹簧的位移随着弹簧阻尼系数的改变有稍微变化,但总体在0.067 mm左右。从两者力的变化来看,弹簧受到了力随阻尼系数的增大而不断加大,从最初的4.84 N左右增大到8.54 N,且未有下降趋势,但液压缸所受到力的变化规律与位移相似,均值在5.63 N左右,可见,由于弹簧和液压缸两者结构形式和对力的敏感程度的差异,导致弹簧+液压支撑形式的悬架系统未能实现良好的减振效果。因此,弹簧+液压支撑形式的悬架系统不能作为减振系统来使用。
|
图 14 不同弹簧阻尼时液压和弹簧位移特性 Fig. 14 Hydraulic and spring displacement characteristics under different spring damping |
|
图 15 不同弹簧阻尼时液压和弹簧支撑力特性 Fig. 15 Hydraulic and spring support force characteristics under different spring damping |
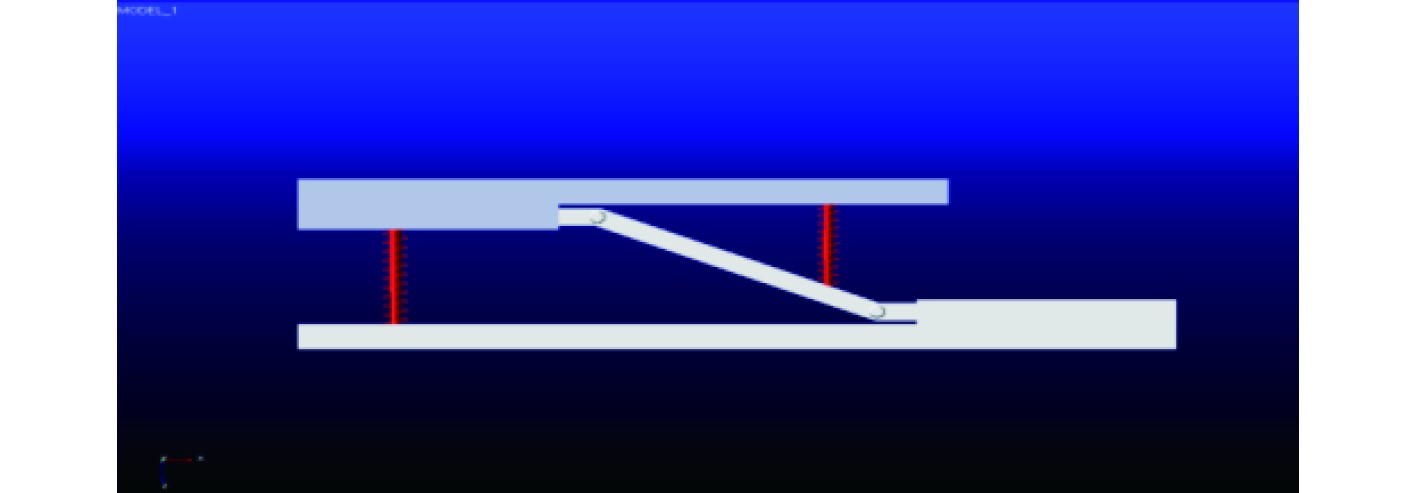
弹簧+液压支撑形式的悬架系统未给船舶的减振效率带来正向增益,但这提供了另外一种思路,即对双弹簧支撑形式在力学属性相似的情况下开展研究。另外,由于液压缸在被动式悬架系统中无法有效控制液压杆在缸套内的位移,故将船首处的液压缸改为弹簧阻尼器,利用弹簧的阻尼性能代替液压缸的运动来减小上船体的运动,这样,前后支撑均变为具有相似力学属性的弹簧形式。除此之外,为了降低连接构件中的轴向力,这里将连接钢架的角度从原来的45°降低到30°,如图16所示,其中位于首部的设置为弹簧阻尼器1,在尾部的为弹簧阻尼器2。
|
图 16 单体构型双弹簧悬架系统模型 Fig. 16 Single configuration double spring suspension system model |
为了研究前后弹簧刚度系数和阻尼系数对减振性能的影响,设置首部弹簧阻尼器刚度系数和阻尼系数分别为k1、c1,尾部弹簧阻尼器刚度系数和阻尼系数分别为k2、c2,通过唯一变量对不同位置处的运动幅值和减振效率展开研究,2组阻尼器设置如表3所示。
|
|
表 3 弹簧阻尼器参数 Tab.3 Spring damper parameters |
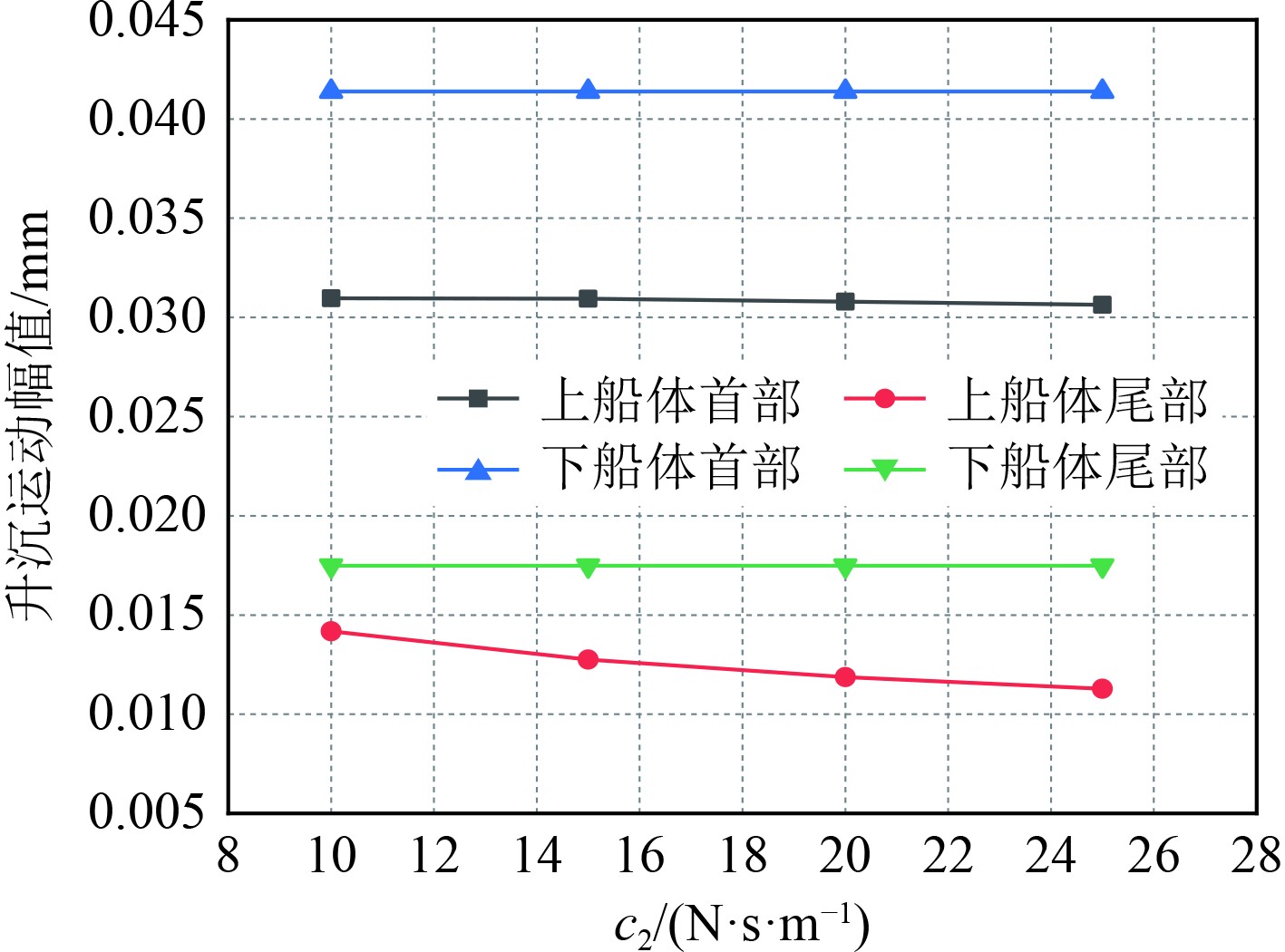
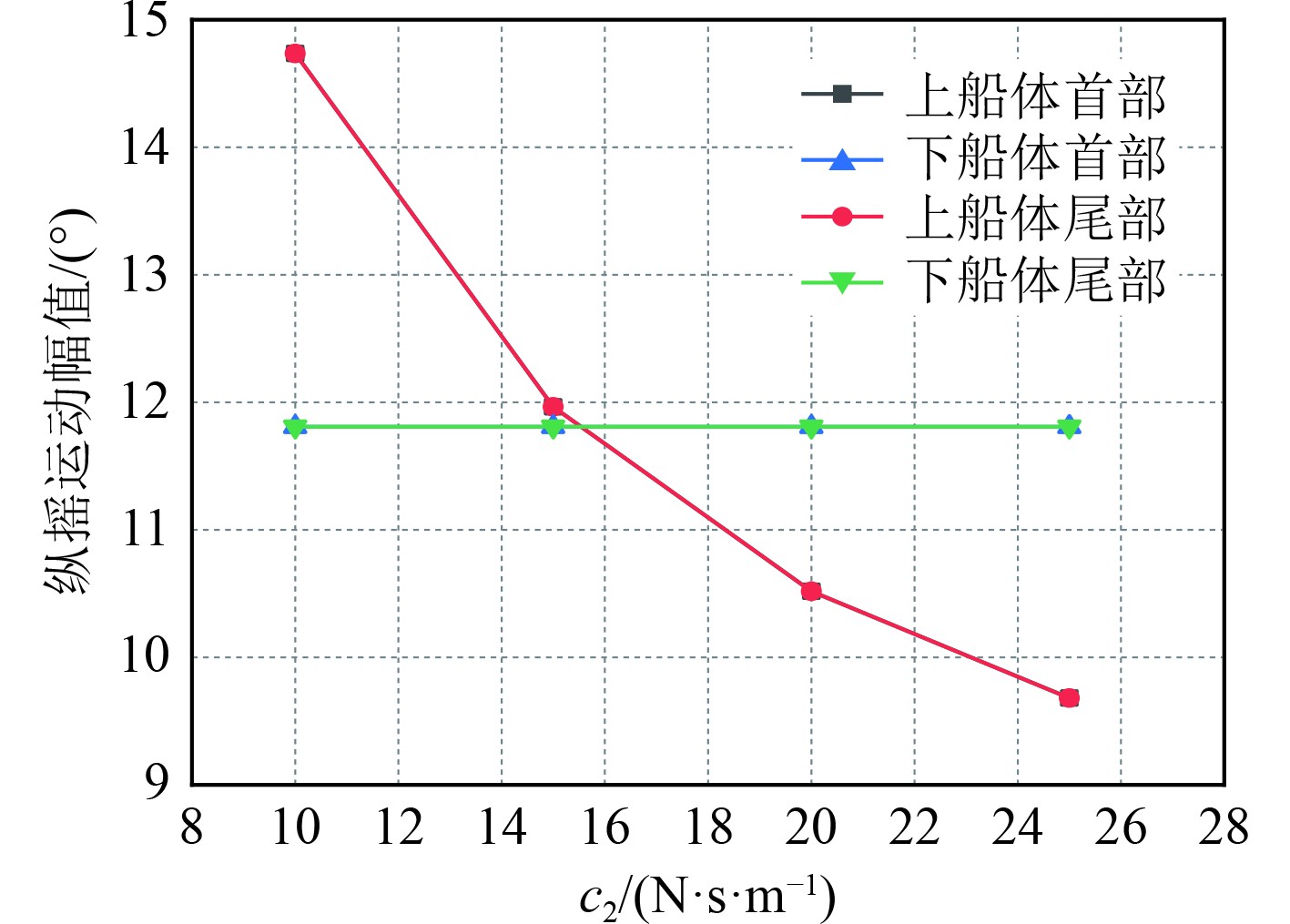
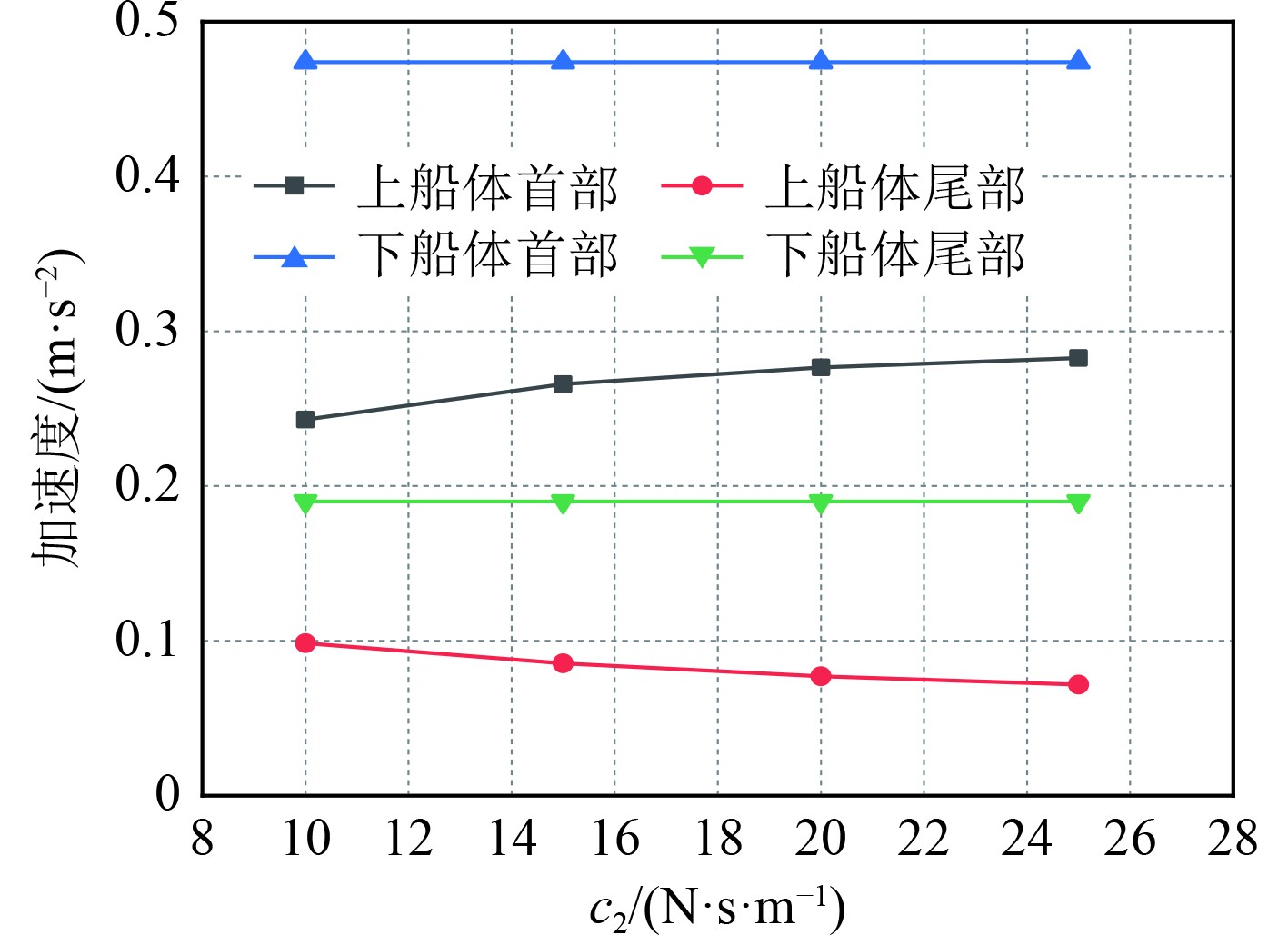
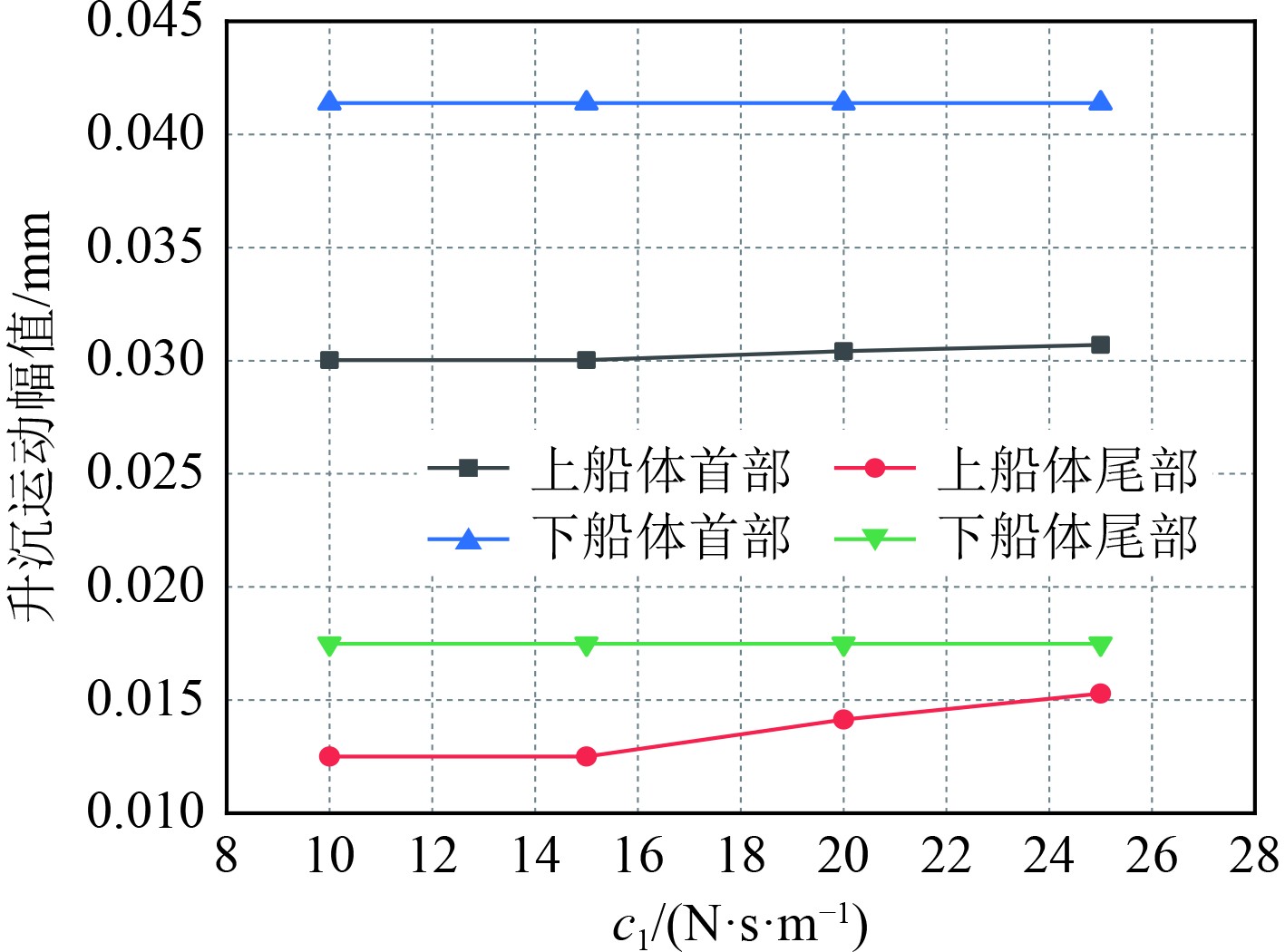
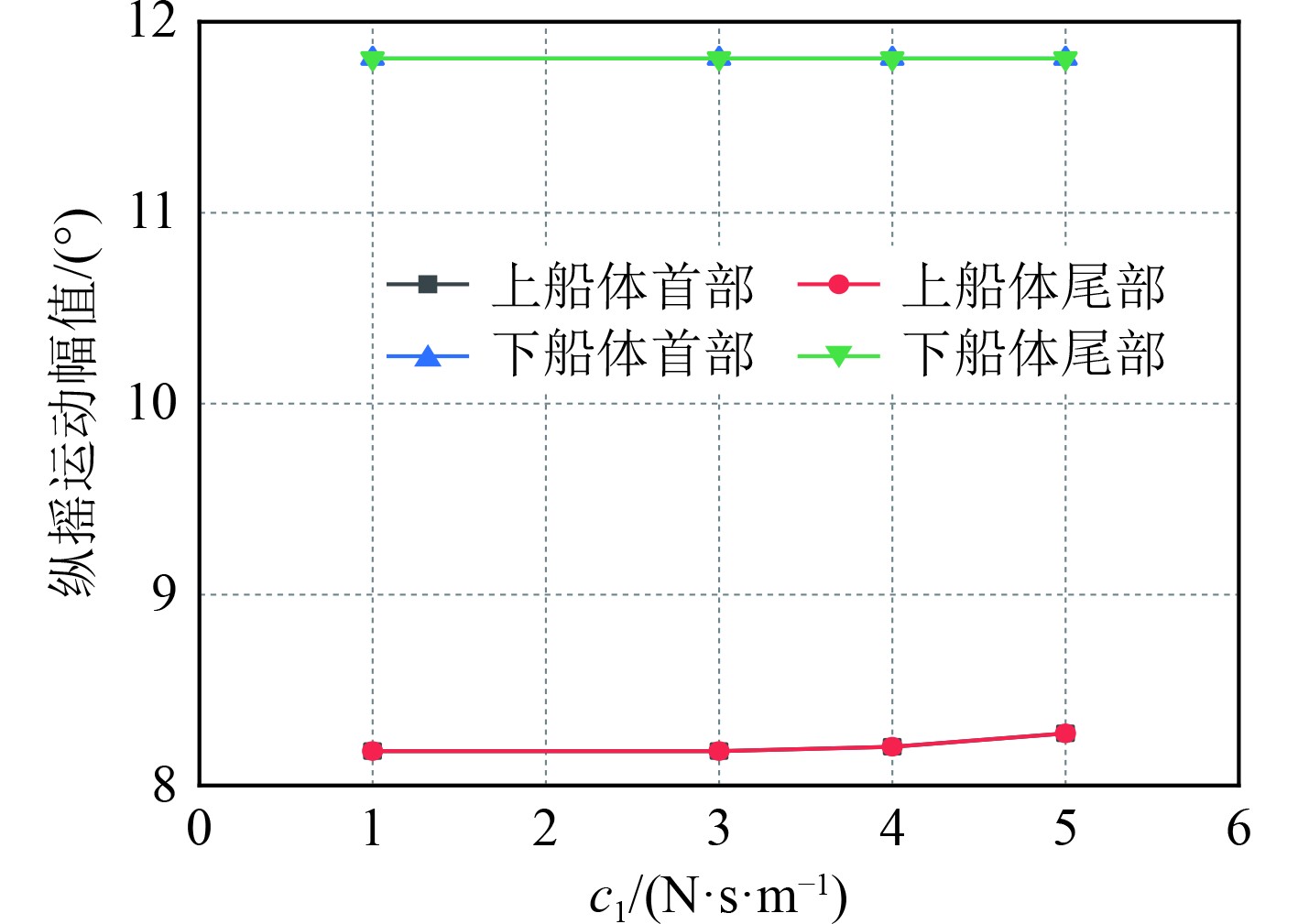
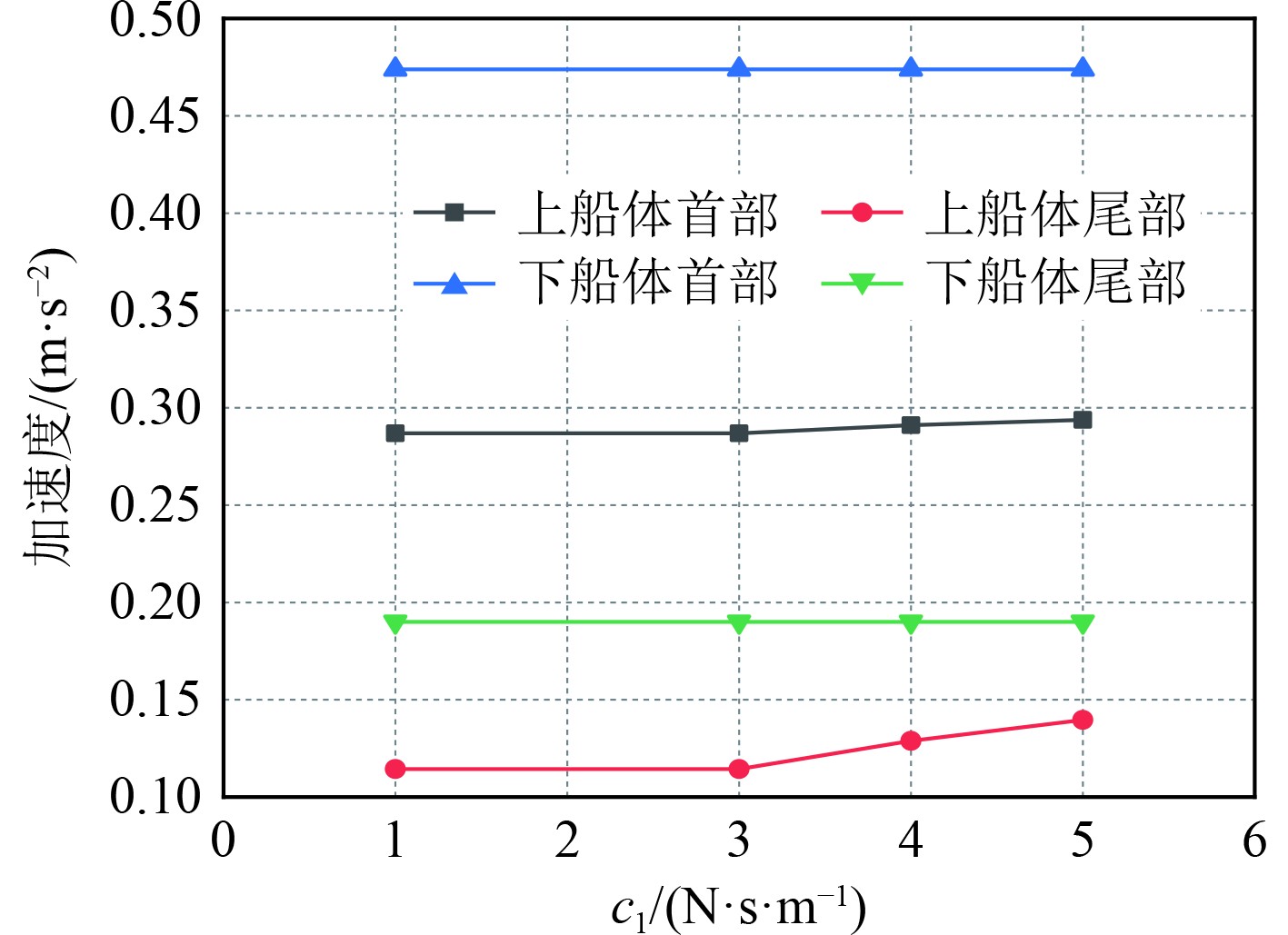
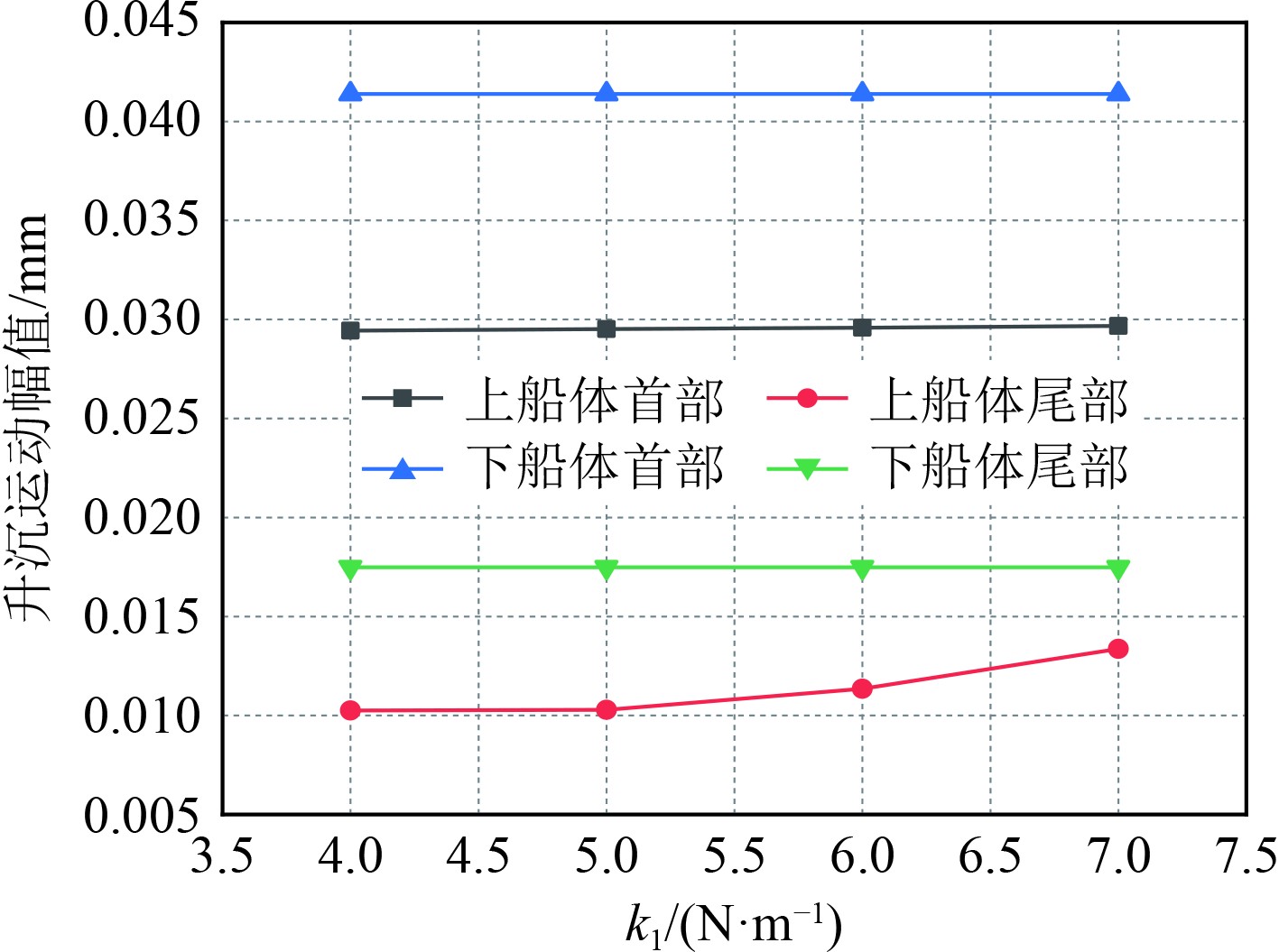
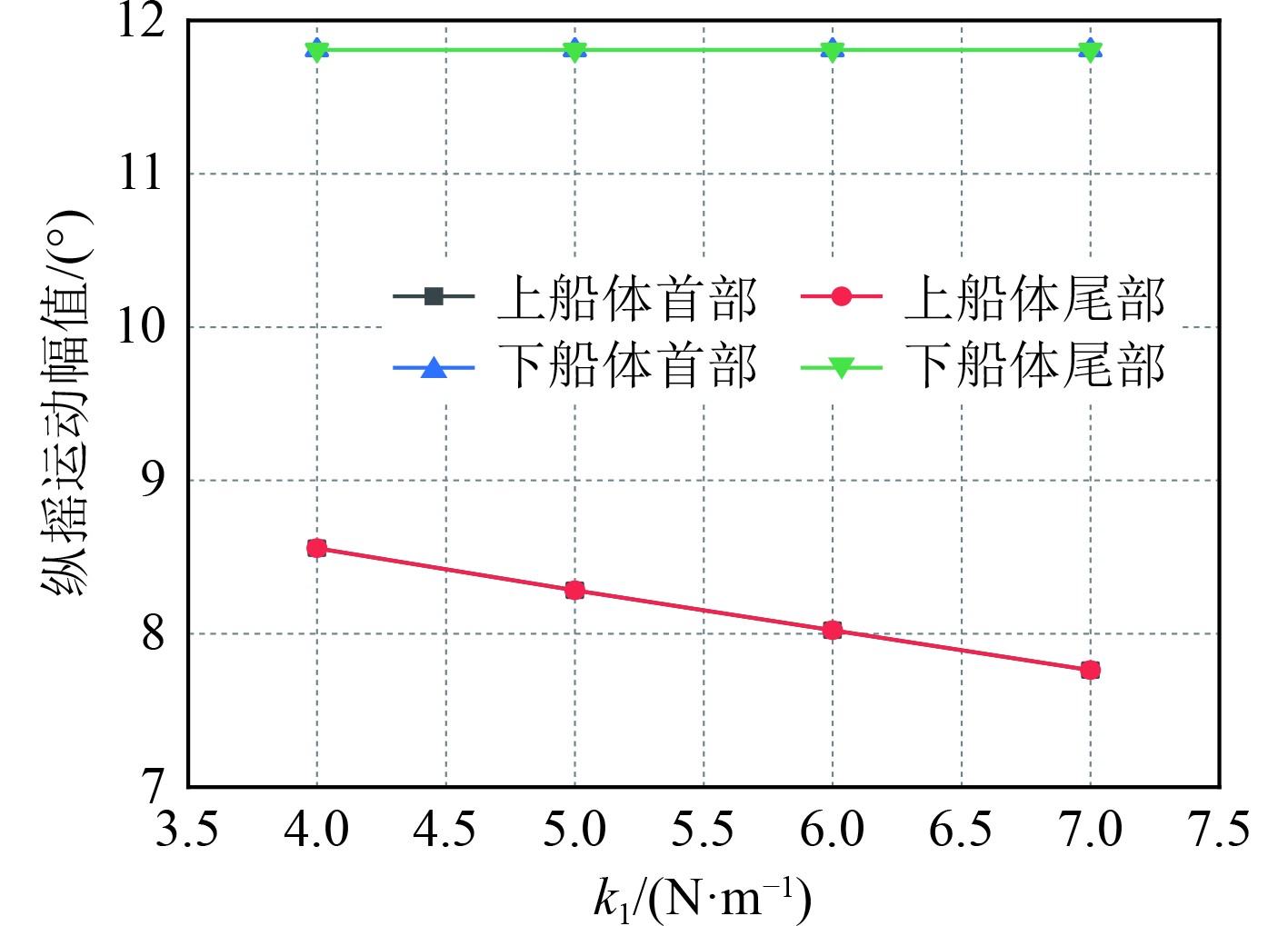
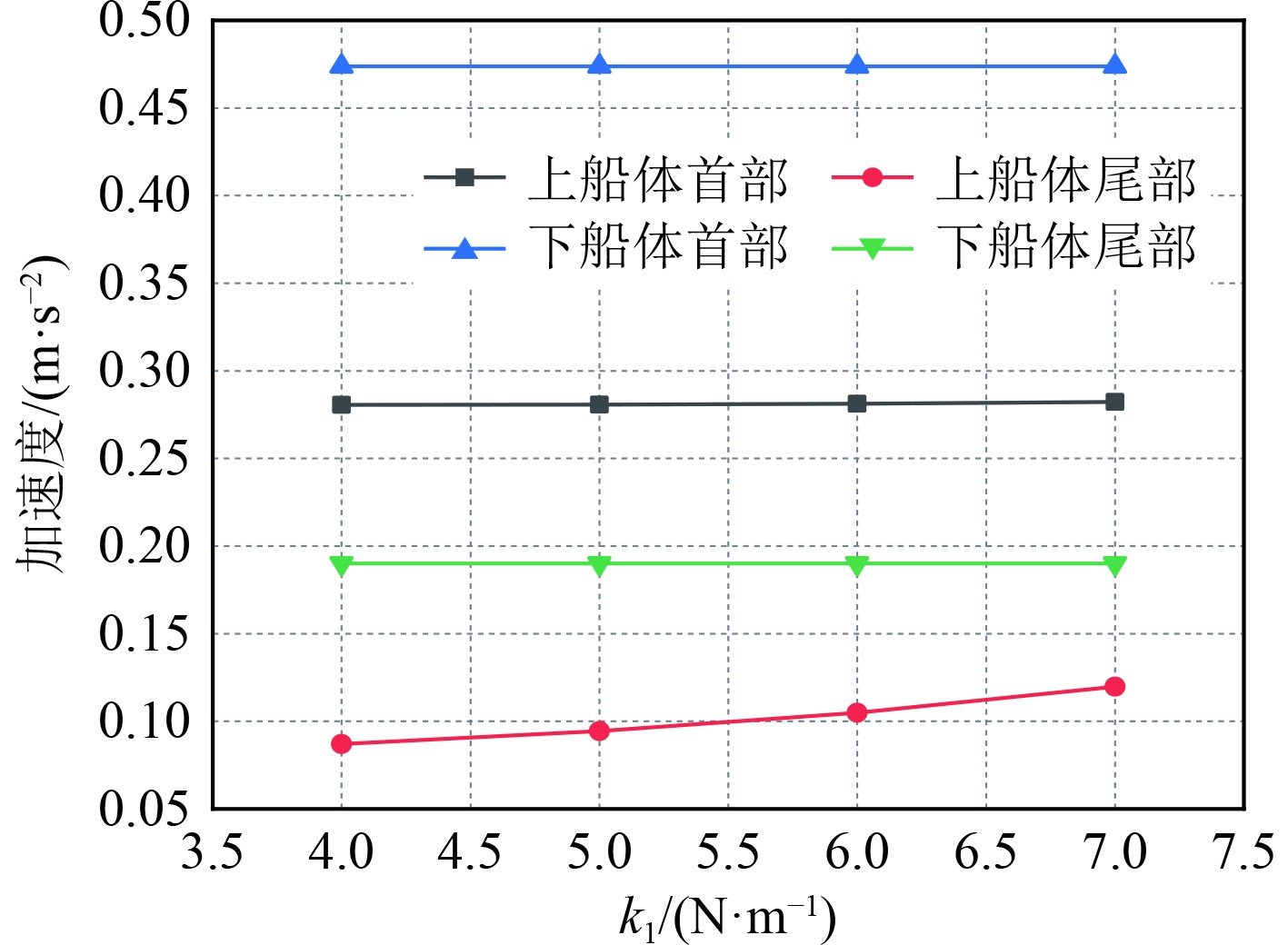
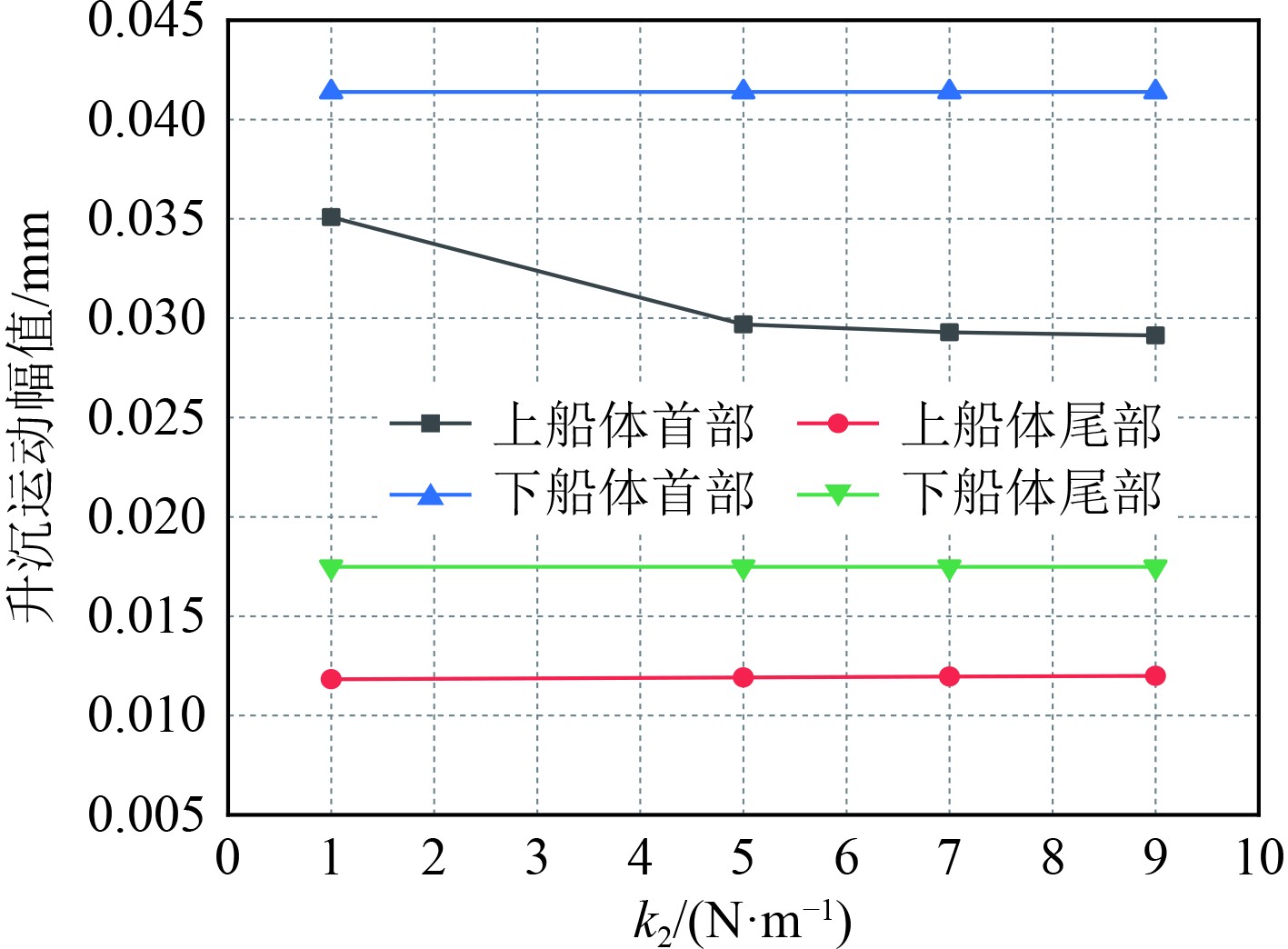
图17~图19为k1 = 2 N/m、c1 = 2 N·s/m、k1= 3 N/m时,不同c2时的计算结果;图20~图22为k1 = 5 N/m、k2 = 7 N/m、c2 = 20 N·s/m时,不同c1时的计算结果;图23~图25为c1 = 2 N·s/m、k2 = 7 N/m、c2 = 20 N·s/m时,不同k1时的计算结果;图26~图28为c1 = 2 N·s/m、k1 = 7 N/m、c2 = 20 N·s/m时,不同k2时的计算结果。由图可知,虽然对于不同的刚度系数和阻尼系数,各个部位的运动参数有一定的差异,但差值没有明显变化,大多数值几乎不变,如图17中上下船体的首部升沉运动分别均值为0.031 mm和0.042 mm,在c2为10 N·s/m和15 N·s/m时两者差别在2%左右,说明双弹簧支撑形式对于保持稳定的运动具有良好效果。在所有纵摇运动中,除了上船体首部纵摇运动有明显降低外,其他船体部分基本不变,说明了此时双弹簧结构下,不同弹簧刚度和阻尼对纵摇运动的影响较小。经过系列定量常量的分析,得到了最佳的弹簧参数,即k1、k2、c1、c2分别为5 N/m、7 N/m、2 N·s/m和20 N·s/m。在此工况下的最佳减振效率如表4所示。
|
图 17 不同c2时船体各部分升沉运动幅值 Fig. 17 Heave motion amplitude of each part of hull under different c2 |
|
图 18 不同c2时船体各部分纵摇运动幅值 Fig. 18 Pitch motion amplitude of each part of hull under different c2 |
|
图 19 不同c2时船体各部分加速度运动幅值 Fig. 19 Acceleration motion amplitude of each part of the hull at different c2 |
|
图 20 不同c1时船体各部分升沉运动幅值 Fig. 20 Heave motion amplitude of each part of hull under different c1 |
|
图 21 不同c1时船体各部分纵摇运动幅值 Fig. 21 Pitch motion amplitude of each part of hull under different c1 |
|
图 22 不同c1时船体各部分加速度运动幅值 Fig. 22 Acceleration motion amplitude of each part of the hull at different c1 |
|
图 23 不同k1时船体各部分升沉运动幅值 Fig. 23 Heave motion amplitude of each part of hull under different k1 |
|
图 24 不同k1时船体各部分纵摇运动幅值 Fig. 24 Pitch motion amplitude of each part of hull under different k1 |
|
图 25 不同k1时船体各部分加速度运动幅值 Fig. 25 Acceleration motion amplitude of each part of the hull at different k1 |
|
图 26 不同k2时船体各部分升沉运动幅值 Fig. 26 Heave motion amplitude of each part of hull under different k2 |
|
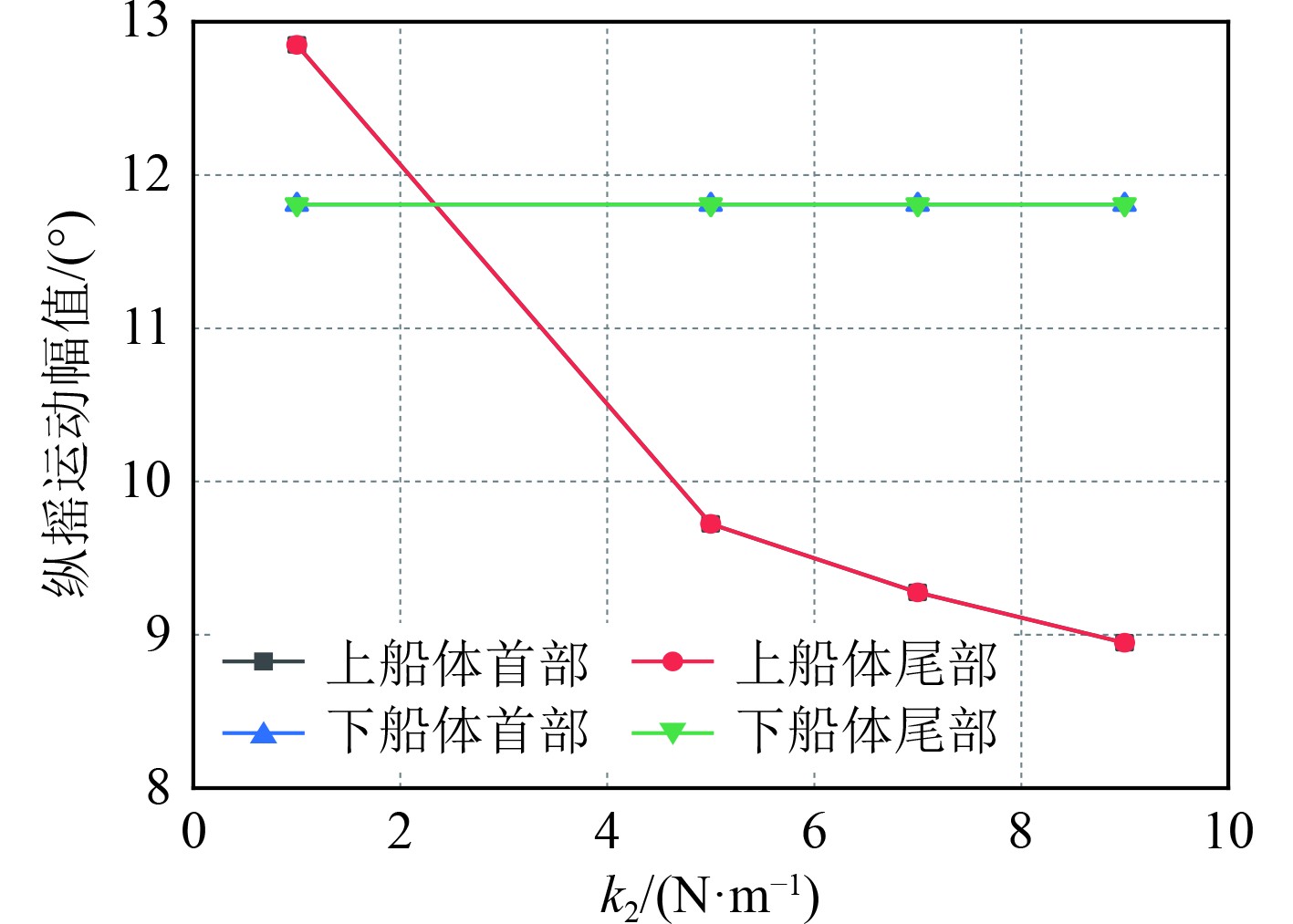
图 27 不同k2时船体各部分纵摇运动幅值 Fig. 27 Pitch motion amplitude of each part of hull under different k2 |
|
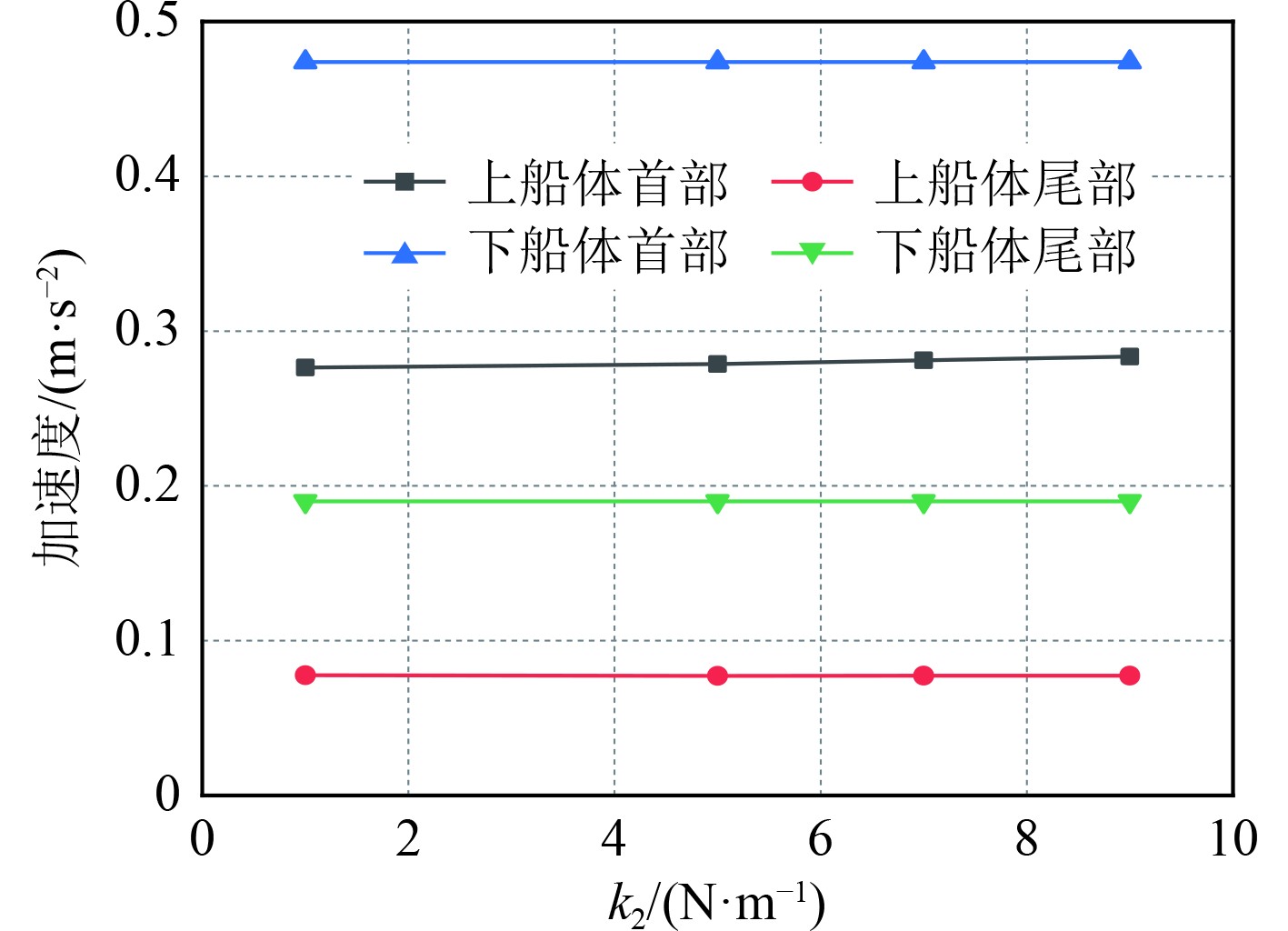
图 28 不同k2时船体各部分加速度运动幅值 Fig. 28 Acceleration motion amplitude of each part of the hull at different k2 |
|
|
表 4 双弹簧支撑最优减振效率 Tab.4 Optimal damping efficiency of double spring support |
1)液压支撑悬架系统构型中,支撑力为2 N时具有最佳的减振效率,综合减振效率达到50%左右,但由于上船体首部的升沉和加速度运动相较于上船体尾部纵摇更为显著,因此其对于前后支撑力的平衡仍有改进空间。
2)弹簧+液压支撑组合由于弹簧和液压缸两者结构形式和对力的敏感程度的差异,导致其未能实现良好的减振效果。
3)经过改进后的双弹簧支撑形式具有更为明显的减振效果,且通过调整刚度系数和阻尼系数可以实现最大减振,最佳弹簧属性下的加速度减振效率最大达到了64%,其他运动参数综合减振效率也可达45%左右。
| [1] |
于婧睿. 高速双体船纵向减摇控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [2] |
怪异“蜘蛛船”[J]. 科学之友(A版), 2009, 2: 15.
|
| [3] |
JOHN F, AHMADIAN A. Multi-body dynamic simulation and analysis of wave-adaptive modular vessels[C]// Hawaii, 11th International Conference on Fast Sea Transportation, 2011.
|
| [4] |
Nauti-craft. Boat models [EB/OL]. 2017.
|
| [5] |
HAN JIALIN, MAEDA TERUO, KINOSHITA TAKESHI, et al. Towing test and motion analysis of a motion-controlled ship-based on an application of skyhook theory[C]// Proceedings of the 12th International Conference on the Stability of Ships and Ocean Vehicles, UK, 2015.
|
| [6] |
JIALIN HAN, DAISUKE KITAZAWA, TAKESHI KINOSHITA, et al. Experimental investigation on a cabin-suspended catamaran in terms of motion reduction and wave energy harvesting by means of a semi-active motion control system[J]. Applied Ocean Research, 2019, 8(3): 88−102.
|
| [7] |
王默, 度红望, 熊伟. 小型救助船舶主动式液压互联悬架系统的设计与仿真[J]. 液压与气动, 2021, 45(8): 138-144. DOI:10.11832/j.issn.1000-4858.2021.08.020 |
| [8] |
白雪松. 波浪适应救助船悬架系统动力学特性研究[D]. 大连: 大连海事大学, 2021.
|
| [9] |
彭婧, 李旭涛, 李胜利. 基于ADAMS的液压支架运动学仿真分析[J]. 煤炭技术, 2023, 42(8): 237-239. |
| [10] |
刘成武, 陈智强. 基于ADAMS的汽车悬架系统仿真分析与优化[J]. 福建工程学院学报, 2012, 10(3): 241-244. |
| [11] |
霍雷刚. 电动汽车悬架系统仿真分析与优化设计[D]. 济南: 齐鲁工业大学, 2020.
|
| [12] |
陈华, 韩霄翰. 基于ADAMS光学检测 平台刚−柔耦合动力学模型仿真[J]. 机械设计与研究, 2023, 39(2): 166-170. |
| [13] |
殷赵民, 滕汉东. 双层液压式动力反共振隔振器动力学研究[J]. 振动与冲击, 2024, 43(12): 307-311. |
| [14] |
夏明悦. 基于变弹性基础Winkler模型的转向机构间隙球铰动力学特性研究[D]. 镇江: 江苏大学, 2022.
|
| [15] |
马啸天. 基于ADAMS的铁路起重机伸缩臂负载伸缩动力学仿真[D]. 南昌: 华东交通大学, 2023.
|
| [16] |
葛正浩, 高创, 张晓亮, 等. 基于ADAMS的Stewart平台运动学分析[J]. 轻工机械, 2024, 42(2): 1-7+22. DOI:10.3969/j.issn.1005-2895.2024.02.001 |
| [17] |
陈远龙, 司晓东, 温信宇. 基于ADAMS的清污机主臂液压缸杆件结构运动学分析[J]. 机械工程与自动化, 2023(1): 84-86. DOI:10.3969/j.issn.1672-6413.2023.01.028 |
 2025, Vol. 47
2025, Vol. 47

