2. 中国船舶集团有限公司第七〇三研究所,黑龙江 哈尔滨 150078
2. The 703 Research Institute of CSSC, Harbin 150078, China
燃气轮机具有稳定性高、经济性好等多方面优点,被广泛用于航空、船舶、发电等重要领域[1 − 2]。燃油控制系统作为燃气轮机重要的附属系统,计算喷入燃烧室的燃油流量,对避免燃气轮机发生超温、超转、喘振等故障,维护燃气轮机的稳定性具有重要作用[3 − 4]。随着燃气轮机技术指标的不断提升,对燃油控制系统的控制精度的要求也越来越严苛[5]。国内外众多学者对于燃油控制系统及其与发动机的耦合进行了深入的研究。
对于单个燃油系统的研究,Reed等[6]建立燃油供油系统的计算模型,利用Matlab编程研究不同工况下燃油供油系统性能参数的变化规律。Ishola等[7]为了控制轻型双引擎飞机燃油系统的流量,监测和优化燃油系统的效率,建立燃油系统的模型并在Matlab/Simulink上进行仿真分析。丁琳等[8]依据涡轴发动机控制原理,建立某型直升机涡轴发动机燃油系统的数学模型,并对该燃油系统进行全数字仿真研究。张东[9]利用AMESim对某型发动机主燃油系统的部件和系统进行建模仿真,通过试验验证模型精度并对燃油系统进行改进设计。刘振刚等[10]对某型发动机的主燃油控制系统进行分析研究,基于试飞数据对该燃油控制系统的主要部件进行Hammerstein辨识建模,仿真结果表明该建模方法可以准确模拟燃油系统执行机构的工作过程。目前文献的研究主要针对燃油控制系统进行建模仿真分析,对建模方法进行优化以建立更高精度的仿真模型,忽略了不同信号强度对燃油系统输出特性的影响研究。
针对燃油系统与发动机的耦合,Shu等[11]利用GT Power和Matlab/Simulink建立双燃料发动机和燃油系统的联合仿真模型,研究发动机燃料模式切换的瞬态过程,并利用布谷鸟搜索算法对传统的燃油PID控制系统进行优化。吴文斐等[12 − 13]基于Simulink平台把主燃油控制系统模型与发动机模型连接起来进行联合仿真,实现燃油系统与发动机的耦合,并对飞机发动机液压控制系统进行优化。目前文献的研究中实现了燃油系统与发动机的耦合,主要集中于利用集成模型对燃油控制系统进行优化,忽略了燃油时滞特性对发动机总体性能影响的研究。
综上所述,本文建立燃气轮机和燃油系统的多系统集成模型,研究燃油系统的时滞特性对发电燃气轮机突变负荷时动态性能的影响,并进行半物理仿真实验的验证。
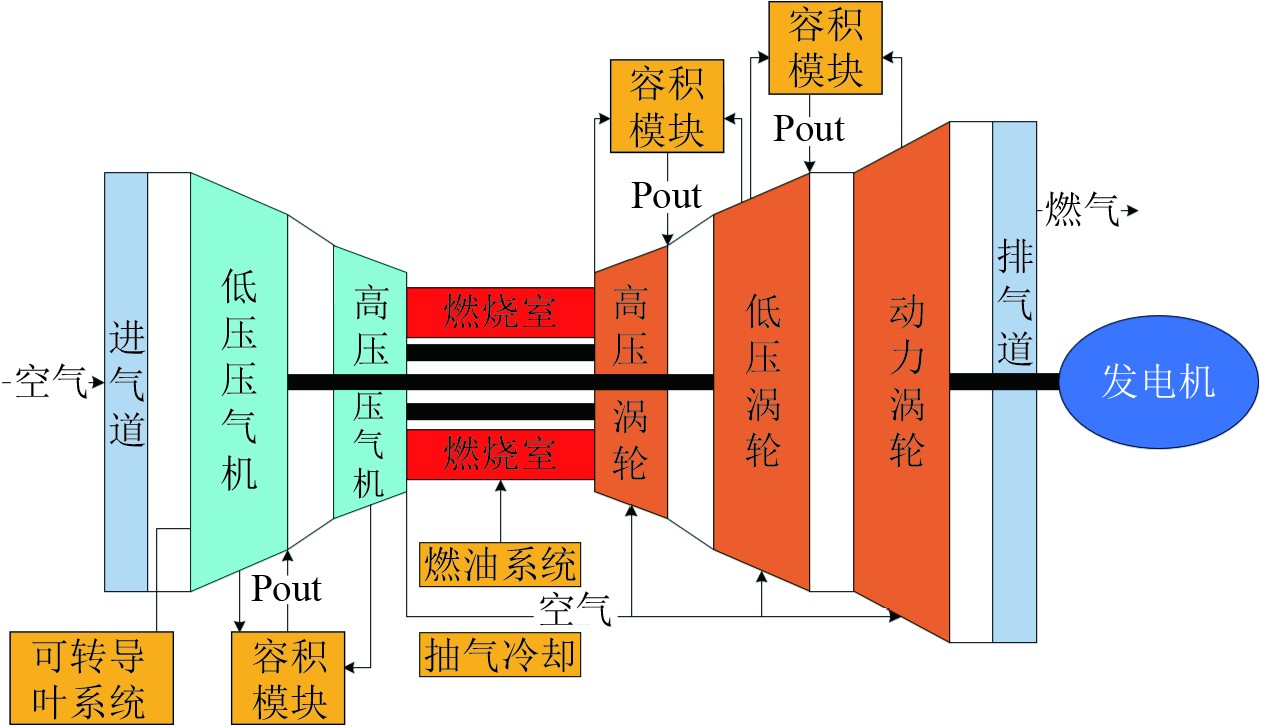
1 燃气轮机与燃油系统建模 1.1 燃气轮机建模与验证 1.1.1 燃气轮机模型建立本文建立了某型三轴发电燃气轮机仿真模型,主要由进排气道、压气机、燃烧室、涡轮、转子等部分组成,其基本结构如图1所示。
|
图 1 发电燃气轮机结构原理图 Fig. 1 Power generation gas turbine structure schematic diagram |
在进行燃气轮机进排气系统建模时,假设进排气道与外界没有能量交换,认为空气在进排气道内总温不变。把流经进排气道的空气视为不可压流体,其数学模型如下:
| $ P\mathrm{_{out}}=P\mathrm{_{in}}-\Delta P\times\left(\frac{G_K}{G_{K0}}\right)^2。$ | (1) |
式中:
对于压气机和涡轮,工作特性用压比/膨胀比、折合转速、折合流量和效率表示[14]。
| $ \frac{{G_{\mathrm {in}}\sqrt {T_\mathrm{in}} }}{{{P_\mathrm{in}}}} = {f_1}\left({\text{π}} ,\frac{n}{{\sqrt {{T_\mathrm{in}}} }}\right) ,$ | (2) |
| $ \eta = {f_2}\left({\text{π}} ,\frac{n}{{\sqrt {{T_{{\mathrm{in}}}}} }}\right)。$ | (3) |
式中:
在对燃烧室进行建模时,可将其简化为一个容腔,根据质量守恒和能量守恒原理,其出口压力和温度计算方程如下:
| $ \frac{{\rm{d}}P_{\mathrm{bout}}}{{\rm{d}}\tau}=\frac{R_gT_{\mathrm{bout}}(G_{bin}+G_f-G_{\mathrm{bout}})}{V}+\frac{P_{\mathrm{bout}}}{T_{\mathrm{bout}}}\frac{{\rm{d}}T_{\mathrm{bout}}}{{\rm{d}}\tau} ,$ | (4) |
| $ \begin{split} \frac{{{\rm{d}}{T_\mathrm{bout}}}}{{{\rm{d}}\tau }} =& \frac{{{R_g}{T_\mathrm{bout}}}}{{{P_b}_\mathrm{out}V{C_P}}}[k({G_\mathrm{bin}}{h_\mathrm{bin}} +{G_f}{H_u}{\eta _b} - \\ & {G_\mathrm{bout}}{h_\mathrm{bout}}) - {h_\mathrm{bout}}({G_\mathrm{bin}} + {G_f} - {G_\mathrm{bout}})] 。\end{split}$ | (5) |
式中:
容积模块用来模拟三轴燃气轮机中压气机之间和涡轮之间的连接部分,根据质量守恒:
| $ \frac{{{\rm{d}}{P_v}}}{{{\rm{d}}\tau }} = \frac{{{R_g}{T_\mathrm{vin}}}}{{{V_v}}}({G_\mathrm{vin}} - {G_\mathrm{vout}})。$ | (6) |
式中:
压气机和涡轮之间通过转动轴连接,本文考虑连接轴的转子惯性,转子动力学方程如下:
| $ \frac{{{\rm{d}}n}}{{{\rm{d}}\tau }} = \frac{{30}}{{J{\text{π}} }}\left( {{M_T} - {M_C}} \right) = \frac{{900}}{{J{{\text{π}} ^2}n}}\left( {{N_T} - {N_C}} \right) 。$ | (7) |
式中:
对燃气轮机仿真模型进行稳态工况点验证。仿真模型的输入参数分别为空载、50%工况和满工况下的进气温度和负载,与试车数据对比的输出参数为低压轴转速、高压轴转速、动力涡轮转速、低压涡轮出口温度和高压压气机出口压力。其中仿真结果中的低压轴转速、高压轴转速和动力涡轮转速是通过1.1.1节中的转子动力学方程计算得到。对结果进行归一化处理,如表1所示。可知,最大相对误差约为2.83%。
|
|
表 1 稳态工况点精度对比(归一化) Tab.1 Comparison of steady-state point accuracy (Normalization) |
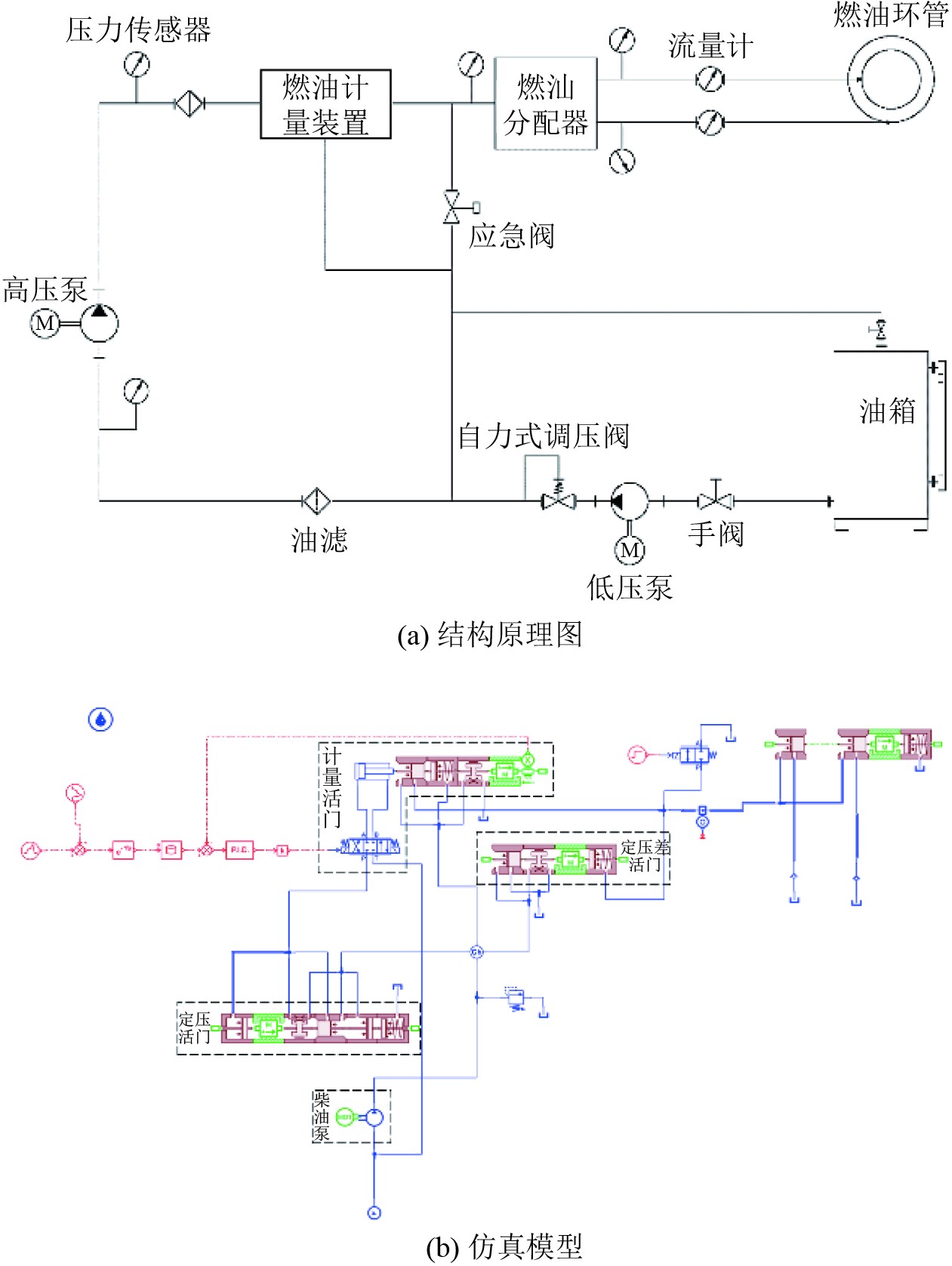
本文基于燃油系统模拟装置的结构和原理建立燃油系统仿真模型,其主要由油箱、低压泵、油滤、高压泵、燃油计量装置、燃油分配器、故障排放阀等部分组成[15],基本结构如图2(a)所示。在AMESim仿真软件建立的燃油系统仿真模型如图2(b)所示。
|
图 2 燃油系统结构原理与仿真模型示意图 Fig. 2 Fuel system structure principle and simulation model diagram |
燃油系统中的主要部件为燃油泵和燃油计量装置。其中高压泵为轴向柱塞泵,低压泵为离心泵。柱塞泵通过缸体内柱塞的运动改变密封容积来造成压差,从而实现吸油和排油过程[16]。单个柱塞泵的排量公式如下:
| $ {V_\mathrm{Pump}} = \frac{{{\text{π}} {d_\mathrm{Pump}}^2{D_\mathrm{Pump}}\tan \gamma }}{4} 。$ | (8) |
式中:
柱塞泵内的实际排出流量公式如下:
| $ {Q_\mathrm{Pump}} = \frac{{z{\text{π}} {d_\mathrm{Pump}}^2{D_\mathrm{Pump}}\tan \gamma {n_\mathrm{Pump}}{\eta _v}}}{4} 。$ | (9) |
式中:
燃油系统中的燃油计量装置主要包括定压活门、定压差活门和计量活门,是燃油系统的核心组成部分。其输出流量公式为:
| $ {Q_F} = {k_F} \times A\sqrt {\frac{{2\left| {\Delta {P_F}} \right|}}{\rho }} 。$ | (10) |
式中:
随着仿真工具的进步,燃气轮机仿真技术逐渐向多学科耦合数值模拟的方向发展[17]。采用多学科集成仿真的方法,实现燃气轮机及其附属系统的集成,可以提高模型仿真的精度,充分模拟实际发电燃气轮机的动态过程。本文利用不同的仿真软件建立燃气轮机和燃油系统仿真模型,为了提高仿真的精度,研究燃油系统时滞性对燃气轮机突变负荷时动态性能的影响,需要进行Simulink模型与AMESim模型的集成。
AMESim中可以创建与其他软件联合仿真的接口,与Simulink集成时,选取“Simulink(co- simulation)”作为联合仿真的接口;AMESim模型进入仿真模式后,会在Simulink中生成可以被S函数调用的文件,实现联合仿真。本文中燃气轮机模型与燃油系统模型之间通过接口传递的参数如表2所示。燃气轮机模型通过数据传递接口向燃油系统模型传递燃油计量阀开度信号,燃油系统模型接收信号后模拟实际的阀门打开,输出对应的燃油流量,采集到的燃油流量信号通过接口传递到燃气轮机模型中进行计算。
|
|
表 2 燃气轮机与燃油系统之间参数传递 Tab.2 Parameter transfer between gas turbine and fuel system |
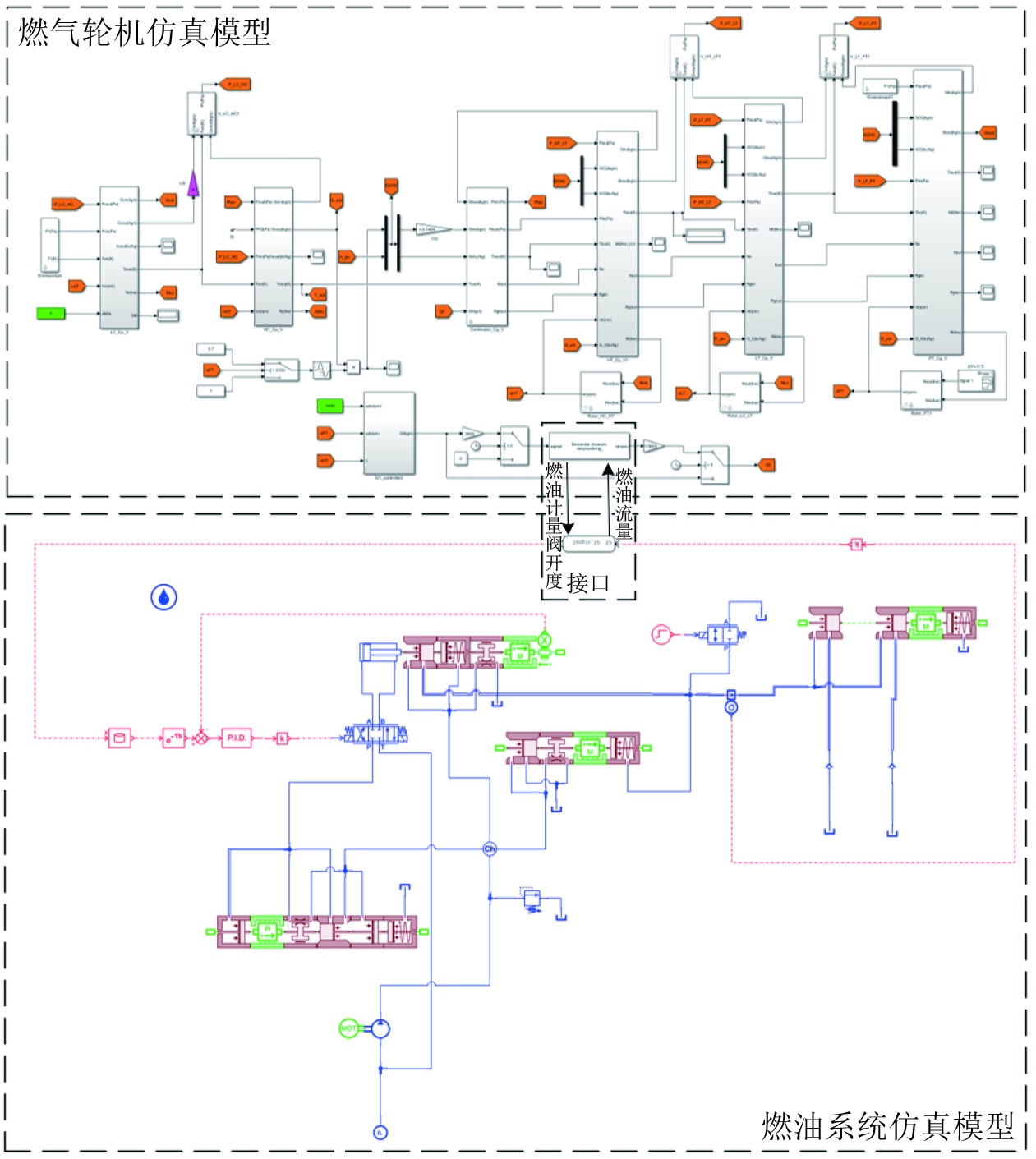
通过配置联合仿真的接口,实现发电燃气轮机模型与燃油系统模型的集成,如图3所示。燃气轮机多系统集成仿真模型的入口边界条件为燃气轮机的负载输入。通过在燃气轮机仿真模型中输入变化的负载,进行燃气轮机多系统集成模型的变工况仿真。
|
图 3 燃气轮机多系统集成仿真模型 Fig. 3 Gas turbine multi-system integration simulation model |
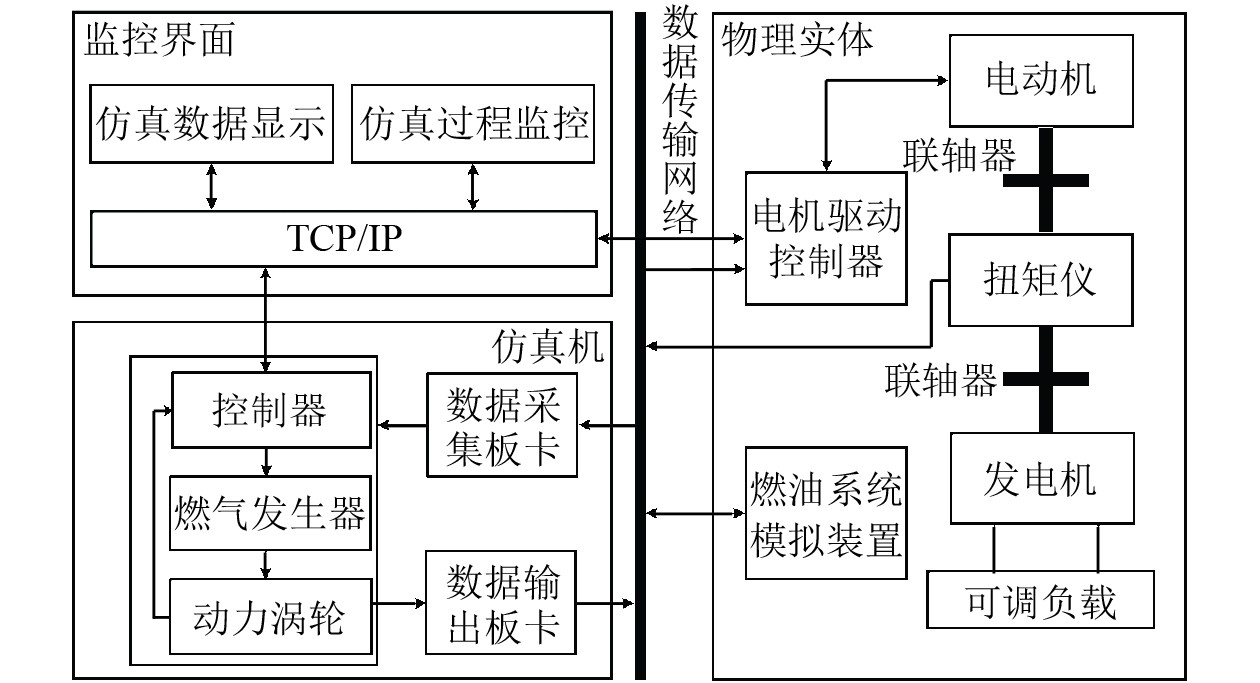
本文基于燃油系统模拟装置和燃气轮机实时仿真系统设计发电燃气轮机半物理仿真实验台,其整体结构示意图如图4所示。燃气轮机以仿真模型的形式运行在燃气轮机实时仿真机上,燃油系统、发电机和负载等以物理实体运行。
|
图 4 半物理仿真平台示意图 Fig. 4 Schematic diagram of semi-physical simulation platform |
在仿真运行过程中,燃气轮机实时仿真机将燃气轮机动力涡轮输出转速的实时信号通过数据输出板卡传送给电机驱动控制器,电动机在仿真时间步长内以恒转速方式运行,从而带动发电机发电,发电机扭矩通过转速扭矩仪及数据采集板卡以数字量的形式传送给燃气轮机实时仿真机,从而构成转速的仿真回路;仿真过程中燃气轮机实时仿真机将燃气轮机PID控制器计算并转换成的燃油计量阀开度通过数据输出板卡传送给燃油系统模拟装置,使其阀门打开并输出燃油流量,燃油流量通过数据采集板卡传送给燃气轮机实时仿真机,从而构成燃油的仿真回路。
发电燃气轮机半物理仿真实验台的运行是在监控界面的控制下进行的,通过TCP/IP通讯,监控界面将仿真模型及仿真参数下载到仿真机中,并控制仿真模型的计算过程。半物理仿真系统中重要参数的数据将通过数据通讯传输给燃气轮机实时仿真机的总控软件,用于显示、存储和分析,总控软件也可以通过数据通讯控制负载箱,从而对实验过程中燃气轮机的工况进行调整。
4 结果分析 4.1 燃油系统时滞特性研究在实验台的监控界面设定燃油流量的阶跃控制信号,采集燃油系统模拟装置输出的燃油流量结果。设定阶跃的信号为500~
|
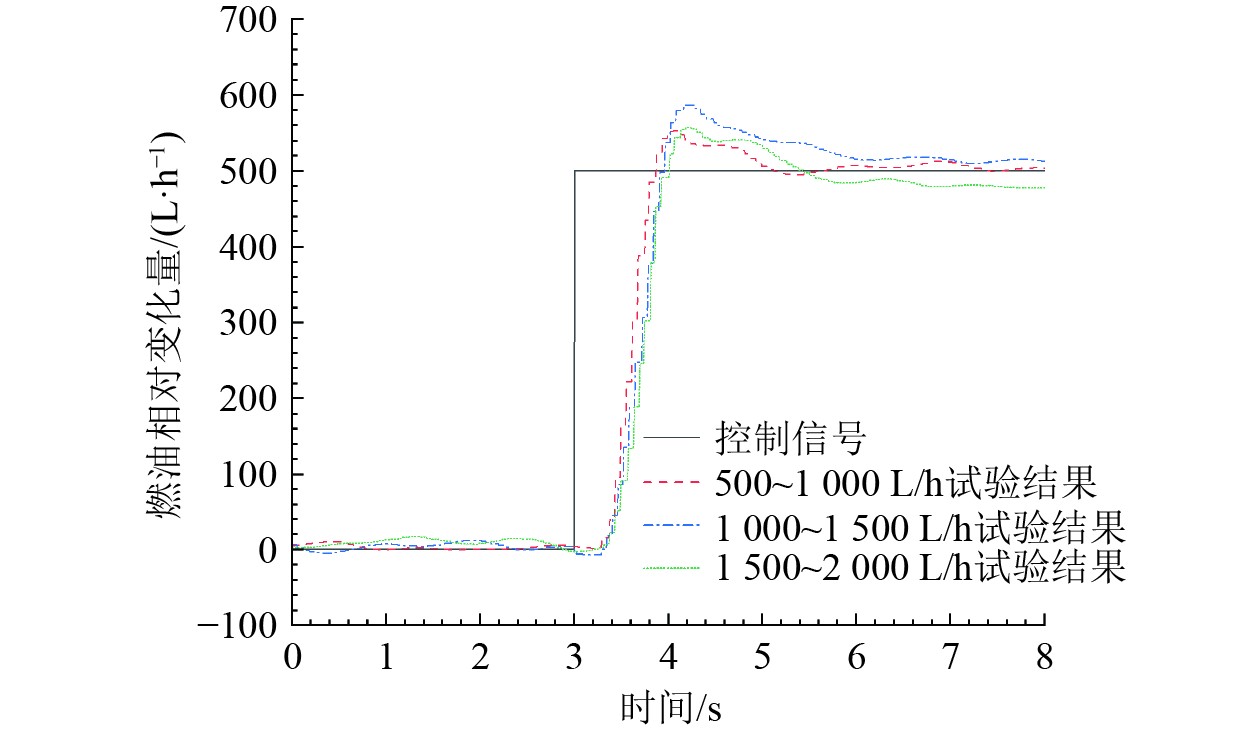
图 5 不同阶跃控制信号下结果对比 Fig. 5 Comparison of results under different step control signals |
可知,控制信号均在第3 s时发生阶跃,而在不同的阶跃控制信号下,燃油计量装置不能跟随控制指令立即输出相应的燃油流量,其具有一定的时滞性。造成这一现象的主要原因包括燃油系统部件运动时受到摩擦、惯性因素、流体粘性因素、流体液压因素以及信号传递速度等。这些因素对稳态信号下输出的燃油流量影响很小,但会对动态信号下的燃油输出产生很大影响。为了得到这一时滞性的规律,对3种不同阶跃控制信号下的试验结果进行对比分析,可以看出当控制信号开始发生变化时,不同信号下的试验结果几乎重合,燃油系统模拟装置输出燃油的时间均滞后了0.3~0.5 s;在阶跃控制信号下燃油流量的响应需要一定的调节时间[18],其响应曲线的延迟时间约0.3 s,响应曲线的上升时间约0.5 s,整个响应的调节时间约0.9 s。
4.2 燃油系统时滞特性对燃气轮机动态性能的影响研究为了研究燃油系统时滞特性对燃气轮机突变负荷时动态性能的影响,并对燃气轮机多系统集成模型进行验证,本文设计了3种仿真方案。方案1是对不考虑燃油系统时滞特性的燃气轮机本体模型进行单独仿真;方案2是对燃气轮机多系统集成模型进行集成仿真;方案3是基于设计的发电燃气轮机半物理仿真实验台进行实验。对这3种方案进行变工况仿真研究,选取这3种方案下燃气轮机的燃油流量、高压轴转速、低压轴转速和动力涡轮转速的数据进行对比分析。
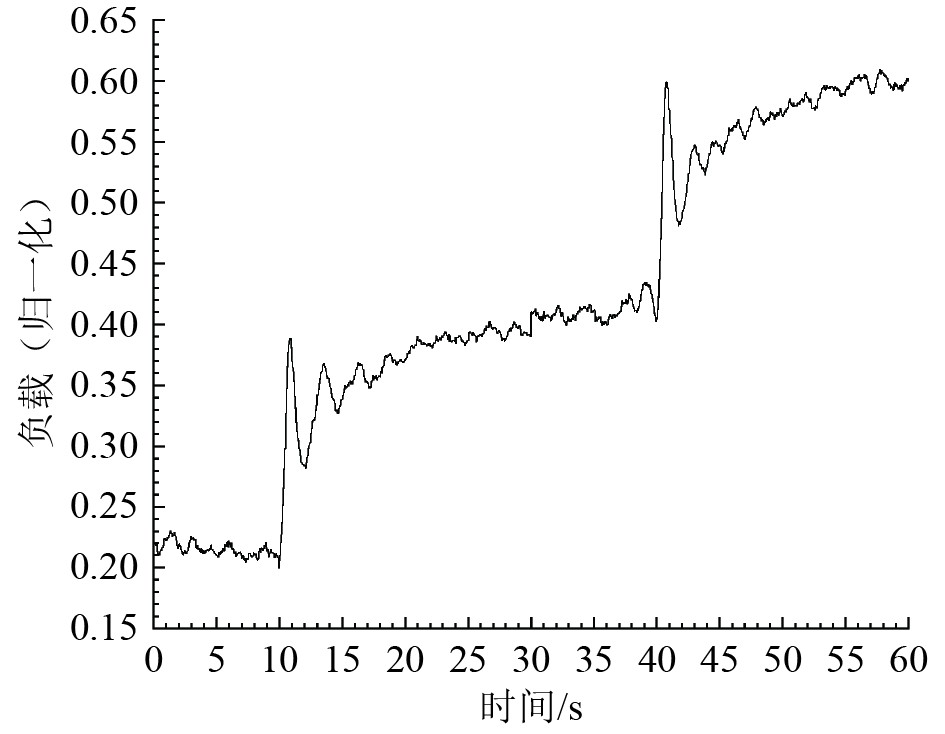
通过发电燃气轮机半物理仿真实验台的监控界面控制负载箱,进行变工况的半物理仿真实验。在监控界面设定阶跃的负载信号,采集到的负载变化如图6所示。负载在0~10 s期间稳定运行在0.2工况,第10 s时阶跃上升至0.4工况并在0.4工况稳定运行30 s,第40 s时阶跃上升至0.6工况并在0.6工况稳定运行20 s,60 s时结束。
|
图 6 变工况过程中负载变化 Fig. 6 Load changes during variable working conditions |
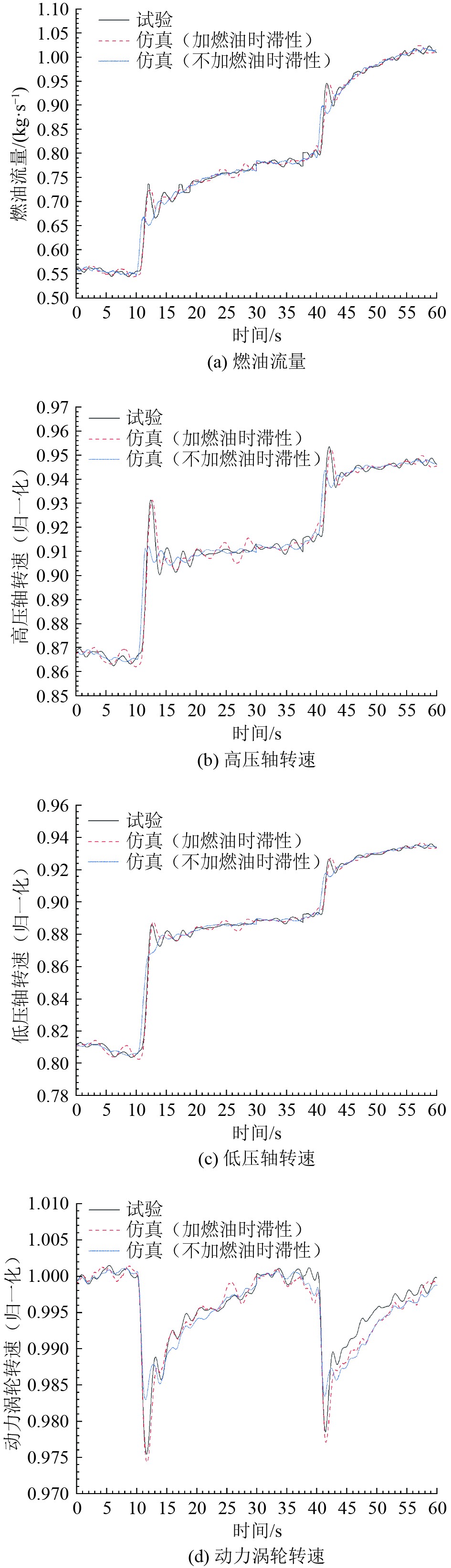
为了保证实验与仿真的入口边界条件一致,将图6中采集的负载作为仿真模型的负载输入进行仿真。由于电流信号传递过程中存在干扰,采集到的负载在阶跃时存在波动。负载明显的动态特征使多系统集成模型的验证更具有挑战性。在这种负载条件下,2种仿真方案中燃气轮机的燃油流量、高压轴转速、低压轴转速和动力涡轮转速的仿真结果如图7中各仿真曲线所示。
|
图 7 变工况过程中3种方案各参数变化 Fig. 7 The parameters of the three schemes change in the process of varying working conditions |
根据图7(a),在突变负载的动态过程中,对于考虑燃油系统时滞性的集成仿真和半物理实验,其燃油流量开始变化的时间相对于不考虑燃油系统时滞性的单独仿真结果滞后了约0.5 s;超调量和调节时间也明显大于单独仿真结果。说明燃油系统的时滞特性导致突增负载时燃气轮机的燃油系统输出燃油滞后,调节能力减弱,调节所需时间增加。
根据图7(b)~图7(d),燃油的变化导致集成仿真和半物理实验结果中的高压轴转速和低压轴转速开始变化的时间相对于不考虑燃油系统时滞性的仿真结果滞后了约0.5 s,且瞬态调速率和调节时间明显更大。动力涡轮转速会在负载突增的时刻直接发生突变,这是由于负载扭矩的增大会直接作用于动力涡轮轴的剩余功率。值得注意的是,这种突变现象不会迅速的反馈至高压轴和低压轴,因为燃气发生器的状态主要由燃油量决定。由于时滞性导致的燃油系统调节燃油能力变弱,燃油流量超调量变大,因此动力涡轮转速的瞬态调速率明显增大。我们使用转速动态变化过程中的最大(最小)转速与额定转速之差的绝对值同额定转速之比,即瞬态调速率作为发动机稳定性的评价指标。变工况过程中的瞬态调速率结果如表3所示。可知,在0.2~0.4工况和0.4~0.6工况的突增负载过程中,半物理实验结果中的动力涡轮转速瞬态调速率相比于不考虑燃油系统时滞性的仿真结果分别增大了44.36%和29.75%。
|
|
表 3 变工况过程中的动力涡轮转速瞬态调速率 Tab.3 Transient speed adjustment of power turbine speed during variable operating conditions |
在2个突增0.2工况的变工况过程中,考虑燃油时滞性的集成仿真结果与半物理实验结果中各参数的最大相对误差如表4所示。可知,在整个突增负载的变工况过程中,集成仿真与半物理实验结果中各参数的最大相对误差为5.19%。
|
|
表 4 集成仿真与半物理实验结果误差 Tab.4 Result error between integrated simulation and semi-physical experiment |
本文利用Matlab/Simulink建立三轴发电燃气轮机仿真模型,利用AMESim建立燃油系统仿真模型,创建联合仿真接口,实现燃气轮机模型和燃油系统模型的集成。设计发电燃气轮机半物理仿真实验台,对不考虑燃油系统时滞特性的燃气轮机本体模型、考虑燃油系统时滞特性的燃气轮机多系统集成模型和发电燃气轮机半物理仿真实验台进行变工况仿真,所得结论如下:
1)燃油系统输出燃油具有一定的时滞性。在不同的阶跃控制信号下,燃油系统输出的燃油流量滞后了0.3~0.5 s才开始发生变化;在阶跃控制信号下燃油流量的响应需要一定的调节时间,其响应曲线的延迟时间约0.3 s,响应曲线的上升时间约0.5 s,整个响应的调节时间约0.9 s。
2)在0.2~0.4工况和0.4~0.6工况的突变负载过程中,燃气轮机多系统集成模型的仿真结果与半物理实验的实验结果中各参数的最大相对误差为5.19%。
3)燃油系统的时滞特性会导致突变负荷动态过程中燃气轮机燃油系统输出燃油滞后约0.5 s,燃油调节能力减弱;造成高、低压轴转速变化时间滞后,瞬态调速率和调节时间增大;造成动力涡轮转速的瞬态调速率增大,在0.2~0.4工况和0.4~0.6工况的突变负荷过程中分别增大44.36%和29.75%。
| [1] |
王旭. 燃气轮机在船舶动力装置中的应用[J]. 内燃机与配件, 2018(9): 46-47. WANG X. Application of gas turbine in ship power plant[J]. Internal Combustion Engine & Parts, 2018(9): 46-47. DOI:10.3969/j.issn.1674-957X.2018.09.024 |
| [2] |
王守相, 孟子涵. 舰船综合电力系统分析技术研究现状与展望[J]. 中国舰船研究, 2019, 14(2): 107-117. WANG S X, MENG Z H. Current status and prospects of analysis technologies of shipboard integrated power system[J]. Chinese Journal of Ship Research, 2019, 14(2): 107-117. |
| [3] |
丁宁. 燃气轮机燃油控制系统建模仿真及故障模拟研究[D]. 哈尔滨: 哈尔滨工程大学, 2023.
|
| [4] |
秦宇. 船用燃气轮机燃油系统故障模拟及诊断研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [5] |
孙建国. 现代航空动力装置控制[M]. 北京: 航空工业出版社, 2009.
|
| [6] |
REED J A, AFJEH A A. Computational simulation of gas turbine: part i foundation of component based models[J]. Journal of Engineering for Gas Turbines and Power, 2000, 12(3): 10−13.
|
| [7] |
ISHOLA A A , RACHEL C , TALIB A . Mathematical modeling and simulation of a twin-engine aircraft fuel system using matlab-simulink[J]. International Journal of Control Science and Engineering, 2018, 8(1): 12.
|
| [8] |
丁琳, 王道波, 李猛, 等. 直升机涡轴发动机燃油调节系统建模与仿真[J]. 航空兵器, 2011(4): 30-34. DING L, WANG D B, LI M, et al. Modeling and simulation of fuel conditioning system for turbo-shaft engine of helicopter[J]. Aero Weaponry, 2011(4): 30-34. DOI:10.3969/j.issn.1673-5048.2011.04.008 |
| [9] |
张东. 发动机主燃油控制系统建模仿真与试验验证[D]. 南京: 南京航空航天大学, 2008.
|
| [10] |
刘振刚, 郭政波. 基于试飞数据的涡扇发动机主燃油系统建模研究[J]. 工程与试验, 2018, 58(3): 77-81. LIU Z G, GUO Z G. Research on main fuel system modeling of turbofan engine based on flight test data[J]. Engineering & Test, 2018, 58(3): 77-81. DOI:10.3969/j.issn.1674-3407.2018.03.017 |
| [11] |
ZEPENG S , HUIBING G , ZHENGUO J , et al. Modeling and optimization of fuel-mode switching and control systems for marine dual-fuel engine[J]. Journal of Marine Science and Engineering, 2022, 10(12): 2004−2004.
|
| [12] |
吴文斐, 郭迎清, 李睿, 等. 涡扇发动机液压机械主控制系统建模与仿真分析[J]. 航空发动机, 2011, 37(1): 16-19. WU W F, GUO Y Q, LI R, et al. Modeling and simulation analysis of hydro-mechanical main control system for turbofan engine[J]. Aeroengine, 2011, 37(1): 16-19. DOI:10.3969/j.issn.1672-3147.2011.01.005 |
| [13] |
吴文斐, 郭迎清, 陆军. 涡扇发动机液压机械式自动加速器优化设计[J]. 航空动力学报, 2010, 25(10): 2379-2385. WU W F, GUO Y Q, LU J. Optimal design of the turbofan engine hydro-mechanical accelerator[J]. Journal of Aerospace Power, 2010, 25(10): 2379-2385. |
| [14] |
李淑英. 船舶动力装置仿真技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2013: 94.
|
| [15] |
关天皓. 船用发电燃气轮机精细化建模仿真及性能优化研究[D]. 哈尔滨: 哈尔滨工程大学, 2023.
|
| [16] |
冯永保, 李锋, 何润生. 液压传动与控制[M]. 西安: 西北工业大学出版社, 2020.
|
| [17] |
曹建国. 航空发动机仿真技术研究现状、挑战和展望[J]. 推进技术, 2018, 39(5): 961-970. CAO J G. Status, challenges and perspectives of aero-engine simulation technology[J]. Journal of Propulsion Technology, 2018, 39(5): 961-970. |
| [18] |
胡寿松. 自动控制原理(第五版)[M]. 北京: 科学出版社, 2007.
|
 2025, Vol. 47
2025, Vol. 47
