2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 江西职业技术大学 船舶工程学院,江西 九江 332007
2. China Ship Development and Design Center, Wuhan 430064, China;
3. Shipbuilding Engineering Department, Jiangxi Polytechnic University, Jiujiang 332007, China
水下航行器是各国军事力量的象征,是公认的战略性武器,其在航行过程中的快速性是在设计阶段需要考虑的重要因素。因此,水下航行器在航行时所受到的流体阻力在水下航行器性能的相关研究中备受关注。国内外专家已经通过各种技术和方式对水下航行器阻力开展了诸多研究。其中数值计算方法已经成为了研究水下航行器水动力性能的必不可少的手段和方法[1]。李鹏等[2]采用商业软件STAR-CCM+对SUBOFF标准模型进行了数值模拟,分析在模拟潜艇的水动力性能时,采用不同湍流模型所造成的差异;卢博等[3]采用延迟分离涡模拟求解了某潜艇模型在不同附体影响下的流场并分析了潜艇的阻力特性;柏铁朝等[4]通过数值模拟发现,潜艇潜深对阻力系数的影响会随着潜深的增大而逐渐减小。
水下航行器的阻力按照承受阻力的部分可以分为主体阻力和附体阻力,由于在水下航行器总阻力中,附体阻力的占比要远高于传统水面船舶,且附体形状较为复杂且多样,包括艏升降舵、指挥台围壳、方向舵、艉升降舵、稳定翼、特种装置和超出主体线型之外的导流罩等部件。其中,水下航行器的桅杆导流罩是造成附体阻力的重要部分,因此,单独关注桅杆导流罩的阻力在优化水下航行器设计中非常必要。在分析研究中,对桅杆导流罩的分析即是对不同剖面下的圆柱体进行水动力分析。自冯·卡门[5]对涡街的诱导速度、稳定性和阻力进行了分析后,越来越多的学者加入到对钝体绕流的分析中来;Parnaudeau等 [6]对雷诺数为
本文对实尺度的水下航行器桅杆导流罩的阻力进行了预报。先通过对比数值计算和模型试验的结果,验证了数值计算结果的准确性。再对模型尺度的桅杆导流罩进行阻力分析并对实尺度桅杆导流罩进行了阻力预报。最后,分别对2种典型工况下的桅杆导流罩进行阻力和力矩的预报。该研究对实尺度下不同形状的桅杆导流罩进行预报分析,对比了2种桅杆导流罩在不同海况下的水动力性能,有效节省了进行实尺度试验的成本。
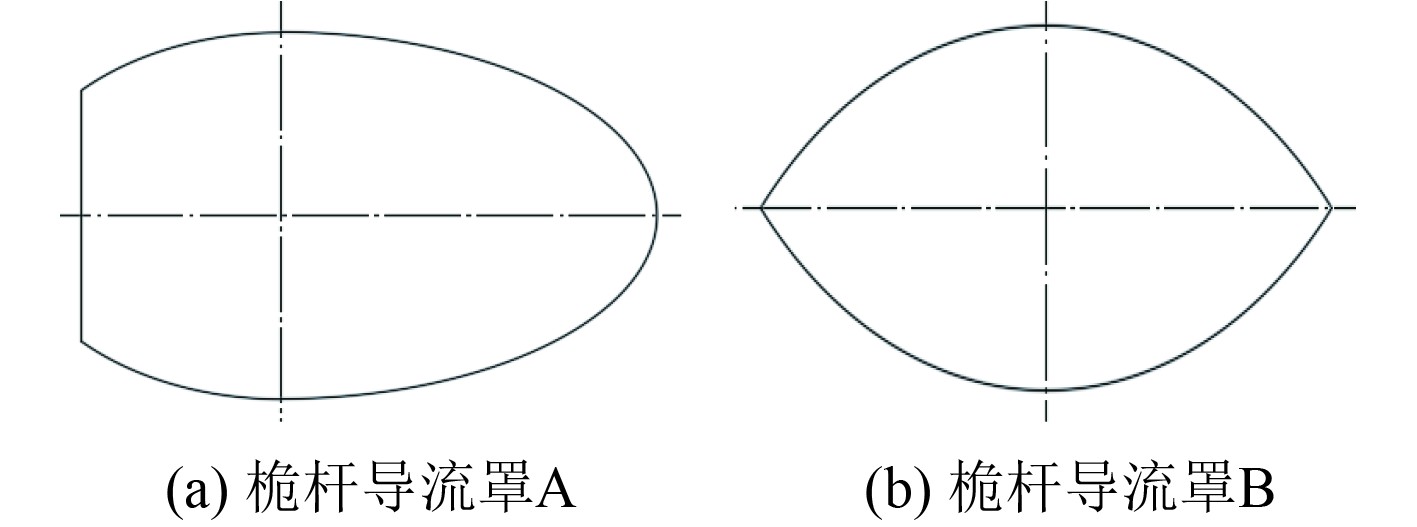
1 研究对象及计算技术 1.1 研究对象分析试验与仿真计算过程中,考虑2种不同剖面的桅杆导流罩,进行试验和三维数值计算,2种桅杆导流罩的剖面形状如图1所示。2种桅杆导流罩分别为桅杆导流罩A、桅杆导流罩B(以下分别简称为A、B)。
|
图 1 不同桅杆导流罩的二维剖面形状 Fig. 1 Two dimensional cross-sectional shapes of different mast fairing |
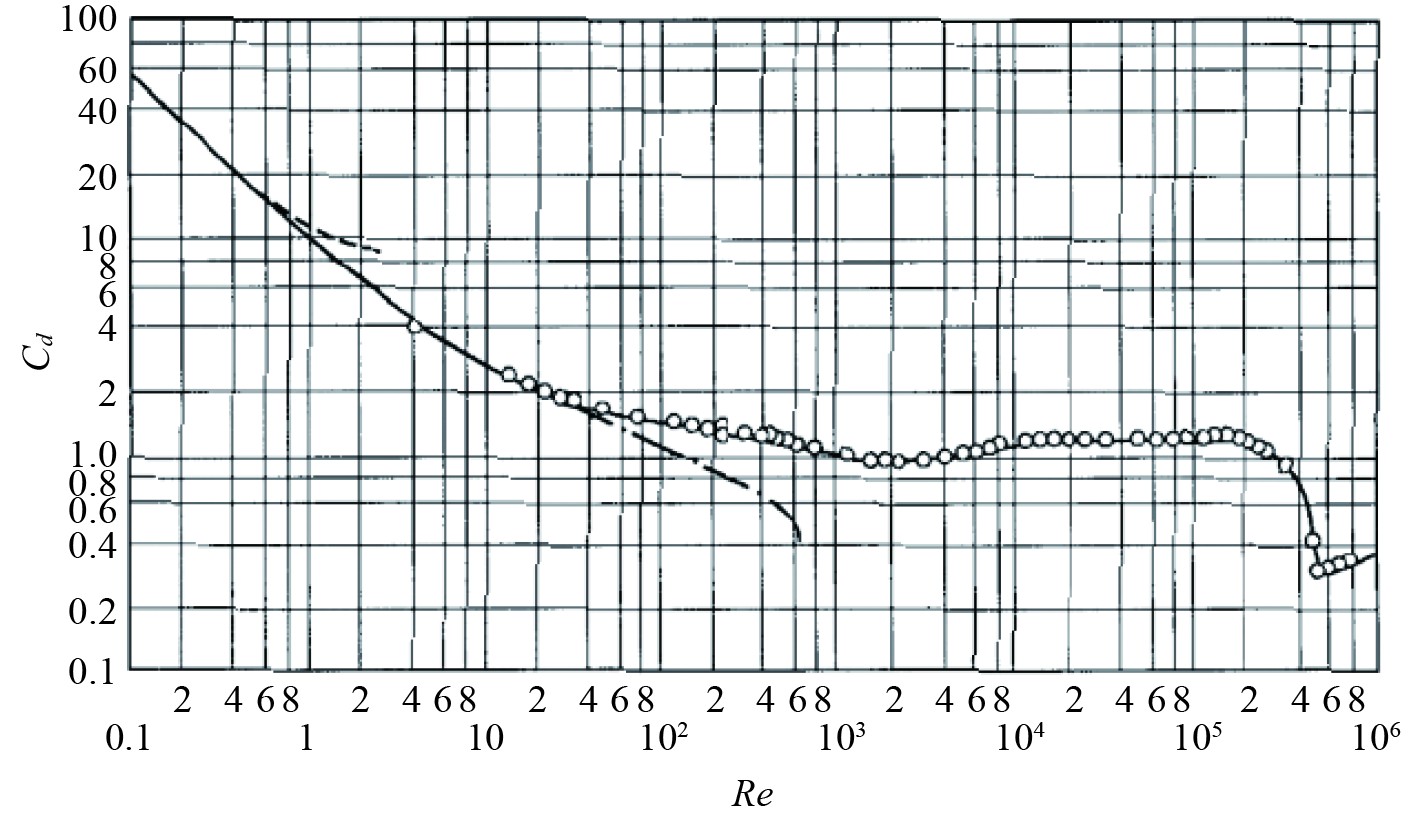
在图1中,导流罩A的迎流直径为0.372 m,在设计航速v=10 kn时,其特征雷诺数为1.61×106,导流罩B的迎流直径为0.29 m,在设计航速v=10 kn时,其特征雷诺数为1.25×106。图2所示为圆柱绕流阻力系数Cd随雷诺数Re的变化,对于经典的圆柱绕流,该量级的雷诺数均位于超临界区域,故对于波浪阻力准确预报存在一定难度。同时上述2个剖面形状在迎流面或背流面与圆柱的外形有重合部分,故在后续水动力学仿真中也可能存在一定的难度。
|
图 2 圆柱绕流阻力系数Cd随雷诺数Re的变化 Fig. 2 Variation of drag coefficient Cd around a cylinder with Reynolds number Re |
在进行桅杆导流罩A、B剖面的三维阻力计算和试验验证时,考虑桅杆导流罩临界出水工况H1和桅杆导流罩部分出水工况H2。
在H1工况中,桅杆顶部与静水面平齐,桅杆贴近水面部分会产生粘性阻力与兴波阻力并受波浪作用产生波浪载荷,桅杆水下部分仅受粘性阻力,桅杆阻力计算的高度为剖面在来流方向的投影宽度。
在H2工况中,桅杆出水部分高度为1/2的有义波高,桅杆近水面部分会产生粘性阻力与兴波阻力并受波浪作用产生波浪载荷,桅杆水下部分仅受粘性阻力,桅杆阻力计算的高度为1/2有义波高加上剖面在来流方向的投影宽度。
1.3 三维阻力计算关键技术桅杆导流罩的三维阻力可以分为水下阻力和水面阻力。对于水下阻力,考虑到三维圆柱阻力分布沿着高度方向变化较小,则桅杆的水下阻力可参照相应剖面的二维的阻力计算结果,即二维阻力计算结果在相应水深高度的积分等于水下阻力值。对于水面阻力,需要先计算相应的圆柱标准模型算例来提高模拟精度,其中圆柱标准模型算例的计算网格及求解模型的选取如下:对于网格设置,三维网格设置使用的网格类型为六面体网格,棱柱层数为20层,对流域和圆柱外围进行额外加密。图3为加密后的计算域网格和圆柱剖面附近的加密网格。

|
图 3 圆柱标准模型算例计算网格划分 Fig. 3 Mesh division of cylindrical standard model example |
对于湍流模型及求解器的选择,在物理模型的选择中,选取VOF波模型,时间项选择隐式不定常,粘滞项选择流态为湍流,在雷诺平均湍流模型中求解方程选择可实现的k-ε模型,材料选择欧拉多相流,流体选择分离流体。在求解器中时间步长设置为0.01 s,时间离散设置为一阶,最大物理时间为40 s,最大内部迭代为15。
1.4 波浪载荷计算关键技术对于波浪载荷计算,利用Ansys-AQWA对桅杆导流罩在不同航速下受到的阻力进行频域预报,得出桅杆导流罩阻力性能预报分析。
Ansys-AQWA基于规则波中的三维射衍射理论,在线性流体理论下可以对各种浮式类和系泊类海洋结构物在不同环境载荷下的运动响应和受力进行模拟,并进行水动力计算和分析。AQWA中结构的网格划分采用表面网格划分法。
对于规则波,对桅杆导流罩的受力进行模拟仿真,主要关注迎浪时(浪向角为0°)桅杆导流罩的受力响应;对于不规则波,选用Pierson-Moskowitz海浪谱,计算浪向角为0°下三级海况、四级海况和五级海况下桅杆导流罩的受力响应。不同海况下的波浪参数如表1所示。本研究Ansys-AQWA的总工况数如表2所示。
|
|
表 1 不同海况下的波浪参数 Tab.1 Wave parameters under different sea conditions |
|
|
表 2 计算工况 Tab.2 Calculate operating conditions |
为验证三维模型阻力计算的可靠性,选取直径D=0.2 m、高H=0.8 m的圆柱在雷诺数Re=1.23×105进行阻力计算,计算得到的阻力系数Cd=1.04。在雷诺数Re=1.23×105时,Yeon等[9]在2016年进行CFD计算的Cd=1.16,可得计算误差为11.5%;故计算模型的选取具有一定的可靠性,能够满足本文对阻力计算的精度要求。
2.2 模型尺度阻力分析 2.2.1 水面阻力对剖面A和剖面B,都考虑缩比2.5的大模型,分别开展水面阻力CFD计算和水面拖曳试验。在水面阻力CFD计算中,模型高度与入水高度与H2工况保持一致;在水面拖曳试验中,模型高800 mm,吃水为400 mm。
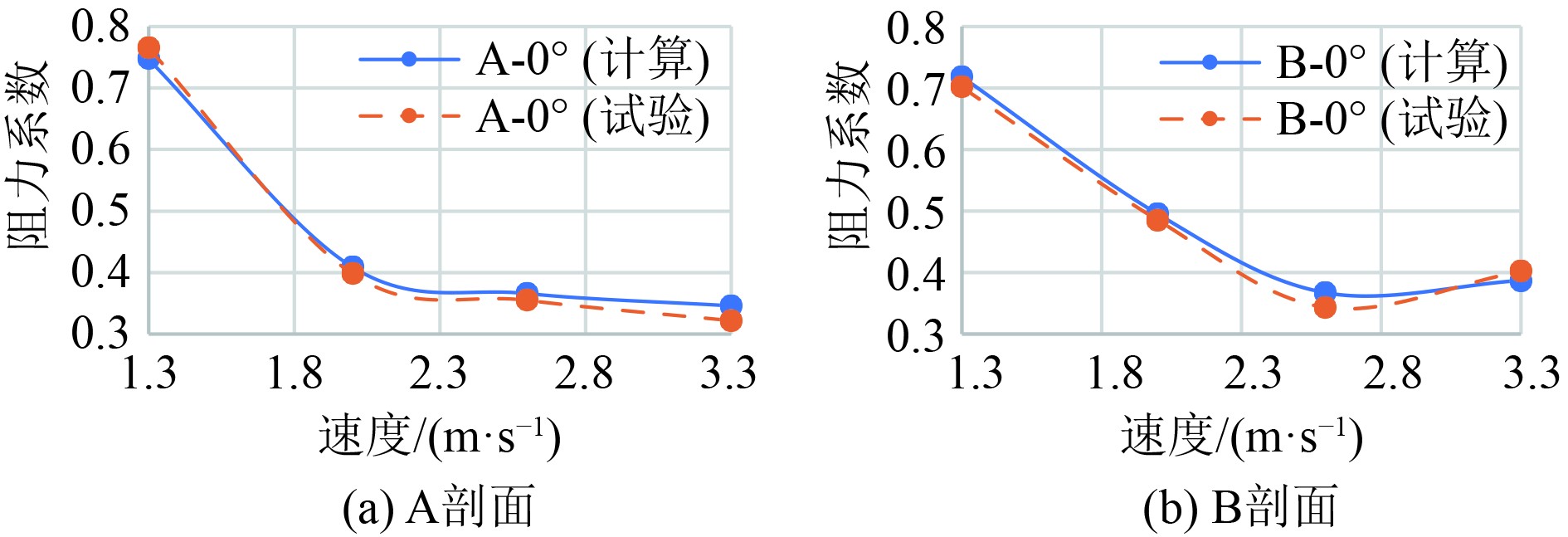
图4所示为通过模型尺度CFD计算和模型试验获得的A剖面大模型和B剖面大模型的水面阻力系数。表3所示为对应的阻力系数与相对误差。
|
图 4 A、B剖面大模型水面阻力系数对比 Fig. 4 Comparison of water surface resistance coefficient between A and B profile large models |
|
|
表 3 A、B剖面大模型水面阻力系数 Tab.3 Water surface resistance coefficient of A and B profile large models |
从图4和表3中可发现,模型尺度CFD计算阻力值与模型试验阻力值吻合较好,最大相对误差为7.4%,验证了模型尺度CFD计算精度。同时,在较高航速下,A剖面的水面阻力系数略小于B剖面。
2.2.2 水下阻力对剖面A考虑缩比为3.9的小模型、对剖面B考虑缩比2.5的大模型;水下阻力CFD计算采用二维剖面计算结果,水下模型拖曳试验通过将总阻力减去水下部分用于连接模型与传感器的长剑杆阻力得到模型水下阻力。对CFD计算结果和模型试验结果分别进行无量纲化处理后,以得到模型水下阻力系数。
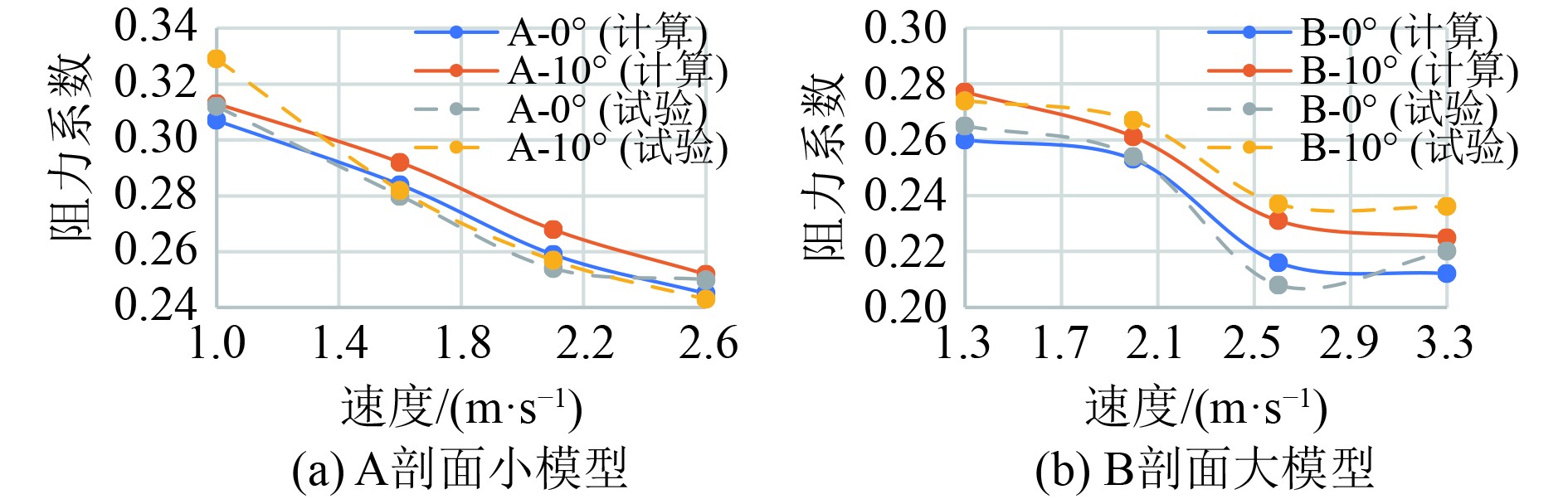
图5所示为通过模型尺度CFD计算和模型试验获得的A剖面小模型和B剖面大模型在攻角分别为0°和10°时的水下阻力系数。表4所示为对应的阻力系数与相对误差。
|
图 5 A剖面小模型、B剖面大模型水下阻力系数对比 Fig. 5 Comparison of underwater resistance coefficient between A profile small model and B profile large model |
|
|
表 4 A剖面小模型、B剖面大模型水下阻力系数 Tab.4 Underwater resistance coefficient of A profile small model and B profile large model |
从图5和表4中可发现,模型尺度CFD计算阻力值与模型试验阻力值吻合较好,最大相对误差为4.6%,验证了模型尺度CFD计算精度。同时,A剖面的水下阻力系数比B剖面的水下阻力系数大;当攻角增加时,2个剖面的水下阻力系数随之增加。
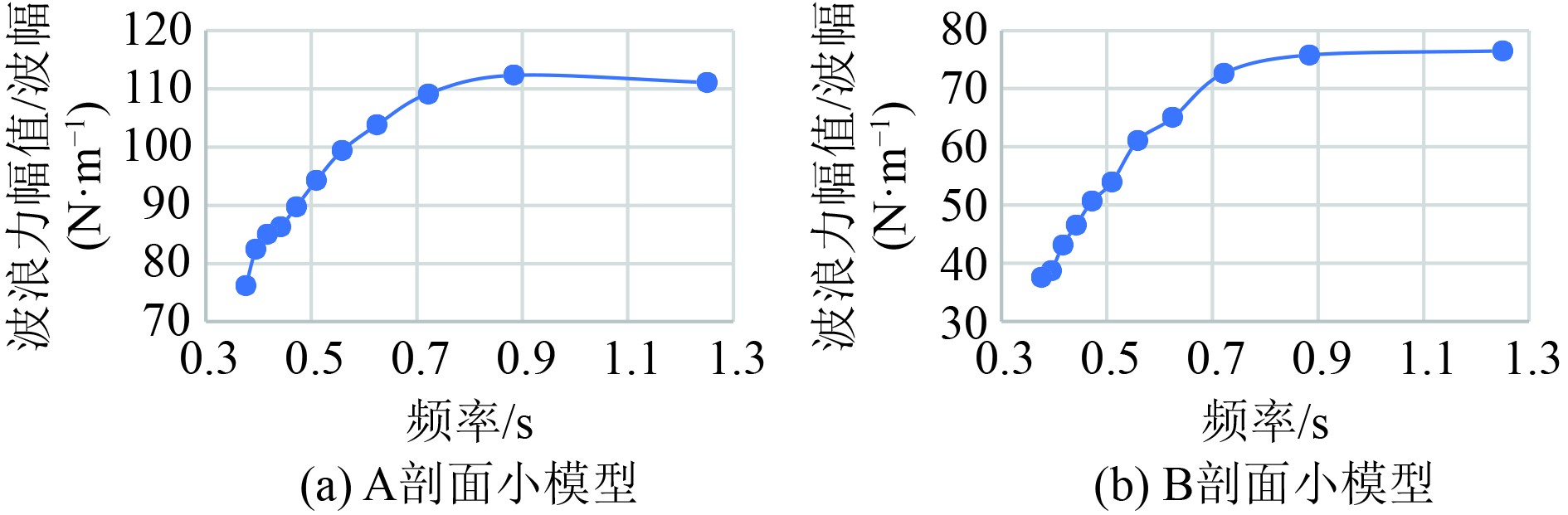
2.2.3 水面波浪力RAO考虑2个剖面,开展缩比为3.9小模型的水面规则波试验。在华中科技大学拖曳水池造波系统造波范围内,选取波长1~11 m。测量2个剖面的波浪力,得2个剖面的波浪力RAO如图6所示。
|
图 6 A、B剖面小模型波浪力RAO对比 Fig. 6 Comparison of wave force RAO between A and B profile small models |
考虑A、B剖面,基于实尺度的CFD计算和缩比2.5大模型的水面拖曳试验,对H2工况中水面部分进行阻力预报。
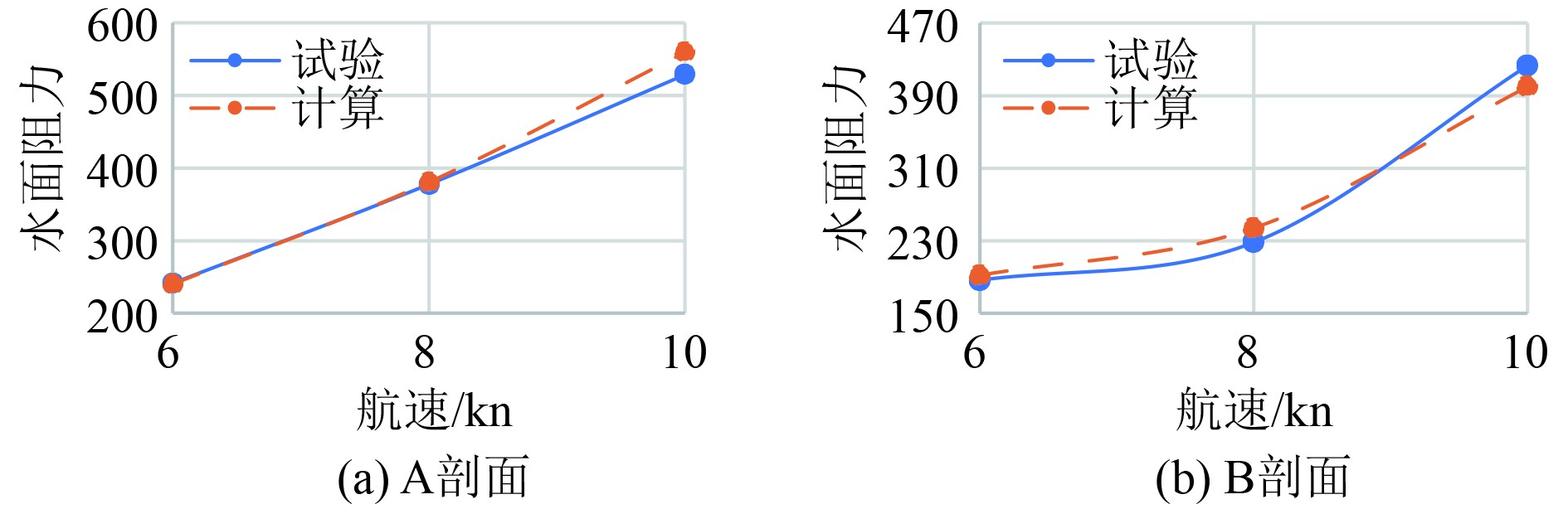
图7所示为通过实尺度CFD计算和模型试验预报获得的A剖面和B剖面的水面阻力。表5所示为对应的阻力与相对误差。
|
图 7 A、B剖面水面阻力对比 Fig. 7 Comparison of water surface resistance between A and B profiles |
|
|
表 5 A、B剖面水面阻力 Tab.5 Water surface resistance of A and B profiles |
从图7和表5中可发现,实尺度CFD计算阻力值与模型试验预报的水面阻力值吻合较好,最大相对误差为7.04%,验证了实尺度CFD计算精度。同时,A剖面的水面阻力大于B剖面的水面阻力。
2.3.2 水下阻力考虑A和B剖面,基于实尺度的二维CFD计算和缩比模型的水下拖曳试验,对H2工况中水面部分进行阻力预报。
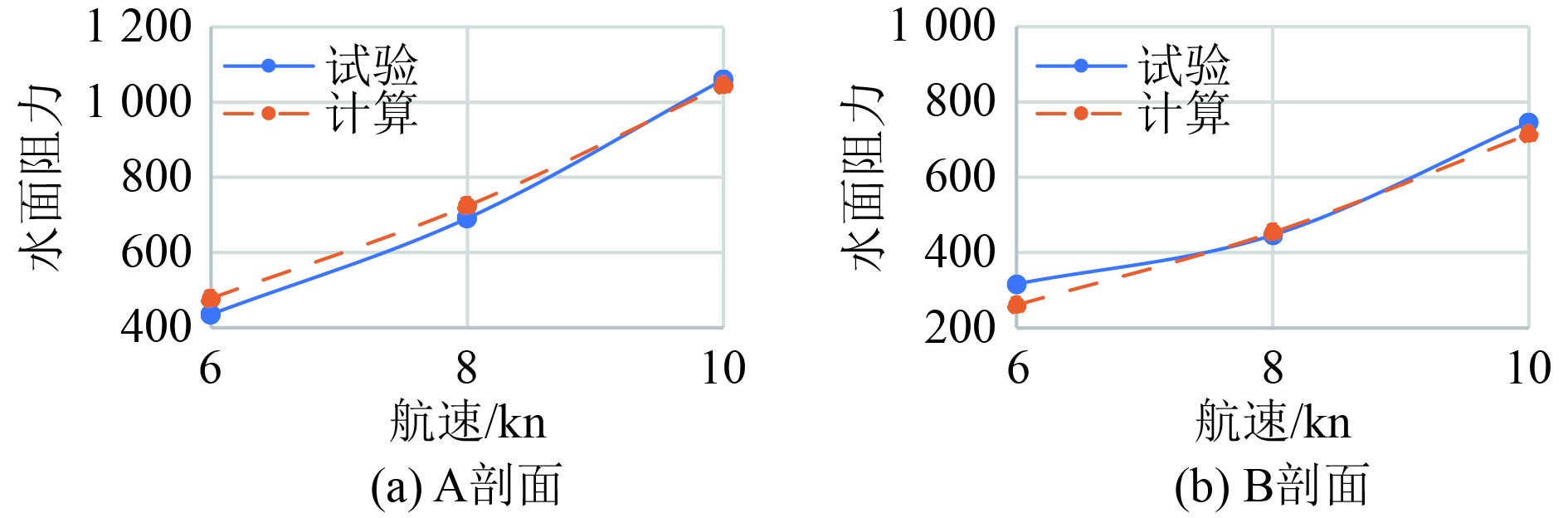
图8所示为通过实尺度CFD计算和模型试验预报获得的A剖面和B剖面的水下阻力。表6所示为对应的阻力值与相对误差。
|
图 8 A、B剖面水下阻力对比 Fig. 8 Comparison of underwater resistance between A and B profiles |
|
|
表 6 A、B剖面水下阻力 Tab.6 Underwater resistance between A and B profiles |
从图8和表6中可发现,实尺度CFD计算阻力值与模型试验预报的水下阻力值吻合较好,仅6 kn时B剖面水下阻力相对误差偏大,其他工况下最大相对误差在9.80%以内,验证了实尺度CFD计算精度。同时,A剖面的水下阻力大于B剖面的水下阻力。
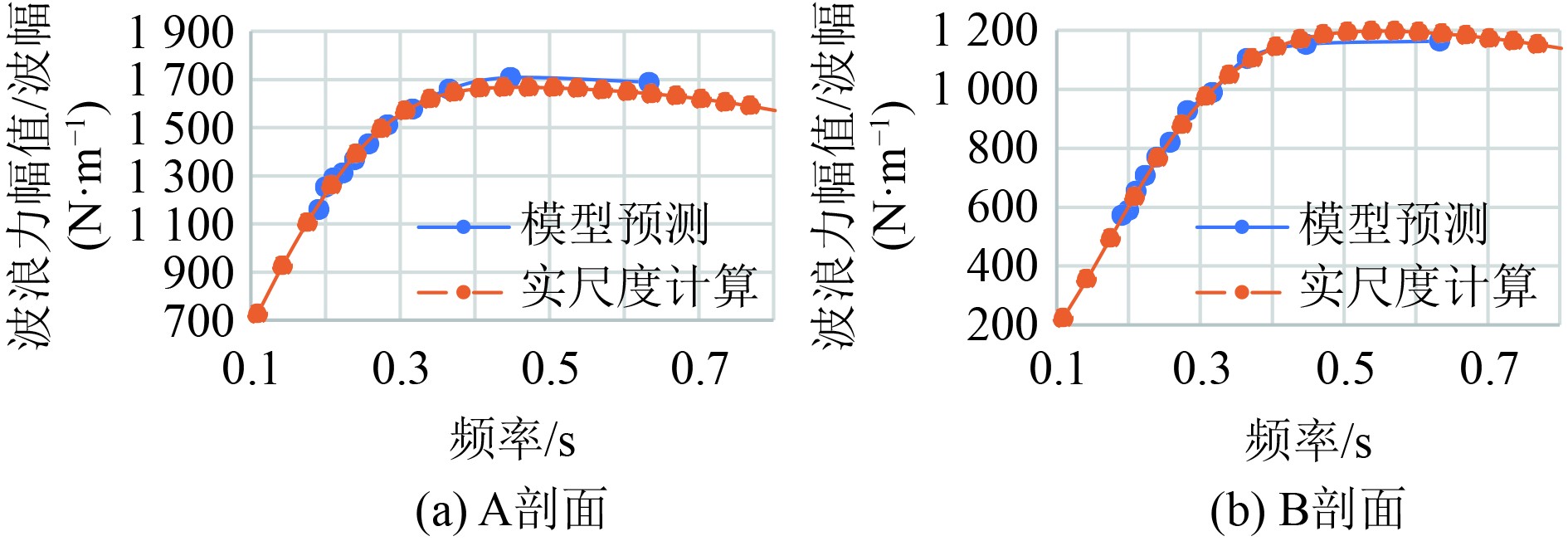
2.3.3 水面波浪载荷首先,基于实尺度势流计算和模型试验,对比A剖面和B剖面波浪力RAO,如图9所示。可发现模型试验预报波浪力RAO与势流计算结果吻合较好,进一步验证了势流计算的准确度。
|
图 9 A、B剖面波浪力RAO Fig. 9 Wave force RAO on A and B profiles |
基于势流计算,获得不同航速下A剖面和B剖面的波浪力统计值,如表7~表9所示。
|
|
表 7 6 kn航速下A、B剖面的波浪力统计值 Tab.7 Statistical values of wave forces on A and B profiles at a speed of 6 kn |
|
|
表 8 8 kn航速下A、B剖面的波浪力统计值 Tab.8 Statistical values of wave forces on A and B profiles at a speed of 8 kn |
|
|
表 9 10 kn航速下A、B剖面的波浪力统计值 Tab.9 Statistical values of wave forces on A and B profiles at a speed of 10 kn |
计算桅杆导流罩A、B剖面的总阻力与阻力矩时,考虑H1和H2工况。
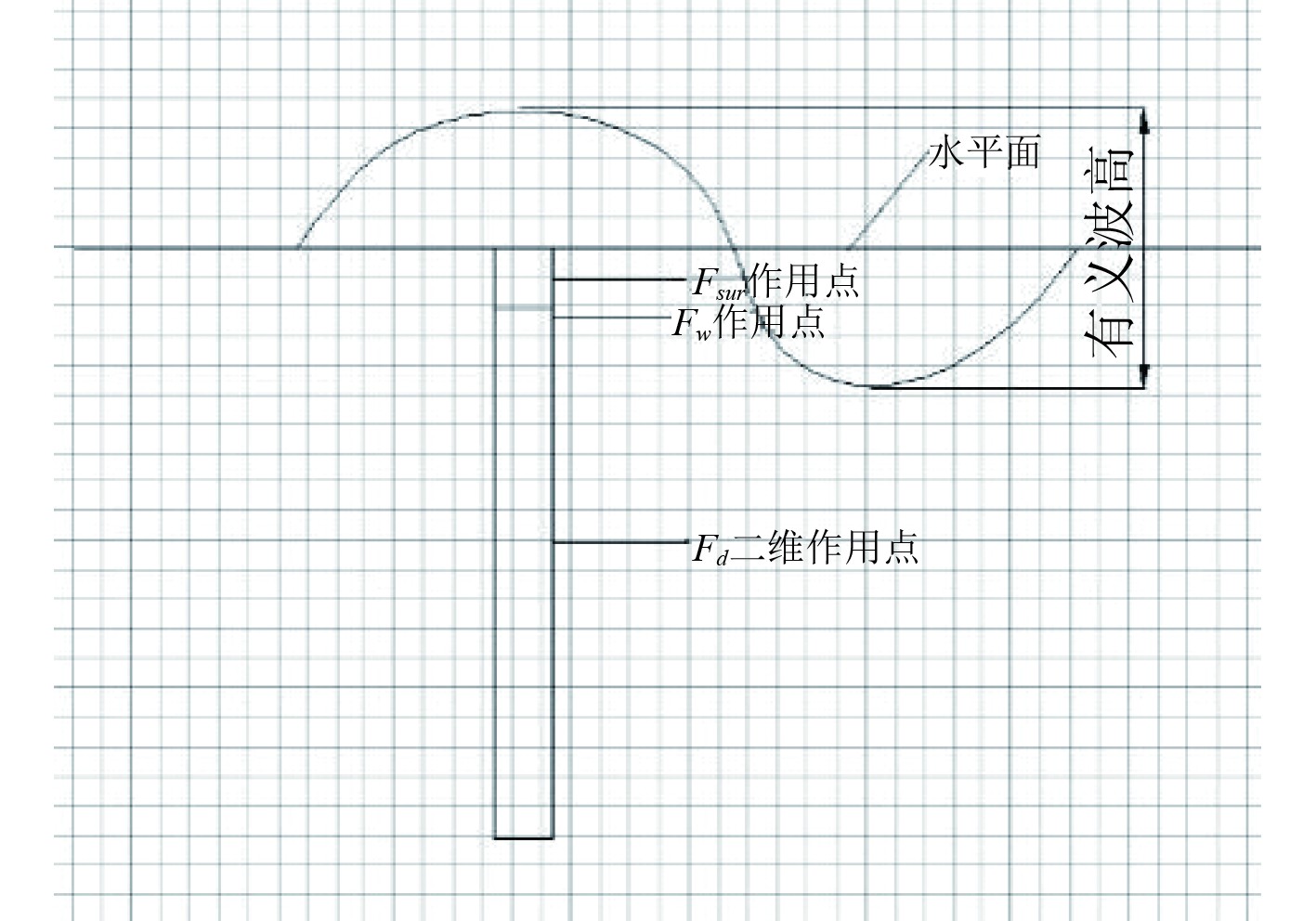
2.4.1 H1工况H1工况下阻力波浪力作用点位置如图10所示,桅杆顶部与静水面平齐,桅杆贴近水面部分会产生粘性阻力与兴波阻力并受波浪作用产生波浪载荷,桅杆水下部分仅受粘性阻力。假设水面部分高度为一倍的特征投影宽度,该部分粘性阻力与兴波阻力采用相应的三维剖面阻力计算结果,假设阻力作用点在该部分高度中间处(图中Fsur作用点处);波浪载荷采用AQWA计算结果,假设波浪载荷作用点在静水面下1/4有义波高处(图中Fw作用点处)。假定水下部分所受粘性阻力在桅杆高度上均匀分布,阻力作用点在该部分高度中间处(图中Fd二维作用点处)。
|
图 10 H1工况下阻力波浪力作用点位置 Fig. 10 Location of resistance wave force application point under H1 working condition |
表10为数值计算的各剖面在不同海况下的总阻力,其中Fsum3、Fsum4、Fsum5分别代表三级~五级海况下桅杆受到的总阻力。
|
|
表 10 H1工况不同海况下各剖面的总阻力 Tab.10 The total resistance of each profile under different sea conditions in H1 working condition |
表11为H1工况不同海况下各剖面的阻力矩的统计表。其中Msum3、Msum4、Msum5分别代表三级~五级海况下桅杆受到的总阻力矩。
|
|
表 11 H1工况不同海况下各剖面的阻力矩 Tab.11 Resistance moment of each profile under different sea conditions in H1 working condition |
在H1工况下,A剖面在不同海况下所受到的总阻力与阻力矩均大于B剖面。
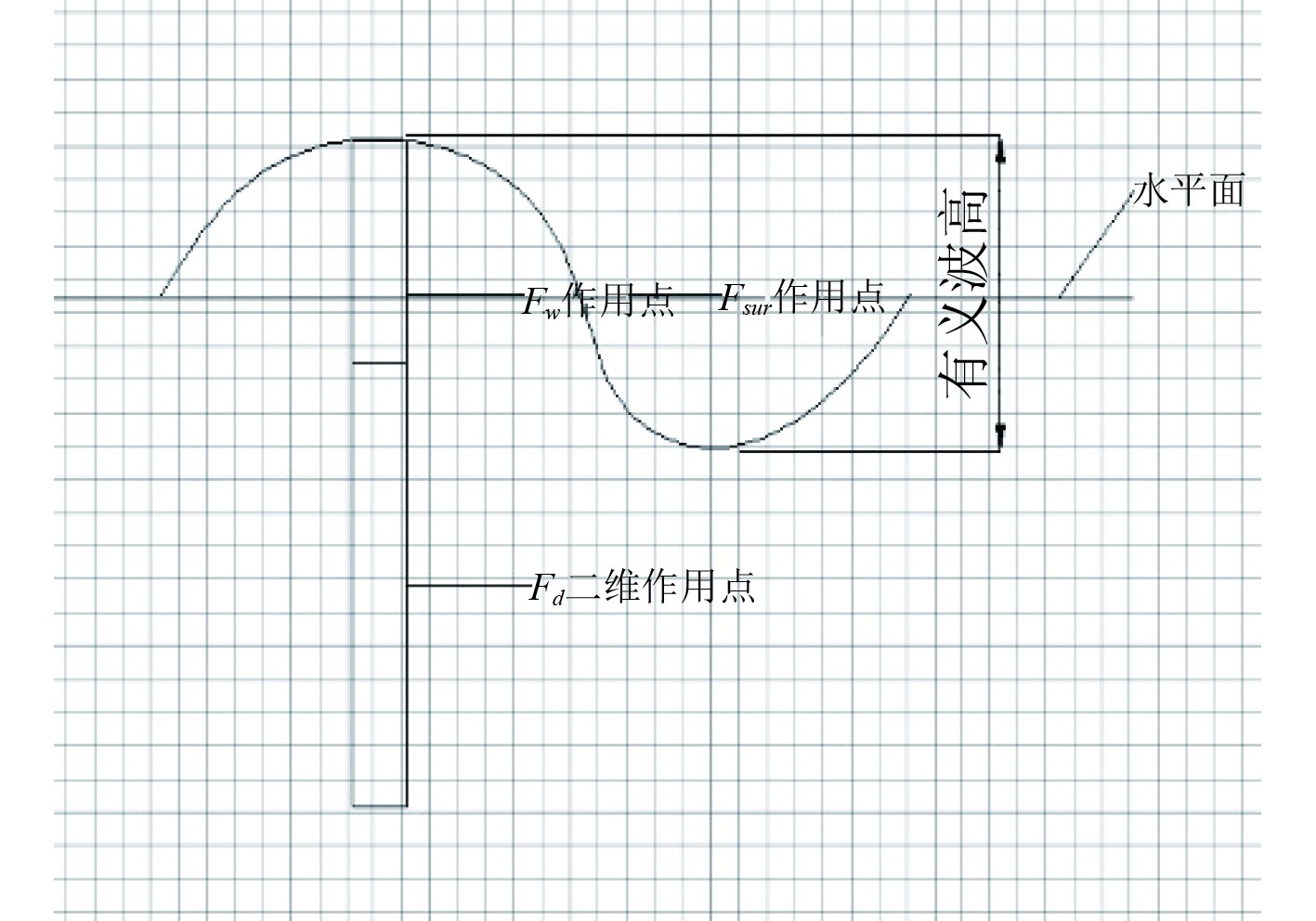
2.4.2 H2工况H2高度下阻力波浪力作用点位置如图11所示,桅杆出水部分高度为1/2的有义波高,桅杆近水面部分会产生粘性阻力与兴波阻力并受波浪作用产生波浪载荷,桅杆水下部分仅受粘性阻力。假设近水面部分高度为1/2的有义波高加剖面在来流方向的投影宽,该部分粘性阻力与兴波阻力采用相应的三维剖面阻力计算结果,假设阻力作用点在静水面处(图中Fsur作用点处);波浪载荷采用AQWA计算结果,假设波浪载荷作用点在静水面处(图中Fw作用点处)。假定水下部分所受粘性阻力在桅杆高度上均匀分布,阻力作用点在该部分高度中间处(图中Fd二维作用点处)。
|
图 11 H2工况下阻力波浪力作用点位置 Fig. 11 Location of resistance wave force application point under H2 working condition |
表12为通过模型试验预报的H2工况不同海况下的总阻力。表13给出了通过数值计算获取的H2工况不同海况下总阻力以及相对误差。通过分析阻力相对误差,发现H2工况下数值计算和模型试验预报结果吻合良好,最大误差小于9.91%。同时A剖面的总阻力显著大于B剖面的。
|
|
表 12 通过模型试验预报的H2工况下不同海况受到的总阻力 Tab.12 The total resistance under different sea conditions predicted by model experiments under H2 operating conditions |
|
|
表 13 通过数值计算预报的H2工况下不同海况的总阻力及误差 Tab.13 The total resistance and error under different sea conditions predicted by numerical calculation under H2 operating conditions |
表14为模型试验预报的H2工况不同海况各剖面的阻力矩。表15为数值计算的H2工况不同海况各剖面的阻力矩及相对误差的统计表。
|
|
表 14 通过模型试验预报的H2工况下不同海况受到的阻力矩 Tab.14 Resistance moment under different sea conditions predicted by model experiments under H2 operating conditions |
|
|
表 15 通过数值计算预报的H2工况下不同海况受到的阻力矩及误差 Tab.15 Resistance moment and error under different sea conditions predicted by numerical calculation for H2 working condition |
通过相对误差分析可以发现,数值计算结果与模型试验预报结果吻合良好,相对误差小于6.36%。同时,在H2工况不同海况下,A2剖面的阻力矩显著大于B2剖面,且这种趋势随航速增加而更加明显。
3 结 语本文对实尺度的水下航行器桅杆导流罩的阻力进行了预报,首先在模型尺度开展关于2个剖面的水面阻力、水下阻力以及水面波浪力RAO的物理试验与数值计算,验证了数值计算结果的精度。再进一步开展实尺度数值计算与模型试验预报对比,发现水面阻力、水下阻力和水面波浪载荷均吻合良好。在此基础上分别针对2个典型工况H1和H2开展了总阻力与阻力矩的预报。
研究结果表明,在实尺度下,剖面A的水面和水下阻力均大于B剖面,这说明该形状的桅杆导流罩具有更优的水动力性能。在2种典型工况中,导流罩受到的阻力大小接近,在三级海况下,H2工况的阻力矩更大;五级海况下,H1工况的阻力矩更大。本研究提出了实尺度桅杆导流罩水动力性能的预报方法,对水下航行器的桅杆导流罩的设计和优化提供了参考和指导。
| [1] |
张楠, 沈泓萃, 姚惠之. 水下航行器阻力与流场的数值模拟与验证及艇型的数值优化研究[J]. 船舶力学, 2005, 2: 1-13. DOI:10.3969/j.issn.1007-7294.2005.05.001 |
| [2] |
李鹏, 王超, 孙华伟, 等. 潜艇阻力及流场数值仿真策略优化分析[J]. 上海交通大学学报, 2022, 56(4): 506-515. |
| [3] |
卢博, 黄桥高, 何幸, 等. 带附体潜艇流场精细化模拟与时空演化特性[J/OL]. 华中科技大学学报(自然科学版), 1−6, 2024−12−03.
|
| [4] |
柏铁朝, 许建, 王国栋, 等. 近冰面航行潜艇阻力及绕流场分析[J]. 中国舰船研究, 2021, 16(2): 36-48. |
| [5] |
VON KARMAN T. Uber den mechanismus des flussigkeits-und luftwiderstandes[J]. Phys. Z. , 1912: 49−59.
|
| [6] |
PARNAUDEAU P, CARLIER J, HEITZ D. Experimental and numerical studies of the flow over a circular cylinder at reynolds number 3900[J]. Physics of Fluids, 2009, 20(8): 85-101. |
| [7] |
延嘉虹, 杨春. 不同雷诺数下圆柱绕流流动特性数值模拟[J]. 流体测量与控制, 2024, 5(4): 1-5. |
| [8] |
余睿洁, 罗良, 陈威, 等. 亚临界雷诺数下粗糙圆柱绕流数值模拟研究[J]. 应用力学学报, 2022, 39(5): 974-980. |
| [9] |
YEON S M, YANG J, STERN F. Large-eddy simulation of the flow past a circular cylinder at sub-to super-critical reynolds numbers[J]. Applied Ocean Research, 2016, 59: 663-675. DOI:10.1016/j.apor.2015.11.013 |
 2025, Vol. 47
2025, Vol. 47
