2. 深海技术科学太湖实验室,江苏 无锡 214082
2. Taihu Laboratory of Deepsea Technological Science, Wuxi 214082, China
目前,面向国际海洋贸易的发展需求,船舶也逐渐朝着快速化发展,而船舶航速的增加使得船舶在海洋环境中承受更大的波浪载荷,对船体结构强度设计提出了新的挑战。相较于船舶受到的水平弯矩、扭转弯矩载荷,船舶受到的垂向弯矩波浪载荷数值较大,是船体结构强度安全评估的重要参数。
水弹性力学作为研究结构运动响应和载荷响应的重要理论,把流体与固体作为一个统一的动力系统考虑,研究流体和结构耦合过程中的动力响应问题,为船体的运动和载荷响应计算提供了重要的手段。Bishop等[1]在《船舶水弹性力学》专著提出了“船舶波激响应的一致性动力分析”观点,将船体结构简化为Euler梁或Timoshenko梁,忽略流体在船体纵向分布上的相互干扰,将耐波性分析中的二维切片理论引入到流固耦合响应分析中,建立了二维船舶水弹性理论,奠定了船舶水弹性理论发展的基础。在三维水弹性力学频域分析方法方面,吴有生等[2]在二维水弹性理论基本概念的基础上,将三维势流理论和结构动力学方程相结合,提出了广义流固耦合边界条件,开创性地发展了适用于波浪中三维弹性体在承受内外激励力时动态响应分析的三维水弹性理论。杜双兴[3]基于三维水弹性力学分析方法基础上,使用分区域展开法发展了无限水深零航速三维振荡源Green函数的快速计算方法,为三维水弹性分析方法向实用化发展奠定了基础。后期通过考虑非均匀稳态流和航速的影响[4],逐步完善了三维水弹性力学频域分析方法,进一步拓展了水弹性理论的应用范围。在三维水弹性力学时域分析方法方面,王大云[5]基于广义流固界面条件和三维时域格林函数,给出了考虑物体弹性变形的三维势流的时域积分方程,并推导了广义水动力系数和广义力,建立了船体运动、受力响应的直接时域分析方法理论。基于以上相关理论和算法,中国船舶科学研究中心自研开发了海洋结构分析通用软件SAM,目前软件的环境载荷模块已广泛应用于船舶、海上浮式平台等海洋结构物的性能评估,并经过了水池模型试验、商业软件计算结果、海上平台实测的数据结果对比验证[6 - 14]。
本文采用SAM软件对某集装箱船的运动和载荷响应进行数值预报,并与模型试验结果进行了比对,分析了航速变化对船体运动、波浪载荷的影响。
1 理论方法基于三维线性水弹性理论,假定流体为均质、无粘、无旋的不可压理想流体,自由表面波为微幅波,结合结构动力学,考虑结构是线弹性的以及结构在相对平衡位置的非定常运动变形微幅的,可得到浮体的广义三维线性频域水弹性运动方程:
| $ [{\boldsymbol{a}} + {\boldsymbol{A}}]\{ \ddot {\boldsymbol{p}}\} + [{\boldsymbol{b}} + {\boldsymbol{B}}]\{ \dot {\boldsymbol{p}}\} + [{\boldsymbol{c}} + {\boldsymbol{C}}]\{ {\boldsymbol{p}}\} = \{ {\bf{Z}}\} + \{ {\boldsymbol{\Delta}} \} + \{ {\boldsymbol{Q}}\} 。$ | (1) |
式中:
广义辐射力相关的流体附加质量矩阵、附加阻尼矩阵,以及与广义恢复力相关的流体恢复力系数矩阵中每个元素的表达式如下:
| $ \left\{ {\begin{aligned} &{{A_{rk}} = \displaystyle\frac{\rho }{{{\omega _e}^2}}{Re} \left\{ {\iint\limits_{\bar S} {\vec {\boldsymbol{n}} \cdot \vec u_r^0({\text{i}}{\omega _e} + \vec W \cdot \nabla ){\varphi _k}({\omega _e}){\text{d}}S}} \right\}},\\ &{{B_{rk}} = - \displaystyle\frac{\rho }{{{\omega _e}}}{Im} \left\{ {\iint\limits_{\bar S} {\vec {\boldsymbol{n}} \cdot \vec u_r^0({\text{i}}{\omega _e} + \vec W \cdot \nabla ){\varphi _k}({\omega _e}){\text{d}}S}} \right\}} ,\\ &{{C_{rk}} = - \rho \iint\limits_{\bar S} {\vec {\boldsymbol{n}} \cdot \vec u_r^0{\text{[}}gw_k^0 + \frac{1}{2}(\vec u_k^0 \cdot \nabla ){W^2}{\text{]d}}S}} 。\end{aligned}} \right. $ | (2) |
式中:
三维频域水弹性方程中右端的广义外力包括广义集中力、广义体积力、广义表面力。广义体积力
| $ {Q_r} = - \iiint\limits_\Omega {{\rho _b}gw_r^0{\text{d}}\Omega }。$ | (3) |
式中:
对船舶或其他波浪中的结构而言,物体所受到的表面分布力主要是作用在湿表面上的流场压力,广义表面分布力
| $ {Z_r}(t) = - \iint\limits_{{\overline {\rm S}}} \mathop {\boldsymbol{n}}\limits^ \rightharpoonup \cdot {\mathop u\limits^ \rightharpoonup }^0_r P{\mathrm{d}}{\text{S}} 。$ | (4) |
式中:
基于以上理论均是基于线性响应系统,因此规则波中的各类响应均可以使用模态叠加法求取,如垂向弯矩
| $ {{\boldsymbol{M}}_y}(x,y,z) = \sum\limits_{r = 7}^m {{p_r}{{\boldsymbol{M}}_{y,r}}} 。$ | (5) |
式中:
本文选取某集装箱船进行水弹性响应计算,船长286 m,型宽40 m,船舶主尺度信息如表1所示。船舶型线关于中纵剖面对称,水动力网格模型如图1所示,包含了
|
|
表 1 船舶尺度参数 Tab.1 Basic parameters of the ship |

|
图 1 船舶湿表面网格 Fig. 1 The ship's wet surface mesh |
在保证试验船模的流体特性以及结构动力特性与实船相似的前提下,将船模沿着垂线间长方向分成3段,分段位置分别位于船模的第5站、第10站和第15站横剖面处,试验船模分段示意图如图2所示。试验船模的各分段使用2根相同的圆管测量梁连接成一个整体。船模在波浪中进行试验时,使用重心位置处的六自由度陀螺仪测量记录船模运动响应,使用分段位置处测量梁上的应变传感器测量记录波浪弯矩载荷。

|
图 2 试验船模 Fig. 2 Test ship model |
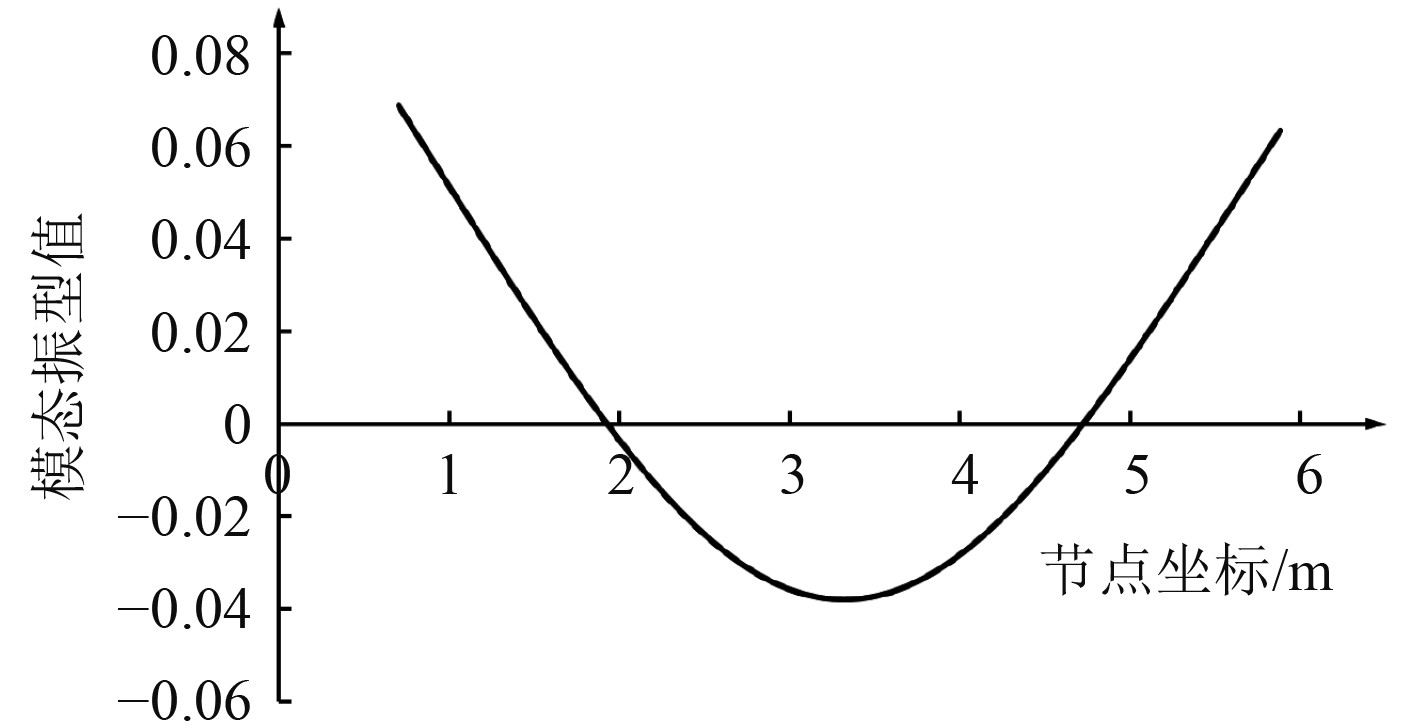
将船体结构简化为二维Euler梁,使用线密度属性模拟沿船舶纵向质量分布,通过模拟船体梁剖面刚度属性,进行结构有限元模态分析,船舶的首阶垂向振动频率分别为0.84 Hz,模型船体首阶垂向二节点弯曲模态如图3所示。
|
图 3 船体梁两节点垂向弯曲振动 Fig. 3 Hull girder 2-node vertical bending vibration |
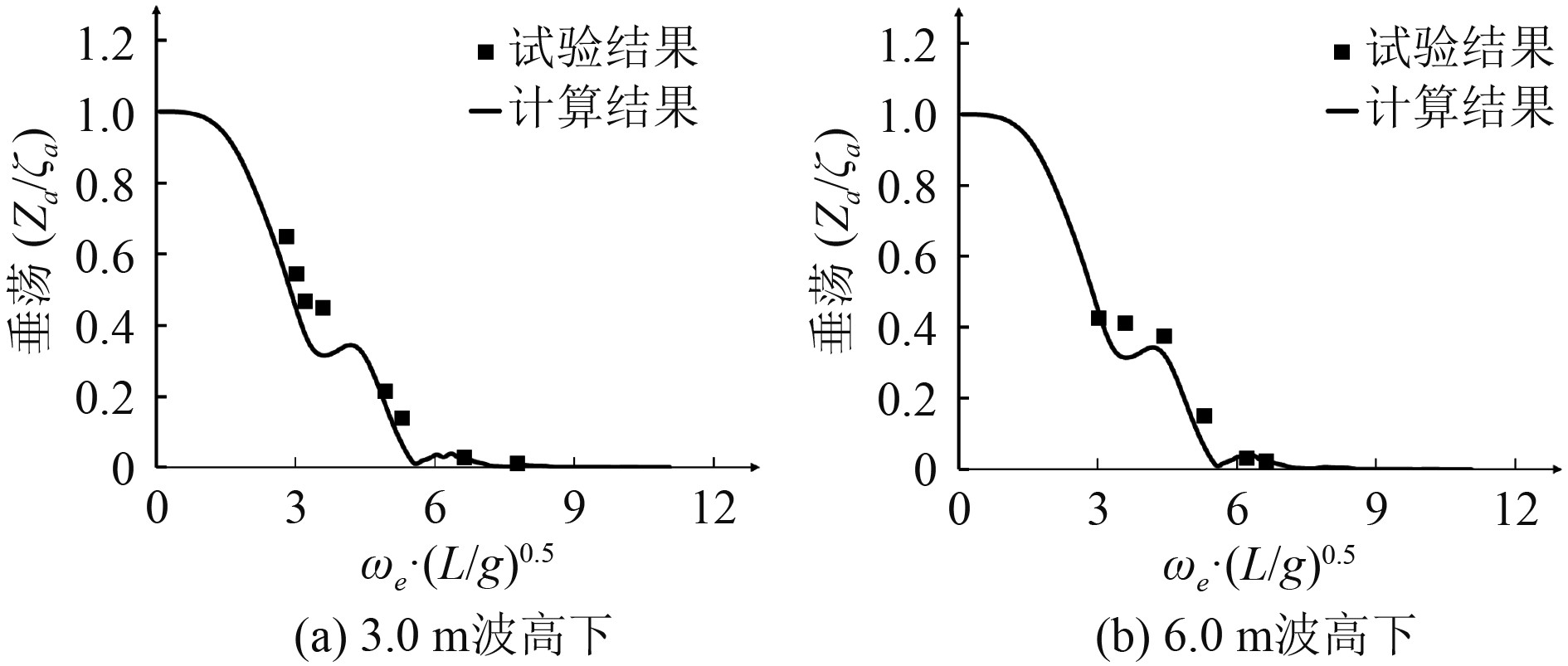
针对航速为11.0 kn的实船在3.0、6.0 m波高下的顶浪航行状态,选用SAM软件对实船在顶浪规则波下的水弹性响应开展计算,将得到的运动和载荷响应计算结果与模型试验结果进行比较,验证了软件的准确性。船舶在规则波下的垂荡、纵摇传递函数试验结果和计算结果如图4~图5所示,图中对遭遇频率、垂荡、纵摇响应进行了无因次化处理,分别用
|
图 4 垂荡传递函数 Fig. 4 Heave transfer function |
|
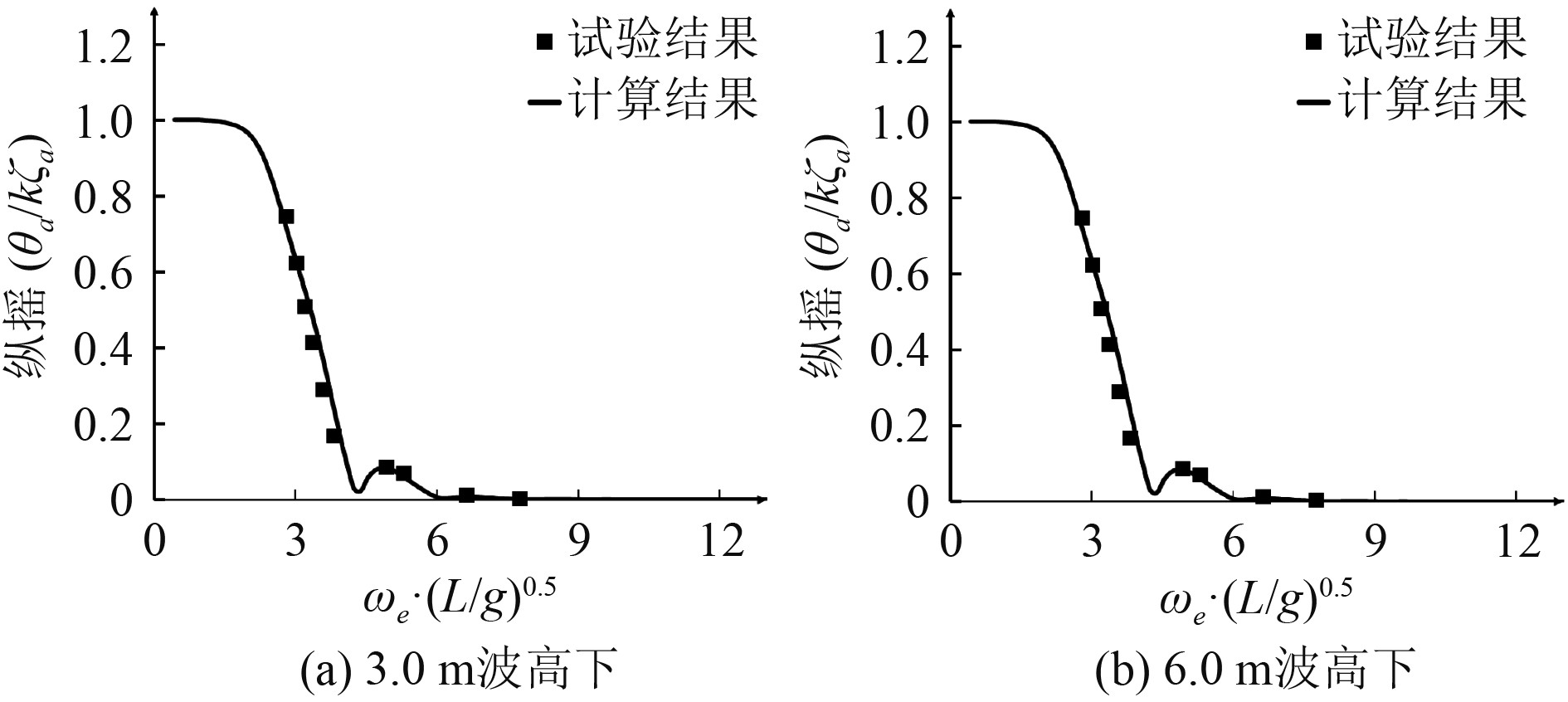
图 5 纵摇传递函数 Fig. 5 Pitch transfer function |
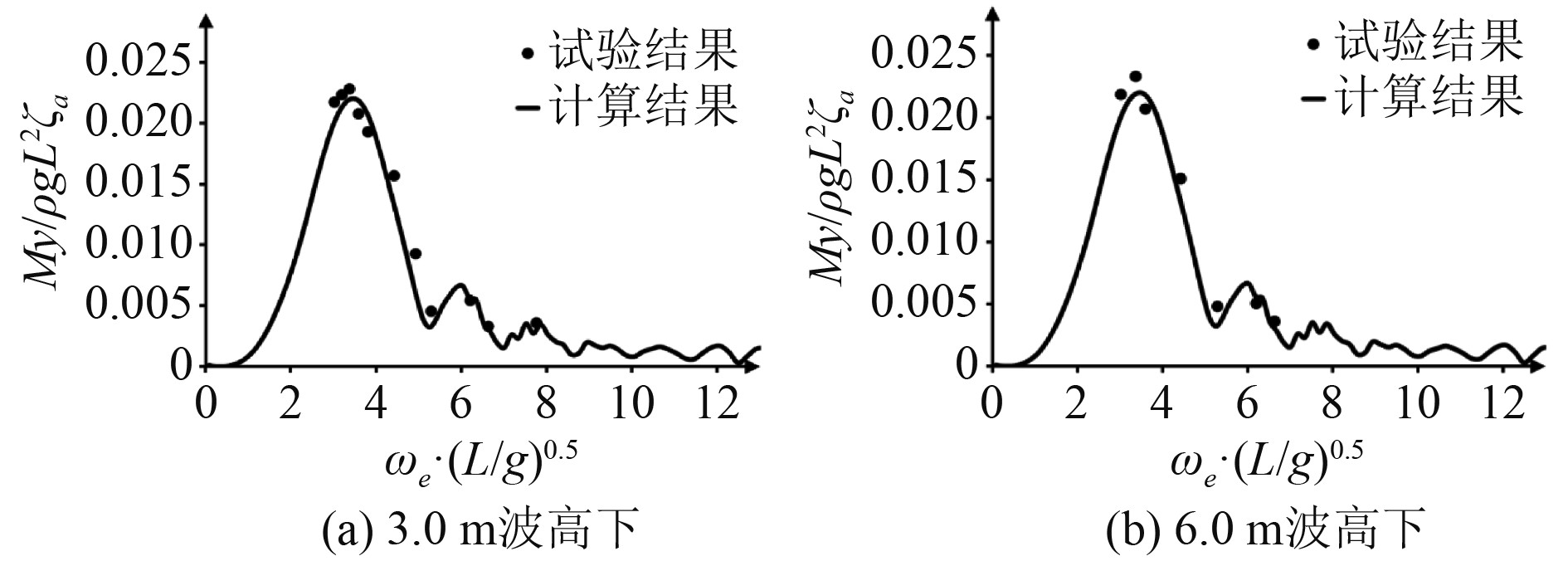
该船船中剖面在规则波下的垂向弯矩传递函数试验结果与计算结果如图6所示,图中对垂向弯矩进行了无因次化处理,用My/ρgL2ζa表示,其中My为船中剖面垂向弯矩。由图可知,SAM软件的剖面载荷计算曲线趋势、峰值位置与试验数据散点均能实现较好地吻合。
|
图 6 3.0 m波高下的船中剖面垂向弯矩传递函数 Fig. 6 Midship vertical bending moment transfer function under 3 m wave height |
通过SAM软件,进一步探究不同航速、浪向下的运动和载荷响应规律。
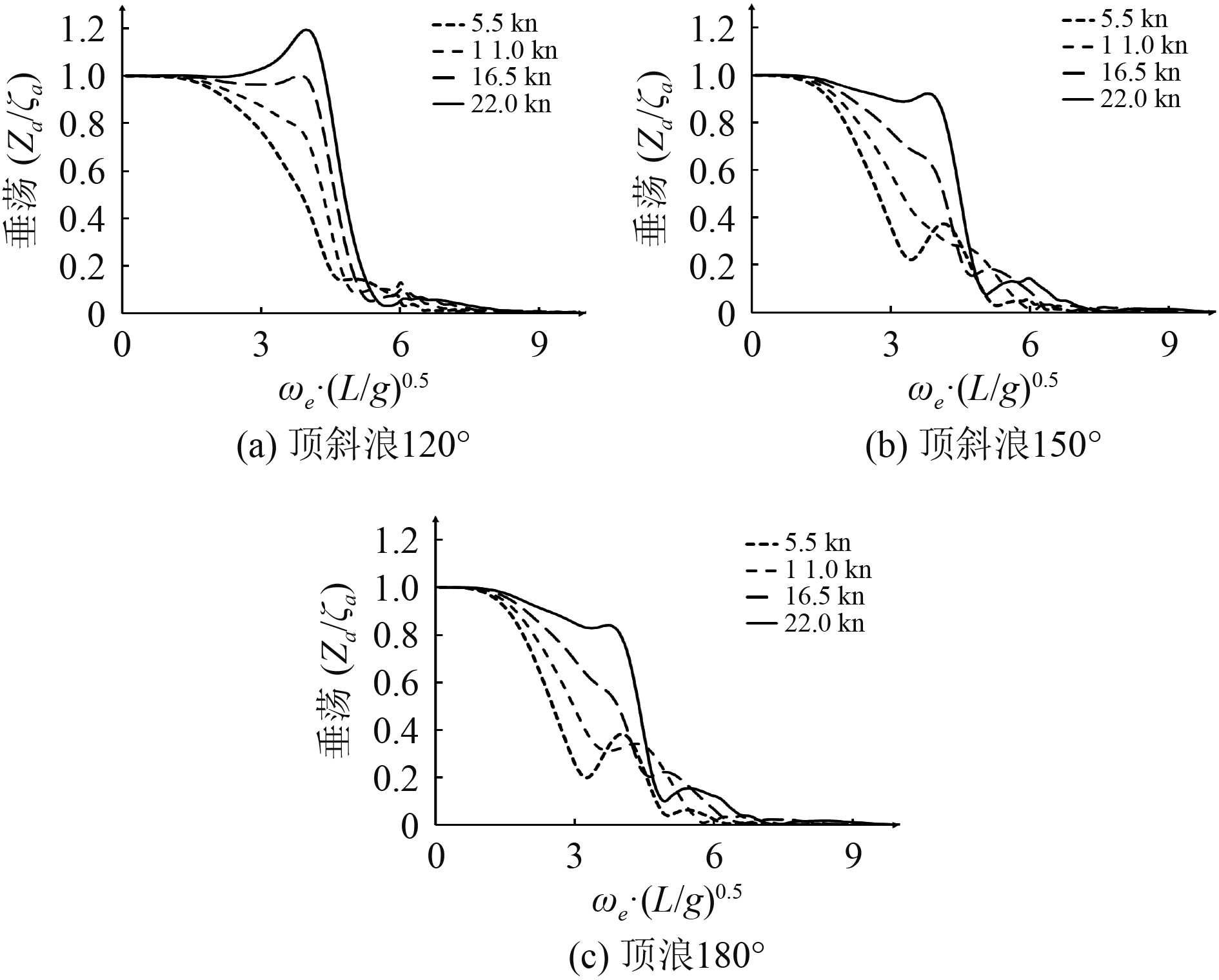
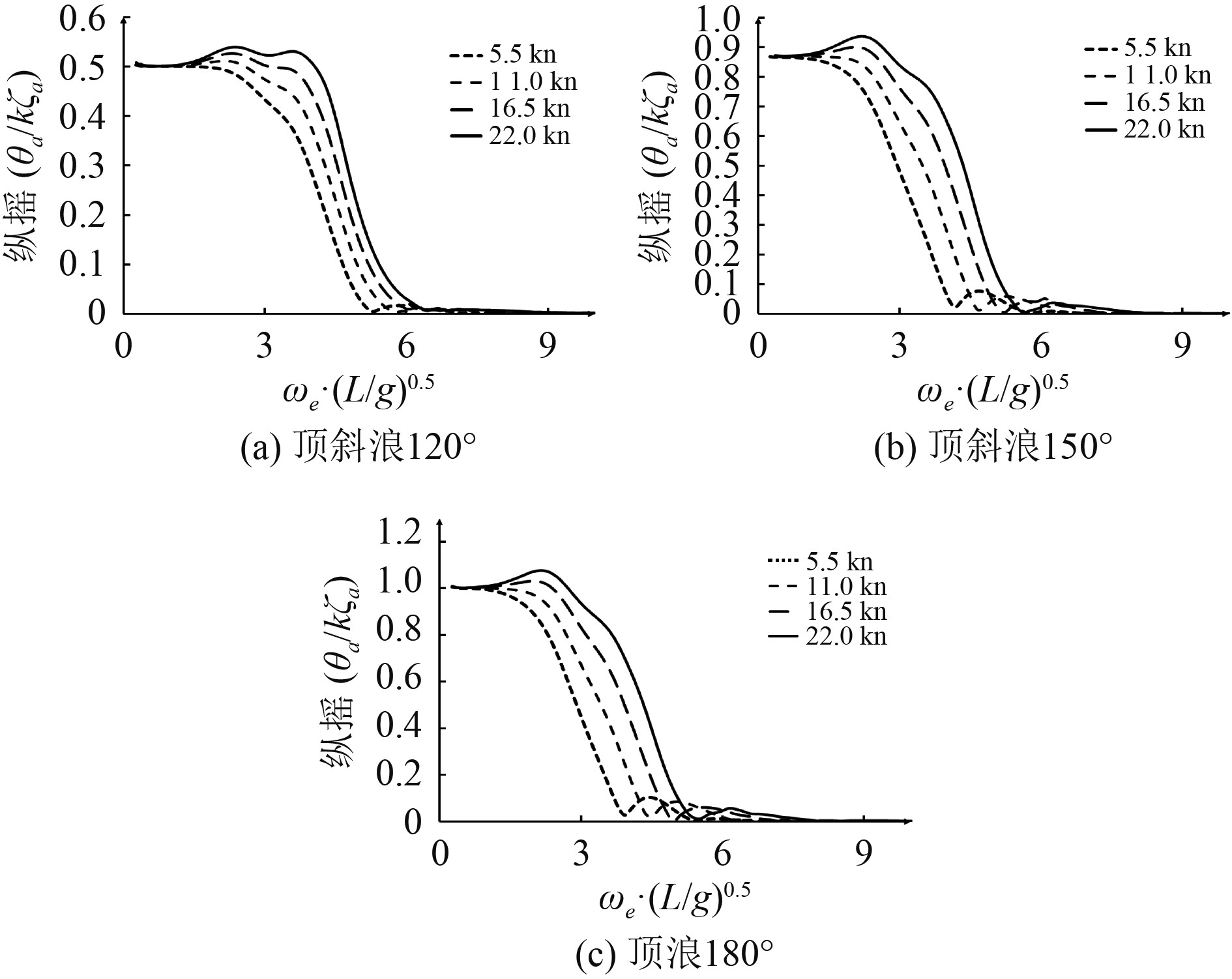
4.1 运动传递函数船舶在顶浪180°、顶斜浪120°以及顶斜浪150°方向上的升沉和纵摇频率响应函数曲线如图7~图8所示。可以发现,各浪向下的升沉响应在随着航速增加的同时,并且在ωe/(L/g)0.5=4.0附近船舶在顶斜浪150°、顶浪180°下的升沉响应曲线出现峰值,由于此处的遭遇频率与船舶升沉固有周期对应的谐振效应引起。同时,在ωe/(L/g)0.5=1.2的遭遇频率内,不同航速下的船舶在同一浪向下的纵摇响应基本一致,并随着航速增加而变大。
|
图 7 不同航速下船舶升沉运动幅频响应传递函数 Fig. 7 Heave RAO at different speeds |
|
图 8 不同航速下船舶纵摇运动幅频响应传递函数 Fig. 8 Pitch RAO at different speeds |
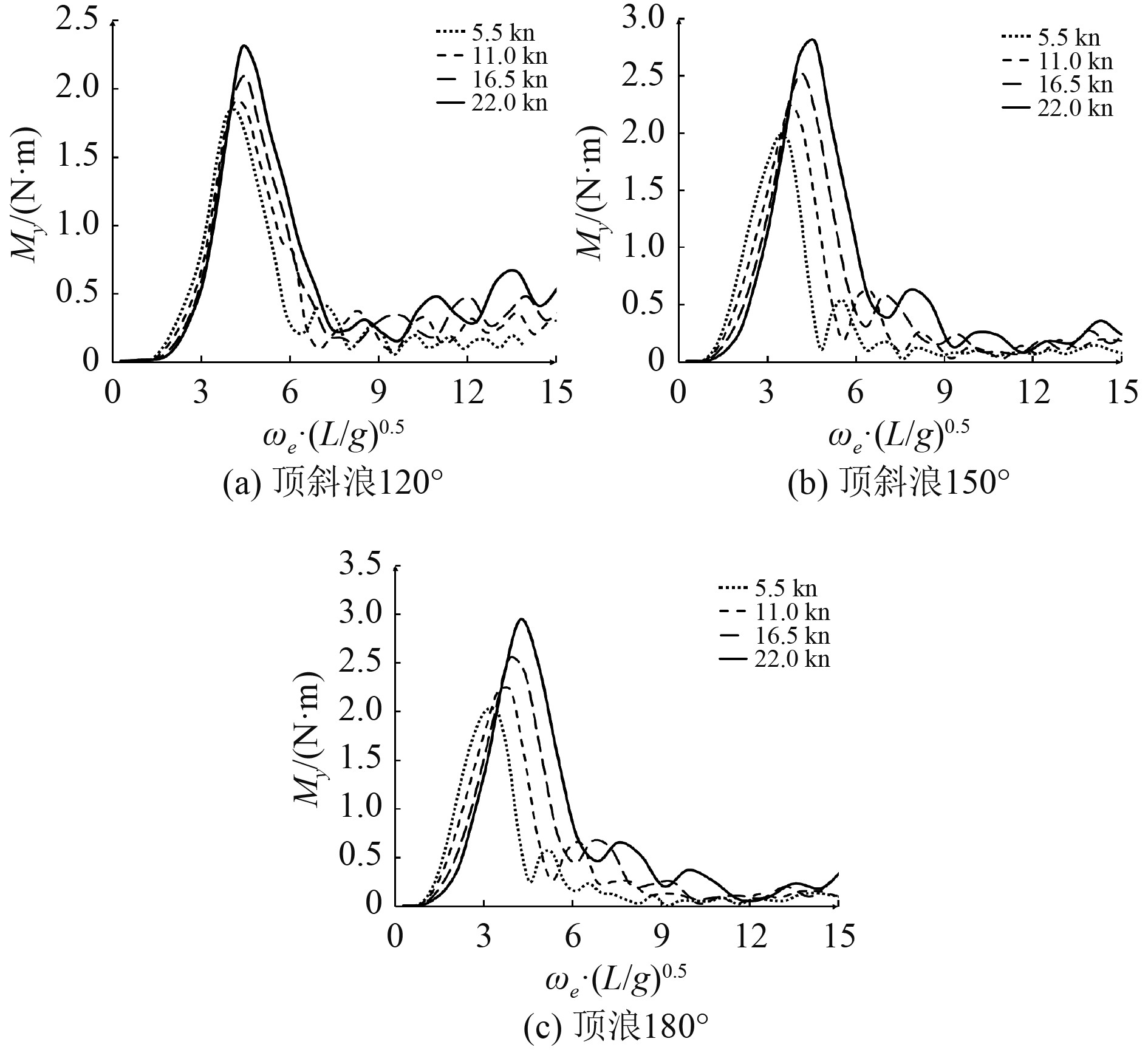
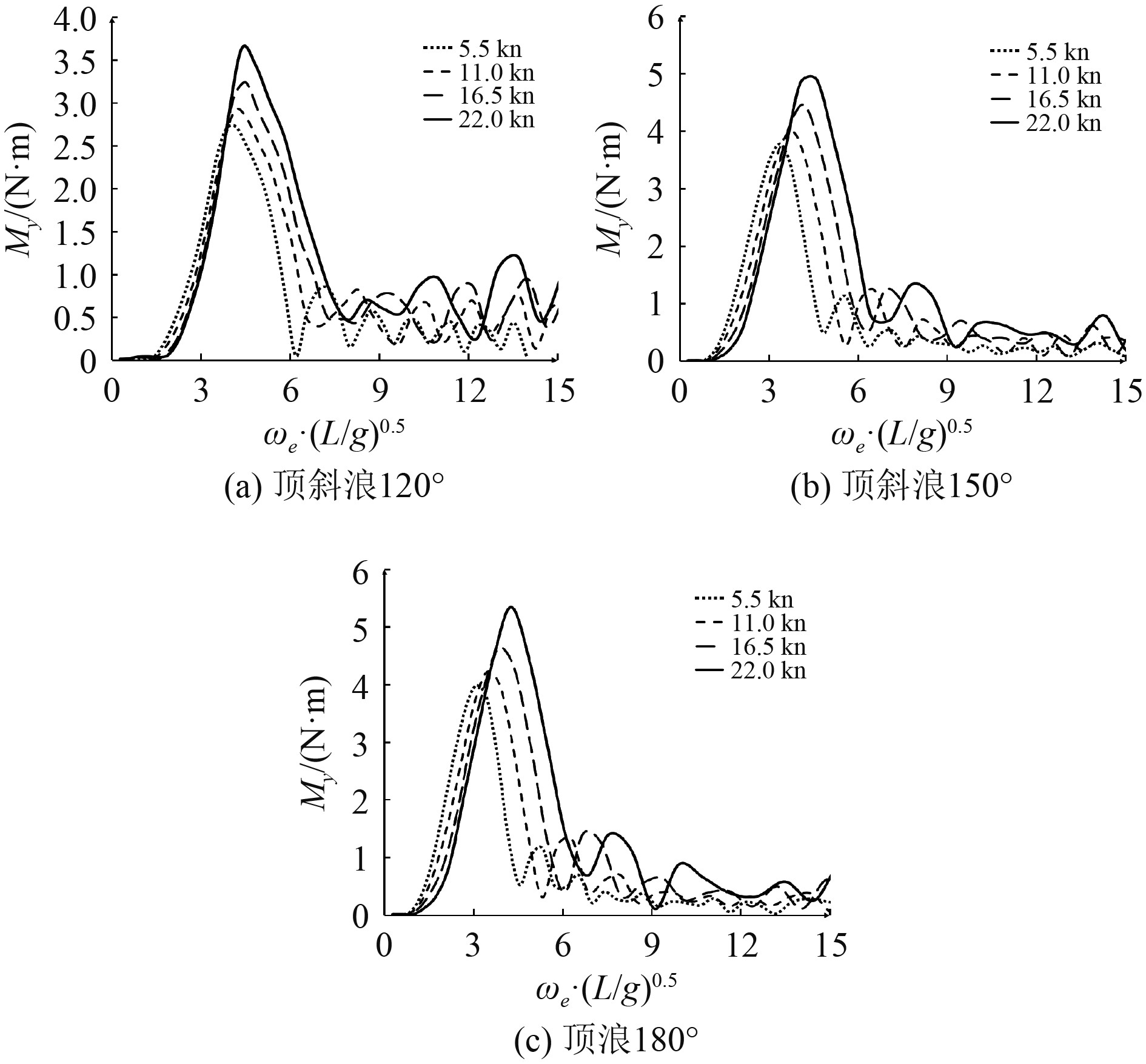
船首、船中以及船尾剖面在各航速下的垂向弯矩幅频响应传递函数如图9~图11所示,可以发现各剖面在垂向弯矩传递函数极值随着航速增加不断变大;相较于顶斜浪状态下,剖面垂向弯矩极值在顶浪状态下最大。
|
图 9 船尾L/4剖面船舶垂向弯矩幅频响应传递函数 Fig. 9 Vertical bending moment RAO at L/4 section |
|
图 10 船中L/2剖面船舶垂向弯矩幅频响应传递函数 Fig. 10 Vertical bending moment RAO at L/2 section |
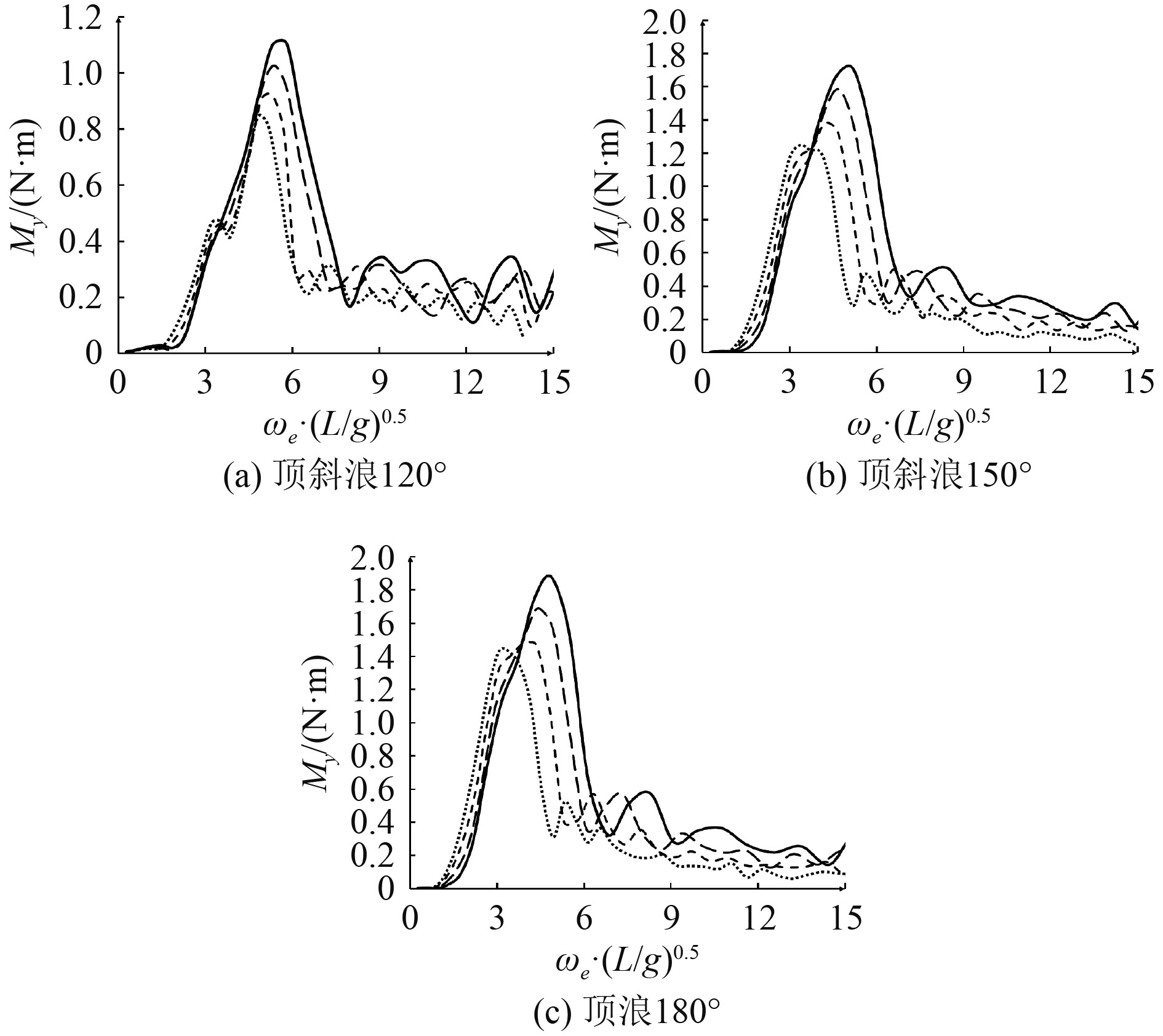
|
图 11 船首3L/4剖面垂向弯矩幅频响应传递函数 Fig. 11 Vertical bending moment RAO at 3L/4 section |
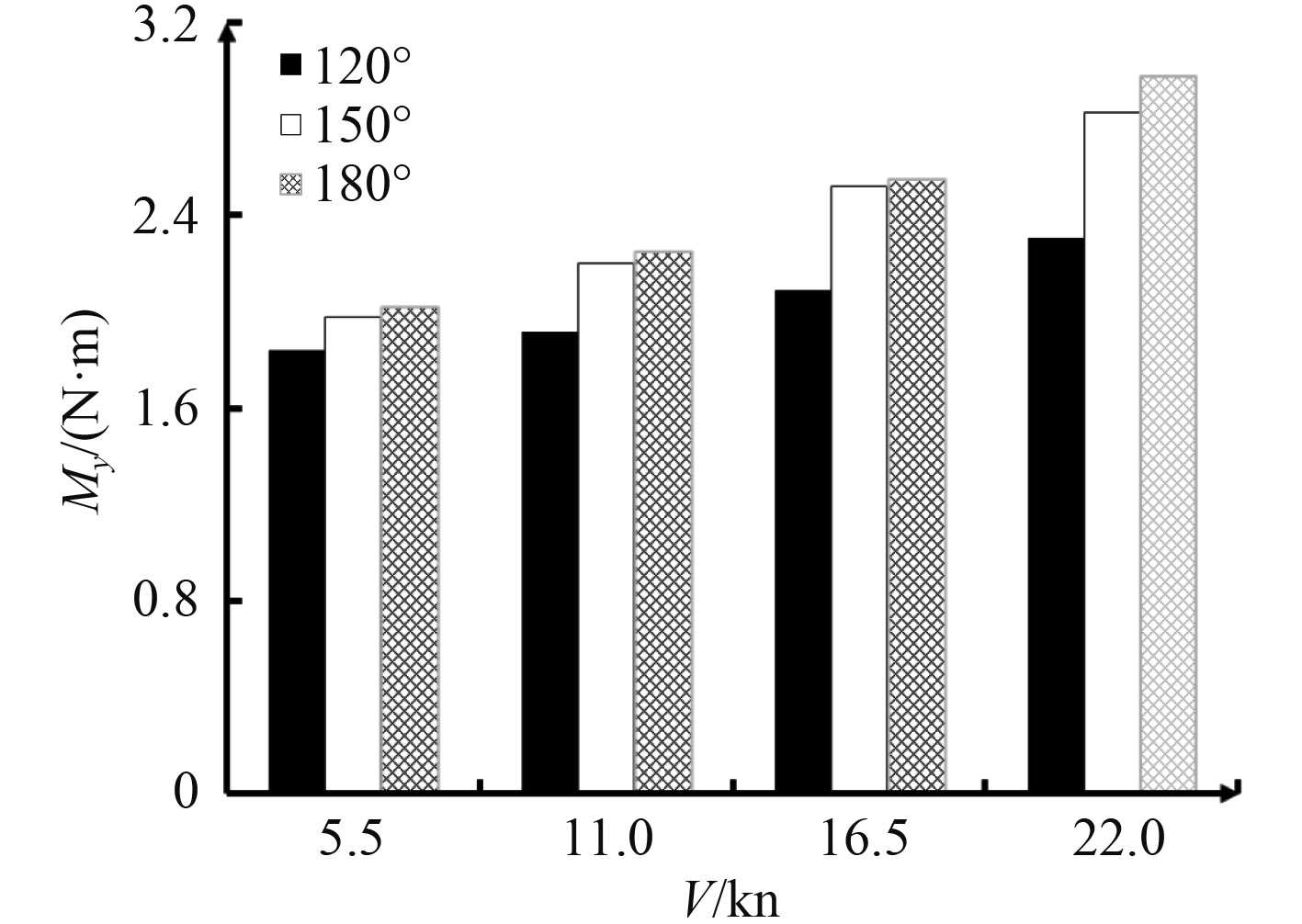
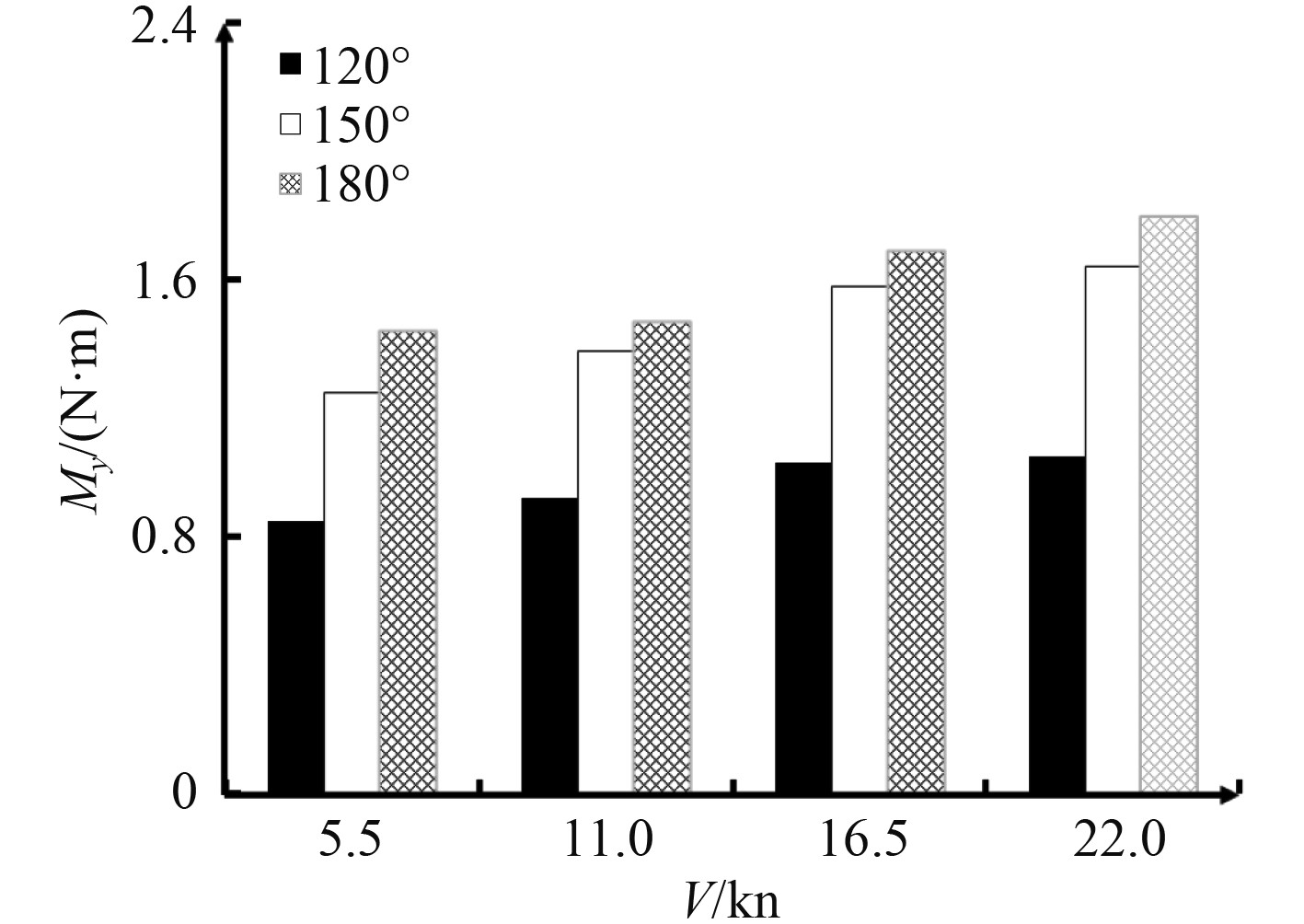
为进一步探究航速变化对船舶不同剖面位置处的波浪载荷的影响,根据船舶船首、船中、船尾剖面在顶浪、斜浪下的垂向弯矩幅频响应传递函数曲线,得到船舶各位置处的垂向弯矩载荷极值如图12~图14所示。可以发现,在各航速下同一剖面在顶浪时垂向弯矩极值最大,并且顶浪180°下与顶斜浪150°下的垂向弯矩极值相差不大。同时,各剖面的垂向弯矩极值随着航速的增加不断变大,并且相较于船首、船中剖面位置,航速增加对船尾剖面的垂向弯矩极值影响最大,船尾剖面垂向弯矩极值由2.02×108 N·m增加至2.98×108 N·m,增长了47.5%;船中剖面垂向弯矩极值由3.99×108 N·m增加至5.33×108 N·m,增长了33.6%;船首剖面垂向弯矩极值由1.44×108 N·m增加至1.80×108 N·m,增长了25.0%。
|
图 12 船尾L/4剖面的垂向弯矩极值 Fig. 12 Extreme value of vertical bending moment at the L/4 section |
|
图 14 船首3L/4剖面的垂向弯矩极值 Fig. 14 Extreme value of vertical bending moment at the 3L/4 section |
根据不同航速下船舶的船首、船中以及船尾剖面的垂向弯矩的幅频响应传递函数曲线的极值分析结果,选择垂向弯矩载荷最大的船中剖面作为主要载荷参数。基于JONSWAP海浪谱,对船舶载荷响应进行短期预报。海浪谱表达式为[15]:
| $\begin{aligned}{S_A}(\omega ) = &487(1 - 0.287{\mathrm{ln}}\gamma )\frac{{H_s^2}}{{T_p^4}}{\omega ^{ - 5}}\times\\ &\exp (\frac{{ - 1948}}{{T_p^4}}){\gamma ^{\exp \left[ {\frac{{ - {{(0.159\omega {T_p} - 1)}^2}}}{{2{\sigma ^2}}}} \right]}}。\end{aligned} $ | (6) |
式中:Hs为有义波高;Tp为波浪谱峰周期;
根据我国国家海洋局发布的浪级标准,选择4级海浪范围中有义波高Hs的最大值为2.5 m。不规则波中的有义波高与周期是相关的联合分布,谱峰周期与有义波高的关系如式(7)所示。基于同一有义波高与谱峰周期的范围以及中国沿海海浪长期分布资料[16],本文选择有义波高2.5 m下的谱峰周期范围的最大值8.7 s进行短期预报。
| $ \sqrt {13{H_s}} \leqslant {T_p} \leqslant \sqrt {30{H_s}}。$ | (7) |
船舶在各航速不同浪向短期预报值的计算结果如表2所示。
|
|
表 2 船中剖面垂向弯矩短期预报有义值 Tab.2 Midship significant values of vertical bending moment in short term |
可知,船中剖面垂向弯矩载荷短期预报值在5.5 kn增加至22.0 kn的过程中,120°下的垂向弯矩载荷数值增加了22.6%,150°下的垂向弯矩载荷数值增加了31.0%,180°下的垂向弯矩载荷数值增加了31.9%,向弯矩载荷在顶浪航行状态下对航速增加较为敏感。各航速下的船中剖面垂向弯矩载荷短期预报值在浪向120°时最大,而由图13发现船中剖面的垂向弯矩传递函数曲线的极大值出现在顶浪180°。这是由于各浪向的载荷短期预报值是根据其传递函数在各频率下的能量积分得到,从而造成各浪向下垂向弯矩传递函数极大值对应的浪向角与各浪向下短期预报极大值对应的浪向角不一致的现象。
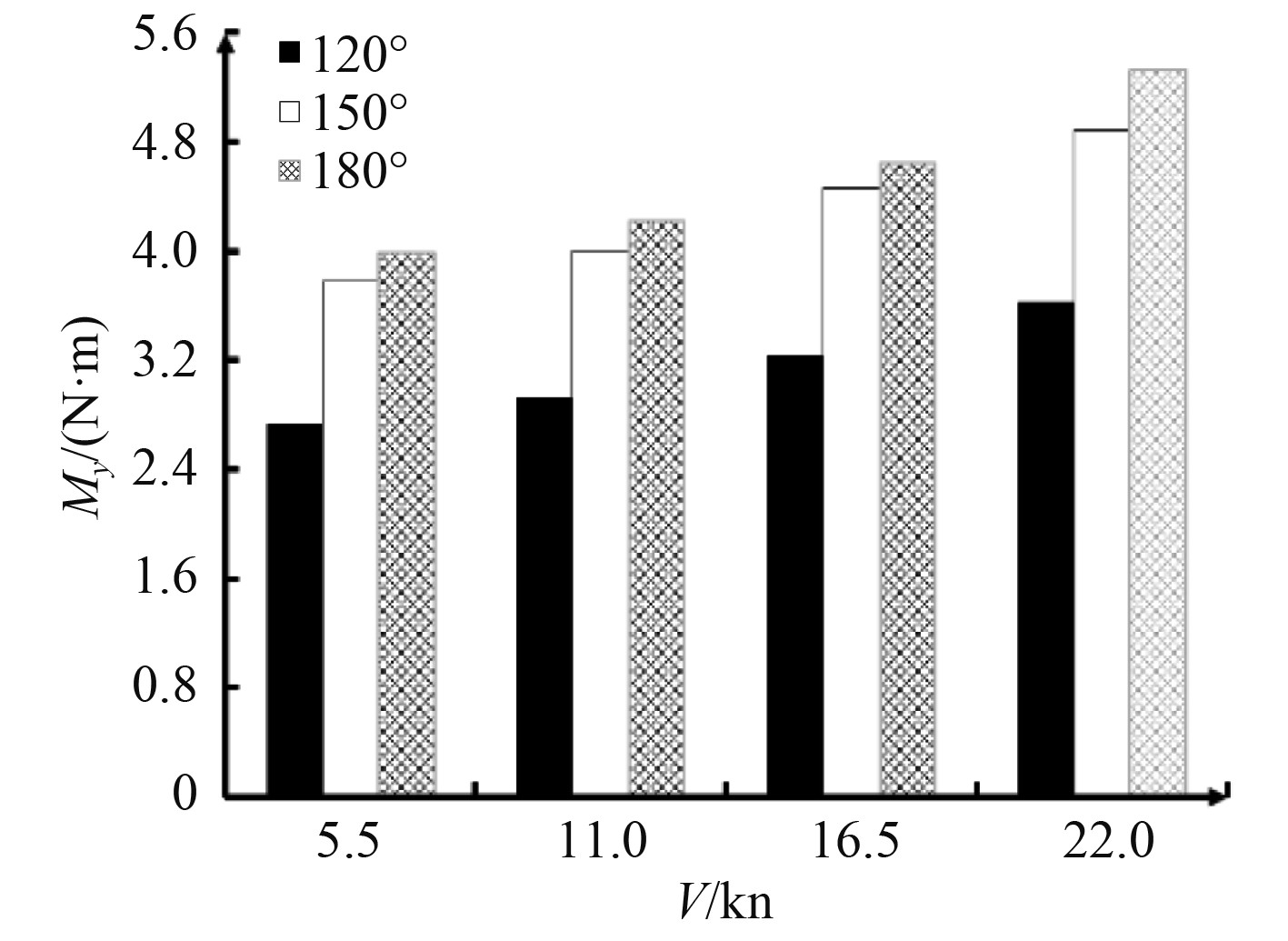
|
图 13 船中L/2剖面的垂向弯矩极值 Fig. 13 Extreme value of vertical bending moment at the L/2 section |
本文针对某集装箱船,利用模型试验数据验证了海洋结构分析通用软件SAM准确性,并研究了航速变化对垂向弯矩载荷响应的影响。具体地,通过研究得到以下结论:
1)通过数值计算结果与模型试验结果对比发现,两者的运动响应以及波浪载荷响应实现了较好地吻合,验证了SAM软件对船模动响应的准确预报;
2)数值结果表明,船舶各测量剖面的垂向弯矩极值在航速由5.5 kn增加至22.0 kn的过程中在不断增加,并且相较于船首剖面以及船中剖面,船尾剖面垂向弯矩增加程度最大;
3)通过对船中剖面的垂向弯矩载荷进行短期预报有义值分析,发现载荷短期预报值与载荷传递函数极值对应的浪向角可能不一致,由此说明对船舶设计载荷进行短期预报阶段进行全浪向下遍历十分有必要。
| [1] |
BISHOP R E D, PRICE W G. Hydroelasticity of Ships[M]. Cambridge University Press, London, 1979.
|
| [2] |
WU Y S. Hydroelasticity of floating bodies[D]. Brunel University, U. K. , 1984.
|
| [3] |
杜双兴. 海洋浮体结构的直接分析方法−三维线性水弹性随机分析理论及应用[D]. 无锡: 中国船舶科学研究中心, 1990.
|
| [4] |
田超. 航行船舶的非线性水弹性理论与应用研究[D]. 上海: 上海交通大学, 2007.
|
| [5] |
王大云. 三维船舶水弹性力学的时域分析方法[D]. 无锡: 中国船舶科学研究中心, 1996.
|
| [6] |
倪歆韵, 王墨伟, 田超. 基于三维水弹性理论的COMPASS-THAFTS软件开发及应用[C]//第三十届全国水动力学研讨会暨第十五届全国水动力学学术会议文集, 2019.
|
| [7] |
NI X Y, CHENG X M, LU Y, et al. Evaluation of hydroelastic responses of a 180k DWT large bulk carrier[J]. Ocean Engineering, 2020, 199: 106948. |
| [8] |
倪歆韵, 丁军, 陈颖, 等. 双模块浮式平台运动性能分析[C]// 第三十二届全国水动力学研讨会论文集, 2021.
|
| [9] |
DING J, TIAN C, WU Y S, et al. Hydroelastic analysis and model tests of a single module VLFS deployed near islands and reefs[J]. Ocean Engineering, 2017, 144: 224-234. DOI:10.1016/j.oceaneng.2017.08.043 |
| [10] |
DING J, WU Y S, ZHOU Y, et al. Investigation of connector loads of a 3-module VLFS using experimental and numerical methods[J]. Ocean Engineering, 2020, 195: 106684. |
| [11] |
DING J, XIE Z Y, WU Y S, et al. Numerical and experimental investigation on hydroelastic responses of an 8-module VLFS near a typical island[J]. Ocean Engineering, 2020, 214: 107841. |
| [12] |
NI X Y, ZHANG Z W, TIAN C, et al. The development of 3d hydroelastic software and its application on platform[C]// Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, June 9−14, 2019, Glasgow, Scotland, OMAE2019−96122.
|
| [13] |
NI X Y, CHENG X M, WU B, et al. Performance analysis of the mooring system of a two-module scientific research and demonstration platform[J]. Journal of Hydrodynamics, 2021, 33(5): 901-914. DOI:10.1007/s42241-021-0080-2 |
| [14] |
DING J, WU Y S, NI X Y, et al. A direct coupling analysis method and its application to the scientific research and demonstration platform[J]. Journal of Hydrodynamics, 2021, 33(1): 13-23. DOI:10.1007/s42241-021-0009-9 |
| [15] |
BERNARD M著. 海洋工程水动力学[M]. 北京: 国防工业出版社, 2012.
|
| [16] |
方钟圣. 西北太平洋波浪统计集[M]. 北京: 国防工业出版社, 1996.
|
 2025, Vol. 47
2025, Vol. 47
