0 引　言

船舶在泊船过程中，环境风、浪等外部因素对船舶运动姿态的影响不可忽视。这些环境因素会显著改变船舶的横摇、纵摇、垂荡等运动姿态，导致船舶的遭遇角出现偏差。遭遇角是船舶航向与外界环境作用力方向之间的夹角，其准确性直接关系到船舶的航向控制和泊船安全性。当遭遇角出现偏差时，船舶无法按预期调整航向，可能导致船舶偏离预定泊位，甚至引发碰撞、搁浅等安全事故，严重威胁船舶和港口设施的安全^{[1 − 2]}。因此，如何有效地控制泊船遭遇角，确保船舶能够安全、精准地完成靠泊任务，成为船舶控制领域亟待解决的问题。

针对泊船遭遇角控制研究，国内外学者已进行了大量的探索和实践。Kim等^[3]运用计算流体力学技术构建泊船航行仿真模型，采用时变自回归模型实时估计航向角。基于估计结果，执行转向操作，有效控制泊船遭遇角。该方法能捕捉时间序列变化，实现实时估计，使系统及时响应环境变化。但其控制中未充分考虑波浪干扰，导致遭遇角控制误差较大，泊船过程存在安全风险。苏文学等^[4]选用RBF神经网络、最小学习参数法构建外界扰动与船舶系统的运动模型，利用非线性反馈控制、李雅普诺夫理论设计泊船航向控制器。该控制器能够实时控制船舶行驶过程中的方向，进而实现对遭遇角的有效控制。但在面对风、浪等动态且不可预测的环境干扰时，其预测精度可能下降，导致控制器无法及时准确地调整航向。黄立文等^[5]以时延最小、外界环境干扰最小作为泊船遭遇角控制条件，利用改进Smith、PID原理调节其航向及舵角值，使泊船遭遇角达到期望值。该方法能迅速精确调整航向和舵角，高效引导泊船遭遇角改变方向。但控制系统鲁棒性不足，难以应对系统动态变化，影响船舶遭遇角精确控制。王伟等^[6]利用模糊控制理论构建泊船遭遇角控制器，并借助反向传播神经网络优化控制器性能。该方法能够有效处理不确定性和非线性问题，对于泊船过程中可能遇到的各种复杂环境和条件，模糊控制器都能灵活应对，提供较为稳健的控制效果。但该方法对泊船运动数据有较强的依赖性，若数据不充分或存在偏差，控制器就无法达到预期的控制效果。

鉴于以上方法的泊船遭遇角控制方法存在问题，提出一种基于运动姿态数据挖掘的高泊船安全性和效率的控制方法。该方法通过挖掘船舶的运动状态频繁项，深入探究船舶运动姿态的内在规律，以此降低泊船遭遇角的控制难度，提升控制效率，进而提高整体作业效率。此外，该方法还融合RBF神经网络、闭环增益成形算法，设计合理的控制器，使泊船遭遇角始终保持在最佳状态，有效避免船舶与泊位或其他障碍物发生碰撞，确保作业质量。

1 FP-growth算法下运动姿态数据挖掘

泊船过程中，船舶会产生大量包含速度、加速度、航向角等多种运动姿态信息的高维混合属性数据。深入挖掘这些数据，能够精准识别出不同遭遇角下船舶的运动特性，进而为优化遭遇角控制策略提供坚实的科学依据。因此，在实施泊船遭遇角控制之前，有必要对船舶的运动姿态数据进行挖掘，以清晰了解姿态运动与遭遇角控制之间的内在联系。FP-growth算法凭借其独特优势，能够直接处理高维数据，并且仅需扫描数据库2次，无需生成候选项集，可减少计算量^{[7 − 8]}。具体而言，借助FP-树，高效挖掘出运动姿态组合与遭遇角控制的关联规则，过程如下：

步骤1　输入泊船运动姿态数据获取与计算阈值。运用ADXL345加速度计、MPU6050陀螺仪获取船舶在泊船过程中的运动姿态数据，如横摇、纵摇、垂荡等，并将这些数据输入到增长树节点中，最低支持度$ \min \gamma (A \to B) $与最低置信度$ \min \lambda (A \to B) $。计算式为：

$ \min \gamma (A \to B) = \ln \frac{{{\text{num}}(AB)}}{{{\text{num}}(\text{total})}} ，$

(1)

$ \min\lambda(A\to B)=\mathrm{lc}\frac{\text{num}(AB)}{\text{num}(A)}。$

(2)

式中：$ {\text{num}}(\text{total}) $为泊船运动姿态数据集；$ {\text{num}}(AB) $为特定姿态组合的出现次数；$ {\text{num}}(A) $为某一运动姿态$ A $与其他相关姿态的平均差异度量。

步骤2　首次扫描与FP树构建。依据式(1)查询支持度大于计算结果的频繁集，基于这些频繁集构建FP树和项目标题并降序排列。

步骤3　再次扫描与节点生成及分支过滤。对步骤2得到的频繁集再次扫描，根据支持度生成相应的姿态数据节点。依据样本分支是否包含运动姿态数据的频繁项来过滤样本分支。若是，则保留；若否，则修剪该分支。修剪后，执行下一次扫描任务，并重新生成项目标题和FP树。

步骤4　遍历表头获取频繁项。以项表头的最后一个头指针作为遍历起点，遍历表头中的各个数据项，从而得出带有递归项的频繁项。

步骤5　筛选频繁项。判断遍历数据项中的数据是否为运动姿态数据的频繁项。若是，则保留此遍历结果；若不是，则舍弃，进行下一轮的遍历。

步骤6　计算支持度与置信度并确定关联规则。针对步骤5保留下来的数据频繁项集，利用步骤1中的2个公式计算各姿态数据的支持度与置信度。将支持度和置信度小于最低支持度与最低置信度的频繁项作为泊船运动姿态数据的关联规则。

将满足最小支持和置信阈值的数据输出视为有效关联规则，至此完成泊船运动姿态数据的挖掘。根据这些关联规则，得出泊船姿态运动与遭遇角控制之间的关联性。

2 泊船遭遇角控制 2.1 泊船系统函数设置

FP-growth算法主要处理离散数据，无法捕捉船舶运动姿态与遭遇角之间的非线性关系。RBF神经网络通过其隐含层的径向基函数（RBF）能够拟合复杂的非线性映射，从而精确描述船舶运动姿态与遭遇角之间的动态关系^{[9 − 10]}。因此，利用RBF网络构建泊船系统函数。

RBF神经网络算法数学表达式为：

$ o(\text{num}(\text{total}))=\boldsymbol{\omega}^{\rm{T}}\Phi(\text{num}(\text{total}))。$

(3)

式中：$ \boldsymbol{\omega}=[\omega_1,\omega_2,...,\omega_l]\in R^l $为输入层和输出层之间的权值矩阵；$ l \gt 1 $为网络节点数总数量；$ \Phi ({\text{num}}({\text{total}})) $为高斯函数。第$ i $个高斯函数的数学表达式为：

$ \Phi_i(\text{num}(\text{total}))=\exp\left\{-\frac{(\text{num}(\text{total})-\mu_i)^{\mathrm{T}+1}}{\eta_i^2}\right\}。$

(4)

式中：$ \mu_i=[\mu_1,\mu_2,...,\mu_l]^{\mathrm{T}} $，$ {\eta _i} $为$ i $的分布曲线的中心向量及其宽度。因RBF神经网络能够在$ {\text{num}}({\text{total}}) $上利用某一精度值逼近任何的连续函数，该计算过程为：

$ o^*(\text{num}(\text{total}))=\omega^{*\mathrm{T}}\Phi(\text{num}(\text{total}))+\varepsilon^* 。$

(5)

式中：$ {\omega ^*} $为理想的常数权重；$ {\varepsilon ^*} $为函数的重构误差。

假设所有的$ {\text{num}}({\text{total}}) $，对于任何一个大于0的常数$ \varepsilon \gt 0 $，都存在理想的常数权重$ {\omega ^*} $使$ |{\varepsilon ^*}| \leqslant \varepsilon $。理想权重矢量$ {\omega ^*} $是一个自定义的量，其目的是便于分析^[11]。$ {\omega ^*} $是$ \omega $的真值，对所有的$ {\text{num}}({\text{total}}) $，使$ |{\varepsilon ^*}| $最小，则有：

$ {\varepsilon ^*}{\text{ = }}\arg \mathop {\min }\limits_\omega \mathop {\sup }\limits_{{\text{num}}({\text{total}})} |h - {\omega ^{\rm T}}\Phi |({\text{num}}({\text{total}})) 。$

(6)

因$ {\omega ^*} $未知，需对其求解，用符号$ \hat \omega $为$ {\omega ^*} $的估计值。通常利用梯度下降法更新$ \hat \omega $值，并定义参数估计误差为$ {\sigma _i} = {\hat \omega _i} - \omega _i^* $，反复求解直至误差值为0.001为止，此时估计值$ {\hat \omega _i} $即为$ {\omega ^*} $值^[12]。然后结合式(5)，得出泊船系统函数$ f({\text{num}}({\text{total}})) $，即：

$ f(\text{num}(\text{total}))=\omega^{\mathrm{T}}\Phi(\text{num}(\text{total}))+\varepsilon 。$

(7)

2.2 泊船遭遇角控制实施

水流和风速等外部环境因素会显著影响船舶的航向。RBF神经网络可能无法准确预测这种随机外部干扰，导致输出可能与实际情况存在偏差，导致船舶无法按预期调整航向，进一步增大遭遇角偏差。三阶闭环增益成形算法通过增益成形，可以有效抑制水流、风速等外部环境干扰的影响，保证控制效果^{[13 − 14]}。

根据泊船数据挖掘结果可知，船舶的运动姿态与航向紧密相关，而航向保持控制是实现精准泊船遭遇角控制的关键环节。为实现对遭遇角的有效控制，从航向控制的角度入手。泊船航向控制属于单输入单输出系统，将舵角$ \delta $作为泊船航向控制系统的输入量，航向$ \psi $作为输出量。在泊船航向控制领域，Nomoto传递函数数学模型被广泛应用，其能够较好地描述船舶在舵角输入下的航向响应特性。则泊船系统函数$ f({\text{num}}({\text{total}})) $的Nomoto传递函数数学模型，即：

$ {G_{\delta \psi }}(s) = \frac{{{K_0}}}{{s({t_0}s + 1)}}。$

(8)

式中：$ s $为拉普拉斯变换算子；$ {K_0} $为操纵性指数，反映了船舶对舵角输入的稳态响应特性；$ {t_0} $为时间常数，体现了船舶的惯性和对舵角输入的响应速度。

通过对式(7)的深入分析，研究人员对泊船的运动特性有了更为透彻的理解。基于此，为实现对泊船遭遇角的有效控制，引入三阶闭环增益成形算法。该算法能可依据式(8)，依据船舶实际运行情况和控制需求调整控制策略^[15]，其控制的数学为为：

$ K = \frac{1}{{G{t_1}s(t_1^2{s^2} + 3{t_1}s + 3)}}。$

(9)

式中：$ {t_1} $为闭环增益成形算法中的时间变量；$ G $为传递函数的增益。

在实际应用中，由于姿态数据通常为离散的数据，为了保证结果有效性，需要将式(8)变换成离散型。为此，运用双线性变换法对式(8)进行离散化，得到离散后的传递函数$ G(z) $：

$ G(z) = \frac{{{K_0}{h^2} + 2{K_0}{h^2}{z^{ - 1}} + {K_0}{h^2}{z^{ - 2}}}}{{2h + 4{t_0} - 8{t_0}{z^{ - 1}} + (4{t_0} - 2h){z^{ - 2}}}}。$

(10)

式中：$ h $为采样周期；$ z $为变换中的延迟算子。接着，对式(9)离散化处理，得到离散型的控制表达式$ K(z) $：

$ K(z) = \frac{{{h^3} + 3{h^3}{z^{ - 1}} + 3{h^3}{z^{ - 2}} + {h^3}{z^{ - 3}}}}{{G(z)(A + B)}}。$

(11)

式中：$ A $、$ B $为系统在不同延迟状态下（由$ z $的幂次为）的动态特性变化对控制阶段的影响。

将式(10)代入式(11)，便可得到最终适用于泊船遭遇角控制的离散型三阶闭环增益成形控制数学表达式。实际应用时，通过设备采集船舶的运动姿态数据，并将其输入到该表达式中。数据经控制运算后，输出航向信号。依据此信号，船舶可实时调整当前运动状态，进而实现泊船遭遇角控制。

3 实验分析 3.1 实验设置

以某艘船舶为例，该船舶满载吃水深度为10.2 m；两柱间长为137 m；船宽为31.8 m；航速为11 kn。在泊船过程中，使用OCTANS-IV BLUE船舶姿态传感器实时采集船舶的姿态数据，借助TH-N10A2能见度监测仪感知周围环境及探测障碍物，并获取遭遇角信息，各设备详情见表1。获取数据后，利用Pandas、NumPy、SciPy等Python库对采集到的数据进行处理和分析；运用Octave软件搭建数学模型，开展仿真分析和可视化工作；同时，采用R语言进行统计分析和数据可视化展示，从而实现对船舶泊船过程的全面评估与分析。

3.2 泊船遭遇角控制效果分析

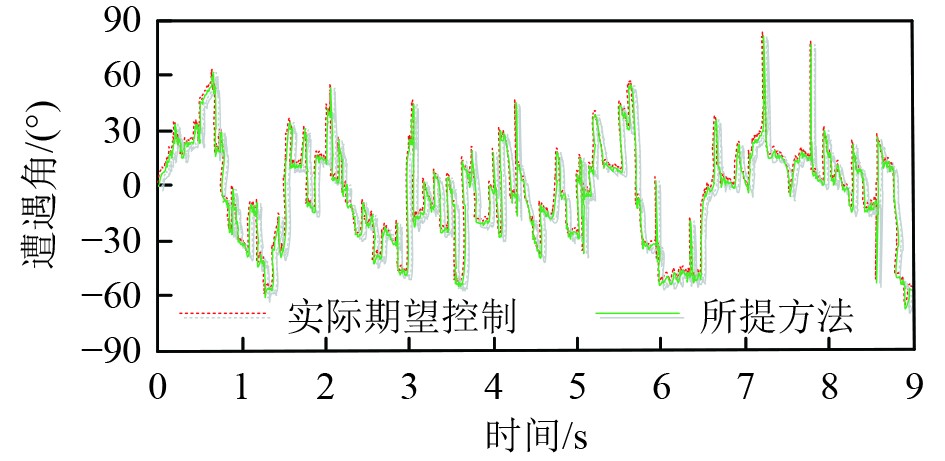
利用设备采集本艘船舶在泊船过程中的运动姿态及周围环境数据，利用所提方法对这些数据进行遭遇角控制，并将控制结果与实际期望控制结果进行对比分析，结果见图1。

可知，所提出的方法在泊船遭遇角控制方面表现出色，各个时刻遭遇角的角度变化情况均与实际期望值保持基本一致。这是因其采用闭环增益成形算法实现泊船遭遇角控制，此算法能够根据船舶不同的运动姿态变化进行恰当调整，从而保证了遭遇角控制的自适应性和鲁棒性。

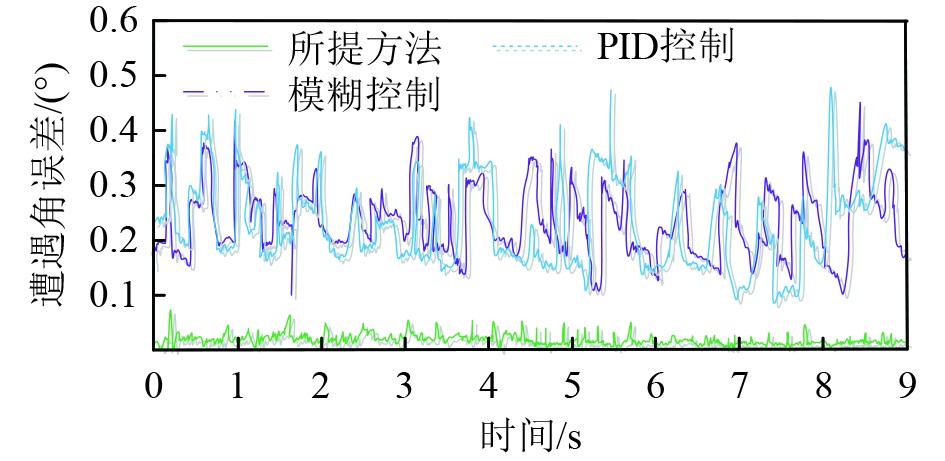
控制误差是检测所提方法遭遇角控制效果的一个关键评估指标。在实验环境不变的情况下，根据泊船作业经验设定遭遇角控制公差为0.25°标准，引入PID控制、模糊控制作为对比方法，对比分析3种方法的航向控制误差情况，结果见图2。

可知，所提方法下泊船遭遇角控制误差曲线最靠近0，且波动范围在0°～0.081°，满足公差0.25°标准，证实所提方法遭遇角控制效果良好，能够将泊船遭遇角控制在合理范围内。这是因为其采用FP-growth算法挖掘泊船运动姿态数据，了解姿态运动与遭遇角控制之间的内在机理，进而有效地缩小遭遇角控制误差。

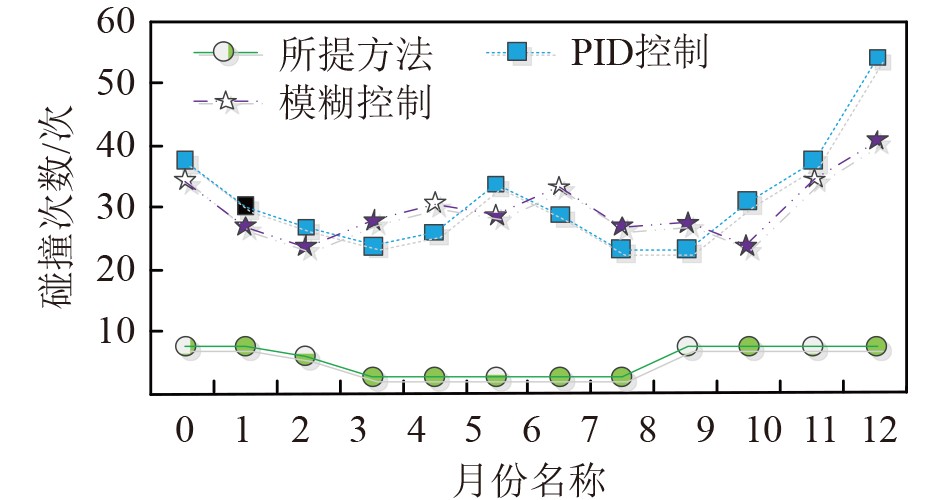
3.3 泊船遭遇角控制性能分析

碰撞次数是指船舶在泊船过程中因遭遇角控制不当导致的碰撞事件数量。为了评估遭遇角控制性能，选此指标，并对2024年本艘船舶在12个月内的泊船过程进行了监测。采用所提出的方法与对比2种方法对泊船遭遇角进行控制，并统计了各方法在各月份的碰撞次数。结果如图3所示。

可知，采用所提方法的船舶在2024年发生碰撞次数最多的月份为9月，但也仅为11次。相比之下，采用对比方法的船舶在各月份的碰撞次数均超出21次。由此可见，所提方法的遭遇角控制性能极佳。这得益于其采用的RBF神经网络能够逼近泊船系统函数，从而准确建立运动姿态数据与遭遇角控制之间的数学关系，显著提升泊船遭遇角的控制精度，进而大幅度降低了泊船碰撞次数。

4 结　语

为了实现精确的遭遇角控制，使船舶能够更好地对准泊位，降低与岸线的碰撞风险，提升泊船的安全性和效率，提出一种基于运动姿态数据挖掘的泊船遭遇角控制方法。运用FP-growth算法和修剪原理，获取泊船运动姿态频繁项，深入挖掘姿态运动与遭遇角控制之间的关系。采用RBF神经网络结合梯度下降法构建泊船系统函数，结合三阶闭环增益成形算法生成泊船遭遇角控制数学模型。将运动姿态输入输入此模型中，经过运算得出控制输出信号（航向信息），根据此信号信息调节航向，最终实现对遭遇角的精准控制。经实验验证，所提方法的遭遇角控制误差小，泊船碰撞次数少，作业质量高。