0 引　言

海洋覆盖了地球表面积的71%，蕴藏着丰富的能源资源，其中海洋可再生能源的利用正日益受到全球关注^[1]。随着可再生能源的发展，水能资源的开发利用逐渐成为研究热点，潮流能以其可预测性的显著优势，在近岸海域展现出了巨大的发电潜力^[2]。为了将潮流动能转化为电能，科研人员设计了多样化的潮流能水轮机，其中水平轴潮流能水轮机因其发电效率高且技术成熟，在潮流能研究领域中得到广泛应用^[3]。与风力发电场不同，水平轴潮流能水轮机通常部署在河流、航道和近海区域，其场地构型受到水深、沟道宽度等多种因素的限制^[4]。因此，潮流能水轮机的阵列布置方式对于整体功率输出的影响至关重要，需要深入研究多个潮流能水轮机之间的相互作用关系^[5]。

O’Doherty等^[6]运用CFD技术深入探讨了小型水轮机阵列的性能，特别关注了机组间距对单个水轮机尾流场及整体阵列性能的影响，研究发现当机组横向间距设定为2D，且纵向间距大于5D时，水轮机的能量捕获效率显著提升。李岩伟等^[7]通过模拟单列布置的双台水轮机，发现纵向间距主要影响下游水轮机后方 5D 范围内的尾流流速亏损，而对远端流场的影响则相对有限。因此，对于纵向排列的双台水轮机流场，流场恢复到初始状态所需的距离与水轮机间的纵向间距并不直接相关。谢永和等^[8]通过物理试验发现，当2台水轮机间距足够近时，会提升2台水轮机的获能效率，但维护难度增加。Mycek等^[4]研究了两台间距为4D水轮机间的相互作用，测量了下游水轮机尾流中的轴向速度和湍流强度，并发现这些关键参数显著受到上游水轮机运行状态的影响。

本文基于有限元数值分析，构建了潮流能水轮机的计算模型，旨在探究上游水轮机对下游水轮机尾流影响的规律。通过与水动力实验结果的对比验证了数值模拟的准确性，研究2个串联水轮机在不同纵向间距（S = 5D、7.5D、10D、12.5D、15D）和叶尖速比（TSR = 4、5、6）条件下，对下游水轮机的水动力性能、尾流场以及湍动能的影响，对于优化水平轴潮流能水轮机的阵列布局具有重要意义。

1 数值理论 1.1 控制方程

假设流体为不可压缩流体，控制方程分为连续方程和动量方程，雷诺平均Navier-Stokes方程可表示为：

$ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ，$

(1)

$ \frac{{\partial \rho {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = \rho {F_i} - \frac{{\partial {P_t}}}{{\rho {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{u_i}{u_j}} } \right]。$

(2)

式中：$ - \rho \overline {{u_i}{u_j}} $为湍流脉动值的雷诺数应力项，$ \mathrm{N} $；${u_i}$为时均流速在x、y、z方向的分量，$ \mathrm{m/s} $；${F_i}$为所受外力；${P_t}$为时均压强，$ \mathrm{Pa} $；$ \rho$为流体密度，kg/m³。

1.2 水动力性能参数

潮流能水轮机水动力性能的无量纲参数有：叶尖速比（TSR）、功率系数（C_P）和推力系数（C_T）。其公式分别为：

$ TSR=\frac{\mathit{\Omega}R}{V_0}，$

(3)

$ C_P=\frac{M\mathit{\Omega}}{\displaystyle\frac{1}{2}\rho AV_0^3} ，$

(4)

$ {C_T} = \frac{T}{{\displaystyle\frac{1}{2}\rho AV_0^2}}。$

(5)

式中：$ \mathit{\Omega} $为水轮机旋转角速度，$ \mathrm{rad/s} $；$R$为叶轮半径，$ \mathrm{m} $；${V_0}$为流速，$ \mathrm{m/s} $。$M$为扭矩，$ \mathrm{N\cdot m} $；$\rho $为流体密度，$ \mathrm{kg/m}^3 $；$A$为叶轮扫掠面积，$ \mathrm{m}^2 $；$T$为推力，N。

2 方法流程及验证 2.1 计算模型及边界条件

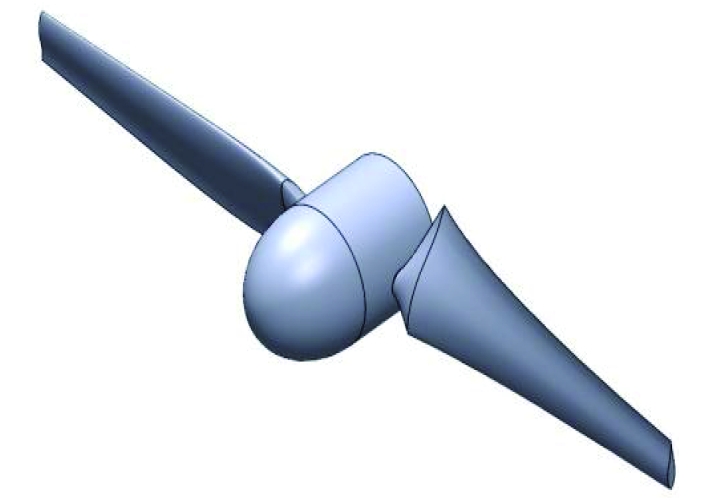
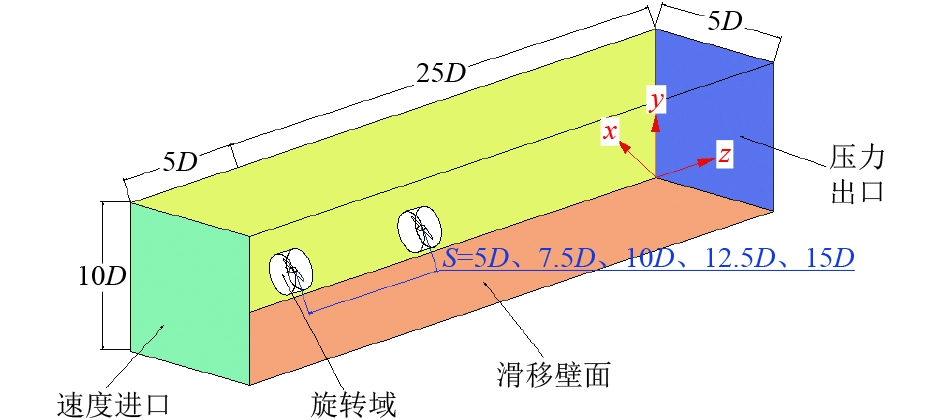
本文的研究基于文献[9]研发的潮流能水轮机展开，在构建数值计算模型的过程中，为简化分析省略了支撑立柱和机箱等非核心部分，仅保留了关键的叶片和轮毂结构，如图1所示。叶片截面翼型为S809，计算域被划分为背景域和旋转域，其中旋转域为包裹叶轮的圆柱体，如图2所示。水轮机直径为D，背景域的长宽高为30D×10D×10D，前台水轮机叶轮盘面至入口边界与出口边界的距离分别为5D和25D，同时叶轮轴线到底部、顶部及两侧壁面的距离均保持5D的间距。设定进口边界为速度入口，采用0.8 m/s的恒定流速模拟水流，顶部、底部和侧壁则设定为滑移壁面，以减少边界效应对模拟结果的影响，出口边界设定为压力出口。叶轮表面为无滑移壁面，采用多重参考系（MRF）模拟叶轮旋转进行稳态求解和SST K-Omega湍流模型进行流动模拟。

2.2 网格划分

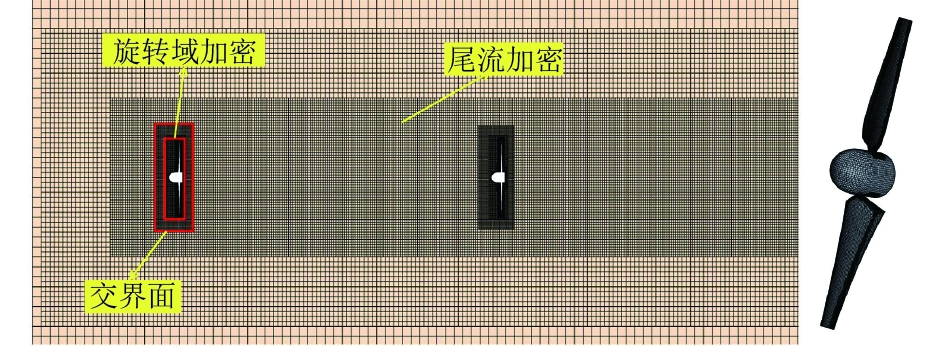
旋转域和静止域都采用切割体网格，为了提高数值结果的准确性，对旋转域及尾流区进行加密。整体网格数为582万，其中静止域网格数为401万，每个水轮机网格数约为904525，如图3所示。

2.3 数值模拟验证

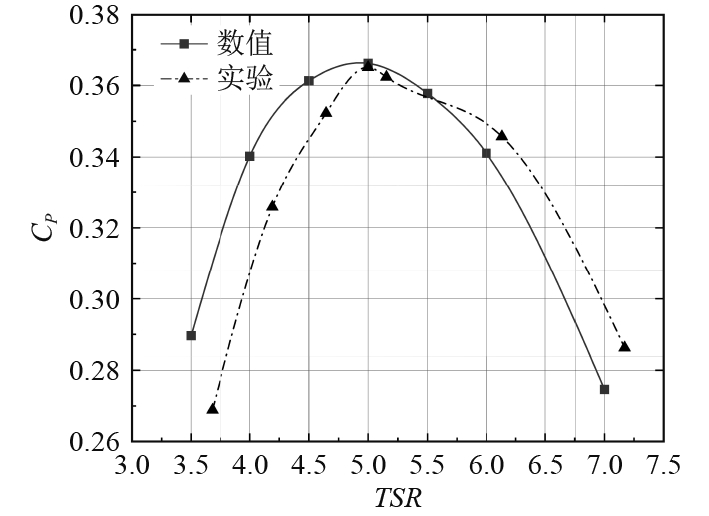
本文从功率系数方面对数值模拟结果进行了验证。将功率系数的计算结果与荆丰梅^[10]的实验数据进行对比，如图4所示。通过对比数值与实验得出的功率曲线，观察出两者在趋势上保持了一致性，有效验证了本文所采用数值方法的准确性与可靠性，但存在一定的差异，这是由于实验中通过测量电机功率来计算水轮机的功率系数，存在一定的功率损失。

3 结果与分析 3.1 水轮机水动力性能分析

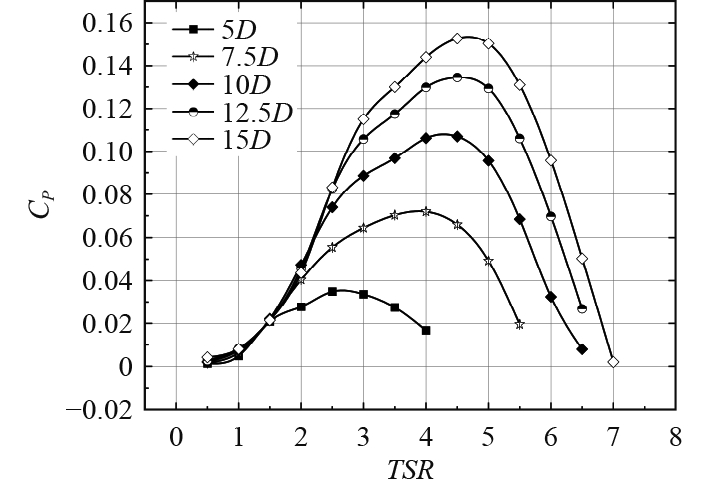
通过改变水轮机组的纵向间距（S）和叶尖速比（TSR），下游水轮机的功率系数（C_P）发生显著变化，如图5所示。可知，随着叶尖速比的增大，下游水轮机的功率首先呈现增长趋势，随后在达到最高点后开始回落，呈现出一致的倒U型曲线趋势，这一现象在不同纵向间距下均有所体现。随着纵向间距的增加，下游水轮机的功率系数也逐步提升，这归因于下游流速随距离增长而逐渐恢复。具体而言，S = 5D时，在TSR = 2.5，C_P达到0.0349；S = 7.5D时，在TSR = 4，C_P达到0.0719；S = 10D时，在TSR = 4.5，C_P达到0.1069；S = 12.5D时，在TSR = 4.5，C_P达到0.1345；S = 15D时，在TSR = 4.5，C_P达到0.1527。因此在S＞10D的条件下，下游水轮机的最佳叶尖速比为4.5，S = 15D时达到最大C_P值。S = 5D时，在TSR = 4，C_P接近0，可判断此时上游水轮机对其干扰严重，当距离为10D、12.5D、15D时，最大C_P值分别为0.1069、0.1345、0.1527，三者近似相等，可认为上游水轮机产生的尾流场在与下游水轮机距离10D处基本恢复。当叶尖速比处于4～5时，水轮机的功率系数显著提升，因此在实际操作中，若将转速精确调控至这一区间，将极大地促进发电量的增加，从而提升能源转换效率。

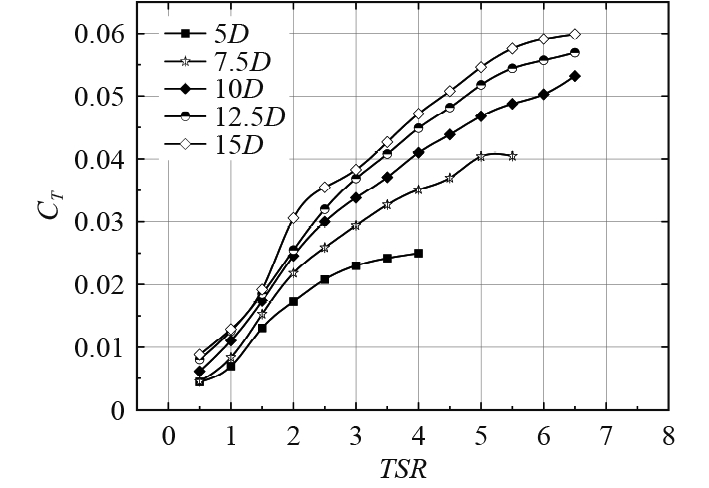
下游水轮机的推力系数随叶尖速比的变化趋势如图6所示。可知，在不同纵向间距条件下，随着叶尖速比的逐渐增加，下游水轮机的推力系数均呈现持续增长的趋势。在同一叶尖速比下，当纵向间距逐渐扩大时，推力系数也随之相应增加。

3.2 尾流场速度分析 3.2.1 尾流场轴向速度分析

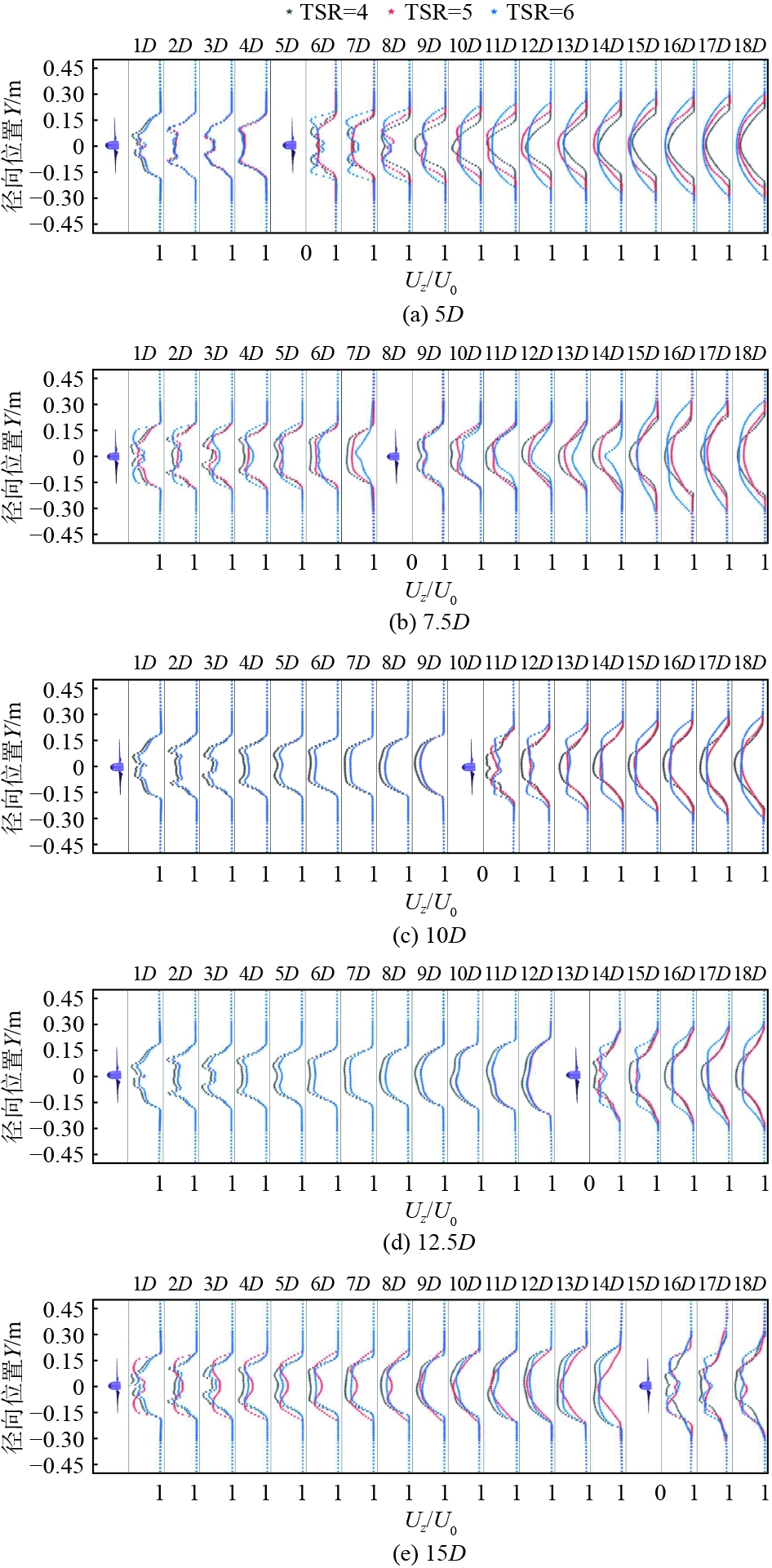
2台串联水轮机组尾流区剖面的瞬时轴向速度分布如图7所示，其中横坐标U_Z/U₀为尾流速度与来流速度的比值。可以看出，轴向速度的恢复呈现出显著的对称分布特性，即速度分布沿中心轴线两侧呈镜像分布。随着轴向距离的递增，速度分布的曲线轮廓由初始的马鞍型逐渐转变为山峰状，这一变化体现了尾流区域速度的逐步回升的动态过程。在下游水轮机尾流场的初始1D～3D区间内，速度损失现象显著，且这些损失主要集中在叶尖两侧区域，而轮毂正后方的速度损失则相对轻微。随着与上游水轮机距离的增加，尾流速度逐渐恢复。当2台水轮机间距达到S = 10D、12.5D，且叶尖速比维持在4～5时，上游水轮机的尾流速度恢复形态近乎重叠，这有力地证明了随着前后水轮机间距的增大，上游水轮机的尾流效应显著减弱，当纵向距离超过10D时，上游水轮机对下游水轮机的干扰基本恢复。

进一步分析，不同叶尖速比条件下，尾流速度的恢复趋势展现出一致性，但细节上有所差异。具体而言，在TSR = 6时，其叶尖位置处的速度损失相比TSR = 4、5时有所减轻，这一现象的成因在于，较高的叶尖转速加剧了流体与叶片间的复杂相互作用，促进了流动分离与失速现象，间接提高了流体通过叶片时的能量转换效率，从而在一定程度上减少了流速的额外损失。此效应在下游水轮机尾流场扩展至7D范围内均有所体现。此外，由数据对比可明确，TSR = 4时水轮机的速度恢复最慢，而TSR = 6时速度恢复最快，这一对比强烈表明较高的叶尖速比有助于加速尾流场的速度恢复。

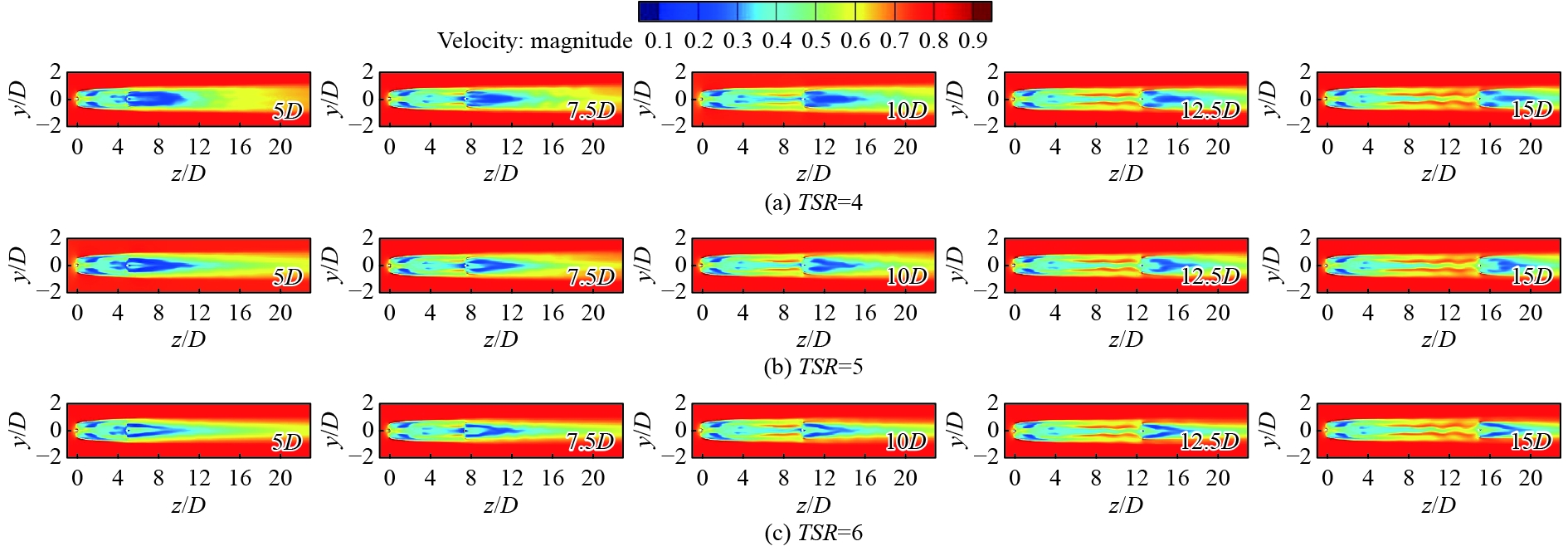
3.2.2 尾流场速度云图

2台串联水轮机组尾流场的速度分布云图如图8所示，x轴和y轴均经过归一化处理，其中D为水轮机直径。可知，流体流经旋转水轮机时的尾流场特性，流体受水轮机阻塞效应驱使，部分高速流体被引导至流场两侧，从而在下游区域形成了一个狭长的低速带。2台水轮机的尾流场速度分布展现出良好的对称性，此外，下游水轮机位于上游水轮机的正后方，由于上游水轮机尾流场的叠加效应，当S = 5D、7.5D时，下游水轮机直接受到上游水轮机产生的高频尾流影响，导致下游水轮机出现严重的失速现象。由图可知，最大速度亏损主要集中在水轮机叶尖的正后方区域，随着距离的增加，上游水轮机对下游水轮机的影响逐渐减弱，导致下游水轮机的低速区域逐渐缩小，尾流形状也逐渐趋于稳定。通过对比不同条件下的尾流速度恢复情况，发现增大叶尖速比能够有效促进下游水轮机尾流场速度的恢复，并减小水轮机后方低速区域的面积，综合图7和图8中的尾流速度恢复情况，建议将串联水轮机组的纵向间距设置在10D以上，以确保水轮机组的稳定高效运行。

3.2.3 尾流湍动能

湍动能（TKE）是指单位质量流体在流动过程中所产生的脉动能量，是表征湍流混合能力的一个重要指标，其计算公式为：

$ {TKE}=\frac{1}{2}\left(\overline{{u}'^2}+\overline{v'^2}+\overline{w'^2}\right)。$

(6)

式中：$ {u}^{{'}}、{v}^{{'}}、{w}^{{'}} $分别为脉动速度。

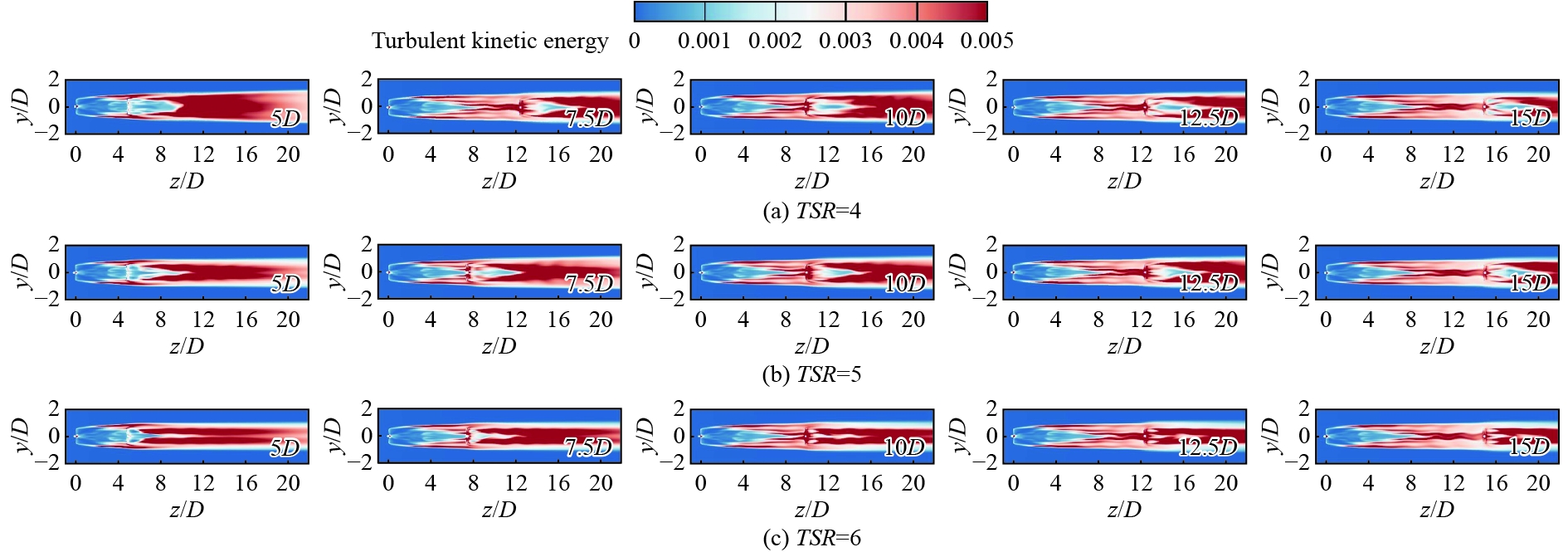
2台水轮机组的尾流场的湍动能分布如图9所示，x轴和y轴均已进行归一化处理，其中D为水轮机直径。整体而言，湍动能呈现出相似的趋势，并且大致呈对称分布。具体而言，下游水轮机因受上游水轮机尾流的显著干扰，导致其周边湍动能的衰减过程尤为突出，当S = 5D时，下游水轮机几乎完全处于上游尾流的影响之下，导致失速现象最为严重。然而，随着两台机组间纵向间距的逐渐增大，湍动能水平开始稳步回升，显示出尾流影响逐渐减弱。随着叶尖速比的增加，高湍动能区域的影响面积逐渐减小，尾流场的速度恢复能力增强。在下游水轮机后方5D的区域内，湍动能逐渐增加至相对均匀的水平，其中最大的湍动能值集中在水轮机叶尖的正后方，而相对较低的湍动能区域则位于轮毂的正后方。

4 结　语

本文以串联水平轴潮流能水轮机组为研究对象，采用数值模拟的方法，通过改变下游水轮机的纵向间距和尖速比研究对水动力性能和尾流场特性的影响，得到主要结论如下：

1）通过对比水动力实验数据与数值模拟结果，验证了数值模拟方法在计算上的准确性，这一验证过程为深入探讨尾流场特性奠定了坚实的基础。

2）根据串联水轮机组的水动力分析，下游水轮机功率系数曲线先增大后下降，呈倒U型曲线趋势，水轮机组的尾流场功率系数在纵向间距10D时基本恢复，当下游水轮机的叶尖速比位于4～5时，其功率系数较高。随着叶尖速比的增大，下游水轮机的推力系数持续增长，随着纵向间距的增大，推力系数也随之增加。

3）根据尾流场速度分析，发现尾流场轴向速度恢复和速度云图、湍动能均呈现以中心轴线为基准的对称分布特性，最大速度损失和湍动能均出现在两侧叶尖位置附近，而轮毂正后方的速度损失和湍动能值则相对较小。随着水轮机之间纵向间距的增加，上游水轮机对下游水轮机的影响逐渐减弱，当纵向间距超过10D时，下游水轮机尾流场的速度逐渐趋于稳定。此外，增大叶尖速比有助于加速尾流场速度和湍动能的恢复，为水轮机组的稳定运行和效率提升提供了有利条件。