0 引　言

随着现代装备对隐身技术需求的增加，闭环消磁系统在舰船中的应用变得愈加重要。闭环消磁系统通过实时测量舰船内部磁场值，推算外部空间磁场，再控制消磁绕组去补偿舰船在一定区域内的磁异常，确保舰船在特定环境下的隐身效果。为实现这一目标，精确的舰船外部磁场推算方法是关键。然而，传统的磁场推算方法在处理复杂舰船结构时往往难以保证较高的精确度，因此亟需一种能够提升磁场推算精度的优化方法。

对于舰船外部磁场推算，目前应用较多的方法主要有2类：一类是磁体模拟法^{[1 − 6]}，该类方法基于物体在若干测量点处产生磁场的相似性，将船舶磁场等效为若干分布于船舶所占空间内模拟体的磁场，对于磁场测量数据的需求较小，但缺乏理论上的严密性，且建模过程对经验性的依赖较高；另一类是依据严格理论公式推算的数字建模法^{[7 − 13]}，如有限元法、边界元法、积分方程法等。这类方法的优点是计算精度较高，但是对数据量要求高，计算量较大。近年来随着计算机技术的快速发展，计算能力快速提升，计算精度与计算量的矛盾得到一定程度的缓解，数字建模法应用的研究也越发活跃。

不容忽视的是，随着数字建模法中三维结构的日益复杂，在推算过程中的系数矩阵病态性问题也愈发突出，直接影响推算结果的精确度与稳定性，这一问题引起了很多学者的关注。Olivier等^[7]通过补充物理方程的方法来降低系数矩阵的病态程度，但在反演计算的最后仍采用传统SVD分解方法，计算效率仍然不高；Neyman^[10]对比了几种有限元方法对于轴对称结构磁场计算的准确性；唐申生等^[8]推导了一般柱面条件下边界元方程组的系数矩阵公式，通过磁场垂直分量来进行空间磁场推算的效果，但未对矩阵病态性问题进行分析；左超等^[11]研究了有限元-边界元混合算法在舰船开域空间静态磁场求解问题中的应用；周家新等^[12]对现有的几种潜艇磁场建模方法进行了理论推导和数值分析对比，发现积分方程法综合结果较优；何保委等^[13]用增加约束方程改进积分方程法近场磁场建模时系数矩阵病态性问题，并开展了仿真试验验证效果，但其最终求解仍采用SVD分解法。

磁场逆推算中矩阵病态性问题对于计算精度有着较大的影响，之前的研究只通过增加约束方程、多种有限元结合等方法来优化此问题，但在磁场逆推算求解时通常采用是传统的正则化手段^[7,8,13]，如SVD分解和吉洪诺夫正则化等。SVD分解法存在着截断参数选取过于依赖经验，优化效果难以保证的问题；吉洪诺夫正则化方法存在着正则化矩阵构造困难，难以适用于三维复杂模型的问题。为弥补这些正则化手段在解决矩阵病态性问题方面的不足，富明慧^[14]引入的预处理精细积分法，相对于常规的正则化方法可以更好地降低矩阵条件数并提高解的精确度，对于矩阵的病态问题有较好的优化效果；刘李楠^[15]将预处理精细积分法应用于电磁层析成像的反演运算中，验证了其稳定性和准确性；王慧蓉^[16]通过单参数进行迭代预处理，进一步优化了预处理精细积分法对于求解病态方程组的效果。

从研究现状分析可以看出，一方面运用积分方程法来解决舰船外部磁场推算方法精度问题和计算效率的关键是降低系数矩阵病态性；另一方面，预处理精细积分法对于降低矩阵病态性有良好的效果。因此，本文将预处理精细积分法与积分方程法相结合，首先通过引入磁本构方程来降低系数矩阵的病态性，在此基础上基于预处理精细积分法进一步优化磁场逆推算求解过程中的病态问题，提出一种基于预处理精细积分法的舰船外部磁场推算优化方法，并通过实测数据和仿真结果进行对比，验证所提出方法的有效性。

1 积分方程法病态性问题分析

在舰船外部磁场推算中，积分方程法因其理论精度较高而得到广泛应用。然而，由于舰船结构的复杂性及推算过程中的多重物理因素，积分方程法中的系数矩阵通常存在严重的病态性问题。该病态性不仅降低了计算结果的精度，还显著增加了计算复杂度，使得求解过程更加困难。因此，本节将通过对系数矩阵进行约化分析病态性问题，并引入磁本构方程以降低系数矩阵的病态程度。

1.1 系数矩阵的约化

对于背景磁场为${{\boldsymbol{H}}^0}$的磁场空间而言，磁性物体$V$会产生感应场${{\boldsymbol{H}}_{{\text{red}}}}$，即：

$ {\boldsymbol{H}} = {{\boldsymbol{H}}^0} + {{\boldsymbol{H}}_{{\text{red}}}}。$

(1)

如果磁性物体$V$的相对磁导率${\mu _r}$较高且厚度相对于尺度而言极薄，则依据瑞利理论^[15]可以假设其感应磁强${{\boldsymbol{M}}^{{\text{ind}}}}$在物体表面呈平行且稳定分布，剩余磁强${{\boldsymbol{M}}^{{\text{rem}}}}$也遵循同样的分布规律，由此假设可得到该磁性物体$V$产生的感应场${{\boldsymbol{H}}_{{\text{red}}}}$的公式为：

$ \boldsymbol{H}_{\text{red}}=\frac{1}{4{\text{π}}} \iiint\limits_V \left(\frac{3(\boldsymbol{M}\cdot\boldsymbol{r})}{r^5}\boldsymbol{r}-\frac{1}{r^3}\boldsymbol{M}\right)\mathrm{d}V 。$

(2)

式中：${\boldsymbol{r}}$为空间中任意点与积分点之间的向量。

空间任意一点的总磁场强度${\boldsymbol{B}}$是由背景场${{\boldsymbol{H}}^0}$和磁性物体$V$受磁化后产生的感应场${{\boldsymbol{H}}_{{\text{red}}}}$的叠加而成，将磁性物体$V$用磁偶极子模型等效后可以得到空间任意一点总磁场强度${\boldsymbol{B}}$为：

$ { {\boldsymbol{B}}(P) = {\mu _0}\left({{\boldsymbol{H}}^0}(P) + \displaystyle\frac{1}{{4{\text{π}} }}\iiint\limits_V {\left(\displaystyle\frac{{3({\boldsymbol{M}}(Q) \cdot {\boldsymbol{r}})}}{{{r^5}}}{\boldsymbol{r}} - \frac{1}{{{r^3}}}{\boldsymbol{M}}(Q)\right)}\right) \mathrm{d}V }。$

(3)

式中：${\mu _0}$为真空磁导率；$P$为空间中的任意一点；$Q$为磁性物体$V$上的积分点；${\boldsymbol{r}}$为$PQ$向量；$r$为${\boldsymbol{r}}$向量的长度。

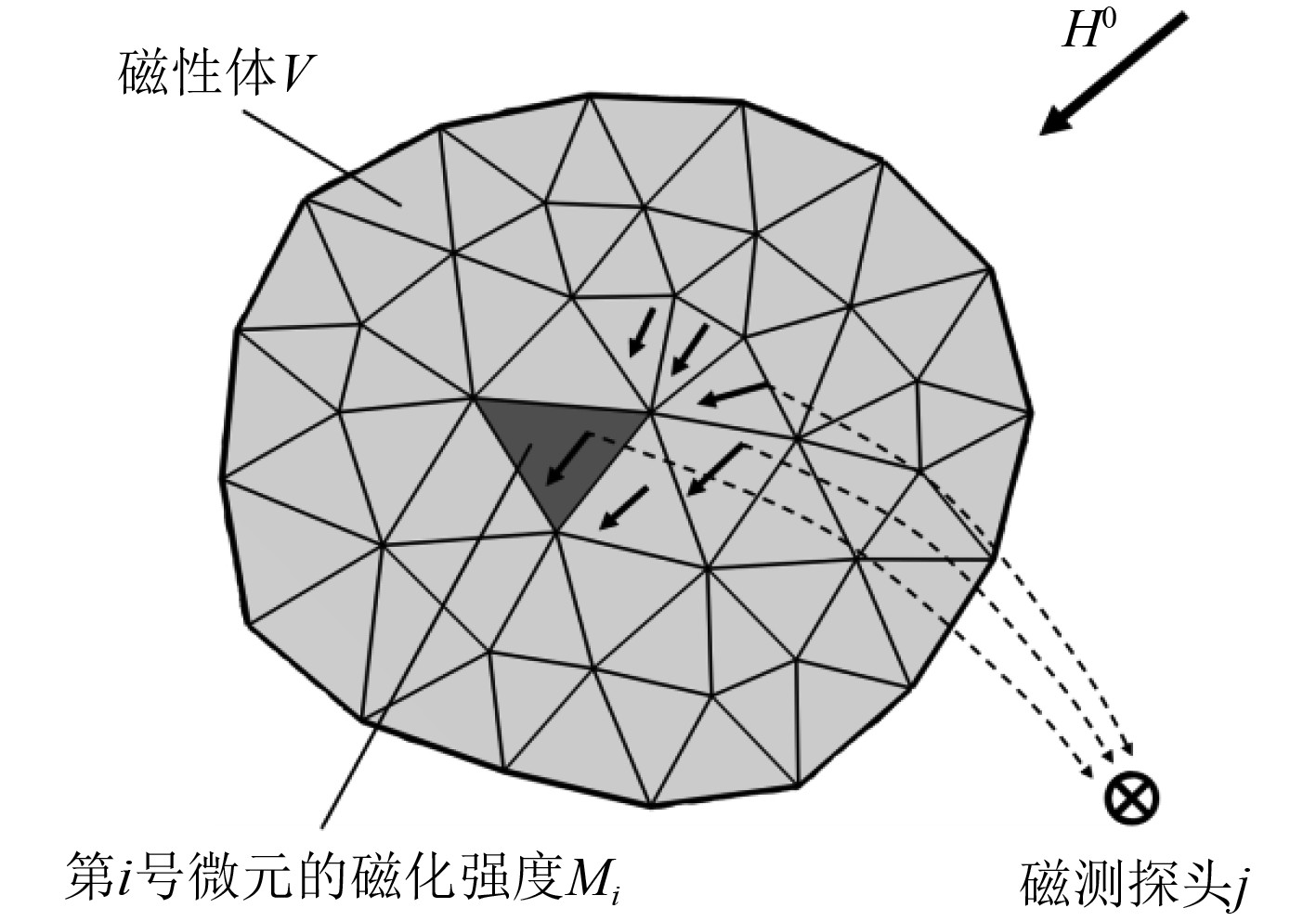
如图1所示，对于上述磁性物体$V$进行格栅化分块成$n$个微元，假设每个微元内的磁场均匀稳定。在磁性物体$V$外部空间布置$m$个三轴测磁探头进行测量，可以得到探头测量值与每个微元的磁场值的关系式：

$ {{\boldsymbol{B}}_j} = {\mu _0}\left({\boldsymbol{H}}_j^0 + \frac{1}{{4 \text{π} }}\sum\limits_i^n {\iiint\limits_{{V_i}} {\left(\frac{{3({{\boldsymbol{M}}_i} \cdot {\boldsymbol{r}})}}{{{r^5}}}{\boldsymbol{r}} - \frac{1}{{{r^3}}}{{\boldsymbol{M}}_i}\right)}} \mathrm{d}{V_i}\right) 。$

(4)

式(4)可以约化为：

$ {\boldsymbol{A}} {\boldsymbol{M}} = {\boldsymbol{b}} 。$

(5)

式中：$ {\boldsymbol{A}} $为着场源与测量点间的空间线性关系；$ {\boldsymbol{M}}$为磁性物体$V$上的未知磁场值；$ {\boldsymbol{b}} $为测量值中去除背景场后属于磁性物体$V$激发的磁场值；$ {\boldsymbol{A}} $为$ 3m \times 3n $矩阵；$ {\boldsymbol{M}} $为$ 3n \times 1 $矩阵；$ {\boldsymbol{b}} $为$ 3m \times 1 $矩阵。

为了求得未知的磁场值$ {\boldsymbol{M}} $，需对系数矩阵$ {\boldsymbol{A}} $进行求逆运算。通常情况下，磁性物体$V$的格栅化分块数量$n$远多于测磁探头数量$m$，因而系数矩阵$ {\boldsymbol{A}} $存在严重的秩亏现象，导致病态性问题非常严重。直接求逆将会引发解的不适定问题，因此需通过多种方法降低系数矩阵的病态性。

1.2 磁本构方程对病态性的优化

根据麦克斯韦感应定律，铁磁性物体的磁化过程存在固有的物理关系，将这些关系表示为方程组便形成了磁本构方程组。将该方程组加入到式(5)中，可以为原方程组增加约束方程，从而优化系数矩阵的病态性。

铁磁性物体的感应磁强由磁场强度$ {\boldsymbol{H}} $决定，即：

$ {{\boldsymbol{M}}^{{\text{ind}}}} = (\mu _r^{{\text{rev}}} - 1){\boldsymbol{H}}。$

(6)

式中：$ \mu _r^{{\text{rev}}} $为材料的相对可逆磁导率。

结合式(1)和式(2)并进行分块可得：

$ \begin{split} {\boldsymbol{M}}_{\boldsymbol{K}}^{{\text{ind}}} = &\ (\mu _r^{{\text{rev}}} - 1)\Biggr({\boldsymbol{H}}_{\boldsymbol{K}}^0 + \frac{1}{{4 \text{π} }} \times \\ &\Biggr(\sum\limits_i^n {\iiint\limits_{{V_i}} {\Biggr(\frac{{3({\boldsymbol{M}}_i^{{\text{ind}}} \cdot {\boldsymbol{r}})}}{{{r^5}}}{\boldsymbol{r}} - \frac{1}{{{r^3}}}{\boldsymbol{M}}_i^{{\text{ind}}}\Biggr)}} \mathrm{d}{V_i} + \\ &\sum\limits_i^n {\iiint\limits_{{V_i}} {\Biggr(\frac{{3({\boldsymbol{M}}_i^{{\text{rem}}} \cdot {\boldsymbol{r}})}}{{{r^5}}}{\boldsymbol{r}} - \frac{1}{{{r^3}}}{\boldsymbol{M}}_i^{{\text{rem}}}\Biggr)}} \mathrm{d}{V_i}\Biggr)\Biggr)。\end{split} $

(7)

上式可以进一步约化为下式：

$ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{C}} + {{\boldsymbol{I}}_{\boldsymbol{d}}}}&{\boldsymbol{C}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}^{{\text{ind}}}}} \\ {{{\boldsymbol{M}}^{{\text{rem}}}}} \end{array}} \right] = \left[ {\boldsymbol{d}} \right] 。$

(8)

式中：$ {{\boldsymbol{I}}_{\boldsymbol{d}}} $为单位矩阵；$ {\boldsymbol{d}} $为由相对可逆磁导率和背景场决定的值。

式(8)是磁本构方程组，其有着$ 6 \times n $个未知量，$ 3 \times n $个方程。因此该方程组的系数矩阵也是秩亏的，将其与式(5)结合起来，可以得到：

$ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{C}} + {{\boldsymbol{I}}_{\boldsymbol{d}}}}&{\boldsymbol{C}} \\ {\boldsymbol{A}}&{\boldsymbol{A}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}^{{\text{ind}}}}} \\ {{{\boldsymbol{M}}^{{\text{rem}}}}} \end{array}} \right] = \left[ \begin{gathered} {\boldsymbol{d}} \\ {\boldsymbol{b}} \\ \end{gathered} \right]。$

(9)

由式(9)可知，结合磁本构方程组后，积分方程法的方程组有$ 6 \times n $个未知量和$ 3 \times (m + n) $个方程，与式(5)的个$ 3 \times n $未知量和$ 3 \times m $个方程相比，得到了显著改善，使得在相同精度要求下对测量探头的需求降低。

然而，即使添加了磁本构方程组，未知量依旧比约束方程多近一倍，系数矩阵的病态性问题仍然存在，因此需通过其他方法对系数矩阵进行整体处理，以进一步降低其病态性。

2 基于精细积分法的病态问题优化

根据矩阵理论，矩阵的条件数反映了其病态程度，因此降低条件数能够有效优化解的不适定问题。当矩阵的所有行或列具有相同的模时，条件数会下降，从而减轻病态性^{[16 - 18]}。因此，范数均衡预处理方法在优化矩阵病态问题上效果良好。本文基于积分方程组中系数矩阵方程重复度高、行列模差异大的特点，将范数均衡法与精细积分法结合，采用范数均衡预处理的精细积分法以降低矩阵的病态性。同时，提出均衡调节参数以进一步优化方程组的解，以应对不适定问题。

2.1 范数均衡预处理精细积分法

对于式(9)进行预处理，使其化为：

$ {\boldsymbol{QAP}} \cdot {\boldsymbol{m}} = {\boldsymbol{b}} 。$

(10)

式中：$ {\boldsymbol{Q}} $和$ {\boldsymbol{P}} $均为进行范数均衡处理的对角矩阵，$ {\boldsymbol{M}} = {\boldsymbol{Q}} \cdot {\boldsymbol{m}} $，将原所求解$ {\boldsymbol{M}} $化为$ {\boldsymbol{m}} $来进行求解，令$ {\boldsymbol{B}} = {\boldsymbol{QAP}} $。

因此对式(10)进行精细积分求解$ {\boldsymbol{m}} $，由$ {\boldsymbol{M}} = {\boldsymbol{Q}} \cdot {\boldsymbol{m}} $即可得到原方程所需的解。

可得：

$ \left\{\begin{aligned} &\boldsymbol m=(\boldsymbol I+(\boldsymbol I+\boldsymbol T\boldsymbol b))\boldsymbol m，\\ &\boldsymbol T\boldsymbol b=2\boldsymbol T\boldsymbol b+\boldsymbol T\boldsymbol b·\boldsymbol T\boldsymbol b 。\end{aligned}\right. $

(11)

其中精细积分展开项：

$ {\boldsymbol{Tb}} = ( - {\boldsymbol{B}}\tau ) + \frac{{{{( - {\boldsymbol{B}}\tau )}^2}}}{2} + \frac{{{{( - {\boldsymbol{B}}\tau )}^3}}}{6}。$

将式(11)经过一定次数的循环迭代，即可得到满足要求的较为精确的解$ {\boldsymbol{m}} $，进一步得到所需要的磁场计算值$ {\boldsymbol{M}} $。

2.2 均衡调节参数

在传统的预处理过程中，范数均衡处理矩阵$ {\boldsymbol{Q}} $和$ {\boldsymbol{P}} $通常是分别对矩阵的行和列进行独立处理。具体而言，传统方法关注的是行和列的单独均衡，忽略了行列之间的相互关系。虽然这种方式在一定程度上能减轻矩阵的病态性，但在行列差异较大的情况下可能存在局限性。因此，本文提出一种基于均衡调节参数的范数均衡处理矩阵构造方法，以更有效地解决这一问题。即构造：

$ \left\{\begin{aligned} &{\boldsymbol Q}_{i}=\frac{\alpha }{{\Vert {\boldsymbol A}_{i}\Vert }_{p}},\\ &{\boldsymbol P}_{j}=\frac{\beta }{{\Vert {\boldsymbol A}_{j}\Vert }_{p}}。\end{aligned} \right. (i,j=1,2,3,\cdots ,n) $

(12)

式中：$ \alpha $和$ \beta $均为均衡调节参数，分别表示行与列之间的均衡关系。通过选择合适的行列关系指示对象，可以有效调节矩阵中行列之间的差异，减少因行列差异过大而引起的病态问题。均衡调节参数的选择对整体均衡处理效果有着较大影响，合适的参数选择能有效提升矩阵计算的稳定性。

在实际计算中，可根据需要选取不同的行列关系指示对象。本文选用矩阵的带宽作为行列关系的指示对象，此时均衡调节参数$ \alpha $和$ \beta $可取为上下带宽的对应反比。通过带宽调整，可以进一步优化矩阵的均衡性，有效提升数值计算的稳定性和效率。

相比传统范数均衡处理方法，该方法在适应性和灵活性方面具有优势，尤其在行列差异较大的矩阵处理中，能更好地平衡不同维度的关系，从而提高计算精度。

3 试验（仿真）设计与结果分析

为验证上述方法在磁场推算中的优化效果，本文构建了与文献[7]中参数相同的单层薄板模型。通过对比处理后的系数矩阵条件数，分析文献[7]中的传统SVD分解法和本文提出的范数均衡预处理精细积分法在矩阵病态性优化方面的效果。此外，使用文献[7]与本文方法分别求解每个微元的磁强值，再推算其在磁测探头处的激发磁场值，并与文献[7]中实测的磁场值（已去除背景场）进行对比。通过比较2种方法的计算结果与实测数据的吻合度，进一步验证本文方法在磁场推算计算精度上的优化效果。

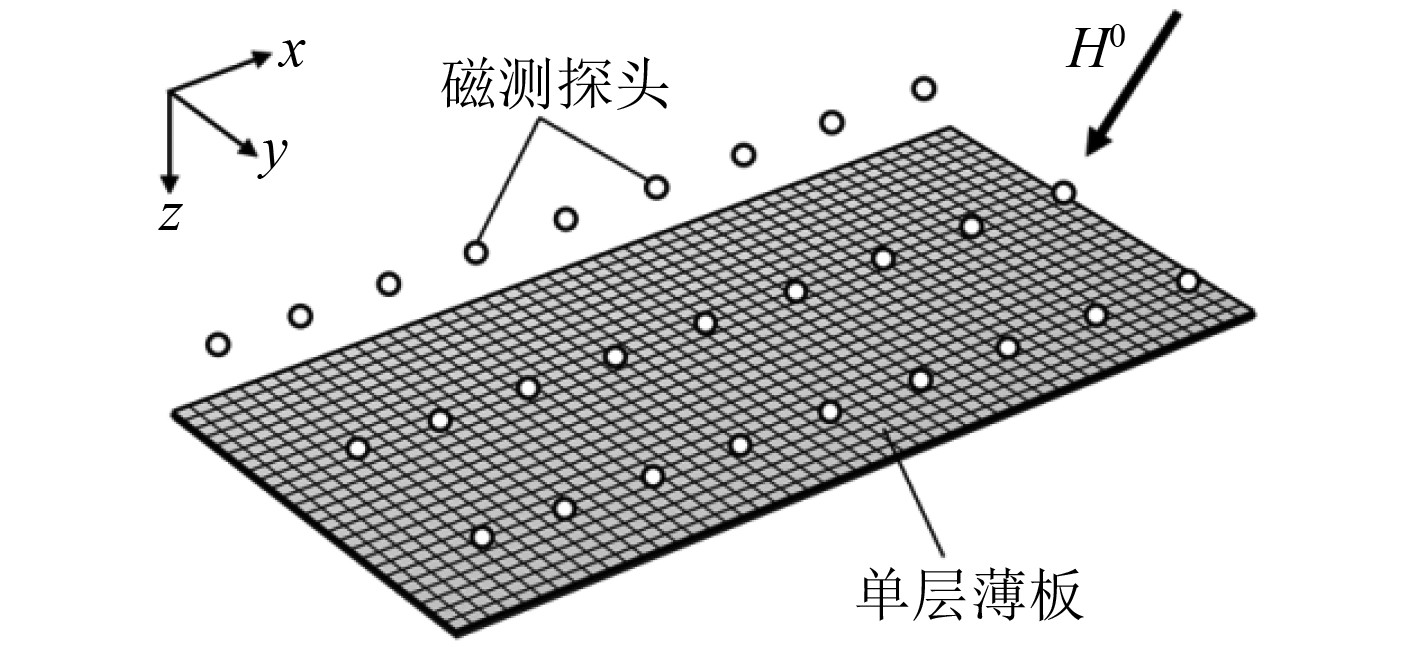
构造如图2所示的单层薄板模型，试验中背景磁场${{\boldsymbol{H}}^0}$为$ \boldsymbol{H}_x^0=-226\;49\text{ }\mathrm{nT} $，$ \boldsymbol{H}_y^0=-421\text{ }\mathrm{nT} $，$ \boldsymbol{H}_z^0= 40671\text{ }\mathrm{nT} $，铁磁性薄板尺寸为900 mm×500 mm×1.4 mm，相对磁导率$ {\mu _r} = 96 $，模型分块数为480，磁测探头数量为27，对于薄板可以忽略z向的分量，因此需求解的未知量数为1920（$ {{\boldsymbol{M}}^{{\text{ind}}}} $2×480个，$ {{\boldsymbol{M}}^{{\text{rem}}}} $2×480个）。

对于系数矩阵条件数结果，在不进行任何处理时，式(9)中系数矩阵的条件数为$ {\xi _0} = 6.53 $；文献[7]中传统SVD分解法处理后所得的系数矩阵条件数为$ {\xi _1} = 5.45 $；用本文的算法在未加入均衡调节参数时的条件数降低为$ {\xi _2} = 5.19 $；而加入矩阵上下带宽的反比作为指示算出的均衡调节参数（$ \alpha = 155 $，$ \beta = 217 $）后，条件数进一步降低为$ {\xi _3} = 4.93 $，结果表明，本文提出的方法相较于传统SVD分解法在优化系数矩阵病态性方面表现出更好的效果。

对于磁场推算结果，首先求解每个微元的磁强值，并利用这些结果计算出在27个磁测探头处的激发磁场值，随后与文献[7]中的实测磁场值（去除背景场）进行对比（见表1），并比较2种方法的推算结果与实测结果的均方根误差（见表2）。

结合表1和表2的结果，可以看出z方向的推算误差相对较大，可能是由于z向分量较小，导致误差的比例被放大。总体来看，本文方法的总场均方根误差为6.81%，显著优于文献[7]中方法所得到的10.71%。因此，可以证明本文提出的方法在外部磁场推算上具有更高的精确度。

通过单层薄板模型验证了本文方法的有效性之后，为了进一步评估该方法在更复杂结构中的适用性和优化效果，本文又构建了T型薄板、工型薄板及圆筒薄板3种更复杂的基础模型。通过对这些复杂结构模型的条件数进行优化，验证了本文方法在应对复杂几何形状时对系数矩阵病态性的改善能力。结果表明，本文提出的范数均衡预处理精细积分法不仅在简单结构上表现良好，也能有效降低复杂结构条件数，改进了矩阵病态性，提升了计算稳定性和精度，具体结果如表3所示。

通过上述计算结果可以看出，本文提出的方法在降低积分方程法系数矩阵的病态性方面表现出显著的效果。具体而言，与传统SVD分解法相比，本文方法通过范数均衡预处理结合精细积分法，有效减少了系数矩阵的条件数，这意味着矩阵的病态程度得到了显著改善。降低条件数能够减少计算过程中数值误差的累积，从而提升了求解的稳定性和准确性。此外，本文方法对不同结构（如T型薄板、工型薄板和圆筒薄板）均能有效降低病态性，这表明该方法具有良好的普遍适用性和鲁棒性。因此，本文提出的方法不仅在降低病态性上效果显著，还在整体上提升了外部磁场推算的精度和可靠性。

4 结　语

本文提出一种基于预处理精细积分法的舰船外部磁场推算方法，旨在提高磁场推算的精度和计算效率。为实现这一目标，本文在积分方程法的基础上，通过引入磁本构方程与预处理精细积分法，优化了系数矩阵的病态性问题，从而改善了磁场推算的稳定性和精确性。仿真计算和实测数据的对比结果表明，与传统方法相比，本文的方法使均方根误差降低至6.81%，显著提升了推算精度。此外，通过对T型薄板、工型薄板、圆筒薄板等复杂模型的验证，结果显示该方法在降低矩阵病态性方面有效，且具备良好的通用性与鲁棒性，系数矩阵条件数降低幅度达到20%～40%。综上所述，本文提出的方法在精度和稳定性上的提升为舰船外部磁场推算提供了一种有效的优化方案，具有工程应用价值。