自动识别系统(Automatic Identification System, AIS)和雷达是船舶十分常用的导航设备。AIS提供高精度定位和船舶信息,雷达独立探测目标物体。两者具有一定的互补性和冗余性,通过数据融合可提升定位精度和导航可靠性,是增强船舶安全性的有效途径。由于2种设备测量船舶位置的原理不同,导致它们所测得的船位并不完全重合,从而产生误差,最终导致实时定位精度等方面存在偏差;这种偏差随着船舶大型化的发展已越来越大,削减该偏差的重要性不仅体现当下,而且对智能船舶的信息感知至关重要,所以有必要进行误差处理后再进行融合。
在雷达系统中,由于机械振动、大气折射和系统内部不完善等因素,系统误差成为影响目标定位精度的主要问题。马军等[1]提出一种基于AIS数据的机载雷达系统误差实时自动标校方法,通过与AIS数据关联来校正雷达系统的误差,该方法具备实时性强、精度高的优点,但对AIS数据的依赖性较高,受限于AIS数据的精度与更新频率;刘敬一等[2]深入分析了AIS船位信息的误差来源,基于运动属性约束的船舶AIS航迹修正方法,提升船舶定位的准确性。常用的船位融合算法包括卡尔曼滤波法、加权平均法、BP神经网络算法等[3 − 5],代广树等[6]分析了AIS与雷达数据的差异,采用聚类方法与高斯-克吕格投影进行时空校准,并使用模糊数学和加权融合算法实现数据融合。严庆新等[7]使用基于最小方差准则的加权平均法对船位融合,并对融合后的误差分析进行仿真验证。Witold等[8]采用交叉协方差准则对真实船舶的船位进行融合处理,强调动态协方差矩阵的选取至关重要。赵海林等[9]基于航迹关联,分析了雷达系统误差致使目标分裂的原因,提出了一种在多雷达多传感器下的自适应误差校正方法,但使用的模型和算法较为复杂,存在计算复杂性高、实时性不足等问题[10]。
多数研究在进行数据融合时选择将雷达测量最近距离数据和AIS数据简化为一维像素点进行融合。这种做法忽略了船舶尺度、相对位置关系以及船型对雷达测量数据的影响,结果仍然不够准确。本文提出基于最小二乘法椭圆拟合的雷达测量位置修正方法,以提高雷达测量数据的准确性。通过针对传统数据融合方法中存在的误差处理问题进行了改进,综合考虑了船舶的尺度、相对位置关系对雷达测量数据的影响,克服了将雷达数据简化为一维像素点所带来的不准确性。最后利用Matlab在动态环境下进行仿真实验,对雷达测量拟合的目标位置点与AIS拟合船位进行融合,并与真实位置点的误差进行对比。实验证明采用最小二乘法椭圆拟合的船舶驾驶台位置为船位相比于采取最近距离点为雷达位置为船位融合后的平均误差减少78.51%,验证该方法的有效性。
1 船位信息预处理由于AIS与雷达在坐标系和时间同步上的差异,进行船位融合之前,需要完成船位信息的预处理。
1.1 坐标转换由于AIS船位与雷达船位在坐标单位和测量原理上的差异,要求在多源数据融合过程中必须进行精确的坐标转换,以确保数据的一致性和准确性。
1.1.1 AIS坐标变换AIS依赖船舶的GPS系统获取位置信息,并通过WGS-84地理坐标系报告经纬度数据,利用VHF无线电频段进行播发[11]。本文运用墨卡托投影将WGS-84坐标系转换为笛卡尔坐标系,再通过距离换算将船位数据整合到以测量点为原点的直角坐标系中。经纬度
| $ \left\{ {\begin{aligned} &{{X_A} = K \cdot \ln \left[ {\tan \left( {\displaystyle\frac{{\text{π}} }{4} + \displaystyle\frac{B}{2}} \right) \cdot {{\left( {\displaystyle\frac{{1 - e \cdot \sin B}}{{1 + e \cdot \sin B}}} \right)}^{\tfrac{e}{2}}}} \right]},\\ &{{Y_A} = K \cdot (L - {L_0})},\\ &{K = \displaystyle\frac{{{a^2}}}{b} \cdot \displaystyle\frac{1}{{\sqrt {1 + {{e'}^2} \cdot {{\cos }^2}{B_0}} }} \cdot \cos {B_0}}。\end{aligned}} \right. $ | (1) |
式中:椭球体长半轴a=
雷达测量方位和距离的原理是基于雷达系统发射电磁波并接收目标物体反射回来的信号。通过分析发射的电磁波与接收到的回波信号之间的时间差与接收回波的方位,雷达可以确定目标物体相对于雷达的距离和方位角。因此,雷达检测到的来船位置信息通常以极坐标系下的距离和方位角来描述。故在雷达坐标变换方面选择将极坐标系转换到以测量点为原点直角坐标系中。
设雷达测得距离为
| $ {X_R} = \rho \sin \theta ,\;{Y_R} = \rho \cos \theta 。$ | (2) |
通过上述处理,确保AIS与雷达的船位数据都转换并同步到以测量点为原点的统一直角坐标系中。
1.2 时间统一根据多源信息融合理论,不同类型传感器的数据融合需要进行时间配准[12]。在进行雷达与AIS数据融合时,必须考虑两者不同的采样周期。为了实现有效的船位融合,雷达与AIS船位融合必须在相同时间点上进行处理。雷达的扫描周期相对固定,一般为每分钟15~30次,时间间隔通常为2~4 s。而AIS的数据播发周期则随着船舶状态的变化而变化,播发周期一般在2~180 s不等,按照IMO NAV 43次会议附录规定,AIS在“自动模式”下动态信息报告间隔如表1所示[11]。本文采用雷达数据更新时间作为数据匹配时间,并使用协调世界时(UTC)作为参考基准。
|
|
表 1 “自动模式”下,AIS动态信息报告间隔 Tab.1 AIS dynamic information reporting intervals in "Automatic Mode" |
插值法适用于船舶保持固定航向和速度的情况下计算位置。然而,相较于插值法,三次样条插值使用三次多项式拟合数据点,生成平滑且连续的曲线,更好地实现时间同步。由于选取雷达数据的更新频率为2 s,而AIS的更新频率不固定。在AIS与雷达数据的时间匹配过程中,由于两者采样频率不同,使用三次样条插值对AIS数据进行处理,以实现与雷达数据的同步。
假设在区间
在实际应用中,通常GPS天线位于船舶驾驶台,由于两设备测量原理不同以及均存在系统误差,导致雷达船位和AIS船位之间存在偏差,以VLCC船舶为例,误差可达数十米甚至上百米。为了提高雷达测距的精度,本文提出一种基于最小二乘法的拟合修正方法,将雷达测量的船舶边界点拟合到GPS天线位置。从而减小由于雷达船位误差带来的数据融合误差。
2.1 雷达工作原理雷达通过发射电磁波并接收反射信号,根据发射与接收的时间差计算目标物体的距离,公式为:
| $ d = \displaystyle\frac{{c\Delta t}}{2} 。$ | (3) |
式中:
雷达通过天线阵列接收信号的相位差来确定目标物体的方位,当接收到反射信号时,系统记录对应的角度以确定目标的方位。
2.2 基于边界点选取的最小二乘法椭圆拟合在船舶导航和定位中,雷达测量通常得到的是船舶的边界点,通过最小二乘法拟合这些边界点,可以得到一个连续的椭圆模型,从而更准确地描述船舶的尺度、相对位置和船型。这种方法不仅适用于静态场景,还可以动态更新观测数据,实现对船舶位置和形态的实时跟踪和修正。本文采用以船长为长半轴,船宽为短半轴的椭圆模型来对船舶进行模拟,从而进行位置修正与计算。
最小二乘法通过构建误差函数,将观测数据与理论模型之间的偏差量化,并通过优化算法寻找使误差函数最小的参数。在拟合椭圆时,首先假设椭圆方程的一般形式为:
| $ A{x^2} + Bxy + C{y^2} + Dx + Ey + 1 = 0 。$ | (4) |
且满足
| $ {F(A,B,C,D,E) = \displaystyle\sum\limits_{i = 1}^n {{{\left( {x_i^2 + {x_i}{y_i}A + y_i^2B + {x_i}C + {y_i}D + E} \right)}^2}}}。$ | (5) |
为了使
| $ \frac{{\partial F}}{{\partial A}} = \frac{{\partial F}}{{\partial B}} = \frac{{\partial F}}{{\partial C}} = \frac{{\partial F}}{{\partial D}} = \frac{{\partial F}}{{\partial E}} = 0 。$ | (6) |
从而可以得到方程:
| $ \begin{split} &\left[\begin{array}{*{20}{c}}\sum_{ }^{ }x_i^2y_i^2 & \sum_{ }^{ }x_iy_i^3 & \sum_{ }^{ }x_i^2y_i & \sum_{ }^{ }x_iy_i^2 & \sum_{ }^{ }x_iy_i \\ \sum_{ }^{ }x_iy_i^3 & \sum_{ }^{ }y_i^4 & \sum_{ }^{ }x_iy_i^2 & \sum_{ }^{ }y_i^3 & \sum_{ }^{ }y_i^2 \\ \sum_{ }^{ }x_i^2y_i & \sum_{ }^{ }x_iy_i^2 & \sum_{ }^{ }x_i^2 & \sum_{ }^{ }x_i^2 & \sum_{ }^{ }y_i \\ \sum_{ }^{ }x_iy_i^2 & \sum_{ }^{ }y_i^3 & \sum_{ }^{ }x_iy_i & \sum_{ }^{ }y_i^2 & \sum_{ }^{ }y_i \\ \sum_{ }^{ }x_iy_i & \sum_{ }^{ }y_i^2 & \sum_{ }^{ }x_i & \sum_{ }^{ }y_i & N\end{array}\right]= \\ &-\left[\begin{array}{*{20}{c}}\sum_{ }^{ }x_i^3y_i & \sum_{ }^{ }x_i^2y_i^2 & \sum_{ }^{ }x_i^3 & \sum_{ }^{ }x_i^2y_i & \sum_{ }^{ }x_i^2\end{array}\right]。\end{split}$ | (7) |
解得
| $ \left\{ {\begin{aligned} &{{X_c} = - \displaystyle\frac{{A \cdot D - 2 \cdot B \cdot C}}{{{A^2} - 4B}}} ,\\ &{{Y_c} = - \displaystyle\frac{{A \cdot C - 2 \cdot D}}{{{A^2} - 4B}}} 。\end{aligned}} \right. $ | (8) |
最终以椭圆中心坐标
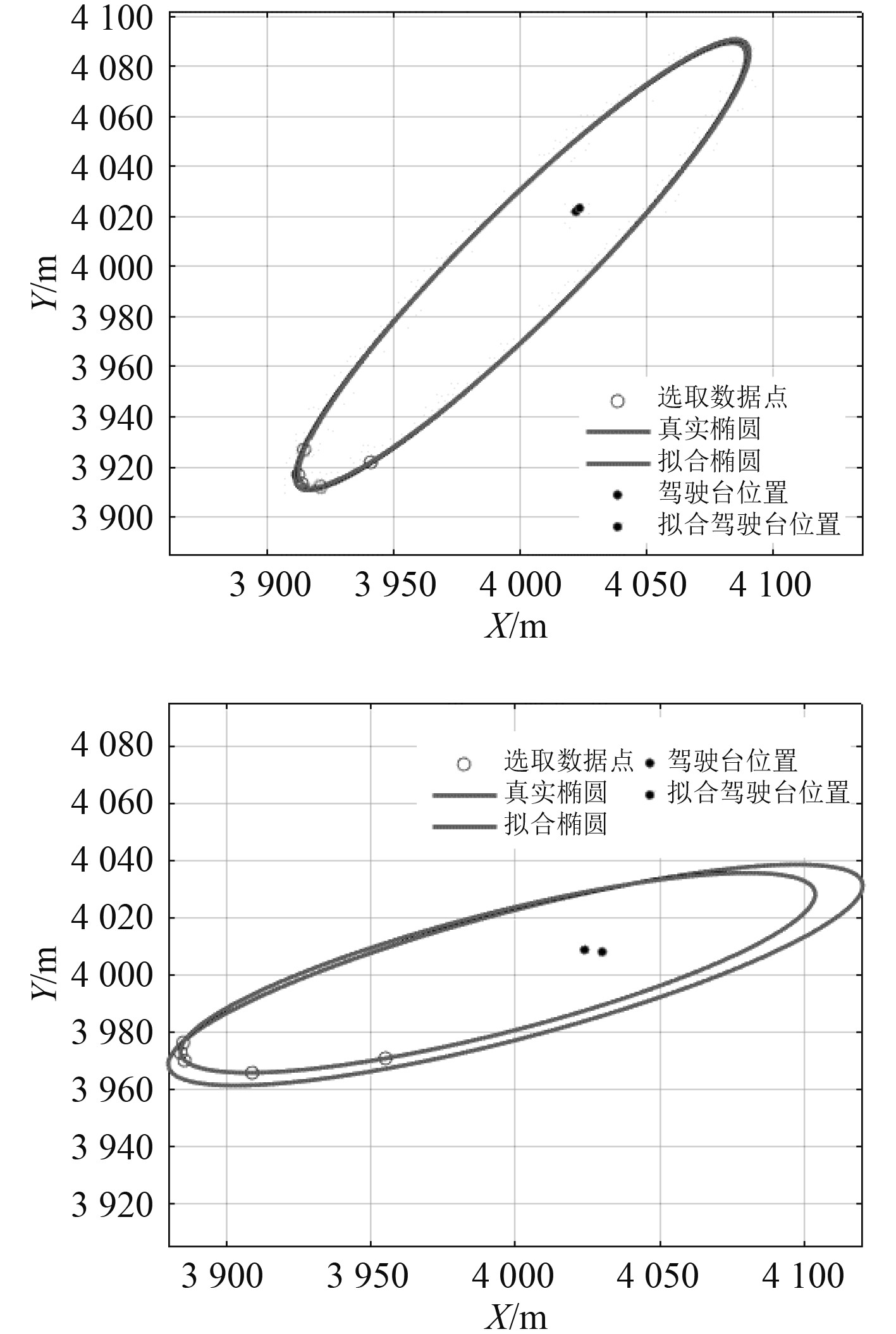
如图1所示,本实验中的设定如下:雷达的测距误差的方差取400 m2,测方位误差的方差取2(°)2[13],假设左侧船舶的真实中心坐标为(
|
图 1 最小二乘法拟合椭圆对比 Fig. 1 Comparison of least squares fitted ellipse |
系统误差导致拟合椭圆相较于真实位置存在一定偏移。然而,相对于所设置方差,拟合椭圆坐标中心点相对于真实中心点坐标误差较小。确定中心坐标、船长、船宽和航向后,可以将船舶中心向船尾移动1/4船长模拟船舶驾驶台的位置,从而更接近实际GPS天线的位置,提升定位精度。
3 AIS与雷达数据融合 3.1 卡尔曼滤波为了提高船舶定位的精度和可靠性,可以在局部传感器获得信息时加上滤波器,滤除噪声并且能很好地跟踪目标[14]。本文分别对AIS和雷达数据进行卡尔曼滤波处理,然后再进行数据融合。这种方法的优势在于,在融合之前,对每个传感器的数据进行去噪和状态估计,能够有效提高单一传感器数据的精度,并为最终的数据融合提供更加精确的输入。
首先,针对AIS和雷达这2种不同的传感器,卡尔曼滤波通过线性动态系统和高斯噪声假设进行状态估计。其基本的状态预测方程为:
| $ {{\boldsymbol{x}}_{\boldsymbol{k}}}={\boldsymbol{ A}}{{{x}}_{{{k - 1}}}} +{\boldsymbol{ B}}{{{u}}_{{{k - 1}}}}{{ + }}{{{w}}_{{{k - 1}}}}。$ | (9) |
式中:
在对AIS数据和雷达数据分别进行卡尔曼滤波时,首先通过船舶的运动状态预测其当前位置,再结合实际测得的数据进行更新和修正。更新步骤的核心是通过卡尔曼增益
| $ {\hat x_{k|k}} = {\hat x_{k|k - 1}} + {K_k}({z_k} - \boldsymbol H{\hat x_{k|k - 1}}) 。$ | (10) |
式中:
| $ K_k=P_{k|k-1}H^{\mathrm{T}}(HP_{k|k-1}H^{\mathrm{T}}+R)^{-1}。$ | (11) |
式中:
自适应加权融合算法的核心是基于各传感器的测量误差方差,通过调整权重来实现AIS和雷达数据的最优融合。假设AIS与雷达数据源的测量位置分别为
| $ {w_{{\rho _1}}} = \frac{1}{{\sigma _{{\rho _1}}^2}},{w_{{\rho _2}}} = \frac{1}{{\sigma _{{\rho _2}}^2}},{w_{{\theta _1}}} = \frac{1}{{\sigma _{{\theta _1}}^2}},{w_{{\theta _2}}} = \frac{1}{{\sigma _{{\theta _2}}^2}}。$ | (12) |
融合后的距离
| $ \hat \rho = \frac{{{w_{{\rho _1}}}{\rho _1} + {w_{{\rho _2}}}{\rho _2}}}{{{w_{{\rho _1}}} + {w_{{\rho _2}}}}}, \hat \theta = \frac{{{w_{{\theta _1}}}{\theta _1} + {w_{{\theta _2}}}{\theta _2}}}{{{w_{{\theta _1}}} + {w_{{\theta _2}}}}}。$ | (13) |
融合后的加权方差
| $ \left\{\begin{aligned} &\hat \sigma _\rho ^2 = \frac{1}{{{w_{{\rho _1}}} + {w_{{\rho _2}}}}} = \frac{{\sigma _{{\rho _1}}^2\sigma _{{\rho _2}}^2}}{{\sigma _{{\rho _1}}^2 + \sigma _{{\rho _2}}^2}}, \\ &\hat \sigma _\theta ^2 = \frac{1}{{{w_{{\theta _1}}} + {w_{{\theta _2}}}}} = \frac{{\sigma _{{\theta _1}}^2\sigma _{{\theta _2}}^2}}{{\sigma _{{\theta _1}}^2 + \sigma _{{\theta _2}}^2}}。\end{aligned} \right.$ | (14) |
通过自适应加权融合算法,可以根据传感器误差动态调整权重,从而实现对船位的更精确融合。该方法在AIS数据更新频率较低、雷达数据受噪声影响较大的情况下,能够有效减少测量误差,提高船舶定位的精度。
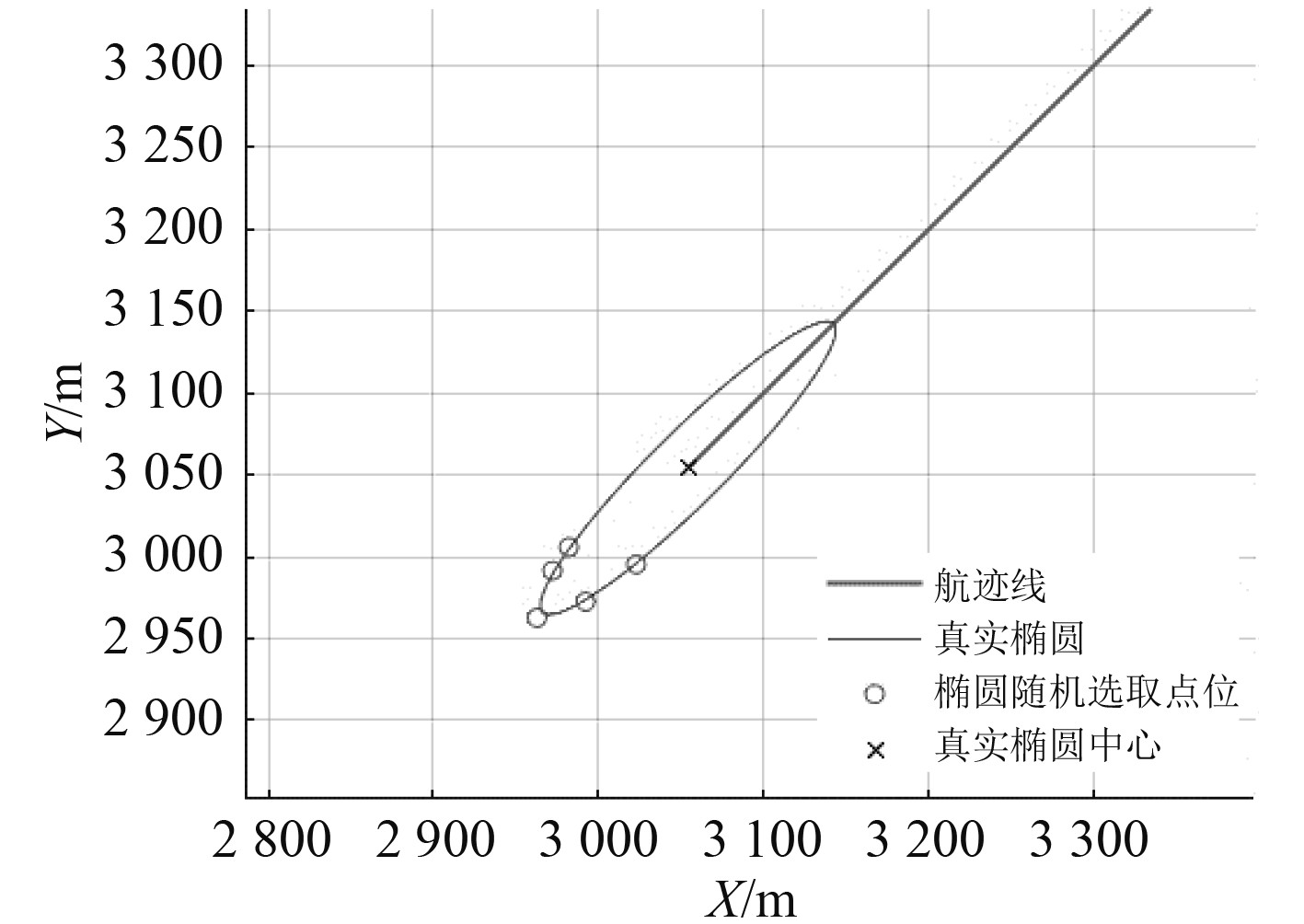
4 算法仿真验证 4.1 仿真试验条件通过对海上雷达系统的误差特性分析,得出了在类似条件下的测距与测向误差方差为[13]:雷达的测距误差的方差取400 m2,测方位误差的方差取2(°)2。目标船GPS提供数据的径向误差的方差取80 m2,方位误差的方差取1.2(°)2。目标船的船长船宽参照真实超大型油船VLCC14 AXEL SPIRIT 1的数据,长为249 m,宽为44 m。航向为225°,航速为10 kn;测量点位于(0,0),目标船初始位置的坐标为(
|
图 2 船舶运动趋势图 Fig. 2 Ship movement trend |
雷达通过对物体外沿边界进行扫描获得多个数据点,通常选取的拟合点位越多,椭圆拟合的准确性就越高。但是考虑到航海实际,雷达发射电磁波会被地物或其他障碍物阻挡或反射,从而导致无法获取较多目标雷达扫描点位;一些特殊物体的物理特性,诸如方向反射率很低等原因,会降低雷达的检测性能,导致目标信息检测不准确[15]。因此,在雷达扫描点位数量不足的情况下,选择可拟合出椭圆轮廓的最少拟合点位数量进行实验,以保证方法在极端情况下的有效性。为增强拟合结果的可靠性和普适性,在实验中随机选择5个外沿边界点,结合随机原理思想,以避免拟合偏差[16]。通过最小二乘法进行椭圆拟合,从而计算出雷达测量下的拟合椭圆的参数。
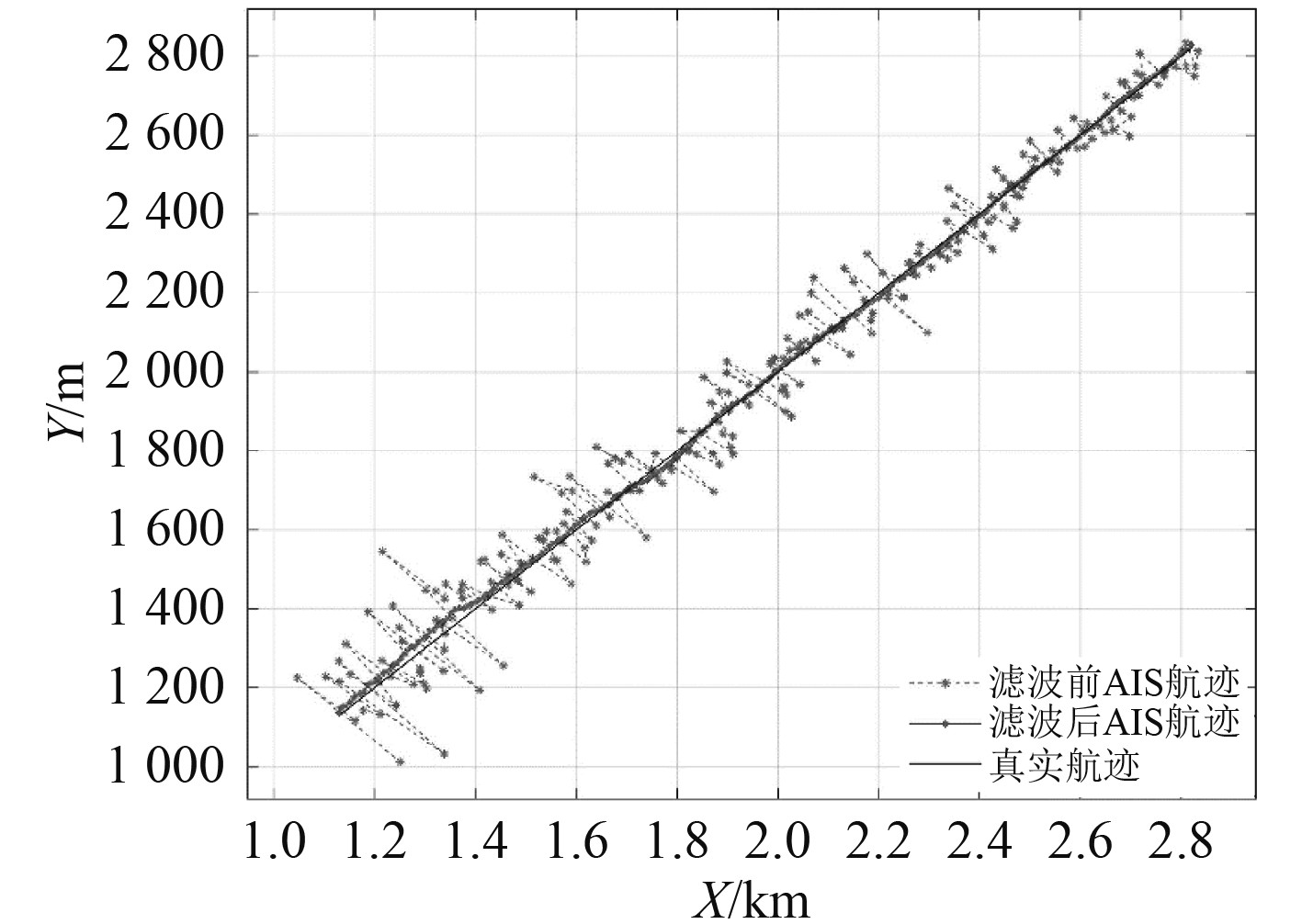
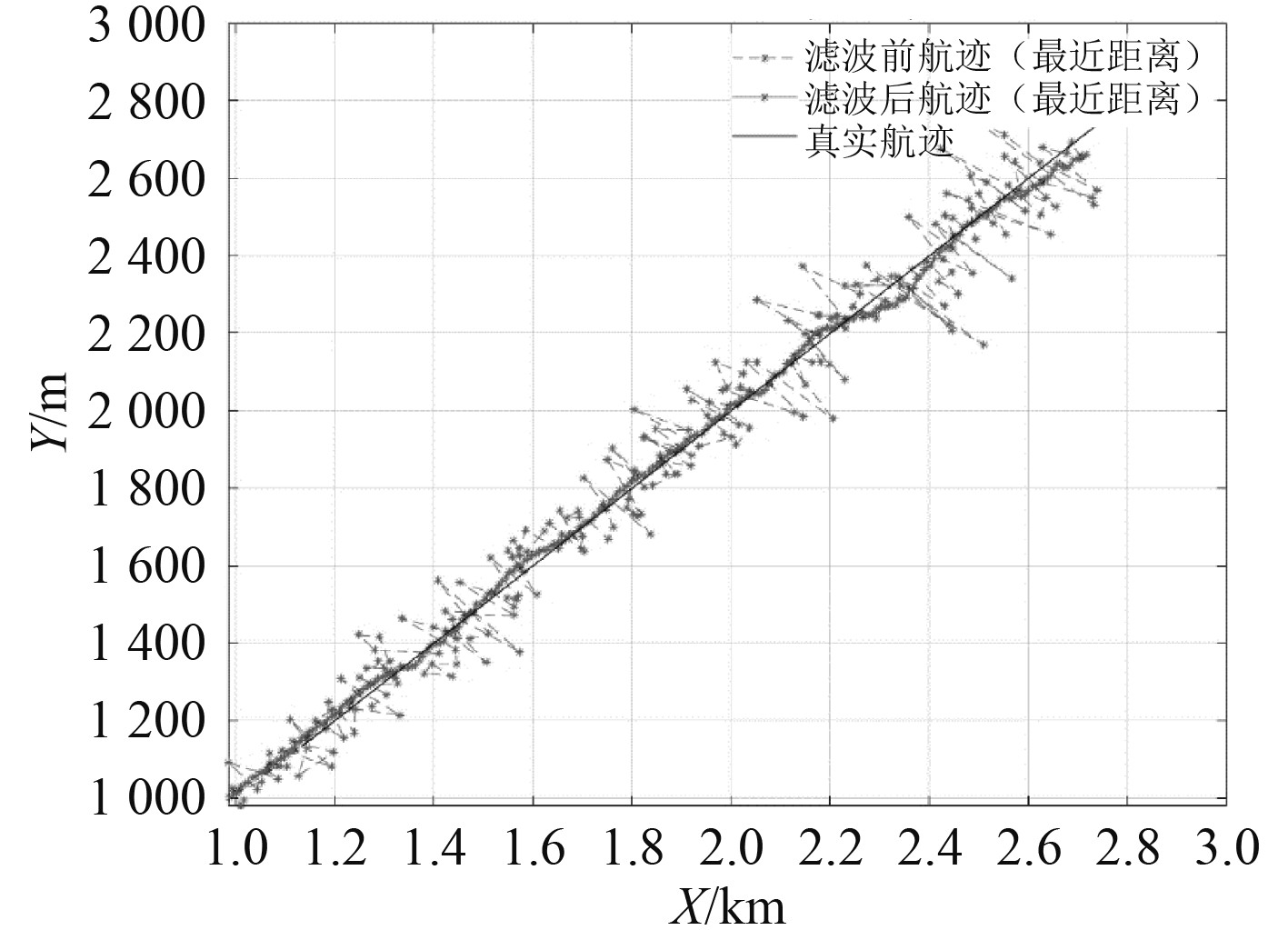
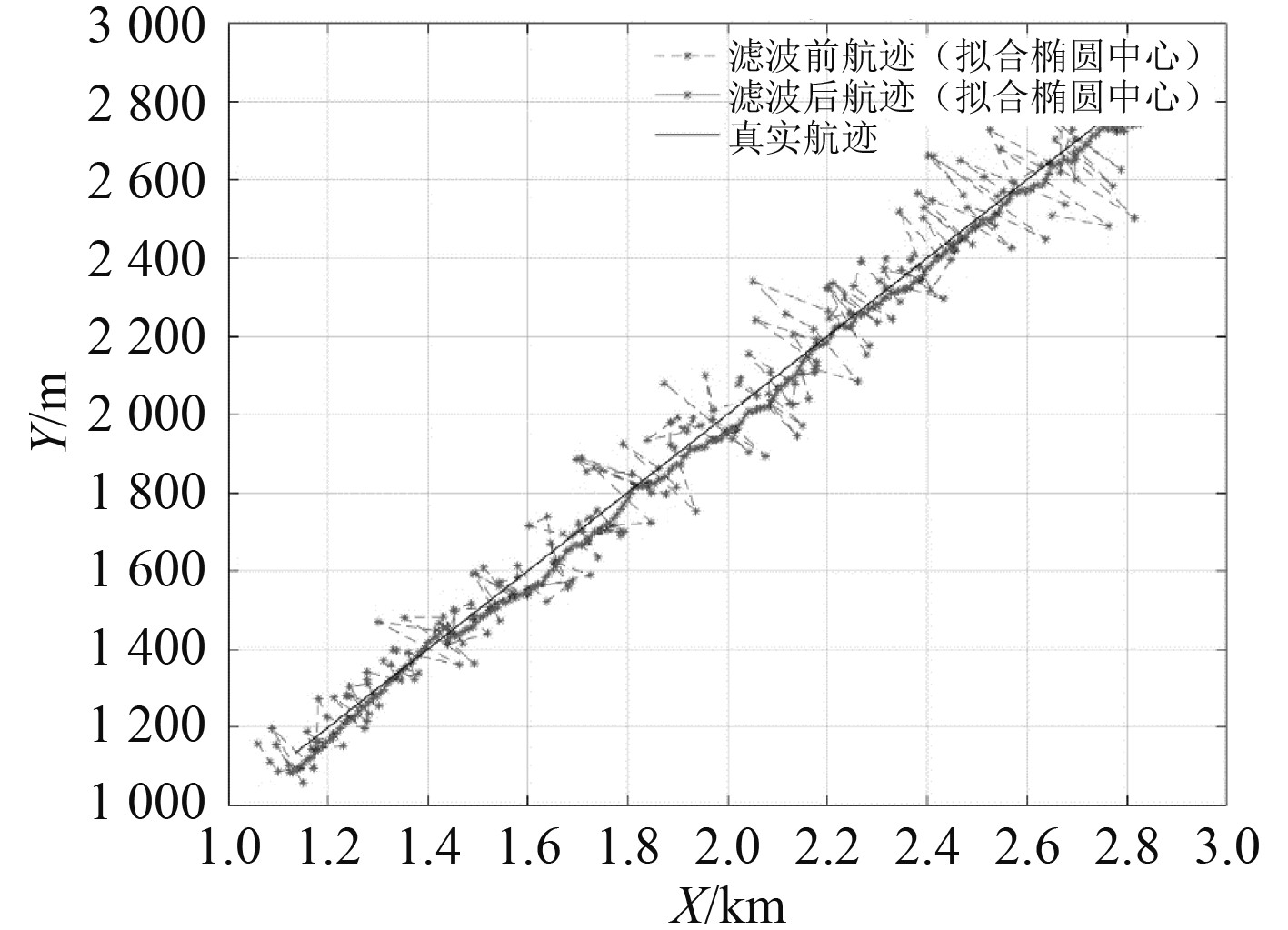
4.2 卡尔曼滤波船位在船舶轨迹预测和目标跟踪中,测量噪声和系统不确定性会影响轨迹估计的精度。卡尔曼滤波在匀速直线运动的轨迹估计方面表现良好,因此在融合雷达与AIS数据之前,通过卡尔曼滤波器对船位进行处理,如图3~图5所示。滤波后的轨迹精度得到明显改善,确保了融合过程中的数据可靠性。
|
图 3 AIS滤波轨迹图 Fig. 3 AIS filtered trajectory |
|
图 4 最近距离点位滤波轨迹图 Fig. 4 Nearest distance point filtered trajectory |
|
图 5 拟合椭圆点位滤波轨迹图 Fig. 5 Fitted ellipse point filtered trajectory |
在最小均方误差情况下,可得加权因子:
|
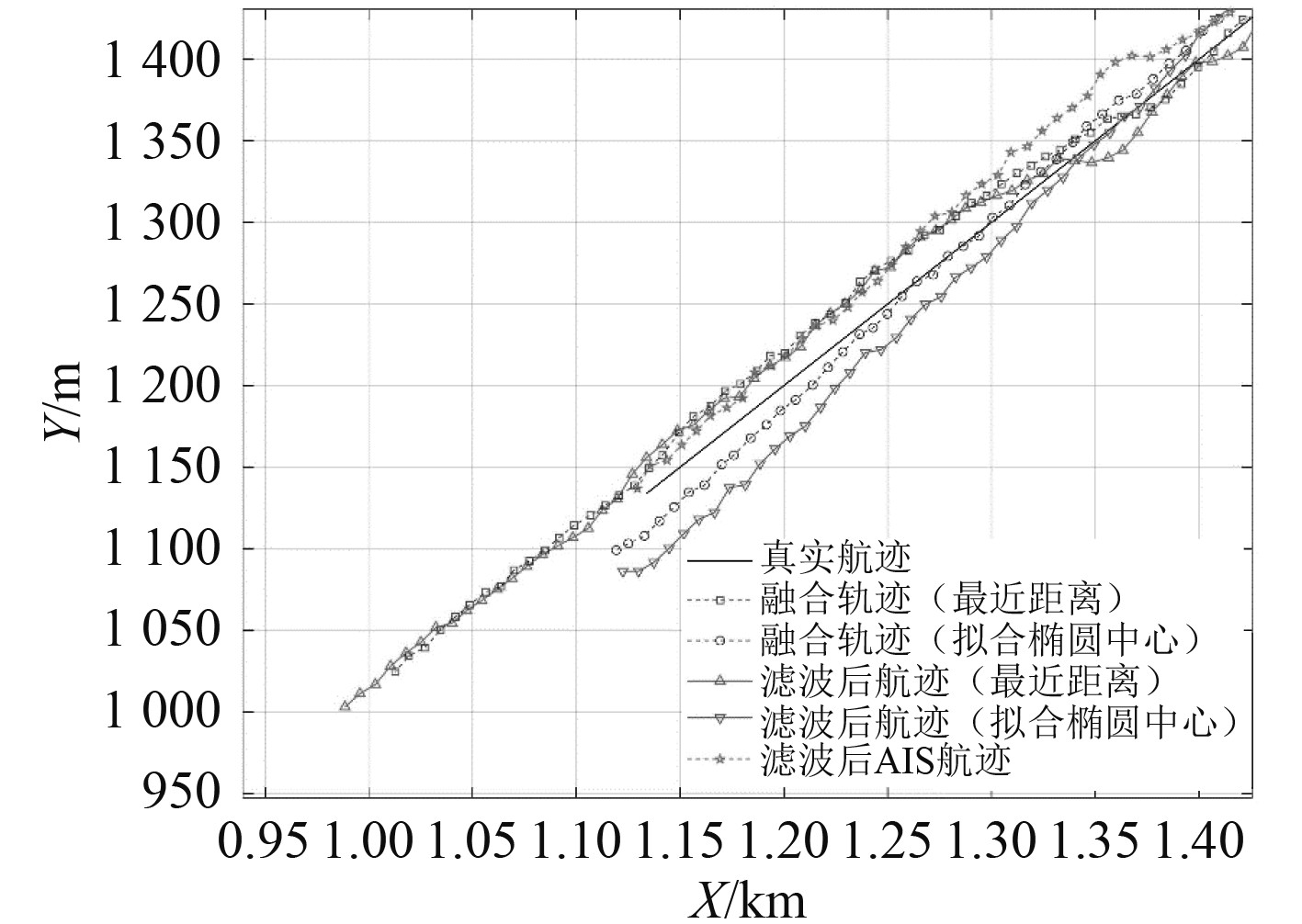
图 6 融合轨迹图 Fig. 6 Fused trajectory |
可知:融合后的船位比未融合时更加接近真实船位。相比于传统的最近距离点方法,采用拟合椭圆位置点进行融合后的船位坐标与真实船位的差异由155.74 m减少到了33.47 m。这表明,拟合椭圆位置点方法在提高船位估计准确性方面效果更佳。
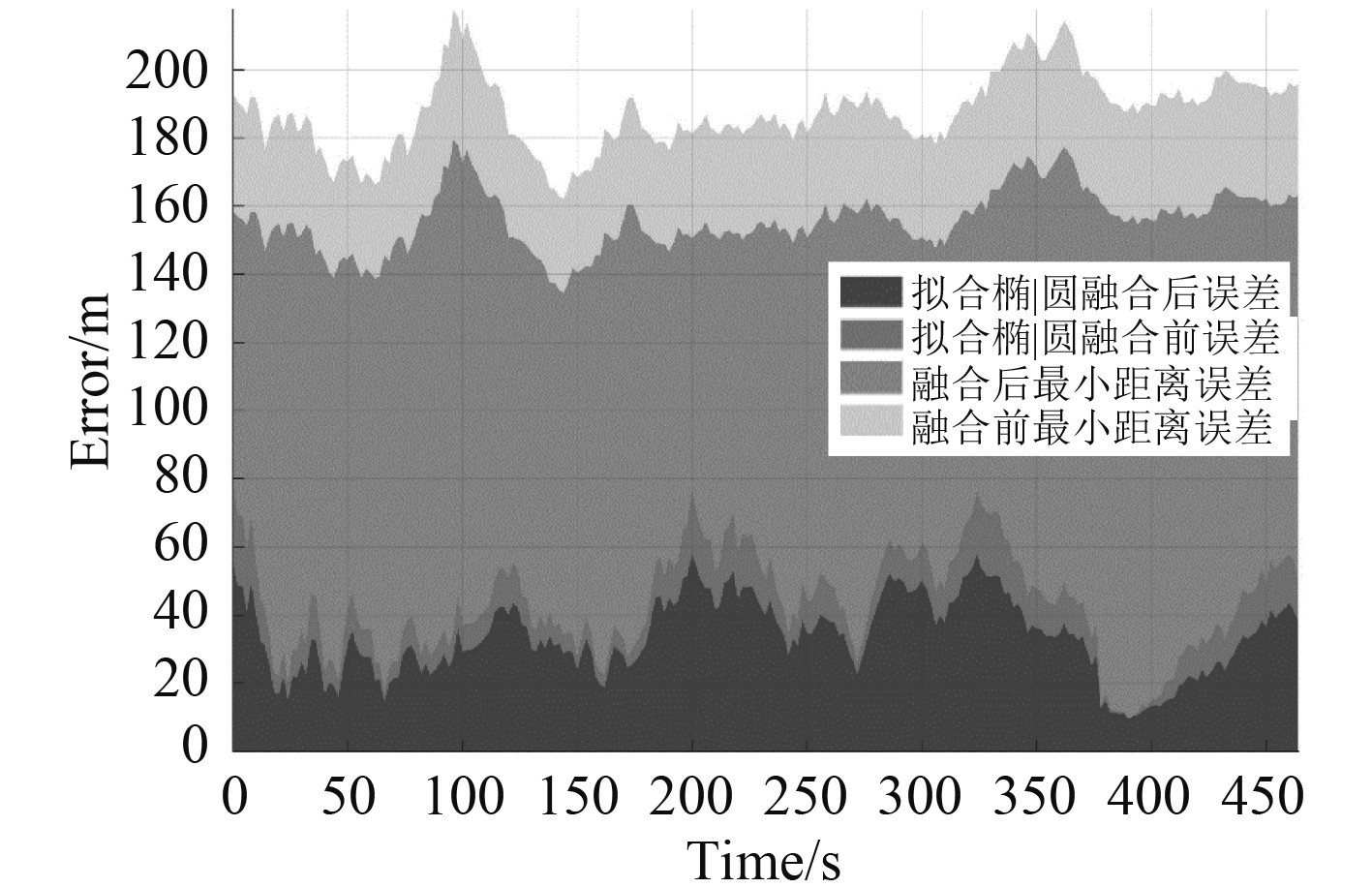
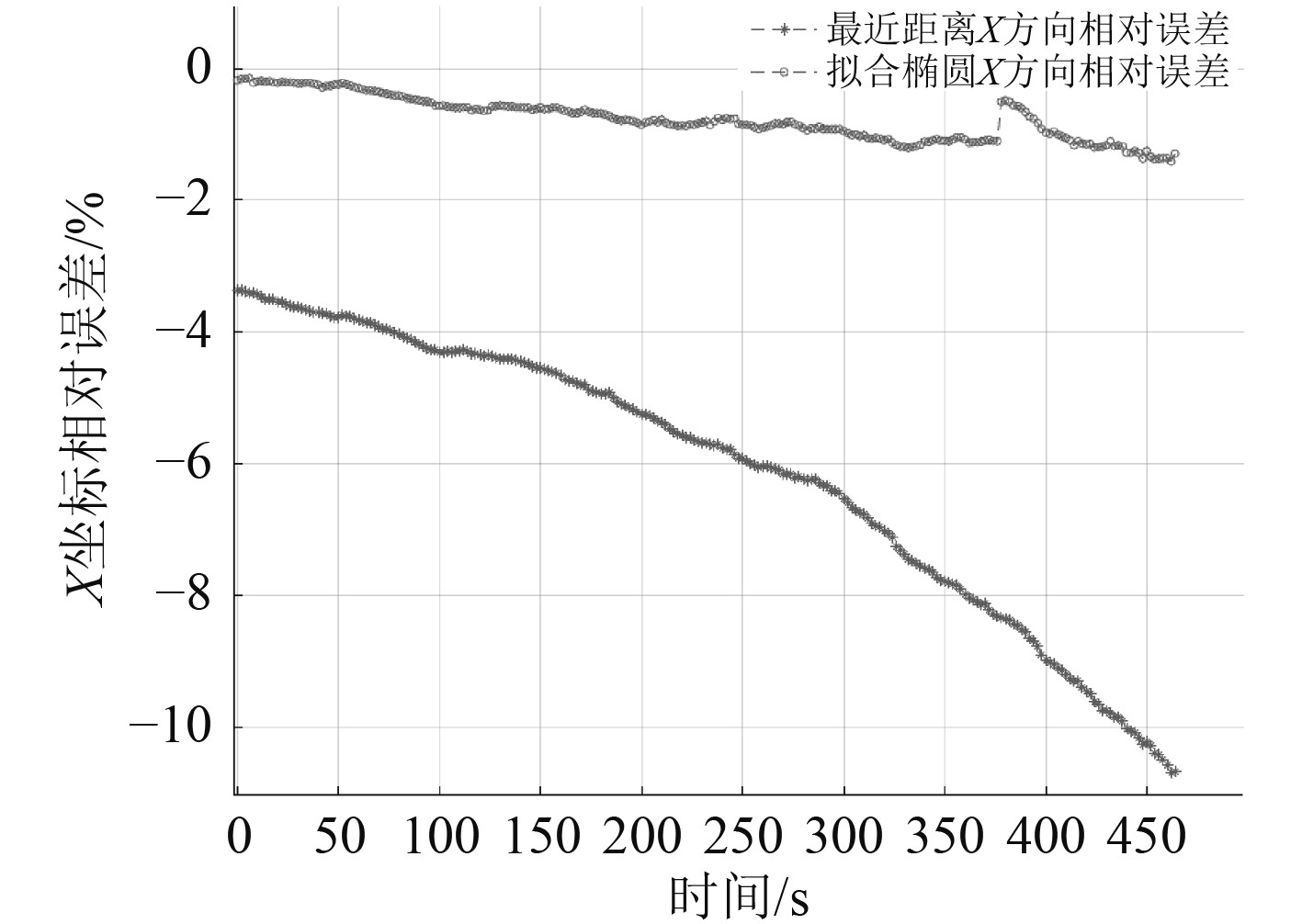
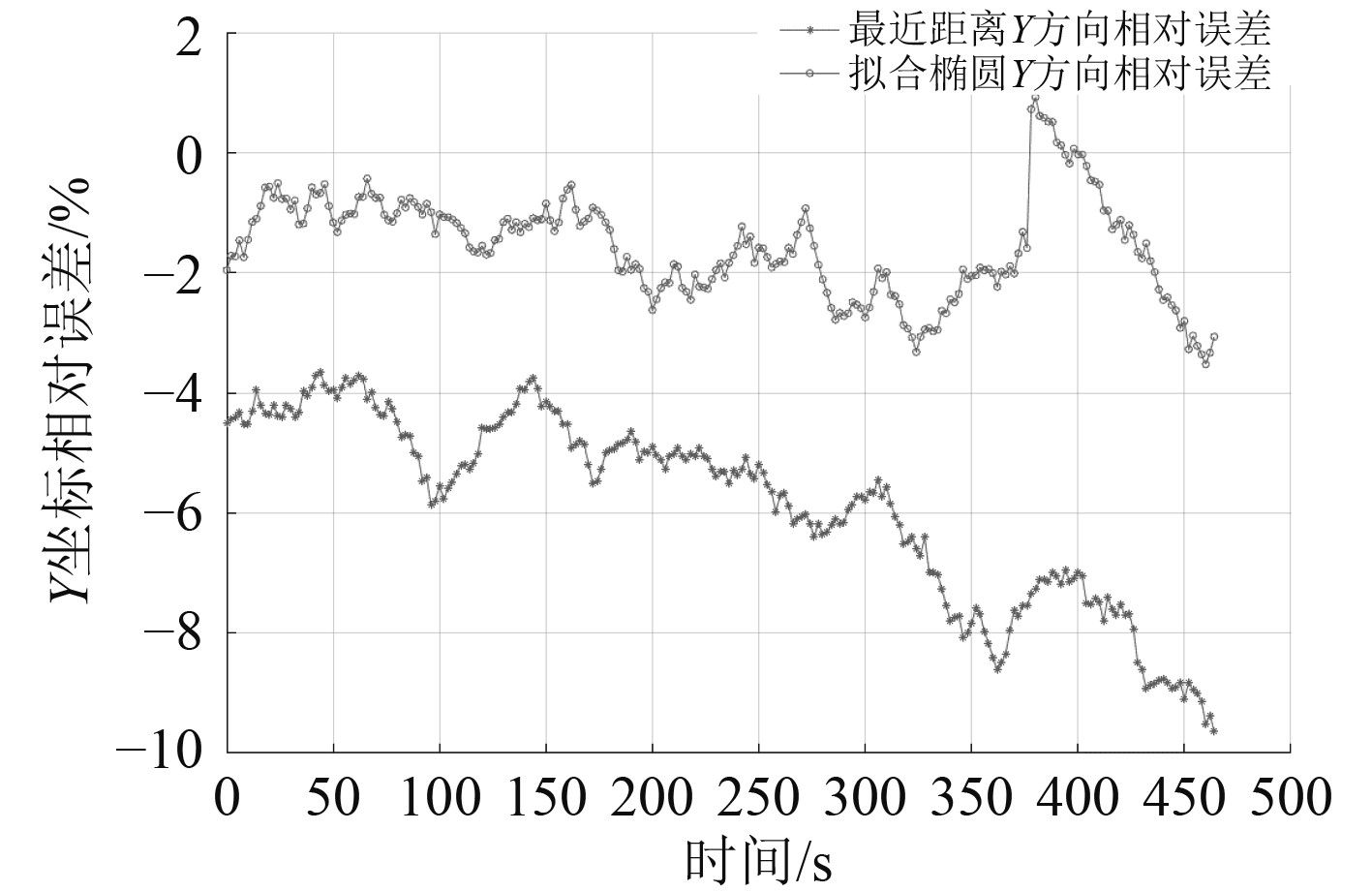
如图7所示,自适应加权算法在2种船位选择方法下均有效降低了误差,拟合椭圆位置点的误差相对较小。从XY坐标位置分析,如图8、图9所示,采用雷达最近距离点位X方向平均相对误均值为
|
图 7 误差对比图 |
|
图 8 X坐标相对误差对比图 Fig. 8 Comparison of the relative error of the X coordinate |
|
图 9 Y坐标相对误差对比图 Fig. 9 Comparison of the relative error of the Y coordinate |
融合前后方差如表2所示。融合后的方差相比融合前有所下降。这表明,通过融合AIS和雷达数据,并使用卡尔曼滤波器优化算法,自适应调整各数据源的权重,能够有效最小化测量方差。具体来说,AIS数据虽然基于GPS,具有较高的精度,但其更新频率较低;雷达数据虽然更新频率较高,但受噪声影响较大。融合两者后,可以平滑各数据源的随机误差,提升整体测量的稳定性与准确性。相较于传统的最近距离点方法,拟合椭圆位置点更适合在复杂环境下的船位估计。这一方法不仅减少了测量误差,也增强了系统的抗干扰能力,从而为导航决策、目标跟踪以及轨迹预测提供了更可靠的数据支持。
|
|
表 2 融合前后方差变化情况 Tab.2 Variance changes before and after fusion |
针对雷达和AIS测量原理导致的船位偏差,提出了一种基于最小二乘法的椭圆拟合位置点的船位融合方法,并与传统的最近距离点方法进行了对比分析。仿真实验结果表明,基于椭圆拟合的位置点融合方法能够有效减少因测量原理的不同从而造成的船位偏差,在仿真中,平均误差比传统方法减少约78.51%,提高了轨迹估计的精度,为海上目标跟踪和航行安全提供了更为可靠的保障。
| [1] |
马军, 丁希雅, 朱文祥. 一种基于AIS数据的机载雷达系统误差实时自动标校方法[J]. 空天预警研究学报, 2024, 38(2): 90-95. MA J, DING X Y, ZHU W X. A method for real-time calibration of airborne radar system errors based on AIS data[J]. Journal of Space and Airborne Early Warning Research, 2024, 38(2): 90-95. DOI:10.3969/j.issn.2097-180X.2024.02.003 |
| [2] |
刘敬一, 高晓倩, 郭琦, 等. 基于运动属性约束的船舶AIS航迹去纠缠方法[J]. 无线电工程, 2023, 53(3): 678-685. LIU J Y, GAO X Q, GUO Q, et al. A method for removing entanglement of ship AIS trajectory based on constraints of motion attributes[J]. Radio Engineering, 2023, 53(3): 678-685. DOI:10.3969/j.issn.1003-3106.2023.03.022 |
| [3] |
S HONG, PENG D, SHI Y. Track-to-track association using fuzzy membership function and clustering for distributed information fusion[C]//2018 37th Chinese Control Conference (CCC). Wuhan, China, 2018.
|
| [4] |
CHEN D, CHEN P, ZHOU C. Research on AIS and radar information fusion method based on distributed Kalman[C]//2019 5th International Conference on Transportation Information and Safety (ICTIS). Liverpool, UK, 2019.
|
| [5] |
武亚伟. 基于雷达和AIS融合的无人船动态避碰系统研究[D]. 武汉: 武汉理工大学, 2021.
|
| [6] |
代广树. 海上无人驾驶技术中的数据融合应用技术[J]. 舰船科学技术, 2019, 41(14): 55-57. DAI G S. Data fusion application technology in marine unmanned driver technology[J]. Ship Science and Technology, 2019, 41(14): 55-57. |
| [7] |
严庆新, 郑帅祥, 关宏旭, 等. 船舶AIS和雷达航迹数据的关联及融合[J]. 武汉理工大学学报(交通科学与工程版), 2023, 47(1): 185-190. YAN Q X, ZHENG S X, GUAN H X, et al. Association and fusion of ship AIS and radar track data[J]. Journal of Wuhan University of Technology (Traffic Science and Engineering Edition), 2023, 47(1): 185-190. |
| [8] |
WITOLD K, ANDRZEJ S. Radar and Automatic Identification System Track Fusion in an Electronic Chart Display and Information System[J]. Journal of Navigation, 2015, 68(6): 1141-1154. DOI:10.1017/S0373463315000405 |
| [9] |
赵海林, 汪永军, 候小丽. 基于航迹关联的系统误差自适应校正方法[J]. 舰船电子对抗, 2023, 46(1): 61−67+77. ZHAO H L, WANG Y J, HOU X L. An Adaptive Correction Method of System Error Based on Track Association [J]. Shipborne Electronic Countermeasure, 2023, 46(1): 61−67+77. |
| [10] |
肖德柱. AIS和ADS-B信息在高频地波雷达中的综合分析方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2021
|
| [11] |
黄善稳. 基于神经网络的AIS和雷达的目标信息融合研究[D]. 重庆: 重庆交通大学, 2023.
|
| [12] |
张津铭. 基于AIS数据的船舶轨迹聚类分析及异常检测研究[D]. 广州: 华南理工大学, 2023.
|
| [13] |
林长川. 雷达与AIS目标位置信息融合方法的研究[C]//2002航海实用新技术论文集, 2002.
|
| [14] |
贾景钧. 基于北斗和AIS信息融合的船舶定位监控系统设计[D]. 桂林: 广西师范大学, 2023.
|
| [15] |
张秋涌, 陈长明. 雷达局限性对船舶引航安全影响的探讨[J]. 中国水运, 2023(8): 126-128. ZHANG Q Y, CHEN C M. Discussion on the impact of radar limitations on ship pilotage safety[J]. China Water Transport, 2023(8): 126-128. |
| [16] |
陈若珠, 孙岳. 基于最小二乘法的椭圆拟合改进算法研究[J]. 工业仪表与自动化装置, 2017(2): 35-38+46. CHEN R Z, SUN Y. Research on improved ellipse fitting algorithm based on least squares method[J]. Industrial Instrumentation and Automation Devices, 2017(2): 35-38+46. DOI:10.3969/j.issn.1000-0682.2017.02.008 |
 2025, Vol. 47
2025, Vol. 47
