0 引　言

汽轮机作为船舶的心脏，其稳定可靠的运行是船舶安全航行的基础。目前，汽轮机控制策略普遍选用比例-积分-微分（PID）算法^[1]，这种方法基于误差，消除误差，不依赖精确的被控对象数学模型，在工程实践中被广为应用。PID控制在电网平稳运行，用电负荷改变不大的情况下取得了满意的控制效果。然而，与陆式汽轮机不同，船用汽轮机作为孤网运行，不能简单假设成地方火电大电网负荷基本不变的情况。此外，在采用全电力推进的新型船舶上，经常要面临剧烈变负荷、急剧甩负荷和频繁的工况变化等情况^{[2 − 3]}，这时传统的PID算法由于参数不能自适应，往往会出现调节时间过长、控制精度不高等缺陷。

针对上述问题，自抗扰控制技术（Active Disturbance Rejection Control，ADRC）继承了PID控制器的优势基础上，将模型的不确定性和外界的干扰看成总扰动，通过扩张状态观测器进行主动的前馈补偿，消除扰动，提供一种简单新颖的控制策略^{[4 - 5]}。自抗扰控制已在航空航天、电力系统等领域广泛应用，并在船舶控制中展现出巨大潜力。钟声等^[6]用自抗扰控律解决了一种深空探测航天器姿态控制问题，并通过仿真验证了控制器的鲁棒性与有效性；GARRIDOR等^[7]提出自抗扰-龙伯格观测器，实现了超声电机的纳米级位置控制；段乐强等^[8]运用自抗扰技术解决了球面磁悬浮万向稳定平台在外部扰动情况下的稳定控制问题；殷虎等^[9]设计了某型船筒盖开关过程自抗扰控制器，其结果表明与PID控制相比，能够精确跟踪指定轨迹。

本文针对船舶发电汽轮机首先设计了线性自抗扰控制器，以满足基本控制需求。接着，为提升控制精度，通过改进原fal函数设计了一种新型自抗扰控制器。通过Matlab平台进行了甩20%、50%、75%、100%负荷的仿真试验，结果表明，相较于线性自抗扰控制，当外界负荷大幅跃迁变化时，所设计的非线性自抗扰控制器能够更有效地抑制转速飞升。此外，为了验证控制器鲁棒性，采用改变油动机环节的时间常数模拟油压故障，仿真验证表明，相较于线性自抗扰控制器，运用改进fal函数的自抗扰控制器有更强的鲁棒性。

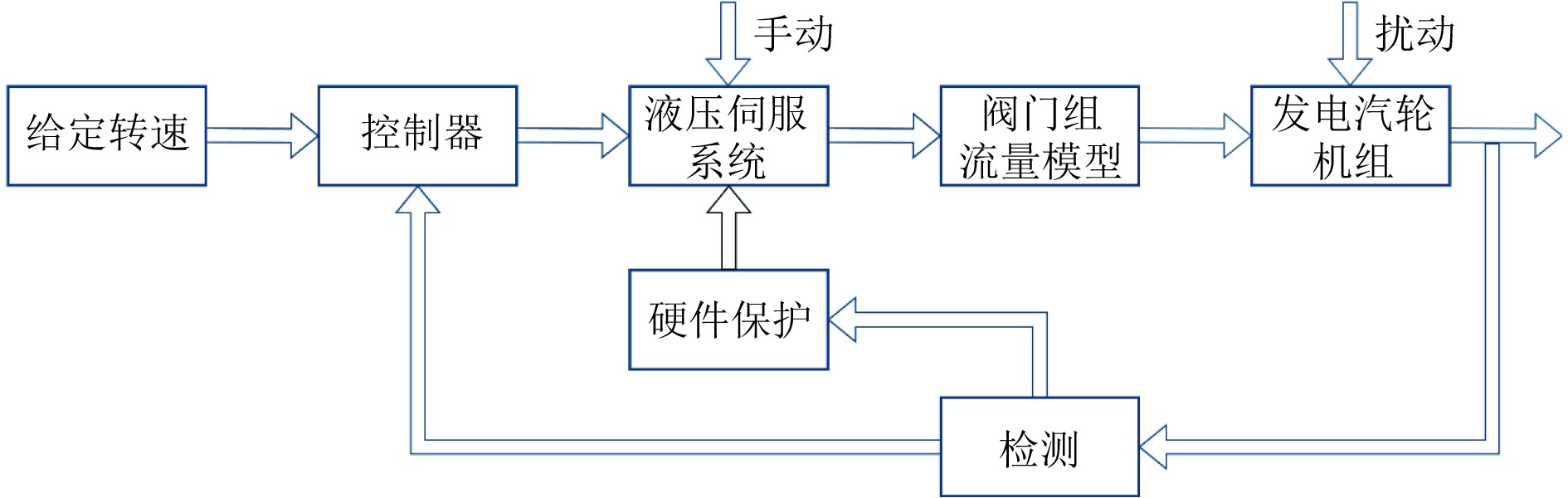
1 汽轮机模型的建立 1.1 汽轮机控制系统组成

汽轮机数字电液控制系统（Digital Electro-Hydraul-ic control system，DEH）由多个组件和精密环节构成，是汽轮机平稳运行的保障。与陆基汽轮机类似，船用汽轮机的调节系统由控制器、伺服放大器、电液转换器、油动机以及反馈机构等多个关键组件构成^[10]。其系统的信号转换流程为：控制器发出的电信号首先被转换为液压信号，然后驱动调节阀门，阀门开度的改变会影响进汽量和蒸汽空间压力，进而控制转子转速。传感器将转子的转速信号转化为电信号，并将该信号反馈给控制器，完成闭环控制。汽轮机调节系统 框图如图1所示。

1.2 传递函数模型

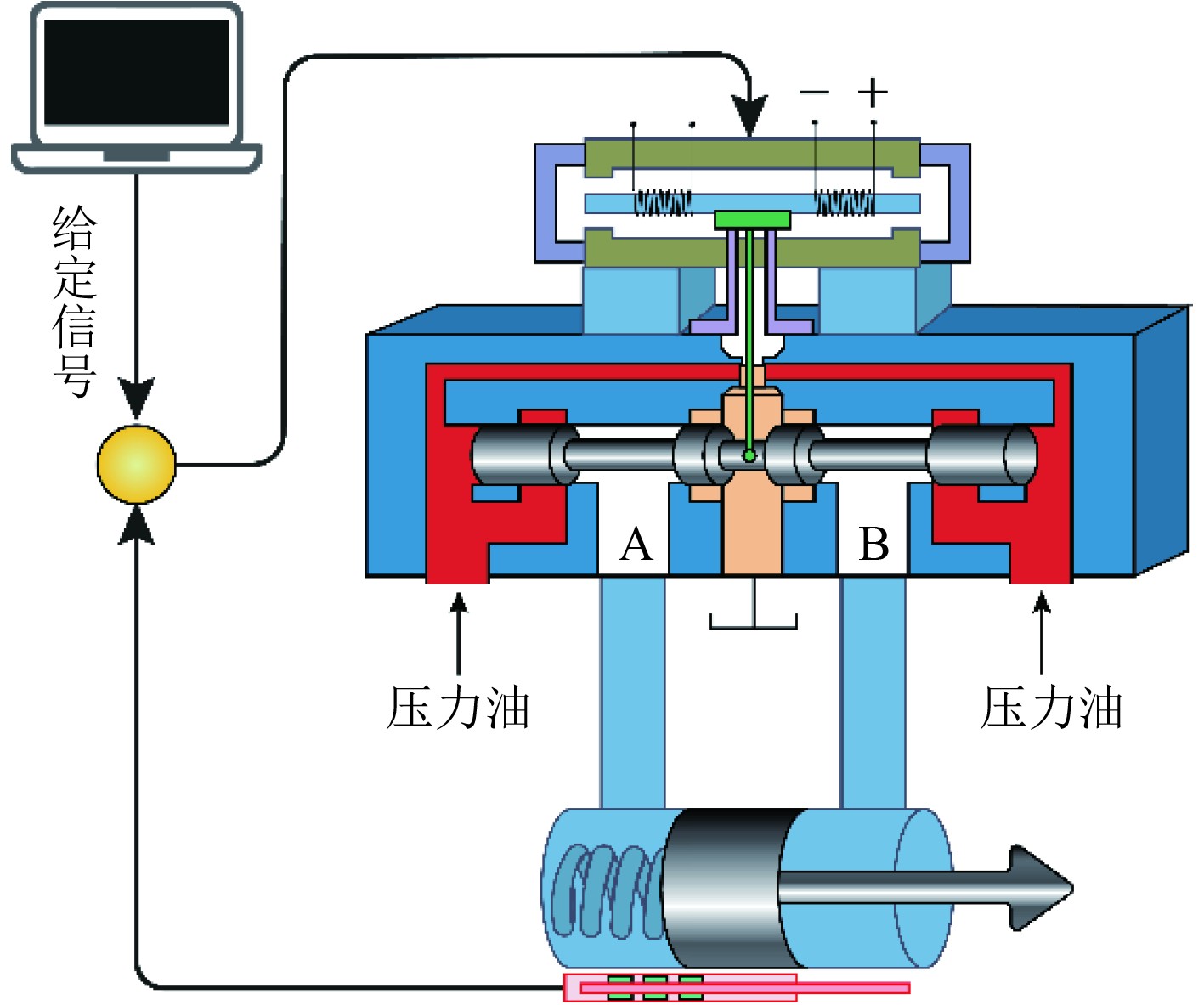
汽轮机调控执行系统如图2所示。电液伺服阀一般选用喷嘴挡板伺服阀。通常情况下，电液伺服阀的响应远快于油动机等液压执行元件，因此在系统建模中常将其简化为一阶惯性环节。

对于油动机环节，由于滑阀位移的高阶导数在我们关心频段内对动态特性影响较小，因此将其忽略，同样简化为一阶惯性环节。设控制器输入电流为i，伺服阀位于${\chi _v}$，油动机阀位为${\chi _z}$，则其传递函数可分别由式(1)、式(2)表示。

$ \frac{\chi_v}{i}=\frac{1}{T_{{e}}s+1}，$

(1)

$ \frac{\chi_z}{\chi_v}=\frac{1}{T_{{o}}s+1}。$

(2)

式中：T_e、T_o表示电液伺服阀与油动机的时间常数。

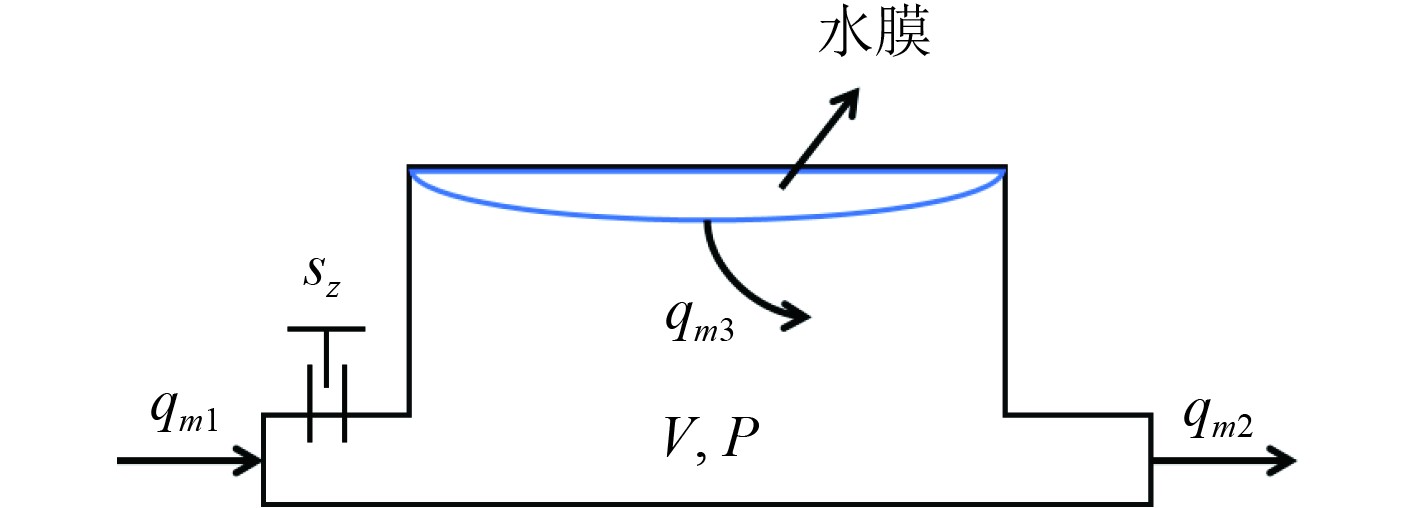
船用汽轮机的工质一般为饱和湿蒸汽，其工作压力较低，焓降较小，因此汽轮机通常为单缸结构且不设置再热器。此外，对于船用汽轮机来说，在其管壁上通常附着一层薄水膜，如图3所示。当调节阀的开度发生变化时，压力也发生改变，从而水膜的饱和度发生变化，一部分蒸汽会从水膜中析出或被水膜吸收，这使得其特性与地方火电汽轮机组存在较大差异。

假设水膜质量为$G$，温度为$T$，焓为$i$，汽化潜热为$\gamma $，管壁温度为${T_{{w}}}$，换热系数为$\alpha $，换热面积为$A$，蒸汽密度为$\rho $，蒸汽流量为${q_{{m}}}$。根据能量守恒、换热公式和质量守恒公式有：

$ Q=G\frac{\mathrm{d\mathit{i}}}{\mathrm{d}t}+\gamma q_{{m3}}，$

(3)

$ Q=\alpha(T_{{w}}-T)A，$

(4)

$ V\frac{\mathrm{d}\rho}{\mathrm{d}t}=q_{{m1}}-q_{{m2}}+q_{{m3}}。$

(5)

将水看成饱和水，且温度与焓均看成关于压力的函数，联立式(3)～式(5)得：

$ A\alpha(T_{{w}}-T(p))=G\frac{\mathrm{d}i}{\mathrm{d}p}\frac{\mathrm{d}p}{\mathrm{d}t}+\gamma\left(V\frac{\mathrm{d}\rho}{\mathrm{d}t}-q_{m1}+q_{m2}\right)。$

(6)

在汽轮机工况稳定时，水膜温度$T$与管壁温度${T_{{w}}}$相差不大，换热量忽略不计，式(6)可改为：

$ G\frac{\mathrm{d}i}{\mathrm{d}p}\frac{\mathrm{d}p}{\mathrm{d}t}=-\gamma\left(V\frac{\mathrm{d}\rho}{\mathrm{d}t}-q_{{m1}}+q_{{m2}}\right)。$

(7)

将流量看成关于阀门开度${s_z}$和蒸汽压力$p$的函数，由于蒸汽容积出口处阀门开度不变，可将出口流量${q_{{{m}}2}}$视为只与压力相关，${q_{{{m}}1}} = {q_{{{m}}1}}({s_{{z}}},p)$，${q_{{{m}}2}} = {q_{{{m}}2}}(p)$。

在汽轮机工作范围内，可将比热${c_{{p}}}$视为常数，有$ \mathrm{d}i=c_{{p}}\mathrm{d}T $。将式(7)在工作点处压力，${p_0}$与阀门开度，${s_{{{z}}0}}$处线性化处理，经过拉普拉斯变化和标幺化最终可得：

$\begin{split} & \left(\frac{{V{{({{\partial \rho } / \partial }p)}_0}{p_0}}}{{{q_{{{m10}}}}}} + \frac{{G{c_{{p}}}{{({{\partial T} / \partial }p)}_0}{p_0}}}{{{q_{{{m10}}}}\gamma }}\right){\chi _{{p}}}(s)s =\\ & {\chi _{{s}}}_{{z}}(s) - \frac{{{{({{{\rm d}{q_{{{m2}}}}} / {{\rm d}p}} - {{\partial {q_{{{m1}}}}} /\partial }p)}_0}{p_0}}}{{{q_{{{m10}}}}}}{\chi _{{p}}}(s)，\end{split}$

(8)

$ (T_{{a}}+T_{{b}})\chi_{{p}}(s)s=\chi_{{sz}}(s)-K\chi_{{p}}(s)。$

(9)

式中：${q_{{{m10}}}}$为额定工况流量，${\chi _{{p}}} = \Delta p/{p_0}$，${\chi _{{{sz}}}} = \Delta {s_{{z}}}/{s_{{{z0}}}}$，$ {T_{{a}}} = {{V{{({{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } \partial }} \right. } \partial }p)}_0}{p_0}} \mathord{\left/ {\vphantom {{V{{({{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } \partial }} \right. } \partial }p)}_0}{p_0}} {{q_{{{m10}}}}}}} \right. } {{q_{{{m10}}}}}} $，${T_{{b}}} = {{G{c_{{p}}}{{({{\partial T} \mathord{\left/ {\vphantom {{\partial T} \partial }} \right. } \partial }p)}_0}{p_0}} \mathord{\left/ {\vphantom {{G{c_{{p}}}{{({{\partial T} \mathord{\left/ {\vphantom {{\partial T} \partial }} \right. } \partial }p)}_0}{p_0}} {{q_{{{m10}}}}\gamma }}} \right. } {{q_{{{m10}}}}\gamma }}$，$K = {{{{({{{\rm d}{q_{{{m2}}}}} \mathord{\left/ {\vphantom {{{\rm d}{q_{{{m2}}}}} {{\rm d}p}}} \right. } {{\rm d}p}} - {{\partial {q_{{{m1}}}}} \mathord{\left/ {\vphantom {{\partial {q_{{{m1}}}}} \partial }} \right. } \partial }p)}_0}{p_0}} \mathord{\left/ {\vphantom {{{{({{{\rm d}{q_{{{m2}}}}} \mathord{\left/ {\vphantom {{{\rm d}{q_{{{m2}}}}} {{\rm d}p}}} \right. } {{\rm d}p}} - {{\partial {q_{{{m1}}}}} \mathord{\left/ {\vphantom {{\partial {q_{{{m1}}}}} \partial }} \right. } \partial }p)}_0}{p_0}} {{q_{{{m10}}}}}}} \right. } {{q_{{{m10}}}}}}$。当处于稳定状态时，${\chi _{{p}}}(s)s = 0$，${\chi _{{{sz}}}}(s) = 1$，${\chi _{{p}}}(s) = 1$可得蒸汽空间传递函数为:

$ G(s)=\frac{1}{(T_{{a}}+T_{{b}})s+1}。$

(10)

式中：${T_{{a}}}$为火电汽轮机的蒸汽容积时间常数；${T_{{b}}}$为由水膜引起的时间常数增大，所以船用汽轮机的时间常数要比火电机组要大。

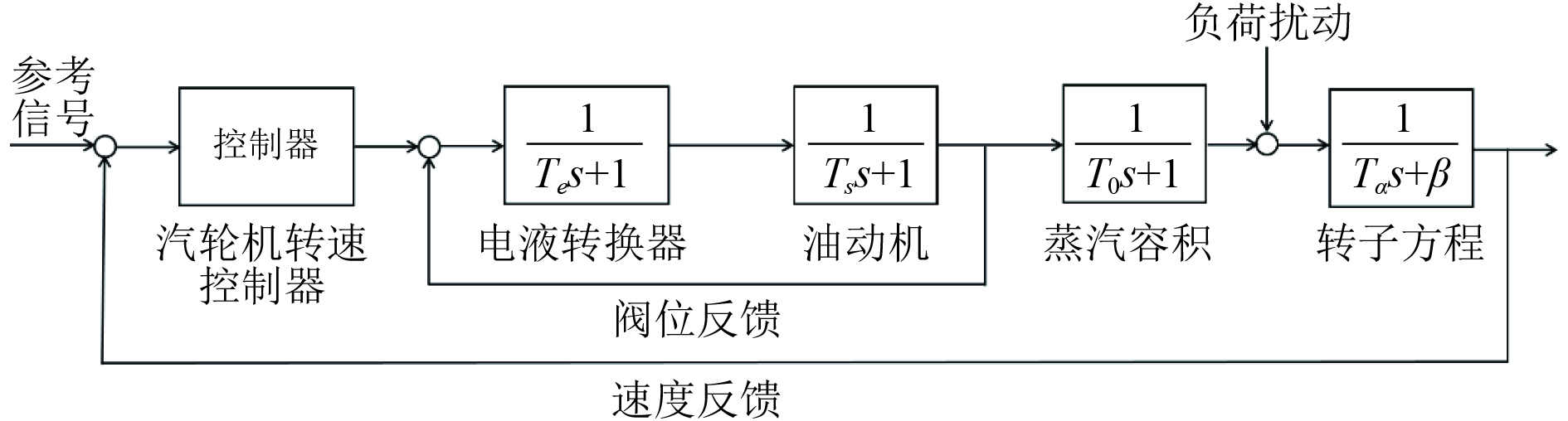
对于转子方程环节，根据牛顿第二定律和在工作点附近的泰勒展开表达式，经过标幺化处理，可表示为：

$ T_{{a}}\dot{\chi}_{\omega}+\beta\chi_{{\omega}}=\chi_{{p}}-\chi_{{pL}}(t)。$

(11)

式中：${T_a}$为转子飞升时间常数；$\beta $为转子自平衡系数；${\chi _\omega }$为转速相对变化量；${\chi _{{p}}}$为压力相对变化量；${\chi _{{{pL}}}}$为负载相对变化量。汽轮机电液控制系统如图4所示。

2 自抗扰控制器设计

自抗扰控制器一般由跟踪微分器、扩张状态观测器和线性或非线性反馈结构组成。跟踪微分器负责将输入信号进行柔化处理，旨在解决快速性和准确性的矛盾。在线性自抗扰控制器设计中，为方便系统的动态特性分析，通常将跟踪微分器省略，简化为线性扩张观测器和PD线性误差反馈控制率的组合。

扩张状态观测器是自抗扰控制的关键部分，负责将式(12)所示的控制系统标准型。转化为式(13)的积分串联型系统。将非线性因素、模型的不确定性和外部扰动统一看成总扰动并作为系统的高阶导数^[11]，通过扩张状态观测器进行主动的前馈补偿，正是该方法的独特之处。

${ x^{(n)} = f(x^{(n-1)} , x^{(n-2)} ,...,\ddot{x} , \dot{x} , \int _{ }^{ }u\mathrm{d}t , ... \int _{ }^{ }... \int _{ }^{ }u\mathrm{d}t) + b_0u(t) + w ，}$

(12)

$ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}} ，\\ {{{\dot x}_2} = {x_3}} ，\\ {......} \\ {{{\dot x}_{{n}}} = {b_0}u(t)}，\\ {y = {x_1}}。\end{array}} \right. $

(13)

式中：x为系统状态，f为非线性因素，u为输入量，w为扰动。

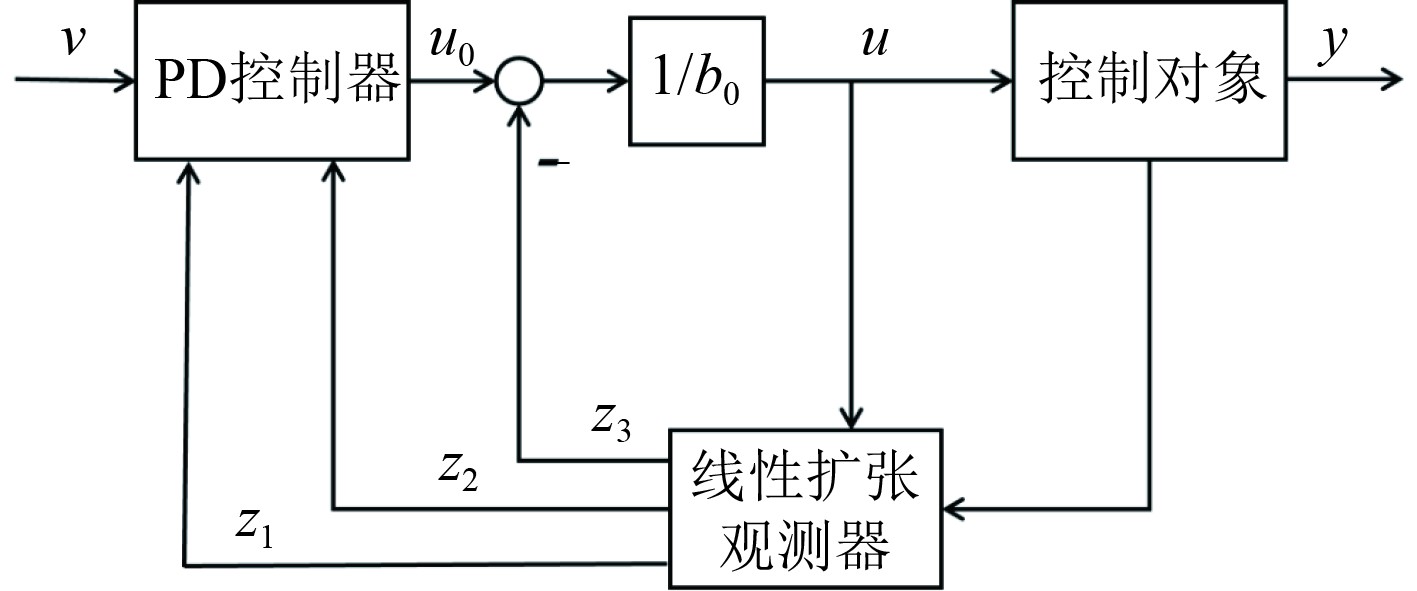
2.1 线性自抗扰控制器设计

自抗扰控制器提出之初，就存在着参数难以整定的问题，不同的控制参数会导致被控对象的控制效果差异明显。针对这一问题，Gao^[12]对原非线性控制器进行了改进，创建了线性自抗扰控制器（Linear Active Disturbance Rejection Control，LADRC ），如图5所示，并从频域角度分析控制系统的性质，提出了用带宽法整定参数。

设计自抗扰控制器一般从线性入手，根据效果考虑提升阶数或引入非线性因素，待整定的控制器参数主要为观测器带宽和控制器带宽，分别用${\omega _{{o}}}$、${\omega _{{c}}}$表示。对于二阶以上控制系统，${b_0}$是一个影响系统稳定的重要参数^[13]，为此将${b_0}$作为一个可调变量以提升系统的控制效果。

经过选取，发现${b_0} = 0.4$时效果最好，系统调节时间${t_s}$设为3 s，控制器带宽取${\omega _c} = 10/{t_s}$，观测器带宽取${\omega _{{o}}} = 4{\omega _{{c}}}$，其余参数按式(14)取值。

$ k_{{p}}=\omega_{{c}}^2,k_{{d}}=2\omega_{{c}},\beta_1=3\omega_{{o}},\beta_2=3\omega_{{o}}^2。$

(14)

2.2 LTfal型非线性自抗扰控制器

在扩张观测器中采用线性函数，虽便于系统分析和参数整定，但抗扰能力有限，且一些非线性因素可以改善系统动态特性，提升控制效果。因此，在系统中适当引入非线性因素，有助于控制质量的提升。

在自抗扰控制器中，一般采用fal函数，其函数表达式如式(15)所示。fal函数中的参数主要有$\alpha $和$\delta $，参数$\alpha $主要决定远离原点处fal(x)输出的增长速度，$\alpha $越大输出增长速度越大。$\delta $负责线性区间的大小和线性函数的斜率。然而，在原点处引入线性区间时，当误差足够小时，fal函数输出可能会在线性高增益段与非线性低增益段频繁切换，从而诱发系统颤振。为此，本文提出通过对数函数和反双曲正切函数的线性组合来构建新扩张状态函数表达式：

$ \mathrm{fal}(x)=\left\{\begin{gathered}\left|x\right|^{\alpha}\mathrm{sign}(x),\left|x\right| > \delta，\\ \frac{x}{\delta^{1-\alpha}},\left|x\right|\leqslant\delta，\\ \end{gathered}\right. $

(15)

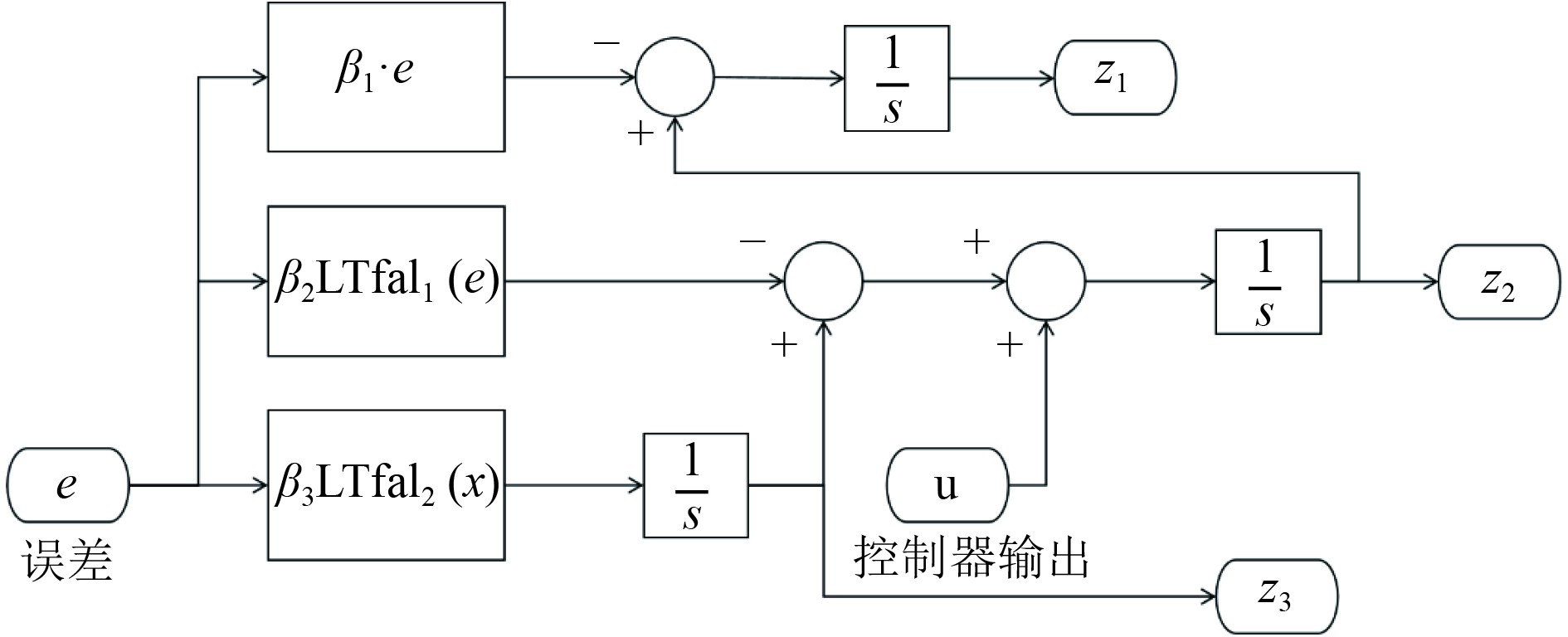
$ \mathrm{fal}LT(x)=\left\{\begin{gathered}\log_a(x+1)+\tanh(bx),x\geqslant0，\\ \log_{1/a}(1-x)+\tanh(bx),x < 0。\\ \end{gathered}\right. $

(16)

${\rm fal}LT$借鉴了fal函数的思路，当输入过大时，$\tanh (bx)$值趋近为1，主要由${\log _a}\left( {x + 1} \right)$或${\log _{{1/a}}}(1 - x)$决定输出，当输入减少时，则主要由$\tanh ({{b}}x)$实现小误差大增益的思想。新型非线性扩张状态观测器（LT型扩张状态观测器）结构图见图6。

2.3 LTfal非线性自抗扰控制器稳定性证明

鉴于该控制器涉及非线性因素复杂，故将其对数项与双曲正切项分离，分别证明各自的稳定性。首先证明对数部分的稳定性。以二阶控制系统为例，当误差大于0时，系统的误差矩阵可表示为：

$ \left\{ \begin{gathered} {{\dot e}_1} = {e_2} - {\beta _1}{e_1}，\\ {{\dot e}_2} = - {\beta _2}\ln ({e_1} + 1)。\\ \end{gathered} \right. $

(17)

$ V(e_1,e_2)=(e_1+1)\ln(e_1+1)-e_1+\frac{1}{2\beta_2}e_2^2。$

(18)

当${\beta _2}$ > 0时该函数正定，对${e_1}、{e_2}$的偏导数为：

$ \left\{\begin{aligned} & \frac{\partial V}{\partial e_1}=\ln(e_1+1)，\\ & \frac{\partial V}{\partial e_2}=\frac{1}{\beta_2}e_2。\end{aligned} \right.$

(19)

式(18)导数为：

$ \begin{split} \dot{V} &=\frac{\partial V}{\partial e_1}\dot{e}_1+\frac{\partial V}{\partial e_2}\dot{e}_2= \\ &\ln(e_1+1)(e_2-\beta_1e_1)+\frac{1}{\beta_2}e_2(-\beta_2\ln(e_1+1))=\\ & -\beta_1e_1\ln(e_1+1)。\end{split} $

(20)

当${\beta _1} > 0$时，$\dot V < 0$，该观测器收敛，当误差${e_1} < 0$时同理。接下来证明双曲正切部分稳定性，由李雅普诺夫引理^[14]，对于误差矩阵：

$ \dot{e}=-\boldsymbol{A}(e)e, $

(21)

$ \boldsymbol{A}(e)=\left[\begin{array}{*{20}{c}}\beta_1 & -1 \\ \beta_2\dfrac{\tanh(be_1)}{e_1} & 0\end{array}\right], $

(22)

若存在对称矩阵$ \boldsymbol{D} $：

$ {\boldsymbol D} = \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&{{d_{12}}} \\ { - {d_{21}}}&{{d_{22}}} \end{array}} \right] 。$

(23)

式中：矩阵D的主对角元素均为正，使得矩阵DA(e)正定，则该系统是李雅普诺夫意义下的稳定。设$ F = {{\tanh (b{e_1})} \mathord{\left/ {\vphantom {{\tanh (b{e_1})} {{e_1}}}} \right. } {{e_1}}} $，则$F \in (0,1)$，且为有界函数，若要满足DA(e) 正定，等价于：

$ \beta_1d_{11}+\beta_2Fd_{12} > 0，$

(24)

$ d_{11}=\beta_1d_{12}-\beta_2Fd_{22}，$

(25)

$ \beta_2Fd_{12}^2+\beta_2Fd_{11}d_{12} > 0。$

(26)

在${\beta _1} > 0 ，{\beta _2} > 0$时，只需令${d_{11}} = 1,\;{d_{12}} = 1,\;{d_{22}} = {{{\beta _1}} \mathord{\left/ {\vphantom {{{\beta _1}} {F{\beta _2}}}} \right. } {F{\beta _2}}}$则可满足李雅普诺夫条件下的稳定。

2.4 LTfal型非线性自抗扰控制器设计

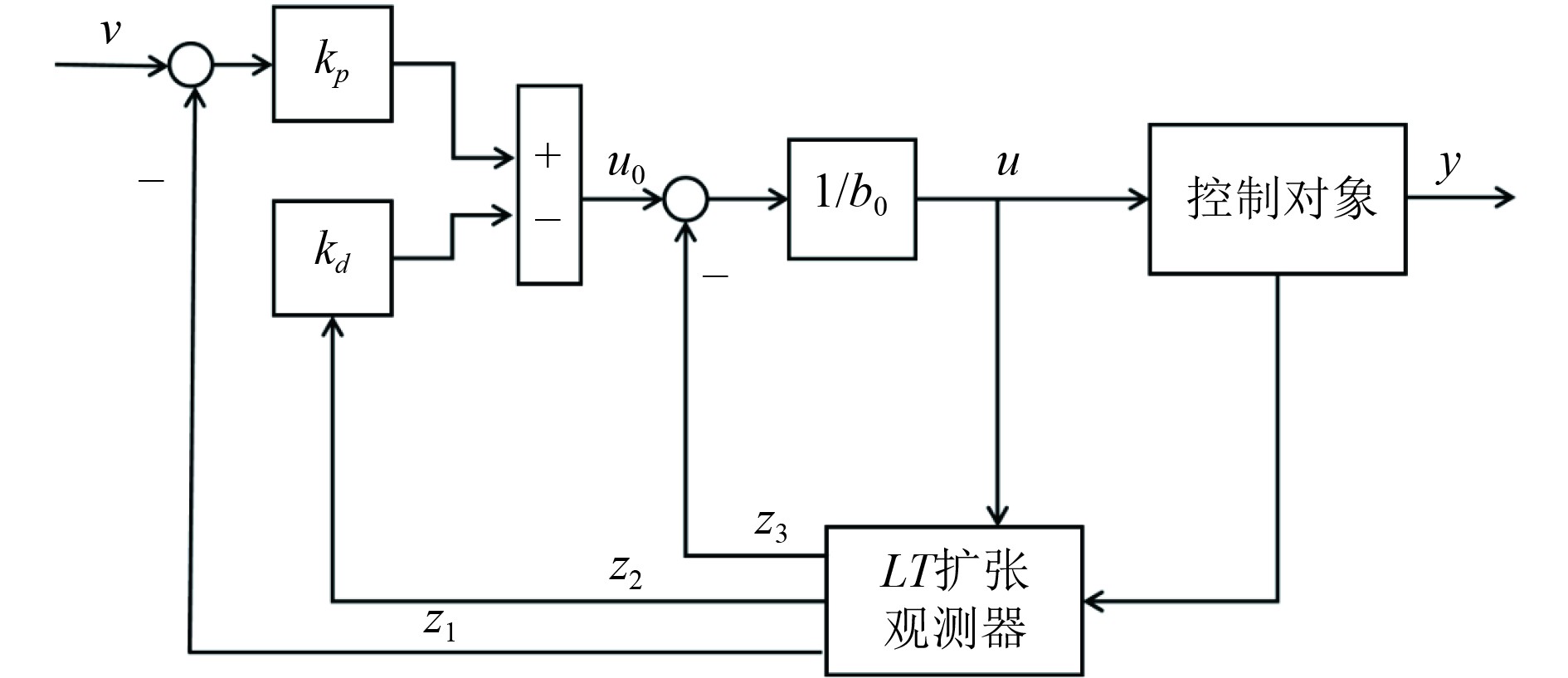
为简化该控制器，采用线性误差反馈组合和非线性扩张状态观测器的组合形式，不考虑跟踪微分器，所设计控制器如图7所示。假设该控制器能够把系统完全化为串联积分标准型，所选极点用$\sigma $表示，根据其传递函数，${{{k}}_{{p}}}$与${{{k}}_{{d}}}$与所选极点的关系为${{{k}}_{{p}}} = {\sigma ^2}$，${{{k}}_{{d}}} = 2\sigma $，理论上对于纯积分串联型系统所选极点与原点距离越远控制效果越好，但考虑实际情况，所选极点过大会对系统稳定性产生影响，最终所选极点$\sigma = 12$。

3 汽轮机负荷扰动仿真

本节主要在Simulink平台上搭建汽轮机控制系统模型，旨在评估线性自抗扰控制器、本文所设自抗扰控制器（LTADRC）和PID控制器在剧烈甩负荷和油动机油压异常的情况下的抗扰能力与鲁棒性。其中，汽轮机额定转速经标幺化为1，扰动在稳定运行第10 s时引入一个负向阶跃信号模拟汽轮机甩负荷，油压异常通过增大油动机环节的时间常数实现。

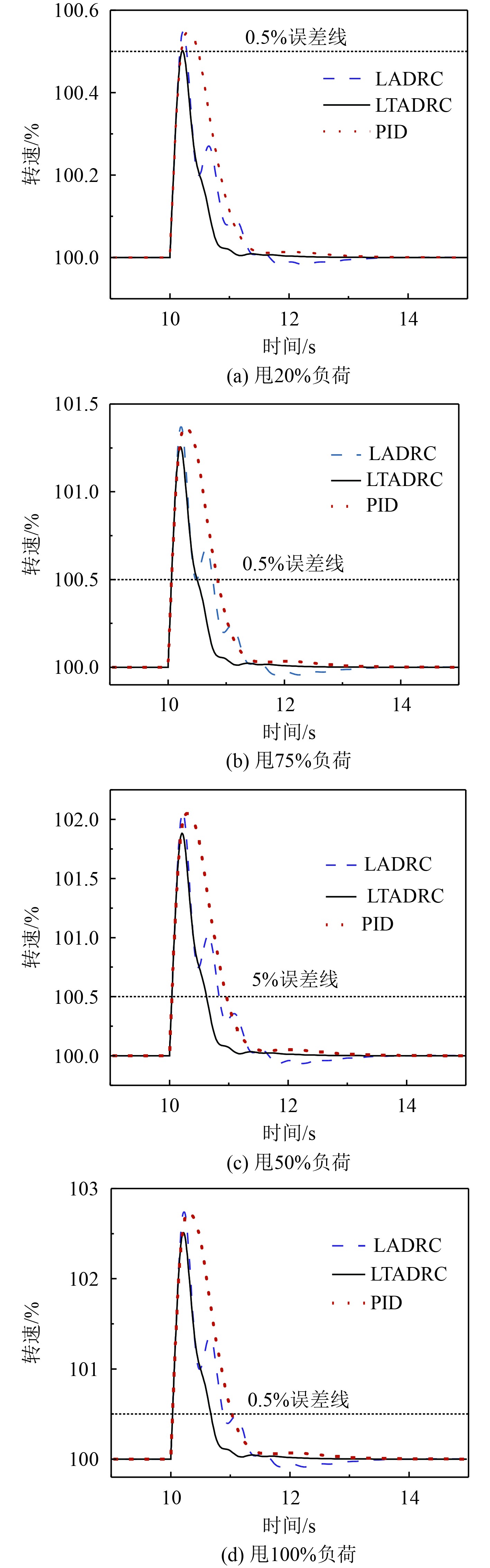
汽轮机在甩不同负荷时，采用3种控制策略的超调量与调节时间总结在表1～表2，其中调节时间定义为引入扰动后恢复到额定转速0.5%误差带内所用时间，超调量定义为转速峰值与额定转速的偏差。可以看出，采用PID控制器、线性自抗扰控制器和本文所设自抗扰控制器均能在负荷突卸时，将转速抑制在3%误差内，且调节时间均小于3 s，满足设计指标，且LTADRC超调量与调节时间最少，其具体过程如图8所示。

从图8可以看出，当采用线性自抗扰控制策略应对机组剧烈甩负荷的情况时，转速并不能平滑的恢复到额定转速，其主要原因是采用低阶线性自抗扰控制高阶系统时，扩张状态观测器由于其结构限制而不能精确跟踪扰动，从而出现振颤。这种情况通常可以适当升高扩张状态观测器的阶数，多利用系统已知息。然而引入合适的非线性因素，在同阶下，其抗扰效果优于线性自抗扰控制策略。

鲁棒性是验证控制器的另一个重要指标，它描述了系统在动态特性发生变化时维持稳定控制的能力。在船舶发电汽轮机的调节控制系统中，油动机油压异常是典型故障，主要表现为油动机环节时间常数的改变，当油动机时间常数减少，截止频率右移，可以更好响应控制信号，稳定裕度增加，为此选择将油动机传递函数的时间常数扩大2倍模拟油压异常，并通过在系统稳定运行10 s时引入负向0.15的跃迁信号，观察控制效果。

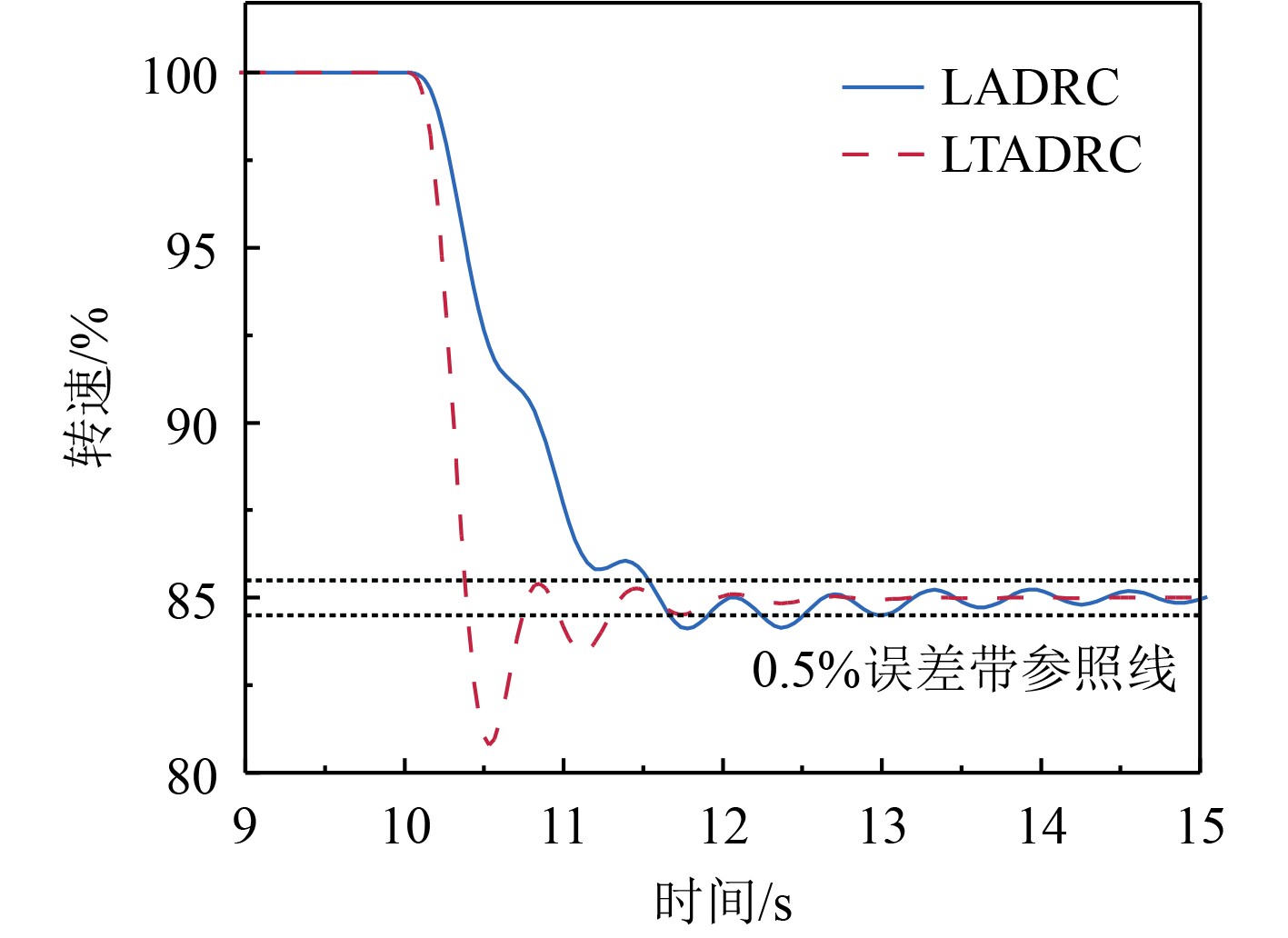
从图9可以看出，当油动机时间常数增大时，线性自抗扰控制和非线性自抗扰控制均出现颤动，LADRC的超调量为0.8%，而LTADRC的超调量为4.1%。LADRC恢复到0.5%误差带的时间大约是2.5 s，而LTADRC则需要3.5 s。尽管从超调量和恢复时间来看，线性控制似乎优于非线性控制，但就颤动频率而言，非线性控制的颤动频率明显低于线性控制，表明其在鲁棒性方面具有优势。

4 结　语

本文针对船用发电汽轮机转速控制系统所面临的挑战，设计了一种基于新型ESO的自抗扰控制器。该控制器利用对数函数和双曲正切函数，构建一种新型扩张状态观测器，继承了传统fal函数小误差大增益、大误差小增益的特点，同时解决了其在分段点处不连续导致的过冲现象。

经仿真验证表明，与PID和LADRC相比，LTADRC在抗扰性能和鲁棒性上均有所增强。在汽轮机甩负荷时，LTADRC能够抑制转速飞升并更快地使转速恢复至额定值。在油动机油压异常的工况下，LTADRC鲁棒性也优于LADRC，更有利于系统的稳定控制。为孤网模式下汽轮机的稳定控制问题提供了潜在解决方案。