0 引　言

近年来，随着海洋工程的大型化，其遭受的环境载荷越来越大，承载能力以及建造质量要求也越来越高，高强度厚钢板在海洋工程中被广泛应用。在焊接过程中，焊缝区域经历高温加热和快速冷却阶段，与其他部分形成显著的温度梯度，导致材料发生不均匀的热膨胀和收缩，进而引起焊接残余应力。针对高强钢厚板焊接结构，其较强的结构约束以及高屈服强度必然会导致高水平的残余应力，可能会诱发冷裂纹或应力腐蚀裂纹，从而缩短焊接结构的使用寿命。为了量化高强钢厚板焊接残余应力的大小及分布情况，一般使用有限元法进行数值模拟^{[1 - 2]}。厚板焊接一般采用多层多道焊工艺，由于需要模拟每道焊接过程，准确的多层多道焊接数值仿真耗时耗力。为了解决这一问题，有学者提出了合并焊道法^{[3 − 6]}，在确保模拟精度的同时有效提高计算效率。然而，如何合并焊道多基于经验，并没有明确的合并焊道方法。此外，大多数研究都集中在厚板对接焊的分析上，而对于大型复杂结构的研究相对较少。本文基于二维焊接热-弹塑性有限元法对自升式平台桩腿主弦管-齿条焊接残余应力进行分析，通过与盲孔法测量的残余应力进行对比，验证数值仿真方法的可靠性。分析了不同合并焊道方法对残余应力分布的影响，得到合适的焊道合并方法，以确保计算结果的准确性和可靠性。通过这一研究，不仅提高了桩腿齿条焊接残余应力的计算效率，也为类似复杂焊接结构的残余应力分析提供了一种有效的数值模拟策略。

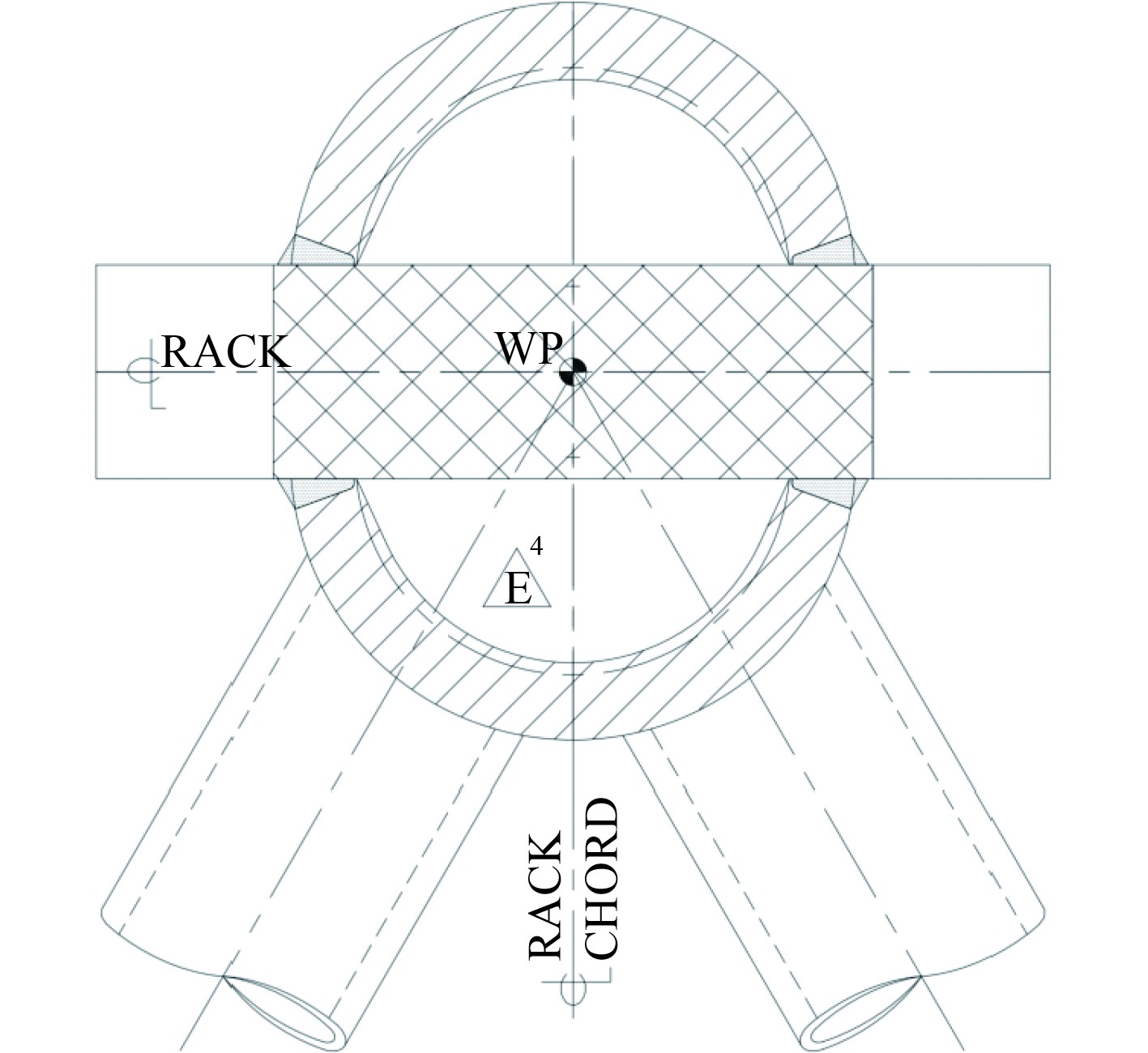
1 主弦管-齿条焊缝情况

本文的研究对象为自升式平台主弦管-齿条焊缝。主弦管-齿条结构作为自升式平台的关键承载部件，由2个半圆管和齿条板焊接而成，共4条焊缝，如图1所示。焊接完成后与撑杆进行总装，形成桩腿主体框架。主弦管和齿条的母材为EH690钢，具有优异的焊接性能和机械性能，能够满足海洋工程中对结构强度和耐久性的要求。

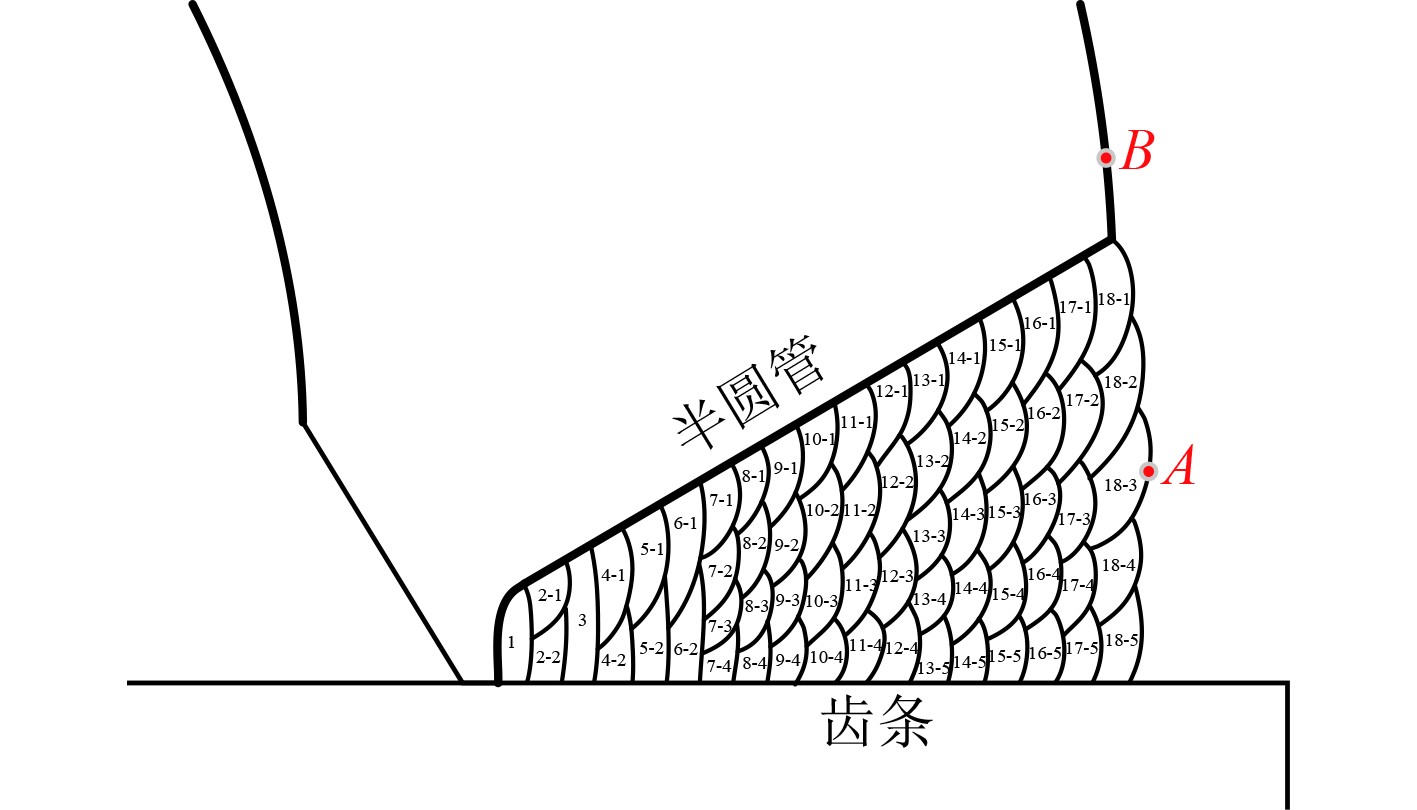
为了保证焊接质量，通常使用多层多道焊进行焊缝填充，本文焊接层数为18层，共64道焊缝，如图2所示。在焊接时，采用手工电弧焊（SMAW）对打底焊道进行焊接，填充焊道和盖面焊道均采用埋弧焊（SAW）进行焊接，预热温度为160℃，焊后立即加热至220～230℃，并保温5 h，随后焊件在空气中自然冷却。具体焊接工艺如表1所示。

2 残余应力试验测量

为了检验后续焊接残余应力数值仿真模型，采用盲孔法对焊接构件表面的残余应力进行测量。盲孔法的原理是当在存在残余应力的材料中钻出一个小孔时，小孔周围的材料由于应力释放而产生应变，通过测量这些应变，结合材料的弹性物理方程，可以反推材料的残余应力状态。该方法通常适用于表面或近表面区域的残余应力测量。本文在焊缝表面靠近中心的位置（A点）和靠近焊缝的半圆管母材（B点）处进行了残余应力测量（见图2）。为了保证测量结果的可靠性，在沿焊缝不同位置取了3个A点和2个B点进行试验。

本试验按照盲孔法残余应力测量标准GB/T 31310-2014^[7]进行。试验采用的是型号为120-3CA的B型应变花，应变花上应变栅的几何中心到钻孔点的距离为10 mm。由于试件体积质量大，测点附近形状不规则，采用现场手持电钻的方式进行打孔，钻头直径为3 mm，钻孔深度为2 mm。使用动态信号采集系统采集钻孔过程中应变信号的变化，通过钻孔后应变换3个方向的应变变化量得到残余应力：

$ \begin{split}\varepsilon = \frac{{1 + \nu }}{E} \times \bar a \times \frac{{{\sigma _x} + {\sigma _y}}}{2} + \frac{1}{E} \times \bar b \times \\ \frac{{{\sigma _x} - {\sigma _y}}}{2}\cos 2\theta + \frac{1}{E} \times \overline b \times {\tau _{xy}}\sin 2\theta 。\end{split}$

(1)

式中：$\varepsilon $为测量的应变变化量；$E$为弹性模量；$\nu $为泊松比；${\sigma _x}$、${\sigma _y}$和${\tau _{xy}}$分别为3个未知残余应力分量；$\bar a$、$\bar b$表示各向同性应力标定常数，可在标准中查到；$\theta $表示3个应变栅与x轴的夹角（0°、45°、90°）；x定义为沿焊缝方向，${\sigma _x}$、${\sigma _y}$分别为焊缝纵向和横向残余应力。

3 有限元分析 3.1 有限元模型

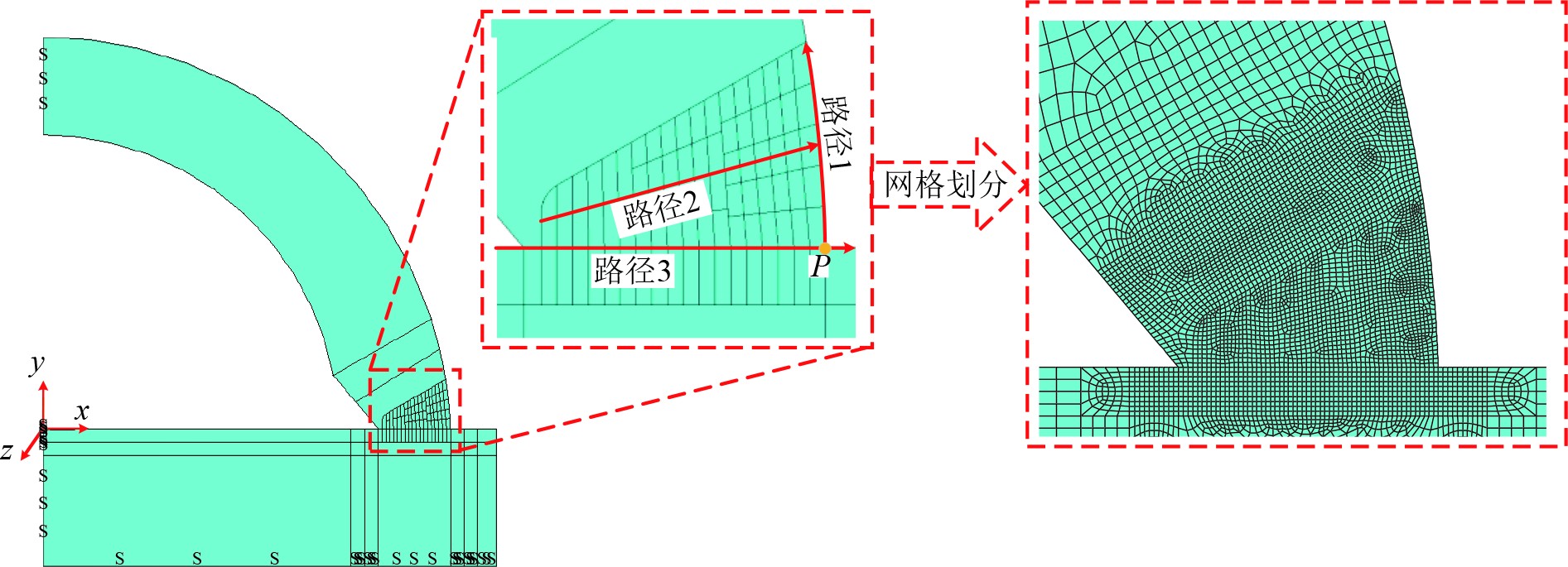
由于主弦管-齿条焊缝长达8 m，且沿焊缝方向焊接变形几乎为0，本文选取一个垂直于主弦管轴线的截面建立二维有限元模型进行分析。在主弦管-齿条焊接过程中，采用了对称施焊的方法。先同时对齿条板一侧的上下两条焊缝进行焊接，其次再对另一齿侧的上下两条焊缝进行焊接。研究表明，4条焊缝同时施焊对于应力和变形的影响与对称施焊的结果相似^[8]。因此，本文只取实际结构的1/4来建立模型，并施加对称边界条件，从而大幅减少计算时间。此外，齿条板的锯齿部分对焊接残余应力和变形的影响微乎其微，因此在数值模型中不包括齿条板的锯齿部分，进一步简化了模型的复杂度。二维平面有限元模型如图3所示。

本文采用有限元软件Ansys（2022R2）进行仿真，采用间接耦合法进行瞬态热-结构分析。该方法将计算过程拆分为2个部分：首先是热分析阶段，采用双椭球热源模型和生死单元技术对焊缝金属的填充过程进行模拟，得到模型的温度场分布；在此基础上，进行结构分析，将热分析中使用的热单元转换为结构分析所需的力学单元，通过将计算得到的节点温度作为外部载荷施加在结构应力分析中，得到残余应力分布情况。由于进行二维数值模拟分析，温度场和应力场分别采用平面单元PLANE55和PLANE182进行计算。在瞬态热-结构分析过程中，单元的节点和编号始终保持不变，仅对单元类型进行相应调整。

为了提高计算效率并保证模拟的准确性，在焊接模拟中对焊缝区域及周边的网格进行了局部细化。经过网格敏感性分析，确定焊缝区域的最小网格尺寸为1 mm。在距焊缝较远的区域，其网格划分较为稀疏，而在焊缝与这些区域之间，采用过渡网格进行有效过渡，有限元网格情况如图3所示。计算机的性能不同，也会对计算时间产生影响，本研究采用的CPU型号为i5-13500H，计算机内存为16 G，数值模拟计算时间约720 min。

在热分析阶段，需要设置相应的边界条件。在焊接过程中，热量主要通过热辐射和热对流从热源传递到焊件，而在焊件内部则以热传导方式传递。通过热对流和热辐射定义热边界条件：对流换热系数为15W/(m²·℃)，热辐射系数为0.85。模型的所有边界只考虑与空气的对流换热，将辐射换热的影响合并到对流换热系数中。在结构分析阶段，需要设置位移边界条件。在对称边界处设置对称约束（见图3）。

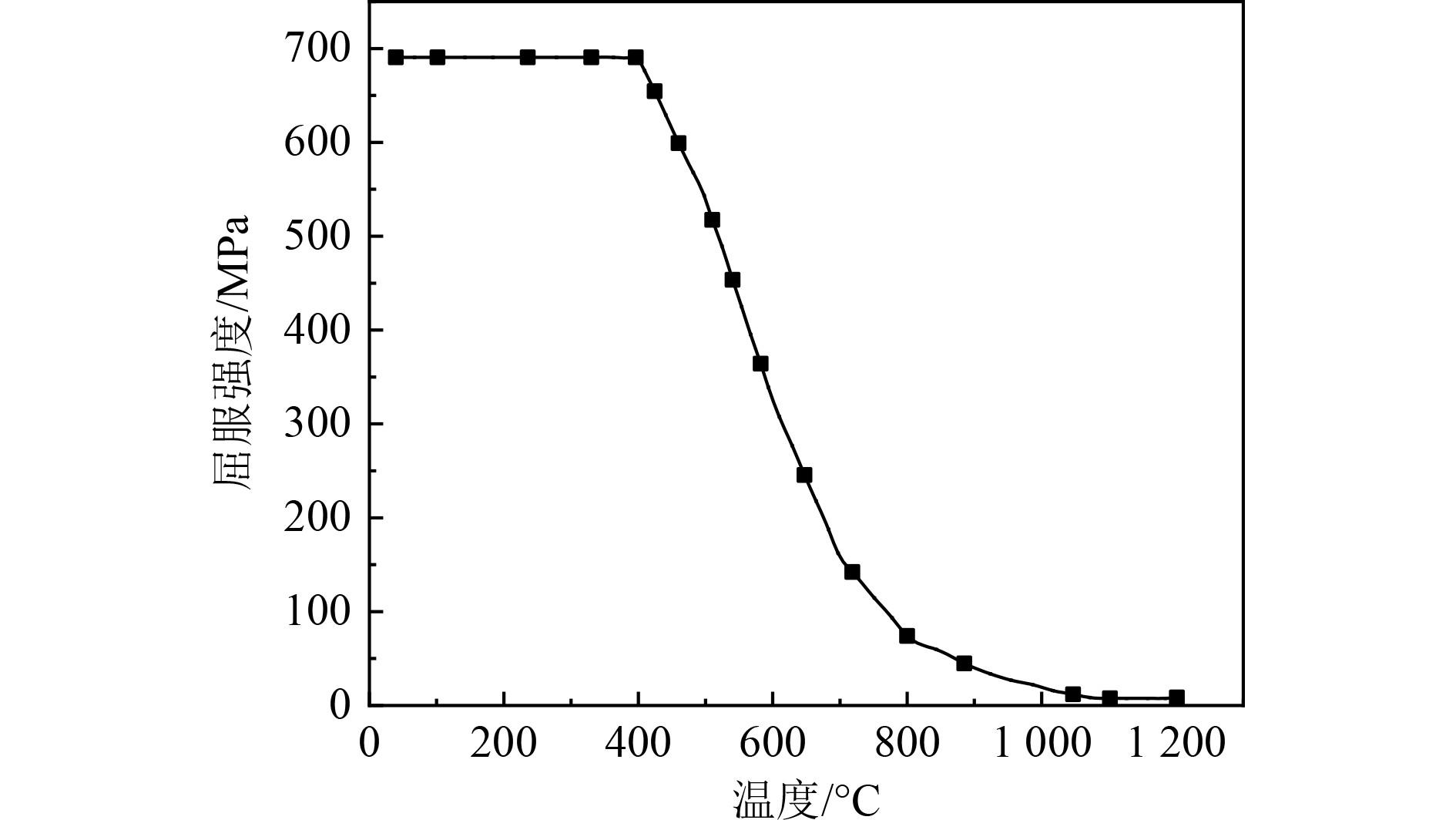
3.2 材料的热力学属性

齿条板和半圆管均为屈服强度不小于690 MPa的高强度调质钢。本文采用文献中相似材料的参数进行仿真分析，热力学性能参数如表2所示^[9]，屈服强度随温度变化曲线如图4所示^[10]。本文为了便于简化计算，在焊接模拟过程中假设母材与填充材料的性能参数一致。这一假设同样被很多已有研究采用^[11-12]，被证明是合理的。

3.3 焊接热源模型

在温度场计算时采用Goldak双椭球体热源模型，前、后半球热源分布函数分别为：

$ {q_1}(x,y,z) = \frac{{{\text{6}}\sqrt {\text{3}} {f_1}Q}}{{{\text{π}} ab{c_1}\sqrt {\text{π}} }}\exp ( - {\text{3}}\frac{{{x^{\text{2}}}}}{{{a^{\text{2}}}}} - {\text{3}}\frac{{{y^2}}}{{{b^2}}} - 3\frac{{{z^2}}}{{{c_1}^2}})。$

(2)

$ {q_2}(x,y,z) = \frac{{6\sqrt 3 {f_2}Q}}{{{\text{π}} ab{c_2}\sqrt {\text{π}} }}\exp ( - 3\frac{{{x^2}}}{{{a^2}}} - 3\frac{{{y^2}}}{{{b^2}}} - 3\frac{{{z^2}}}{{{c_2}^2}})。$

(3)

式中：$ {q_1} $和$ {q_2} $分别为前、后椭球热源的热流密度；${f_1}$和${f_2}$为分配给前后椭球热源的热量比例系数，且${f_1} + {f_2} = {\text{2}}$，通常取${f_1} = 0.6$，${f_2} = 1.4$；$Q$为焊接过程中的总热量，$Q = \eta UI$（$\eta $为热源效率，取$\eta = 0.8$，$U$、$I$分别为焊接电压、焊接电流）；$a$、$b$、${c_1}$、${c_2}$为定义双椭球热源形状的参数。假定焊缝的形状为规则的几何形状，忽略试样表面的残余高度。根据实际焊道尺寸来定义$a$和$b$，$a$的值为焊道宽度的一半，$b$的值为焊道深度，并取${c_1} = a$，$ {c_2} = 2a $^[13-14]。

对于多层多道焊接，可将一定数量的焊道合并为一个焊道，缩短计算时间。将合并焊道后的焊接热输入${Q_0}$定义为多个焊道的热输入之和^[15]。

$ {Q_0} = n \times Q 。$

(4)

式中：n为合并焊道数。

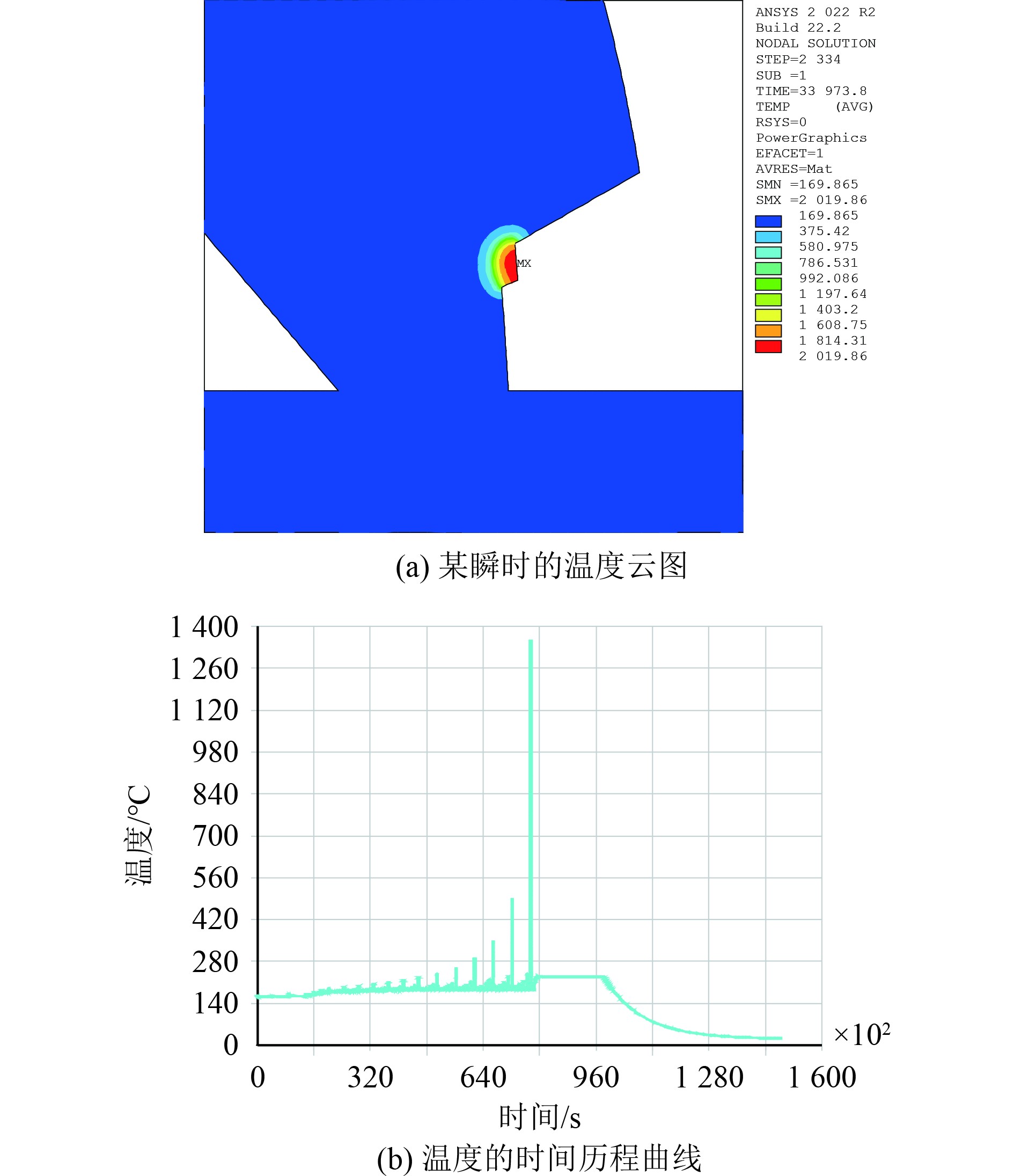
4 模拟结果分析 4.1 温度场

图5(a)为焊接过程中某焊道刚刚填充至分析截面时的温度云图。可以看出，采用生死单元技术实现了焊缝的逐步填充。在此瞬时焊道填充金属的内部，温度范围为1403～2019℃，这一温度范围超过了焊接材料的熔合线温度，确保了焊接材料充分熔化并实现完全穿透。在该道填充金属以外的区域，温度迅速下降到约170℃，接近焊接预热温度。

为了更直观的反映焊缝处温度随时间的变化过程，选取齿条板上与表层焊道相交点P（见图3），绘制了焊接过程中该点温度的时间历程曲线，如图5(b)所示。在焊接过程中，随着焊道越来越靠近P点，该点处的温度变化更加剧烈。在所有焊道填充完成后，模型整体加热到220～230℃，使得模型整体温度分布均匀，保温5 h，然后冷却到室温。图5(b)的温度时间曲线符合实际焊接过程中温度场的变化趋势。

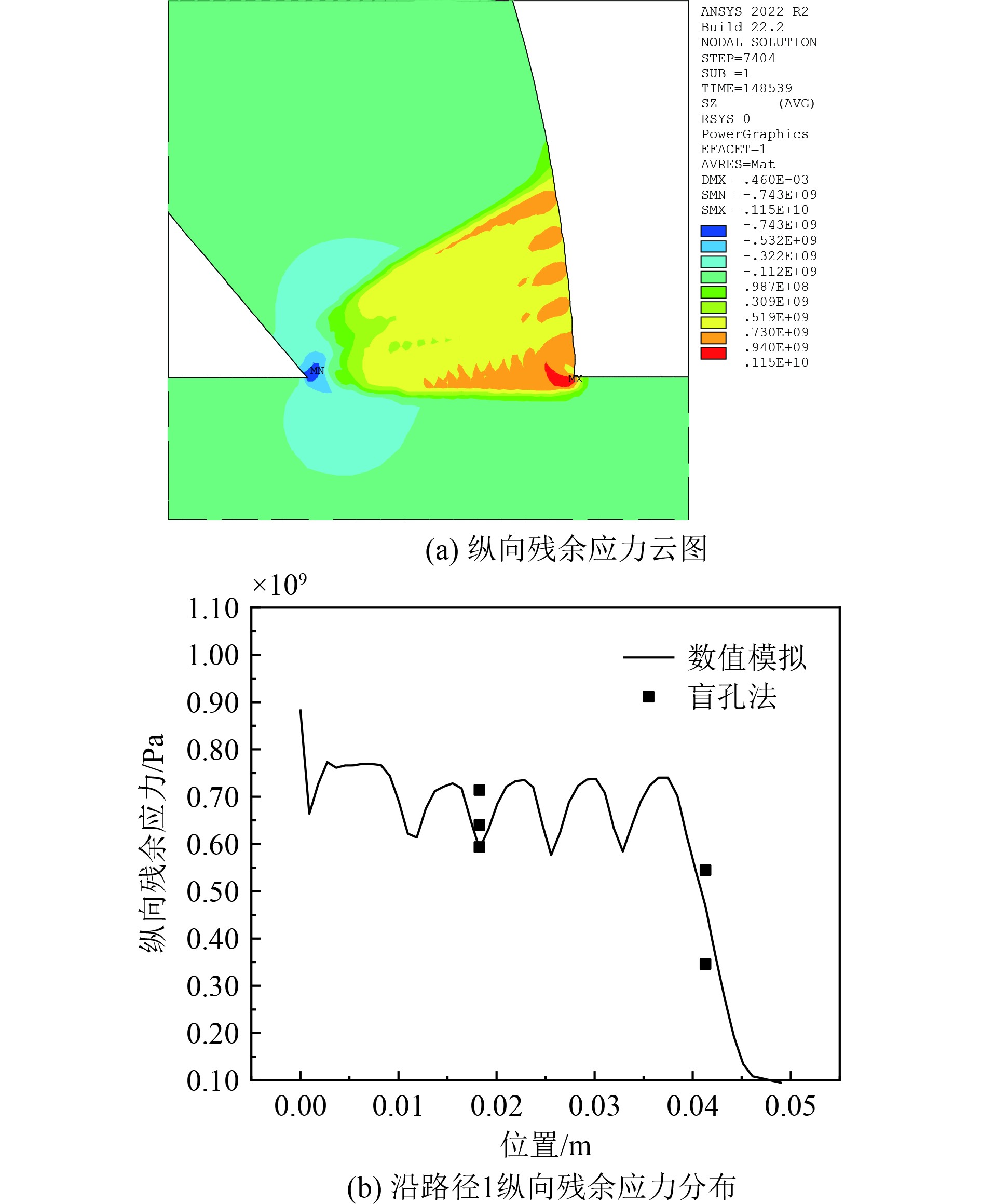
4.2 应力场

在完成模型的热分析后，进一步进行结构分析得到了焊接残余应力。由于试件沿焊缝方向约束大，焊缝纵向残余应力显著高于横向残余应力，本文只显示了纵向残余应力的结果。图6为纵向残余应力云图以及焊缝表面沿图3路径1的纵向残余应力分布。该路径的起始点为P点。试验测量数据也显示在了图中。

由纵向残余应力云图可以发现，焊接模型中纵向残余应力在近焊缝区为拉应力，稍远离焊缝处急剧改变为压应力，最大纵向残余应力出现在焊缝内部且靠近母材的区域，而非焊缝表面位置。盲孔法测得A和B两点的纵向残余应力均值分别为649 MPa和445 MPa。与试验结果相比，数值模拟结果的误差分别为10%和4.8%。可见，数值模型较为准确地预测了残余应力的大小及分布。通过与试验数据的对比，验证了数值模型的可靠性。

5 合并焊道对焊接残余应力的影响

合并焊道是简化多层多道焊接过程数值模拟的有效方法，但可能对焊缝残余应力分布预测结果产生影响。合并焊道可能无法完全模拟实际焊接过程中的复杂热循环和材料响应，这种简化可能会导致模拟结果与实际情况存在偏差，因此需要选择合适的焊道合并方法。

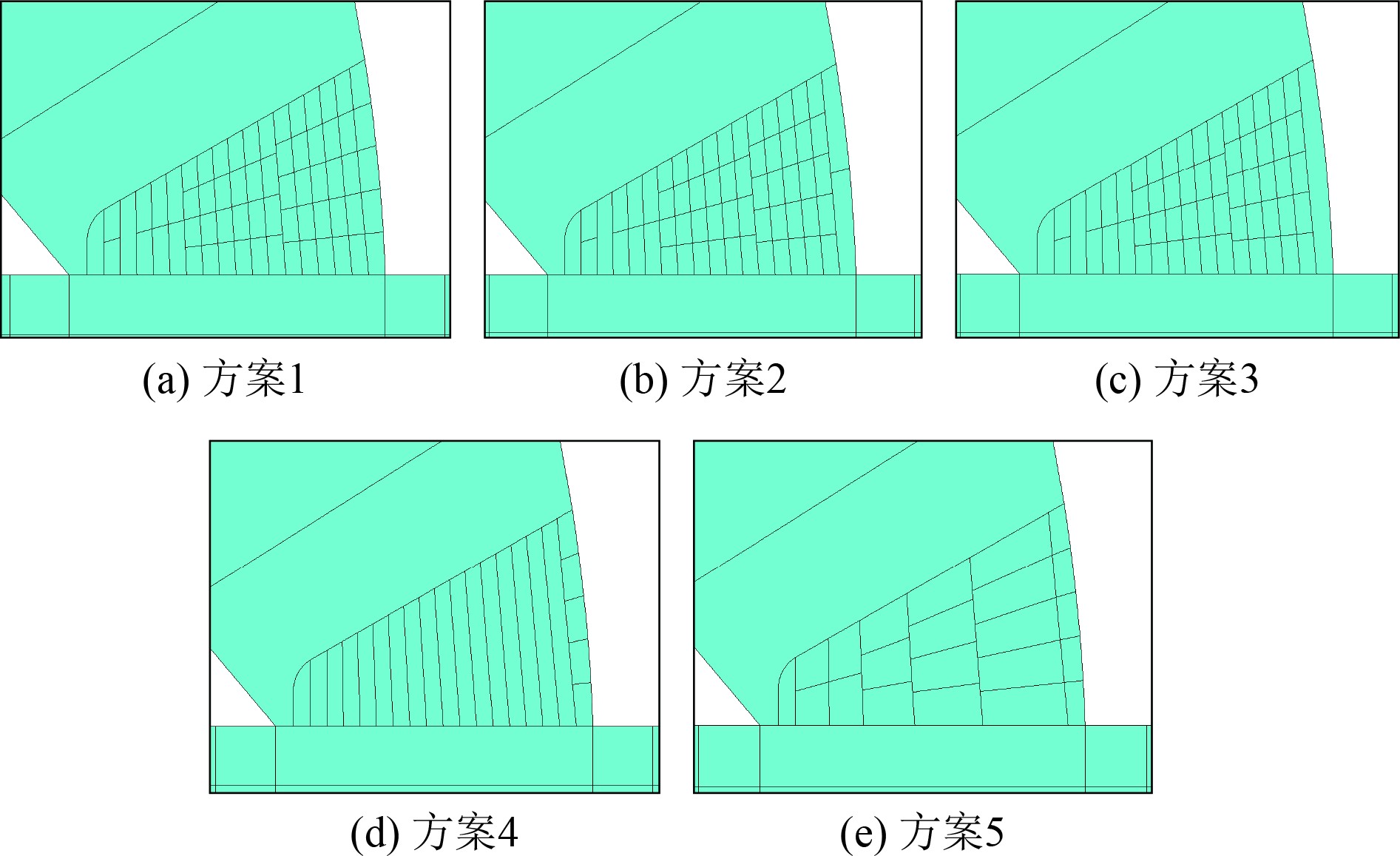
本文对比了5种焊道合并方案，目的是探究焊道合并对焊接残余应力产生的影响。其中，图7(a)为未合并焊道时的焊道分布图；图7(b)、图7(c)为针对焊缝表面焊道的合并；图7(d)、图7(e)为针对焊缝内部焊道的合并。

为便于对模型中的残余应力进行定量分析，在模型的中心截面上定义了如图3所示的3条路径。其中，路径1位于焊缝外表面上；路径2是焊缝深度方向的中心线上；路径3位于齿条板上，经过最大残余应力区域。

5.1 合并表层焊道的影响

在大型构件的焊接中，盖面焊是确保焊缝外观质量和力学性能的关键步骤，其工艺参数对控制焊接变形和残余应力至关重要。本研究对比了3种盖面焊合并方案，如图7(a)～图7(c)所示。

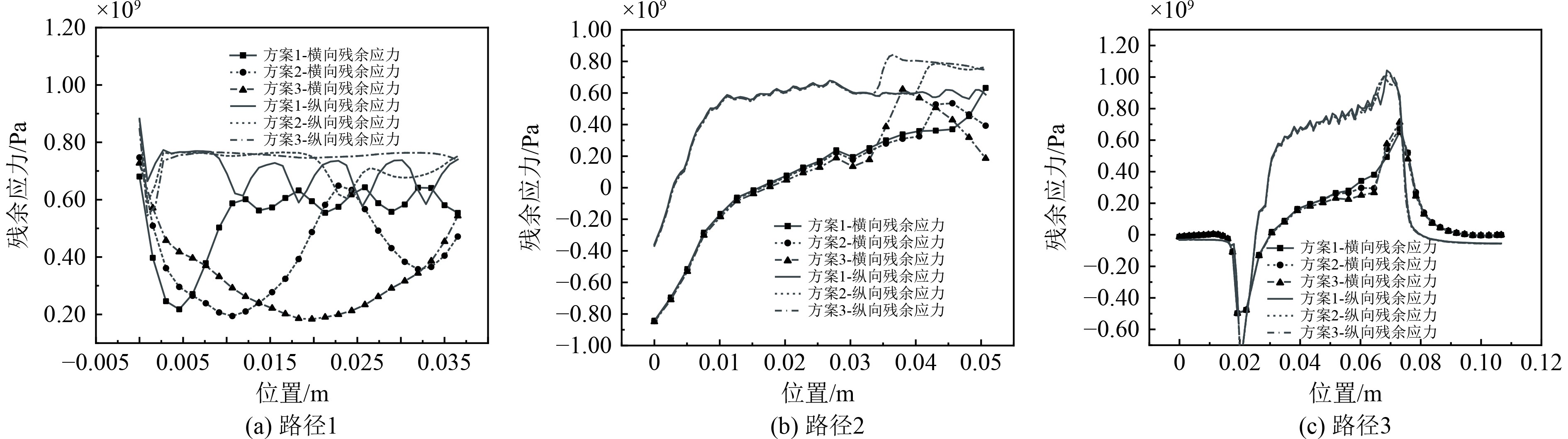
研究显示，合并表层焊道对焊缝残余应力的分布产生了显著影响。图8(a)为焊缝表面残余应力的分布情况，可以看出合并表层焊道会严重低估焊缝表面的横向残余应力，这主要是因为将表层焊道的合并扩大了熔化区域，减少了横向约束力，进而导致横向残余应力减小^[4]。此外，合并表层焊道使得焊缝表面的纵向残余应力分布变得均匀，纵向残余应力有所增加，但使得靠近焊缝与齿条板相交位置处的纵向残余应力降低。图8(b)为沿焊缝深度方向的纵向与横向残余应力分布情况，可以明显看出，合并表层焊道后导致内部的残余应力有所增加，特别是横向残余应力。因此合并表层焊道计算不仅对试件表面残余应力的分布影响较大，对内部的焊接残余应力也存在较大的影响。图8(c)显示合并表层焊道对热影响区的残余应力影响非常小，主要是由于合并表层焊道后的热输入相对均匀，导致热影响区的温度梯度较小，从而使得残余应力的变化不明显。

5.2 合并内部焊道的影响

由于合并表层焊道对残余应力分布的影响较大，所以本文不考虑表层焊道的合并，仅针对内部焊道进行合并，如图7(d)和图7(e)所示。其中，图7(d)是将内部的焊道沿焊缝宽度方向横向合并；图7(e)则是将内部的焊道沿焊缝厚度方向纵向合并。2种合并方式合并的焊道数均从1个逐渐增加到5个。

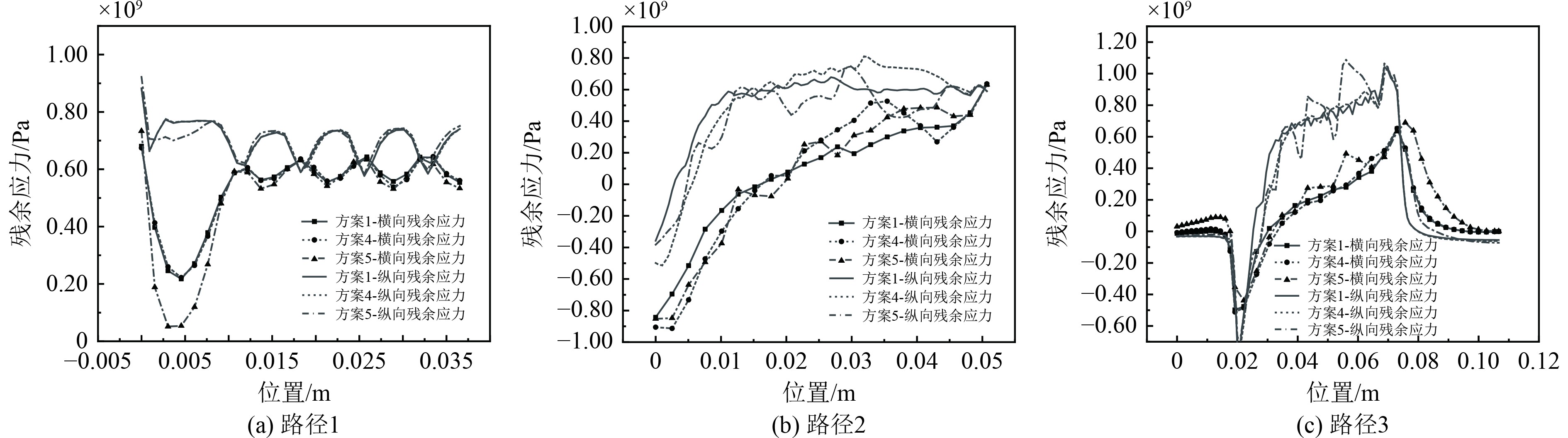
图9展示了合并内部焊道后沿3条路径的残余应力分布情况。图9(a)比较了3种不同方案下焊缝表面的残余应力，发现横向合并方式得到的残余应力分布趋势与未合并时的非常一致，这表明横向合并方式对焊缝表面残余应力的影响相对较小。然而，纵向合并方式对焊缝的残余应力影响较为显著。具体来说，纵向合并方式使得焊缝表面横向残余应力减小，尤其是靠近母材的焊缝表面位置。

从图9(b)、图9(c)显示了焊缝内部以及热影响区的残余应力情况，可以看出，当横向和纵向合并焊道数达到3个以上时，得到的残余应力会产生较大的误差。从图9(c)可以明显观察到，焊道合并对热影响区的残余应力分布具有显著影响。特别是纵向合并方式，导致了热影响区残余应力的显著增加。这种增加可能是由于纵向合并焊接过程中，热循环的累积效应以及材料在冷却过程中的不均匀收缩，这些因素共同作用于热影响区，导致应力的重新分布和集中。因此，纵向合并焊接相较于其他合并方案，可能会在热影响区产生更高的残余应力水平。

5.3 最佳合并方式

考虑以上合并方案对残余应力产生的影响，本文采用适当的合并方式（方案6）对焊道进行简化，以更好地模拟残余应力。由于合并表层焊道对残余应力分布的影响较大，所以不考虑表层焊道的合并。对于内部焊道，采取横向与纵向相结合的合并方式。鉴于纵向合并对残余应力的影响较为显著，尽量降低纵向合并焊道数，横向与纵向合并的焊道数均不超过3个，简化后焊道总数减至20道，如图10所示。数值模拟计算时间约200 min，计算时间缩短了大约70%。

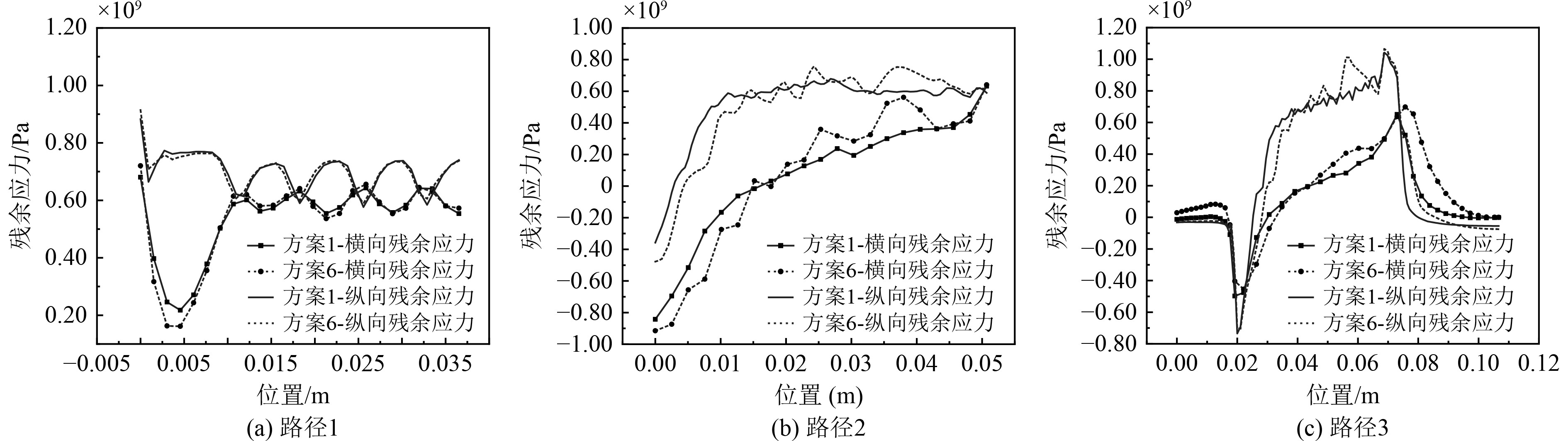
图11为方案6计算得到的残余应力分布图。图11(a)是沿焊缝表面（路径1）残余应力的分布情况，可以看出，采用合适的焊道合并方式对焊缝的应力分布与大小的影响微乎其微。图11(b)是焊缝深度方向上（路径2）的残余应力分布情况，方案6计算的残余应力与方案1的结果虽然有一些差距，但整体上应力分布情况基本一致。图11(c)是沿路径3上的残余应力分布图，焊缝区域的应力分布情况比较吻合，但热影响区的残余应力分布有些差异，主要受焊道纵向合并的影响。

6 结　语

1）二维热-弹塑性有限元法较为准确地预测了主弦管-齿条焊接残余应力，应力状态沿着焊缝方向呈现出显著的梯度变化。近焊缝区域主要表现为拉应力，而稍远区域则快速过渡到压应力。应力峰值并非位于焊缝表面，而是位于焊缝内部接近母材的区域。

2）合并表层焊道对焊缝区域残余应力分布具有显著影响，但对热影响区的影响较小。合并表层焊道使得焊缝表面的纵向残余应力分布变得均匀，纵向残余应力有所增加，但使得靠近焊缝与齿条板相交位置处的纵向残余应力减小。合并表层焊道还会严重低估焊缝表面横向残余应力。此外，这种合并方式不仅影响结构表面残余应力的分布，对内部的焊接残余应力也存在较大的影响。

3）内部焊道横向合并方式对焊缝表面残余应力的影响微乎其微，但纵向合并方式使得焊缝表面横向残余应力减小，尤其是靠近母材的焊缝表面位置。无论是横向合并还是纵向合并均会对焊缝内部残余应力产生影响。此外，焊道合并对热影响区的残余应力分布也有显著影响，相较于其他合并方案，纵向合并焊接可能在热影响区产生更高的残余应力水平。

4）不考虑表层焊道的合并，采取内部焊道的横向与纵向相结合的合并方式，并且尽量减少纵向合并焊道数，是一种简化多层多道焊接过程数值模拟的有效方法。