2. 哈尔滨工程大学 智能科学与工程学院,黑龙江 哈尔滨 150001
2. College of Intelligent Systems Science and Engineering, Harbin Engineering University, Harbin 150001, China
在海洋任务中,无人船(USV)编队的避障能力直接关系到任务成败。海洋环境中可能存在暗礁、浮冰、废弃船舶等天然或人为障碍,编队航行时若发生碰撞,轻则导致设备损坏、产生昂贵维修费用,重则引发编队失联甚至任务完全失败[1 − 3]。在军事侦察、联合搜救等关键场景中,此类事故还可能造成人员安全威胁或敏感信息泄露。因此,实现安全、智能的自主避障及避障轨迹跟踪,是无人船编队发挥集群优势的基础保障[4 − 7],也是当前研究的重点方向。
近年来,研究者提出多种无人船路径规划与避障方法。在避障层面,Wan等[8]将A*算法与自适应动态窗口算法(DWA)相结合,同时实现静态和动态避障。为解决USV自主导航中的避障策略问题。Chen等[9]将决策树分类器与DWA算法融合,提出一种基于决策树的动态窗口方法(DT-DWA)算法,实现了自适应规划调整权重。Zhou等[10]提出混合动态路径规划算法GIBi-RRT-IDWA,结合Bi-RRT的全局能力与DWA的局部路径优化。Han等[11]为了防止USV在避开动态障碍物后陷入局部最小值,采用动态选择的父节点作为改进动态窗口方法的局部目标。Tan等[12]针对DWA路径绕过密集障碍导致路径变长、靠近动态障碍物等问题,提出改进的DWA局部路径规划方法。Wang等[13]基于DWA构建了适用于USV的运动模型与路径评价函数。
Zhou等[14]将人工势场融入偏微分方编队控制器,实现全驱动USV的协同避碰与构型重构。Wei等[15]针对传统的A*和DWA融合算法无法统一终端航向问题,添加全局路径关键点,形成引导路径统一航向范围,提高USV编队聚合效率。Li等[16]引入快速扩展随机树(RRT),并将避碰规则量化纳入评价系统中。Wang等[17]针对标准DWA算法中固定权重机制不合理的问题,结合了A*算法,引入与方位角相关的可变权重,提升了路径规划中的目标定向能力。
在编队轨迹跟踪层面,Jiang[18]基于滑模控制(SMC)方法,设计了一种考虑环境干扰下USV队形调节控制算法。Duan等[19]针对模型不确定性、扰动和输入饱和问题,融合神经网络、干扰观测器和非奇异滑模技术提出复合控制方法。Rabiee H等[20]设计了一个自适应滑模干扰观测器,并提出了一个用于不确定非线性系统的终端滑模控制方案。Liu等[21]提出分层滑模控制策略,解决多USV采样通信下的编队包围控制问题。Zhang等[22]在控制环路中,通过迭代滑模控制器抑制切换系统引起的抖动。
尽管已有研究在避障规划与轨迹控制方面取得积极进展,但仍存在两方面不足:一是很多研究以单船为对象,未考虑USV间的协同避障;二是文献虽探讨了滑模控制的抗扰能力,但对欠驱动USV中横向速度变化引起的控制量抖振问题研究仍不充分。本文将从USV编队的避障规划出发,基于DWA算法进行协同避障算法设计,并充分考虑横向速度的影响,提出一种集成改进DWA的协同避障机制与鲁棒轨迹跟踪策略的滑模控制方法。
1 建模与问题描述在USV运动控制研究中,针对轨迹跟踪等平面控制需求,本文采用水平面三自由度动力学模型进行设计。设定编队由N艘USV组成,基于USV的平面对称特性,根据刚体动量与动量矩定理,建立第
| $ \left\{\begin{aligned} & \dot{x}_i=u_i\cos\psi_i-v_i\sin\psi_i,\\ & \dot{y}_i=u_i\sin\psi_i+v_i\cos\psi_i,\\ & \dot{\psi}_i=r_i,\\ & \left(m_i+m_{xi}\right)\dot{u}_i-\left(m_i+m_{yi}\right)v_ir_i= \\ & X_{uui}u_i^2+X_{vvi}v_i^2+X_{vri}v_ir_i+X_{rri}r_i^2+X_{Pi}\text{ + }X_{di},\\ & \left(m_i+m_{yi}\right)\dot{v}_i+\left(m_i+m_{xi}\right)u_ir_i= \\ & Y_{vi}v_i+Y_{ri}r_i+Y_{vvi}v_i\left|v_i\right|+Y_{vri}r_i\left|v_i\right|+Y_{rri}r_i\left|r_i\right|+Y_{di},\\ & (I_{zzi}+J_{zzi})\dot{r}_i=N_{vi}v_i+N_{ri}r_i+ \\ & N_{vvri}v_i^2r_i+N_{vrri}v_ir_i^2+N_{vvi}v_i\left|v_i\right|+N_{Ri}+N_{di}。\end{aligned}\right. $ | (1) |
式中:
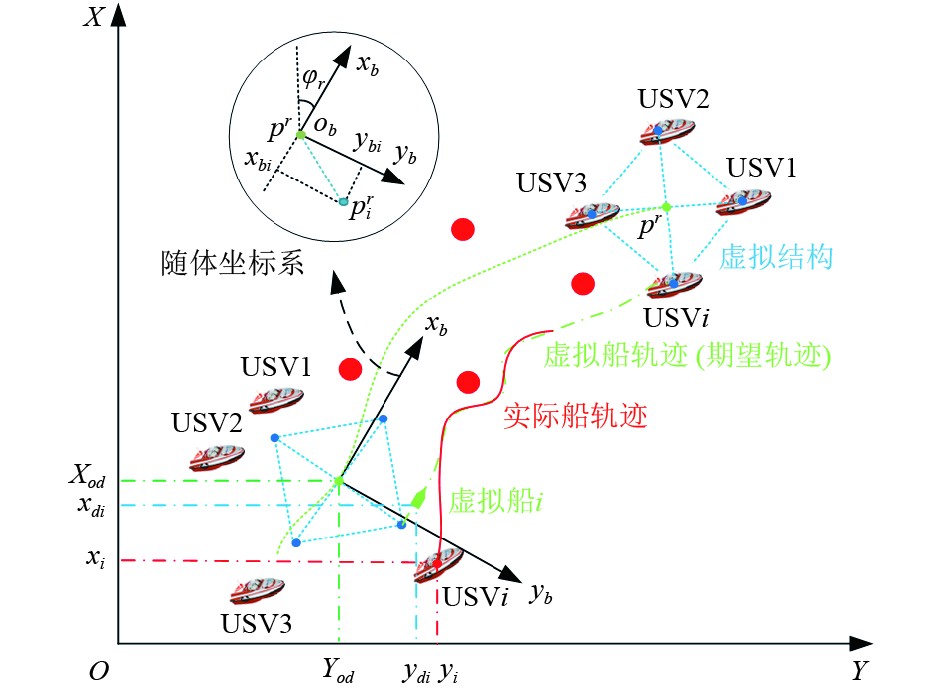
针对外界海洋干扰下的USV编队避障控制问题如图1所示。
|
图 1 USV避障控制示意图 Fig. 1 diagram of USV obstacle avoidance control |
图中:
基于刚体运动学原理的虚拟结构法将整个队形结构视为刚体,如图1中的虚线矩形结构。而刚体队形结构的生成是基于此时的参考轨迹(即图1中虚线轨迹对应的参考点)和对应的队形坐标(即各船在随体坐标系中的位置)。生成刚体队形结构后可以确定各虚拟结构点的大地坐标:
公式具体要求如下:
| $ \left[ \begin{gathered} {x_{oi}} \\ {y_{oi}} \\ \end{gathered} \right] = \left[ \begin{gathered} {X_{od}} \\ {Y_{od}} \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _r}}&{ - \sin {\varphi _r}} \\ {\sin {\varphi _r}}&{\cos {\varphi _r}} \end{array}} \right]\left[ \begin{gathered} {x_{bi}} \\ {y_{bi}} \\ \end{gathered} \right]。$ | (2) |
式中:
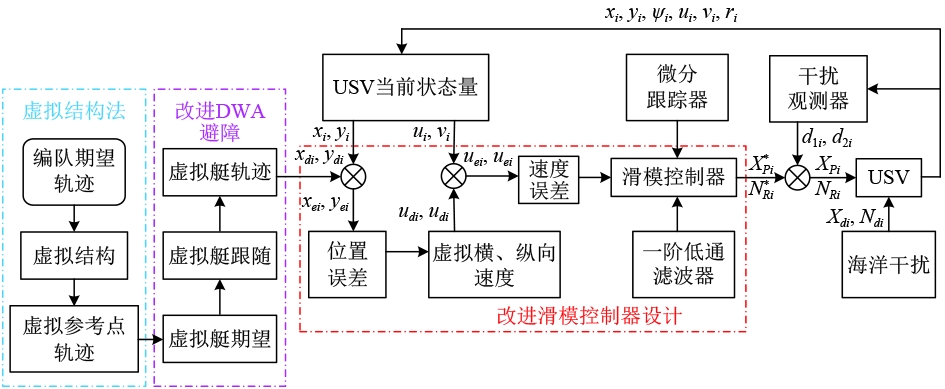
理论上以虚拟点轨迹坐标作为USV轨迹跟踪目标点,即可实现编队的轨迹跟踪与队形保持任务,但在实际轨迹跟踪过程中,需要考虑USV与外界障碍物以及USV之间的避碰。本文对经典动态窗口法进行评价函数优化改进,并创新性地在虚拟结构点映射关系中引入可移动虚拟领航船(图实心小船标识),通过在该中介节点上应用改进避障算法,动态生成避障轨迹,并以此作为各USV的期望目标轨迹。实际USV通过跟踪虚拟船的轨迹来完成避障与轨迹跟踪任务。算法设计流程如图2所示。
|
图 2 USV编队避障控制器设计流程图 Fig. 2 Flowchart of USV formation obstacle avoidance controller design |
由图2可知,虚拟结构法获取结构点位置信息后,将由改进DWA避障算法规划出各USV的期望轨迹,然后根据位置信息进行滑模控制控制器设计。
2 改进DWA规划轨迹算法由于USV通常在二维水面上进行运动,其运动特点包括速度、艏向角、动力学限制等,USV的运动约束与移动机器人有所不同。考虑到仿真预测时间
| $ \begin{split} &\left[ \begin{gathered} {x_{di}}(t + 1) \\ {y_{di}}(t + 1) \\ {\psi _{\beta i}}(t + 1) \\ \end{gathered} \right] = \left[ \begin{gathered} {x_{\beta i}}(t) \\ {y_{\beta i}}(t) \\ {\psi _{\beta i}}(t) \\ \end{gathered} \right] + \\ &dt\left[ \begin{gathered} {u_{\beta i}}(t)\cos ({\psi _{\beta i}}(t)) - {v_{\beta i}}(t)\sin ({\psi _{\beta i}}(t)) \\ {u_{\beta i}}(t)\cos ({\psi _{\beta i}}(t)) - {v_{\beta i}}(t)\sin ({\psi _{\beta i}}(t)) \\ {\text{ }}{r_{\beta i}}(t) \\ \end{gathered} \right] \end{split}$ | (3) |
式中:
经过速度采样后获取速度集,DWA算法通过目标评价函数来对可行速度集进行评价最后选择出最优路径。传统的目标函数是由3部分评价指标:方位角评价函数(
| $ \begin{split} & G_{\max}(u_i,r_i)=\sigma(\alpha\cdot\mathrm{heading}(u_i,r_i)+ \\ & \quad\quad\beta\cdot\mathrm{dist}(u_i,r_i)+\gamma\cdot\mathrm{vel}(u_i,r_i))。\end{split} $ | (4) |
式中:
传统的DWA障碍规避架构虽建立了运动规划框架,但其方位角评价子空间不能很好贴切实际欠驱动USV的最优航行路径。USV的欠驱动特性对整体预测轨迹的顺滑性具有更高的设计需求。对此做出如下3点改进:修正方位角评价函数
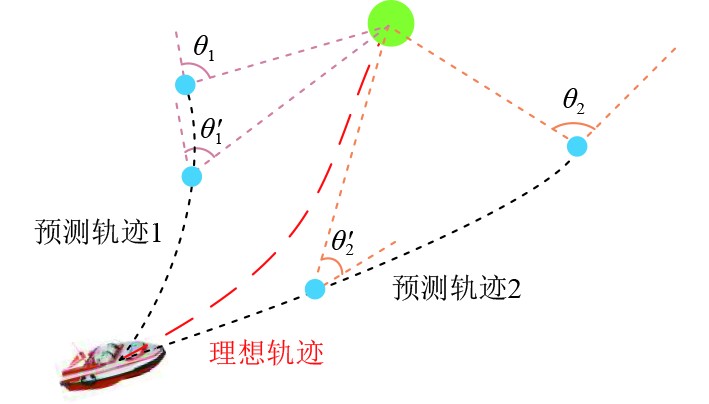
传统DWA在评价方位角时,是以预测轨迹末端的切线方向与目标点连线方向夹角的最小作为理想路径,但在较为接近目标点的情况下,如图3所示。
|
图 3 方位角评价示意图 Fig. 3 Schematic Diagram of Heading Evaluation |
图3中,预测轨迹1和预测轨迹2的评价函数对比中,
| $ n_{dt,h}=\mathrm{round}(d_{\mathrm{mid}}/u_i)。$ | (5) |
式中:
| $ {\rm{heading}}'({u_i},{r_i}) = {180^{\circ}} - abs[(\theta ({n_{dt,h}},aim) - \psi ({n_{dt,h}})]。$ | (6) |
式中:
在传统DWA算法中,在避障后不需要考虑轨迹的复原需求,而本文设计的USV编队轨迹跟踪控制中,在完成避障需求后,USV需要尽可能快的返回到编队队形的指定位置。故添加目标点距离函数,对预测轨迹终点和目标点距离进行评价,距离越近,得分越高:
| $ \mathrm{goal}(u_i,r_i)=10/d{_{goal}} $ | (7) |
式中:
在DWA算法中,转向角速度的平滑性对轨迹的顺滑性也至关重要。突然的艏向角变化不仅影响USV本身的运动稳定性,还可能导致其目标偏离。可以通过控制艏向角速度的变化来降低轨迹的转弯急剧程度:
| $ {\rm{smooth}}({u_i},{r_i}) = {\sum\limits_n {\left( {\frac{{r({t_{n + 1}}) - r({t_n})}}{{\Delta t}}} \right)} ^2} 。$ | (8) |
式中:
结合式(4)、式(6)~式(8)可得改进后的DWA算法评价函数为:
| $ \begin{split} & G'_{\max}(u_i,r_i)=\sigma(\alpha\cdot\mathrm{heading}'(u_i,r_i)+\beta\cdot\mathrm{dist}(u_i,r_i)+ \\ & \gamma\cdot\mathrm{vel}(u_i,r_i)+\lambda\mathrm{goal}(u_i,r_i)+\kappa\mathrm{smooth}(u_i,r_i))。\end{split} $ | (9) |
通过上述改进DWA算法可以实现第i艘虚拟船对虚拟结构目标点的轨迹跟踪与避障任务。由此得到的虚拟船轨迹即可作为第i艘USV的期望轨迹,对此设计第i艘USV轨迹跟踪位置误差系统:
| $ \left[ {\begin{array}{*{20}{c}} {{x_{ei}}} \\ {{y_{ei}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_i} - {x_{di}}} \\ {{y_i} - {y_{di}}} \end{array}} \right]。$ | (10) |
其中:
可以看出当每艘USV的位置误差收敛到0(
首先基于误差系统对虚拟纵向速度控制律和虚拟横向速度控制律进行相关设计。对式(10)两边进行求导可得:
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot x}_{ei}}} \\ {{{\dot y}_{ei}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\dot x}_i} - {{\dot x}_{di}}} \\ {{{\dot y}_i} - {{\dot y}_{di}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos ({\psi _i})}&{ - \sin ({\psi _i})} \\ {\sin ({\psi _i})}&{\cos ({\psi _i})} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{u_i}} \\ {{v_i}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{\dot x}_{di}}} \\ {{{\dot y}_{di}}} \end{array}} \right]。$ | (11) |
为了让USV轨迹位置误差趋近于零,设计纵向虚拟控制律
| $ \left[ \begin{gathered} {\alpha _{ui}} \\ {\alpha _{vi}} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\cos ({\psi _i})}&{\sin ({\psi _i})} \\ { - \sin ({\psi _i})}&{\cos ({\psi _i})} \end{array}} \right]\left[ \begin{gathered} {{\dot x}_{di}} - {{{k_{1i}}{x_{ei}}} \mathord{\left/ {\vphantom {{{k_{1i}}{x_{ei}}} {{w_i}}}} \right. } {{w_i}}} \\ {{\dot y}_{di}} - {{{k_{2i}}{y_{ei}}} \mathord{\left/ {\vphantom {{{k_{2i}}{y_{ei}}} {{w_i}}}} \right. } {{w_i}}} \\ \end{gathered} \right] 。$ | (12) |
式中:
| $ \left[ \begin{gathered} {\alpha _{ui}} \\ {\alpha _{vi}} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\cos ({\psi _i})}&{\sin ({\psi _i})} \\ { - \sin ({\psi _i})}&{\cos ({\psi _i})} \end{array}} \right]\left[ \begin{gathered} {{\dot x}_{di}} - {{{k_{1i}}{x_{ei}}} \mathord{\left/ {\vphantom {{{k_{1i}}{x_{ei}}} {{w_i}}}} \right. } {{w_i}}} \\ {{\dot y}_{di}} - {{{k_{2i}}{y_{ei}}} \mathord{\left/ {\vphantom {{{k_{2i}}{y_{ei}}} {{w_i}}}} \right. } {{w_i}}} \\ \end{gathered} \right] $ | (13) |
根据式(1),首先定义如下控制量
步骤1 定义第i艘USV的纵向速度误差:
| $ {u_{ei}} = {u_i} - {\alpha _{ui}} 。$ | (14) |
考虑到系统的稳态误差项,我们在滑模面的设计中加入
| $ s_{1i}=u_{ei}+\lambda_{1i}\int_0^tu_{ei}(\tau_i)\mathrm{d}\tau_i,\lambda_{1i} > 0。$ | (15) |
其中:
| $ {\begin{split} &{{\dot s}_{1i}} = {{\dot u}_i} - {{\dot \alpha }_{ui}} + {\lambda _{1i}}{u_{ei}}= \frac{{{m_i} + {m_{yi}}}}{{{m_i} + {m_{xi}}}}{v_i}{r_i} + \\ &\frac{{{{\hat X}_{uui}}{u_i}^2 + {{\hat X}_{vvi}}{v_i}^2 + {{\hat X}_{vri}}{v_i}{r_i} + {{\hat X}_{rri}}{r_i}^2 + X_{Pi}^ * }}{{{m_i} + {m_{xi}}}} - {{\dot \alpha }_{ui}} + {\lambda _{1i}}{u_{ei}}。\end{split} }$ | (16) |
步骤2 由于虚拟纵向速度控制律的复杂表达式,导数计算过程中可能出现“微分爆炸”现象,导致算法的计算复杂度显著增加。为此,本文设计了一阶低通滤波器,以滤波器的输出替代原始的微分计算结果,从而有效地缓解了“微分爆炸”问题。一阶滤波器的设计如下:
| $ \left\{ \begin{gathered} {T_{1i}}{{\dot A}_{ui}} + {A_{ui}} = {\alpha _{ui}},\\ {A_{ui}}\left( 0 \right) = {\alpha _{ui}}\left( 0 \right)。\\ \end{gathered} \right. $ | (17) |
式中:
步骤3 针对传统滑模控制中符号函数引发的高频抖振问题,本节提出改进型指数趋近律,采用具有连续饱和特性的双曲正切函数
| $ {\dot s_{1i}} = - {\varepsilon _{1i}}\tanh ({s_{1i}}) - {\sigma _{1i}}{s_{1i}}。$ | (18) |
式中:
结合式(16)~式(18),最终设计的欠驱动USV纵向推进力滑模控制律为:
| $ {\begin{gathered} X_{Pi}^ * = - \left( {{m_i} + {m_{yi}}} \right){v_i}{r_i} - {{\hat X}_{uui}}{u_i}^2 - {{\hat X}_{vvi}}{v_i}^2 - {{\hat X}_{vri}}{v_i}{r_i} - \\ {{\hat X}_{rri}}{r_i}^2 + ({m_i} + {m_{xi}})\left[ {{{\dot A}_{ui}} - {\lambda _{1i}}{u_{ei}} - {\varepsilon _{1i}}\tanh ({s_{1i}}) - {\sigma _{1i}}{s_{1i}}} \right]。\\ \end{gathered} }$ | (19) |
根据式(1),首先定义如下控制量
步骤1 定义无人船的横向速度误差变量如下:
| $ {v_{ei}} = {v_i} - {\alpha _{vi}}。$ | (20) |
针对USV欠驱动系统在横向运动自由度上缺乏直接控制量的特性,本文提出融合比例-积分结构的滑模面综合设计方法。所构建的复合滑模面表达式为:
| $ s_{2i}=\dot{v}_{ei}+\lambda_{2i}v_{ei}+\lambda_{3i}\int_0^tv_{ei}\rm{d}t。$ | (21) |
式中:
| $\begin{split} &{\dot s_{2i}} = {\ddot v_i} - {\ddot \alpha _{vi}} + {\lambda _{2i}}{\dot v_{ei}} + {\lambda _{3i}}{v_{ei}} =\\ &{\ddot v_i} - {\ddot \alpha _{vi}} + {\lambda _{2i}}\left( {{{\dot v}_i} - {{\dot \alpha }_{vi}}} \right) + {\lambda _{3i}}\left( {{v_i} - {\alpha _{vi}}} \right)。\end{split}$ | (22) |
式(22)中关于
| $ \left\{ \begin{gathered} {{\dot \alpha }_{vi}} = - {r_i}{\alpha _{ui}} + {p_i} ,\\ {{\ddot \alpha }_{vi}} = - {{\dot r}_i}{\alpha _{ui}} - r{{\dot \alpha }_{ui}} + {{\dot p}_i} 。\\ \end{gathered} \right. $ | (23) |
式中:
| $ {\begin{aligned} {p_i} =& - [{{\ddot x}_{di}} - {k_{1i}}({w_i}^{ - 1} - {w_i}^{ - 3}x_{ei}^2){{\dot x}_{ei}} + {k_{1i}}{w_i}^{ - 3}{x_{ei}}{y_{ei}}{{\dot y}_{ei}}]\sin ({\psi _i}) + \\ &[{{\ddot y}_{di}} - {k_{2i}}({w_i}^{ - 1} - {w_i}^{ - 3}y_{ei}^2){{\dot x}_{ei}} + {k_{2i}}{w_i}^{ - 3}{x_{ei}}{y_{ei}}{{\dot x}_{ei}}]\cos ({\psi _i})。\\ \end{aligned}} $ | (24) |
步骤2 为简化
| $ \left\{ \begin{gathered} {T_{2i}}{{\dot B}_{Pi}} + {B_{Pi}} = {p_i},\\ {B_{Pi}}\left( 0 \right) = {p_i}\left( 0 \right) 。\\ \end{gathered} \right. $ | (25) |
式中:
步骤3 设计基于双曲正切函数的指数滑模控制律如下:
| $ {\dot s_{2i}} = - {\varepsilon _{2i}}\tanh \left( {{s_{2i}}} \right) - {\sigma _{2i}}{s_{2i}}。$ | (26) |
式中:
结合式(22)、式(23)、式(25)和式(26),转艏力矩的表达式为:
| $ \begin{split} &N_{Ri}^ * = [ - {{\ddot v}_i} + {{\dot B}_{Pi}} - {r_i}{A_{ui}} - {\lambda _{2i}}\left( {{{\dot v}_i} - {{\dot \alpha }_{vi}}} \right) - {\lambda _{3i}}\left( {{v_i} - {\alpha _{vi}}} \right) - \\ &{\varepsilon _{2i}}\tanh \left( {{s_{2i}}} \right) -{\sigma _{2i}}{s_{2i}} ]({I_{zzi}} + {J_{zzi}})/{\alpha _{ui}} - {{\hat N}_{vi}}{v_i} - {{\hat N}_{ri}}{r_i} - \\ &{{\hat N}_{vvri}}{v_i}^2{r_i} - {{\hat N}_{vrri}}{v_i}{r_i}^2 - {{\hat N}_{vvi}}{v_i}\left| {{v_i}} \right| 。\\[-1pt] \end{split} $ | (27) |
步骤4 设计横向速度微分跟踪器平滑控制量。针对式(27)中横向速度二阶导数直接求导引发的噪声放大问题,这里引入关于横向速度一阶导
| $ \left\{ \begin{gathered} {x_{1i}}\left( {k + 1} \right) = {x_{1i}}(k) + h{x_{2i}}\left( k \right),\\ {x_{2i}}\left( {k + 1} \right) = {x_{2i}}(k) + \\ h\left\{ { - D_i^2[{x_{1i}}\left( k \right) - {{\dot v}_i}(k)] - 2{D_i}{x_{2i}}\left( k \right)} \right\}。\end{gathered} \right. $ | (28) |
式中:
通过横向速度微分跟踪器的输出,使用
| $ \begin{split} & N_{Ri}^ * = [ - {x_{2i}} + {{\dot B}_{Pi}} - {r_i}{A_{ui}} - {\lambda _{2i}}\left( {{x_{1i}} - {{\dot \alpha }_{vi}}} \right) - {\lambda _{3i}}\left( {{v_i} - {\alpha _{vi}}} \right) -\\ &{\varepsilon _{2i}}\tanh \left( {{s_{2i}}} \right) - {\sigma _{2i}}{s_{2i}}]{{\left( {{I_{zzi}} + {J_{zzi}}} \right)} \mathord{\left/ {\vphantom {{\left( {{I_{zzi}} + {J_{zzi}}} \right)} {{\alpha _{ui}}}}} \right. } {{\alpha _{ui}}}}- {{\hat N}_{vi}}{v_i} - \\ &{{\hat N}_{ri}}{r_i} - {{\hat N}_{vvri}}{v_i}^2{r_i} - {{\hat N}_{vrri}}{v_i}{r_i}^2 - {{\hat N}_{vvi}}{v_i}\left| {{v_i}} \right|。\\[-1pt] \end{split} $ | (29) |
针对外部未知海洋干扰的影响,设计了一种非线性干扰观测器来估计和补偿由海洋环境干扰引起的干扰,扰动观测器构造如下:
| $ \left\{ \begin{aligned} &{{\hat d}_{1i}} = {z_{1i}} + {L_{1i}}({m_i} + {m_{xi}}){u_i} ,\\ &{{\dot z}_{1i}} = - {L_{1i}}{{\hat d}_{1i}} - {L_{1i}}[({m_i} + {m_{yi}}){v_i}{r_i} + {{\hat X}_{uui}}{u_i}^2 + \\ &\quad{{\hat X}_{vvi}}{v_i}^2 + {{\hat X}_{vri}}{v_i}{r_i} + {{\hat X}_{rri}}{r_i}^2 + {X_{Pi}}],\\ &{{\hat d}_{2i}} = {z_{2i}} + {L_{2i}}({I_{zzi}} + {J_{zzi}}){r_i} ,\\ &{{\dot z}_{2i}} = - {L_{1i}}{{\hat d}_{2i}} - {L_{2i}}\Big( {{\hat N}_{vi}}{v_i} + {{\hat N}_{ri}}{r_i} + {{\hat N}_{vvri}}{v_i}^2{r_i} + \\ &\quad{{\hat N}_{vrri}}{v_i}{r_i}^2 + {{\hat N}_{vvi}}{v_i}\left| {{v_i}} \right| + {N_{Ri}} \Big)。\end{aligned} \right. $ | (30) |
式中:
定义观测值与实际干扰的误差如下:
| $ \left\{ \begin{gathered} {e_{1i}} = {{\hat d}_{1i}} - {X_{di}} ,\\ {e_{2i}} = {{\hat d}_{2i}} - {N_{di}} 。\\ \end{gathered} \right. $ | (31) |
对式(31)中
| $ \begin{split} {{\dot e}_{1i}} =& {{\hat d}_{1i}} - {{\dot X}_{di}} = {{\dot z}_{1i}} + {L_{1i}}({m_i} + {m_{xi}}){{\dot u}_i} - {{\dot X}_{di}} =\\ & - {L_{1i}}{{\hat d}_{1i}} + {L_{1i}}{d_{1i}} - {{\dot X}_{di}} - {L_{1i}}{e_{1i}} - {{\dot X}_{di}}。\end{split} $ | (32) |
同理,
结合式(19),式(29)和式(30),最终的控制律可以设计为:
| $ {\left\{ \begin{aligned} &{X_{Pi}} = X_{Pi}^ * - {{\hat d}_{1i}}= - \left( {{m_i} + {m_{yi}}} \right){v_i}{r_i} + \\ & ({m_i} + {m_{xi}})\left[ {{{\dot A}_{ui}} - {\lambda _{1i}}{u_{ei}} - {{\hat \varepsilon }_{1i}}\tanh ({s_{1i}}) - {\sigma _{1i}}{s_{1i}}} \right] -\\ & {{\hat X}_{uui}}{u_i}^2 - {{\hat X}_{vvi}}{v_i}^2 - {{\hat X}_{vri}}{v_i}{r_i} - {{\hat X}_{rri}}{r_i}^2 - {{\hat d}_{1i}},\\ &{N_{Ri}} = N_{Ri}^ * - {{\hat d}_{2i}}= [ - {x_{2i}} + {{\dot B}_{Pi}} - {r_i}{A_{ui}} - {\lambda _{2i}}\left( {{x_{1i}} - {{\dot \alpha }_{vi}}} \right) - \\ &{\lambda _{3i}}\left( {{v_i} - {\alpha _{vi}}} \right) - {{\hat \varepsilon }_{2i}}\tanh \left( {{s_{2i}}} \right) - {\sigma _{2i}}{s_{2i}}]{{\left( {{I_{zzi}} + {J_{zzi}}} \right)} \mathord{\left/ {\vphantom {{\left( {{I_{zzi}} + {J_{zzi}}} \right)} {{\alpha _{ui}}}}} \right. } {{\alpha _{ui}}}}- \\ & {{\hat N}_{vi}}{v_i} - {{\hat N}_{ri}}{r_i} - {{\hat N}_{vvri}}{v_i}^2{r_i} - {{\hat N}_{vrri}}{v_i}{r_i}^2 - {{\hat N}_{vvi}}{v_i}\left| {{v_i}} \right| - {{\hat d}_{2i}} 。\end{aligned} \right.} $ | (33) |
本节将验证上述设计控制律的稳定性,在设计过程中由于一阶滤波器的引入,会出现替代值与实际值的误差,下面定义滤波器的误差项:
| $ \left\{ \begin{gathered} {e_{3i}} = {A_{ui}} - {\alpha _{ui}} ,\\ {e_{4i}} = {B_{Pi}} - {p_i} 。\\ \end{gathered} \right. $ | (34) |
对式(34)求导得:
| $ \left\{\begin{aligned} &{\dot{e}}_{3i}=-\displaystyle\frac{{e}_{3i}}{{T}_{1i}}+{\beta }_{1i}(·),\\ &{\dot{e}}_{4i}=-\frac{{e}_{4i}}{{T}_{2i}}+{\beta }_{2i}(·)。\end{aligned} \right. $ | (35) |
式中,
为证明控制律的稳定性,设计如下全局Lyapunov函数:
| $ \begin{split}{V_{1i}} =& \frac{1}{2}x_{ei}^2 + \frac{1}{2}y_{ei}^2 + \frac{1}{2}s_{1i}^2 + \frac{1}{2}s_{2i}^2 + \\ &\frac{1}{2}e_{1i}^2 + \frac{1}{2}e_{2i}^2 + \frac{1}{2}e_{3i}^2 + \frac{1}{2}e_{4i}^2。\end{split}$ | (36) |
对式(36)求导得:
| $ {\begin{split} &{{\dot V}_{1i}} = {x_{ei}}{{\dot x}_{ei}} + {y_{ei}}{{\dot y}_{ei}} + {s_{1i}}{{\dot s}_{1i}} + {s_{2i}}{{\dot s}_{2i}} + {e_{1i}}{{\dot e}_{1i}} + {e_{2i}}{{\dot e}_{2i}} + {e_{3i}}{{\dot e}_{3i}} +\\ & {e_{4i}}{{\dot e}_{4i}} = - ({{{k_{1i}}x_{ei}^2 + {k_{2i}}y_{ei}^2)} \mathord{\left/ {\vphantom {{{k_{1i}}x_{ei}^2 + {k_{2i}}y_{ei}^2)} {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }}} \right. } {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }} +{s_{1i}}[ - {{\hat \varepsilon }_{1i}}\tanh ({s_{1i}}) \\ & -{\sigma _{1i}}{s_{1i}}] + {e_{1i}}{{\dot e}_{1i}} + {e_{2i}}{{\dot e}_{2i}} +{s_{2i}}[ - {{\hat \varepsilon }_{2i}}\tanh ({s_{2i}}) - {\sigma _{2i}}{s_{2i}}] + \\ & {e_{3i}}( - {{{e_{3i}}} \mathord{\left/ {\vphantom {{{e_{3i}}} {{T_{1i}}}}} \right. } {{T_{1i}}}} + {\beta _{3i}}) + {e_{4i}}( - {{{e_{4i}}} \mathord{\left/ {\vphantom {{{e_{4i}}} {{T_{2i}}}}} \right. } {{T_{2i}}}} + {\beta _{4i}})\leqslant \\ &- ({{{k_{1i}}x_{ei}^2 + {k_{2i}}y_{ei}^2)}\mathord{\left/ {\vphantom {{{k_{1i}}x_{ei}^2 + {k_{2i}}y_{ei}^2)} {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }}} \right. } {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }} -{{\hat \varepsilon }_{1i}}\left| {{s_{1i}}} \right| -{\sigma _{1i}}s_{1i}^2 - \\ & {{\hat \varepsilon }_{2i}}\left| {{s_{2i}}} \right| - {\sigma _{2i}}s_{2i}^2- {L_{1i}}e_{1i}^2 - {{\dot d}_{1i}} - {L_{2i}}e_{2i}^2 - {{\dot d}_{2i}} - {{e_{3i}^2} \mathord{\left/ {\vphantom {{e_{3i}^2} {{T_{1i}}}}} \right. } {{T_{1i}}}} + \\ &{e_{3i}}{\beta _{3i}} - {{e_{4i}^2} \mathord{\left/ {\vphantom {{e_{4i}^2} {{T_{2i}}}}} \right. } {{T_{2i}}}} + {e_{4i}}{\beta _{4i}}\leqslant - ({{{k_{1i}}} \mathord{\left/ {\vphantom {{{k_{1i}}} {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }}} \right. } {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }})x_{ei}^2 - \\ &({{{k_{2i}}} \mathord{\left/ {\vphantom {{{k_{2i}}} {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }}} \right. } {\sqrt {x_{ei}^2 + y_{ei}^2 + {C_i}} }})y_{ei}^2 - {\sigma _{1i}}s_{1i}^2 - {\sigma _{2i}}s_{2i}^2 - {L_{1i}}e_{1i}^2- {L_{2i}}e_{2i}^2 - \\ &({1 \mathord{\left/ {\vphantom {1 {{T_{1i}}}}} \right. } {{T_{1i}}}} -{\alpha _{1i}})e_{3i}^2 -({1 \mathord{\left/ {\vphantom {1 {{T_{2i}}}}} \right. } {{T_{2i}}}} - {\alpha _{2i}})e_{4i}^2 - {{\dot d}_{1i}} - {{\dot d}_{2i}} + {{B_{3i}^2} \mathord{\left/ {\vphantom {{B_{3i}^2} {4{\alpha _{1i}}}}} \right. } {4{\alpha _{1i}}}} + \\ &{{B_{4i}^2} \mathord{\left/ {\vphantom {{B_{4i}^2} {4{\alpha _{2i}}}}} \right. } {4{\alpha _{2i}}}}\leqslant - {\mu _{1i}}{V_{1i}} + {N_{1i}} 。\\[-3pt] \end{split}} $ | (37) |
上式(37)中,
| $ \left\{\begin{gathered}\mu_{1i} = \min\left( \begin{gathered}2k_{1i}\mathord{\left/\vphantom{k_{1i}\sqrt{x_{ei}^2+y_{ei}^2+C_i}}\right.}\sqrt{x_{ei}^2+y_{ei}^2+C_i},2k_{2i}\mathord{\left/\vphantom{k_{2i}\sqrt{x_{ei}^2+y_{ei}^2+C_i}}\right.}\sqrt{x_{ei}^2+y_{ei}^2+C_i} \\ 2\sigma_{1i},2\sigma_{2i},2L_{1i},2L_{2i},2\mathord{\left/\vphantom{2T_{1i}}\right.}T_{1i} - 2\alpha_{1i},2\mathord{\left/\vphantom{2T_{2i}}\right.}T_{2i} - 2\alpha_{2i} \\ \end{gathered} \right),\\ N_{1i}=-\dot{d}_{1i}-\dot{d}_{2i}+B_{3i}^2\mathord{\left/\vphantom{B_{3i}^24\alpha_{1i}}\right.}4\alpha_{1i}+B_{4i}^2\mathord{\left/\vphantom{B_{4i}^24\alpha_{2i}}\right.}4\alpha_{2i}。\\ \end{gathered}\right. $ | (38) |
解式(37)可以得:
| $ 0 \leqslant {V_{1i}} \leqslant {N_{1i}}/{\mu _{1i}} + [{V_{1i}}(0) - {N_{1i}}/{\mu _{1i}}]{e^{ - {\mu _{1i}}t}} 。$ | (39) |
根据Lyapunov稳定性理论分析式(39)可知,系统
为验证所提出的欠驱动USV编队避障控制算法有效性及鲁棒性,针对直线轨迹、曲线轨迹与正弦轨迹3种期望轨迹开展对比仿真实验。在DWA算法改进对比中,将传统DWA算法记为DWA,本文改进的DWA算法记为IDWA。在轨迹跟踪效果对比中,将未采取横向速度微分跟踪器优化的滑模控制方法记为方法1,改进滑模控制记为方法2,其具体模型参数配置见表1。
|
|
表 1 USV模型参数 Tab.1 Parameters of USV Model |
鉴于USV执行机构的物理约束特性,为提高仿真置信度,在数值仿真中对推进控制力和力矩及其变化率施加幅值约束:
| $ \left\{ \begin{gathered} {N_d}\left( t \right) = 2\sin \left( {0.1t + {\text{π}} /4} \right) + 1,\\ {X_d}\left( t \right) = 10\sin 0.1t + 1,\\ {Y_d}\left( t \right) = 2\cos \left( {0.1 + {\text{π}} /3} \right) 。\\ \end{gathered} \right. $ |
1)仿真实验1:直线工况
仿真实验中,直线目标轨迹为
| $ \begin{gathered} \left[ {{x_1},{y_1},{\psi _1},{u_1},{v_1},{r_1}} \right] = \left[ { - 5, - 2, - \pi /9,0.01,0,0} \right] ,\\ \left[ {{x_2},{y_2},{\psi _2},{u_2},{v_2},{r_2}} \right] = \left[ {13, - 26,\pi /7,0.01,0,0} \right] ,\\ \left[ {{x_3},{y_3},{\psi _3},{u_3},{v_3},{r_3}} \right] = \left[ {24,47,\pi /9,0.01,0,0} \right]。\\ \end{gathered} $ |
|
|
表 2 控制器参数 Tab.2 Parameters of controller |
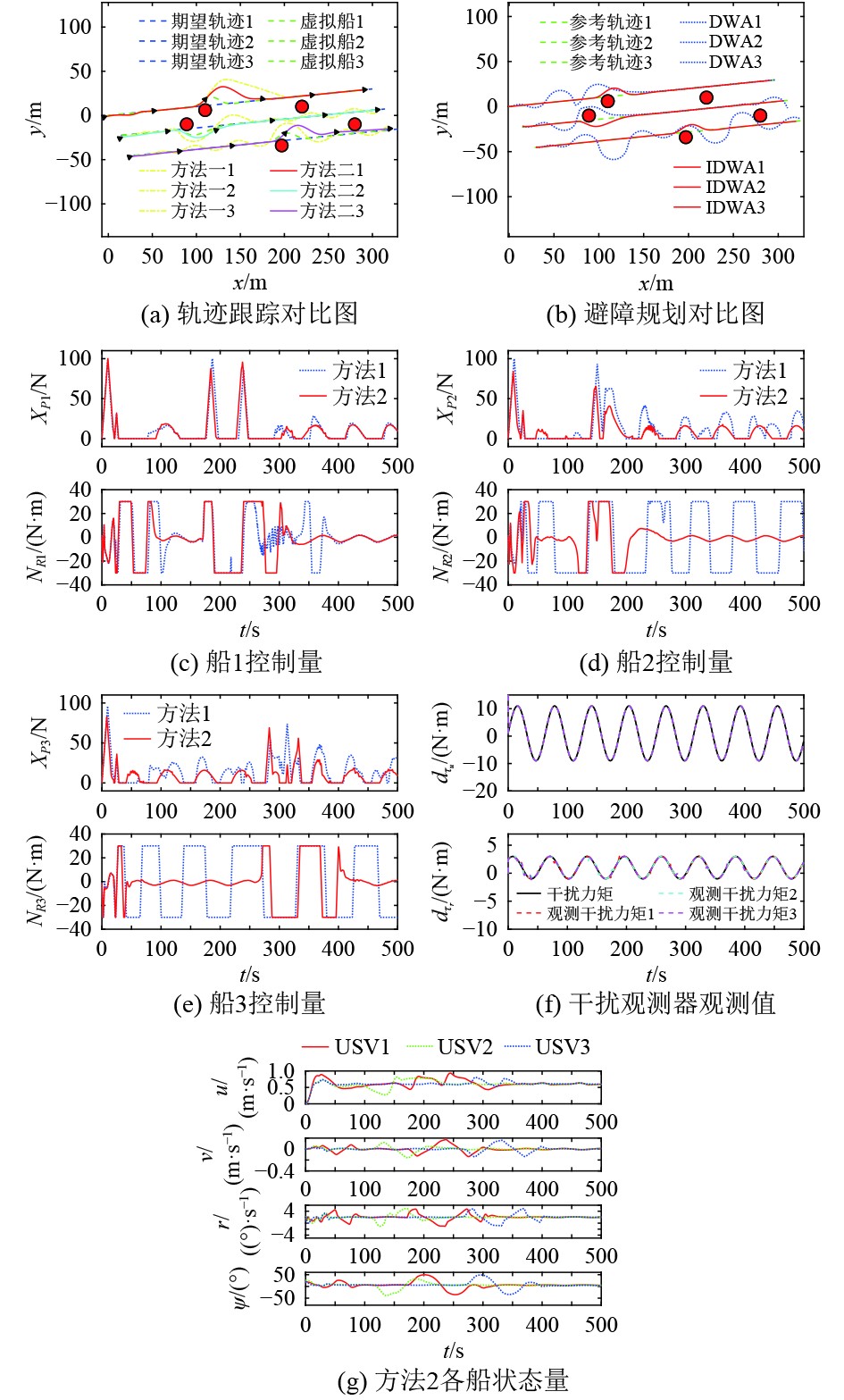
|
图 4 直线工况仿真结果图 Fig. 4 Simulation results under linear trajectory condition |
2)仿真实验2所示:圆形工况
仿真实验中,直线目标轨迹为
| $ \begin{gathered} \left[ {{x_1},{y_1},{\psi _1},{u_1},{v_1},{r_1}} \right] = \left[ { - 2, - 55,0,0.01,0,0} \right] ,\\ \left[ {{x_2},{y_2},{\psi _2},{u_2},{v_2},{r_2}} \right] = \left[ { - 1, - 76,0,0.01,0,0} \right],\\ \left[ {{x_3},{y_3},{\psi _3},{u_3},{v_3},{r_3}} \right] = \left[ { - 1, - 97,0,0.01,0,0} \right]。\\ \end{gathered} $ |
|
|
表 3 控制器参数 Tab.3 Parameters of controller |
|
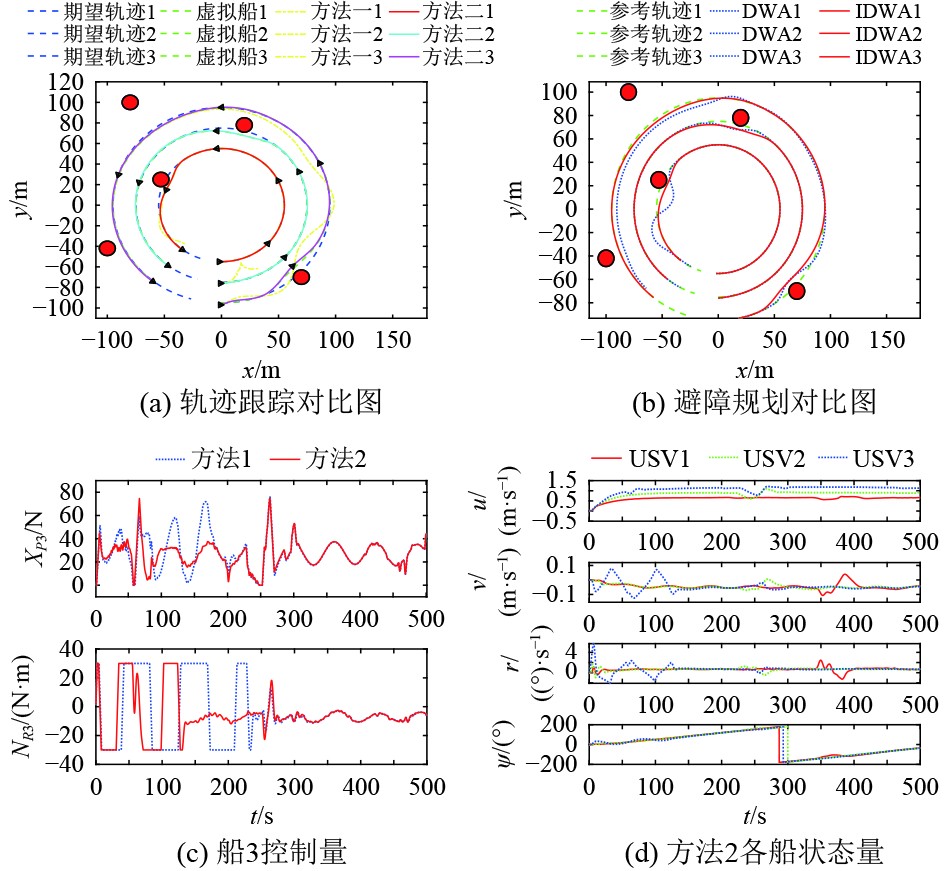
图 5 圆形工况仿真结果图 Fig. 5 Simulation results under circular trajectory condition |
3)仿真实验3:正弦工况
仿真实验中,直线目标轨迹为
| $ \begin{gathered} \left[ {{x_1},{y_1},{\psi _1},{u_1},{v_1},{r_1}} \right] = \left[ { - 18,10,\pi /6,0.01,0,0} \right],\\ \left[ {{x_2},{y_2},{\psi _2},{u_2},{v_2},{r_2}} \right] = \left[ { - 5, - 2,\pi /6,0.01,0,0} \right],\\ \left[ {{x_3},{y_3},{\psi _3},{u_3},{v_3},{r_3}} \right] = \left[ {10, - 18,\pi /6,0.01,0,0} \right]。\\ \end{gathered} $ |
|
|
表 4 控制器参数 Tab.4 Parameters of controller |
|
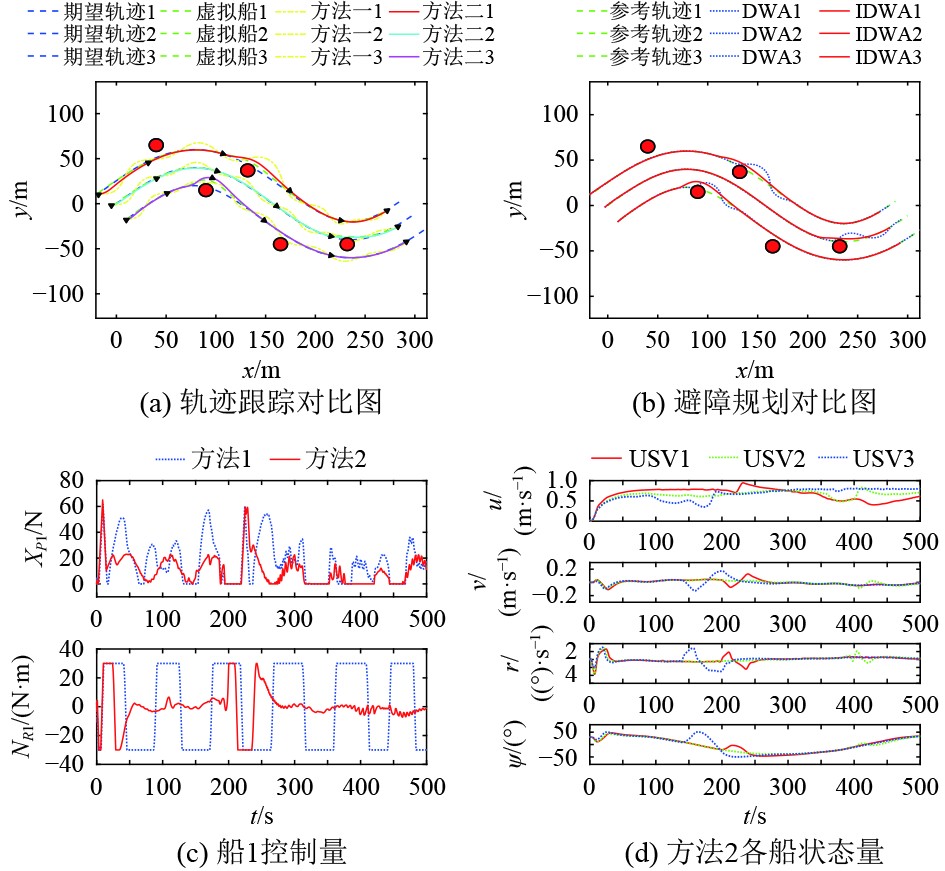
图 6 正弦工况仿真结果图 Fig. 6 Simulation results under sinusoidal trajectory condition |
分析以上3组仿真实验数据,在DWA算法避障规划方面,如图4(b)、图5(b)和图6(b),分别展示了不同工况下改进DWA算法与未改进DWA算法的规划对比结果,可以清晰看出,改进后的DWA算法轨迹波动小,更加符合USV避障期望与航行能力。在轨迹跟踪效果方面,图4(a)、图5(a)和图6(a)分别为2种控制方法的轨迹跟踪效果,显而易见,改进滑模控制(方法2)的各USV轨迹相较于未改进的滑模控制(方法1图中点划线)较快的跟踪上期望轨迹且波动幅度较小。
图4(c)~图4(e)、图5(c),图6(c)分别给出了直线工况下三船与另外工况下部分船的控制量变化图,从图中可以看出,改进后的滑模控制(方法2)在控制力上明显波动程度小于未改进的滑模控制(方法1);在控制力矩上,改进后的方法2基本处于平稳状态,仅在避障需求时出现较大波动,而未改进的方法1则全程处于较大幅度的波动状态中。图4(g)、图5(d)与图6(d)给出了改进滑模控制的各船状态量,均处于较为平稳的状态。图4(f)展示了所设计的干扰观测器的观测值与实际值的变化,可以看出观测取得较为满意的结果,基本能够补偿外界干扰带来的影响。
6 结 语针对USV编队的避障和轨迹跟踪问题,本文提出一种基于改进DWA算法的滑模控制避障算法。对DWA避障算法进行了评价函数的改进,使用规划轨迹更加符合USV编队的特点,轨迹更加平滑,并在避障结束后较快的回归到编队轨迹当中。针对滑模控制中横向速度微分引起的控制量抖振问题,利用微分跟踪器有效的抑制了控制力矩的高频抖振,提高了控制量输出的稳定性,对整体的编队轨迹跟踪的效果起到了良好的优化作用。3组不同工况的仿真实验,也进一步的验证了所提出算法的有效性和优越性。
| [1] |
DU Z, LI W, SHI G. Multi-USV collaborative obstacle avoidance based on improved velocity obstacle method[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2024, 10(1): 04023049. DOI:10.1061/AJRUA6.RUENG-1174 |
| [2] |
DONG Z, ZHOU W, TAN F, et al. Simultaneous modeling and adaptive fuzzy sliding mode control scheme for underactuated USV formation based on real-time sailing state data[J]. Ocean Engineering, 2024, 314: 119743. DOI:10.1016/j.oceaneng.2024.119743 |
| [3] |
WANG J, WANG R, LU D, et al. USV dynamic accurate obstacle avoidance based on improved velocity obstacle method[J]. Electronics, 2022, 11(17): 2720.
|
| [4] |
DONG Z, TAN F, YU M, et al. A Bio-Inspired sliding mode method for autonomous cooperative formation control of underactuated usvs with ocean environment disturbances[J]. Journal of Marine Science and Engineering, 2024, 12(9): 1607. DOI:10.3390/jmse12091607 |
| [5] |
SONG A L, SU B Y, DONG C Z, et al. A two-level dynamic obstacle avoidance algorithm for unmanned surface vehicles[J]. Ocean Engineering, 2018, 170: 351-360. DOI:10.1016/j.oceaneng.2018.10.008 |
| [6] |
LIU Y, ZHANG J, ZHANG Y, et al. Virtual Streamline Traction: Formation Cooperative Obstacle Avoidance Based on Dynamical Systems[J]. Applied Sciences, 2024, 14(14): 6087. DOI:10.3390/app14146087 |
| [7] |
TANG X, YU J, LI X, et al. Distributed formation control with obstacle avoidance for multiple underactuated unmanned surface vehicles[J]. Journal of the Franklin Institute, 2024, 361(12): 107008. DOI:10.1016/j.jfranklin.2024.107008 |
| [8] |
WAN L, LI J, ZHOU M. A hybrid path planning strategy unified with COLREGS for the unmanned surface vehicle[J]. Ships and Offshore Structures, 2025: 1-15.
|
| [9] |
CHEN H, LIN Z, CHEN Z, et al. Adaptive DWA algorithm with decision tree classifier for dynamic planning in USV navigation[J]. Ocean Engineering, 2025, 321: 120328. DOI:10.1016/j.oceaneng.2025.120328 |
| [10] |
ZHOU Y, LI W, CHENG K, et al. Enhanced USV path planning through integrated Bi-RRT and DWA algorithms considering environmental factors[J]. Journal of Marine Engineering & Technology, 2024: 1-17.
|
| [11] |
HAN S, WANG L, WANG Y, et al. A dynamically hybrid path planning for unmanned surface vehicles based on non-uniform Theta* and improved dynamic windows approach[J]. Ocean Engineering, 2022, 257: 111655. DOI:10.1016/j.oceaneng.2022.111655 |
| [12] |
ZHOU Y, WU N, YUAN H, et al. PDE formation and iterative docking control of USVs for the straight-line-shaped mission[J]. Journal of Marine Science and Engineering, 2022, 10(4): 478. DOI:10.3390/jmse10040478 |
| [13] |
WEI G A, ZHANG J Q. Research on Unmanned Surface Vessel Aggregation Formation Based on Improved A* and Dynamic Window Approach Fusion Algorithm[J]. Applied Sciences, 2023, 13(15): 8625. DOI:10.3390/app13158625 |
| [14] |
LI J, LU H, ZHANG H, et al. Dynamic target hunting under autonomous underwater vehicle (AUV) motion planning based on improved dynamic window approach (DWA)[J]. Journal of Marine Science and Engineering, 2025, 13(2): 221. DOI:10.3390/jmse13020221 |
| [15] |
WANG X, CHENG M, ZHANG S, et al. Multi-uav cooperative obstacle avoidance of 3d vector field histogram plus and dynamic window approach[J]. Drones, 2023, 7(8): 504. DOI:10.3390/drones7080504 |
| [16] |
TAN Z, WEI N, LIU Z. Local path planning for unmanned surface vehicle based on the improved DWA algorithm[C]//2022 41st Chinese Control Conference (CCC). IEEE, 2022.
|
| [17] |
WANG Z, LIANG Y, GONG C, et al. Improved dynamic window approach for Unmanned Surface Vehicles’ local path planning considering the impact of environmental factors[J]. Sensors, 2022, 22(14): 5181. DOI:10.3390/s22145181 |
| [18] |
JIANG X, XIA G. Sliding mode formation control of leaderless unmanned surface vehicles with environmental disturbances[J]. Ocean Engineering, 2022, 244: 110301. DOI:10.1016/j.oceaneng.2021.110301 |
| [19] |
DUAN H, YUAN Y, ZENG Z. Distributed robust learning control for multiple unmanned surface vessels with fixed-time prescribed performance[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2023.
|
| [20] |
RABIEE H, ATAEI M, EKRAMIAN M. Continuous nonsingular terminal sliding mode control based on adaptive sliding mode disturbance observer for uncertain nonlinear systems[J]. Automatica, 2019, 109: 108515. DOI:10.1016/j.automatica.2019.108515 |
| [21] |
LIU Z W, HOU H, WANG Y W. Formation-containment control of multiple underactuated surface vessels with sampling communication via hierarchical sliding mode approach[J]. ISA Transactions, 2022, 124: 458-467. DOI:10.1016/j.isatra.2019.12.003 |
| [22] |
ZHANG H, ZHANG X, XU H, et al. Heterogeneous cooperative trajectory tracking control between surface and underwater unmanned vehicles[J]. Ocean Engineering, 2024, 301: 117137. DOI:10.1016/j.oceaneng.2024.117137 |
| [23] |
GAO H, ZOU Z J, XIA L, et al. Application of the NIPC-based uncertainty quantification in prediction of ship maneuverability[J]. Journal of Marine Science and Technology, 2021, 26: 555-572. DOI:10.1007/s00773-020-00754-1 |
| [24] |
DONG Z, TAN F, ZHOU W, et al. Distributed formation control of underactuated UMVs based on nonlinear model prediction algorithm with obstacle avoidance strategy incorporating relative velocity constraints[J]. Ocean Engineering, 2024, 312: 119272. DOI:10.1016/j.oceaneng.2024.119272 |
 2025, Vol. 47
2025, Vol. 47
