无人艇(Unmanned Surface Vehicle,USV)具有自主性、智能化高等优点,可用于高风险或者适宜无人操作的任务,在民用和军事上都有广阔的发展前景[1]。
无人艇的路径规划一直备受关注。研究人员根据对环境信息的了解程度,将路径规划大体上分为两类:一种是基于已经知道环境信息的无人艇全局的路径规划;另一种是针对未知环境信息的无人艇局部的路径规划[2]。全局路径规划常使用的一些算法有A*算法[3]、Dijkstra算法[4]和蚁群算法[5]等,而一些常用的局部路径规划算法包括粒子群算法[6]、人工势场法[7]和动态窗口法[8]等。
陈侠等[9]将人工势场法与RRT算法相结合,通过附近的环境信息指引随机树向着终点发展,但因其所选用的地图过于简单,故缺乏代表性。许万等[10]针对陷阱问题对环境进行采样,填补了凹形区域防止机器人进入陷阱,提高了路径的平滑度,这种方法对传感器要求也更高,同时在补齐的过程中会产生较大的实时计算量,无法适用于在多特殊障碍物组合的情景。李龙等[11]提出了一种改进的绕行方法,采用适用于机器人的基于势函数和关节空间的人工势场法。这种方法结合了基于接近感知的机器人避障路径规划方法,以提高路径规划的效率和性能。秦克斌等[12]针对无人机陷入局部极小值的问题提出了一种解决方案,即建立自膨胀函数,通过改变自膨胀系数,增加距离最近的障碍物对无人机的排斥力,从而改变无人机的受力情况。然而,在障碍物密度极高的小地图情况下,自膨胀系数的增大可能会导致无人机与障碍物发生碰撞,增加了风险。XIE等[13]提出了一种分布式运动规划算法,利用人工势场法确保自动驾驶汽车在动态环境中安全超车。PAN等[14]提出了一种有效的基于改进人工势函数的路径规划方法,通过引入旋转势场,无人机可以有效地逃离常见的局部最小值和振荡。
本文对于局部最优解问题提出了障碍物移动法,当无人艇陷入局部最优解时,对于简单障碍物,将移动障碍物来改变斥力的方向,打破当前状态来解决这一问题,进而继续向目标点前进;在U型障碍物情况下,通过在加入自膨胀系数的基础之上引入模拟退火算法,使无人艇摆脱在U型障碍物情况下的局部最优状态。为了解决人工势场法中的目标不可达问题,提出了对引力势场函数进行改进的方法,当障碍物与目标点距离较近而障碍物产生的斥力过大时,通过调节引力的大小来解决这一问题。
1 人工势场法人工势场法[15 − 17]的基本思想是在障碍物周围创建斥力势场,使得无人艇受到斥力而远离障碍物;同时在目标点建立引力势场,使得无人艇受到引力吸引朝向目标移动。
1.1 引力势场引力势场是全局性的,其源头是目标点,其势能的强度随着机器人与目标点之间的距离变化而变化。常用的势场函数为:
| $ {U_{att}}\left( X \right) = \frac{1}{2}{\lambda _1}{d^2}\left( X \right)。$ | (1) |
式中:
引力势场函数的负梯度为引力:
| $ {{\boldsymbol{F}}}_{att}\left(X\right)=-\nabla {U}_{att}\left(X\right) =- {\lambda }_{1}d\left(X\right) 。$ | (2) |
斥力势场是一种局部性的势场,由障碍物生成,也只在无人艇靠近障碍物一定的范围内起作用,这个范围称为斥力影响范围。常用的斥力势场函数为:
| $ {U_{rep}}(X) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{\lambda _2}{{\left( {\dfrac{1}{{D(X)}} - \dfrac{1}{d}} \right)}^2},D(X) \leqslant d} ,\\ {0,D(X) \geqslant d}。\end{array}} \right. $ | (3) |
式中:
斥力势场函数的负梯度为斥力:
| $ {F_{rep}}\left( X \right) = - \nabla {U_{rep}}\left( X \right)= $ |
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _2}\left( {\dfrac{1}{{D(X)}} - \dfrac{1}{d}} \right)\dfrac{1}{{{D^2}(X)}}\dfrac{{\partial D(X)}}{{\partial X}},D(X) \leqslant d},\\ {0,D(X) \geqslant d} 。\end{array}} \right. $ | (4) |
无人艇所受合力势场即引力势场和斥力势场的矢量叠加,因此可以表示为:
| $ {\boldsymbol{U}}\left( X \right) = {{\boldsymbol{U}}_{att}}\left( X \right) + {{\boldsymbol{U}}_{rep}}\left( X \right)。$ | (5) |
若无人艇受到
| $ {\boldsymbol{F}}\left( X \right) = {{\boldsymbol{F}}_{att}}\left( X \right) + \mathop \sum \limits_{i = 1}^n {{\boldsymbol{F}}_{rep}}\left( X \right)。$ | (6) |
局部最优解问题是指当无人艇靠近障碍物时,障碍物的排斥力与目标的吸引力相互抵消,导致无人艇无法继续向目标移动。无人艇可能会错误认为已到达目标点而停止移动,实际上并未到达目标点,只是受到了错误信息的误导。这种情况会导致在传统人工势场法中无人艇在行进过程中自动停止的问题,如图1所示。
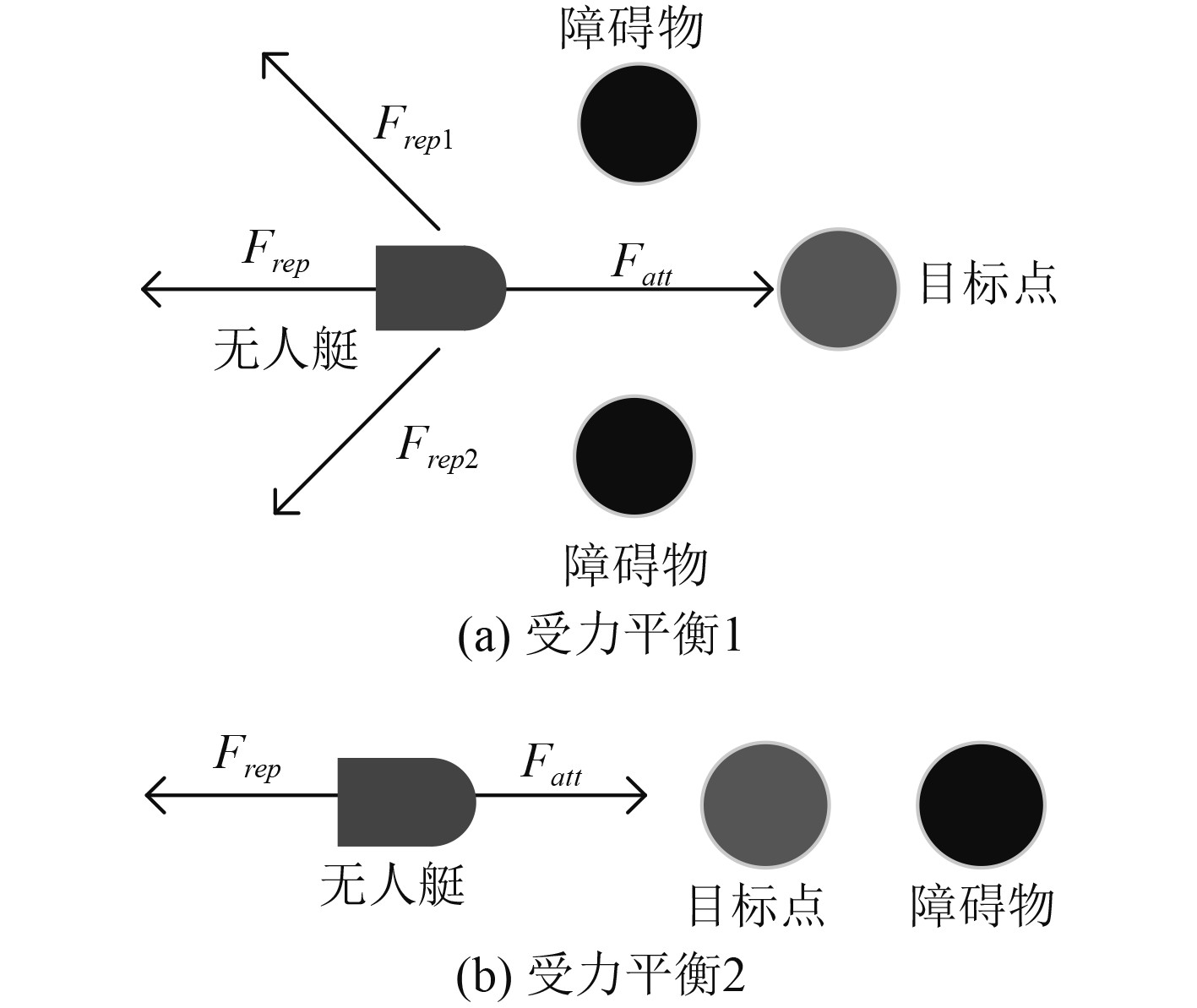
|
图 1 局部最优解问题图 Fig. 1 Local optimal solution problem diagram |
目标不可达问题是指随着无人艇逐渐靠近目标点,其受到的吸引力不断变小,同时如果目标点周围存在障碍物,随着其接近目标点,与障碍物的直线距离不断变小,导致排斥力增大,使得其不能实际到达目标点,如图2所示。
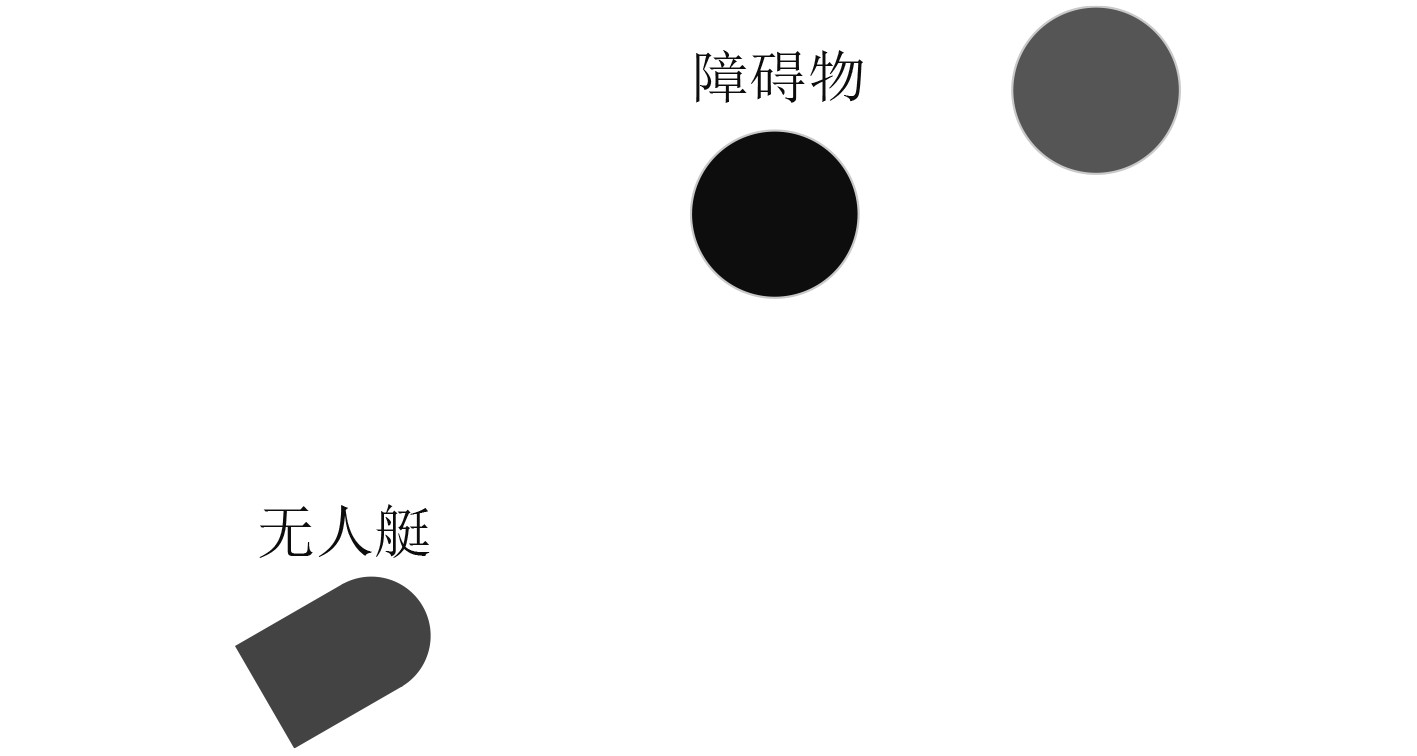
|
图 2 目标不可达问题图 Fig. 2 Target inaccessible problem diagram |
在无人艇运行过程中首先会对无人艇进行检测是否落入局部最优解陷阱,检测步骤如下:首先设定一个局部最优解的判定值
虽然实际运行中很少会出现无人艇所受到引力和斥力刚好方向相反和大小相同的情况,但仍然存在这种情况。当出现这种情况时,提出将障碍物朝着障碍物多的方向移动一段距离,通过如此移动,可以改变斥力的大小和方向,使无人艇逃逸出局部最优状态,并且有利于无人艇在较为安全的环境中进行路径规划,如图3所示。其中,
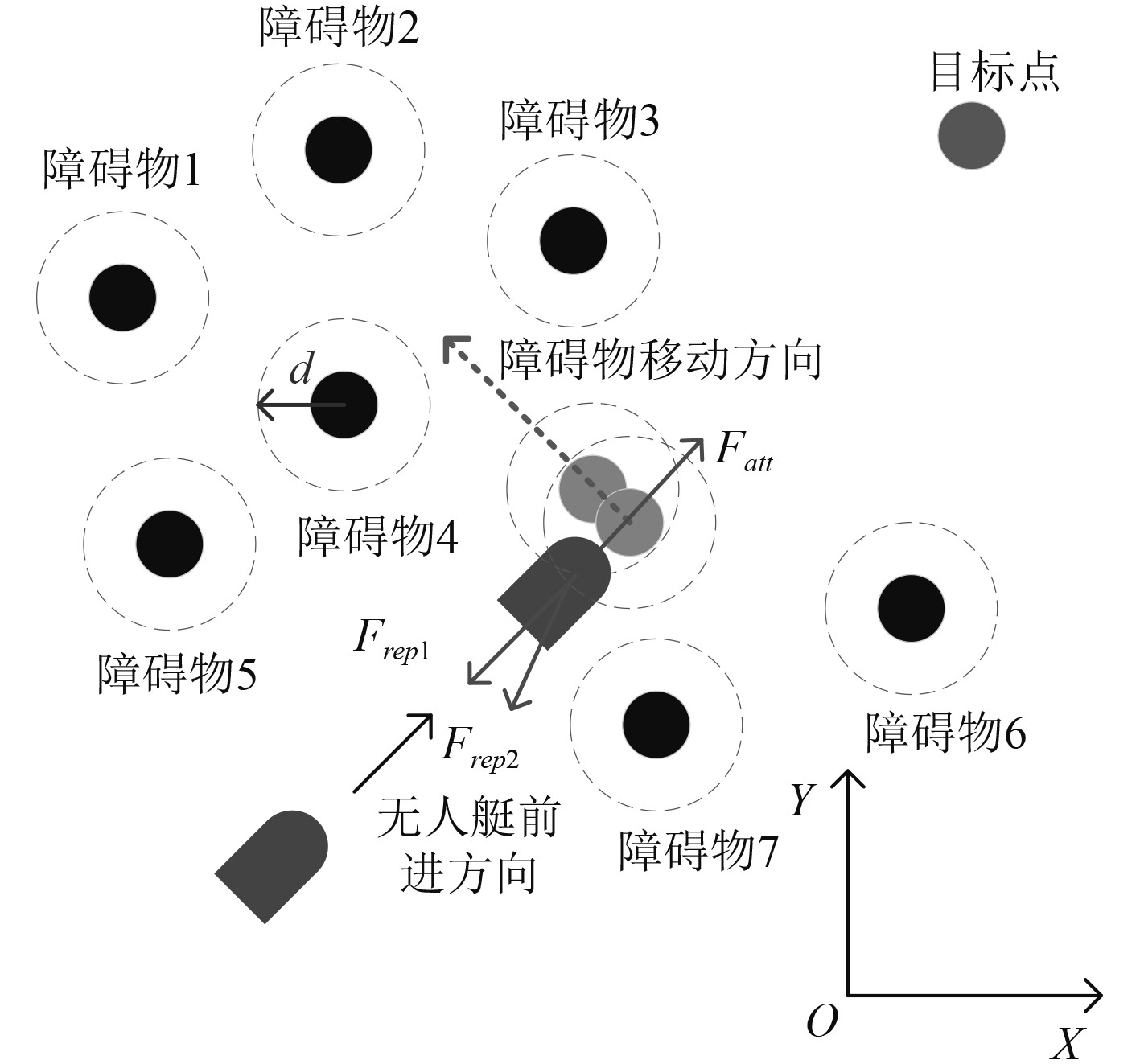
|
图 3 局部最优-受力平衡改进方法图 Fig. 3 Local optimal-force balance improvement method diagram |
障碍物移动的步骤为:
步骤1 计算障碍物的位置差,得到一个表示障碍物数量较多方向的向量。
步骤2 对通过计算得到的方向向量进行归一化处理,即将其长度调整为1。这是为了确保移动的步长一致,不受方向向量长度的影响。
步骤3 设置移动步长,步长可以根据实际需要进行调整。
另一种局部最优解问题则是无人艇在一个小区域不断震荡,当出现这种情况时,提出将障碍物朝着无人艇方向运动。法向量是从无人艇指向障碍物的单位向量,是以障碍物位置与无人艇位置在
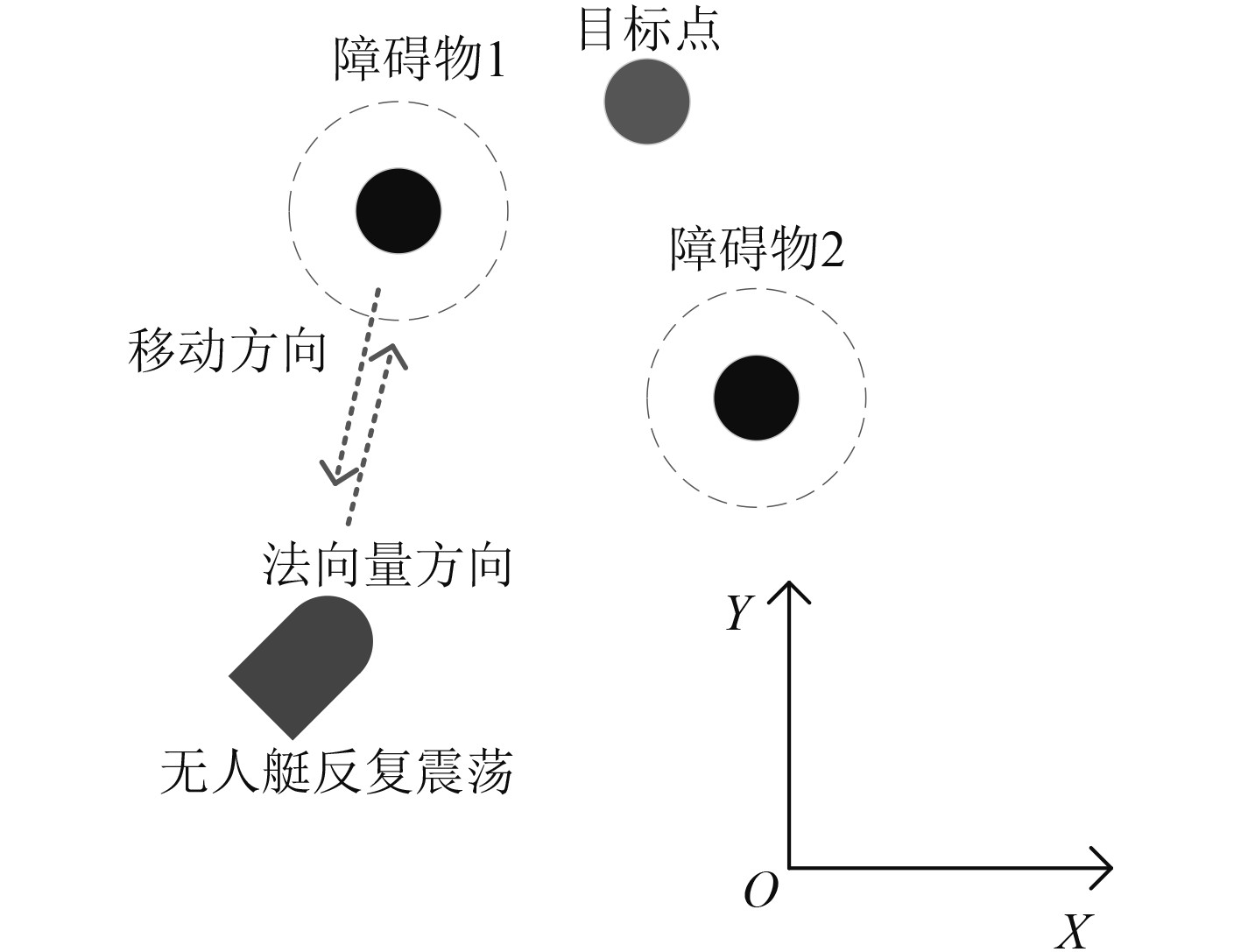
|
图 4 局部最优-震荡改进方法图 Fig. 4 Local optimity-oscillation improvement method diagram |
| $ normal\_vector = \left( {\frac{{x - {x_{obs}}}}{{D\left( X \right)}},\frac{{y - {y_{obs}}}}{{D\left( X \right)}}} \right) 。$ | (7) |
式中:
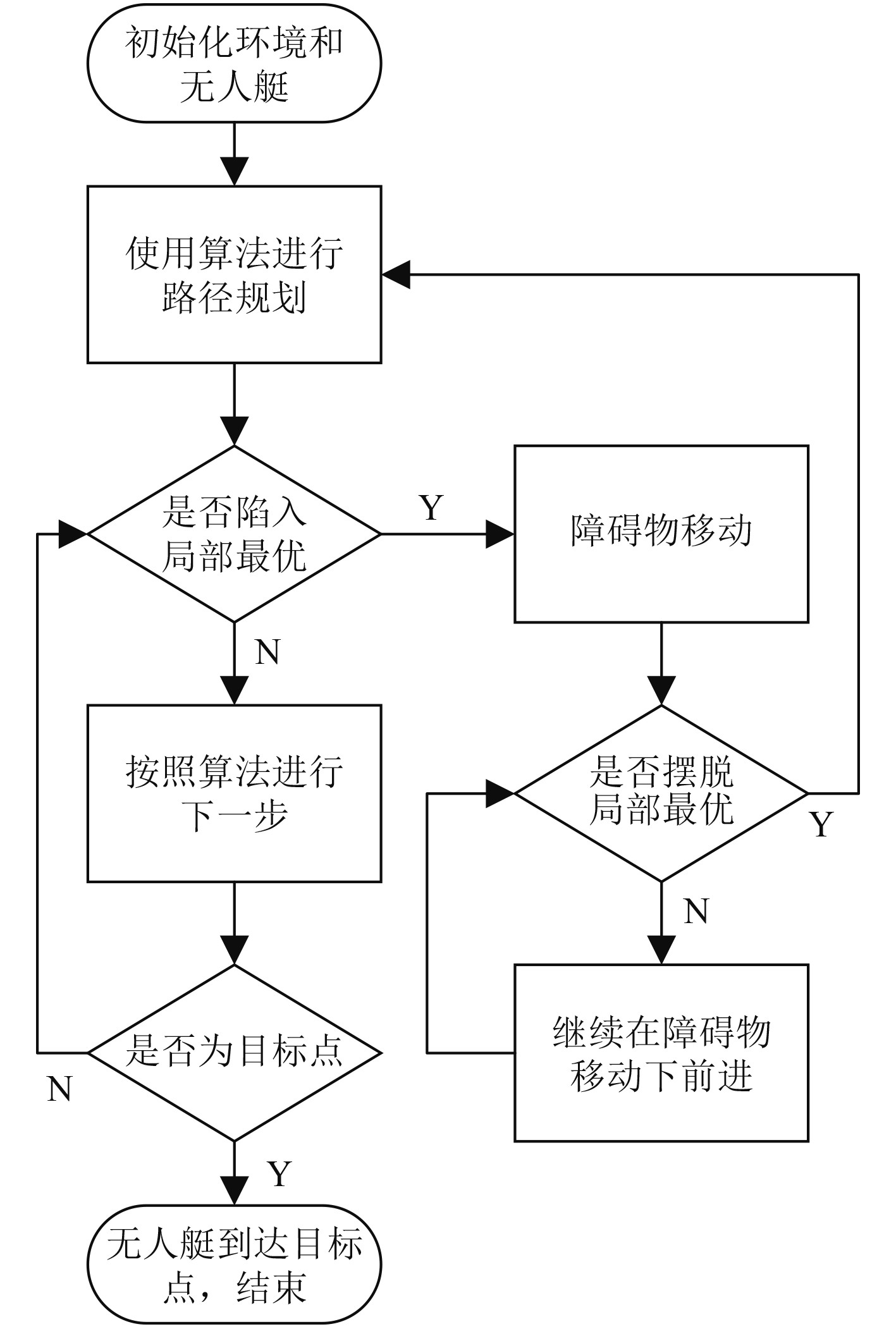
在无人艇和环境信息初始化后,无人艇会使用算法进行路径规划,在前进过程中,记录每次迭代的位置信息,并定期检测是否陷入局部最优状态。如果成功摆脱局部最优状态,将移动的障碍物还原,处理流程图如图5所示。
|
图 5 局部最优问题处理流程图 Fig. 5 Local optimal problem processing flowchart |
在无人艇的路径规划中,当无人艇遇到包含复杂形状障碍物的环境情况如U型障碍时,此时无人艇若陷入局部最优则将被困在该U型区域内,针对这种情况,采用文献[12]所提方法。但加入自膨胀系数的人工势场法在障碍物密度极大的情况下(如U型障碍物),可能存在因自膨胀系数增大而导致与障碍物发生碰撞的可能。为了避免出现这种情况,引入模拟退火算法。
| $ {U_{{{req}}}}(X) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}k{{\left( {\dfrac{1}{{D(X)}} - \dfrac{1}{d}} \right)}^2}\omega ,0 \leqslant D(X) \leqslant d} ,\\ {0,D(X) > d} 。\end{array}} \right. $ | (8) |
| $ \omega = \sigma \left( {\frac{1}{{D\left( X \right)}}\left( {\mathop \sum \limits_{n = 0}^N F = 1} \right)} \right) 。$ | (9) |
式中:
| $ \sigma=\vec{a}=\left(x_{\text{goal}}+x\mathit{_{{o}}},y_{\text{goal}}+y\mathit{_{{o}}}\right),$ | (10) |
| $ \left( {{x_{{o}}},{y_{{o}}}} \right) = {\mathrm{min}}\left( {{x_{{o}}},{y_{{o}}}} \right) 。$ | (11) |
式中:(
模拟退火算法通过模拟固体退火过程中的温度变化,随机探索解空间,并以一定的几率接纳比当下解相对差的解。本文采用模拟退火算法来改进无人艇的路径规划。为了避免因自膨胀系数的增大而可能导致发生碰撞的情况,在其当下位置周围随机挑选一个点,并得出此刻位置和周围随机点的势场大小,如果该点较小,意味着更有可能是无人艇的下一个航向点,因为相对于当前位置更安全。但是,如果该点的势能较大,则以一定的几率
| $ \left\{\begin{array}{*{20}{l}}P=\mathrm{exp}\left(-\Delta/T\right),\\ \Delta=U\left(x_1\right)-U\left(x\right),\\ T\left(t\right)=\alpha T\left(t-1\right)。\end{array}\right. $ | (12) |
式中:
为了解决这个问题,提出了改进引力势场函数的方法。通过引进一临界值
| $ {U_{att}}\left( X \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{\lambda _1}{d^2}\left( X \right), d\left( X \right) \geqslant K},\\ {\dfrac{1}{2}{\lambda _1}{d^2}\left( X \right) + \dfrac{A}{{d\left( X \right)}},d\left( X \right) < K} 。\end{array}} \right. $ | (13) |
式中:
本文选择使用Matlab平台进行仿真和验证,仿真设置为在一个10 m×10 m的开放空间中,有若干个圆形障碍物,无人艇的起点为矩形(0 m,0 m),目标点位置为三角形(10 m,10 m),障碍物用填充圆圈表示,势场函数参数设置为
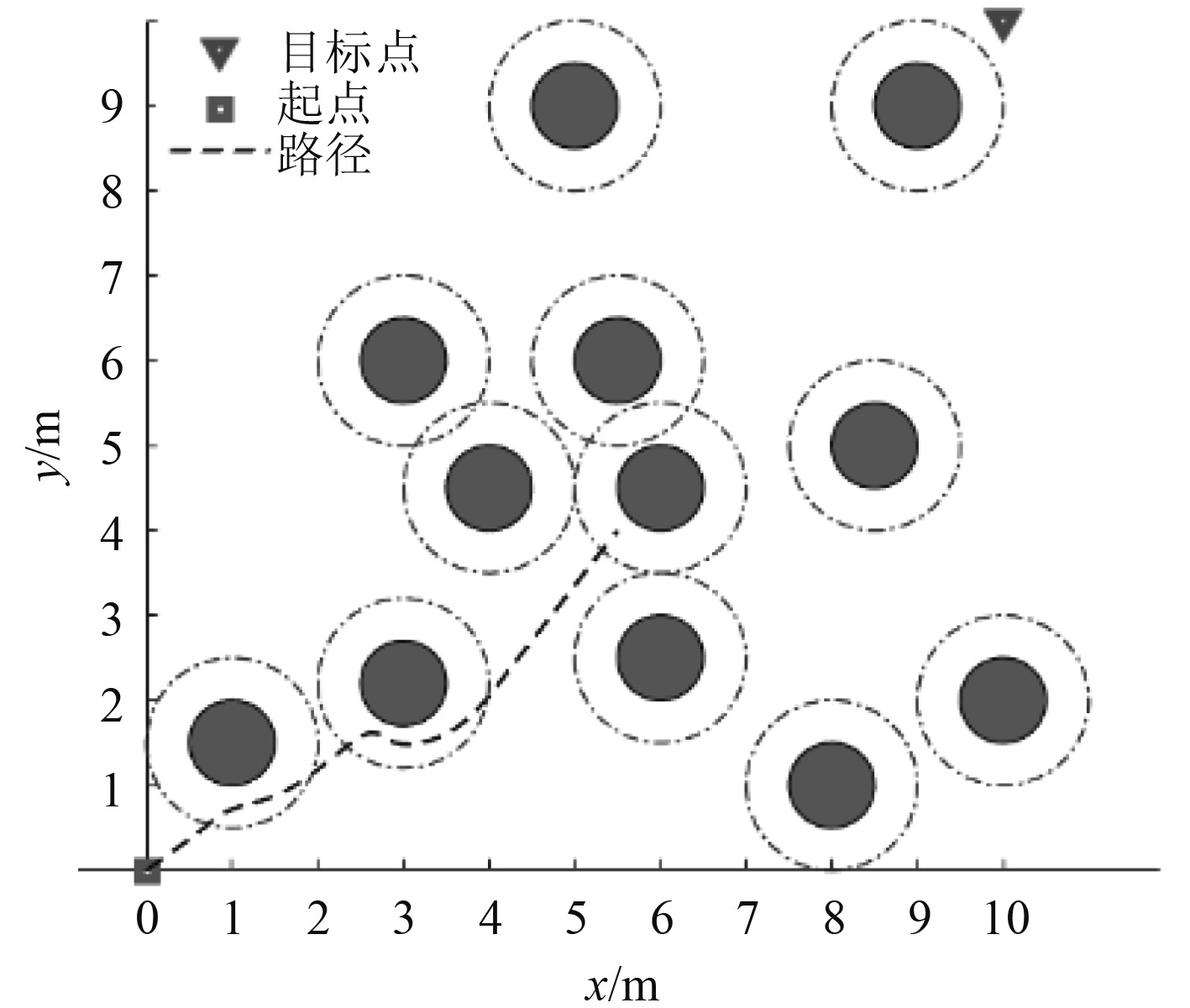
|
图 6 陷入局部最优状态 Fig. 6 Fall into a local optimal state |
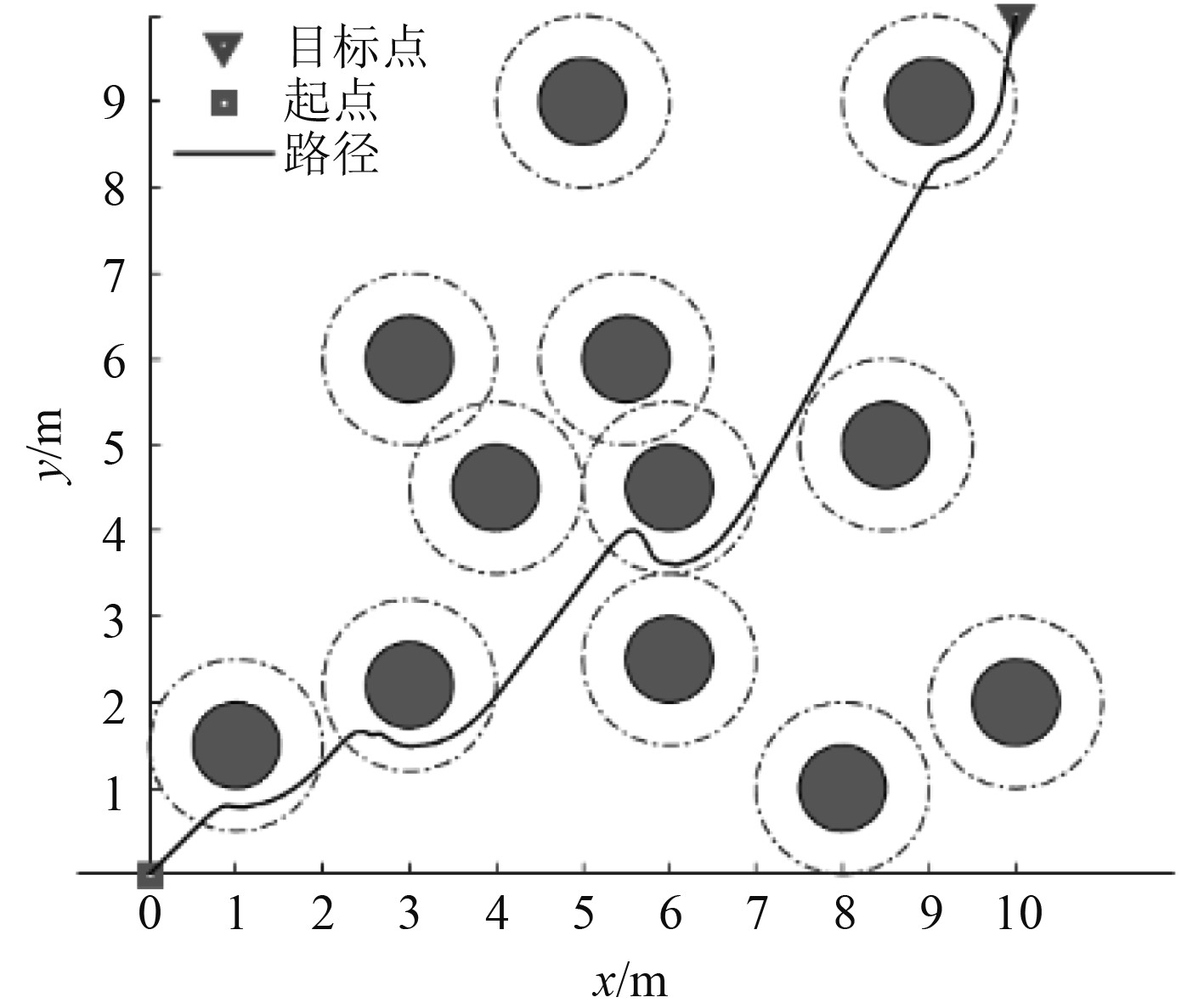
|
图 7 改进算法摆脱局部最优状态 Fig. 7 The improved algorithm gets rid of the local optimal state |
|
|
表 1 路径长度和时间 Tab.1 Path length and time |
针对于无人艇遇到包含复杂形状障碍物的环境情况如U型障碍物时,通过在自膨胀系数的基础上改进,引入模拟退火算法,模拟退火算法中控制参数初值To =10,
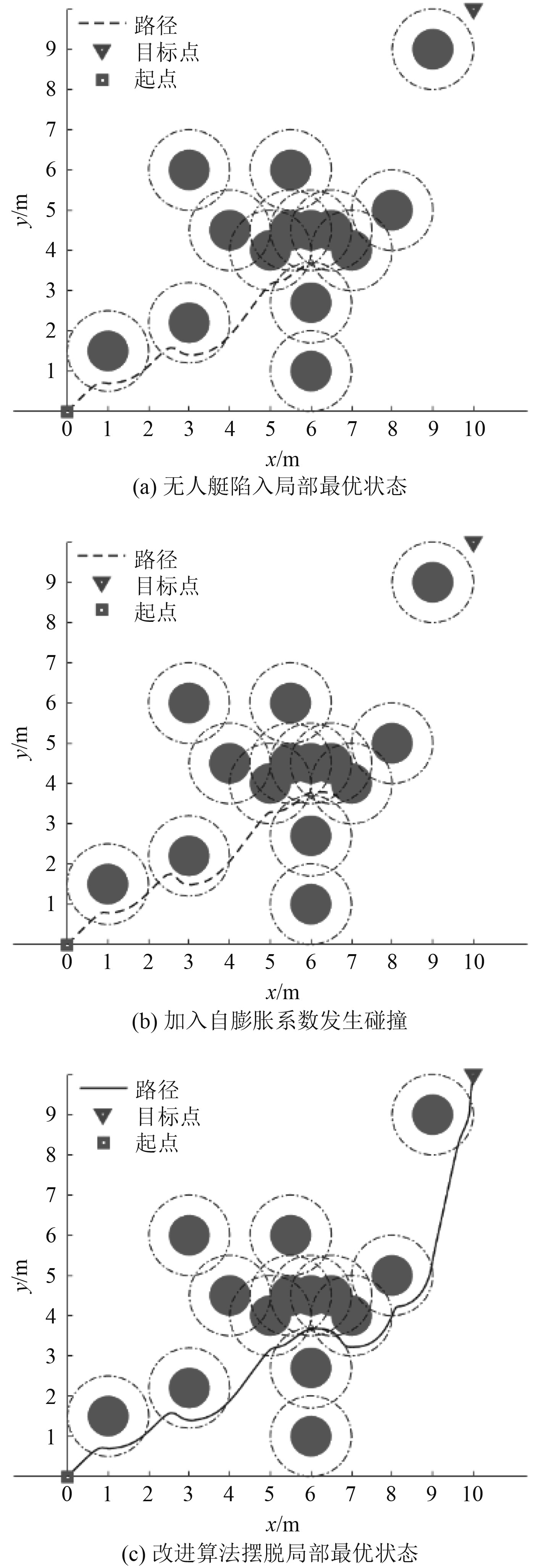
|
图 8 U型障碍物-改进算法摆脱局部最优状态 Fig. 8 U-shaped obstacle - improved algorithm to get rid of local optimal state |
|
|
表 2 路径长度和时间 Tab.2 Path length and time |
对于人工势场法中的目标不可达问题,如图9所示。提出了对引力势场函数进行改进的方法,通过引入一临界值
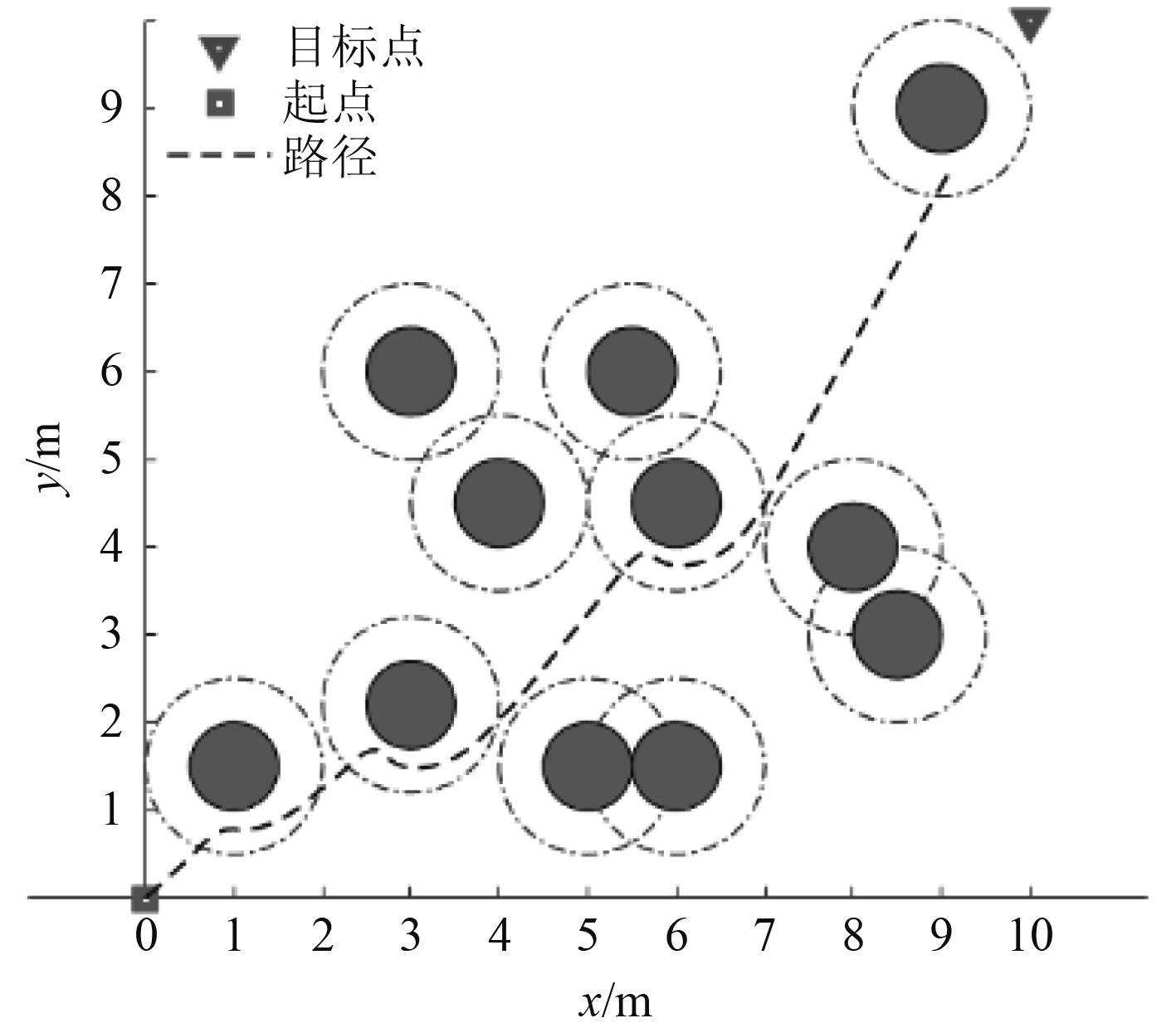
|
图 9 陷入目标不可达状态 Fig. 9 Get stuck in an unreachable state |
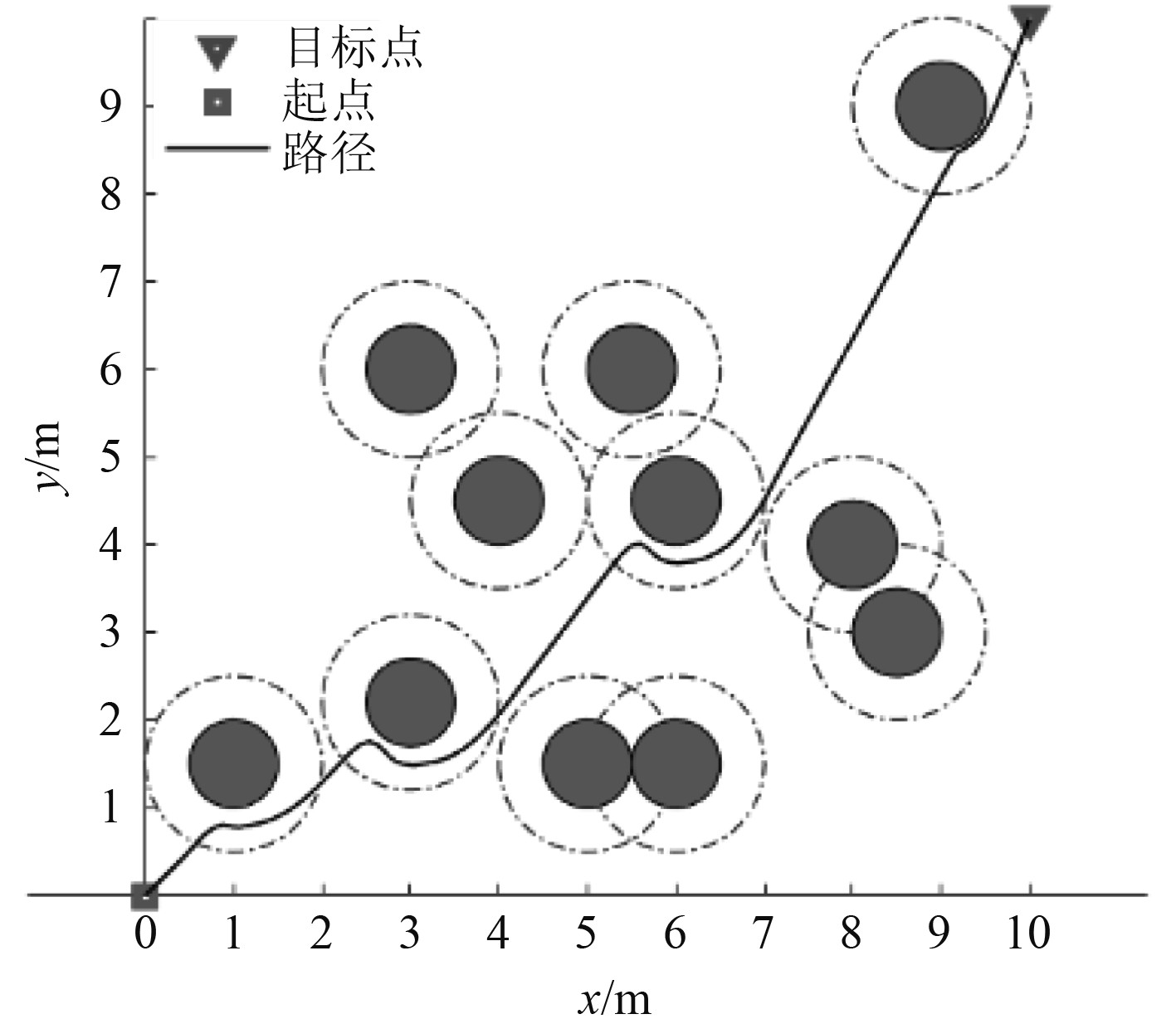
|
图 10 改进算法摆脱目标不可达状态 Fig. 10 The improved algorithm gets rid of the unreachable state |
|
|
表 3 路径长度和时间 Tab.3 Path length and time |
本文针对局部最优解问题,在简单障碍物的情况下,提出障碍物移动法,使无人艇改变当前的受力状态,摆脱局部最优状态,继续朝着目标点进行路径规划;在U型障碍物情况下,通过在加入自膨胀系数的基础之上引入模拟退火算法,使无人艇摆脱在U型障碍物情况下的局部最优状态;针对目标不可达问题,提出通过改进引力势场函数,增加引力,从而解决问题。经过实验验证,改进后的算法已成功解决了现有主要问题,并且取得了不错的效果。但提出的方法尚未在实物平台上进行验证,也未考虑环境中存在动态障碍物的情况,这也是接下来的研究方向。
| [1] |
刘澳霄, 周永录, 刘宏杰. 基于改进人工势场法的医疗配送机器人路径规划[J]. 计算机应用研究, 2024, 41(3): 842-847. |
| [2] |
高霄鹏, 刘冬雨, 霍聪. 水面无人艇运动规划研究综述[J]. 舰船科学技术, 2023, 45(16): 1-6. GAO X P, LIU D Y, HUO C. Summary of research on surface unmanned boat sports planning[J]. Ship Science and Technology, 2023, 45(16): 1-6. |
| [3] |
龙厚云, 李光, 谭薪兴, 等. 融合A*的改进RRT机械臂路径规划[J]. 计算机工程与应用, 2024, 60(4): 366-374. |
| [4] |
MENG L, FENG Z, JING Y F. Optimal path sol-ution based on dijkstra aigorithm[J]. Frontiers in Economics and Management, 2021, 2(6): 135-143. |
| [5] |
王星宇, 胡燕海, 徐坚磊, 等. 基于改进蚁群算法的机器人路径规划方法[J]. 电子技术应用, 2023, 49(1): 75-80. |
| [6] |
白响恩, 孙广志, 徐笑锋. 基于改进粒子群算法的海流环境下无人水面艇路径规划[J]. 上海海事大学学报, 2023, 44(4): 1-7. |
| [7] |
MA B, WEI C, HUANG Q, et al. APF-RRT*: An efficient sampling-based path planning method with the guidanceof artificial potential field[C]//2023 9th International Conferenceon Mechatronics and Robotics Engineering (ICMRE), IEEE, 2023.
|
| [8] |
王豪杰, 马向华, 代婉玉, 等. 改进DWA 算法的移动机器人避障研究[J]. 计算机工程与应用, 2023, 59(6): 326-332. |
| [9] |
陈侠, 刘奎武, 毛海亮. 基于APF-RRT算法的无人机航迹规划[J]. 电光与控制, 2022, 29(5): 17-22. |
| [10] |
许万, 程兆, 朱力, 等. 一种基于改进人工势场法的局部路径规划算法[J]. 电子测量技术, 2022, 45(19): 83-88. |
| [11] |
李龙, 陈禾炜, 汪田鸿, 等. 基于接近觉的机械臂避障路径规划[J]. 机器人, 2022, 44(5): 601-612. |
| [12] |
秦克斌, 王帅淇, 郭晓宇, 等. 改进人工势场法无人机脱离局部极小值问题[J]. 现代电子技术, 2024, 47(10): 107-110. |
| [13] |
XIE S, HU J, BHOWMICK P, et al. Distributed motion planning for safe autonomous vehicle overtaking via artificial potential field[J]. IEEE Transaction on Intelligent Transportation Systems, 2022, 23(11): 21531−21547.
|
| [14] |
PAN Z, ZHANG C, XIA Y, et al. An improved artificial potential field method for path planning and formation control of the multi-UAV systems[J]. IEEE Transactions on Circuits Systems, II Exp. Briefs, 2022, 69(3): 1129−1133.
|
| [15] |
贾胜伟, 张艳春, 陈磊, 等. 考虑运动特性的水面无人艇局部路径规划[J]. 舰船科学技术, 2024, 46(9): 71-75. JIA S W, ZHANG Y C, CHENG L, et al. The local path planning of unmanned surface vehicle considering motion characteristics[J]. Ship Science and Technology, 2024, 46(9): 71-75. |
| [16] |
闫为佳, 杨旗, 黄星卓, 等. 改进人工势场法解决局部最小值路径规划研究[J]. 组合机床与自动化加工技术, 2024(5): 36-39. |
| [17] |
李永正, 陈怡, 赵师纬, 等. 基于改进人工势场法的船舶静态避碰研究[J]. 舰船科学技术, 2023, 45(21): 76-80. LI Y Z, CHEN Y, ZHAO S W, et al. Research on ship static collision avoidance based on improved artificial potential field method[J]. Ship Science and Technology, 2023, 45(21): 76-80. |
 2025, Vol. 47
2025, Vol. 47
