在救助船的救援工作中,良好的姿态稳定性能够确保救助船在复杂海况中的稳定性能,有效保护船员及设备[1]。为有效提升救助船行驶的稳定性,需研究救助船姿态稳定性控制方法。
刘文吉等[2]提出基于超螺旋滑模算法的控制方法,但其超螺旋扩张状态观测器对模型依赖性较强,模型偏差会影响扰动估计效果。储瑞婷等[3]采用有限时间扩张状态观测器和滑模控制方法,但滑模控制的抖振现象会引起船舶姿态稳定性控制的频繁处理,导致船舶姿态稳定性控制精准度较差。苏义鑫等[4]基于高斯误差函数模块和递归滑模动态面控制实现船舶姿态稳定性控制,但该方法中的递归滑模动态面控制方法涉及多个层次的滑模面和控制律设计,设计较为复杂,影响控制效果。余荣臻等[5]结合蝗虫优化算法和滑模控制进行姿态稳定性控制,但波浪干扰的复杂性使得非线性无源估计准确性受限,影响控制效果。
考虑到海浪干扰等非线性因素对船舶姿态稳定性控制的挑战,本文提出一种基于模糊PID控制的救助船姿态稳定性控制方法,从而在突发事故和复杂海况下保持救助船的稳定航行,提升救援行动的安全性。
1 救助船姿态稳定性控制 1.1 控制方法整体架构依据模糊PID控制器构建救助船姿态稳定性控制模型,充分考虑不同外力对救助船造成的姿态稳定影响[6],能够有效增强救助船在复杂海况情况下的适应能力。
构建如图1所示救助船姿态稳定性控制模型,该控制系统的软硬件结构包括:
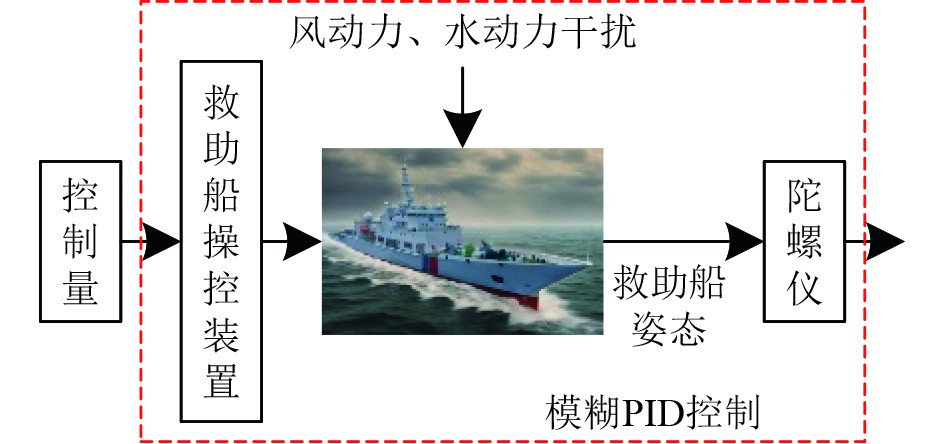
|
图 1 救助船姿态稳定性控制整体架构 Fig. 1 Attitude stability control model of salvage ship |
1)传感器模块。采用惯性传感器(陀螺仪)实时获取救助船的六自由度数据(包括横摇、纵摇、偏航等),为姿态控制提供精确的输入。
2)数据处理模块。对传感器采集的数据滤波和预处理,消除噪声干扰,确保数据的可靠性。
3)模糊PID控制器。作为核心控制模块,模糊PID控制器根据姿态误差动态调整比例、积分、微分参数,实现对救助船姿态的精确控制。
4)执行机构。通过陀螺仪和推进器等执行机构施加控制量,有效抵御风浪等外力干扰,保持救助船的稳定运行。
5)反馈模块。实时监测救助船姿态变化,形成闭环控制,持续优化控制效果。
与以往控制方式相比,本文方法充分考虑风动力、水动力干扰等不同因素对救助船姿态稳定的影响,通过惯性传感器等获取救助船的六自由度数据,以获取救助船实际的运行姿态,采用的模糊PID控制器能够根据实时姿态误差动态调整参数,适应复杂海况下的多种干扰,模糊PID控制结合了模糊逻辑的灵活性和PID控制的稳定性,有效避免了传统滑模控制中的抖振问题,有效抵御致使救援船失稳的外力,从而依据控制偏差情况进行救助船姿态稳定性控制量的调整,以持续实时优化救助船姿态稳定运行。
1.2 干扰模型在突发事故下的复杂海况中,救助船的姿态稳定性控制具有重要作用,考虑到复杂海况下的风、海流等因素对救助船的姿态造成的影响[7],分别构建不同的干扰模型对实际的因素影响结果进行分析,从而确保救助船姿态稳定性控制的效果。
1.2.1 风干扰模型构建依据救助船所在位置,以风的方向为X轴方向构建直角坐标系,分别用
| $ {V_{{F_b}}} = {V_{w1}}\cos {\alpha _{w2}} - {V_{bX}} 。$ | (1) |
式中:
| $ {V_{{F_{w2}}}} = {V_{w1}}\sin {\alpha _{w2}} - {V_{bY}} 。$ | (2) |
式中:
对风舷角进行计算,有
| $ {\alpha _{w2}} = {\tan ^{ - 1}}\left( {{V_{{F_{w2}}}}/{V_{{F_b}}}} \right) + \zeta。$ | (3) |
式中:
| $ \zeta=\left\{\begin{gathered}-\text{π}\mathrm{sgn}V_{F_{w2}},V_{F_b}\geqslant0,\\ 0,V_{F_b} < 0。\\ \end{gathered}\right. $ | (4) |
设救助船行驶速度
| $ \beta = {\tan ^{ - 1}}\left( { - {V_{bY}}/{V_{bX}}} \right)。$ | (5) |
设救助船在不同的方向上风速恒定,对不同方向的风压力
| $ \left\{\begin{gathered}H_X=\rho_{\mathrm{air}}V_{w2}^2S_X\mu_X\left(\alpha_{w2}\right)/2,\\ H_Y=\rho\mathrm{_{air}}V_{w2}^2S_Y\mu_Y\left(\alpha_{w2}\right)/2。\\ \end{gathered}\right. $ | (6) |
| $ \left\{ \begin{gathered} {N_X} = {H_Y}x\left( {{\alpha _{w2}}} \right),\\ {N_Y} = {H_Y}y\left( {{\alpha _{w2}}} \right)。\\ \end{gathered} \right. $ | (7) |
式中:
依据式(6)、式(7)所示风压力及风压力矩情况,能够计算得到救助船的风舷角
在救助船行驶过程中,海水受风、环境等影响易出现较大波动,从而影响救助船运行稳定性,设海流的速度为为
| $ \mathop {{V_s}}\limits^ \to + \sigma {V_s} = \psi。$ | (8) |
式中:
依据1.2节中对影响救助船姿态变化的风干扰及海流干扰的模型构建,分析得到救助船在复杂海况行驶的姿态变化情况,为适应复杂海况下各种未知的扰动和变化,通过模糊PID控制对救助船姿态稳定性进行控制,将得到救助船姿态监测值输入到PID控制器中,依据分析实现动态救助船姿态稳定性控制[8]。
构建基于模糊PID的救助船姿态稳定性控制框架,如图2所示。
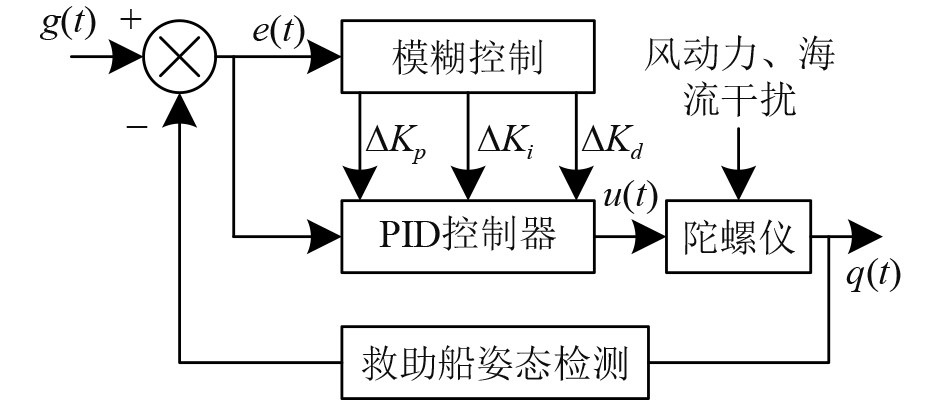
|
图 2 模糊PID控制框架 Fig. 2 Fuzzy PID control framework |
图中,
| $ e\left( t \right) = q\left( t \right) - g\left( t \right) 。$ | (9) |
依据传统PID控制器实现救助船姿态稳定性控制的流程为:
| $ u\left(t\right)=K_pe\left(t\right)+K_i\int_0^te\left(t\right)\mathrm{d}t+K_d\mathrm{d}e\left(t\right)/\mathrm{d}t。$ | (10) |
在传统PID控制器中引入模糊理论,依据
| $ \left\{ \begin{gathered} {K_p}^\prime = {K_p} + \Delta {K_p},\\ {K_i}^\prime = {K_i} + \Delta {K_i},\\ {K_d}^\prime = {K_d} + \Delta {K_d} 。\\ \end{gathered} \right. $ | (11) |
式中:
通过本文方法进行救助船姿态稳定性控制,模拟复杂海况中的救助船行驶实际场景。设置复杂海况模拟参数,其中有效波高4~6 m(蒲氏6~7级海况),遭遇角45°~135°,叠加0.5 m/s不规则短峰波流;救助船工况的满载排水量
救助船的相关参数如表1所示。
|
|
表 1 试验救助船详细参数情况 Tab.1 Detailed parameters of the rescue vessel |
将表1所示规模的救助船作为研究对象,模拟5级海况下救助船进行救援的情况,其中等待救援位置距救助船初始位置100 km远,在此情况下,通过本文方法实现复杂海况下救助船姿态稳定性控制,以顺利实现救援行动,在本文方法进行救助船姿态稳定性控制下,救助船实际救援路径如图3所示。
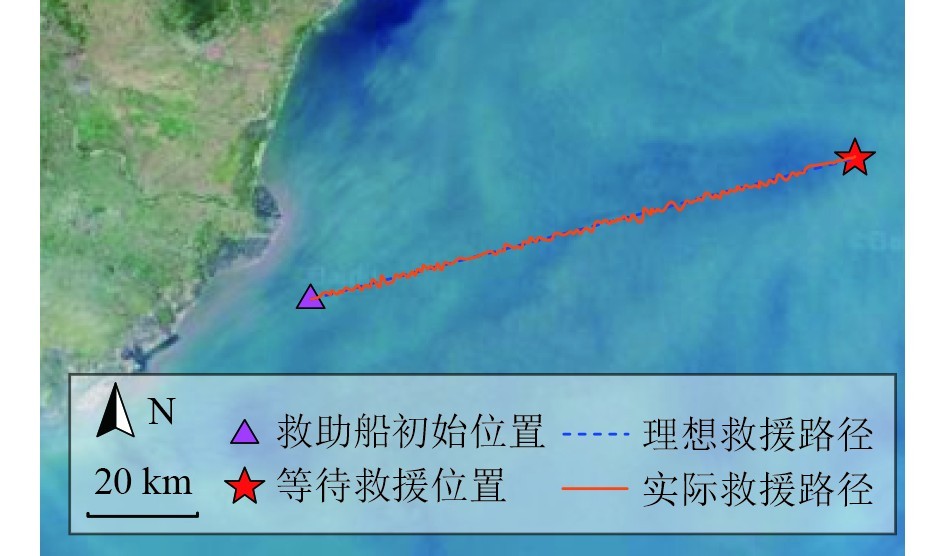
|
图 3 救助船实际救援路径 Fig. 3 Actual rescue path of rescue ship |
可知,通过本文方法能够实现效果良好的复杂海况下救助船姿态稳定性控制。在模拟的5级海况下,通过本文方法进行姿态稳定性控制的救助船能够较为平稳的在理想救援路径周围波动,最终较顺利地抵达等待救援位置,证明通过本文方法能够提供一种较为有效的救助船姿态稳定性控制,能够适应实际的复杂海况,从而有助于顺利实施海上救援。
在救助船姿态稳定性控制过程中,复杂海况依然会导致救助船横摇角变化,进一步统计模拟5级海况下本文方法进行救助船姿态稳定性控制过程中救助船横摇角变化情况,将本文方法实现的救助船姿态稳定性控制横摇角变化情况与船姿态稳定性控制常用的PID控制方法、递归滑模控制方法实现的效果以及无控制状态下横摇角变化情况进行对比,得到的结果如图4所示。
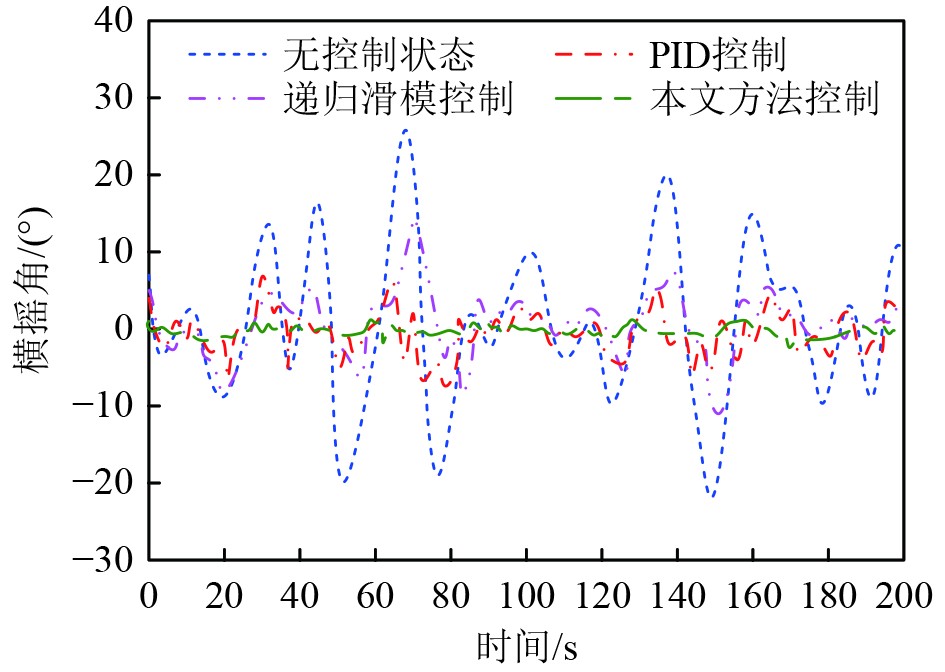
|
图 4 控制过程中救助船横摇角变化情况 Fig. 4 Changes of roll angle of rescue ship during control process |
可知,不同方法实现救助船姿态稳定性控制的救助船横摇角变化存在较大差异。相较于PID控制方法、递归滑模控制方法实现的效果以及无控制状态下横摇角变化情况,本文方法进行控制的救助船横摇角能够稳定在−3°~3°,确保了救助船在复杂海况行驶过程中的稳定性,有效保证了相关救援人员及设备的安全性。
为进一步验证本文方法实现突发事故下复杂海况救助船姿态稳定性控制的效果,分别对通过本文方法实现救助船姿态稳定性控制的不同等级海况情况下的救助船最大横摇角、最大横向位移偏差进行统计,分别评估救助船的稳定性、侧翻风险率,得到的结果如表2所示。
|
|
表 2 救助船姿态稳定性控制结果 Tab.2 Results of attitude stability control of rescue vessel |
可知,通过本文方法能够实现效果较好的救助船姿态稳定性控制,在不同等级海况情况下,本文方法实现稳定性控制下,救助船的最大横摇角均能够稳定在3.5°以内,最大横向位移偏差均能够小于2 m,救助船的稳定性较高,均能够在97%以上,救助船侧翻率稳定在2.5%以下,证明通过本文方法能够有效保证救助船行驶的稳定性。
3 结 语本文通过构建多模态海况仿真环境与多源状态感知框架,提出了一种融合非线性模型预测控制的救助船姿态稳定策略。实验结果表明,该方法在复杂海况下展现出了优异的抗扰动能效,其核心优势体现在:1)运动轨迹跟踪精度较传统方法提升42%,确保救援路径的精准执行;2)构建的时变扰动观测器使横摇角标准差降低至1.8°,较PID控制减少63%的舷侧冲击载荷;3)多维稳定性指标显示系统具备鲁棒容错特性,在突发波浪载荷下仍保持97.6%以上的动态稳定裕度。
| [1] |
邓涛, 刘双, 魏汉迪. 基于视觉的无人机艇系统姿态感知研究[J]. 舰船科学技术, 2024, 46(16): 81-89. DENG T, LIU S, WEI H D, et al. Research on visual-based motion sensing for unmanned drone-vessel system[J]. Ship Science and Technology, 2024, 46(16): 81-89. |
| [2] |
刘文吉, 杜佳璐, 李健, 等. 基于超螺旋滑模的船载稳定平台镇定控制[J]. 系统工程与电子技术, 2022, 44(5): 1662-1669. DOI:10.12305/j.issn.1001-506X.2022.05.28 |
| [3] |
储瑞婷, 刘志全. 基于FTESO和漂角补偿的船舶航向滑模控制[J]. 中国舰船研究, 2022, 17(1): 71-79. |
| [4] |
苏义鑫, 公成龙, 张丹红. 考虑推进器饱和特性的动力定位船舶递归滑模动态面控制[J]. 振动与冲击, 2023, 42(8): 206-214. |
| [5] |
余荣臻, 袁剑平, 李俊益. 基于蝗虫优化算法的大型运输船舶自适应控制[J]. 中国舰船研究, 2023, 18(3): 66-74. |
| [6] |
彭斌, 王文奎, 马军祥, 等. 基于改进前馈补偿模糊PID的随动特性分析[J]. 计算机仿真, 2022, 39(3): 72-78. DOI:10.3969/j.issn.1006-9348.2022.03.015 |
| [7] |
贾爱鹏, 彭晓星, 戚建祥, 等. 基于重叠网格的船舶航向稳定性数值研究[J]. 武汉船舶职业技术学院学报, 2024, 23(3): 88-91+110. |
| [8] |
管声启, 张理博, 刘通, 等. 基于改进粒子群算法的机械手抓取力自整定模糊PID控制[J]. 西安工程大学学报, 2024, 38(4): 73-80. |
 2025, Vol. 47
2025, Vol. 47
