海上运输时,液态货物的晃荡和蒸发现象会同时发生并相互影响,现有的研究工作主要是单独研究了液舱或货物围护系统内的热效应,而没有将两者耦合。Ferrín等[1]对小型储罐内LNG的流动情况进行了数值模拟,研究了静止储罐内充液量对蒸发率和分层程度的影响。Lee等[2]提出了一种预测船舶货物围护系统保温壁温度的计算方法。Chen等[3]提出了一种能够准确预测LNG在运输途中的老化情况的热力学模型。Lin等[4]提出了一种将相邻流体层和甲烷蒸汽的流动相结合的等效导热模型,有效地估算了不同填充比下蒸发气体的质量。Jeon等[5]通过仿真模拟对低温液体的蒸发率和蒸发量进行了高精度的数值计算。
Lee等[6]模拟了泄漏LNG的扩散行为和传热特性。Choi等[7]通过数值计算模拟了低温液体在货物围护系统多孔结构中的扩散过程,以及LNG泄漏对船体钢板的影响。
本文将二者耦合,进一步了解在货物围护系统出现破损时,储罐内的实际传热情况,并分析特定条件下储罐内部甲烷蒸汽生成和液体泄漏到多孔隔热层内的热质传递过程。对于深入了解海洋动载下多孔隔热层泄漏的船舶LNG储罐内热质传递过程具有重要意义,为后续船舶液货舱的设计以及优化提供了参考。
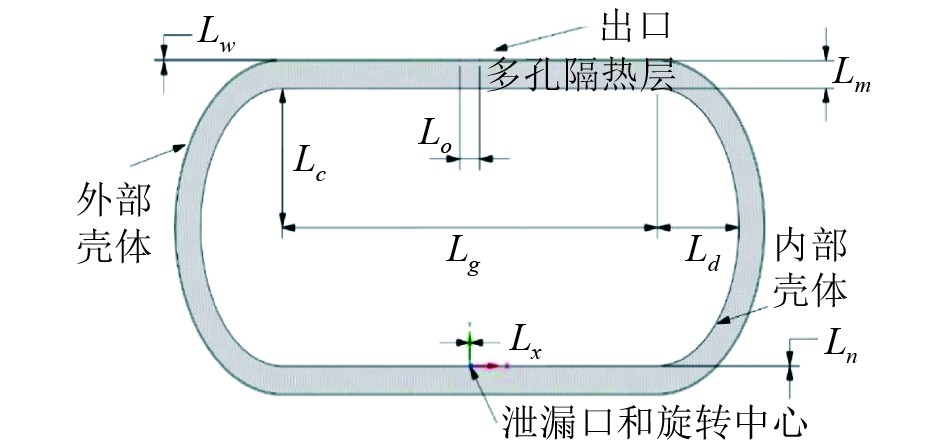
1 物理模型本文选用的C型储罐模型如图1所示。储罐的主罐体Lg=1.5 m,两端的C型封头短轴半径Ld=0.325 m,长轴半径Lc=0.5 m,储罐由内部壳体、多孔隔热层和外部壳体3部分组成,其中内部壳体Ln=0.7 mm,多孔隔热层厚度Lm=100 mm,外部壳体厚度Lw=5 mm。3部分对应的材料分别为殷瓦钢、玻璃棉和9%的镍钢,材料的属性见表1。储罐泄漏点Lx=2 mm,出口Lo=80 mm。由于主要研究储罐在晃荡激励下多孔隔热层泄漏时储罐内部和多孔隔热层的热效应和水动力特性,因此忽略了鞍座等支撑系统。
|
图 1 LNG储罐二维示意图 Fig. 1 Two-dimensional diagram of LNG storage tank |
|
|
表 1 储罐材料属性 Tab.1 Tank material properties |
针对海洋动载下多孔隔热层泄漏船舶LNG储罐热质传递的研究,本文采用流体体积法(VOF)以及Lee模型模拟了液化天然气的流动与相变过程。
连续方程为:
| $ \nabla \cdot \left(\rho \overrightarrow{V}\right)=0。$ | (1) |
式中:
动量方程为:
| $ \begin{split} \nabla\cdot\left(\rho\overrightarrow{V}^2\right)= & -\nabla P+\nabla\cdot\left[\frac{\mu}{\varepsilon}\left(\nabla\overrightarrow{V}+\nabla\overrightarrow{V}^{\text{T}}\right)\right]- \\ &\left(\frac{\mu}{K}\overrightarrow{V}+\frac{C\rho_{\text{v}}}{\sqrt{K}}\overrightarrow{V}^2\right)+\rho v+\overrightarrow{F{_{{C}}}}。\end{split} $ | (2) |
式中:
| $ K = \frac{{{d_{{p}}}^2{\varepsilon ^3}}}{{180 \times {{(1 - \varepsilon )}^2}}},$ | (3) |
| $ C = \frac{{3.5 \times (1 - \varepsilon )}}{{{d_{{p}}}{\varepsilon ^3}}} 。$ | (4) |
能量方程为:
| $ \nabla \cdot \left|\overrightarrow{V}\left(\rho E+p\right)\right|=\nabla \cdot \left({k}_{{eff}}\nabla T\right)+{S}_{{h}}。$ | (5) |
式中:E为内能,J;能量源相等于总的传质量乘以汽化潜热,计算公式为
| $ {S_{{h}}} = {S_{{m}}}{h_{{{fg}}}}。$ | (6) |
由于LNG在储罐和隔热层内会发生相变,实际过程包含了蒸发和冷凝,当液体温度超过给定压力下的饱和温度时,会发生蒸发。冷凝是蒸发的反过程,当蒸汽温度降至饱和温度以下时,会发生冷凝。本文选用Lee模型作为模拟蒸发-冷凝过程的相变模型[8],计算公式为:
| $ \left\{\begin{aligned} &{S_{{{vl}}}} = \frac{{{r_{{v}}}{\alpha _{{v}}}{\rho _{{v}}}\left( {{T_{{{sat}}}} - {T_{{v}}}} \right)}}{{{T_{{{sat}}}}}},{T_{{{sat}}}} > {T_{{v}}},\\ &{S_{{{lv}}}} = \frac{{{r_\text{{l}}}{\alpha _\text{{l}}}{\rho _\text{{l}}}\left( {{T_{{l}}} - {T_{{{sat}}}}} \right)}}{{{T_{{{sat}}}}}}{\text{ }},{T_{{{sat}}}} \leqslant {T_{\text{l}}}。\end{aligned} \right.$ | (7) |
式中:
本文采用正弦激励来模拟海浪对船舶储罐的影响[9],旋转中心位于储罐底部的泄漏点的中心(见图1),外部激励方式为:
| $ y = A\sin \left( {\frac{{2{\text{π }}}}{T}t} \right),$ | (8) |
| $ v = y' = A\frac{{2{\text{π }}}}{T}\cos \left( {\frac{{2{\text{π }}}}{T}t} \right) ,$ | (9) |
| $ a = y'' = - A\frac{{4{{\text{π }}^2}}}{{{T^2}}}\sin \left( {\frac{{2{\text{π }}}}{T}t} \right)。$ | (10) |
式中:
使用Ansys Fluent用于求解上述方程,采用双精度求解器对非稳态晃动特性进行模拟仿真,采用标准
为了研究网格数量对模拟结果的影响,本文选取了4种不同网格数量进行网格独立性测试,并选择泄漏到隔热层的液体的质量为监测对象。在储罐内的充液高度为0.50 m外部激励为f=0.40 Hz ,A=0.10 m的条件下,以50 s内的晃荡情况为例。网格数量对液体质量的影响(见表2),当网格数量为
|
|
表 2 网格独立性验证 Tab.2 Grid independence verification |
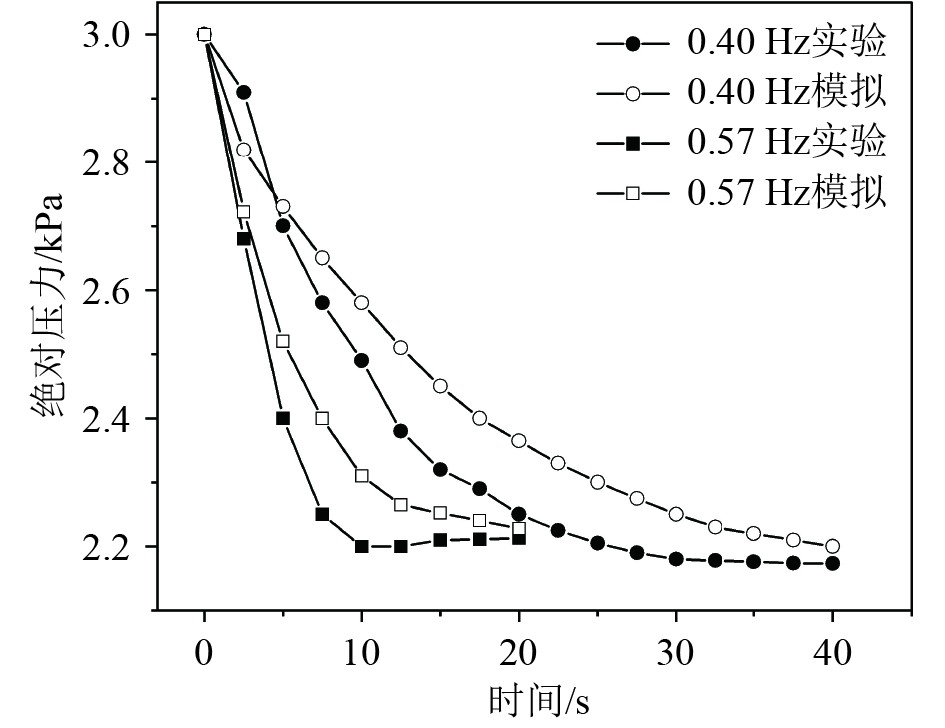
为了验证数学模型和数值分析方法的可行性,与Grotle等[10]进行的液体晃动实验进行对比,参考引文中的实验条件[10 - 11],图2为实验和模拟的压力结果对比图数值模拟结果与实验结果最大相对误差为2.9 %。综上,本数值模型准确度较高。
|
图 2 模拟结果与实验结果对照 Fig. 2 Comparison of simulated and experimental results |
共振频率通常位于固有频率附近,晃动在共振时最剧烈。根据参考文献[12]给出的公式计算C型独立罐中液体的一阶固有频率。计算方程如下:
| $ T = a\sqrt {\frac{L}{{g\tanh ({\text{π}}h/L)}}} ,$ | (11) |
| $ a = 1.8\sqrt {1 - \frac{h}{D}} + 2.5。$ | (12) |
式中:
由公式计算可得,当充液高度为0.50 m和0.80 m时,储罐的一阶固有频率分别为0.41 Hz和0.54 Hz。为了充分了解频率对蒸发和泄漏的影响,本研究选取 2种充液高度(0.50 m、0.80 m)以及3种晃荡频率(0.30、0.40、0.50 Hz)。如图3和图4所示,显示了在3种晃动频率下储罐内的和多孔隔热层中的相位轮廓,图中深色为天然气的液相区域。储罐内的流体由于外部晃动激励,气液界面发生了变化,晃荡频率由0.30 Hz增大到0.50 Hz,储罐内液体晃动的程度由平稳趋于剧烈。

|
图 3 不同晃荡频率影响下的液相分布图 Fig. 3 Liquid phase distribution under the influence of different shaking frequencies |
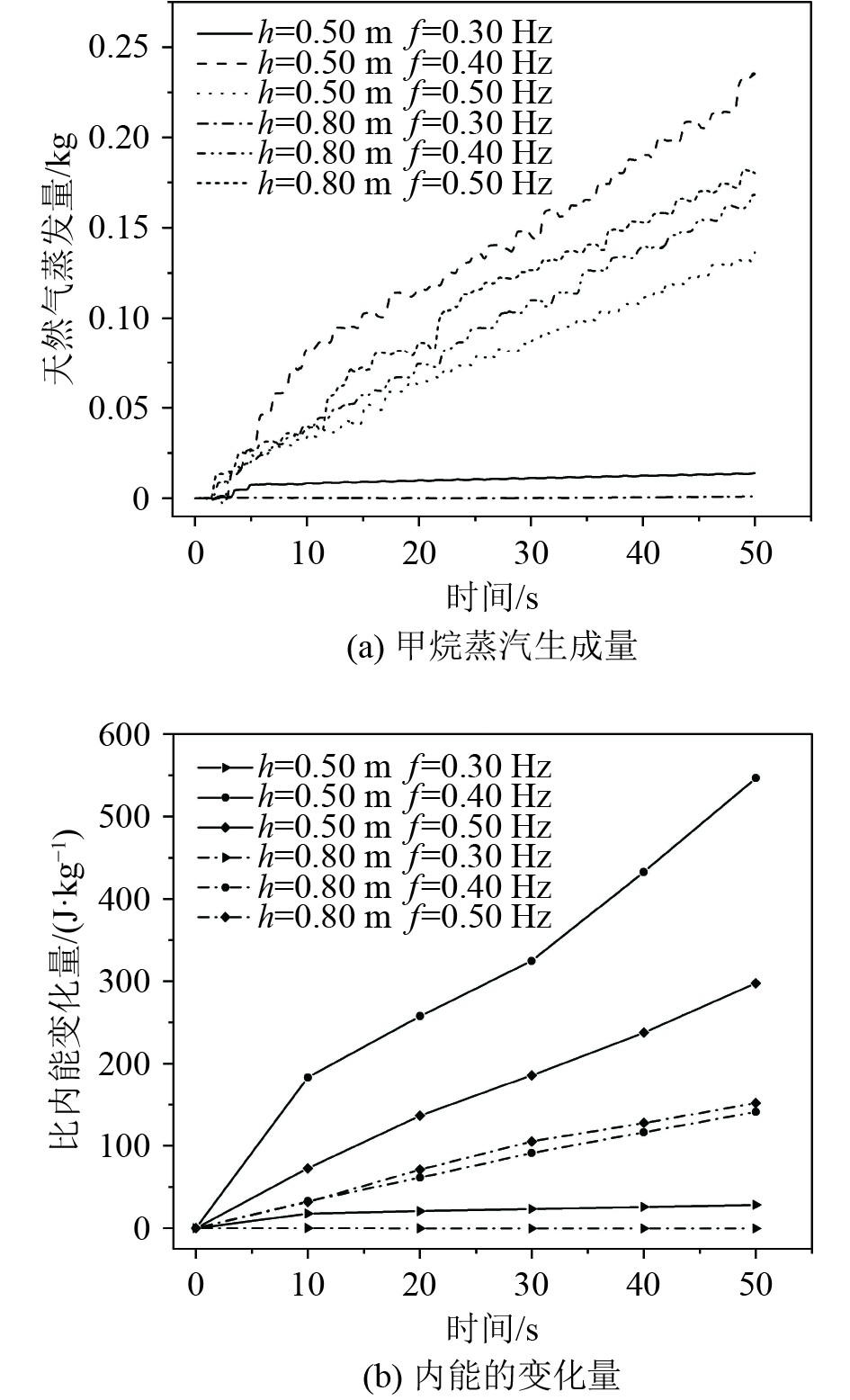
|
图 4 晃荡频率对储罐内蒸发的影响 Fig. 4 Effect of shaking frequency on evaporation in storage tanks |
另外,图4为晃动条件下天然气的生成量和比内能的变化量。当晃荡频率接近固有频率时,甲烷蒸汽生成量和内能增加量达到较大值。造成这种现象的主要原因:1)由于C型独立储罐结构的特殊性,左右两侧有球形封头,储罐晃荡时,内部的液体晃荡到储罐顶部,圆形封头会使液体高速返回形成射流,最终以一定的倾斜角度撞击液体表面,增大了液相与气相的接触面积,增强了液相与气相之间的传热和传质;2)由于粘度的存在,储罐晃动的机械能转化为LNG的内能,导致LNG温度升高,从而促进了LNG的蒸发。
值得注意的是,储罐内生成气体的质量会呈现出周期性的减少,这是由于储罐是一个密闭的容器,当液体在撞击到储罐壁面后冲击到原来的气相区域时,使得气相区域的局部压力增大,导致一部分的甲烷气体液化,因此气体质量会有一定程度的降低。
由图5(a)可知,随着液体的晃荡,泄漏点处的压力呈现出周期性的变化,并且这种变化与晃动周期吻合,监测点处的压差随晃荡频率的增大而增大,当晃荡频率较低时,压力的波动比较平缓;当晃荡频率增大到0.40 Hz时,压力波动十分明显。由于压力的波动程度不同,导致泄漏到多孔隔热层的液体的质量也有所变化。根据图5(b)所示,选取的2种充液高度,液体泄漏的质量皆与晃荡频率呈正相关。
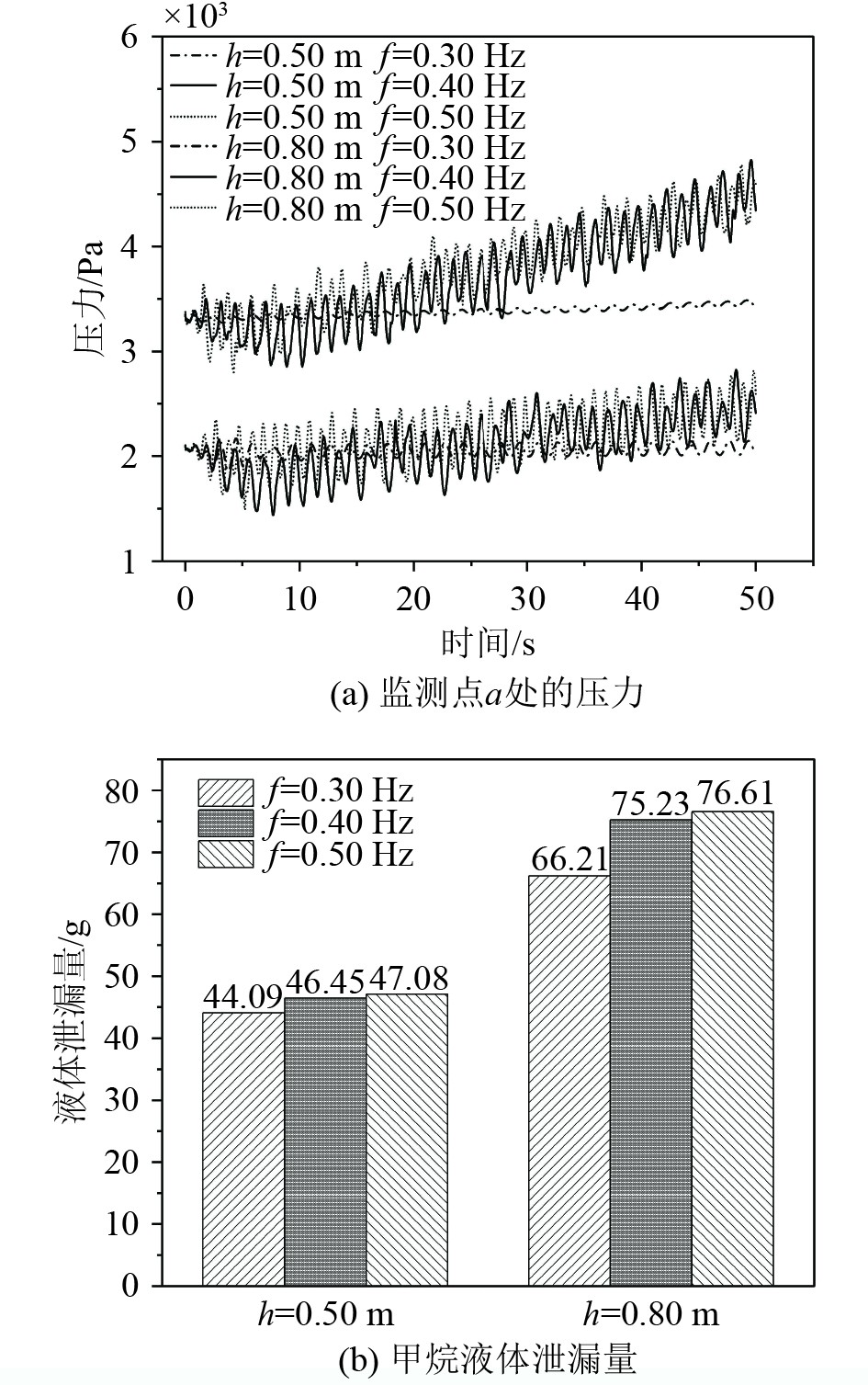
|
图 5 晃荡频率对多孔隔热层内泄漏的影响 Fig. 5 Effect of shaking frequency on internal leakage in porous thermal barriers |
本节主要研究LNG储罐在不同晃动振幅下的晃动特性,默认晃荡频率为0.40 Hz。晃荡振幅选取了0.05、0.10和0.15 m 三种高度。图6分别为充液高度为0.5 m和0.8 m时不同振幅的相位轮廓。当晃动幅度为0.05 m时,气液界面几乎没有波动,液体在罐内的运动相对稳定;当晃动幅度增大到0.1 m时,可以发现液面有明显的波动,波动程度变大;当振幅增大到0.15 m时,晃荡的剧烈程度进一步增强,气液界面被破坏,液体会晃荡到储罐顶部形成射流,如图6(b)可知,液体在晃荡到50 s时,液体已经完全脱离储罐侧的壁面,并且晃荡形成的射流能够完整地贯穿整个储罐顶部。
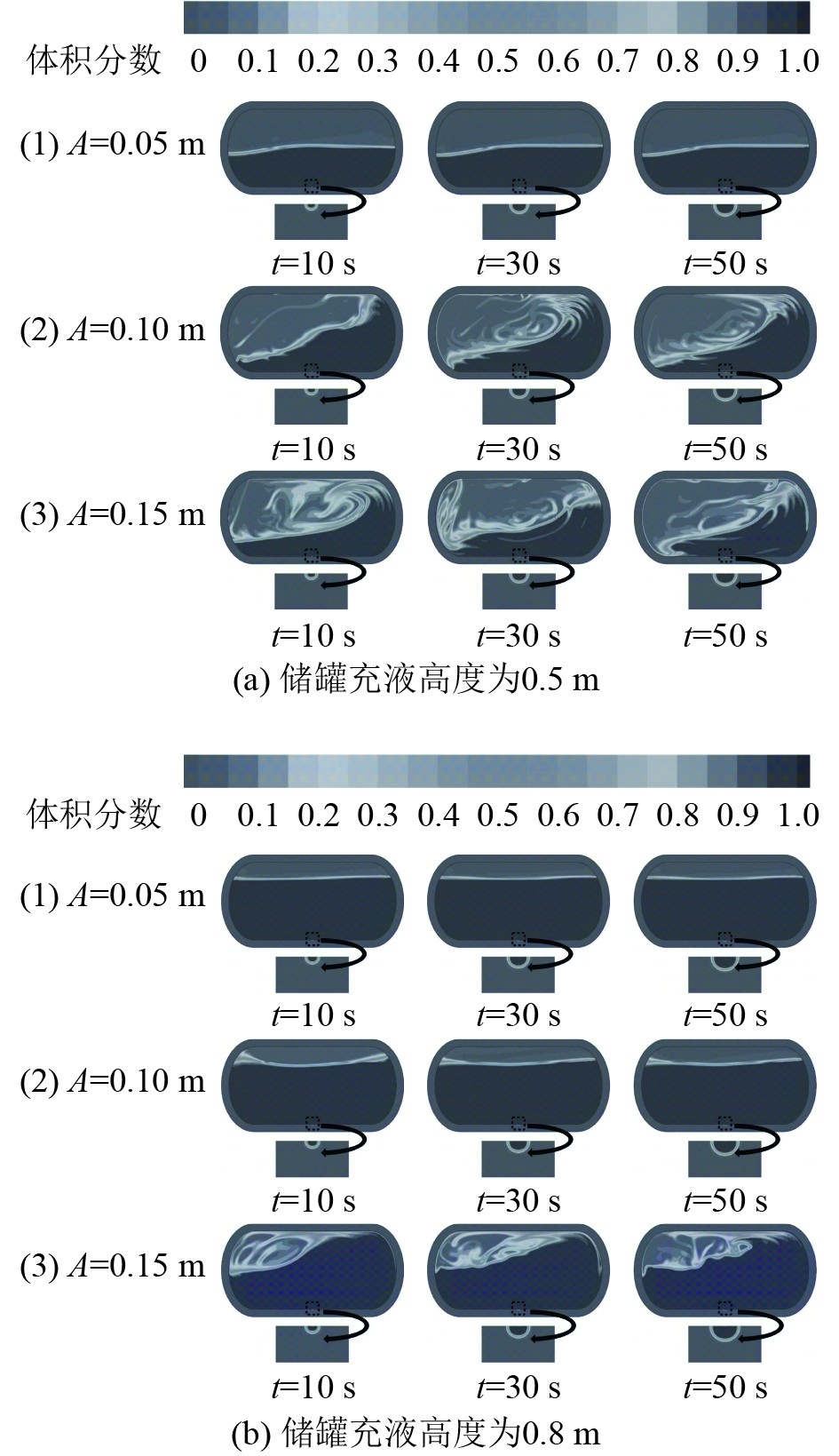
|
图 6 不同晃荡振幅影响下的液相分布图 Fig. 6 Liquid phase distribution under the influence of different shaking amplitudes |
由图7可知,在相同充液高度的前提下,储罐内产生的蒸汽质量和内能的增加量与振幅呈正相关。这是因为晃动幅度越大,液体在储罐内的波动越剧烈,增加了气液接触面积,促进了液体蒸发,并且在晃动过程中外部的机械能通过做功传递到储罐内部并转化为内能。由图8可知,由于振幅不同,导致了监测点处的压差呈现出不同的变化。振幅越大,压差波动越大,在泄漏点处对多孔隔热层的冲击力越强,因此在相同时间内泄漏到多孔层的液体的质量就越多,尤其是当充液高度为0.8 m时上述现象更明显。
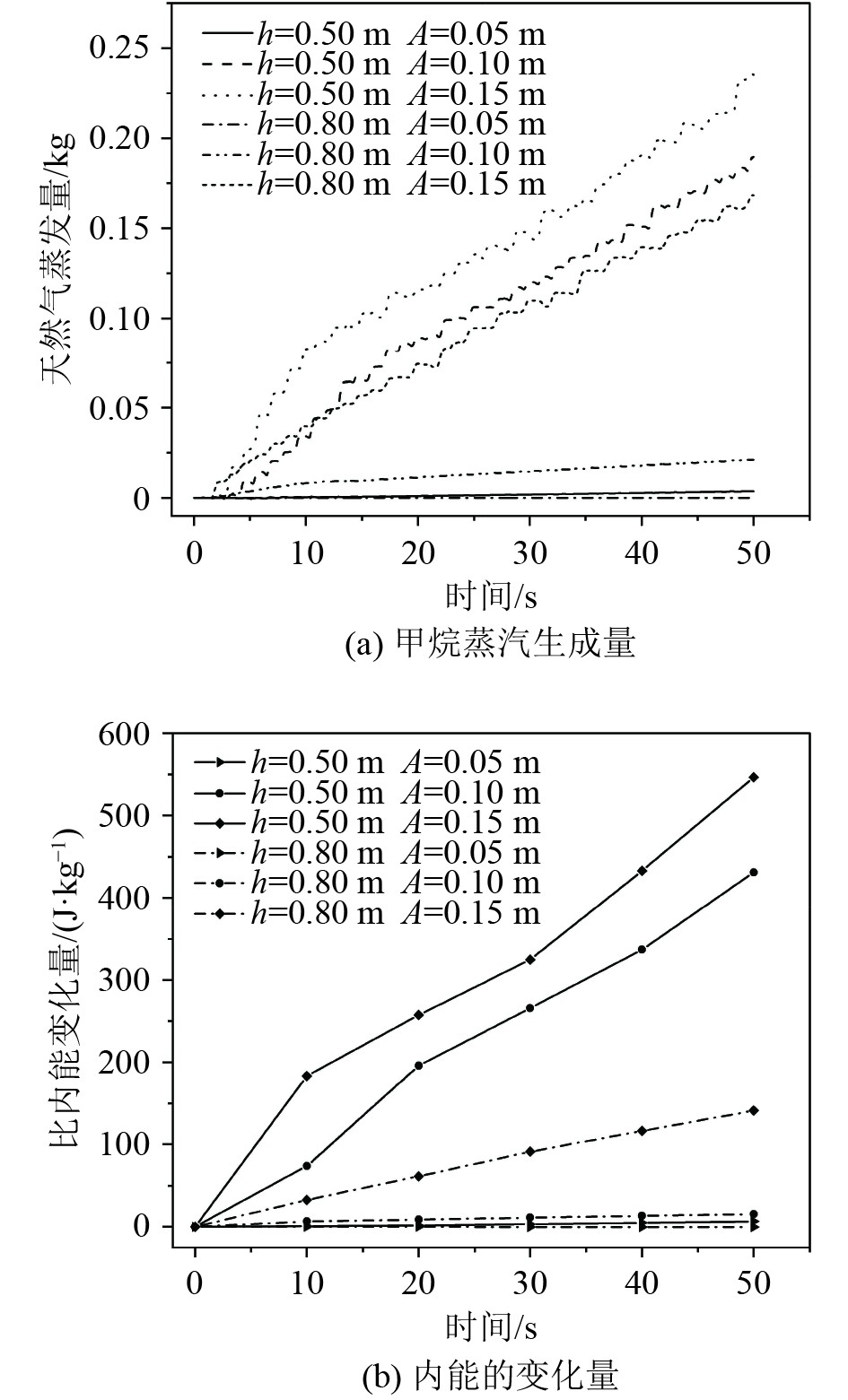
|
图 7 晃荡振幅对储罐内蒸发的影响 Fig. 7 Effect of shaking amplitude on evaporation in storage tanks |
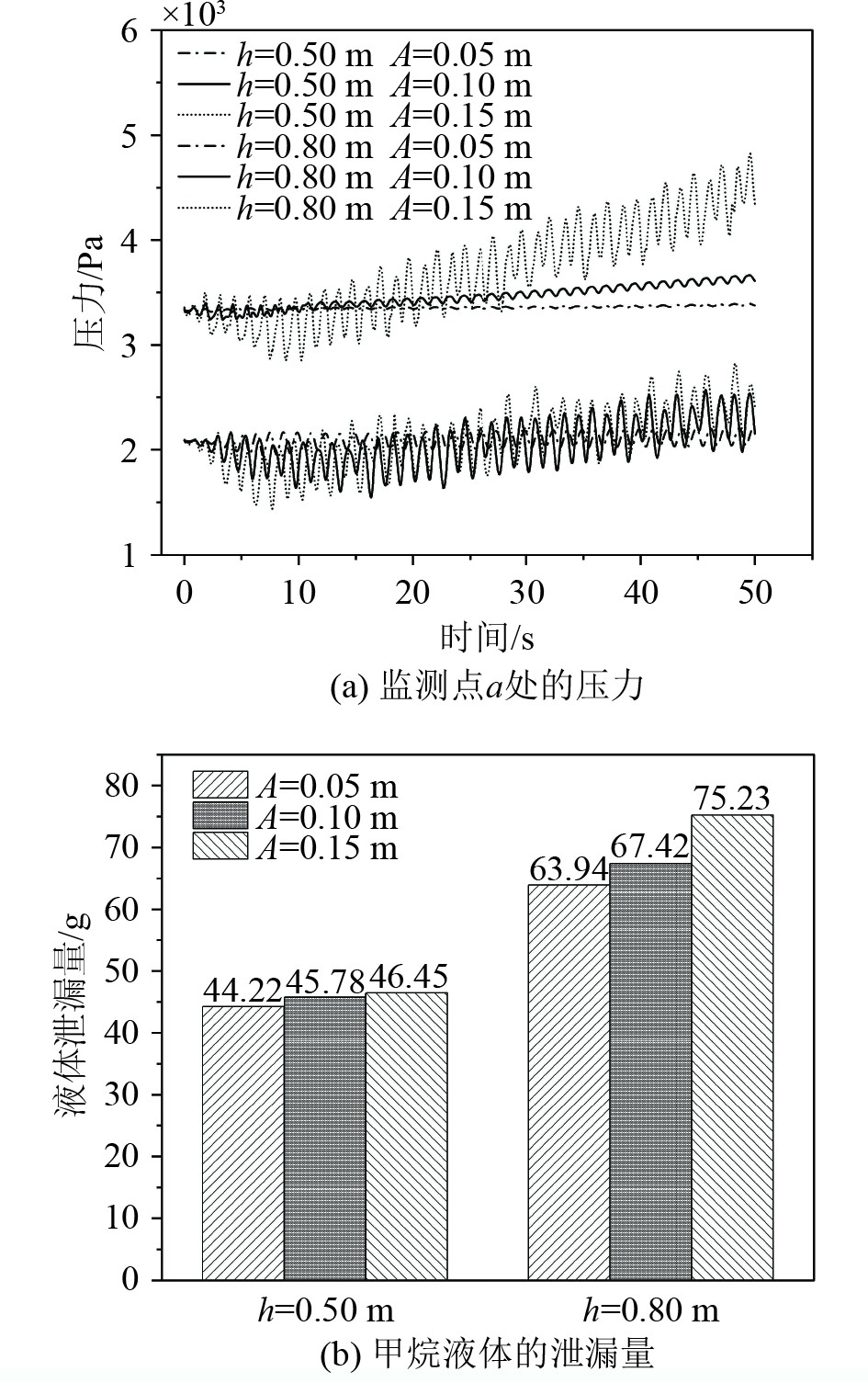
|
图 8 晃荡振幅对多孔隔热层内泄漏的影响 Fig. 8 Effect of shaking amplitude on internal leakage in porous insulation layers |
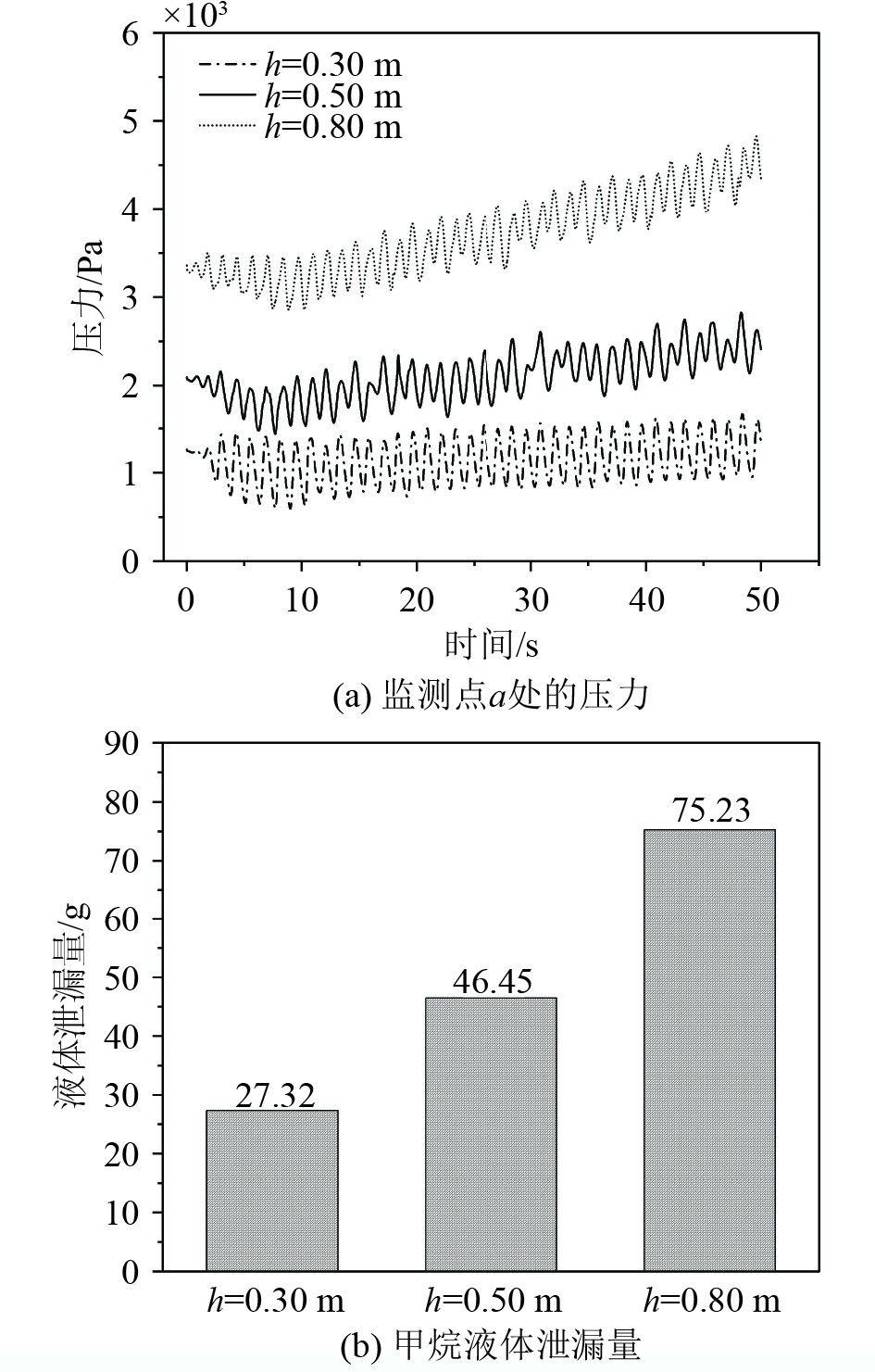
本节主要研究船舶在航行中,不同的充液高度对蒸汽产生和液体泄漏的影响。本节中,默认晃荡频率为0.40 Hz,振幅为0.15 m;分别选取了0.30、0.50和0.80 m 三种液面高度。由图10(a)可知,当其他参数不变时,随着充液高度的增加,储罐内蒸汽的产生量逐渐递减,这是由于在相同的晃荡条件下,储罐内的液体由于质量的增加而具有更大的惯性,并且较多的液体增大了液体与储罐的接触面积,从而增大了阻尼效应。因此,在图9(a)中,相同的外部激励下,液面越高,液体晃荡的越平稳。气相和液相之间的传热与传质降低导致了产生蒸汽量的减少。根据图11(a)可知,受重力的影响,较高的充液高度会使得泄漏点处的压力较大,在相同时间内会有更多的液体渗透到多孔隔热层内,如图11(b),充液高度每增加0.1 m,泄漏到多孔层的液体质量多增加9.61 g。

|
图 9 不同充液高度和多孔隔热层孔隙率影响下的液相分布图 Fig. 9 Liquid phase distribution under the influence of different filling heights and porosity of porous insulation layer |
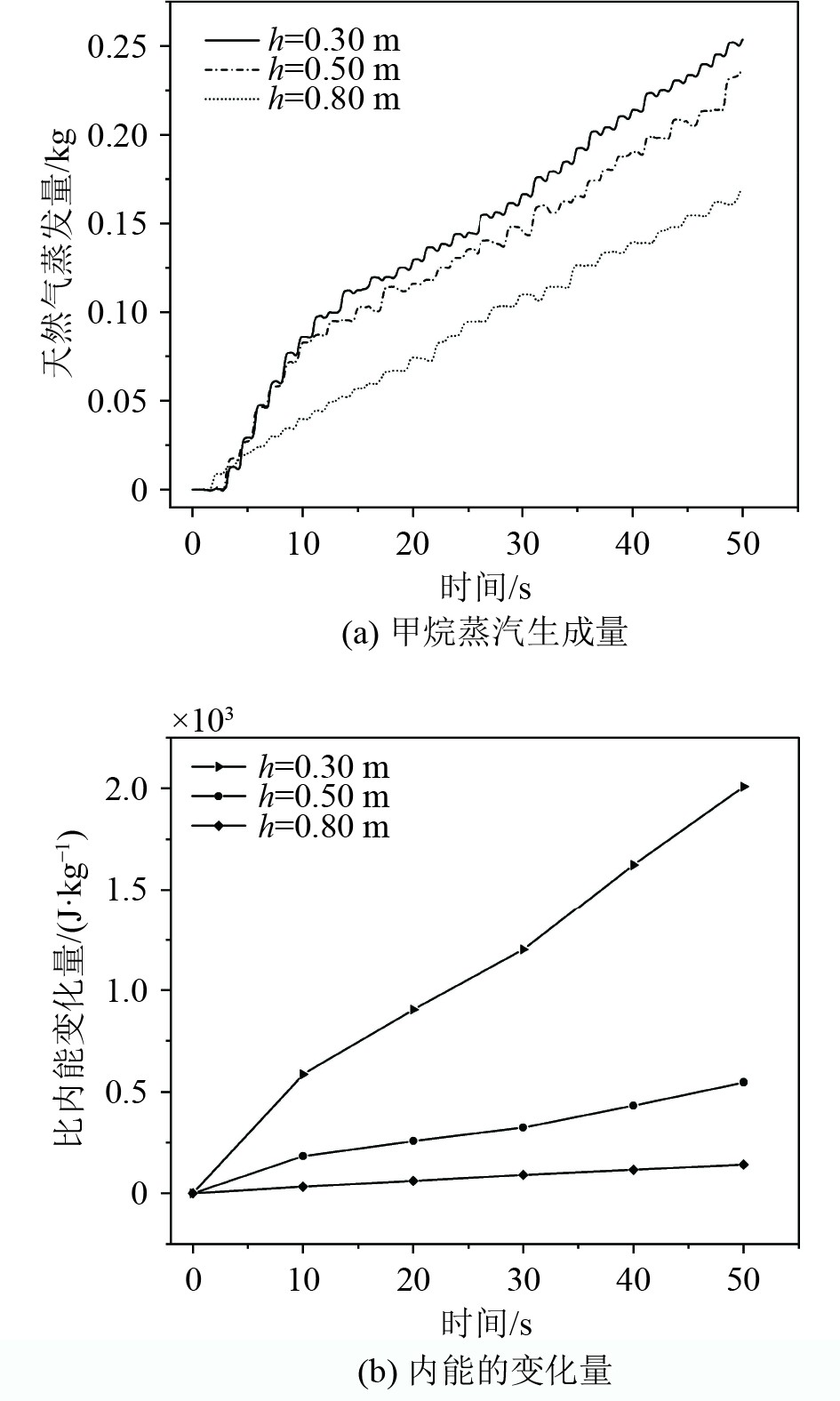
|
图 10 充液高度对储罐内蒸发的影响 Fig. 10 Effect of filling height on evaporation in storage tanks |
|
图 11 充液高度对多孔隔热层内泄漏的影响 Fig. 11 Effect of filling height on internal leakage in porous insulation layers |
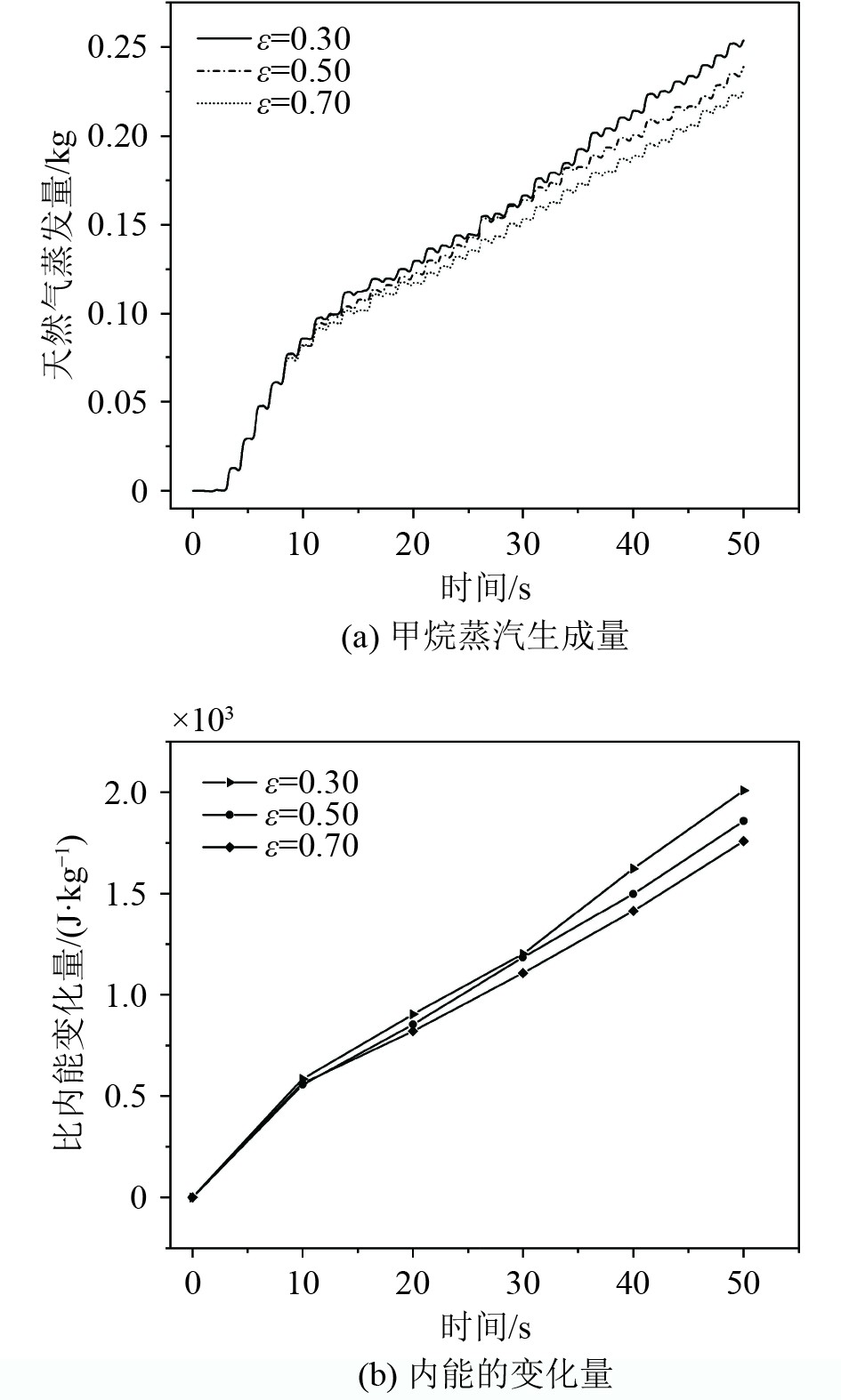
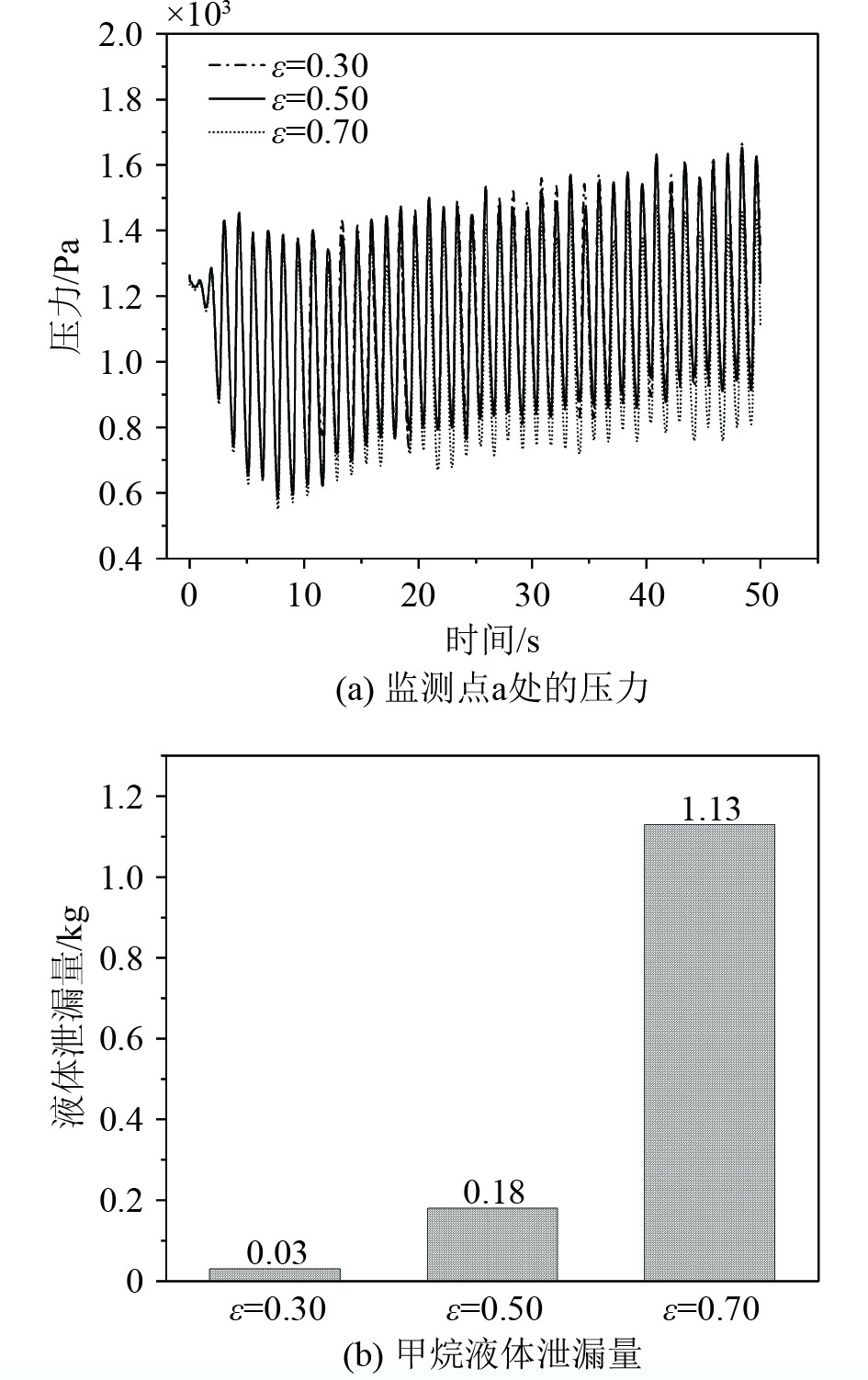
为了研究多孔隔热层材料孔隙率对于蒸发和泄漏的影响,在外部激励为频率0.40 Hz和振幅为0.1 m时且边界条件不变的情况下,分别设置多孔层的孔隙率为0.30、0.50和0.70。由图12(a)知,在50 s内,ε=0.3、0.5、0.7时,储罐内的液体在晃荡的情况下分别产生了254、239、225 g的气体,孔隙率每增加0.2,储罐内约减少15 g的蒸汽。随着多孔隔热层孔隙率的增加,储罐内生成的气体呈递减趋势。这是由于孔隙率的增大,使得相同体积的隔热层内有更多的空气间隙,而空气比玻璃纤维的导热率更低,相同时间内通过泄漏点进入储罐的热量更低。由图9(b)和图13(a)可知,孔隙率的改变对储罐内的低温液体流动影响甚微,但由于孔隙率的增大,使得固体的体积减少,多孔隔热层内有更多的空间来为液体提供流动的路径和储存空间,并且较大的孔隙率能够减少液体流动的阻力,较大的孔隙率使得液体与固体表面的接触面积相应减少,降低了粘性力和摩擦力的作用,减少了可能阻碍液体流动的界面效应。因此如图13(b),随着孔隙率的增大,进入到多孔隔热层的液体质量增多。
|
图 12 隔热层孔隙率对储罐内蒸发的影响 Fig. 12 Effect of insulation porosity on evaporation in storage tanks |
|
图 13 孔隙率对多孔隔热层内泄漏的影响 Fig. 13 Effect of porosity on internal leakage in porous thermal barriers |
本文分析了晃荡频率、振幅,以及储罐内部充液高度和隔热层的孔隙率对储罐及多孔层内蒸发和泄漏的影响。可知:较高晃荡频率会导致储罐内LNG更多的蒸汽产生;在晃荡频率接近储罐的固有频率时,储罐内可获得较大的蒸发量。较大的晃荡振幅会导致储罐内LNG更多的蒸汽产生,但对泄漏的影响并不明显;在给定储罐条件下,受阻力和重力的影响,相同频率下蒸汽产生量与储罐的充液高度呈负相关,其充液高度增加0.1 m,可增加9.61 g LNG泄漏量;多孔隔热层的孔隙率每增大0.2,甲烷蒸汽的产生量减少约15 g,而泄漏的甲烷液体的质量将增大6倍。
| [1] |
FERRÍN J L, PÉREZ-PÉREZ L J. Numerical simulation of natural convection and boil-off in a small size pressurized LNG storage tank[J]. Computers & Chemical Engineering, 2020, 138: 106840.
|
| [2] |
LEE H B, PARK B J, RHEE S H, et al. Liquefied natural gas flow in the insulation wall of a cargo containment system and its evaporation[J]. Applied Thermal Engineering, 2011, 31(14−15): 2605-2615. DOI:10.1016/j.applthermaleng.2011.04.028 |
| [3] |
CHEN H, YANG G, WU J. A multi-zone thermodynamic model for predicting LNG ageing in large cryogenic tanks[J]. Energy, Elsevier BV, 2023, 283: 128503. |
| [4] |
LIN Y, YE C, YU Y, et al. An approach to estimating the boil-off rate of LNG in type C independent tank for floating storage and regasification unit under different filling ratio[J]. Applied Thermal Engineering, 2018, 135: 463–471.
|
| [5] |
JEON G M, PARK J C, KIM J W, et al. Experimental and numerical investigation of change in boil-off gas and thermodynamic characteristics according to filling ratio in a C-type cryogenic liquid fuel tank[J]. Energy, 2022, 255: 124530. DOI:10.1016/j.energy.2022.124530 |
| [6] |
LEE J H, KIM Y J, HWANG S. Computational study of LNG evaporation and heat diffusion through a LNG cargo tank membrane[J]. Ocean Engineering, 2015, 106: 77-86. DOI:10.1016/j.oceaneng.2015.06.045 |
| [7] |
CHOI S W, KIM H S, LEE W I. Analysis of leaked LNG flow and consequent thermal effect for safety in LNG cargo containment system[J]. Ocean Engineering, 2016, 113: 276-294. DOI:10.1016/j.oceaneng.2015.12.046 |
| [8] |
LEE W H. Pressure iteration scheme for two-phase flow modeling[C]// Veziroglu, T N. Multiphase Transport: Fundamentals, Reactor Safety, Applications. Miami Beach, FL. 1980.
|
| [9] |
钱希鸿, 陈威. 船舶LNG储槽晃荡热动响应特性分析[J]. 舰船科学技术, 2020, 42(15): 82-87. QIAN X H, CHEN W. Thermodynamic response analysis of sloshing ship in marine LNG storage tank[J]. Ship Science and Technology, 2020, 42(15): 82-87. |
| [10] |
GROTLE E L, ÆSØY V. Dynamic modelling of the thermal response enhanced by sloshing in marine LNG fuel tanks[J]. Applied Thermal Engineering, 2018, 135: 512-520. DOI:10.1016/j.applthermaleng.2018.02.086 |
| [11] |
GROTLE E, ÆSØY V. Numerical simulations of sloshing and the thermodynamic response due to mixing[J]. Energies, 2017, 10(9): 1338. DOI:10.3390/en10091338 |
| [12] |
戴经武. 全压式液化气船设计[J]. 船舶, 1993(1): 1-10+18. |
 2025, Vol. 47
2025, Vol. 47
