现代鱼雷是一种战术技术性能日趋先进、结构精密复杂、耗资很大的精确制导武器[1]。目前鱼雷主要的使用方式包括线导和自导,自导方式包括声自导和尾流自导[2]。在攻击中远距离目标时,由于目标运动要素解算误差导致的目标散布范围较大,鱼雷散布也大,自导鱼雷命中概率较低。所以,通常采用“线导+声自导[3 − 4]”或“线导+尾流自导[5 − 6]”攻击中远距离目标,鱼雷发射后利用线导通道导引鱼雷攻击目标,以提高鱼雷命中概率。
在线导鱼雷导引过程中有可能出现鱼雷穿越目标航迹线(或目标尾流),而没有进行自动跟踪的情况,这时候采用人工导引是比较有效的补救导引办法。但是,传统人工导引方法需要操作人员快速准确指定鱼雷导向位置点,操作难度较大易于出现失误,导致鱼雷导引失败捕获不到目标。为了解决上述问题,实现线导鱼雷人工导引过程自动化控制,本文提出了一种基于目标运动要素的线导鱼雷人机相辅导引方法,构建了目标位置导引和鱼雷占位导引2种鱼雷导向位置点计算模型,并设计了线导鱼雷人机相辅导引控制过程。在鱼雷尾流自导攻击不能满足入尾流角要求情况下,先使用鱼雷占位导引计算模型计算鱼雷导向位置点,在鱼雷占位过程中,当满足入尾流要求时,再调用目标位置导引计算模型计算鱼雷导向位置点;在鱼雷声自导攻击情况下,直接采用目标位置导引计算模型计算鱼雷导向位置点。
1 目标运动要素目标运动要素主要包括目标方位
目标运动要素误差是指实际用于计算的目标运动要素与目标真实运动要素的差值,是影响自导鱼雷和线导鱼雷发现目标概率的主要因素。目标航向误差
经过大样本统计,目标运动要素解算求得的目标运动要素误差导致的目标位置散布可以近似看作服从正态分布[8],散布区域近似为椭圆。
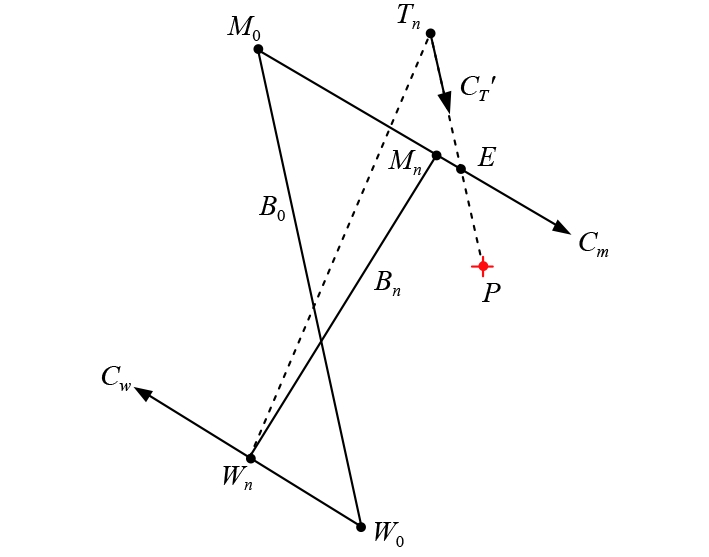
2 人工导引方法人工导引方法[9]是在鱼雷攻击过程中通过人工干预确定鱼雷导向位置点,计算鱼雷当前位置到该导向位置点的方向(即下一时刻鱼雷导引航向),并控制鱼雷导向该位置点。人工导引示意图如图1所示。
|
图 1 人工导引示意图 Fig. 1 Manual guidance diagram |
图中:
| $ {C_T}^\prime = \arctan \frac{{{X_P} - {X_T}(n)}}{{{Y_P} - {Y_T}(n)}}。$ | (1) |
根据线导鱼雷导引时雷目态势以及鱼雷自导弹道要求,本文分别设计了目标位置导引和鱼雷占位导引[10]2种鱼雷推荐导向位置点计算模型,以及人机相辅导引方法控制过程。
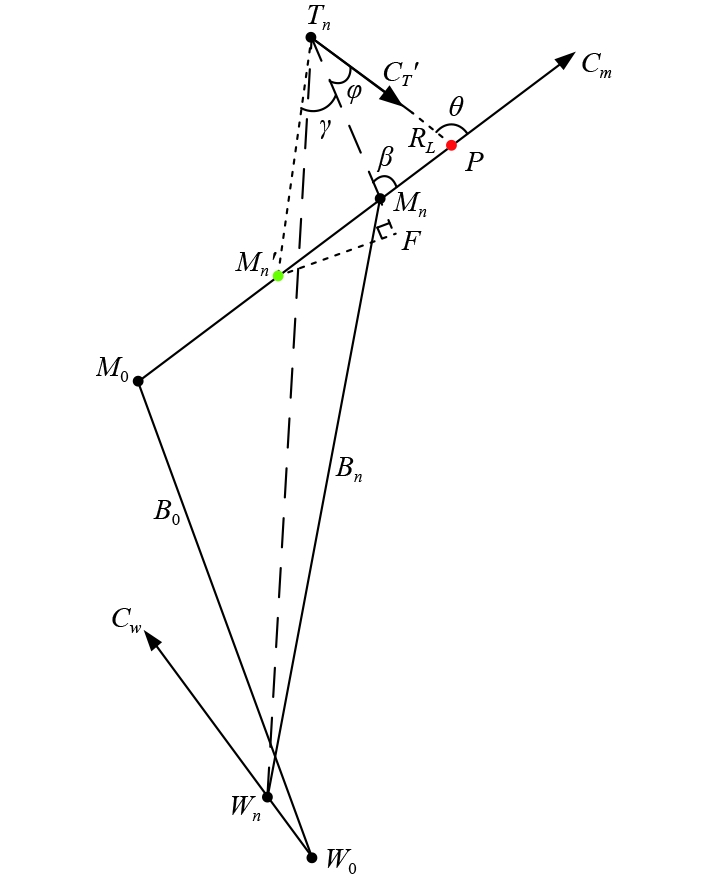
3.1 目标位置导引计算模型根据当前时刻目标位置和目标运动要素信息,以及鱼雷当前时刻位置信息和鱼雷速度,计算目标与鱼雷相遇点位置以及鱼雷到相遇点的航向,该相遇点就是鱼雷导向位置点。声自导鱼雷与目标相遇实际上是鱼雷声自导扇面形心[11]与目标相遇;尾流自导鱼雷与目标相遇实际上是鱼雷与目标尾流瞄准点[12]相遇。目标位置导引示意图如图2所示。
|
图 2 目标位置导引示意图 Fig. 2 Target position guidance diagram |
假设目标与鱼雷再次相遇点
1)计算当前时刻鱼雷相对目标的方位
| $ {B_{MT}} = \arctan \frac{{{X_T}(n) - {X_m}(n)}}{{{Y_T}(n) - {Y_m}(n)}} 。$ | (2) |
2)在直角三角形
| $ {T_n}{M_n} = \sqrt {{{\left[ {{X_T}(n) - {X_m}(n)} \right]}^2} + {{\left[ {{Y_T}(n) - {Y_m}(n)} \right]}^2}},$ | (3) |
| $ \gamma = \arctan \frac{{m \times {R_L} \times \sin \beta }}{{{T_n}{M_n} + m \times {R_L} \times \cos \beta }} 。$ | (4) |
3)在三角形
| $ \frac{{\sin (\gamma + \varphi )}}{{\sin (\beta - \gamma )}} = \frac{{{M_n}^\prime P}}{{T{}_nP}} = m,$ | (5) |
| $ \varphi = \arcsin \left[ {m \times \sin (\beta - \gamma )} \right] - \gamma 。$ | (6) |
4)计算鱼雷航向
| $ {C_T}^\prime = {B_{MT}} + \pi + \varphi \times SIGN({Q_{MT}}),$ | (7) |
| $ \theta = {C_m} - {C_T}^\prime 。$ | (8) |
5)计算相遇时间
| $ \Delta t = \left| {\frac{{{T_n}{M_n} \times \sin \beta }}{{{V_T} \times \sin \theta }}} \right|,$ | (9) |
| $ \left\{ \begin{gathered} {X_P} = {X_m}(n) + \left(\Delta t - \frac{{{R_L}}}{{{V_T}}}\right) \times {V_m} \times \sin ({C_m}),\\ {Y_P} = {Y_m}(n) + \left(\Delta t - \frac{{{R_L}}}{{{V_T}}}\right) \times {V_m} \times \cos ({C_m})。\\ \end{gathered} \right. $ | (10) |
式中:
如果鱼雷自导方式为尾流自导,当采用3.1节方法计算的命中角(尾流自导时也是入尾流角)不能满足鱼雷对入尾流角要求
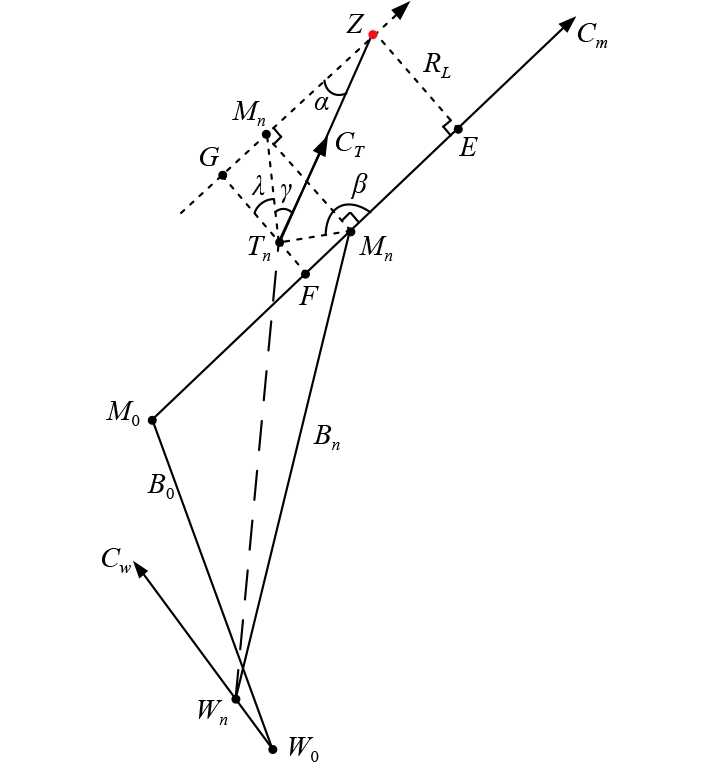
鱼雷占位导引示意图如图3所示。
|
图 3 鱼雷占位导引示意图 Fig. 3 Torpedo occupation guidance diagram |
首先设计鱼雷占位点
1)使用3.1节中式(2)计算当前时刻鱼雷相对目标的方位
2)计算当前时刻鱼雷到
| $ \left\{ \begin{aligned} &{T_n}G = {R_L} - {T_n}F,{{T_n}F < {R_L}},\\ &{T_n}G = {T_n}F - {R_L},{{T_n}F > {R_L}},\\ &{T_n}G = 0,{{T_n}F = {R_L}}。\\ \end{aligned} \right. $ | (11) |
| $ {T_n}{M_n}^\prime = \sqrt {{{({M_n}^\prime G)}^2} + {{({T_n}G)}^2}} 。$ | (12) |
3)在三角形
| $ \sin \alpha = \frac{{{T_n}G}}{{{T_n}Z}},$ | (13) |
| $ \frac{{{M_n}^\prime Z}}{{\sin \gamma }} = \frac{{{T_n}{M_n}^\prime }}{{\sin \alpha }} \Rightarrow \frac{{{T_n}Z \times m}}{{\sin \gamma }} = {T_n}{M_n}^\prime \times \frac{{{T_n}Z}}{{{T_n}G}} ,$ | (14) |
| $ \gamma = \arcsin \frac{{{T_n}G \times m}}{{{T_n}{M_n}^\prime }} ,$ | (15) |
| $ \lambda = \arcsin \frac{{{M_n}^\prime G}}{{{T_n}{M_n}^\prime }},$ | (16) |
| $ \alpha = \frac{\text{π} }{2} - (\gamma + \lambda )。$ | (17) |
4)计算占位点位置坐标
| $ \left\{ \begin{aligned} &{T_n}Z = \frac{{{T_n}G}}{{\sin \alpha }},{{T_n}G \ne 0},\\ &{T_n}Z = \frac{{{M_n}^\prime G}}{{1 - m}},{{T_n}G = 0} 。\\ \end{aligned} \right. $ | (18) |
| $ \left\{ \begin{aligned} &{C_T}^\prime = {C_m} + \alpha \times {\mathrm{sign}}({Q_{MT}}),{{T_n}F < {R_L}},\\ &{C_T}^\prime = {C_m} - \alpha \times{\mathrm{sign}}({Q_{MT}}),{{T_n}F > {R_L}} ,\\ &{C_T}^\prime = {C_m},{{T_n}F = {R_L}} 。\\ \end{aligned} \right. $ | (19) |
| $ \left\{ \begin{gathered} {X_Z} = {X_T}(n) + {T_n}Z \times \sin ({C_T}^\prime ) ,\\ {Y_Z} = {Y_T}(n) + {T_n}Z \times \cos ({C_T}^\prime )。\\ \end{gathered} \right. $ | (20) |
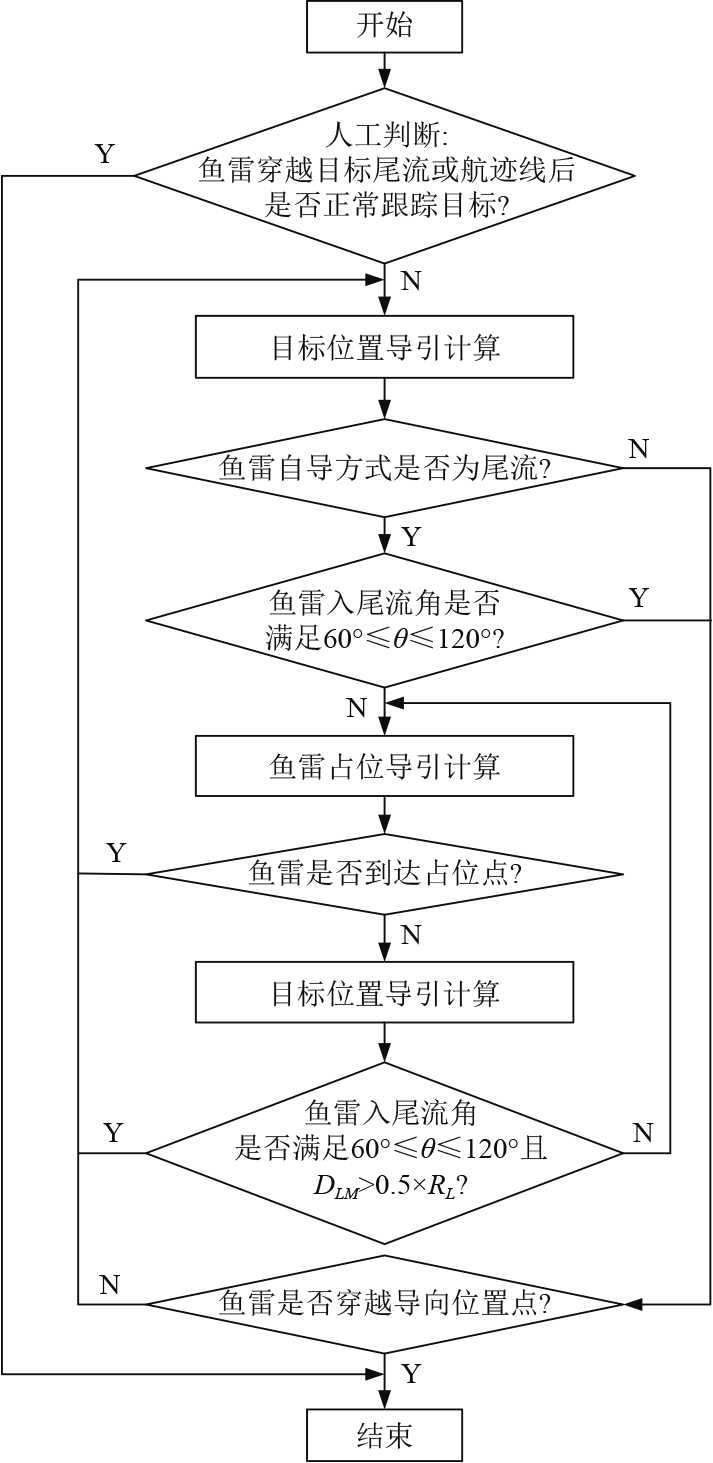
线导鱼雷人机相辅导引方法控制过程如图4所示。
|
图 4 线导鱼雷人机相辅导引控制流程图 Fig. 4 Control flow chart of man-machine guidance for wire-guided torpedo |
1)在人工判断鱼雷穿越目标尾流或航迹线基础上,调用目标位置导引计算模型计算鱼雷航向、命中角以及鱼雷导向位置点信息,并控制鱼雷导向该位置点;
2)当为尾流自导鱼雷时,在判断出鱼雷命中角(入尾流角)不满足弹道要求情况下(考虑到误差影响实际入尾流角判断范围为
3)在鱼雷向占位点机动过程中,同时使用3.1中的方法周期计算命中角,当鱼雷命中角满足
在发射平台和目标都在进行匀速直航运动情况下,根据已发表的文献资料选择典型的鱼雷攻击态势对人机相辅导引方法进行仿真验证。根据文献[13]设计声自导鱼雷发现目标判断方法,声自导扇面开角100°,声自导作用距离
根据目标舷角大、中、小,目标航速高、中、低,目标距离远、中,设计18个典型态势进行仿真测试。发射平台态势:航速6 kn,航向10°。目标具体态势如表1所示。
|
|
表 1 目标态势信息表 Tab.1 Torpedo detection of target trajectory statistics table |
针对目标方位
1)目标方位误差
2)目标距离误差
3)目标航速误差
4)目标航向误差
根据上述18个典型态势进行仿真测试,针对声自导和尾流自导鱼雷每个态势各测试
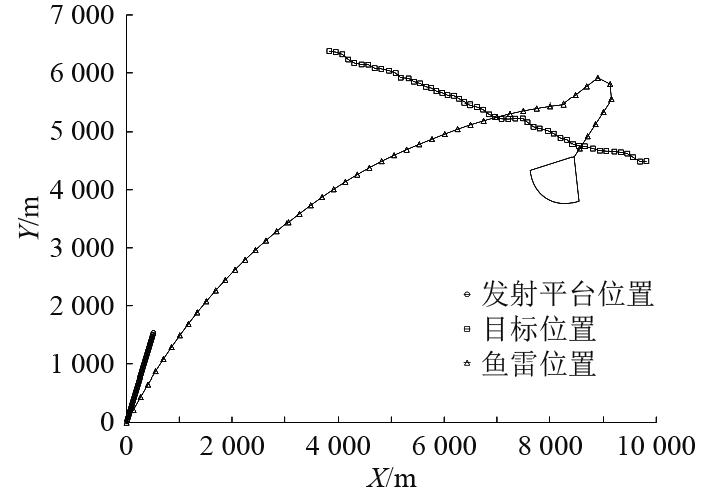
|
图 5 线导+尾流自导鱼雷导引弹道示意图 Fig. 5 Schematic diagram of guided trajectory of a wire-guided and wake homing torpedo |
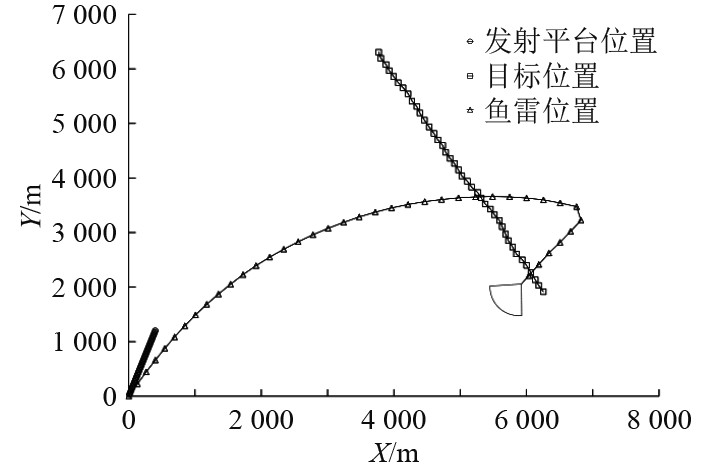
|
图 6 线导+声自导鱼雷导引弹道示意图 Fig. 6 Schematic diagram of guided trajectory of a wire-guided and acoustic homing torpedo |
|
|
表 2 鱼雷发现目标情况统计表 Tab.2 Torpedo detection of target trajectory statistics table |
在发射平台和目标都是进行匀速直航运动情况下,针对目标方位、距离、航速和航向分别增加正态分布随机误差,系统设定为判断出鱼雷穿越目标航迹线(或目标尾流)60 s后调用人机相辅导引方法导引鱼雷,可以有效控制鱼雷重新搜索发现目标。具体情况如下:
1)线导+声自导鱼雷在上述典型态势中经过人机相辅导引重新发现目标概率为100%。经分析数据,声自导鱼雷穿越目标航迹线60 s后距目标最大理论距离约为
2)线导+尾流自导鱼雷在上述典型态势中经过人机相辅导引重新发现目标概率超过88%。经分析数据,目标尾流长度随目标速度降低而减小,目标高速时尾流长度约为
3)后续还需要进一步研究在特殊态势下目标运动要素误差对鱼雷发现目标概率影响情况。
5 结 语本文提出一种基于目标运动要素的线导鱼雷人机相辅导引方法,在人工确认鱼雷没有正常跟踪目标前提下,利用目标运动要素和线导鱼雷位置信息,自动计算推荐鱼雷导向位置点,系统控制鱼雷导向该位置点,可以实现人工导引过程自动控制,缩短系统反应时间,减少操作失误风险,有利于提升线导鱼雷发现目标概率。经仿真验证,在典型态势中鱼雷经过人机相辅导引重新发现目标概率很高,线导+声自导鱼雷发现目标概率为100%,线导+尾流自导鱼雷发现目标概率超过88%。
| [1] |
孟庆玉, 张静远, 宋保维. 鱼雷作战效能分析[M]. 北京: 国防工业出版社, 2003.
|
| [2] |
司广宇. 潜艇指控系统理论与应用[M]. 北京: 电子工业出版社, 2018.
|
| [3] |
李家腾, 邱长卿, 范学满. 一种基于目标指示的现在时刻推算方位导引法[J]. 软件, 2021, 42(10): 50-53. |
| [4] |
李家腾, 刘剑, 范学满. 基于目指信息的潜射线导鱼雷环形搜索方案研究[J]. 舰船电子工程, 2021, 41(10): 24-29. |
| [5] |
野学范, 朱伟良, 张靖康, 等. 一种改进的线导+尾流自导鱼雷导引方法[J]. 火力与指挥控制, 2015, 40(9): 172-175. |
| [6] |
王顺杰, 朱伟良, 李斌. 基于过去方位导引法的线导+尾流自导鱼雷攻击问题研究[J]. 兵工自动化, 2014, 33(11): 11-13. |
| [7] |
王顺杰, 张玉玲, 罗向前. 目标运动要素误差对尾流自导鱼雷齐射影响[J]. 指挥控制与仿真, 2020, 42(3): 52-56. |
| [8] |
刘强, 袁富宇. 声自导鱼雷发现概率统计计算新思路[J]. 制造业自动化, 2011, 33(24): 79-83,111. |
| [9] |
李斌, 张靖康, 李刚. 基于模糊控制的线导鱼雷方位导引法[J]. 兵工自动化, 2014, 33(5): 11-14. |
| [10] |
曲丰. 提升线导鱼雷捕获概率的方法[D]. 武汉: 华中科技大学, 2017.
|
| [11] |
徐继华, 袁富宇. 基于折线简化的方位导引方法的可用性研究[J]. 指挥控制与仿真, 2017, 39(2): 31-35. |
| [12] |
武志东, 李斌, 夏佩伦. 潜射鱼雷命中结果的解析计算方法[J]. 数学的实践与认识, 2016, 46(17): 149-153. |
| [13] |
崔滋刚, 张仪, 李志伟. 潜射鱼雷攻击水面舰船时的声自导发现概率仿真研究[J]. 计算机测量与控制, 2017, 25(6): 92-94. |
| [14] |
王顺杰, 丁文强, 朱伟良. 目标对抗条件下自导+线导鱼雷连射方法[J]. 火力与指挥控制, 2020, 45(5): 82-86. |
| [15] |
龚小林, 李志伟. 尾流自导鱼雷快速攻击目标发现概率仿真分析[J]. 舰船电子工程, 2021, 41(9): 97-101. DOI:10.3969/j.issn.1672-9730.2021.09.022 |
| [16] |
李长文, 毛俊超, 初磊. 目标运动要素稳定性的图形表达探讨[J]. 鱼雷技术, 2016, 24(2): 137-140. |
 2025, Vol. 47
2025, Vol. 47
