2. 机械传动与制造工程湖北省重点实验室,湖北 武汉 430081
2. Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering, Wuhan 430081, China
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)因其较高的可靠性和成本优势,被广泛用于新能源绿色船舶电力推进系统中[1]。PMSM本质上是个多变量且紧密耦合的非线性系统,容易受到系统参数变化以及外界负载扰动的影响[2]。传统PI控制器过于依赖电机参数,仅通过该算法进行电机控制无法满足精度要求[3],为了增强控制性能,在调速系统中采用了许多非线性控制技术,包括模型预测控制、自抗扰控制、滑模控制、线性最优控制[4 − 6]。滑模控制因其快速性、鲁棒性强、抗外部扰动性强等优点而被广泛应用。
传统滑模控制使用线性滑模曲面逐渐收敛,收敛时间过长且无法估计。结合有限时间稳定理论,提出终端滑模控制[7]的永磁同步电机调速控制策略,通过在线性滑模曲面上引入非线性分量,提高系统的收敛速度。但是该滑模曲面中有负指数项,容易导致控制量无穷大进而产生奇异点。非奇异快速终端滑模控制(Non-singular Fast Terminal Sliding Mode Control,NFTSMC)系统[8]规避这个问题,但不同的初始状态对收敛速度有着明显的影响。将其与固定时间稳定理论相结合,提出一种固定时间非奇异终端滑模控制器[9],能够保证在不同初始状态下都能够在一个固定时间内收敛到平衡,固定时间控制理论对于收敛时间的估计是过度的且与控制器可调参数无明显关系,且控制器不显含时间上界。预定义时间控制(Predefined-time Sliding Mode Control,PTSMC)正好解决了这一问题。预定义时间控制器[10]的可调参数为稳定时间的上界,相对于固定时间滑模控制算法,不仅收敛时间显含在控制器中,而且收敛时间相较于固定时间滑模控制算法更快。
当控制系统中出现外部扰动时,必须增大控制器增益,才能满足系统的稳定控制。但是过大的控制增益会严重影响系统的控制器性能。负载观测器[11]可用于准确估算系统扰动转矩并前馈补偿到永磁同步电机系统中,避免了因采用高增益导致的控制器性能下降的问题,从而提高系统抗扰动性。
船舶本体、船舶推进电机及螺旋桨构成了船-机-桨的电力推进系统,为了满足性能指标的要求,必须对动力推进系统进行整体研究[12],为了确保电力推进系统的稳定性就需要对搭建的系统进行仿真分析,刘英杰等[13]基于船桨的基本特性,搭建船桨的数学模型,分析螺旋桨负载特性在不同工作环境下的动态响应,但缺乏对电机控制方面的研究。李浩等[14]建立了螺旋桨负载和永磁推进电机矢量控制的联合仿真模型,但仅使用传统PI速度环控制器,缺乏对控制器的参数设计。
针对以上问题,本文提出一种基于新型预定义时间稳定理论的滑模面。相较于现有的滑模曲面,减少了滑模参数数量,降低运算复杂程度,相较于有限时间控制算法,其收敛时间在控制器参数显性表示。同时使用该滑模面设计了永磁同步电机速度环矢量控制器,针对负载变化造成的系统控制稳定性下降的问题,设计了滑模扰动观测器对永磁同步电机系统进行前馈补偿,最后结合船-机-桨模型进行了仿真试验,验证了本文所设计的控制器收敛速度更快,能够实现预定义时间收敛且具有较好的抗干扰性能。
1 船舶电力推力系统建模 1.1 PMSM永磁同步电机数学模型永磁同步电机是一种复杂的系统,具有非线性、多变量和强耦合性等特点。建立永磁同步电机数学模型需要作出以下假设[15]:空间磁场呈正弦分布,忽略永磁同步电机铁芯饱和,不考虑涡流和磁耗。永磁同步电机的定子电压方程为:
| $ \left\{\begin{aligned} & u_d=Ri_d+L_d\frac{\mathrm{d}i_d}{\mathrm{d}_t}-p_n\omega_mL_qi_q,\\ & u_q=Ri_q+L_d\frac{\mathrm{d}i_q}{\mathrm{d}t}-p_n\omega_m\left(L_di_d+\varphi_f\right)。\end{aligned}\right. $ | (1) |
式中:
电磁转矩方程为:
| $ {{{\boldsymbol{T}}}_e} = \frac{3}{2}{p_n}{i_q}\left[ {{i_d}({L_d} - {L_q}) + {\varphi _f}} \right]。$ | (2) |
永磁同步电机的运动方程表示为:
| $ J\frac{\mathrm{d}\omega_m}{\mathrm{d}t}=T_e-T_L-B\omega_m。$ | (3) |
对于表贴式永磁同步电机,由于转子磁路对称,即
| $ \frac{\mathrm{d}\omega_m}{\mathrm{d}t}=\frac{3p_n\varphi_fi_q}{J}-\frac{T_L}{J}-\frac{B}{J}\omega_m。$ | (4) |
式中:
考虑以下非线性系统:
| $ \dot x(t) = f(x(t)),x(0) = {x_0}。$ | (5) |
式中:
定义1 若该系统能够在一个有限时间
定义2 若系统存在一个与系统初始状态无关的常数
定义3 若系统状态收敛时间
理论1 文献[10]提出一种预定义时间稳定的Lyapunov函数的一个新的充分条件,设预定义常数
| $ \dot{V}\leqslant-\frac{1}{T_c}\frac{2}{\alpha}\left(2V+V^{1-\frac{\alpha}{2}}+V^{1+\frac{\alpha}{2}}\right)。$ | (6) |
其中,
将系统状态变量定义为:
| $ \left\{\begin{gathered}e=\omega^*-\omega_m,\\ \dot{e}=-\dot{\omega}_m=-\frac{3P_n\varphi_f}{2J}i_q+\frac{B}{J}\omega_m+\frac{T_L}{J}。\end{gathered}\right. $ | (7) |
预定义时间滑模面可设计为:
| $ s=e+\int_0^t(c_1e+c_2\left|e\right|^{1+\alpha}+c_3\left|e\right|^{1-\alpha})\mathrm{sign}(e)\mathrm{d}t。$ | (8) |
其中,
对式(8)预定义时间滑模面求导可得:
| $ \dot{s}=\dot{e}+c_1e+c_2\left|e\right|^{1+\alpha}+c_3\left|e\right|^{1-\alpha}。$ | (9) |
结合式(7)、式(9)可得控制器为:
| $ \begin{gathered} {i_q} = \frac{{2J}}{{3{P_n}{\varphi _f}}}\left[ {{c_1}e + {c_2}\left( {1 + \alpha } \right){{\left| e \right|}^\alpha } + } \right. \\ {c_3}\left( {1 - \alpha } \right){\left| e \right|^{ - \alpha }}\left. { + \frac{B}{J}\dot e + qs + k{\mathrm{sign}}\left( s \right)} \right]。\\ \end{gathered} $ | (10) |
对于永磁同步电机控制系统,选用所设计的滑模面和控制器时,系统为全局实际预定义时间稳定系统,该系统状态能够在预定义时间
选取全局正定的Lyapunov函数:
| $ V_S=\frac{1}{2}S^2。$ | (11) |
对式(11)求导可得:
| $ \begin{aligned}\dot{V}=s\cdot\dot{s}=s(\dot{e}+c_1e+c_2\left|e\right|^{1-\frac{a}{2}}+c_3\left|e\right|^{1+\frac{a}{2}})= \\ \begin{array}{*{20}{c}} & s\left(-qs-k\mathrm{sign}\left(s\right)\right)\end{array}=-\left(qs^2+k\left|s\right|\right)\leqslant 0。\\ \end{aligned} $ | (12) |
所设计的预定义时间滑模控制器满足上述理论,证明了稳定性,且根据理论1可知系统误差可在预定义时间
在滑模控制中鲁棒性越强,趋近速率越快,但抖振也会越大。为减小滑模控制的抖振问题,使用连续的饱和函数
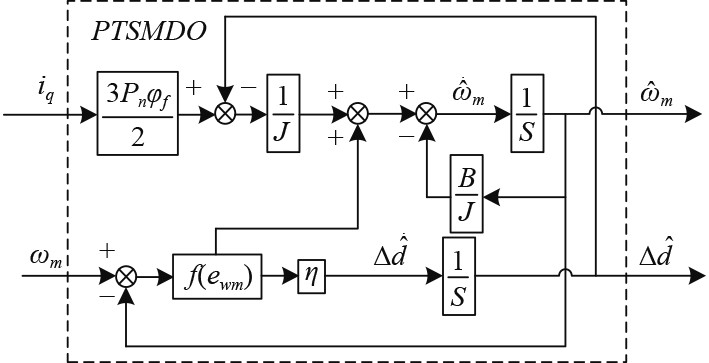
设计了一种滑模观测器来估计负载值并将其反馈给永磁同步电机速度环控制,增强系统的抗扰动性能,增加系统的稳定性,观测器结构如图1所示。
|
图 1 预定义时间滑模扰动观测器结构框图 Fig. 1 Structure block diagram of the PTSMDO |
考虑电机内部参数摄动和外部位置干扰[8],方便将式(4)改写为:
| $ \left\{\begin{aligned} & \frac{\mathrm{d}\omega_m}{\mathrm{d}t}=\frac{3p_n\varphi_fi_q}{J}-\frac{B}{J}\omega_m-\frac{\Delta d}{J},\\ & \Delta d=\Delta T_e+T_L。\end{aligned}\right. $ | (13) |
式中:
| $ \left[\begin{gathered}\dot{\omega}_m \\ \Delta\dot{d} \\ \end{gathered}\right]=\left[\begin{array}{*{20}{c}}-\displaystyle\frac{B}{J} & -\displaystyle\frac{1}{J} \\ \; \; 0 & 0\end{array}\right]\left[\begin{array}{*{20}{c}}\omega_m \\ \Delta d\end{array}\right]+\left[\begin{array}{*{20}{c}}\displaystyle\frac{1}{J} \\ 0\end{array}\right]T_L。$ | (14) |
以机械角速度
| $ {\begin{split} \left[ \begin{gathered} {{\dot \hat \omega }_m} \\ \Delta {\dot\hat{ d}} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{B}{J}}&{ - \displaystyle\frac{1}{J}} \\ 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\hat \omega }_m}} \\ {\Delta \hat d} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{1}{J}} \\ 0 \end{array}} \right]{T_L} + \left[ {\begin{array}{*{20}{c}} 1 \\ \eta \end{array}} \right]f\left( {{e_{\omega m}}} \right)。\end{split} }$ | (15) |
式中:
联合式(14)和式(15)可得:
| $ \left[ \begin{gathered} {{\dot e}_{\omega m}} \\ {{\dot e}_d} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{B}{J}}&{ - \displaystyle\frac{1}{J}} \\ 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\hat \omega }_m}} \\ {\Delta \hat d} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} 1 \\ \eta \end{array}} \right]f\left( {{e_{wm}}} \right)。$ | (16) |
其中,
| $ \begin{split} f\left( {{e_{\omega m}}} \right) = &\left( {{c_1} + {c_2}\left( {1 + \alpha } \right){{\left| e \right|}^\alpha } + \left. {{c_3}\left( {1 - \alpha } \right){{\left| e \right|}^{ - \alpha }}} \right)\dot e +} \right. \\ &\frac{B}{J}\dot e + p\mathrm{sign}\left( s \right)。\end{split} $ | (17) |
通过
选取全局正定的Lyapunov函数:
| $ \begin{split} \dot V = s \cdot \dot s = s(\dot e + {c_1}e + {c_2}{\left| e \right|^{1 - \frac{a}{2}}} + {c_3}{\left| e \right|^{1 + \frac{a}{2}}})= \\ \begin{array}{*{20}{c}} {}&{ s\left( { - p\mathrm{sign}\left( s \right)} \right) = - p\left| s \right| \leqslant 0}。\end{array} \end{split} $ | (18) |
上述可证明所设计的滑模扰动观测器符合稳定性原理。
1.5 螺旋桨负载的动态数学模型螺旋桨是驱动船舶运动的主要装置,船舶螺旋桨系统是推进电机带动螺旋桨旋转,当该推力方向与船舶前进方向相同时,推动船舶前进,船体则受到水流的反作用力,形成推进系统的负载力矩,同时船速和螺旋桨转速的任何变化都会直接影响螺旋桨负载转矩和推力。依据螺旋桨的工作原理[12],其旋转时产生的推力
| $ \left\{ \begin{aligned} &P = {K_P}\rho {n^2}D_P^4,\\ &{T_L} = {K_M}\rho {n^2}D_P^5。\\ \end{aligned} \right. $ | (19) |
式中:
| $ J = \frac{{{h_p}}}{D} = \frac{{{V_p}}}{{nD}}。$ | (20) |
文献[14]通过螺旋桨敞水试验给出了
螺旋桨旋转时会使得附近水流压力下降,导致船舶首尾形成压力差,产生额外的阻力,推力减额系数
| $ {P_e} = P\left( {1 - t} \right)。$ | (21) |
当考虑到船舶主体后,螺旋桨进速
| $ {V_P} = {V_s}\left( {1 - \omega } \right)。$ | (22) |
其中,伴流系数
| $ kM_s\frac{\mathrm{d}V_s}{\mathrm{d}t}=P_e-R。$ | (23) |
式中:
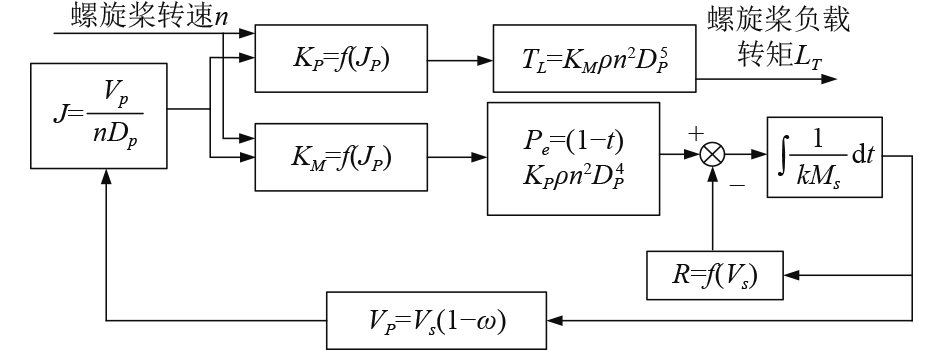
|
图 2 螺旋桨负载模型 Fig. 2 Propeller load model |
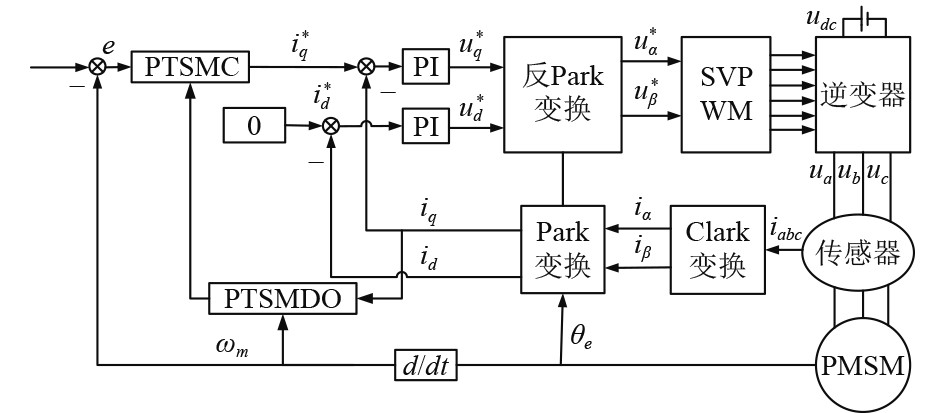
为了验证本文所设计的控制策略在永磁同步电机驱动系统中的有效性和可行性,基于Matlab/Simulink平台搭建永磁同步电机矢量控制仿真模型,具体PMSM控制系统结构如图3所示,选取电机参数与文献[8]相同,控制器相关参数如表1所示。本文将NFTSMC控制策略与PTSMC控制策略在电机空载启动和突变负载下的性能进行对比。
|
图 3 PMSM控制系统结构框图 Fig. 3 PMSM control system |
|
|
表 1 控制器参数 Tab.1 Controller parameters |
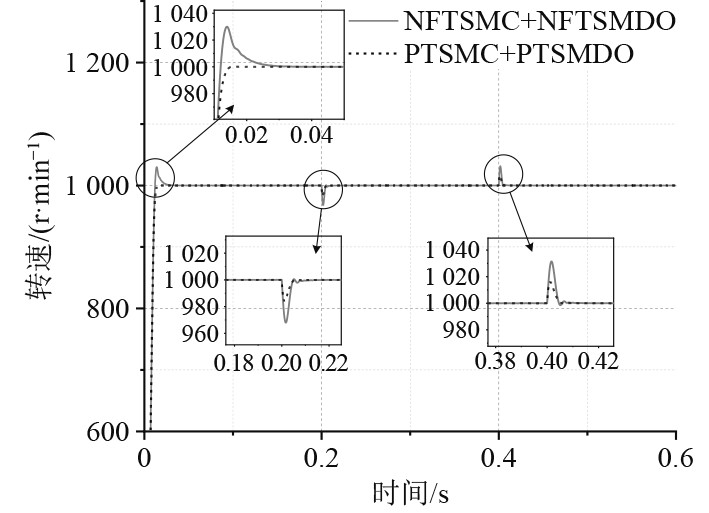
图4显示系统在0~
|
图 4 速度响应曲线对比 Fig. 4 Comparison of speed response |
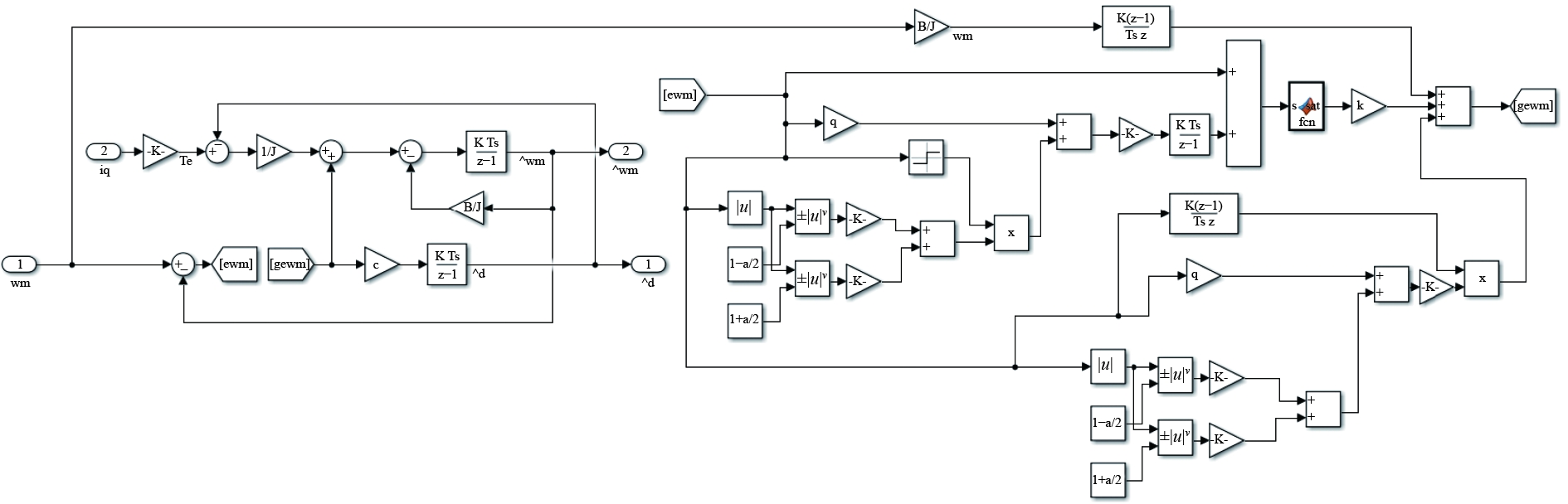
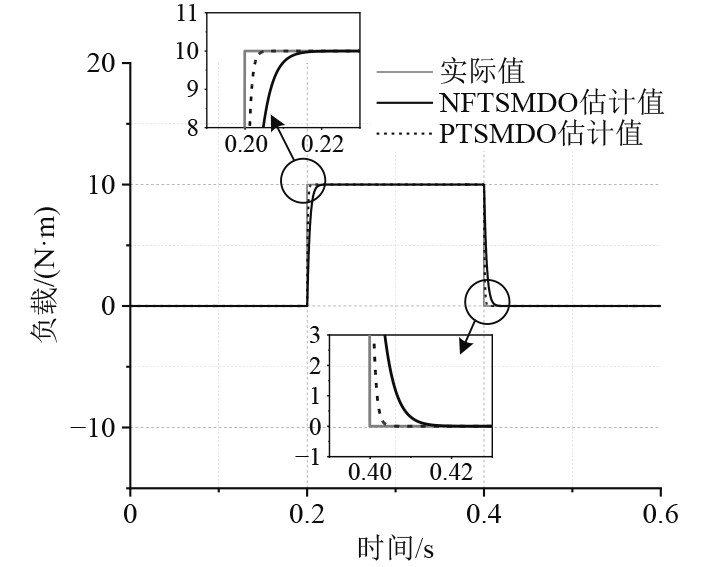
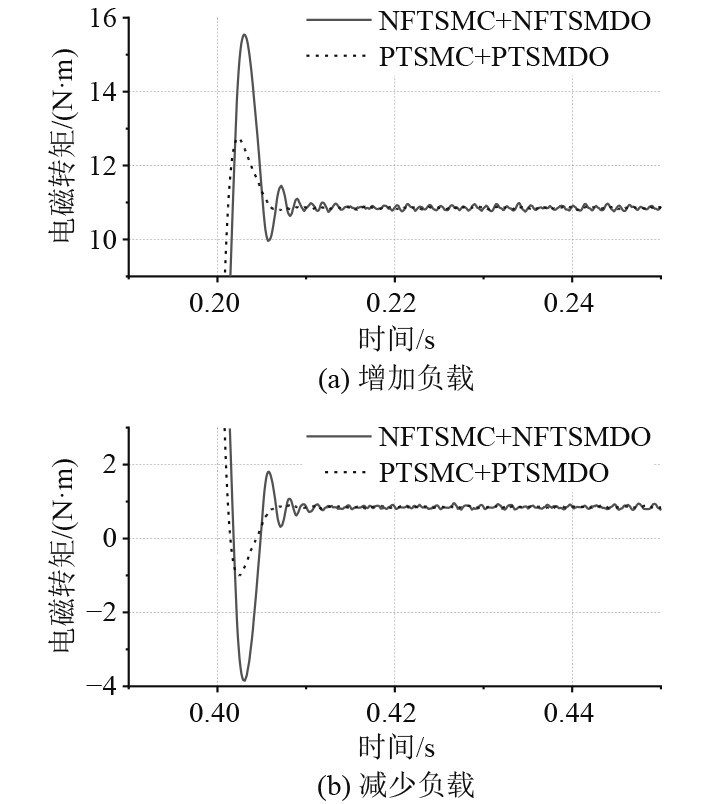
图5为PTSMDO的仿真模型,图6对比了NFTSMDO和PTSMDO的负载估计值。可以看出,PTSMDO比NFTSMDO响应速度更快且准确的估计扰动值。图7为突变负载时的电磁转矩局部放大图,可以看出PTSMC-PTSMDO的稳定性能明显大于另一种控制策略,能明显降低因负载突变所引起的电磁转矩变化,使速度波动最小化,综上所述本研究的控制策略具有较好动态跟踪特性和抗干扰性能。
|
图 5 预定义时间滑模观测器仿真模型 Fig. 5 Simulation model of PTSMDO |
|
图 6 负载实际值与观测器估计值 Fig. 6 Load disturbance observation |
|
图 7 电磁转矩响应曲线对比 Fig. 7 Comparison of electromagnetic torque response |
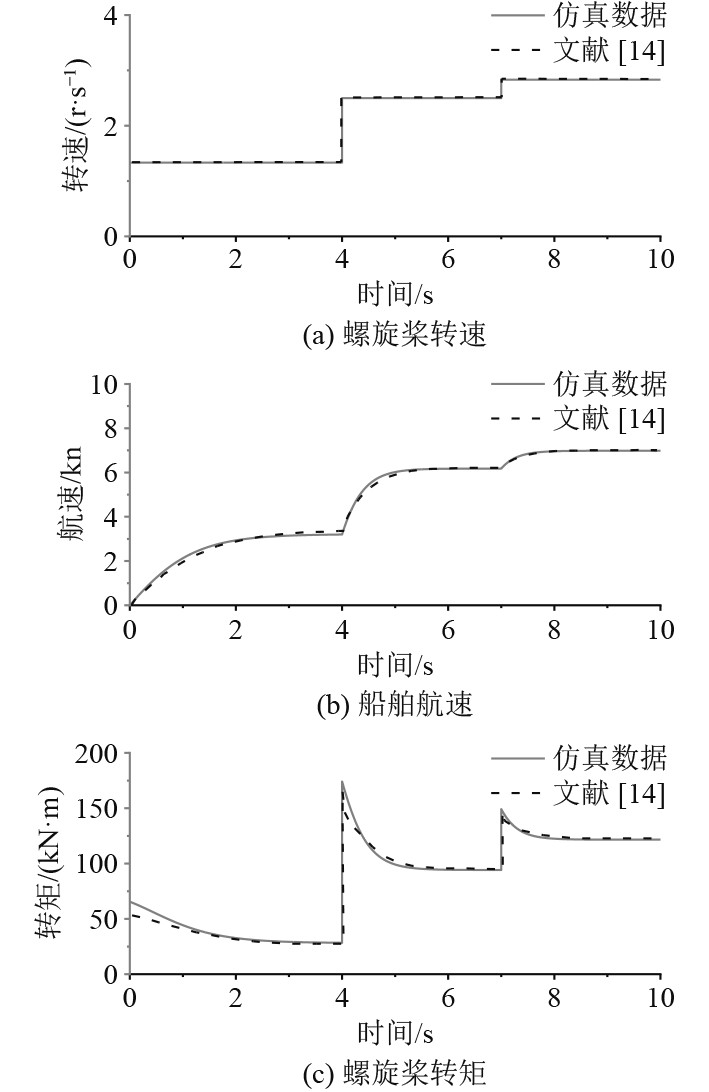
为了验证模型的准确性,本文采用中铁渤海铁路“轮渡1号”船舶[14]的简化船桨模型,使用相同的模型参数和工况进行仿真验证,参数如表2所示。仿真结果与文献的结果对比情况如图8所示,可以看出仿真结果与参考文献基本相符。本文结果中转矩初值过大是由于使用阶跃信号模拟转速变化,导致加速度过大,但基本趋势一致,故该模型能够用于后续仿真研究。
|
图 8 分级启动 Fig. 8 Stepwise start-up |
将简化后的船桨模型联合船用永磁同步电机模型进行仿真,船用永磁同步电机参数如表3所示。在实际船舶正车当中,一般采用分级启动将电机从静止加速到给定转速150 r/min。该过程分为3个阶段,初始阶段为50 r/min,在3 s时提速至100 r/min,6 s时提升至150 r/min,总仿真时间为10 s。
|
|
表 3 船用永磁同步电机参数 Tab.3 Parameters of marine PMSM |
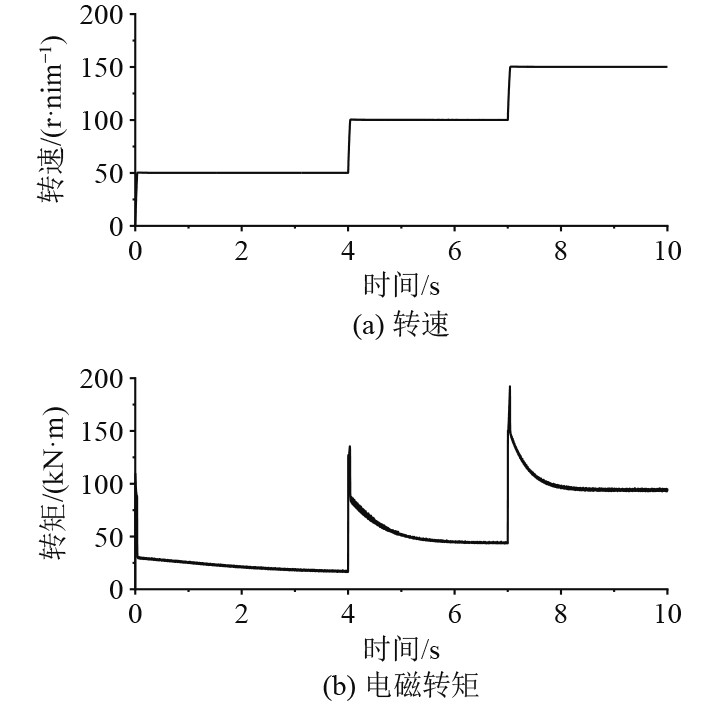
图9为永磁同步电机在船舶分级启动的运行工况,在启动过程中每次加速阶段均没有超调,且响应迅速。电磁转矩在加速阶段的最大转矩为195.2 kN·m,船速稳定后的转矩为94.27 kN·m,均小于该电机的额定电磁转矩,证明该控制策略在船舶运行工况中的合理性。
|
图 9 船用永磁同步电机运行工况 Fig. 9 Operation of marine PMSM |
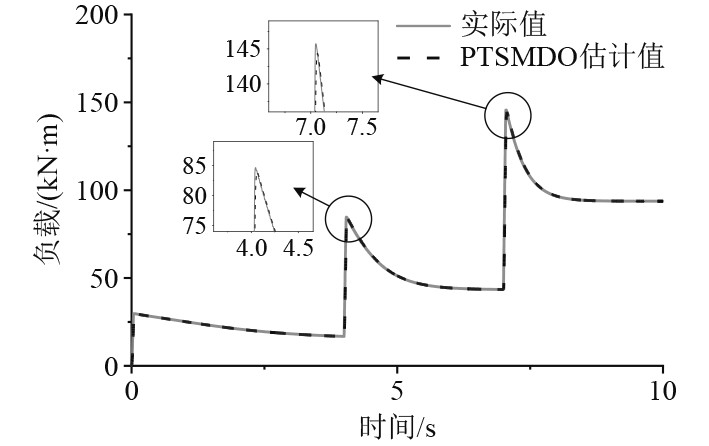
图10对比了电机负载转矩实际值与PTSMDO的估计值,在每级启动的时刻负载转矩都有一次突变,随后又稳定在与螺旋桨转速相对应的转矩值上,突变时的最大估计值与最大实际值如表4所示。船速稳定后电机负载转矩为94.23 kN·m,估计值为94.23 kN·m,可以看出观测器可以快速并准确地估计扰动值,结果表面该控制策略适用于船用永磁同步电机的航行工况中,且具有一定的控制效果。
|
图 10 船舶时变负载实际值与观测器估计值 Fig. 10 Time-varying load of the ship and the estimated value of the observer |
|
|
表 4 观测值与实际值对比数据 Tab.4 Comparison data of observed and actual value |
本文以船用永磁同步推进电机为研究对象,通过船-机-桨之间的基本特性分析,搭建船-机-桨在分级启动工况下的简化模型,基于Lyapunov稳定性理论提出了一种新型预定义时间滑模控制策略,通过仿真分析得出以下结论:
1)针对基于传统滑模速度环控制器收敛速度慢,渐进稳定和时间不显含于参数的问题,将预定义时间滑模的控制策略运用到调速系统中,提高了电机系统响应速度,保证系统能在预定义时间内达到预设值。
2)针对电机负载突变问题和易受外部扰动问题,负载变化值通过PTSMDO快速精准地跟踪时变负载,并前馈补偿至速度环控制器中,相较于NFTSMDO提高了响应速度和估计精度,提高了系统的抗干扰能力和鲁棒性。
3)利用Simulink结合船-机-桨仿真模型试验证明,采用预定义时间控制滑模策略可以在无超调的前提下更快速且精确的达到参考转速,且保证系统具有良好的抗扰动特性以及,可作为一种新型的控制策略用于船舶永磁同步电机。
| [1] |
王凯, 卢博闻, 李仁祥, 等. 船舶多清洁能源混合动力系统及其关键技术[J]. 舰船科学技术, 2020, 42(17): 6-11. WANG K, LU B W, LI R X, et al. Research progress on multi-clean energy hybrid system and the key technologies of ships[J]. Ship Science and Technology, 2020, 42(17): 6-11. |
| [2] |
ZHAO K H, LIU W C, ZHOU R R, et al. Model-free fast integral terminal sliding-mode control method based on improved fast terminal sliding-mode observer for PMSM with unknown disturbances[J]. ISA Transactions, 2023, 143: 572-581. DOI:10.1016/j.isatra.2023.09.025 |
| [3] |
LU P, GU M, YANG Y, et al. 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC) [C] //Chongqing: Research on Adaptive Control of PMSM based on Fuzzy PID, 2019.
|
| [4] |
HUANG Q W, XIE Z H, LIU H G. Active control for stick-slip behavior of the marine propeller shaft subjected to friction-induced vibration [J]. Ocean Engineering, 2023, 268.
|
| [5] |
NIU S, LUO Y, FU W, et al. Robust model predictive control for a three-phase PMSM motor with improved control precision[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 838-849. DOI:10.1109/TIE.2020.3013753 |
| [6] |
陈睿炜. 永磁同步电机在舰船推进系统中的滑模控制研究[J]. 舰船科学技术, 2017, 39(14): 82-84. CHEN R W. Sliding mode control of permanent magnet synchronous motor in ship propulsion system[J]. Ship Science and Technology, 2017, 39(14): 82-84. |
| [7] |
LI S H, ZHOU M M, YU X H. Disturbance Observer Based Terminal Sliding Mode Control Method for PMSM Speed Regulation System [C] //Jiangsu: The 30th Chinese Control Conference (International), 2011.
|
| [8] |
ZHANG L, TAO R, ZHANG Z X, et al. PMSM non-singular fast terminal sliding mode control with disturbance compensation [J]. Information Sciences, 2023, 642.
|
| [9] |
LIU H X, MEI K Q, LIU L, et al. Fixed-time non-singular terminal sliding mode control for PMSM drive systems[J]. Journal of Power Electronics, 2023, 24(2): 258-268. |
| [10] |
ZHANG M J, ZANG H Y, BAI L Y. A new predefined-time sliding mode control scheme for synchronizing chaotic systems [J]. Chaos, Solitons & Fractals, 2022, 164.
|
| [11] |
LI T, ZHAO Y, HOU L. Adaptive sliding mode control with disturbance observer for speed regulation system of permanent magnet synchronous motor[J]. IEEE Access, 2023, 11: 17021-17030. DOI:10.1109/ACCESS.2023.3245635 |
| [12] |
MENG F, ZHANG C, ZHAO Y. Modeling and simulation of marine propeller load [C] //Heilongjiang: 2016 IEEE International Conference on Mechatronics and Automation, 2016.
|
| [13] |
刘英杰, 张周, 王婷. 船舶电力推进系统螺旋桨负载特性动态仿真[J]. 舰船电子工程, 2018, 38(2): 78-82. LIU Y, ZHANG Z, WANG T. Dynamic simulation of propeller load characteristics in ship electric propulsion system[J]. Ship Electronic Engineering, 2018, 38(2): 78-82. |
| [14] |
李浩, 王川, 郭昊昊, 等. 船舶推进电机运动控制系统仿真研究[J]. 舰船科学技术, 2020, 42(13): 114-119. LI H, WANG C, GUO H H, et al. Research on simulation of ship propulsion motor motion control system[J]. Ship Science and Technology, 2020, 42(13): 114-119. |
| [15] |
YANG H, TANG J-W, CHIEN Y-R. Application of new sliding mode control in vector control of PMSM[J]. IEICE Electronics Express, 2022, 19(13): 20220156-20220156. DOI:10.1587/elex.19.20220156 |
| [16] |
LI X, WANG Y, GUO X, et al. An improved model-free current predictive control method for SPMSM drives[J]. IEEE Access, 2021, 9: 134672-134681. DOI:10.1109/ACCESS.2021.3115782 |
 2025, Vol. 47
2025, Vol. 47
