2. 水路交通控制全国重点实验室,湖北 武汉 430063;
3. 武汉理工大学 交通部船舶动力工程技术交通行业重点实验室,湖北 武汉 430063;
4. 中远海运特种运输股份有限公司,广东 广州 510510
2. National Key Laboratory of Waterway Traffic Control, Wuhan University of Technology, Wuhan 430063, China;
3. Key Laboratory of Ship Power Engineering and Transportation, Wuhan University of Technology, Wuhan 430063, China;
4. COSCO Shipping Special Transportation Co., Ltd., Guangzhou 510510, China
随着光伏技术的进步和成本的降低,越来越多适装光伏的船舶和平台选用光伏发电系统实现绿色减排和能效提升。但由于光伏接入船舶电网,引入了大量电力电子器件,改变了船舶电网原有的电力系统结构,电力系统的运行和控制方式也随之发生变化,因此与传统的船舶电力系统相比,光伏电-船电系统往往会产生以下问题:
1)在光伏发电量大且船舶电网出现空载或负载较小的情况时,光伏电源提供的过剩电力将使沿线局部电压升高,导致部分节点电压高于规定范围[1];
2)并网逆变器中的电力电子器件会引入大量的谐波分量,对并网后的船舶电力系统电能质量造成影响[2];
3)光伏发电系统在接入船舶电网时会造成较大的冲击电流,且分布式电源的启动和停止没有明显的规律性,导致输出功率和电参数的无规则变化[3]。
在船舶电力系统中定义光伏渗透率为光伏额定功率占在网发电机组额定功率的百分比,将大容量光伏集成到船舶电力系统中,相当于为系统增添了一个无惯性阻尼特性的逆变电源[4]。基于上述问题,本文以“中远盛世 ”轮电力系统为研究对象,以光伏渗透率为变量,采用系统仿真建模的方法,分析光伏渗透率提升对船舶电力系统电能质量的影响,探究船舶电力系统中光伏渗透率进一步提升的可行性。
1 船舶电能质量参数规范及系统建模 1.1 船舶电能质量参数规范船舶电能质量主要指电压偏差、频率偏差、三相不平衡和谐波等指标[5]。其中电压偏差
| $ \delta U=\frac{U-U_{\mathrm{normal}}}{U_{\mathrm{normal}}},$ | (1) |
| $ \delta f=\frac{f-f_{\mathrm{normal}}}{f_{\mathrm{normal}}}。$ | (2) |
式中:
三相平衡的定义是指三相交流船舶电力系统中,三相电压相位之间的夹角为120°的系统[7]。船舶电力系统作为低压系统,光伏电源的随机性可能影响到低压电网的三相不平衡性,同时由于短路故障、两相断线、负荷不对称以及单相接地等原因也都会引起三相不平衡[8]。所以三相不平衡度作为一项衡量电能质量的指标被引入,三相电压不平衡度可表示为:
| $ \varepsilon_2=\left|\frac{U_2}{U_1}\right|\times100\text{% },$ | (3) |
| $ \varepsilon_0=\left|\frac{U_0}{U_1}\right|\times100\text{% }。$ | (4) |
式中:
由于船舶电力系统采用三相三线制,不含有零序分量,因此在已知三相电压向量的情况下,可根据式(5)求得负序电压不平衡度:
| $ \varepsilon_2=\sqrt{\frac{1-\sqrt{3-6\displaystyle\frac{U_a^4+U_b^4+U_c^4}{(U_a^2+U_b^2+U_c^2)^2}}}{1+\sqrt{3-6\displaystyle\frac{U_a^4+U_b^4+U_c^4}{(U_a^2+U_b^2+U_c^2)^2}}}}\times100\%。$ | (5) |
在光伏并网系统谐波检测中,谐波的主要参数包括电流、电压的畸变程度、谐波总量和各次谐波的含有率[10],谐波的表示方法如下:
| $ \left\{\begin{array}{l}HR{U}_{n}=\displaystyle\frac{{U}_{n}}{{U}_{1}}\times 100\text{%},\\ HR{U}_{i}=\displaystyle\frac{{I}_{n}}{{I}_{1}}\times 100\text{%},\\ TH{D}_{u}= \sqrt{\underset{n=2}{\overset{\infty }{{{\displaystyle \sum }}^{\text{}}}}{(HR{U}_{n})}^{2}}\times 100\text{%},\\ TH{D}_{i}= \sqrt{\underset{n=2}{\overset{\infty }{{{\displaystyle \sum }}^{\text{}}}}{(HR{U}_{i})}^{2}}\times 100\text{%}。\end{array}\right. $ | (6) |
式中:
针对光伏并网电能质量问题,中国船级社(CCS)在2014年的《太阳能光伏系统及磷酸铁锂电池系统检验指南》和2023年的《钢质海船入级规范》针对光伏系统在并网波动、三相不平衡和谐波等方面均做出了具体规范,如表1所示。
|
|
表 1 船舶电网及逆变器电能质量规范要求 Tab.1 Power quality specifications for marine power grids and inverters |
并网型光伏发电系统因其效率高和经济性好,是目前应用的主流形式[11]。本文以“中远盛世”5300 PCTC船舶电力系统为研究对象,通过该船《电力负荷计算书》可知该船正常航行工况电气总负荷约为600 kVA,由3台柴油发电机联合供电,参数如表2所示。根据“中远盛世”轮电力系统结构和主要参数,在Matlab/Simulink中搭建光伏并网发电模型,仿真参数如表3所示。
|
|
表 2 发电机及主要负载参数表 Tab.2 Generator and main load parameter table |
|
|
表 3 光伏电-船电仿真系统主要参数 Tab.3 Main parameters of the photovoltaic electric-ship electric simulation system |
为研究不同渗透率的船舶光伏并入/切出前后对船舶电网电压和频率的影响,采用#2柴油同步发电机并网,并且分2个阶段进行仿真分析。阶段1:(0~0.8 s)光伏并网后与柴油发电机混合供电;阶段2:(0.8~1.0 s)光伏切出电网后柴油发电机单独带载。
图1和图2为不同渗透率下光伏船电系统中船舶光伏并入/切出前后的电压和频率波动瞬时偏差响应曲线,参数见表4。由图可知,随着光伏渗透率的提高电压和频率的波动幅度和峰值均呈现增长趋势,电压和频率在光伏并入/切出船舶电网后的0.1 s内均出现最大峰值,电压和频率瞬时偏差也呈现增长趋势,在光伏渗透率达到40%时,电压和频率偏差最大分别达到3.39%和2.09%,光伏在接入电网过程中的电压和频率偏差及其恢复时间普遍大于光伏切出电网过程,且随着渗透率的提高系统所需的恢复时间也逐渐增加,船电系统的整体电压也会出现不同幅度的抬高。

|
图 1 不同渗透率下的电压波动曲线 Fig. 1 Voltage fluctuation curves under different permeability |

|
图 2 不同渗透率下的频率波动曲线 Fig. 2 Frequency fluctuation curve under different permeability |
|
|
表 4 船舶电力系统电压和频率偏差 Tab.4 Voltage and frequency deviation of ship power system |
光伏并网切入对电能质量参数的影响明显高于光伏切出,因此以下研究只考虑光伏接入电网时的电能质量参数情况,图3为在不同渗透率的光伏并网系统接入后的负序电压不平衡度曲线图,表5表示在暂态(0 ~ 0.3 s)和稳态(0.3 ~ 1 s)下公共连接点短时负序不平衡值

|
图 3 不同光伏渗透率下的三相不平衡度曲线 Fig. 3 Three-phase unbalance curve under different photovoltaic permeability |
|
|
表 5 不同渗透率下的三相不平衡度 Tab.5 Three phase unbalance degree under different permeability |
从总体上看,随着光伏渗透率的提高,系统的三相不平衡度呈现被抬高的趋势。当渗透率达到40%时,系统公共点和逆变器的暂态不平衡度分别达到3.71%和1.12%,公共点和逆变器稳态不平衡度分别达到2.14%和0.89%。公共点负序不平衡已接近规定值。
2.3 谐波分析仿真分析快速傅里叶变换(Fast Fourier Transform,FFT)通过将时域信号转换为频域信号,可以快速识别信号中存在的不同频率成分,即谐波。进行谐波分析的思想是通过FFT将畸变波形分解为基波分量和谐波分量,通过分析各次谐波分量的幅值和相位来确定电压和电流的畸变水平[12]。本节将基于FFT分析光伏电-船电系统不同渗透率等级下的光伏并入/切出产生的谐波是否满足相关规范[13]。
对于以T为周期的函数
| $ f_T(t)=a_0+\sum_{k=1}^{\infty}\left(a_k\mathrm{cos}k\omega_1t+b_k\mathrm{sin}k\omega_1t\right)。$ | (7) |
式中:k=1,2,3,…;
函数的第k次谐波为:
| $ f_T(t)=a_k\mathrm{cos}k\omega_1t+b_k\mathrm{sin}k\omega_1t=A_k\sin\left(k\omega_1t+\varphi_k\right)。$ | (8) |
式中:
在复指数形式中,第k次谐波表达式为:
| $ \begin{split} f_T(t)= & a_k\mathrm{cos}k\omega_1t+b_k\mathrm{sin}k\omega_1t= \\ &\displaystyle\frac{a_k-jb_k}{2}e^{jk\omega_1t}+\frac{a_k+jb_k}{2}e^{-jk\omega_1t}。\end{split} $ | (9) |
可以得到各次谐波振幅按照频率高低变化的频谱图,这种频谱图仅显示各次谐波分量的振幅。频谱的图形为离散频谱,可以清晰地表明一个周期函数内的谐波分量和所占比重,《太阳能光伏系统及磷酸铁锂电池系统检验指南》规范中各次谐波电流含有率如表6所示。
|
|
表 6 各次谐波电流含有率限值 Tab.6 Each harmonic current contains rate limits |
图4与图5分别为不同渗透率下光伏接入时的实际电压和电流谐波总畸变率分析图,表7为不同光伏渗透率下的电压电流总谐波含量。在8个不同等级渗透率的光伏并网切入过程中,总体上电压总畸变率相比于电流总畸变率更小,谐波含量和畸变率均表现为随渗透率增加而提高的趋势。在光伏渗透率达到40%时可以满足相关规范,若光伏渗透率进一步提高,将对船舶电力系统产生危害。
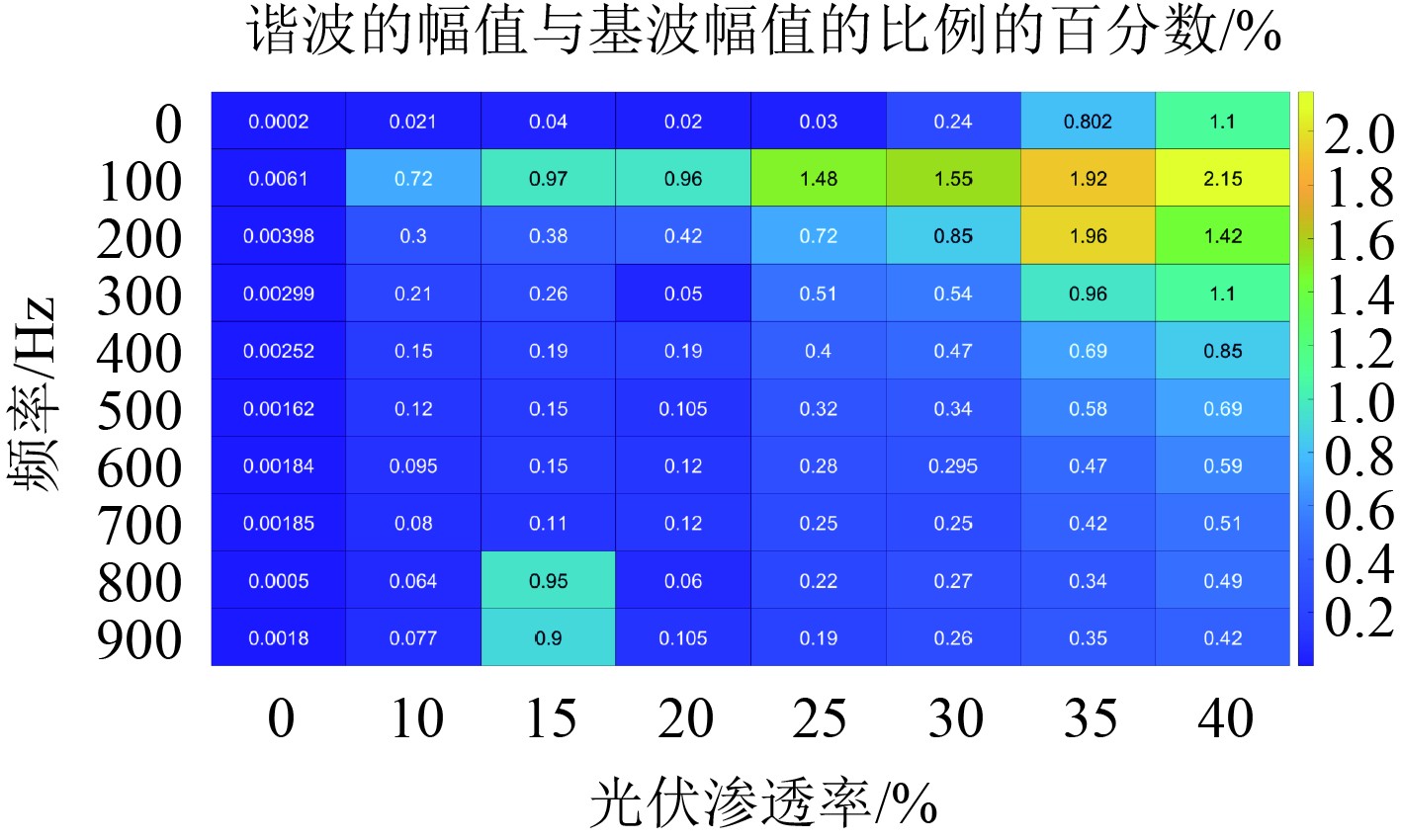
|
图 4 不同光伏渗透率下的电压谐波畸变率 Fig. 4 Voltage harmonic distortion rate under differentphotovoltaic permeability |
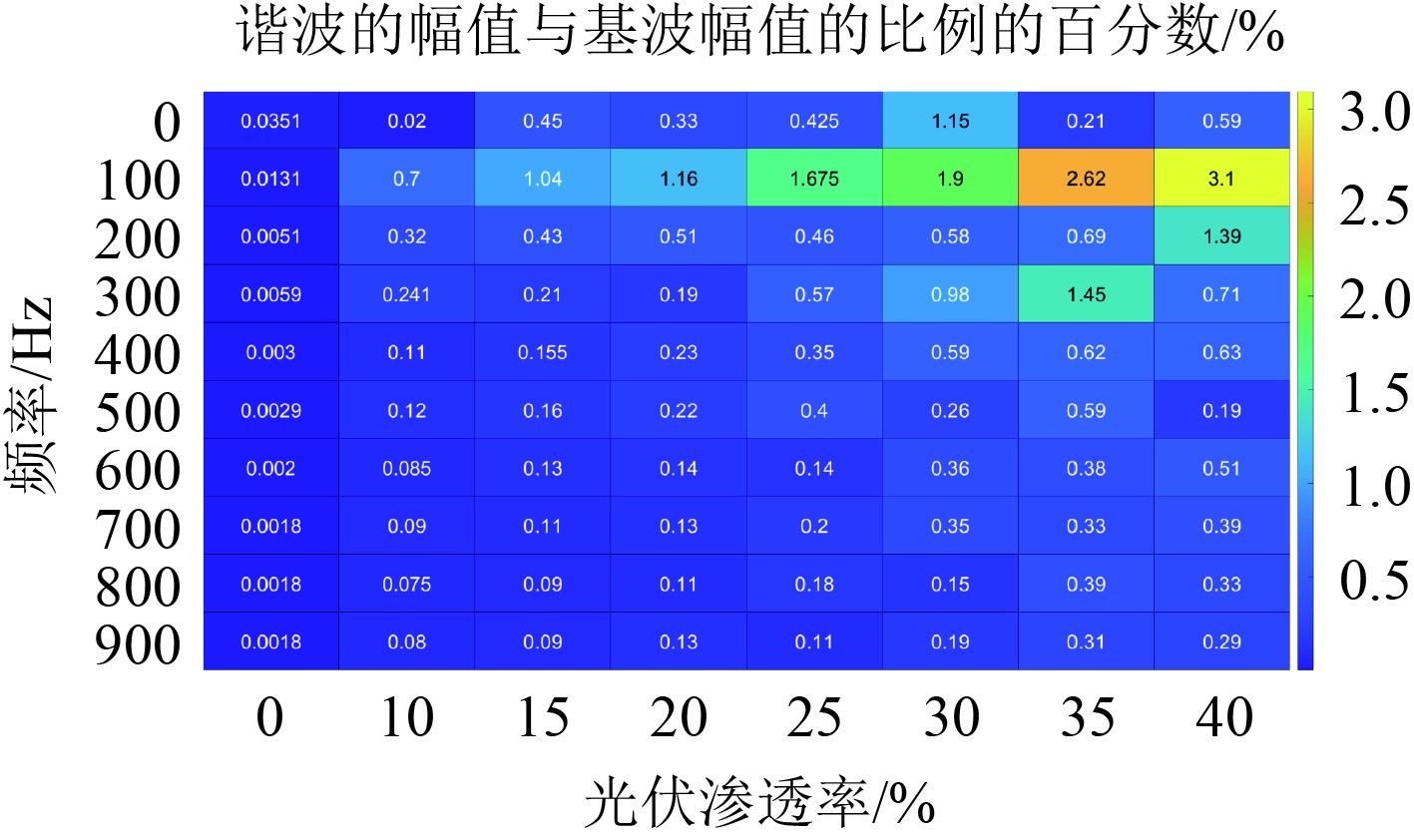
|
图 5 不同光伏渗透率下的电流谐波畸变率 Fig. 5 Current harmonic distortion rate under different photovoltaic permeability |
|
|
表 7 不同光伏渗透率下的电压电流总谐波含量 Tab.7 Each harmonic current contains rate limits |
前述研究表明当系统处于稳定运行状态时,在满足规范要求的相关电能质量指标条件下,光伏渗透率可提升至40%。为进一步探究光伏渗透率对船舶电力系统暂态因素的影响,本节在并网点模拟三相短路故障,采用10%、20%、30%、40%等4个光伏渗透率梯度,0.3 s瞬时光伏接入点发生三相短路故障,0.35 s时故障清除。
光伏并网发电系统三相曲线如图6所示,光伏电源接入船舶电网必然会引起原有短路电流的变化,其中三相短路故障发生时,系统短路电流的峰值和暂态电流的过渡时间随着光伏渗透率的提高而显著增大,光伏渗透率达到40%时最大短路电流峰值约为故障前稳态电流的1.7倍,随后电流达到稳态值,约为故障前电流的1.1倍左右。表8为系统短路故障时的谐波分量,在短路故障开始到切出时谐波含量大幅度提高,若不及时切出故障,将会严重降低系统供电的可靠性。

|
图 6 三相短路波形图 Fig. 6 Three-phase short circuit waveform diagram |
|
|
表 8 三相短路故障时系统谐波含量 Tab.8 Harmonic content of system when three-phase short circuit fault occurs |
有功功率和无功功率是表示光伏逆变系统运行效率的重要指标,在故障条件下不同光伏渗透率下的功率波动曲线如图7所示。随着光伏渗透率的提高光伏逆变器总有功和无功功率呈现增长趋势,且有功功率的增加率高于无功功率的增长率,系统的瞬时波动性增强。当渗透率提高至40%时,系统无功功率在0.05 s前会出现大幅度的提高,在0.05 s内系统功率因数最低值小于0.90,这是由于光伏输出功率等效折减了在网发电机实际负担的有功功率,使光伏功率因数降低,此时系统需要进行无功补偿,而当系统稳定运行时各渗透率的功率因数趋于一致,均位于0.99以上。
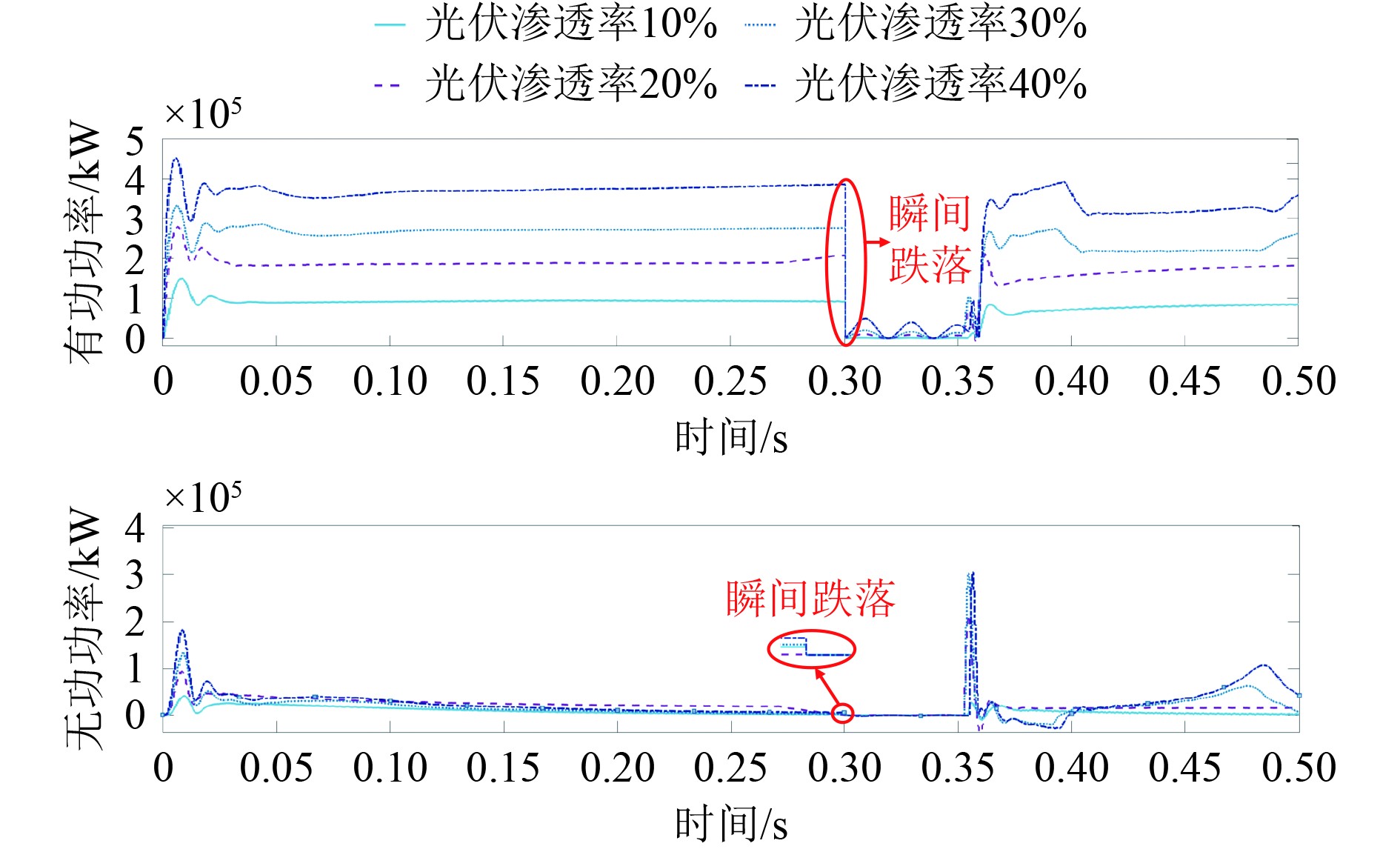
|
图 7 不同渗透率下的有功和无功功率曲线 Fig. 7 Active and reactive power curves under different permeability |
在0.3 s出现三相短路故障后有功和无功功率出现了瞬时跌落,系统随着渗透率的提高出现小幅度振荡,渗透率越高故障时的振荡幅度越大,对系统造成的损耗也越大。随着有功功率提高,光伏系统恢复到初始状态,有功功率参数的变化规律说明在短路故障情况下,光伏并网发电装置渗透率的变化不会导致系统发生失稳现象,但渗透率的改变会使系统恢复稳定时间发生变化,光伏发电系统也不像同步发电机组一样具有强励磁功能,不具有惯性支撑能力,在低压穿越故障时有功功率输出迅速下降,随着渗透率的提高,故障期间这部分功率会缺失严重,导致暂态稳定性变差,系统发生失稳的可能性越高,若故障长时间存在,存在失稳的可能性。
4 结 语本文以船舶电力系统电压频率偏差、三相不平衡度和谐波为技术指标,分析了船用并网型光伏电源不同渗透率下,并网和切出对船舶电力系统电能质量的影响及发生三相短路故障时船舶电力系统的暂态响应,得到结论如下:
1)随着光伏渗透率的提高,光伏系统对船舶电力系统的耦合影响逐渐增大。在电能质量参数均满足相关规范的前提下,船舶电力系统中光伏渗透率可提升至40%,但三相不平衡和谐波参数已接近指标上限值。
2)高渗透率光伏电源接入会导致船舶电力系统的不稳定性和输送功率的不确定性等。同时在发生短路故障时,光伏渗透率越高的船舶电力系统也越容易失稳。因此需要在光伏接入船舶电网时对其渗透率进行一定的控制。
绿色能源技术以其环保、可再生特性及显著的经济和社会效益,正日益成为全球能源领域的发展趋势,但高渗透率光伏并网对船舶电力系统的稳定运行带来了许多挑战,未来研究需要综合考虑光伏系统的特性、船舶电力系统的运行需求以及高渗透率逆流保护装置等多个方面,以推动船舶电力系统的绿色、安全和高效发展。
| [1] |
朱武, 王浩然, 杨可欣, 等. 带自适应谐波补偿功能的光伏并网控制策略[J]. 控制工程, 2024, 31(1): 10−17. ZHU W, WANG H R, YANG K X, et al. Grid-connected photovoltaic control strategy with adaptive harmonic compensation [J]. Control Engineering, 2024, 31(1): 10−17. |
| [2] |
招景明, 苏洁莹, 潘峰, 等. 考虑光伏波动的有源配电网分布式储能双目标优化规划[J]. 可再生能源, 2022, 40(11): 1546-1553. ZHAO J M, SU J Y, PAN F, et al. Dual-objective optimization planning of distributed energy storage in active distribution network considering photovoltaic fluctuations[J]. Renewable Energy, 2022, 40(11): 1546-1553. |
| [3] |
VINOTHKUMAR V. KANIMOZHI R. Power quality improvement by PV integrated UPQC using multi-level inverter with resilient back propagation neural network approach[J]. Journal of Intelligent & Fuzzy Systems, 2022, 43(5).
|
| [4] |
王孝元, 黄宇晴, 曹建萍. 基于粒子群算法的电池船运行优化[J]. 船舶工程, 2022, 44(2): 94-98+133. WANG X Y, HUANG Y Q, CAO J P. Optimization of battery ship operation based on particle swarm optimization[J]. Ship Engineering, 2022, 44(2): 94-98+133. |
| [5] |
刘治江. 混合动力船舶复合储能系统控制策略仿真研究[D]. 武汉: 武汉理工大学, 2020.
|
| [6] |
SONG S J, XIONG H, LIN Y Z, HUANG, et al. Robust three-phase state estimation for PV-Integrated unbalanced distribution systems[J]. Applied Energy, 2022, 322.
|
| [7] |
刘可真, 陈雪鸥, 陈镭丹等. 光伏发电系统动态离散等值模型研究[J]. 上海交通大学学报, 2023, 57(4): 414−421. LIU K Z, CHEN X O, CHEN L D, et al. Research on dynamic discrete equivalent Model of photovoltaic power generation System [J]. Journal of Shanghai Jiao Tong University, 2023, 57(4): 414−421. |
| [8] |
RAJBIR S , GEENA K. THD reduction and power quality improvement in grid connected PV system[J]. Journal of Trend in Scientific Research and Development, 2017, 1(4): 429−433.
|
| [9] |
张晓刚, 马俊祥, 马信等. 一种基于FCS-MPC的光伏并网电能质量控制方法[J]. 机械研究与应用, 2022, 35(3): 126-131. ZHANG X G, MA J X, MA X, et al. A grid-connected photovoltaic power quality control method based on FCS-MPC[J]. Mechanical Research and Application, 2022, 35(3): 126-131. |
| [10] |
庄静茹. 分布式光伏并网的电能质量分析与评估[D]. 济南: 山东大学, 2022.
|
| [11] |
HIROKI N , YOSHIFUMI Z , NAOTO Y , et al. A study on the configuration of low‐voltage distribution networks for high penetration of photovoltaic power sources [J]. IEEE Transactions on Electrical and Electronic Engineering, 2021, 16 (7): 965−972.
|
| [12] |
马启鹏, 郝正航, 张裕等. 含高渗透率分布式光伏配电网的网络分区与电压协调控制[J]. 电网与清洁能源, 2023, 39(3): 93-102+108. MA Q P, HAO Z H, ZHANG Y, et al. Network zoning and voltage coordination control of distributed photovoltaic power distribution Network with high permeability[J]. Power Grid and Clean Energy, 2023, 39(3): 93-102+108. DOI:10.3969/j.issn.1674-3814.2023.03.012 |
| [13] |
颜湘武, 梁白雪, 贾焦心等. 高渗透率光伏并网对系统暂态频率稳定性影响的量化评估[J]. 可再生能源, 2022, 40(9): 1232-1240. YAN X W, LIANG X B, JIA J X, et al. Quantitative evaluation of the effect of high permeability photovoltaic grid connection on transient frequency stability of system[J]. Renewable Energy Sources, 2022, 40(9): 1232-1240. DOI:10.3969/j.issn.1671-5292.2022.09.014 |
 2025, Vol. 47
2025, Vol. 47
