0 引　言

近20年来水下无人航行器步入了发展的快车道，作为可长期在水下自主航行并可回收的智能化装备，受到国内外海洋强国的重视^[1]，AUV作为其中自主控制的航行器，是未来水下无人系统的发展重点。AUV作为一种在复杂水下环境运行的欠驱动机器人，具有本质非线性、欠驱动特性、可控性、约束特性等特点^[2]，当AUV动力学及其环境发生重大变化时，具有固定增益的传统控制方法不能保证整个系统的高质量响应^[3]。

运动控制技术作为AUV的关键技术之一，是水下机器人能够完成任务的前提。赵蕊等^[4]提出一种基于分数阶PID技术的航向控制器，并使用遗传算法对其中需要确定的参数进行自动整定。CHEN等^[5]提出一种利用RBFNN和扰动观测器的自适应滑模控制器，其中RBFNN逼近和补偿建模的不确定性，扰动观测器用来估计和补偿外部扰动的影响。夏国清等^[6]针对AUV特点，采用了带衡量因子的动态BP神经网络控制器控制AUV航向，通过仿真结果表明神经网络控制器在扰动存在的情况下有更好的自适应性。Khodayari等^[7]设计一种基于非线性多输入、多输出结构的自适应模糊PID控制器，通过仿真实验验证了该方法在AUV系统中的可靠性。敖邦乾等^[8]设计一种基于神经网络-PID的USV控制系统，利用神经网络自学习能力修正控制参数，使航行器沿着规划的路径行驶。Li等^[9]打破传统小俯仰角假设的限制，根据航行器非线性运动方程提出了一种半全局稳定的神经网络自适应控制方案的潜水控制AUV。Yang等^[10]在ROV不确定性和存在外部干扰的条件下，提出一种基于递归神经网络的模糊滑模控制方法，实现四自由度ROV的稳定运动，通过实验证明了该方法的良好性能。Mukund等^[11]在自主水下航行器模型参数完全未知的假设下，设计一种由在线参数估计器、状态估计的观察器和最优控制器组成的间接自适应控制系统，通过仿真实验证明了尽管系统参数存在较大的不确定性，该系统仍能进行精确的深度控制。郭琳钰等^[12]设计了基于RBF神经网络的模型预测控制器，使用模型预测控制进行路径跟踪，利用实时数据在线训练神经网络补偿AUV模型的不确定性。

本文针对AUV航向控制问题，建立水下六自由度运动数学模型，采用PID控制器计算控制变量，为解决PID固定增益在AUV复杂运动中不能保证高质量响应问题，设计了一种基于多层感知器人工神经网络的自适应控制系统，并通过动量梯度下降法将动量项引入参数更新法则中，加速收敛过程并减少收敛过程中的振荡。通过在Matlab中仿真实验证明该方法可以动态调整PID控制器参数，具有良好的跟踪效果。

1 AUV运动模型

AUV由于其外形结构复杂，导致其空间运动具有非线性、强耦合的特点，为了使AUV在水下空间的航行控制能够反映运动的真实情况，单平面的运动数学模型不能满足需求。因此要实现更真实的偏航控制，整体仿真控制系统的设计面临很多挑战，为此本文根据AUV六自由度运动数学模型，采用Matlab搭建六自由度仿真模型。

1.1 运动学模型

水下航行器在水中的运动一般被假设为刚体的空间运动，根据六自由度运动方程，AUV的运动学模型可以分开表示为式(1)的位置-速度方程和式(2)的姿态-角速度方程：

$ \left\{\begin{aligned} & \dot{x}= u\cos\psi \cos\theta +v\left(\cos\psi \sin\theta \sin\varphi -\sin\psi \cos\varphi \right)+\\ &w(\cos\psi \sin\theta \cos\varphi +\sin\psi \sin\varphi )，\\ & \dot{y}=u\sin\psi \cos\theta +v\left(\sin\psi \sin\theta \sin\varphi +\cos\psi \cos\varphi \right)+\\ & w(\sin\psi \sin\theta \cos\varphi -\cos\psi \sin\varphi )，\\ &\dot{z}=u\left(-\sin\theta \right)+v\cos\theta \sin\varphi +w\cos\theta \cos\varphi 。\end{aligned}\right. $

(1)

$ \left\{\begin{array}{l}\dot{\varphi }=p+q\sin\varphi \tan\theta +r\cos\varphi \tan\theta ，\\ \dot{\theta }=q\cos\varphi -r\sin\varphi，\\ \dot{\psi }=q\sin\varphi /\cos\theta +r\cos\varphi /\cos\theta 。\end{array}\right. $

(2)

式中：$ [x,y,z,\varphi ,\theta ,\psi {]}^{\rm T} $为地面坐标系下的位置和姿态向量；$ [u,v,w,p,q,r{]}^{\rm T} $为随体坐标系速度向量。

1.2 动力学模型

为简化模型推导，做出如下假设：

1）AUV的运动为刚体运动，不考虑内部相互作用；

2）惯性系下可以不考虑地球自转的影响；

3）水下航行器在水下运动时处于全黏湿状态。

基于做出的假设和动量及动量矩定理，AUV的动力学方程如下：

$\begin{split} &{{\boldsymbol{M}}}_{RB}\dot{V}+{{\boldsymbol{C}}}_{RB}\left(V\right)V+{{\boldsymbol{M}}}_{A}\dot{V}+{{\boldsymbol{C}}}_{A}\left(V\right)V+\\&{\boldsymbol{D}}\left(V\right)V+g\left(\eta \right)=\tau 。\end{split}$

(3)

式中：$ {{\boldsymbol{M}}}_{RB}\in {R}^{6\times 6} $为航行器刚体质量的惯性矩阵；$ {{\boldsymbol{C}}}_{RB}\left(V\right)\in {R}^{6\times 6} $为航行器刚体质量的科里奥利力和向心力矩阵；$ {{\boldsymbol{M}}}_{A}\in {R}^{6\times 6} $为附加质量惯性矩阵；$ {{\boldsymbol{C}}}_{A}\left(V\right)\in {R}^{6\times 6} $为附加质量科里奥利力和向心力矩阵；$ {\boldsymbol{D}}\left(V\right)\in {R}^{6\times 6} $为线性阻尼矩阵；$ g\left(\eta \right)\in {R}^{6\times 1} $为水下航行器恢复力和力矩向量；$ \tau \in {R}^{6\times 1} $为航行器上的外部作用力及其力矩；$ \eta =[x,y,z,\varphi ,\theta ,\psi {]}^{\rm T} $，$ V=[u,v,w,p,q,r{]}^{\rm T} $。

仿真模型参考Remus 100型AUV，根据运动学方程和动力学方程在Matlab/Simulink平台上构造，驱动装置来自尾部螺旋桨，通过垂直方向舵和水平尾翼操纵。考虑到AUV执行器的物理限制，在被控对象的模型构建中对垂直舵和水平尾翼最大偏转角度进行限制。

2 控制算法设计

水下航行器的运动存在着复杂性、非线性、时变性、不确定性等特点，无法获得精确的数学模型，而实际的运动过程包含的控制任务复杂，传统的控制任务要求不高，面对复杂的控制任务无法完成任务要求。为了解决被控对象存在的诸多问题，实现复杂控制任务，将控制理论的方法和人工智能技术结合的智能控制得到快速发展。神经网络控制将神经网络引入控制领域，从机理上简单模拟人类大脑的生理拓扑结构，具有并行机制、模式识别、记忆和自学习能力的特点，能学习和适应不确定系统的动态特性，有很强的鲁棒性和容错性，基于神经网络逼近的自适应神经网络控制是神经网络的更高形式。

2.1 神经网络理论

神经网络的设计使用大量神经元，将神经元以一定拓扑结构排列进行学习和调整的自适应控制方法，表现出丰富的特性，在智能控制的参数、结构或环境的自适应、自组织和自学习等控制方面具有独特的能力。神经网络的研究已经有几十年的历史，作为一种运算模型，节点具有不同的连接方式，而每个称为节点的神经元都代表一种特定的输出函数，称为激励函数，每个相邻两层相连的节点之间存在称为权重的加权值，相当于神经网络的记忆，输出也会随着连接方式、权重值、激励函数的不同而不同。

随着神经网络理论的快速发展，现在神经网络模型的种类已经极大丰富，其中典型的有多层前向传播网络（BOP网络）、Hopfield网络、CMAC小脑模型、ART自适应共振理论、BAM双向联想记忆、SOM自组织网络、Blotzman机网络和Madaline网络等。神经网络自适应、自组织和自学习能力的实现通过学习算法来实现，可分为有教师学习、无教师学习和再励学习等，其根本原理都是通过某种规则动态调整权值使网络具备相应的功能。本文神经网络采用多层感知器神经网络，使用动量梯度下降法对权值进行更新。

1）多层感知器神经网络（MLP-ANN）

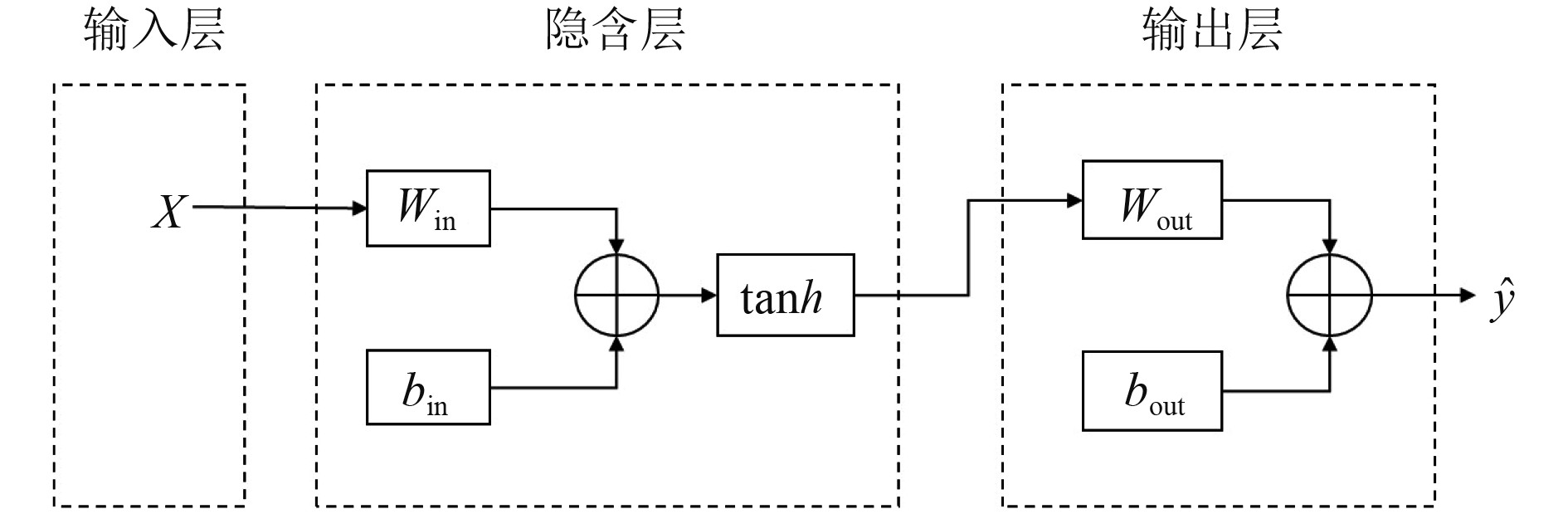
多层感知器（Multilayer Perceptron，MLP）神经网络也被称为前馈神经网络，或者被称为人工神经网络（Artificial Neural Network，ANN），包括输入层、隐含层和输出层，其学习目标是为了使输出逼近期望输出。多层感知器神经网络拓扑结构如图1所示。

各层具体关系如下：

第1层为输入层。该层主要将需要输入的数据传入到隐含层，在具体设计时需要结合具体问题考虑是否要对输入数据做相对应的预处理，因此输入层的输出为：

$ {O}_{l}^{\left(1\right)}={x}_{l}\text{，}l=\mathrm{1,2},3\dots n 。$

(4)

式中：$ {O}_{l}^{\left(1\right)} $为输入层输出；$ {x}_{l} $为输入层第$ l $个输入；$ n $为输入变量的个数；$ {x}_{l} $组成$ n\times 1 $的矩阵$ {\boldsymbol{X}} $。

第2层为隐含层。该层的每一个隐含节点都代表对输入层输入的变量先进行加权运算，然后对得到的数据使用激活函数进行处理。隐含层的输入是输入层的输出，隐含层的输出为：

$ T={W{\mathrm{in}}}_{m\times n}{\boldsymbol{X}}+{b{\mathrm{in}}}_{m\times 1}，$

(5)

$ {O}_{m\times 1}^{\left(2\right)}=g\left(T\right)\text{，}m=\mathrm{1,2},3\dots i。$

(6)

式中：$ m $为隐含层神经元序号；$ {O}_{m}^{\left(2\right)} $为隐含层第$ m $个节点输出；$ {W{\mathrm{in}}}_{m\times n} $、$ {b{\mathrm{in}}}_{m\times 1} $为人工神经网络输入层到隐含层的权值和贝叶斯值；$ i $为隐含层节点个数。

第3层为输出层。该层为对输入经过神经网络计算得到的输出结果，该层的输入为隐含层的输出，输出为：

$ {y}_{j}^{\left(3\right)}={W{\mathrm{out}}}_{j\times m}{O}_{m\times 1}^{\left(2\right)}+{b{\mathrm{out}}}_{j\times 1}\text{，}j=\mathrm{1,2},3\dots k 。$

(7)

式中：$ k $为输出的个数；$ {y}_{j}^{\left(3\right)} $为第$ j $个输出；$ {W{\mathrm{out}}}_{j\times m} $、$ {b{\mathrm{out}}}_{j\times 1} $为人工神经网络隐含层到输出层的权值和贝叶斯值。

其中，隐含层的激活函数$ g\left(x\right) $采用由双曲正弦和双曲余弦推导的双曲正切函数，双曲正切函数表达式如下：

$ g\left(x\right)=\tan {\mathrm{h}}x=\frac{\sin {\mathrm{h}}x}{\cos {\mathrm{h}}x}=\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}。$

(8)

2）动量梯度下降法

在对神经网络进行训练时，通常应设置一个需要优化的损失函数作为判断该神经网络训练好坏的标准，通过对神经网络中权值矩阵的动态调整选择合适的参数使损失函数的值尽量小，损失函数通常为实际值与预估值误差的函数，形式如下：

$ E=\frac{1}{2}\sum {\left(e\right)}^{2}=\frac{1}{2}\sum {(y-\widehat{y})}^{2}。$

(9)

因此很多学者引入梯度下降的算法作为误差反向传播的方式。这里的梯度是一个向量，指多元函数在某一点处方向导数最大值的方向，前提假设各个方向导数均存在，这样就可以使用原有参数减去损失函数梯度的常数更新方式令目标损失函数朝着下降最快的方向更新。但是在很多实际问题中并非只有一个极值点作为全局最优点，在使用梯度下降法时会存在陷入局部最优和下降速度慢等问题，无法得到想要的结果。

为了解决上述问题，引入动量梯度下降法作为优化算法，用于加速梯度下降的收敛速度并减少路径中的振荡。动量方法通过引入一个动量项来累积之前梯度的方向，从而在更新参数时考虑之前梯度的历史信息。

在标准的梯度下降中，每次迭代的参数基于当前梯度：

$ {\theta }_{t+1}={\theta }_{t}-\eta {\nabla }_{\theta }J\left({\theta }_{t}\right) 。$

(10)

式中：$ {\theta }_{t} $为第$ t $次迭代时的参数；$ \eta $为学习率，设置为0.9；$ {\nabla }_{\theta }J\left({\theta }_{t}\right) $为损失函数$ J $对参数$ \theta $的梯度。由于这样更新梯度会存在速度慢、结果不稳定的特点，引入动量项$ {v}_{t} $表示第$ t $次迭代时动量的累积值，则动量梯度下降法的参数更新公式为：

$ {v}_{t+1}=\beta {v}_{t}+(1-\beta ){\nabla }_{\theta }J\left({\theta }_{t}\right) ，$

(11)

$ {\theta }_{t+1}={\theta }_{t}-\eta {v}_{t+1} 。$

(12)

式中：$ {v}_{t} $为梯度指数加权移动平均的动量项；$ \beta $为动量系数，取值范围在0～1之间，设置为0.8；$ {\nabla }_{\theta }J\left({\theta }_{t}\right) $为当前梯度。

通过引入动量项，参数更新可以在下降方向上加速，能够更快达到最小值，对于振荡的损失函数可以平滑更新路径，引入动量还可以摆脱模型中的局部极值和鞍点，找到更优的全局最小值。在神经网络的训练中，动量梯度下降法可以加速权重和偏置的更新，减少训练时间，并提高收敛的稳定性，神经网络可以更快地找到最优参数，从而提高模型的性能和训练效率。

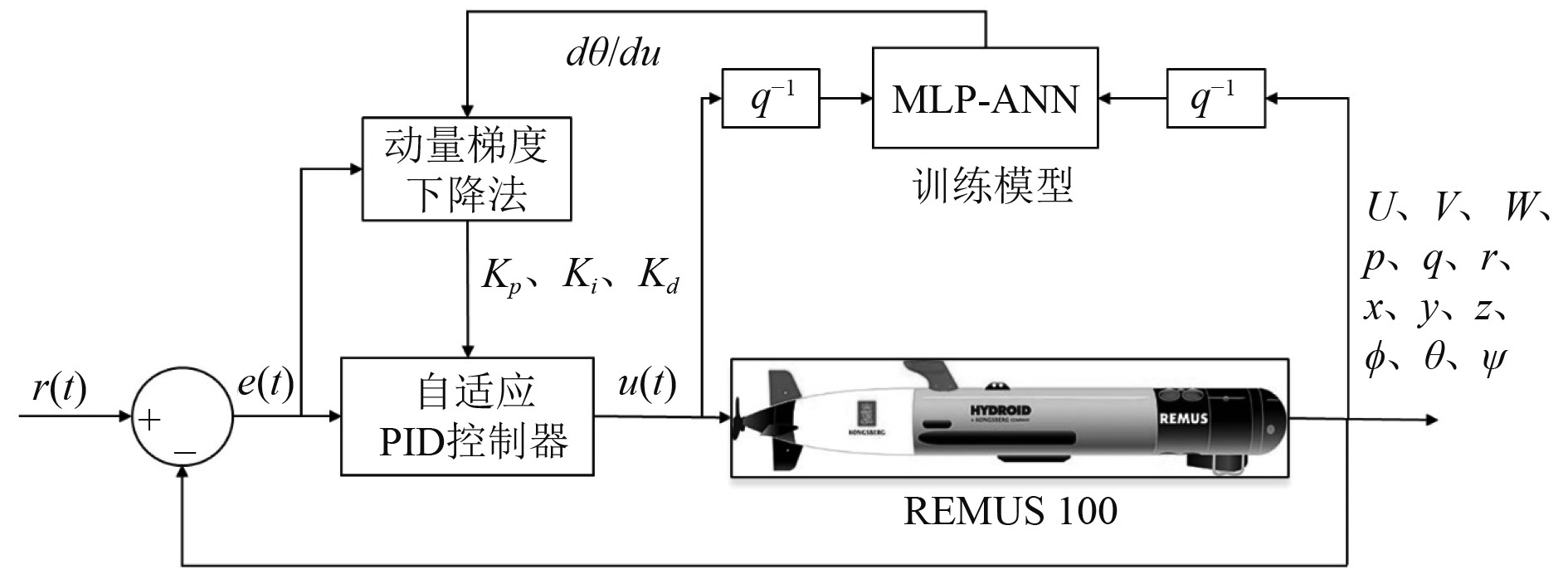
2.2 自适应控制算法

基于上述MLP-ANN训练模型，在每次控制循环中计算被控对象系统模型的雅可比矩阵，根据计算得到的结果使用动量梯度下降法迭代更新PID控制器参数，实现自适应控制算法，自适应PID控制算法如图2所示。

结合训练得到的MLP-ANN模型，根据自适应PID控制算法可计算得到输出对输入的雅可比矩阵，由于本文针对水下航行器航向控制进行研究，因此雅可比矩阵如下：

$ \frac{{\mathrm{d}}\theta }{{\mathrm{d}}u}\cong \frac{{\mathrm{d}}\widehat{y}}{{\mathrm{d}}X}=W{\mathrm{out}}W{\mathrm{in}}\frac{{\mathrm{d}}{O}_{m\times 1}^{\left(2\right)}}{{\mathrm{d}}T}。$

(13)

式中：$ \dfrac{{\mathrm{d}}{O}_{m\times 1}^{\left(2\right)}}{{\mathrm{d}}T}=1-{\tan {\mathrm{h}}}^{2}\left(T\right) $表示激活函数输出对其输入变量的导数。这里应设置的损失函数应为期望值与实际输出的函数：

$ E=\frac{1}{2}\sum {\left(e\right)}^{2}=\frac{1}{2}\sum {(r-\theta )}^{2} 。$

(14)

因此损失函数对PID控制参数的梯度为：

$ \frac{{\mathrm{d}}E}{{\mathrm{d}}{K}_{p,i,d}}=\frac{{\mathrm{d}}E}{{\mathrm{d}}e}\frac{{\mathrm{d}}e}{{\mathrm{d}}\theta }\frac{{\mathrm{d}}\theta }{{\mathrm{d}}u}\frac{{\mathrm{d}}u}{{\mathrm{d}}{K}_{p,i,d}} 。$

(15)

为实现PID参数自适应更新，应用动量梯度下降法计算动量项，得到的新的PID参数，更新算法如下：

$ \vee {K}_{p,i,d}\left(n\right)=\beta {\nabla }_{{K}_{p,i,d}}\left(n-1\right)+(1-\beta ){\nabla }_{{K}_{p,i,d}}\left(n\right)，$

(16)

$ {K}_{p,i,d}\left(n\right)={K}_{p,i,d}\left(n-1\right)-\eta \vee {K}_{p,i,d}\left(n\right)。$

(17)

式中：$ {K}_{p,i,d} $为PID控制器参数；$ {{\mathrm{d}}u}/{{\mathrm{d}}{K}_{p,i,d}} $表示控制输入对控制器参数的偏导数，分别为$ e\left(t\right)、{\int }_{0}^{\infty }e\left(t\right){\mathrm{d}}t、{{\mathrm{d}}e\left(t\right)}/{{\mathrm{d}}t} $，这些量由闭环控制系统的PID计算公式得到；$ {\nabla }_{{K}_{p,i,d}}={{\mathrm{d}}E}/{{\mathrm{d}}{K}_{p,i,d}} $为梯度；n为第n次迭代的数值；$ \alpha 、\eta $分别为学习速率和动量系数。

2.3 仿真模型搭建

结合上述理论，在具体实现过程中需要结合具体的问题进行分析，由于本文是设计实现水下航行器航向自适应控制系统，根据水下航行器六自由度数学模型，对航向运动进行解耦可以发现航向角的实际值与$ x、y、u、v、r、\psi $和控制输出$ U\left(t\right) $有关，故设置神经网络为3层拓扑结构，输入向量为7个，分别为上一时刻的$ x、y、u、v、r、\psi $和这一时刻的控制输出，隐含层节点数选取为30个，输出为预测的这一时刻输出。

因此要搭建的仿真模型应由2个部分构成，分别为MLP-ANN训练模型和Simulink仿真模型，具体设计如下：

1）MLP-ANN训练模型

神经网络训练模型主要通过对数据的训练，实现对非线性系统的辨识，算法如图3所示。

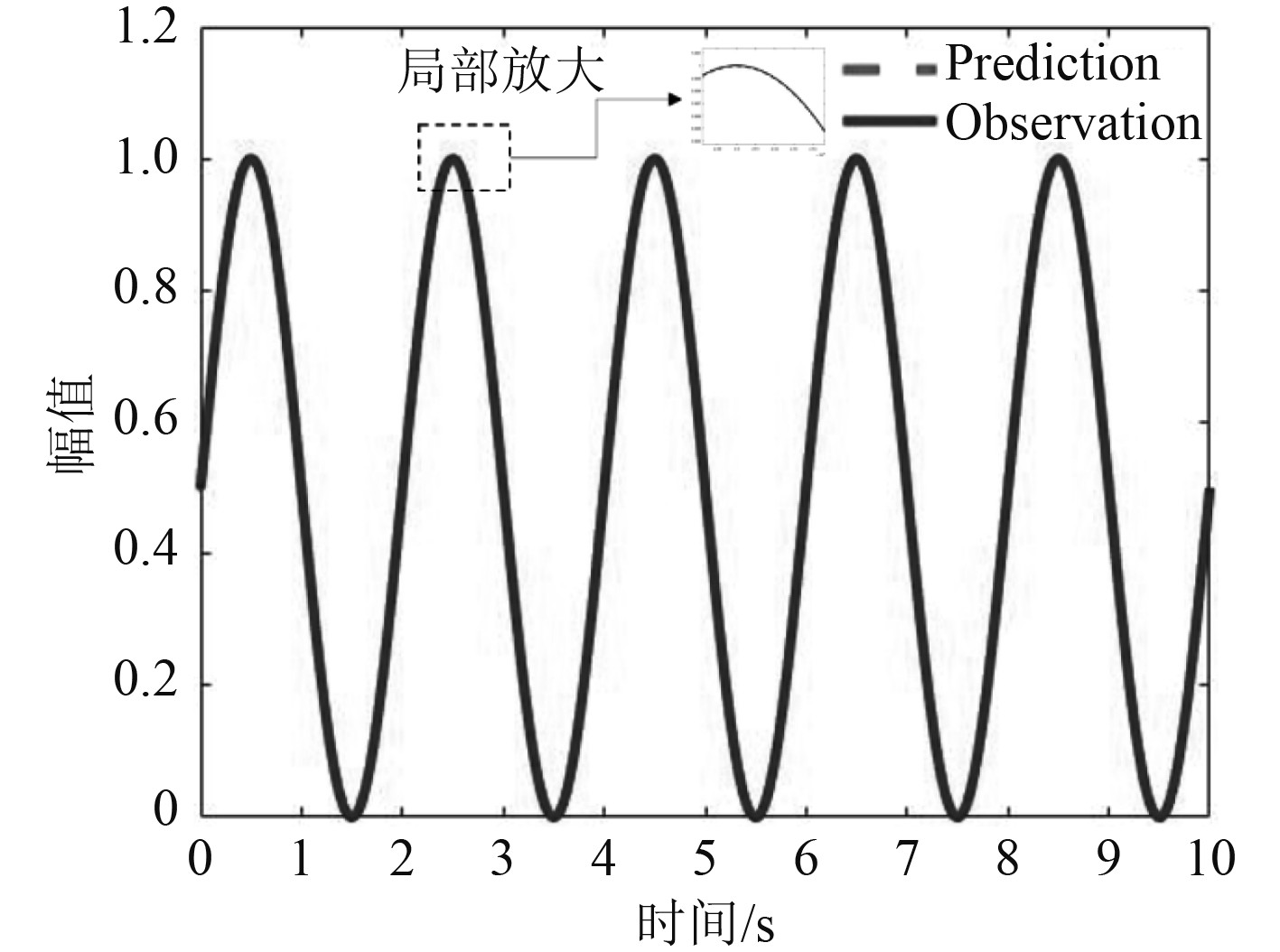
其中LM优化算法是一种结合梯度下降和高斯牛顿法的非线性优化算法，综合了梯度下降法初值不敏感和高斯牛顿法在最优值附近收敛速度快的特点，可以加快网络训练过程。训练模型对数据的训练拟合结果如图4所示，通过对局部放大图的观测可知训练模型对数据的拟合仅存在可以忽略的误差，表明训练模型准确性效果极好。

2）Simulink仿真模型

本文已经给出AUV仿真模型、神经网络模型、动量梯度下降法更新自适应PID参数模型，将其在Matlab2021b/Simulink中模块化搭建仿真模型。

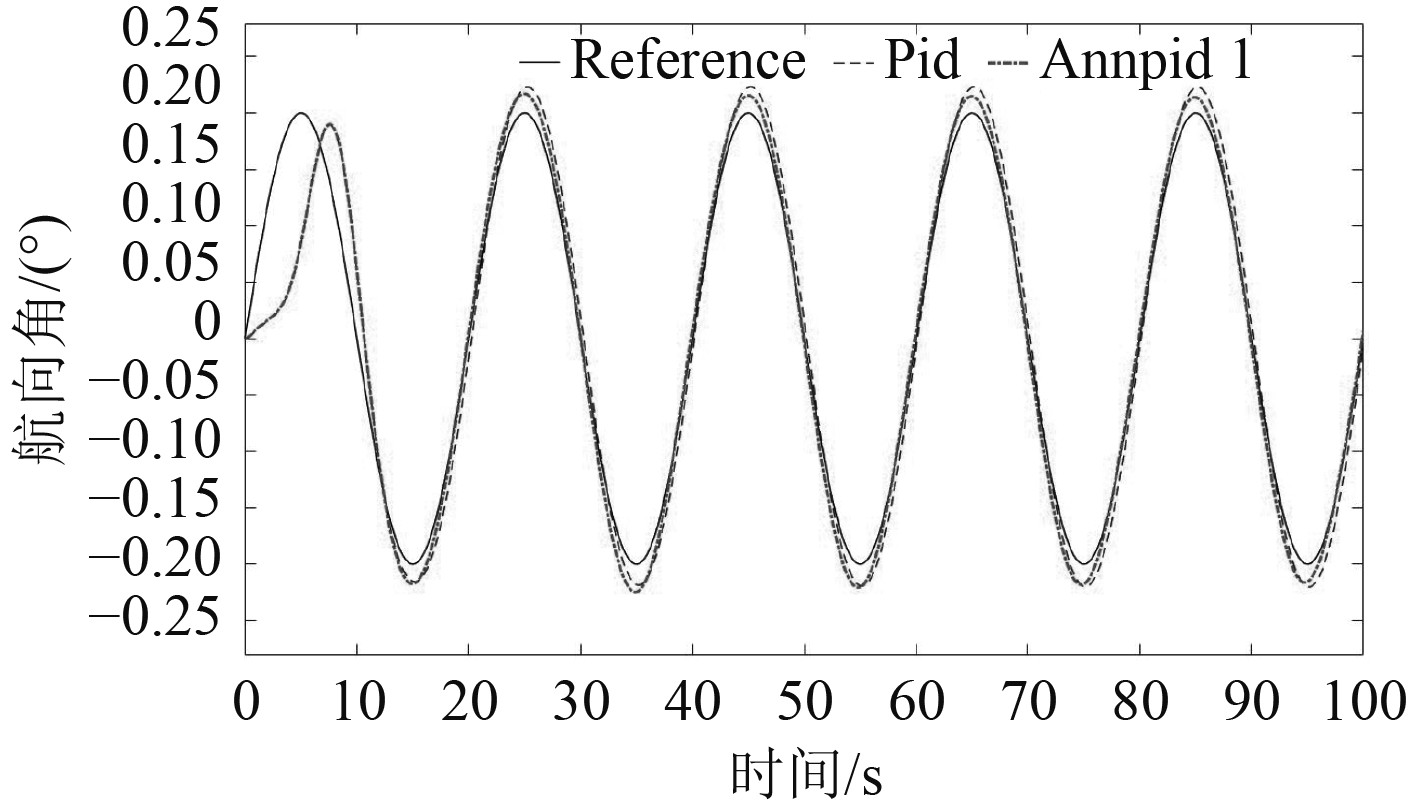
3 结果分析与对比

实验仿真在本文搭建的仿真模型中进行，首先以输入向量为$ {\boldsymbol{X}}=[x\left(t-1\right),y\left(t-1\right),u\left(t-1\right),v\left(t-1\right), r\left(t-1\right), \psi \left(t-1\right),U(t\left)\right] $对设计的MLP-ANN模型进行训练得到权重和偏置。然后在使用m函数编写得到的AUV模型上测试开发的自适应PID控制算法，其中时滞算符为$ {q}^{-1} $，初始PID参数值为K_p=68、K_i=0.5、K_d=30，用推导得到的动量梯度下降公式对PID参数进行更新。在对控制器性能的对比中，可使用对阶跃信号和正弦信号的跟踪结果验证系统跟随性^[13-14]。为对比仿真结果，搭建PID控制并设置与自适应PID控制参数初始值一致的仿真模型，设置输入信号为0.05 Hz，幅值为0.2的正弦信号作为期望输入信号，仿真时间设置为100 s，得到输出响应如图5所示。

可以看出，自适应PID方法可以成功跟踪正弦信号，并且响应速度要优于传统PID，使用绝对误差积分（IAE）和时间乘以绝对误差积分（ITAE）2种性能指标对2种方法进行量化比较，结果对比如表1所示。

表中IAE是对误差的绝对值直接积分所得，代表系统在整个响应过程中的累计误差；ITAE将误差乘以时间来加权，除了考虑误差的大小，还更关注后期误差的表现。自适应PID在这2项指标上都有更好的表现，说明该方法不仅能有效减少误差，还能更快调整系统使其达到稳定状态，表明自适应PID在性能上优于传统PID，尤其是在需要迅速减少误差和加快响应时间的控制任务中有突出表现。

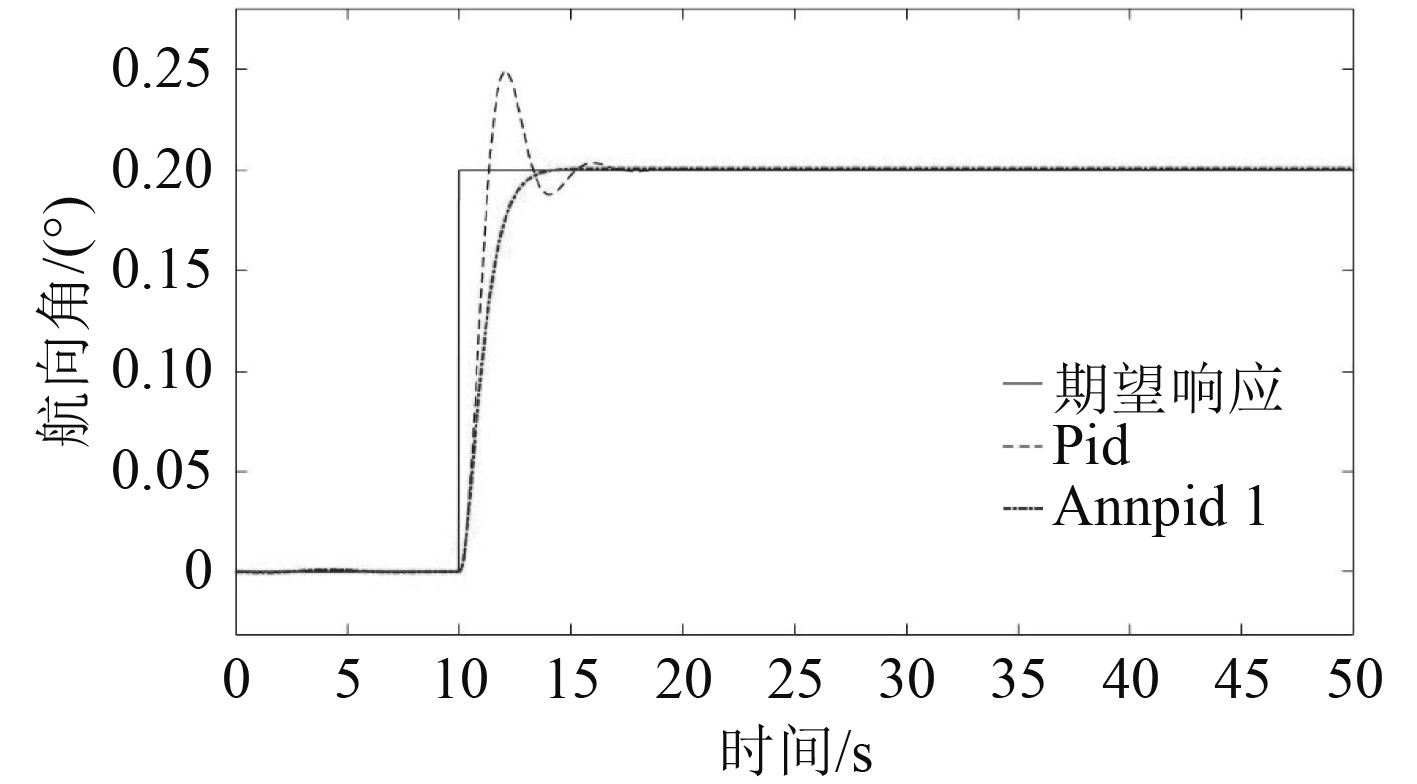
在阶跃信号下传统PID和自适应PID的响应如图6所示。

可以得到传统PID响应存在振荡过程，需要较长的振荡调节直至稳定，调节时间为4.85 3s，最大超调量为24.6%，但是稳定状态下误差在2%范围内；而自适应PID响应控制效果比传统PID控制效果好，无振荡现象和超调量，调节时间为3.2195 s，较传统PID减少1.6335 s，稳态误差满足要求。上述获得的结果都证明了自适应PID相比于传统PID能够得到较好的性能。

4 结　语

针对AUV在复杂环境下航行控制问题，固定增益的PID控制无法实现较好的控制效果，本文提出一种基于MLP-ANN的自适应PID控制方案，搭建基于多层感知器的人工神经网络模型，使用非线性LM算法代替梯度下降法训练模型，将神经网络模型计算得到的雅可比矩阵和控制律建立联系推导控制参数自适应更新律，并引入动量梯度下降法更新参数。

仿真实验基于Matlab平台搭建的实验模型实现，通过对正弦信号和阶跃信号的跟踪对比实验证明该方案的可行性和优越性，相比于传统PID控制方案，该方案可以通过更新控制参数实现自适应控制，在AUV航向控制实现方法方面具有一定的工程应用价值。