国际航运业,包括南海航线和北海航线的活动造成了2.7%的全球空气污染或8.7亿吨二氧化碳[1]。除二氧化碳外,二氧化硫、二氧化氮和颗粒物的排放也是空气污染的关键问题。为减少污染,提出了包括使用氢、液化天然气(LNG)等替代方案。氢气作为一种清洁能源,燃烧时只产生水,不产生二氧化碳,因此被视为理想的零排放燃料[2]。然而,氢气的存储和运输具有一定的挑战性,尤其是在海洋环境中。因此,将氢气与LNG混合使用,成为一种折中的选择,既能利用现有的LNG基础设施,又能减少碳排放。然而,LNG的泄漏可能导致窒息、火灾、蒸汽云爆炸(VCE)等危险[3 − 5]。气体泄漏、火灾、VCE、沸腾液体膨胀蒸汽爆炸等后果可能同时或连续发生,将压力液体容器加热到沸点的射流火灾会导致沸腾液体扩展蒸气云爆炸(BLEVE),从而导致灾难性事故[6 − 7]。单次爆炸可能导致爆炸源周围的气体泄漏和火灾,而爆炸、高温或碎片可能会损坏邻近的系统,导致设备故障。计算流体力学(CFD)方法可以用于进行爆炸分析或研究[8]。近年来,CFD方法取得了相当大的进步,现在可以预测复杂的VCE。但是,必须先对CFD代码进行验证,并进行网格灵敏度分析,以保证计算结果的准确性[9 − 10]。因此,本文通过模拟研究船舱内的预混燃气爆炸,分析火焰传播特性,总结爆炸规律,为船舶防爆和布局优化提供参考。
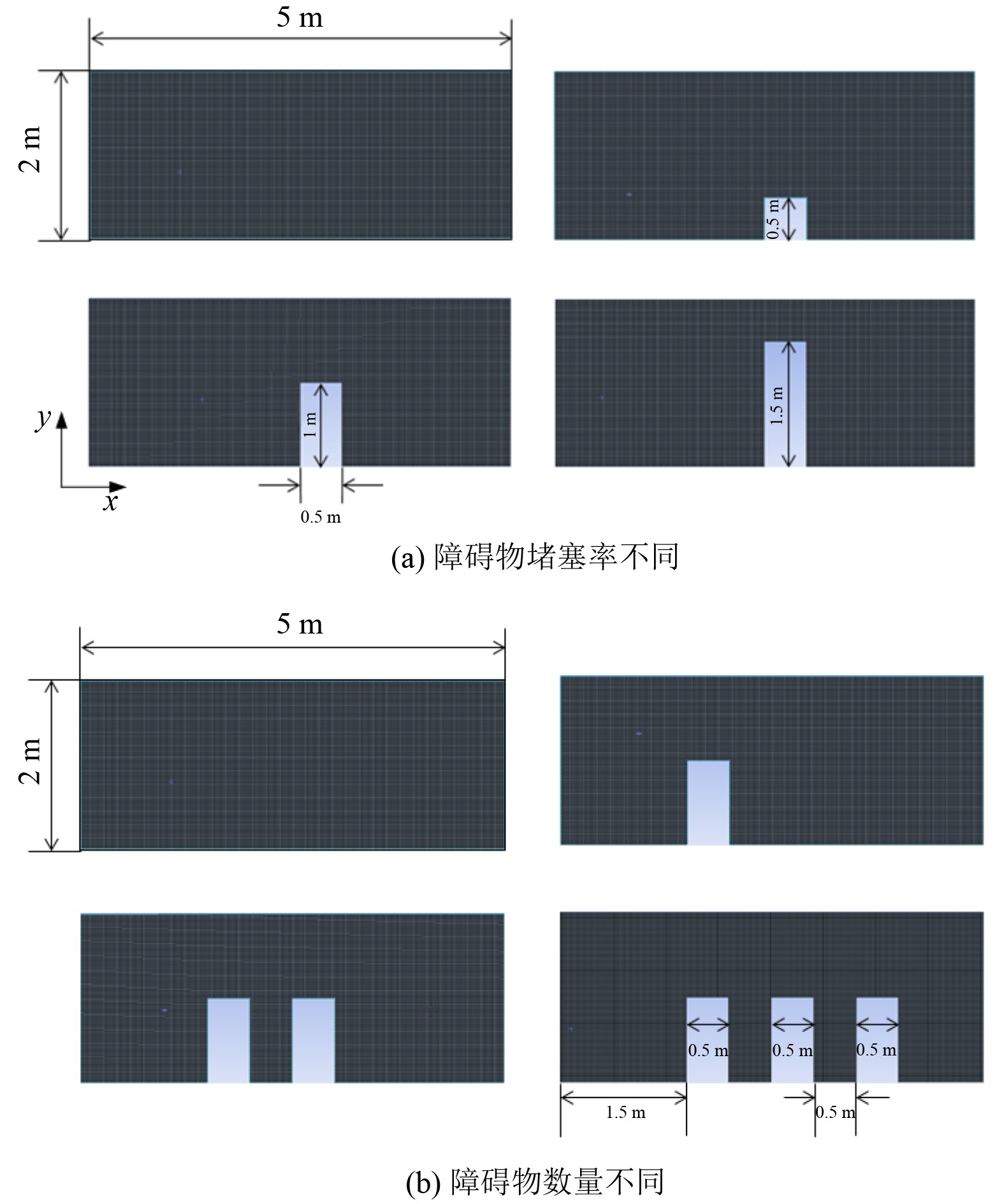
1 模型建立与参数设置 1.1 物理模型建立本文探讨障碍物对密闭船舱内部预混燃气爆炸行为的影响,主要考虑本来障碍物的存在与否对爆炸过程火焰传播和压力峰值的影响。由于研究的重点在于舱内有无障碍物对爆炸行为的影响,因此在模拟过程中对复杂的三维问题进行了简化,选择将船舱简化为长方形的二维模型进行研究,这样可以在保持准确性的同时大大减少计算量和复杂性[11]。本文使用Fluent软件进行数值模拟,为了准确模拟爆炸过程中湍流的生成和传播,选择了经典的K-epsilon湍流模型。利用Ansys mesh软件对物理模型进行网格划分,生成粗(533 179)、中(731 274)、细(
| $ RE=\frac{\left|{X}_{i}-{X}_{ref}\right|}{{X}_{ref}}\times 100\text{%}。$ | (1) |
式中:
结果表明,粗网格的误差为3.17%,中网格的误差为1.89%。从整体误差角度分析,中网格与精细网格之间的误差相对较小,可以认为两者在捕捉主要流场特征和火焰传播规律方面表现相似。鉴于计算资源及效率的平衡,本文选取了中等质量的网格进行分析如图1所示。当前网格为四面体形状,其最大质量评分为0.967,最小质量评分为0.274,而平均质量评分为0.837。
|
图 1 密闭船舱网格划分 Fig. 1 Grid division of enclosed cabin |
燃烧问题中,流体介质不仅要时刻遵循质量守恒方程、动量守恒方程、能量守恒方程,介质中参与燃烧反应的化学成分还要满足组分守恒方程[12]。在用Fluent模拟扰流柱流道内的燃烧过程时,假设预混气体和空气及其混合物为理想气体。采用SIMPLE压力校正算法处理可压缩流动,可以计算区域内压力、燃烧浓度、温度等参数的变化。
连续性方程是质量守恒的一种具体形式,任何流体流动都必须符合。连续性方程可表示为[13]:
| $ \frac{\partial }{\partial t}\left(\rho \right)+\nabla \left(\rho \overrightarrow{\nu }\right)=0。$ | (2) |
式中:
| $ \rho =\sum _{k=1}^{n} {\alpha }_{k}{\rho }_{k} ,$ | (3) |
| $ \overrightarrow{\nu }=\frac{\displaystyle\sum _{k=1}^{n} {\alpha }_{k}{\rho }_{k}{\overrightarrow{\nu }}_{k}}{\rho } 。$ | (4) |
动量方程可以用 Navier Stokes (N–S) 方程表示,该方程表示为:
| $\begin{split} \displaystyle\frac{{\partial \left( {\rho u} \right)}}{{\partial t}} +& \displaystyle\frac{{\partial \left( {\rho uu} \right)}}{{\partial x}} + \displaystyle\frac{{\partial \left( {\rho uv} \right)}}{{\partial y}} + \displaystyle\frac{{\partial \left( {\rho uv} \right)}}{{\partial z}} = \\ &-\displaystyle\frac{{\partial p}}{{\partial x}} + \mu \left( {\displaystyle\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \displaystyle\frac{{{\partial ^2}u}}{{\partial {y^2}}} + \displaystyle\frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right) + {F_x},\end{split}$ | (5) |
| $ \begin{split} \displaystyle\frac{{\partial \left( {\rho v} \right)}}{{\partial t}} +& \displaystyle\frac{{\partial \left( {\rho uv} \right)}}{{\partial x}} + \displaystyle\frac{{\partial \left( {\rho vv} \right)}}{{\partial y}} + \displaystyle \frac{{\partial \left( {\rho uv} \right)}}{{\partial z}} = \\ &- \displaystyle\frac{{\partial p}}{{\partial y}} + \mu \left( {\displaystyle\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \displaystyle\frac{{{\partial ^2}v}}{{\partial {y^2}}} + \displaystyle\frac{{{\partial ^2}v}}{{\partial {z^2}}}} \right) + {F_y},\end{split} $ | (6) |
| $ \begin{split} \displaystyle\frac{{\partial \left( {\rho w} \right)}}{{\partial t}} +& \displaystyle\frac{{\partial \left( {\rho uw} \right)}}{{\partial x}} + \displaystyle\frac{{\partial \left( {\rho vw} \right)}}{{\partial y}} + \displaystyle\frac{{\partial \left( {\rho ww} \right)}}{{\partial z}} = \\ &-\displaystyle\frac{{\partial p}}{{\partial z}} + \mu \left( {\displaystyle\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \displaystyle\frac{{{\partial ^2}w}}{{\partial {y^2}}} + \displaystyle\frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right) + {F_z}。\end{split}$ | (7) |
式中:u为动态粘度,N·s/m2,是粘性力的组成部分。
能量守恒方程:
| $ \frac{\partial}{\partial t}\left(\rho h\right)+\frac{\partial}{\partial x_j}\left(\rho u_jh-\frac{u_e}{\sigma_h}\frac{\partial h}{\partial x_j}\right)=\frac{Dp}{Dt}+R_uQ_s+S_h。$ | (8) |
式中:
| $ \tau_{ij}=\mu_e\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\frac{2}{3}\mu_e\frac{\partial u_k}{\partial x_k}。$ | (9) |
组分守恒方程:
| $ \frac{\partial}{\partial t}\left(\rho Y_u\right)+\frac{\partial}{\partial x_j}\left(\rho u_iY_u-\frac{\mu_e}{\sigma_{fu}}\frac{\partial Y_{fu}}{\partial x_j}\right)=R_u $ | (10) |
式中:
理想气体状态方程
| $ \mathit{PV} \mathrm= \mathit{mRT}。$ | (11) |
式中:P为气体压力,Pa;V为气体体积;m为气体的质量;R为气体常数;T为热力学温度。
组分输运模型。由于本研究不涉及化学反应,故选用一般有限速率模型,材料为甲烷/氢气-空气,组分输运方程为:
| $ \nabla \cdot \left(\rho \nu {Y}_{i}\right)=\nabla \cdot \left[\left(\rho {D}_{i,m}+\frac{{\mu }_{i}}{S{c}_{i}}\right)\nabla {Y}_{i}+{D}_{T,i}\frac{\nabla T}{T}\right]+{R}_{i} 。$ | (12) |
式中:
湍流动能k与湍流耗散率
| $ \frac{\partial}{\partial t}\left(\rho_lk\right)+\frac{\partial}{\partial x_i}\left(\rho_lk\overrightarrow{v_i}\right)=\frac{\partial}{\partial x_j}\left(\delta_k\mu_e\frac{\partial k}{\partial x_j}\right)+G_k+\rho_l\varepsilon,$ | (13) |
| $ \begin{split} \frac{\partial }{{\partial t}}\left( {{\rho _l}\varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {{\rho _l}\varepsilon \overrightarrow {{v_i}} } \right)= & \frac{\partial }{{\partial {x_j}}}\left( {{\delta _k}{\mu _e}\frac{{\partial k}}{{\partial {x_j}}}} \right) + \\ &\frac{{{C_{1\varepsilon }}}}{k}{G_k} - {C_{2\varepsilon }}{\rho _l}\frac{{{\varepsilon ^2}}}{k} - R\varepsilon 。\end{split} $ | (14) |
式中:k、ε、v分别为湍动能、湍动能耗散率、湍流动能粘度系数;
为了保证数值模拟的精确度,Fluent计算采用了与实验一致的设置和参数,并在模拟中布置了压力监测点,以实时监测模拟过程中的压力变化。以便后续验证数值模拟结果的可靠性。实验条件下,入口和出口均设为压力边界,压力值均为2个大气压;壁面为恒温壁面,温度设置为300 K。燃料混合物的初始组成为:甲烷0.74 mol,氢气0.26 mol,点火方式为电火花点火。实验过程记录了火焰传播的结构、压力变化及其他重要参数,为数值模拟提供了对比数据。将入口和出口设置为压力边界,压力值均为2个大气压。壁面条件采用绝热无滑移壁面假设,即所有边界设置为绝热壁面,假设气体在壁面上无滑动,流速为0。
通过比较数值模拟和实验结果中的压力峰值、火焰传播速度及形态等关键参数,分析两者之间的差异。图2所示结果表明,数值模拟能够较好地再现实验中火焰传播的主要特征,特别是在火焰前锋的形变与压力上升速率方面,两者的趋势一致,但在某些局部区域,数值模拟结果的压力峰值略高于实验结果。

|
图 2 爆炸压力对比曲线 Fig. 2 Explosion pressure comparison curve |
由图3可知,当没有障碍物时,初始阶段,燃烧处于层流状态,火焰前锋呈现光滑的半球形结构,传播速度相对较慢。当火焰传播速度逐渐增加、空间内的速度梯度和压力梯度增大时,火焰会由层流转变为湍流燃烧。湍流增强了燃料与空气的混合[14],使燃烧更加剧烈。在中期阶段,火焰前锋接触到壁面后,火焰形态受到壁面效应的影响,火焰前锋的传播路径被改变。壁面附近的流动速度减慢,火焰前锋在壁面区域发生形变和拉伸,出现明显的湍流特征。

|
图 3 不同堵塞率下火焰传播云图 Fig. 3 Flame propagation cloud map under different blockage rates |
在堵塞率为25%、50%、75%时,可以发现火焰刚刚被点燃,火焰前锋呈现圆形结构,传播速度较慢。此时火焰主要表现为层流燃烧特征,燃烧反应主要集中在局部区域,火焰面较为平滑。但是在中期阶段,火焰前锋的形状变得不规则,开始受到障碍物的影响而发生明显的形变和拉伸。当火焰遇到障碍物时,产生了局部湍流,火焰被挤压和拉伸,形成了复杂的火焰结构。障碍物的存在增强了流动的湍流效应,同时使火焰前锋发生更大幅度的形变。火焰继续向上蔓延,并逐渐填满整个空间。火焰的传播速度在遇到障碍物后有所减缓,火焰形态趋于复杂,湍流效应加剧。在最后一个时间点(80.00 ms),火焰穿越障碍物后,流动结构变得更加混乱,表现出明显的湍流燃烧特征。较高的堵塞率导致了更多的障碍物,这增加了流体的扰动和湍流效应,从而加速了火焰的传播。这种现象在流体力学中表现为火焰受阻碍物的作用产生局部加速,这种加速效应随着堵塞率的增加而更加显著[15]。结果表明,在较高的堵塞率下,火焰传播不仅更快,而且结构也更加不规则且湍动更强。合理布置障碍物和控制混合气体的初始条件,对于燃烧过程的优化和安全控制具有重要意义。
2.2 障碍物堵塞率对爆燃压力的影响由图4可知,在没有任何堵塞的情况下,3个测点分别为 (1,1.5)、(4,1.5)、(5,1.5)的爆炸压力曲线几乎重合,显示出类似的趋势。随着时间的增加,压力逐渐升高,并且在0.1 s左右达到峰值。由于没有障碍物,爆炸压力的上升是比较平缓的,波动性较小。在25%的堵塞率下,3个测点的爆炸压力曲线仍然非常接近,但可以注意到,压力上升的速率比无堵塞情况变快,并且峰值压力略有增加。堵塞物部分阻碍了气体的流动,导致局部压力的快速升高。当堵塞率增加到50%时,压力曲线之间的差异开始显现,特别是在时间0.06~0.08 s。总体趋势仍然是压力快速上升并达到峰值,但由于堵塞率的增加,气体流动受到更大阻碍,压力上升更快,并且峰值压力进一步增加。在堵塞率达到75%时,3个测点的压力曲线出现了明显的差异。压力在初期阶段迅速上升,并且在时间约为0.02 s时达到峰值,然后逐渐减小。这是因为高度堵塞导致气体流动受到极大限制,压力迅速累积到一个较高的值,然后由于能量释放,压力略有下降。随着堵塞率的增加,预混燃气的爆炸压力曲线表现出更快的上升速率和更高的峰值压力。这是由于障碍物的存在使得气体流动受阻,局部压力迅速累积,并且在燃烧过程中能量释放更为集中所致。在高堵塞率下,测点之间的压力差异可能增加,因为气体流动受到更复杂的干扰。

|
图 4 不同堵塞率下Pmax变化趋势 Fig. 4 Trend of Pmax variation under different blockage rates |
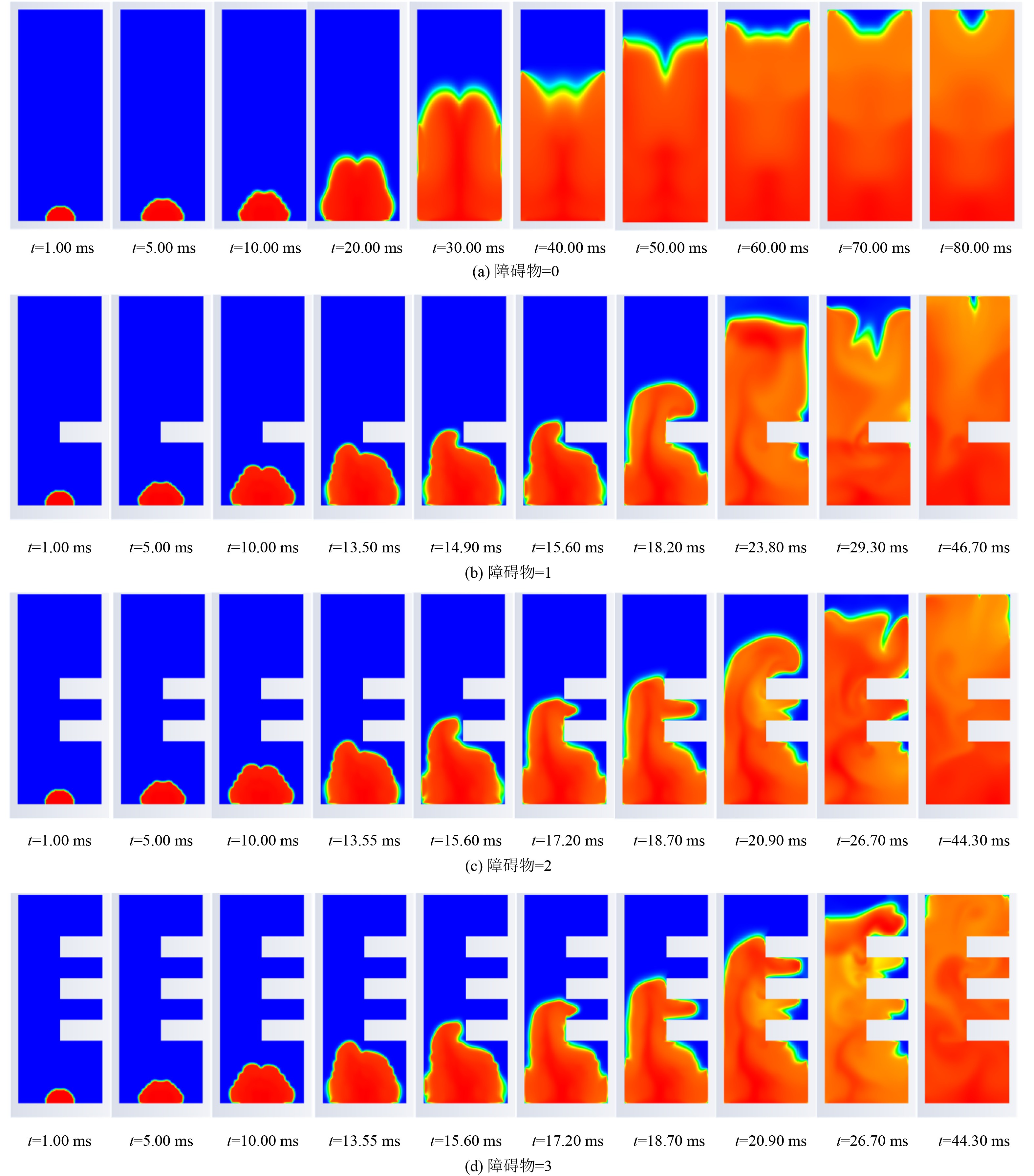
如图5所示,在火焰接近障碍物之前,障碍物对火焰的影响较小。在此阶段,火焰的传播保持相对稳定,呈现出预混层流燃烧的特征。单一障碍物的设置距离点火源较远(2.5 m),火焰在到达障碍物前的传播不会受到明显的干扰。当火焰到达障碍物时(t=18.80 ms),由于障碍物引起的流动压缩和压力波的反射,火焰前沿发生形变,从层流状态转变为湍流状态。当设置多个障碍物(1、2、3个),第1个障碍物的距离缩短至1.5 m,使得火焰更早地受到影响。第1个障碍物的存在使得火焰在t = 13.50 ms时就开始发生明显的形变。当火焰与障碍物碰撞时,会发生分裂。火焰的一部分沿着障碍物之间的涡旋区域传播,而另一部分继续沿轴线方向传播。这种分裂现象增加了火焰的表面积,并在障碍物间形成更复杂的流动模式。火焰通过障碍物后,结构会变得更加复杂,尤其是当有多个障碍物时,火焰会在涡旋区域内经历更多的湍流,导致火焰加速传播。随随着障碍物数量的增加,火焰传播的复杂性和速度明显增加。这是因为障碍物会增加流体的扰动,导致火焰前沿产生湍流和涡旋[16],使得火焰传播更快且更加不规则。
|
图 5 不同障碍物数量下火焰传播云图 Fig. 5 Flame propagation cloud map under different numbers of obstacles |
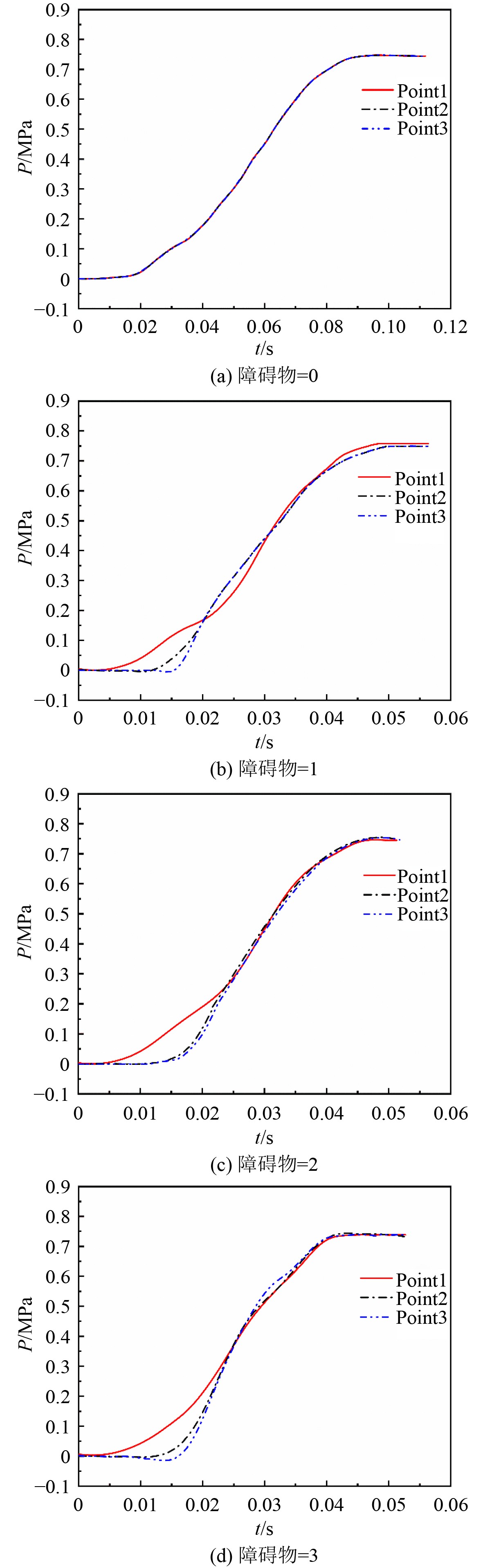
图6分别对应障碍物数量为0、1、2、3的情况。当没有障碍物时,3个测点的压力曲线几乎重合,且呈现出较为平缓的上升趋势。在0.1 s左右达到稳定的峰值压力。由于没有障碍物,气体的流动较为均匀,压力随时间的变化较为平稳,没有明显的波动。随着障碍物数量的增加,预混燃气的爆炸压力曲线表现出更快的上升速率和更显著的空间差异。这是因为障碍物阻碍了气体的自由流动,导致局部压力迅速积累,并引发了更大的压力梯度和波动。这种现象在多个障碍物情况下尤为明显,表明障碍物的增加对燃气爆炸过程有重要影响。原因在于障碍物扰动形成的涡流加剧了组分输送速率和燃烧速率,从而加速了火焰由层流向湍流的转变[17 − 18]。
|
图 6 不同障碍物数量下火焰传播监测点曲线图 Fig. 6 Curve diagram of flame propagation monitoring points under different numbers of obstacles |
如图7和图8所示,随着初始压力的增加,最大爆炸压力Pmax 逐渐增大。不同堵塞率(0%、25%、50%、75%)的曲线非常接近,说明堵塞率对 Pmax的影响相对较小。虽然堵塞率75%时,压力略高,但总体来看各曲线趋势一致。障碍物数量的增加对 Pmax的影响较小,曲线基本上重合,说明障碍物数量对最大爆炸压力的影响并不显著。随着初始压力的增加,最大压力上升速率 (dp/dt)max 也明显增大。堵塞率越高(尤其是75%时),(dp/dt)max 的增长更为显著。这是因为堵塞率的增加加剧了气体流动的阻力,使得压力在较短时间内迅速积累[19]。这种局部压力的快速积累会导致压力上升速率加快,进而可能增加爆炸的强度。障碍物数量越多(尤其是3个障碍物时),(dp/dt)max 的增幅更为显著。这表明障碍物数量的增加使得气体的流动路径变得更加复杂,导致压力快速上升的速率更大。这些变化趋势表明,爆炸压力和压力上升速率的变化受初始条件(如初始压力)、系统结构(如堵塞率和障碍物数量)的影响显著。理解这些原理对于设计更安全的燃气系统,防止爆炸事故的发生具有重要意义。

|
图 7 堵塞率对Pmax和(dp/dt)max的影响 Fig. 7 The influence of blockage rate on Pmax and (dp/dt) max |

|
图 8 障碍物数量对Pmax和(dp/dt)max的影响 Fig. 8 The influence of the number of obstacles on Pmax and (dp/dt) max |
1) 障碍物堵塞率增加,火焰的传播速度加快,同时火焰前沿的形状也变得更加复杂。较高的堵塞率导致了更多的障碍物,这增加了流体的扰动和湍流效应,从而加速了火焰的传播。
2)障碍物数量增加,火焰通过每个障碍物后的变形程度加剧,尤其是在多个障碍物条件下,火焰传播的结构会变得更加复杂。障碍物数量增加也会导致最大爆炸压力上升率的增大,这意味着更多的障碍物会加剧爆炸的剧烈程度。
3)在火焰传播初期,爆炸超压逐渐增大,增长速度较慢。随着火焰传播的加速,特别是在火焰接近和穿过障碍物时,超压迅速增加。火焰完全穿过障碍物后,超压逐渐达到平衡并趋于稳定。
4)爆炸压力和压力上升速率的变化受初始条件(如初始压力)、系统结构(如堵塞率和障碍物数量)的影响显著。理解这些原理对于设计更安全的燃气系统,防止爆炸事故的发生具有重要意义。
| [1] |
QIN Y, CHEN X. Flame propagation of premixed hydrogen-air explosion in a closed duct with obstacles[J]. International Journal of Hydrogen Energy, 2019, 44: 3944-3952. |
| [2] |
龚慧芝, 赵忠超. LNG在微小通道中沸腾流动与换热特性的数值研究[J]. 舰船科学技术, 2024, 46(5): 126-132. DOI:10.3404/j.issn.1672-7649.2024.05.023 |
| [3] |
JOHANSEN CT, CICCARELLI G. Visualization of the unburned gas flow field ahead of an accelerating flame in an obstructed square channel[J]. Combust and Flame, 2009, 156: 405-416. |
| [4] |
MCGARY J, AHMED K. Flame-turbulence interaction of laminar premixed deflagrated flames[J]. Combust and Flame, 2017, 176: 439-450. |
| [5] |
束元超, 王珂, 白旭. LNG船舶舱室泄漏爆炸动态响应模拟研究[J]. 舰船科学技术, 2023, 45(24): 14-19. DOI:10.3404/j.issn.1672-7649.2023.24.003 |
| [6] |
GUBBA SR, IBRAHIM SS, MALALASEKERA W, et al. Measurements and LES calculations of turbulent premixed flame propagation past repeated obstacles[J]. Combust and Flame, 2011, 158: 2465-2481. |
| [7] |
DI SARLI V, DI BENEDETTO A, RUSSO G. Sub-grid scale combustion models for large eddy simulation of unsteady premixed flame propagation around obstacles[J]. Journal of Hazardous Materials, 2010, 180: 71-78. |
| [8] |
COATES A, MATHIAS D, CANTWELL B. Numerical investigation of the effect of obstacle shape on deflagration to detonation transition in a hydrogeneair mixture[J]. Combust and Flame, 2019, 209: 278-290. |
| [9] |
汪焓煜. 生物质油在内燃机上应用基础特性[D]. 杭州: 浙江大学, 2020.
|
| [10] |
钟安昊. 生物质热裂解油的层流燃烧特性研究[D]. 杭州: 浙江大学, 2018.
|
| [11] |
ZHOU Q, CHEUNG CS, LEUNG CW, et al. Effects of fuel composition and initial pressure on laminar flame speed of H2/CO/CH4 bio-syngas[J]. Fuel, 2019, 238: 149-158. |
| [12] |
崔锦泉, 周伟, 王智磊, 等. 船舶双燃料发动机LNG供气系统模拟仿真技术应用研究[J]. 舰船科学技术, 2022, 44(18): 122-125. DOI:10.3404/j.issn.1672-7649.2022.18.024 |
| [13] |
BRADLEY D. Instabilities and flame speeds in large-scale premixed gaseous explosions[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1999, 1764: 3567-3581. |
| [14] |
WANG X, FU J, XIE M, et al. Numerical investigation of laminar burning velocity for methane-hydrogen-air mixtures at wider boundary conditions[J]. Aerospace Science and Technology, 2022, 121: 107393. |
| [15] |
MARINOV NM. A detailed chemical kinetic model for high temperature ethanol oxidation[J]. International Journal of Chemical Kinetics, 1999, 31: 183-220. |
| [16] |
XIANG L, JIANG H, REN F, et al. Numerical study of the physical and chemical effects of hydrogen addition on laminar premixed combustion characteristics of methane and ethane[J]. International Journal of Hydrogen Energy, 2020, 45: 20501-20514. |
| [17] |
ECKART S, PIZZUTI L, FRITSCHE C, et al. Experimental study and proposed power correlation for laminar burning velocity of hydrogen-diluted methane with respect to pressure and temperature variation[J]. International Journal of Hydrogen Energy, 2022, 47: 6334-6348. |
| [18] |
BRADLEY D, LAWES M, MUMBY R,et al. The stability of laminar explosion flames[J]. Proceedings of the Combustion Institute, 2019, 37: 1807-1813. |
| [19] |
OPPONG F, XU C, LUO Z, et al. Cellularization of 2-methylfuran expanding spherical flame[J]. Combustion and Flame, 2019, 206: 379-389. |
 2025, Vol. 47
2025, Vol. 47
