2. 哈尔滨工程大学,黑龙江 哈尔滨 150006
2. Harbin Engineering University, Harbin 150006, China
随着全球贸易一体化进程的不断推进,海上航运日益频繁,为确保船舶在极端恶劣海洋环境条件下稳定安全航行和港口等浅狭窄海域机动调度[1 - 3],避免因操纵与控制能力不足引发碰撞、搁浅、失事等生命财产安全灾害事故[4],国际海事组织(IMO)要求在船舶方案设计阶段开展船舶的操纵性评估[5],同时出于对船舶机动特性和航运成本效益的考虑,极大地促进了对全球船舶动态操控性特性的研究[6]。
船舶操纵性预报方法分为直接预报、操纵模拟、数值模拟以及机器学习4类[7],其中直接预报和操纵模拟需通过船模拖曳和回转试验辨识操纵运动模型参数,存在耗时长、成本高等问题[8],因此,随着并行计算能力的增强和计算流体力学(CFD)的快速发展,CFD数值模拟已成为船舶方案设计阶段快速预报船舶操纵性的重要手段,而且SIMMAN、ITTC等国际会议针对KVLCC2、KCS等常规船型提供了大量试验数据,极大促进了船舶操纵数值模拟的发展[9]。
船舶操纵数值模拟研究主要分为自航船模操纵运动参数预报和约束船模水动力参数预报[8 - 10]。自航船模操纵运动参数预报方面,Mofidi等[11]联合螺旋桨体积力模型和CFD求解器,对KCS标准船模进行了回转操纵性预报;Jin等[12]分别采用BFM和DPM螺旋桨模拟技术联和非定常RANS方程对DTMB5415标准船模的回转和Z形操纵试验进行了模拟,可以较好地预报操纵运动参数;王建华等[13]采用动态重叠网格技术及自主研发的CFD求解器对波浪载荷下的船−桨−舵的回转操纵试验进行了数值模拟。约束船模水动力参数预报方面,Balagopalan等[14]对KCS船模进行了约束船模数值试验,并利用船模试验对数值试验精度进行了校核;Liu等[15]利用STAR-CCM+针对KCS标准船模分析了垂荡和纵倾对船体水动力的影响;Zhang等[16]利用OpenFOAM对ONRT船模进行斜航拖曳试验,求解得出了相关水动力系数;Kim等[17]通过求解RANS方程,对KCS船模进行了PMM数值试验,除纯艏摇模拟结果存在一定误差,其横荡等数值试验结果满足操纵性预报精度要求。
虽然目前国内外众多学者对船舶操纵性数值预报作出了大量研究贡献,在求解器选择方面既有Fluent、STAR-CCM+等通用商业软件,也有OpenFOAM开源软件,更有自主研发CFD求解器;在模型选取方面有缩比模型也有实船尺度模型;在螺旋桨模拟技术方面有BFM和DPM;在网格处理方面有重叠网格也有滑移网格。总之,对于船舶方案设计阶段操纵性数值预报方面尚未形成一套既定的流程,而且对数值结果的准确性存在一定争议。
因此,本文为验证现有船舶动力学数值仿真模拟对船舶运动预测的准确性,利用STAR-CCM+分别以KVLCC2油轮回转运动和S175集装箱船在规则波中的摇摆运动为例进行了操纵性预报,并与SIMMAN试验结果进行了对比,验证了数值模拟方法的可靠性,表明数值模拟方法可作为船舶方案设计阶段操纵性预报的主要手段。
1 船舶回转运动 1.1 确定问题研究对象是1∶58比例的KVLCC2油轮模型。KVLCC2油轮1∶58缩比模型的几何特性:水线间长LPP为5.51 m,船宽B为1 m,船高H为0.51 m,吃水T为0.35 m,排水量Δ为

|
图 1 船模随船坐标系 Fig. 1 Ship model's accompanying coordinate system |
在三维矩形计算区域内,船舶进行回转运动。计算区域大小:长为30LPP,宽为14LPP,高为14LPP。除顶部外,所有边界表面都是具有滑动壁面条件。上表面是压力输出条件(P = 0)。在所有固体壁上施加阻尼条件,以调节表面波浪可能的反射。
1.2 参数设置这项工作的主要特点之一是考虑自由曲面。此选项允许解析船舶周围的波浪,从而可以分析船体的波浪阻力。此外,如果没有自由曲面模型,则不可能确定纵倾角、倾斜角和浮出角。因此,任务采用了具有以下物理参数的多相设置:
1)空气:密度为
2)水:密度为
3)重力正指向Z轴,等于标准9.81 m/s2。
1.3 数学模型本文考虑了一个多相非稳态物体运动问题,该问题有6个自由度:沿x、y和z轴运动,以及摇摆、倾斜和偏航。物体的运动和旋转由以下方程决定:
| $ m\frac{{\mathrm{d}\vec v}}{{\mathrm{d}t}} = \vec f,$ | (1) |
| $ m\frac{{\mathrm{d}\vec \omega }}{{\mathrm{d}t}} + \vec \omega \times M\vec \omega = \vec n 。$ | (2) |
式中:m为体质量;
相位运动(水或空气)是用雷诺平均Navier–Stocks方程组和封闭的湍流模型模拟的。雷诺平均Navier–Stocks方程组:
| $ \left\{\begin{array}{l}\nabla\cdot\overrightarrow{V}=0,\\ \displaystyle\frac{\partial\overrightarrow{\overline{V}}}{\partial t}+\nabla\cdot\left(\overrightarrow{\overline{V}}\overrightarrow{\overline{V}}\right)=-\displaystyle\frac{1}{\rho}\nabla\overline{p}+\displaystyle\frac{1}{\rho}\nabla\left(\tau_m+\tau\right)+\overrightarrow{\overline{g}}。\end{array}\right. $ | (3) |
式中:
| $ \left\{\begin{aligned} &\rho\dfrac{{\mathrm{d}}k}{{\mathrm{d}}t}=\nabla\cdot((\mu+\sigma_k\mu_t)\nabla k)+P_k-\beta^{\ast}\rho\omega k ,\\ &\begin{split} \rho\dfrac{{\mathrm{d}}\omega}{{\mathrm{d}}t}=&\nabla\cdot((\mu+\sigma_{\omega}\mu_t)\nabla\omega)+\gamma\displaystyle\frac{\rho}{\mu_t}P_k- \\ &\beta\rho\omega^2+\left(1-F_1\right)D_{kw}。\end{split}\end{aligned}\right. $ | (4) |
式中:k为湍流的动能,
为了计算自由曲面的位置,使用了VOF方法。该方法解决了一个相对变量C的守恒方程,该变量C的值为0~1,并描述了单元中液相的数量:
| $ \frac{\partial C}{\partial t}+\overrightarrow{V}\cdot\nabla C=0。$ | (5) |
在STAR-CCM+项目中进行了网格构建、计算和结果可视化。需要注意的是,在将空间乘以控制体积时,使用了嵌套网格法(Overset方法)。它的本质是将网格分为外部块和内部块。外部块是一个普通的六面体网格,Overset是一个内部块,里面嵌套有一个移动的物体。此内部块与外部块内的主体一起移动。内部块块内的网格如图2所示。

|
图 2 船舶嵌套网格法示意 Fig. 2 Schematic diagram of nested grid method for ships |
网格类型为六面体。为了解决船体边界层的问题,在船体边界上对网格进行加密。因为本文考虑了KVLCC2为缩比船舶模型,而不是实际尺寸的物体,并采用了低雷诺数下的湍流模型,该模型要求边界层单元中心与最近壁面无量纲距离y+<1。
计算网格数量约为700万。在舵面、波浪面和船体表面附近进行了局部加密。此外,网格在自由曲面周围的整个计算区域被加密,以提高相对边界的分辨率,如图3所示。
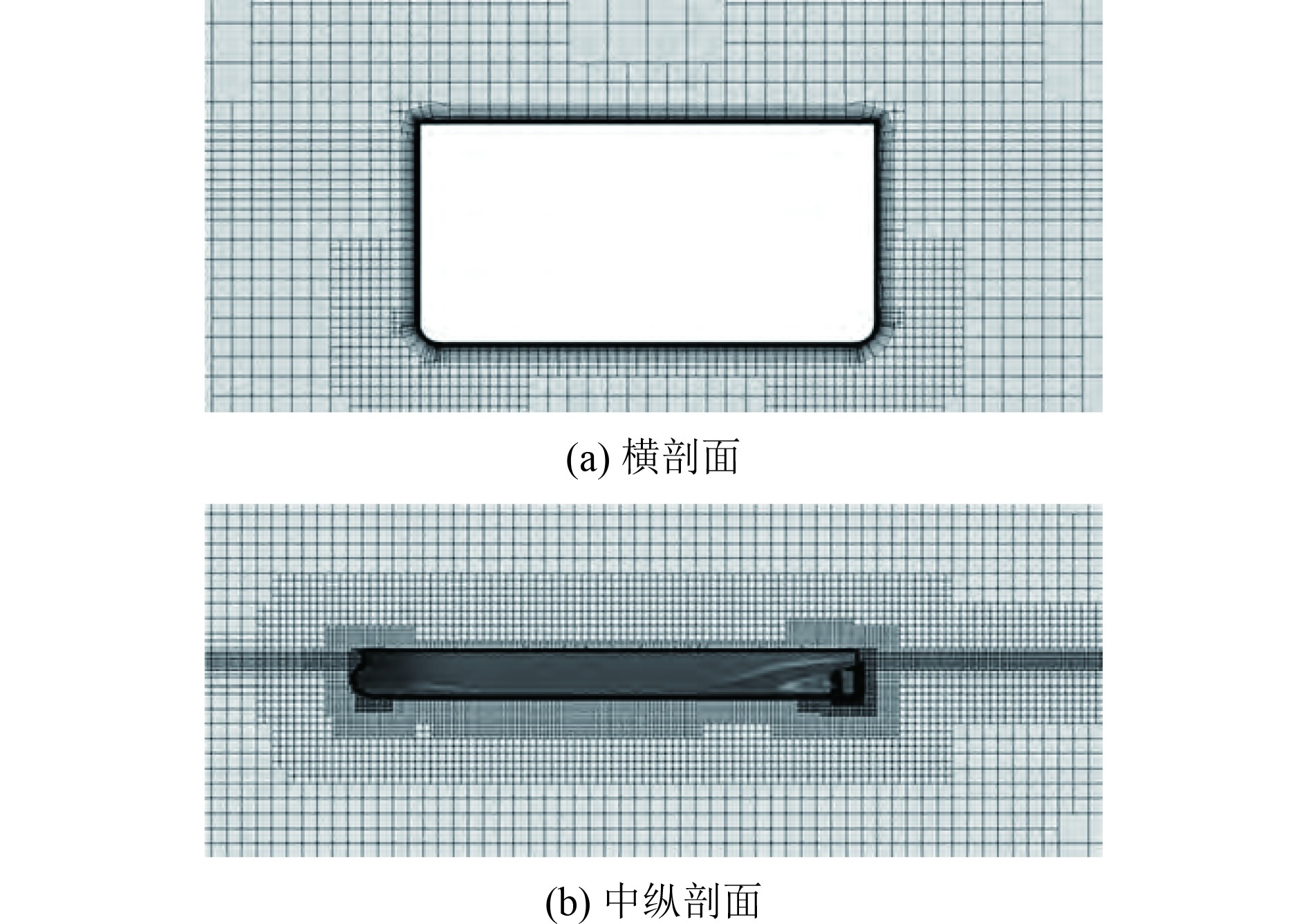
|
图 3 不同截面的计算网格 Fig. 3 Calculation grids of different cross-sections |
为避免引入旋转螺旋桨带来的大量网格计算成本,本文对螺旋桨的处理采用虚拟桨盘技术,因此对于可信的螺旋桨模型,有必要了解推力系数、力矩系数和效率与进气的关系,即推力系数、力矩系数和效率与进气的关系。KVLCC2螺旋桨的推进系数曲线由从Simman Work Shop网站得知[18],但此处未考虑运动与螺旋桨相互作用系数的影响。
由于采用虚拟桨盘,船舶转舵时不应立即转向,而是仍以相应速度运动,并保持船体周围波浪相对稳定,为此,考虑2种基本的运动模式:直线加速和回转模式。这2种模式之间的转换和过渡通过以下过程解决:当船舶进入准静止状态时,舵被重新定位,然后整个几何结构和局部网格密度从初始坐标系统移动到与物体相关的坐标系统。这种迁移需要从解决方案停止的那一刻开始,而不是从解决方案初始化的那一刻开始。然后重新调整网格,进行求解外推,读取新的几何结构,并在重新调整的方向盘上继续计算,因此船舶开始在回转模式下移动。
所有的计算都是用二阶速度势和有限差分方法,时间迭代步长t = 0.005 s,总计算时长16 s,耗费
回转开始时的实验速度为1.047 m/s。为了实现这一目标,给虚拟桨盘分配了与最大效率值相对应的推力和扭矩KVLCC2:KT =
为了实现计算的自动化,开发了一个基于现有数据调节虚拟桨盘转速的程序。随着船的速度加快,转速降低,船的速度加快。船舶回转速度曲线如图4所示。

|
图 4 船舶速度与时间的关系 Fig. 4 Relationship between ship speed and time |
分析可以发现,加速25 s后,当船舶达到1.047 m/s的速度时,精度为2%,舵面重新调整为转角35°。
针对船舶3个自由度(沿X轴、Y轴和偏航角移动)进行了回转运动计算。首先,船舶必须加速到实验速度[19],否则将导致数值计算的回转直径与试验直径不同,因此,在没有改变虚拟桨盘位置的情况下进行了加速,即在直线行驶。根据数值模拟的结果,回转直径为D = 3.03LPP,根据文献[19],试验值回转直径为3.1LPP。因此,通过数值模拟得出的数值与类似的试验数据之间的误差−2.3%。船舶回转运动轨迹如图5所示,可以发现,船舶不会立即进入稳定循环,而是从第2次才进入回转运动。

|
图 5 船舶运动轨迹轨迹 Fig. 5 Ship motion trajectory trajectory |
另外,在考虑船舶6个自由度进行类似计算时,回转直径D = 3.078LPP,比试验值小0.7%。因此,六自由度的引入可以提高计算精度1.6%,而且船舶从第一轮即可进入稳定的回转运动。此时,船舶回转纵距6.9 m,横距4.1 m,战术直径11.58 m,180°回转时间24.6 s。
2 规则波浪中的船舶摇摆问题 2.1 确定问题研究对象是1∶50比例的S175[20]集装箱船模型(见图6)。S175集装箱船1∶50缩比模型的几何特性:水线间长LPP = 3.6 m,船宽B = 0.51 m,船高H = 0.33 m,吃水T = 0.19 m,排水量Δ = 196 kg。

|
图 6 S175集装箱模型 Fig. 6 S175 Container model |
在三维矩形计算区域内,船舶在规则波中运动。计算区域大小:长为8LPP,宽为6.5LPP,高为1.4LPP。除左、上、右外,所有边界表面都是具有滑动条件的壁面,左面是波浪输入速度的条件,上表面和右表面是压力输出条件(P = 0)。在所有固体壁上施加阻尼条件,以消除波的可能反射。
2.2 环境的数学模型和参数数学模型和环境参数与船舶回转运动类似,只是S175与KVLCC2不同,只有3个自由度运动:升沉、横摇和纵摇。
2.3 计算网格和数值参数在构建计算网格时,使用与回转运动相同的方法−Overset方法。但由于船舶运动计算量大且计算耗时长,为研究以上船舶运动数值计算的网格收敛性,以一种简化的形式进行了网格收敛性研究,即自由面无波浪载荷,通过给定船舶一个初始横倾角(20°),数值模拟船舶横摇运动,将摇摆周期作为网格收敛性研究指标,并与类似的试验数据对比。研究结果如表1所示,130万和400万个网格的计算结果并不好,与实验的差异分别为4.2%和5.48%。830万和
|
|
表 1 网格收敛性研究 Tab.1 Study on grid convergence |
在船体以及波长和高度上进行了局部网格浓缩,以获得高质量的波纹分辨率。网格总体情况如图7所示。

|
图 7 网格总体情况 Fig. 7 Overall situation of the grid |
波浪采用斯托克斯一阶波浪理论近似模拟方法,具有规律的周期性正弦波性质。
水平速度方程:
| $ v_h=aw\mathrm{cos}\left(\overrightarrow{K}\cdot\overrightarrow{X}-wt\right)e^{Kz} 。$ | (6) |
垂直速度方程:
| $ v_{\nu}=aw\mathrm{sin}\left(\overrightarrow{K}\cdot\overrightarrow{X}-wt\right)e^{Kz}。$ | (7) |
曲面高度方程:
| $ \mu=a\mathrm{cos}\left(\overrightarrow{K}\cdot\overrightarrow{X}-wt\right)。$ | (8) |
式中:a为波幅;ω为波的频率;
为了与试验数据进行比较,升沉、横摇和纵摇计算结果被无量刚化处理,横摇和纵摇角的非量纲化是相对于波浪坡度的角度,升沉的非量纲化是相对于波幅。图8、图9所示分别为航向与波浪的夹角分为90°和135°计算结果。

|
图 8 航向与波浪的夹角为90°时数值与试验结果对比 Fig. 8 Comparison between numerical and experimental results when the angle between heading and wave is 90° |

|
图 9 航向与波浪的夹角为135°时数值与试验结果对比 Fig. 9 Comparison between numerical and experimental results when the angle between heading and wave is 135° |
由图8可知,横摇和升沉结果与试验结果非常接近。最大的差异只出现在ω = 0.91 rad/s频率。纵倾角的显著差异是由于所获得的数值非常小(度的1/10),因此很难比较结果。由图9可知,航向与波浪的夹角为135°时,数值模拟的结果在横摇和升沉方面与试验结果非常吻合。数值与试验结果之间的纵摇差异不如航向与波浪的夹角为90°的差异强烈,因为在航向与波浪的夹角为135°时,S175的纵摇角较大。
3 结 语1)回转运动的数值仿真需先通过直线加速再转入回转运动,虽然造成计算流程复杂,但仿真结果与实际更符;
2)三自由度下,回转直径预测值与试验误差为−2.3%;六自由度下,回转直径预测值与试验误差为−0.7%,计算耗时约为
3)横摇与升沉数值预报结果与试验值吻合度非常好,纵摇结果的差异主要归因于纵摇角数值非常小;
4)所获得的数值预测结果与试验数据非常一致,说明数值计算足以准确解决各种外部条件下的船舶运动问题。
| [1] |
牙政谋. 大型船舶浅水航行安全研究[J]. 中国水运, 2022(2): 117-119. YA Z M. Research on safety of shallow water navigation for large ships[J]. China Water Transport, 2022(2): 117-119. |
| [2] |
张星. 大型集装箱船风浪作用下的操纵性仿真[J]. 舰船科学技术, 2022, (44)23: 149−151. ZHANG X. Simulation of maneuverability of large container ships under wind and waves[J]. Ship Science and Technology, 2022, (44)23: 149−151. |
| [3] |
张昊翔. 浅水对港内船舶操纵的影响研究[J]. 中国水运, 2023, 23: 20-23. ZHANG H X. Study on the Impact of Shallow Water on Ship Maneuvering in Ports[J]. China Water Transport, 2023, 23: 20-23. DOI:10.3969/j.issn.1006-7973.2023.12.zgsy202312008 |
| [4] |
李永成, 李迎华, 潘子英, 等. 浅水效应下智能技术试验船回转操纵性数值模拟[J]. 舰船科学技术, 2024, 46(3): 46-49. LI Y C, LI Y H, PAN Z Y, et al. Numerical simulation of turning maneuverability of intelligent technology test ship under shallow water effect[J]. Ship Science and Technology, 2024, 46(3): 46-49. |
| [5] |
IMO. Explanatory notes to the standards for ship man-oeuvrability: MSC/Circ. 1053[S]. London, UK: IMO, 2002.
|
| [6] |
郑茂, 丁世淦, 兰加芬. 基于数值计算的非常规船型操纵运动建模[J/OL]. 上海交通大学学报, 1−15[2024-07-08]. ZHENG M, DING S G, LAN J F. Modeling of unconventional ship maneuvering motion based on numerical calculation [J/OL]. Journal of Shanghai Jiao Tong University, 1−15[2024-07-08]. |
| [7] |
LI S , LIU C , CHU X , et al. Ship maneuverability modeling and numerical prediction using CFD with body force propeller[J] . Ocean Engineering, 2022, 264: 112454.
|
| [8] |
孙寒冰, 肖佳峰, 王伟, 等. 船舶操纵水动力导数的数值求解及敏感度分析[J]. 中国舰船研究, 2022, 17(1): 60-70. SUN H B, XIAO J F, WANG W, et al. Numerical solution and sensitivity analysis of hydrodynamic derivatives in ship maneuvering[J]. China Shipbuilding Research, 2022, 17(1): 60-70. |
| [9] |
王建华, 万德成. 船舶操纵运动CFD数值模拟研究进展[J]. 哈尔滨工程大学学报, 2018, 39(5): 813−824. WANG J H, WAN D C. Research progress on CFD numerical simulation of ship maneuvering motion [J]. Journal of Harbin Engineering University, 2018, 39 (5): 813−824 |
| [10] |
WANG J, ZOU L, WAN D. Numerical simulations of zigzag maneuver of free running ship in waves by RANS-Overset grid method[J] . Ocean Engineering, 2018, 162: 55−79.
|
| [11] |
MOFIDI A, MARTIN E J, CARRICA M P. Propeller/rudder interaction with direct and coupled CFD/ potential flow propeller approaches, and application to a zigzag manoeuvre[J]. Ship Technology Research, 2018, 65(1): 10-31. DOI:10.1080/09377255.2017.1399970 |
| [12] |
JIN Y T, DUFFY J, CHAI S H, et al. DTMB 5415M dynamic manoeuvres with URANS computation using body-force and discretised propeller models[J]. Ocean Engineering, 2019, 182: 305-317. DOI:10.1016/j.oceaneng.2019.04.036 |
| [13] |
王建华, 万德成. CFD数值模拟船舶在波浪中的回转操纵运动[J]. 中国舰船研究, 2019, 14(1): 1-8. WANG J H, WAN D C. CFD numerical simulation of ship turning and maneuvering motion in waves[J]. China Shipbuilding Research, 2019, 14(1): 1-8. |
| [14] |
BALAGOPALAN A, TIWARI K, RAMEESHA T V, et al. Manoeuvring prediction of a container ship using the numerical PMM test and experimental validation using the free running model test[J]. Ships and Offshore Structures, 2020, 15(8): 852−865.
|
| [15] |
LIU Y , ZOU L , ZOU Z J, et al. Predictions of ship maneuverability based on virtual captive mode tests[J]. Engineering Applications of Computational Fluid Mechanics, 2018, 12(1): 334−353.
|
| [16] |
ZHANG C L, LIU X J, WAN D C, et al. Experimental and numerical investigations of advancing speed effects on hydrodynamic derivatives in MMG model. Part I: XVV, YV, NV[J]. Ocean Engineering, 2019, 179: 67-75. DOI:10.1016/j.oceaneng.2019.03.019 |
| [17] |
KIM H, AKIMOTO H, ISLAM H. Estimation of the hydrodynamic derivatives by RANS simulation of planar motion mechanism test[J]. Ocean Engineering, 2015, 108: 129-139. DOI:10.1016/j.oceaneng.2015.08.010 |
| [18] |
MOERI Tanker KVLCC2. Workshop on verification and validation of vessel maneuvering simulation methods[EB/OL] http://www.simman2008.dk/KVLCC/KVLCC2/kvlcc2_ geometry.html.
|
| [19] |
TOXOPEUS S L, LEE S W. Comparison of manoeuvring simulation programs for SIMMAN test cases[C]//SIMMAN 2008 Workshop on Verification and Validation of Ship Manoeuvring Simulation Methods. Denmark, 2008.
|
| [20] |
Report of the seakeeping committee, S-175 comparative model experiments[C]// Proc. 18th International Towing Tank Conference (ITTC). Vol. 1. Kobe, Japan. October, 1987.
|
 2025, Vol. 47
2025, Vol. 47
