2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 中国人民解放军91388部队,广东 湛江 524000
2. China Ship Development and Design Center, Wuhan 430064, China;
3. No. 91388 Unit of PLA, Zhanjiang 524000, China
水下航行器机械设备运转过程中产生的振动通过其下面的基座结构传递到航行器的船体结构,因此,减弱基座结构的振动及其振动传递对减小水下航行器的结构振动具有重要意义。
迄今为止,从结构声学设计的角度出发,通过在局部设置变厚度板的方法降低水下航行器设备基座结构、船体结构振动的研究已经取得了大量的成果。在局部采用厚度按幂函数衰减规律变化且幂函数的指数不小于2的一维或二维板结构[1 − 4],利用有限元分析方法研究了盒式结构[5 - 6]、浮筏结构[4]、设备基座[7]等结构的振动特性,或通过结构振动试验与理论研究对比[8 − 10]的方式分析变厚度板的结构参数、结构形式等对目标结构减振效果的影响,均得出了变厚度板能降低目标结构的中高频振动的结论。另外,现有的数值仿真模型中大多数都采用体单元对含变厚度板的结构进行离散,单元规模较大,计算效率不高。
在上述研究中,几乎都是把变厚度板嵌在目标结构中,比如嵌在基座的面板或腹板上,但是由于受到目标结构强度要求、尺寸等方面的限制,变厚度板的尺度相对较小,对目标结构的振动控制的频率范围大多表现在中高频,然而,对水下航行器低频段结构振动的控制是急需解决的问题。因此,本文通过使用重量轻的材料使附加的变厚度板相对目标结构较小,从而避免产生因为目标结构重量增大而引起振动特性改变的现象。另外,为了提高计算效率,采用面单元模拟变厚度板结构,为水下航行器减振降噪设计提供新的思路和参考。
1 变厚度消波阻尼板消波减振的基本理论在薄板中,当不考虑转动惯量和剪切变形的影响时,弯曲波的波速计算式[11]为:
| $ {c_b} = {\left[ {2\text{π} fh\sqrt {\frac{E}{{12\rho \left( {1 - {\mu ^2}} \right)}}} } \right]^{\frac{1}{2}}}。$ | (1) |
式中:
| $ h\left(x\right)=\varepsilon x^m。$ | (2) |
式中:
| $ c_b^{ }\left(x\right)=\left[\frac{E\omega^2h^2\left(x\right)}{12\rho\left(1-\mu^2\right)}\right]^{\frac{1}{4}}。$ | (3) |
式中:
| $ k=\left[\frac{12\rho\omega^2\left(1-\mu^2\right)}{Eh\left(x\right)^2}\right]^{\frac{1}{4}}。$ | (4) |
当波传播到零厚度区域时,群速度
当结构不在液体中并且
| $ NWV = \frac{{{\mathrm{d}}k}}{{{\mathrm{d}}x}}\frac{1}{{{k^2}}} \ll 1 。$ | (5) |
将式(4)代入式(5)中可得
| $ \frac{1}{2}{\left[ {\frac{E}{{12\rho {\omega ^2}\left( {1 - {\mu ^2}} \right)}}} \right]^{\frac{1}{4}}}\frac{1}{{h{{\left( x \right)}^{\frac{1}{2}}}}}\frac{{\mathrm{d}h\left( x \right)}}{{\mathrm{d}x}} \ll 1 。$ | (6) |
根据式(6)可知,在变厚度区域内,归一化波数
| $ \varepsilon\ll\left(\frac{3\rho\omega^2}{E}\right)^{\frac{1}{2}}。$ | (7) |
若使变厚度板结构对弯曲波起到聚焦的作用,波长
| $ \omega_{c1}=\frac{h_1}{x_1^2}\sqrt{\frac{E}{12\rho\left(1-\mu^2\right)}}。$ | (8) |
式中:
根据式(3)和式(4),当板厚按照幂律连续变化且最薄处厚度变为0时,弯曲波无法到达板厚等于0的位置。本文根据上述现象设计变厚度消波阻尼板,设计的思路是,变厚度消波阻尼板由等厚度板、变厚度板和阻尼板构成,变厚度消波阻尼板布置在目标结构振动较大的位置,通过调节变厚度板的长度、材料及板厚等参数改变板的固有频率,实现与振源的耦合共振,从而吸收并耗散弯曲振动能量。由于在实际工程当中无法将板的边缘处的厚度加工为零厚度,因此,在板的最薄处贴一块阻尼板以吸收振动能量。
本文中,
为了验证本文提出的变厚度板有限元模型和变厚度板对振动控制分析的准确性,将数值仿真的结果与实验结果进行对比,验证数值仿真的正确性。实验装置、各个参数以及实验结果等均来自文献[16]。2块变厚度板内嵌到矩形板,矩形板的尺寸如图1所示,钢的材料参数如表1所示,变厚度板的
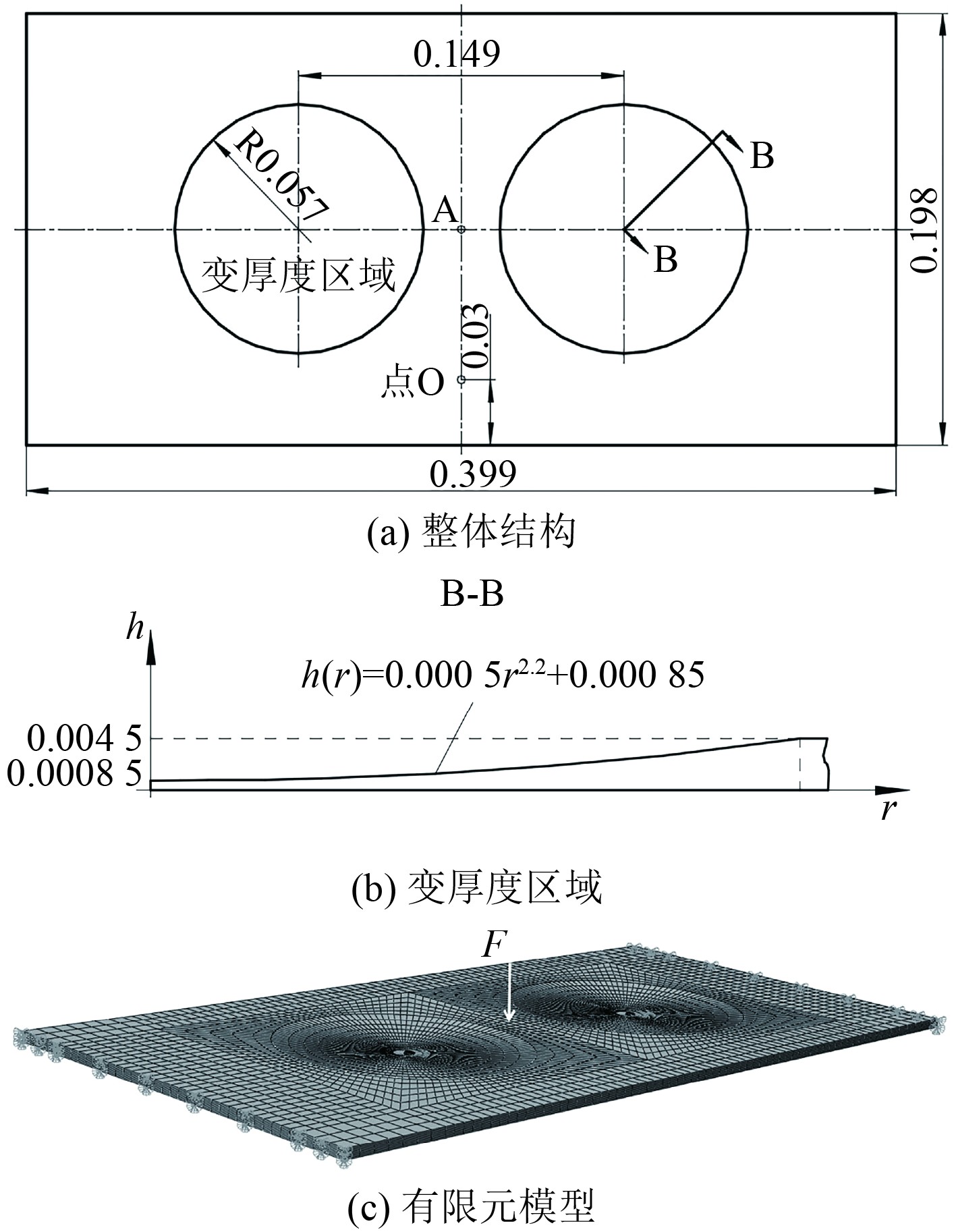
|
图 1 内嵌2块变厚度板的矩形板模型 Fig. 1 Rectangular plate model with two plates of variable thickness embedded |
|
|
表 1 材料参数表 Tab.1 Material parameters table |
| $ h\left(r\right)=0.000\;5r^{2.2}+0.000\;85。$ | (9) |
式中:
用Abaqus软件建立图1(c)所示的有限元模型,分析内嵌变厚度板的矩形板的振动频率响应。在建模中,为了与文献保持一致从而进行比较,采用体单元进行建模,将计算结果与实验结果[16]进行对比,结果如图2所示。在全频段范围内,2条频响曲线差异较小,在最后2个峰值处,频率存在一定的差别,约2%,主要是实验用的内嵌2块变厚度板的矩形板模型在铣削加工过程中引起的几何误差以及矩形板的边界与数值仿真模型边界设置的差别所引起的,总体来看,仿真与实验的整体响应趋势基本吻合,验证了有限元仿真模型和数值仿真方法的可靠性。
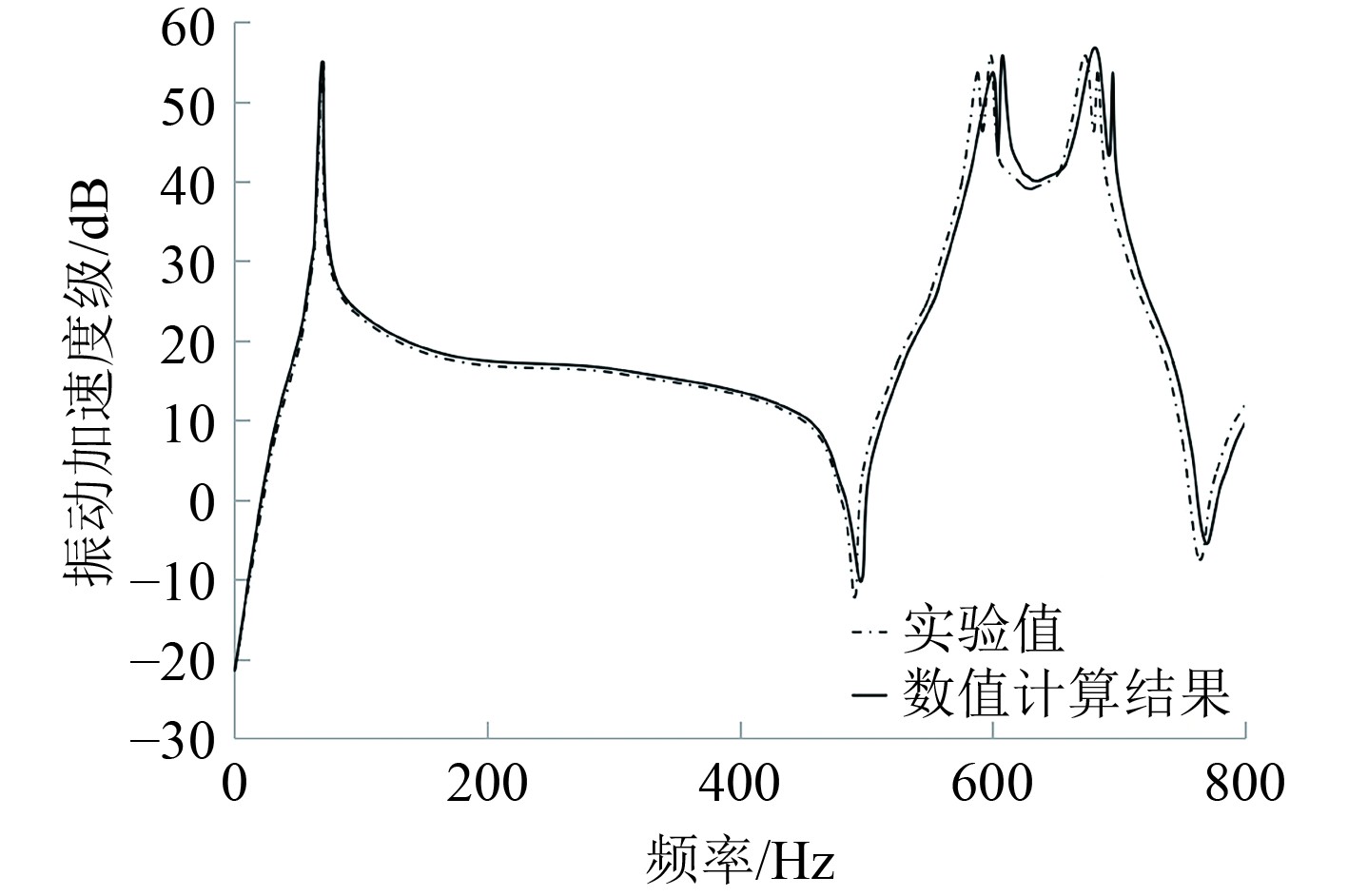
|
图 2 计算结果与实验结果的对比 Fig. 2 Comparison between calculation results and experimental results |
建立水下航行器动力舱及舱内旋转设备基座的有限元模型,如图3所示。舱段、舱段壳板上肋骨、基座面板及支撑工字钢的几何尺寸如表2所示。舱段、基座面板及支撑工字钢材料均为钢材,参数如表1所示,壳板、肋骨、工字钢等均采用板单元建模,在基座面板上表面矩形的面积中心施加垂向、单频、单位正弦激励力F,用来模拟旋转设备工作时在垂向给基座面板的作用力。计算结构振动响应,对于每一个频率,提取基座面板上所有节点的振动加速度并比较,找到加速度的最大值。然后绘制加速度最大值随频率的变化函数曲线,即得到振动加速度的最大值的频响曲线如图4所示。

|
图 3 水下航行器动力舱及旋转设备基座面板有限元模型 Fig. 3 Finite element model of the base panel of the rotating equipment of the power module of the underwater vehicle |
|
|
表 2 模型几何尺度 Tab.2 Model geometric scale |
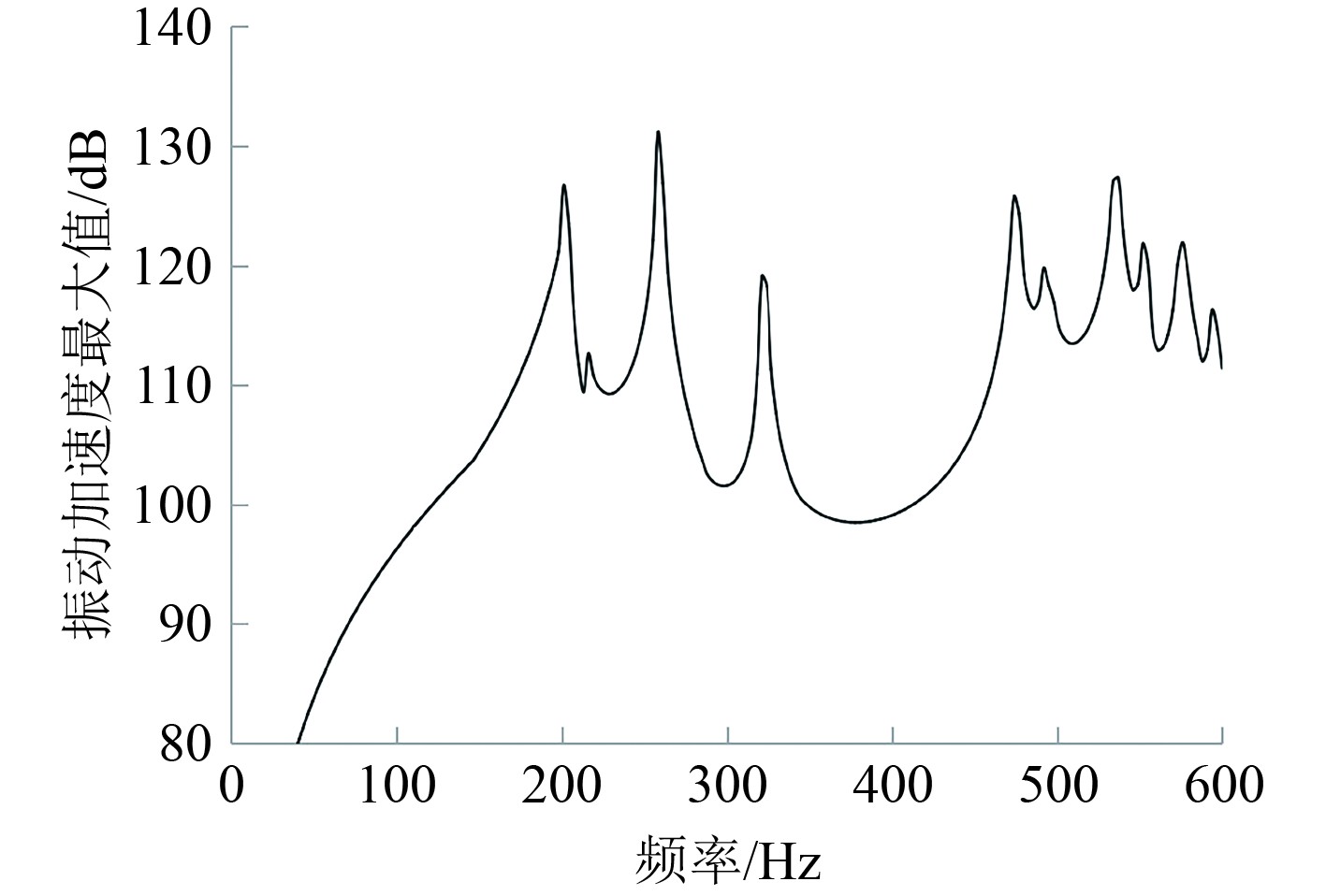
|
图 4 基座面板振动频率响应 Fig. 4 Vibration frequency response of the base panel |
可知,振动峰值分别位于201、258、321、474、537和576 Hz处,这6个峰值频率分别记为f1~f6,出现这6个峰值的基座面板的位置分别记作P1~P6,如图5所示。其中,P1和P4点相距较近,P2与P6点相距较近。为了降低这6个峰值,设计6块变厚度消波阻尼板,使板的第1阶固有频率分别在f1~f6附近,并将板分别安装在P1~P6处,实现与振源的耦合共振,从而吸收并耗散弯曲振动能量,达到降低基座面板振动的目的。
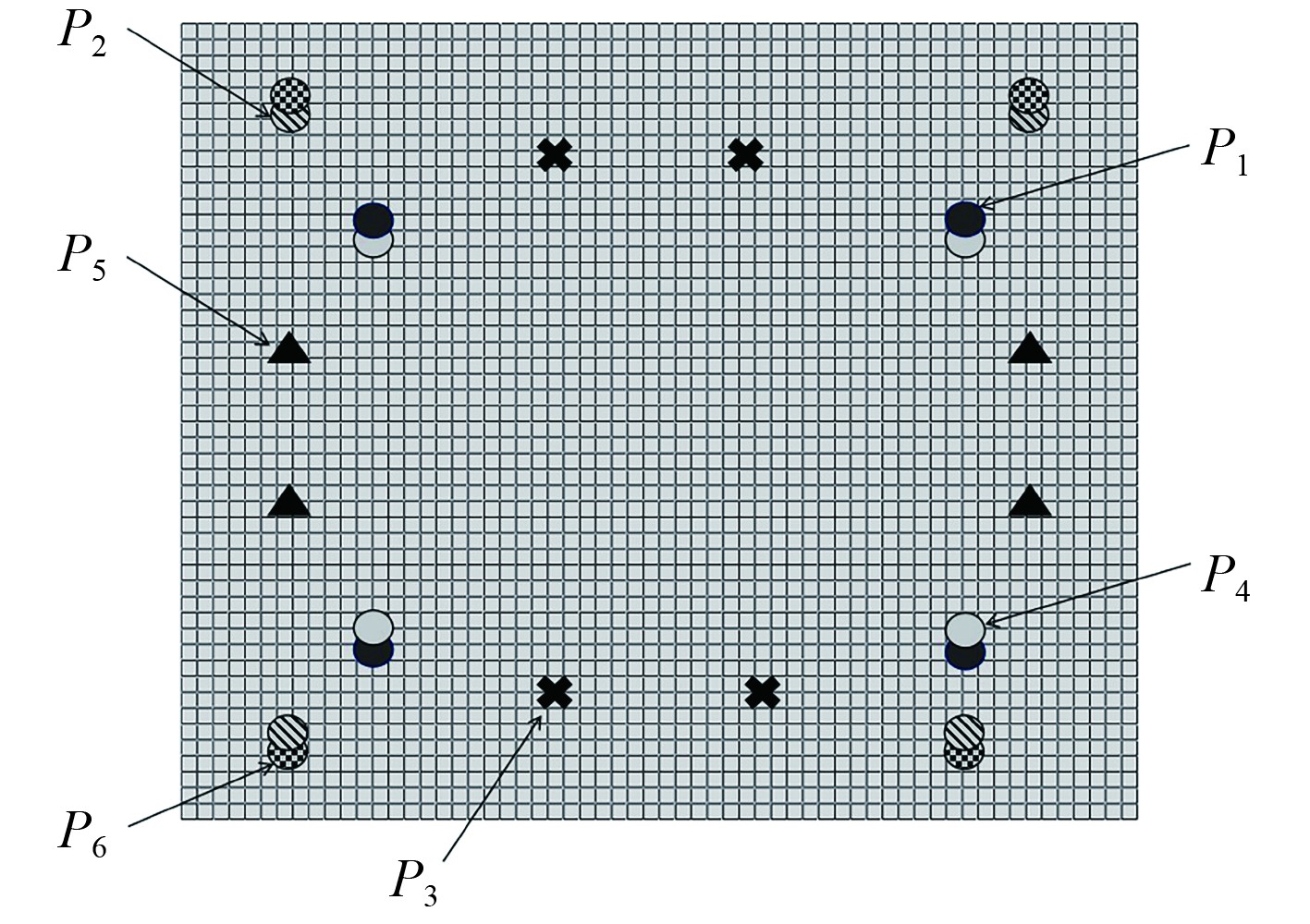
|
图 5 点P1~P6位置图 Fig. 5 Position map of P1~P6 |
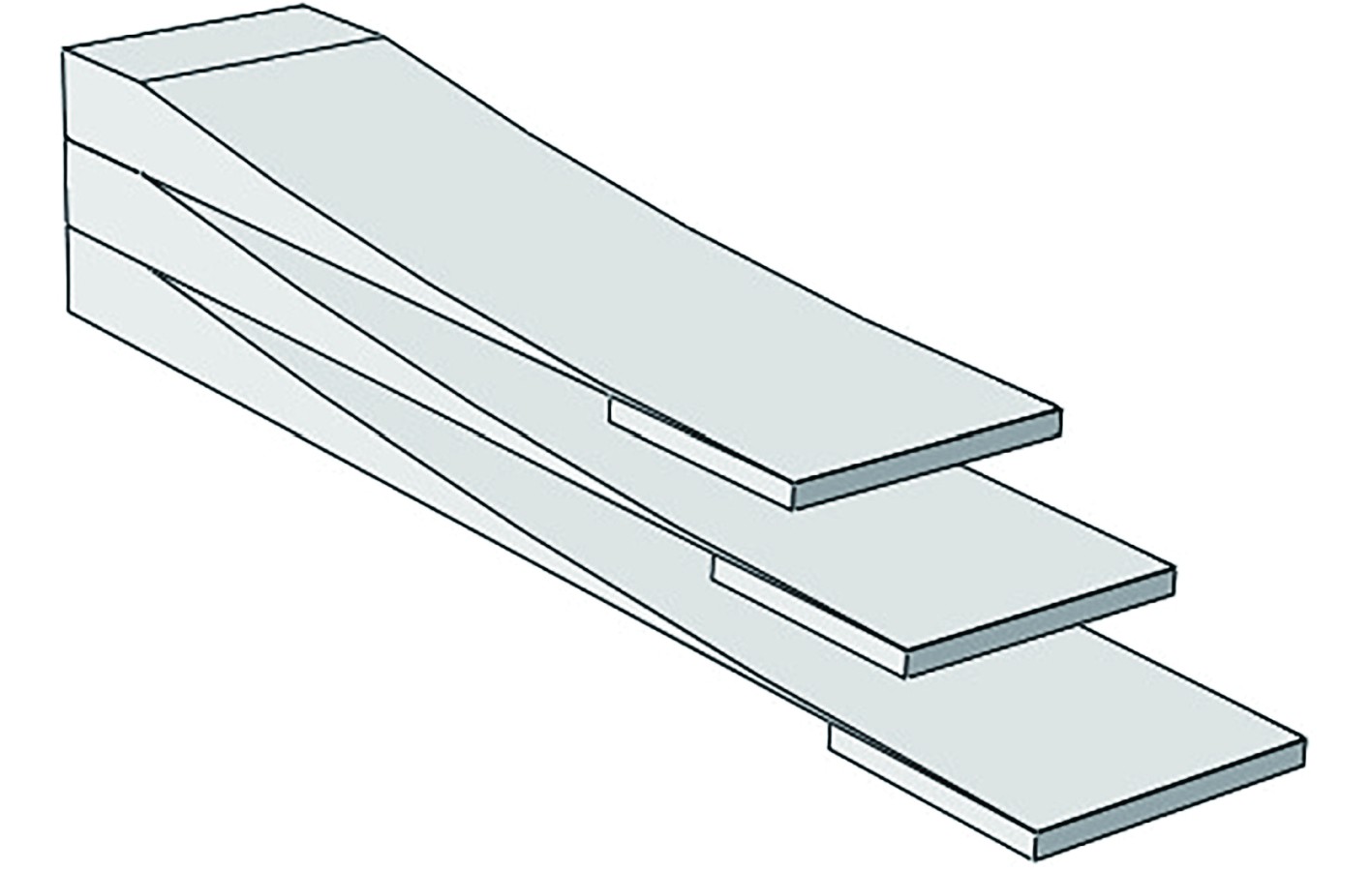
变厚度消波阻尼板是一种利用声波传播特性实现振动控制的创新型附加结构,可以以单片或多个固有频率不同的单片组合的形式固连到基座面板振动较大的位置处,吸收振动能量,由3块单片变厚度板构成的复合型变厚度消波阻尼板如图6所示。
|
图 6 复合型变厚度消波阻尼板结构图 Fig. 6 Composition of composite wave absorbing damping plates with variable thickness |
根据文献[17],每个结构波长范围内需要划分10个网格以保证数值仿真结果能准确反映结构波的聚集情况,变厚度结构中弯曲波的波长

|
图 7 变厚度板有限元模型 Fig. 7 Finite element model of variable thickness plate |
|
|
表 3 前三阶固有频率比较 Tab.3 First three order natural frequency comparison |
| $ \lambda = \frac{{{c_b}}}{f} = \sqrt {\frac{{2\text{π} h\left( x \right)}}{f}} {\left[ {\frac{E}{{12\rho \left( {1 - {\mu ^2}} \right)}}} \right]^{\frac{1}{4}}} 。$ | (10) |
1)根据3.1节的基座面板振动峰值频率设计6块变厚度板,分别记为B1~B6,将变厚度板一端的边界条件设为固支,另一端边界条件设为自由状态,如图7所示,同时,通过调节变厚度板的长度使B1~B6的厚度变化部分的第1阶固有频率分别接近峰值频率f1~f6,从而得到变厚度板的主要参数,宽度均为0.05 m,等厚度部分的板厚为0.016 m,幂指数
|
|
表 4 变厚度板参数ε取值
Tab.4 Parameters of |
|
|
表 5 变厚度板第1阶固有频率 Tab.5 The first natural frequency mode of variable thickness plate |
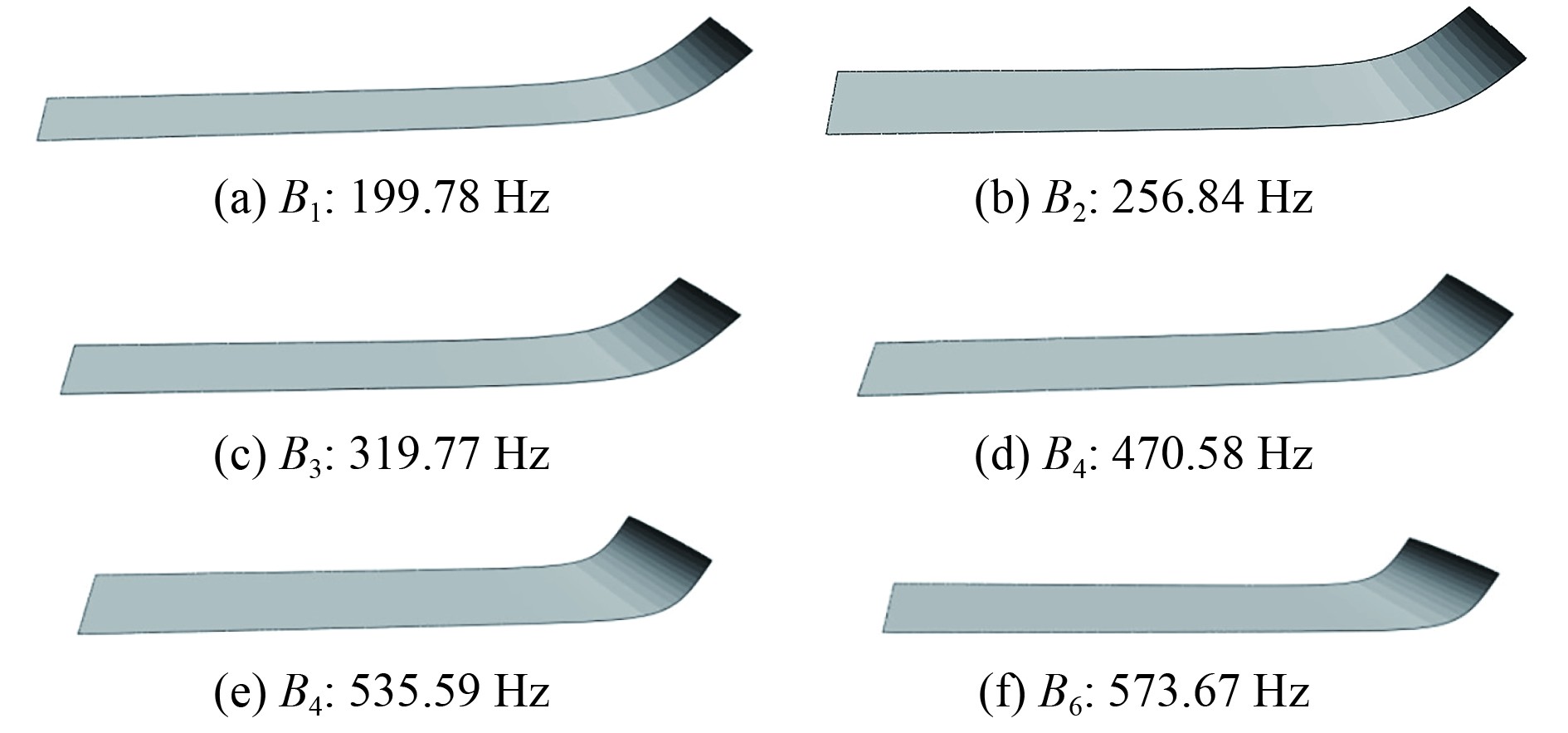
|
图 8 变厚度板第1阶模态振型 Fig. 8 The first modal shape of variable thickness plate |
|
|
表 6 复合型变厚度消波阻尼板的固有频率 Tab.6 Natural frequency of composite variable thickness wave absorbing damping plate |

|
图 9 复合型变厚度消波阻尼板的模态振型 Fig. 9 Modal shape of composite variable thickness wave absorbing damping plate |
2)将得到的变厚度板分别固连在基座面板下方相应的位置处,如图10所示,通过改变变厚度板的长度,使固连到基座面板上的变厚度板的厚度变化部分的第1阶固有频率分别接近峰值频率f1~f6,这里以B2为例,图11为通过改变变厚度板的长度改变其固有频率,并使之趋近于谱峰频率258 Hz的过程。

|
图 10 变厚度板安装示意图 Fig. 10 Installation diagram of variable thickness plate |
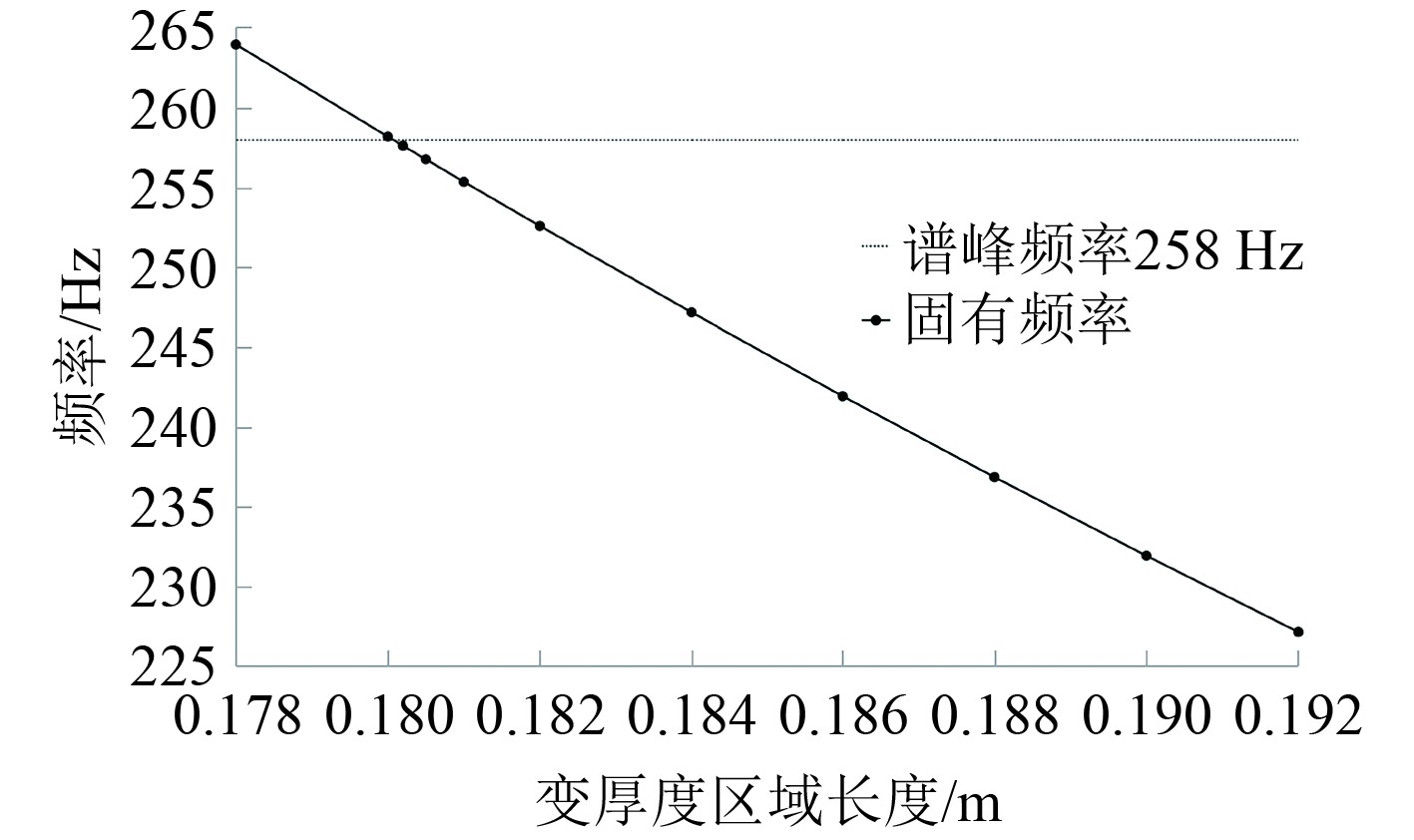
|
图 11 变厚度板固有频率随其长度变化规律(以258 Hz为例) Fig. 11 Natural frequency of variable thickness plate varying with its length (taking 258 Hz as an example) |
由于变厚度板的材料密度远小于基座面板的材料密度,因此6块变厚度板的总重量仅为基座面板重量的1.7%,保证了变厚度消波阻尼板的重量对目标结构振动性能影响不大。
3.3 安装消波阻尼板的基座面板振动分析为了研究变厚度消波阻尼板对基座面板振动的控制作用,将3.2节设计的变厚度板固连在基座面板下方相应的位置处,如图10所示,激振力的频率范围是5~600 Hz。对于每一个频率,计算得到安装变厚度消波阻尼板后的基座面板上的结构振动,提取基座面板上所有节点的振动加速度并比较,找到加速度的最大值,然后绘制加速度最大值随频率的变化函数曲线,即得到振动加速度的最大值的频响曲线,并与图4所示的安装变厚度板前的振动响应进行比较,结果如图12所示。

|
图 12 安装变厚度板前、后基座面板的振动频率响应 Fig. 12 Vibration frequency response of base panels before and after installation of variable thickness plates |
可以看出,安装变厚度消波阻尼板后,在整个频段范围内,基座面板振动峰值都获得了较大幅度的降低,在频率201、258和321 Hz处振动峰值降低最为明显,大约为20 dB。
4 结 语1)采用本文提出的网格划分方法等建模和计算方法能够保证与变厚度板相关的问题的计算精度,同时能够提高计算效率。
2)通过使变厚度板与振源的耦合共振吸收并耗散弯曲振动能量,能够达到降低结构(基座面板)振动的目的。
3)通过将变厚度板组合或单片安装在目标结构上,能够同时降低目标结构在低频和高频的振动峰值。
4)与内嵌式变厚度板相比,本文采用的将变厚度板安装在目标结构上的建模方法既能降低结构的振动,又不降低目标结构的强度,另外,通过采用密度较小的复合材料以减小变厚度板的重量,从而避免了因为重量过大而影响目标结构的振动特性。
本文研究结果可以为船舶结构声学设计提供参考。
| [1] |
GAUTIER F, KRYLOV V V. Special issue: recent advances in acoustic black hole research[J]. Journal of Sound and Vibration, 2020, 476(2)115335. |
| [2] |
LI M, LI C. Numerical and experimental benchmark solution vibration and sound radiation of an acoustic black hole plate[J]. Applied Acoustics, 2020, 163: 107223. |
| [3] |
GUASCHO, SNCHEZ-MARTNP, GHILARDID. Application of the transfer matrix approximation for wave propagation in a Meta fluid representing an acoustic black hole duct termination[J]. Applied Mathematical Modelling, 2020, 77: 1881-1893. DOI:10.1016/j.apm.2019.09.039 |
| [4] |
刘尊程, 温华兵, 李志远, 等. 声学黑洞浮筏系统的隔振性能分析[C]//第十七届船舶水下噪声学术讨论会, 衢州, 2019.
|
| [5] |
何璞, 王小东, 季宏丽. 基于声学黑洞的盒式结构全频带振动控制[J]. 航空学报, 2020, 41(4): 134-143. |
| [6] |
赵业楠, 杨德庆, 王博涵. 声学黑洞俘能器在气垫船舱室噪声控制中的应用研究[J]. 中国造船, 2020, 61(3): 58-67. |
| [7] |
赵楠, 王禹, 陈林, 等. 分布式声学黑洞浮筏系统隔振性能研究[J]. 振动与冲击, 2022, 41(13): 75-80. |
| [8] |
李熙. 一维声学黑洞结构力学性能研究[D]. 天津: 天津大学, 2018.
|
| [9] |
罗静. 基于激光超声技术的一维声学黑洞结构研究[D]. 南京: 南京航空航天大学, 2017.
|
| [10] |
ZHAO L X. Low-frequency vibration reduction using a sandwich plate with periodically embedded acoustic black holes[J]. Journal of Sound and Vibration, 2019, 441: 165-171. DOI:10.1016/j.jsv.2018.10.046 |
| [11] |
J. B. F F S S C. Passive control of vibration and sound transmission for vehicle structures via embedded Acoustic Black Holes[J]. Inter noise and Noise Congress and Conference Proceedings, 2013, 246(1): 176-184. |
| [12] |
KRYLOV V V, SHUVALOV A L. Propagation of localized flexural vibrations along plate edges described by a power law[J]. Institute of Acoustics, 2000, 22: 263-270. |
| [13] |
KRYLOV V V. Localized acoustic modes of a quadratically-shaped solid wedge[J]. Moscow University Physics Bulletin, 1990, 45(6): 65-69. |
| [14] |
A P F , C S C , FABIO S . A normalized wave number variation parameter for acoustic black hole design [J]. The Journal of the Acoustical Society of America, 2014, 136(2): 148−152.
|
| [15] |
CONLON S C , FAHNLINE J B , Semperlotti F. Numerical analysis of the vibroacoustic properties of plates with embedded grids of acoustic black holes [J]. The Journal of the Acoustical Society of America, 2015, 137(1): 447−457.
|
| [16] |
贾秀娴, 杜宇. 声黑洞理论应用于板类结构的轻量化减振分析[J]. 振动工程学报, 2018, 31(3): 434-440. |
| [17] |
王宁. 附加式声学黑洞的设计及振动抑制研究[D]. 南京: 南京航空航天大学, 2023.
|
 2025, Vol. 47
2025, Vol. 47
