2. 深海技术科学太湖实验室,江苏 连云港 150006;
3. 上海交通大学,上海 200240
2. Taihu Lake Laboratory of Deep Sea Technology and Science, Lianyungang 150006, China;
3. Shanghai Jiao Tong University, Shanghai 200240,China
双层圆柱壳是水下航行器的主要结构形式,其受到声波激励下会产生包含结构形式、几何参数以及表面敷设材料等信息的声散射场[1 − 2],深入研究双层圆柱壳声散射特性激励,有助于降低水下装备散射信号,提高结构隐身性能,有效避免敌方声呐探测[3 − 4]。
国内外围绕这个问题进行了广泛而深入的研究,提出了一系列的声散射理论解法、近似解法[5 − 6]和数值解法,其中针对圆柱壳的解析求解方面,最早由Doolittle等[7]给出了圆柱壳的散射解,后经研究学者逐步推导得出含夹层介质、含多层敷设层以及多层圆柱壳的理论解[8]。其中,Akay等[9]利用弹性理论开展了三层圆柱壳夹层介质对外壳声散射特性的影响分析;范军等[1]采用弹性薄壳理论和Fourier变换求解得出了无限长双层充液圆柱薄壳散射声场的解析解,研究分析了双层充液、单层充液和空气圆柱壳在不同入射角的散射特性;李静等[3]采用板块元方法以BeTSSi Ⅱ标准模型为例,研究了圆柱壳内腔敷设吸声材料的声散射方位特性和频率特性;吴杰等[10]利用COMSOL研究了表面吸声材料参数、壳体结构对声散射的影响。为进一步实际水下装备实际结构,周富霖等[10]针对周期加肋圆柱薄壳声散射场进行了近似解析解进行了推导,研究了角度频率谱的共振散射;童韫哲等[11]结合薄壳Donnell方程、梁壳弯曲振动方程研究了离散周向波数频率谱对纵肋对圆柱壳的弹性共振散射;张占阳等[12]针对加肋圆柱壳内部振动声辐射和外部声源激励下声散射耦合问题进行了理论分析和试验验证;王世博等[13]采用有限元方法对比分析了单层圆柱壳内部空气和腔内缘敷设声学材料2种情况下,复合敷设材料结构模量、厚度等参数对外壳散射的影响;孙阳等[14]利用Rayleigh简正级数方法推导得出了圆柱壳覆盖消声层的声散射场函数,研究了壳外敷设多层材料参数对声散射特性的影响。
本文基于动态弹性理论和变量分离方法,针对无限液体介质各向同性双层圆柱壳对稳态谐波声音信号的散射问题,结合各向同性介质Lame运动方程和Hemholtz方程,推导水中无限长双层圆柱壳填充不同夹层介质时外壳散射场的严格解,计算分析一定波长和内外壳相对厚度范围内单、双壳体内部不同介质下稳态信号散射的频率依赖性。
1 理论基础 1.1 研究对象假设单位振幅和频率ω(ω=2πf,f为信号频率,Hz)的平面声波落在给定的双层圆柱壳上,入射波的波向量k垂直于壳层Z轴,并将三维问题平面化,即平面入射声波场中的双层圆柱壳如图1所示。外壳材料的物理性质由密度ρ和体积模量λ、剪切模量μ来描述,其中λ = υE/(1+υ)(1−2υ);μ = E/2(1+υ);E、υ分别为外壳材料的杨氏模量和泊松系数。内部区域I是真空,中间区域II是气体或液体,外部区域III是密度为ρ0、声速c0、入射波pi和反射波ps中的声压液体介质。R1和R2分别为外壳内径和外径,R3和R4分别为内壳内径和外径。

|
图 1 平面入射声波场中的双层圆柱壳 Fig. 1 Double layered cylindrical shell in a plane incident acoustic field |
基于弹性力学中的连续性方程、运动方程以及本构方程,假设是δ/r<<1,不考虑圆柱壳弯矩和扭矩作用,忽略中面位移,即忽略ε3等次要应变,推导可得到在柱坐标系下由位移矢量u(ur,uφ,uz)表示的各向同性物体的弹性动力学Lame方程,如下式:
| $ \left(\lambda+\mu\right)\mathrm{graddiv}{\boldsymbol{u}}+\mu\Delta{\boldsymbol{u}}=-\omega^2\rho{\boldsymbol{u}}。$ | (1) |
已知弹性介质位移矢量u可表示为:
| $ {\boldsymbol{u}} = - {\mathrm{grad}}\varPhi + rot{\boldsymbol{\varPsi }}。$ | (2) |
式中:Φ为标量位移势函数,表示体积变化引起的位移;Ψ为向量位移势函数,描述涡类型位移势。
将式(2)代入式(1)可以得到2个Helmholtz方程:Φ的标量方程和Ψ的矢量方程:
| $ \left\{ \begin{aligned} & \Delta \varPhi + k_l^2\varPhi = 0, \\ & \Delta {\boldsymbol{\varPsi }} + k_\tau ^2{\boldsymbol{\varPsi }} = 0。\\ \end{aligned} \right. $ | (3) |
式中:kl = ω/c1;kτ = ω/c2为波数;c1、c2分别为弹性介质中纵向波和横向波的速度。
在这个问题的平面设置中,式(3)中的变量分开,所有矢量势只有1个不同于零的分量,即Ψz,后续简称为Ψ。
对于满足广义Hooke定律的各向同性环境,坐标系选择不变,应力通过常数Lame和应变来表示。对于圆柱坐标系中的小变形,这些变形分量通过位移向量分量表示,并根据所考虑的圆柱壳和内部填充方案求解得出。
1.2.1 单层圆柱壳散射角特征值单层圆柱壳即在如图1基础上去掉内壳。根据圆柱形坐标系中Helmholtz方程的基本解形式,可将弹性位移势和声压表示为:
| $ \left\{ \begin{aligned} &{\boldsymbol{\varPhi}} = \sum\limits_{m = 0}^\infty {\left[ {{B_m}{J_m}\left( {{k_l}r} \right) + {C_m}{N_m}\left( {{k_l}r} \right)} \right]} {\mathrm{cos}}(m\varphi), \\ &{\boldsymbol{\varPsi}} = \sum\limits_{m = 0}^\infty {\left[ {{D_m}{J_m}\left( {{k_\tau }r} \right) + {F_m}{N_m}\left( {{k_\tau }r} \right)} \right]} {\mathrm{sin}}(m\varphi), \\ &{p_i} = \sum\limits_{m = 0}^\infty {\varepsilon _m}{{\left( { - i} \right)}^m}{J_m}\left( {kr} \right){\mathrm{cos}}(m\varphi), \\ &{p_s} = \sum\limits_{m = 0}^\infty {A_m}H_m^{(1)}\left( {kr} \right){\mathrm{cos}}(m\varphi)。\\ \end{aligned} \right. $ | (4) |
式中:k = ω/c0为外部液体环境中声波的波数;εm = 1(m = 0),εm = 2(m ≠ 0)。Am、Bm、Cm、Dm、Fm分别为来自边界条件的未知系数;pi为入射波和ps为反射波。
由于外壳内缘的正常应力(r = R1)等于液体介质中的声压;在弹性层和液体介质的边界上,弹性层中没有切线应力;外壳2个表面的正常位移分量连续;弹性层中的正常应力等于液体介质中的总(衍射)压力(p∑ = pi+ps),即可将式(4)代数化为边界条件,如下式:
| $ \left\{ \begin{aligned} &\lambda k_l^2\varPhi + 2\mu \left( - \frac{{{\partial ^2}\varPhi }}{{\partial {r^2}}} - {r^{ - 2}}\frac{{\partial \varPsi }}{{\partial \varphi }} + {r^{ - 1}}\frac{{{\partial ^2}\varPsi }}{{\partial r\partial \varphi }}\right) = {\left. {{p_1}} \right|_{r = {R_1}}}, \\ &\mu \left( { - 2{r^{ - 1}}\frac{{{\partial ^2}\varPhi }}{{\partial r\partial \varphi }} + 2{r^{ - 2}}\frac{{\partial \varPhi }}{{\partial \varphi }} - k_\tau ^2\varPsi - 2\frac{{{\partial ^2}\varPsi }}{{\partial {r^2}}}} \right) = 0 {\left|_{\begin{subarray}{l} r = {R_1} \\ r = {R_2}\end{subarray}}, \right.} \\ & - \frac{{\partial \varPhi }}{{\partial r}} + {r^{ - 1}}\frac{{\partial \varPsi }}{{\partial \varphi }} = {\omega ^2}\rho _1^{ - 1}{\left. {\frac{{\partial {p_1}}}{{\partial r}}} \right|_{r = {R_1}}}, \\ &- \frac{{\partial \varPhi }}{{\partial r}} + {r^{ - 1}}\frac{{\partial \varPsi }}{{\partial \varphi }} = {\omega ^2}\rho _0^{ - 1}{\left. {\left( {\frac{{\partial {p_i}}}{{\partial r}} + \frac{{\partial {p_s}}}{{\partial r}}} \right)} \right|_{r = {R_2}}}, \\ & \lambda k_l^2\varPhi + 2\mu \left( { - \frac{{{\partial ^2}\varPhi }}{{\partial {r^2}}} - {r^{ - 2}}\frac{{\partial \varPsi }}{{\partial \varphi }} + {r^{ - 1}}\frac{{{\partial ^2}\varPsi }}{{\partial r\partial \varphi }}} \right) = {\left. {{p_i} + {p_s}} \right|_{r = {R_2}}}。\end{aligned} \right. $ | (5) |
进一步使用三角函数cos(mφ)和sin(mφ)的正交性,为每个模m找到1个6阶代数系统,以找到未知的固定指数分解因子。通过对式(5)中的1类
| $ D\left(\varphi\right)=-\exp\left(-i \text{π}/4\right)\left(\text{π} k\right)^{-1}\sum\limits_{m=0}^{\infty}\left(-i\right)^mA_m\mathrm{cos}(m\varphi)。$ | (6) |
通过定义Kramer规则解的系数Am,即可计算散射角特性值
在外壳内部是一个内部空壳,具有相同的常数λ、μ和位移标量势Φ1、位移矢量势Ψ1。中间区域II的特点是声压为
| $ \left\{ \begin{gathered} {\varPhi _1} = \sum\limits_{m = 0}^\infty {\left[ {{K_m}{J_m}\left( {{k_l}r} \right) + {L_m}{N_m}\left( {{k_l}r} \right)} \right]} {\mathrm{cos}}(m\varphi), \\ {{\boldsymbol{\varPsi}} _1} = \sum\limits_{m = 1}^\infty {\left[ {{S_m}{J_m}\left( {{k_\tau }r} \right) + {T_m}{N_m}\left( {{k_\tau }r} \right)} \right]} {\mathrm{sin}}(m\varphi), \\ {p_1}^\prime = \sum\limits_{m = 1}^\infty {\left[ {{G_m}{J_m}\left( {kr} \right) + {H_m}{N_m}\left( {kr} \right)} \right]} {\mathrm{cos}}(m\varphi)。\\ \end{gathered} \right. $ | (7) |
式中:Km、Lm、Sm、Tm、Gm、Hm分别为与以下附加边界条件相关的额外未知系数。
由于真空和弹性层边界上无应力(r = R3);在弹性层和液体介质(r = R4)的外部边界上,弹性层中没有应力切线;正常位移分量连续;弹性层中的正常应力等于液体介质中的压力
| $ \left\{ \begin{aligned} & \lambda k_l^2{\varPhi _1} + 2\mu \left( - \frac{{{\partial ^2}{\Phi _1}}}{{\partial {r^2}}} - {r^{ - 2}}\frac{{\partial {\varPsi _1}}}{{\partial \varphi }} + {r^{ - 1}}\frac{{{\partial ^2}{\varPsi _1}}}{{\partial r\partial \varphi }}\right) = {\left. 0 \right|_{r = {R_3}}}, \\ & \mu \left( { - 2{r^{ - 1}}\frac{{{\partial ^2}{\varPhi _1}}}{{\partial r\partial \varphi }} + 2{r^{ - 2}}\frac{{\partial {\varPhi _1}}}{{\partial \varphi }} - k_\tau ^2\varPsi - 2\frac{{{\partial ^2}\varPsi }}{{\partial {r^2}}}} \right) = {\left. 0 \right|_{r = {R_4}}}, \\ & - \frac{{\partial {\varPhi _1}}}{{\partial r}} + {r^{ - 1}}\frac{{\partial {\varPsi _1}}}{{\partial \varphi }} = {\omega ^2}\rho _0^{ - 1}{\left. {\frac{{\partial {p_1}}}{{\partial r}}} \right|_{r = {R_4}}}, \\ & - \frac{{\partial {\varPhi _1}}}{{\partial r}} + {r^{ - 1}}\frac{{\partial {\varPsi _1}}}{{\partial \varphi }} = {\omega ^2}\rho _0^{ - 1}{\left. {\frac{{\partial {p_1}}}{{\partial r}}} \right|_{r = {R_4}}}, \\ & \lambda k_l^2{\Phi _1} + 2\mu \left( { - \frac{{{\partial ^2}{\varPhi _1}}}{{\partial {r^2}}} - {r^{ - 2}}\frac{{\partial {\varPsi _1}}}{{\partial \varphi }} + {r^{ - 1}}\frac{{{\partial ^2}{\varPsi _1}}}{{\partial r\partial \varphi }}} \right) = {\left. {{p_1}} \right|_{r = {R_4}}}。\end{aligned} \right. $ | (8) |
通过将式(4)和式(7)代数化为边界条件式(5)和式(8),同样使用三角函数cos(mφ)和sin(mφ)的正交性,为每个模m得到1个11阶代数系统,用于确定未知分解系数Am、Bm、Cm、Dm、Fm、Km、Lm、Sm、Tm、Gm、Hm,即可根据式(6)计算散射角特性值
在以下外壳和介质物理参数下,计算波长kR1 为0.95~25.0的范围内D(0°)的频率依赖性,对于以下外壳和介质的物理参数:
1)外壳−钢:ρ = 7.8×103 kg/m3,λ = 2×1011 N/m2,μ = 8.1×1010 N/m2;
2)中间区域I−水:ρ1 = 1.0×103 kg/m3,c1 = 1.5×103 m/s;空气:ρ1' = 1.0 kg/m3,c1' = 340 m/s;
3)区域Ⅲ−水:ρ3 = 1.0×103 kg/m3,c3 = 1.5×103 m/s;
4)外壳相对厚度:h1 = (R2−R1)/R1,kh1为壳层的波厚度。
分别针对h1 =

|
图 2
散射角特性值|D(0°)|在h = 0.002 Fig. 2
Scattering angle characteristic value |D(0°)| at h = 0.002
Fig. 2
Scattering angle characteristic value |D(0°)| at h = 0.002
|

|
图 3
散射角特性值|D(0°)|在h = 0.02 Fig. 3
Scattering angle characteristic value |D(0°)| at h = 0.02
Fig. 3
Scattering angle characteristic value |D(0°)| at h = 0.02
|
结果表明,真空散射的信号水平比其他填充变体的信号水平平均高出3~20 dB。此外,对于真空壳,横向散射与阴影区散射相当,对于气体和液体填充,声学上“软”散射类型占主导地位。
在kh1 = 0.01~0.02(见图2(c)和图3(b))范围内,空壳散射信号水平与其他填充方案相比不超过1~3 dB。在kh1 = 0.02~0.04范围内,超出率为5%~10%,随着波厚度的进一步增加,这个值减少到3%~5%(见图3(c)),这一趋势可归因于填充外壳的硬度增加和变形程度降低。对于液体填充物,还可以注意到与外壳厚度的特定增加相对应的内液附着质量的影响。
为进一步分析壳内介质对散射信号量的影响,如图4~图6所示,分别计算了h1 为

|
图 4
h1 = |
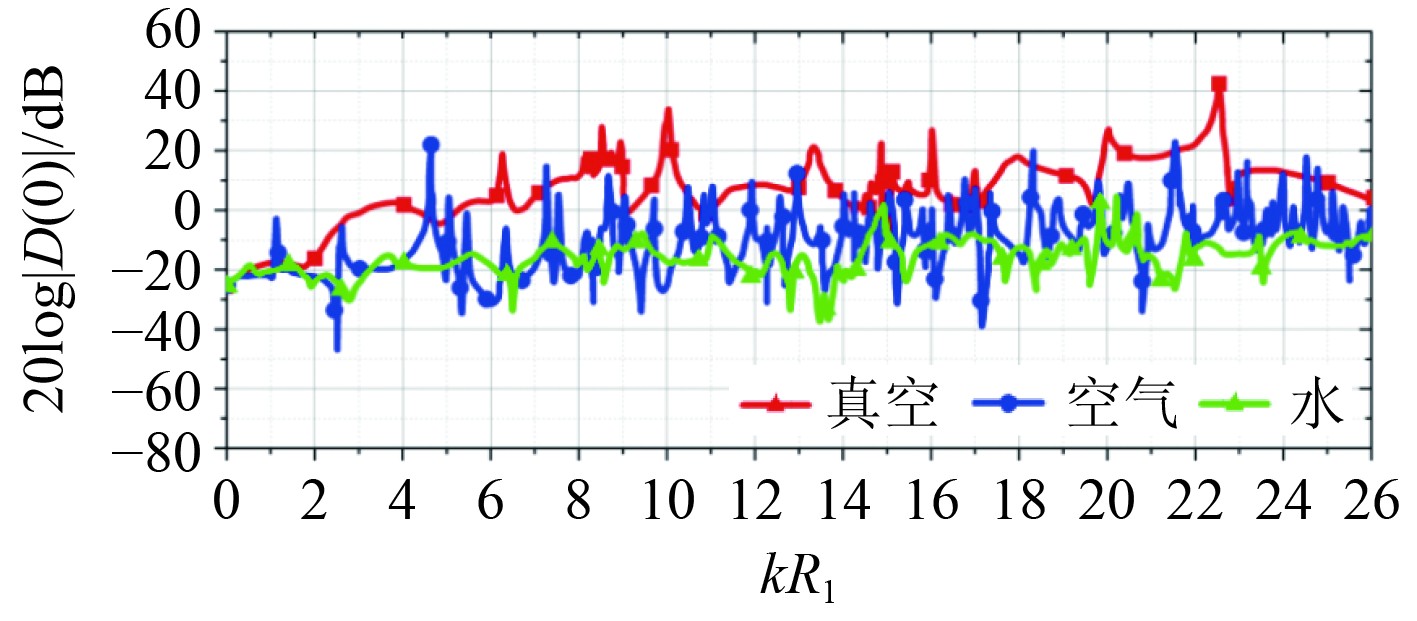
|
图 5 h1 = 0.002下的散射频率依赖性 Fig. 5 Scattering frequency dependence at h1 = 0.002 |

|
图 6 h1 = 0.012下散射频率依赖性 Fig. 6 Scattering frequency dependence at h1 = 0.012 |
结果表明,弹性共振的形成主要发生在kR1>4上,空间重合共振在某些情况下也表现在kR1为2、3上。对于空壳,例如,在kR1为7.5、10、14、20等处可以观察到Sholte-Stonley波的共振,Lamb弹性波的共振在kR1为7~9、14~17等范围内。液态填料的存在降低了共振频率的值,分别为kR1 = 4、kR1 = 7.5等,并有助于减少频率依赖,其中一个可能的原因是在内部区域I形成反射波,当Sholte-Stonley波和Lamb弹性波在封闭的包壳回路上传播时,可以堆积其半波的整个长度,并在激发点进行相位匹配,从而产生散射信号振幅共振。从所获得的频率依赖性类型表明,在液体填料的情况下,这种相匹配的可能性要高得多,因此有利于降低共振频率。
在h1≤0.002范围内,散射信号特征值随着h1的增加而减少一半,平均减少3~6 dB,特别是在共振中;在h1≥0.01范围内,这些水平主要由壁材料的弹性特性决定,填充材料类型的影响大大降低。对于充满水或空气的外壳,h1变化时散射信号水平的差异几乎只在kR1在12~15范围内表现出来,主要是在h1加倍时平均降低2~3 dB(不包括kR1为15、20、25时相匹配引起的共振,其中这种差异可以增加到10 dB)。
2.2 双层壳的散射特性分析相对于单层壳的几何和介质物理参数不变,在内部增加内壳,如图1所示,增加如下参数:
1)内壳−钢:ρ' = 7.8×103 kg/m3,λ' = 2×1011 N/m2,μ' = 8.1×1010 N/m2;
2)中间区域I−空气:ρ1 = 1.0 kg/m3,c1 = 340 m/s;
3)中间区域II−水:ρ2=1.0×103 kg/m3,c2=1.5×103 m/s;空气:ρ2' = 1.0 kg/m3,c2' = 340 m/s;
4)外壳相对厚度:h1 = (R2−R1)/R1;
5)内壳相对厚度:h2 = (R4−R3)/R3,R3 = 0.7R1。
对于内部填充空气和水的双层圆柱壳,分别针对h1为
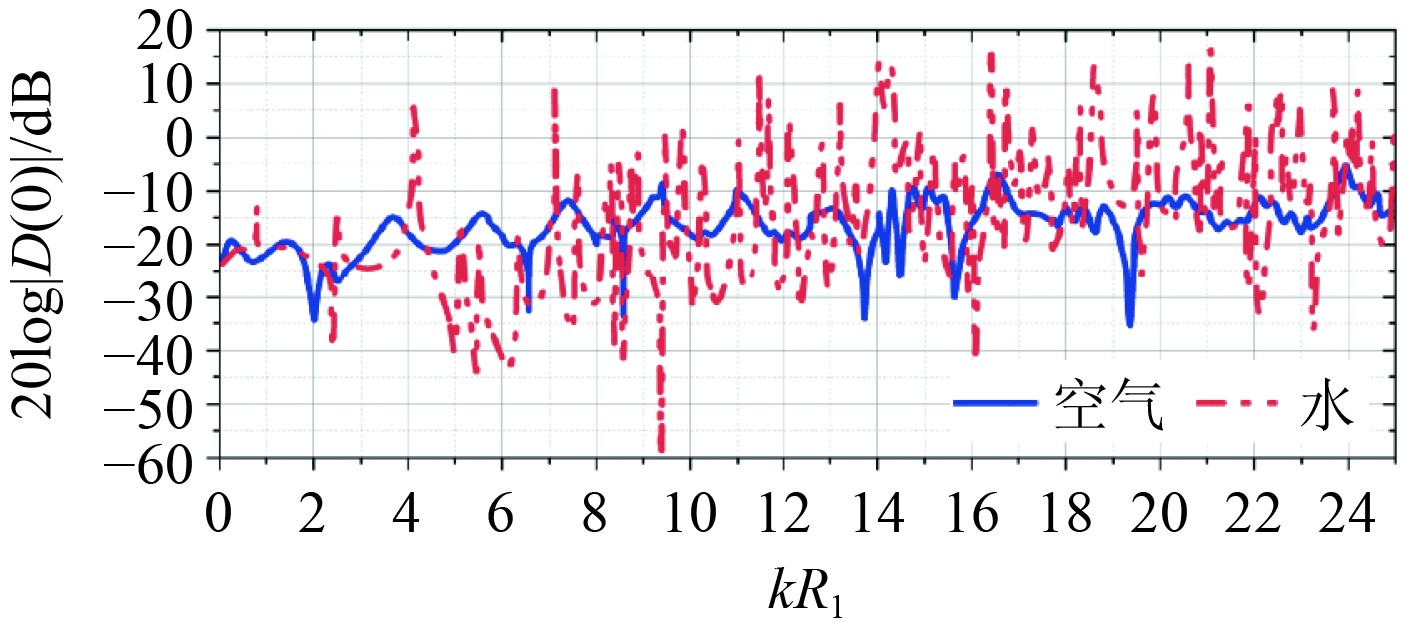
|
图 7
在h1 = |

|
图 9 在h1 = 0.012时,散射信号与外壳的频率依赖性 Fig. 9 Frequency dependence of scattered signal and shell at h1 = 0.012 |
当kR1<1~2(入射声波波长λ0(λ0 = c0/f)大于2R1)时,所有考虑的h1值都没有指定的匹配共振。液体填料有助于更大的频率依赖性,其中可能的原因是内外壳体之间形成了反射波。在h1≥0.012的范围内,从外壳内侧反射到内壳外侧相应声波的超额信号是最重要的,在范围为2<kR1<7(R1<λ0<3R1),平均高达10 dB(见图9)。在较低的h1值下,这种超标在kR1>7范围内约为5 dB,在较低的频率下几乎不存在(见图7~图8)。
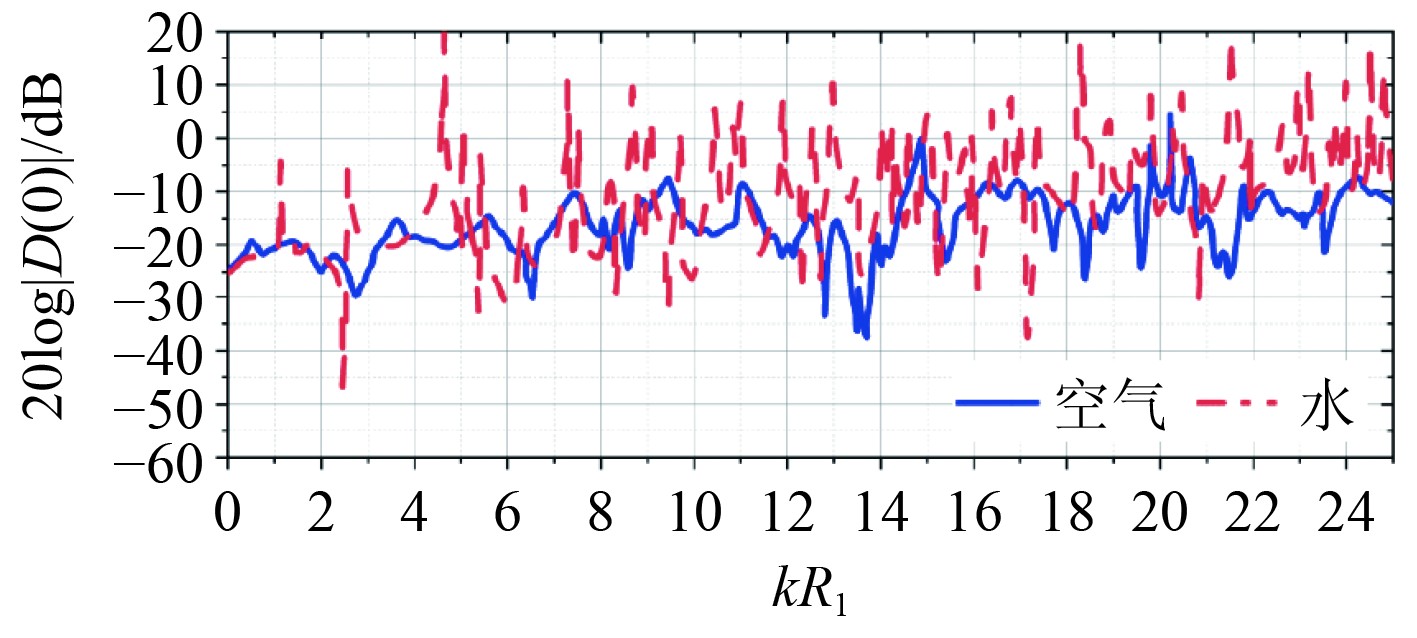
|
图 8 在h1 = 0.002时,散射信号与外壳的频率依赖性 Fig. 8 Frequency dependence of scattered signal and shell at h1 = 0.002 |
在h1≥0.012下,壳体厚度增加有助于液体和空气2种填充物质在散射信号上水平趋同,但液体填料中的单个共振峰除外,这表明在这种情况下声波信号与外壳固有频率相匹配的可能性更高。散射信号振幅共振的物理性质的明确识别复杂,因为共振频率的值还与所考虑的具有分散性的弹性波的相速以及附着液体质量的影响有关。
为进一步分析内壳相对厚度对散射信号量的影响,如图10所示,分别计算了h1为
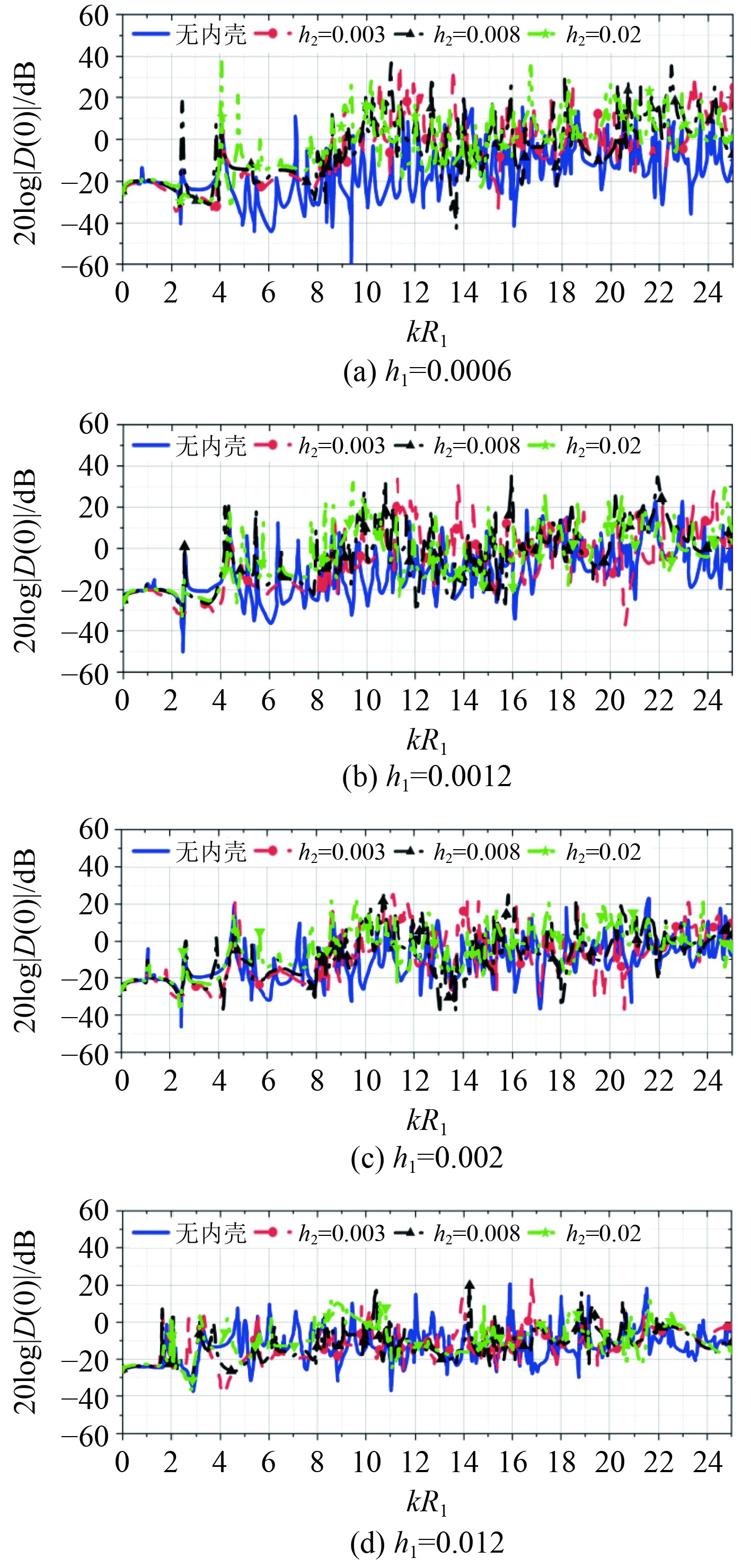
|
图 10 散射信号与双层外壳的频率依赖性 |
当h1 =
一般来说,由于内层厚度而导致的散射信号水平差在20log|D(0°)|左右,随着h1的增加,平均从约17 dB(见图10(a))减少到5~10 dB(见图10(d))。
3 结 语通过对水中无限长双层圆柱壳填充不同夹层介质时外壳散射场的严格解的推导以及单、双圆柱壳外壳散射特性计算分析得出:
1)对于单层圆柱壳,外壳厚度的增加和液体填充物均有利于降低外壳散射信号水平,且可降低共振频率和振幅;
2)对于双层圆柱壳,外壳厚度的增加有助于液体和空气2种填充介质在散射信号水平趋同,其中液体填充介质对外壳固有频率具有更大的依赖性,且共振振幅显著增加;
3)对于双层圆柱壳,外壳相对厚度的增加导致共振振幅平均从25 dB降低至15 dB;内壳厚度导致的外壳散射信号水平变化约为20log|D(0°)|,并随外壳厚度增加,平均从约17 dB降低至5~10 dB。
| [1] |
范军, 刘涛, 汤渭霖. 水中双层无限长圆柱壳体声散射[J]. 声学学报, 2003(4): 345-350. DOI:10.3321/j.issn:0371-0025.2003.04.010 |
| [2] |
周子翔, 任春雨. 轴对称壳体结构声散射高效计算方法[J]. 舰船科学技术, 2020, 42(15): 55-59. DOI:10.3404/j.issn.16727649.2020.08.010 |
| [3] |
李静, 马晓川, 李璇. 敷设空腔覆盖层水下复杂目标的声散射特性研究[J]. 声学技术, 2023, 42(4): 409-418. |
| [4] |
吴杰, 陶猛, 刘凯磊, 等. 敷设空腔覆盖层的水下弹性球壳散射特性研究[J]. 科学技术与工程, 2020, 20(21): 8622-8628. DOI:10.3969/j.issn.1671-1815.2020.21.029 |
| [5] |
陈昌雄, 彭子龙, 宋昊, 等. 水下双层加肋圆柱壳全空间收发分置散射声场快速预报方法[J]. 声学学报, 2024, 49(1): 78-88. DOI:10.12395/0371-0025.2022157 |
| [6] |
苗涛, 葛青, 王志伟, 等. 有限长双层弹性圆柱壳体声散射研究[J]. 舰船科学技术, 2010, 31(1): 71-75. DOI:10.3404/j.issn.1672-7649.2010.01.012 |
| [7] |
DOOLITTLE R D, ÜBERALL H. Sound scattering by elastic cylindrical shells.[J]. The Journal of the Acoustical Society of America, 1966, 39(2): 272−275.
|
| [8] |
BRILL D, GAUNAURD G C. Acoustic resonance scattering by a penetrable cylinder[J]. The Journal of the Acoustical Society of America, 1983, 73(5): 1448-1455. DOI:10.1121/1.389432 |
| [9] |
AKAY A. Scattering of sound from concentric cylindrical shell[J]. The Journal of the Acoustical Society of America, 1991, 89(4): 1572-1578. DOI:10.1121/1.4794490 |
| [10] |
ZHOU F L, FAN J, WANG B, et al. Numerical and experimental studies of the acoustic scattering from an externally ring-stiffened cylindrical shell[J]. Journal of Ship Mechanics, 2019, 23(6): 728-740. |
| [11] |
童韫哲, 潘谢帆, 邓红超, 等. 加纵肋无限长圆柱壳声散射[J]. 船舶力学, 2022, 26(5): 750-760. DOI:10.3969/j.issn.1007-7294.2022.05.013 |
| [12] |
张占阳, 吕世金, 白振国. 有限长圆柱壳水下声辐射与散射耦合特性研究[J]. 声学技术, 2019, 38(2): 76-79. |
| [13] |
王世博, 胡博, 张昊阳, 等. 含覆层圆柱空腔的声学材料水下吸声特性研究[J]. 振动与冲击, 2024, 43(14): 103-111+141. DOI:10.13465/j.cnki.jvs.2024.14.012 |
| [14] |
孙阳, 安俊英, 徐海亭. 覆盖消声层圆柱壳的共振频率与声散射特性[J]. 声学技术, 2015, 34(6): 125-126. |
 2025, Vol. 47
2025, Vol. 47
