2. 中国船舶科学研究中心,江苏 无锡 214082
2. China Ship Scientific Research Center, Wuxi 214082, China
北极地区蕴藏着极为丰富的煤气资源,面对能源紧缺的今天,北极无疑成为地球上“最后的宝藏”,而全球气候变暖导致北极冰川急剧融化[1 − 2],使得北极开发成为可能。但是,北极地区长时间的低气温,以及极地航线上漂浮的大面积海冰无疑为北极航行增加了难度。
在极地环境下,船舶结构受低气温的影响膨胀或收缩,产生不同程度的温度应力。在20世纪就有学者对船舶结构的温度应力进行研究,JASPER[3]基于解析推导得到船体结构温度场,将计算平板热应力的方法推广至计算等剖面船体梁的热应力。杜忠仁[4]基于热应力理论,推导和建立了船体纵向构件热应力计算表达式。近年来,随着仿真软件的技术革新,滕晓青等[5]通过Abaqus对舱段模型进行了温度场和热应力的数值分析,结果显示构件温度在横向纵向上均呈现不均匀状态。程玉莹[6]用Workbench对在极地作业的起重机进行瞬态热分析,得到结构瞬态温度场分布。MOATSOS等[7]针对一艘在极地日照下油轮结构的温度变化及热应力进行了研究,进一步评估了结构的极限承载能力,分析结果显示,由温度变化引起的热应力对船体结构的极限承载能力产生了显著的影响。
除了极地低温,漂浮的海冰也易与船舶发生挤压碰撞造成船体结构损伤变形,Mihkel[8]根据塑性设计准则,考虑船舶的永久变形,研究了某艘冰区加强船舶的横向板架和加强结构的过载响应。陆锁芳[9]基于结构力学理论,通过程序实现舷侧板架结构极限载荷快速求解方法。曾佳等[10]依据规范设定冰载荷尺寸,使用理想弹塑性材料,研究极区船舶冰带构件的极限承载能力。贺福等[11]基于能量法,考虑不同浮冰形状和作用位置对舷侧结构的影响。
目前来看,大多单一的研究温度对船体结构的影响或仅研究冰载荷对船体结构的影响,但实际航行中,冰载荷的存在往往伴随着低温。若产生的温度应力与冰载荷作用效果相同,对船体结构的安全存在极大的威胁,因此,本文开展温度效应和冰载荷联合作用下船舶舷侧极限承载能力研究。
1 理论方法 1.1 VOF模型在数值模拟中,选择流体体积(Volume of Fluid,VOF)模型,其可以精确地捕捉气液界面形状随时间的动态变化,特别适用于具有清晰气液界面的流动问题。数值计算的控制方程如下所示。
动量方程:
| $ \frac{\partial }{{\partial t}}\left( {\rho \nu } \right) + \nabla \cdot \left( {\rho \nu \nu } \right) = - \nabla p + \nabla \cdot \left[ {\mu \left( {\nabla \nu + \nabla {\nu ^{\rm T}}} \right)} \right] + \rho g + F 。$ | (1) |
式中:v为平均速度;F为气液相互作用项;ρ为密度;μ为流体黏度;
能量方程:
| $ \frac{\partial }{{\partial {\text{t}}}}\left( {\rho E} \right) + \nabla \cdot \left[ {\nu \left( {\rho E + P} \right)} \right] = \nabla \cdot \left( {{K_{e}}\nabla T} \right) + {S_h} 。$ | (2) |
式中:P为气相压力;Ke为有效导热系数;Sh为源项,包括辐射及其他体积热源;E为总能量;
目前有理论分析、模型实验、经验公式、数值仿真和实船测量5种方式确定冰载荷的大小,本文选用经验公式,根据CCS颁布的《钢制海船入级规范》[12]设计冰载荷,在该规范中对非首部区域设计冰载作了如下定义:
| $ w_{\mathrm{NowBow}}=F_{\mathrm{NowBow}}/Q_{\mathrm{NowBow}},$ | (3) |
| $ b_{\mathrm{NowBow}}=w_{\mathrm{NowBow}}/3.6,$ | (4) |
| $ P\mathrm{_{avg}}=F_{\mathrm{NonBow}}/\left(b_{\mathrm{NowBow}}\cdot w_{\mathrm{NowBow}}\right)。$ | (5) |
式中:wNowBow为设计载荷板的宽度;bNowBow为设计载荷板的高度;Pavg为载荷板范围内的平均压力;FNonBow和QNonBow分别为设计压力时所采用的力和线载荷。
1.3 载荷变形曲线与极限载荷准则在载荷-变形曲线中使用相对位移来描述板材的局部变形更为合理[13 − 14],相对位移的定义如图1所示。
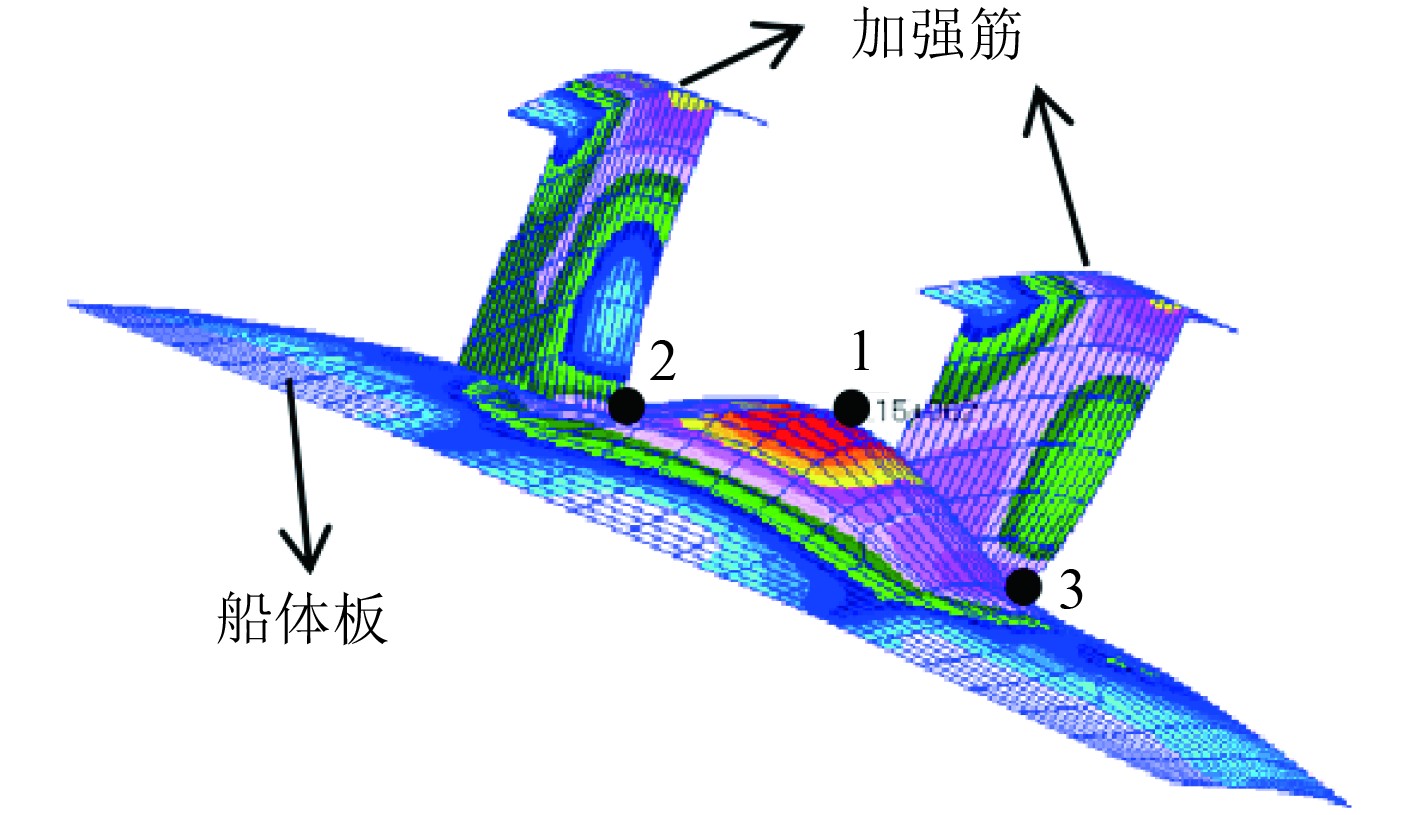
|
图 1 船体板相对位移 Fig. 1 Deflection defination for shell plating |
具体计算公式如下:
| $ \delta = {\delta _1} - \frac{{{\delta _2} + {\delta _3}}}{2} 。$ | (6) |
式中:δ1、δ2和δ3分别为图中点1、点2和点3处的位移;δ为相对位移,也称为变形。
在极限载荷求解过程中,两倍弹性斜率法能使得结构有更大的安全保障,因此本文选取两倍弹性斜率法来判定船舶舷侧的极限承载能力,具体流程为:从坐标原点做1条直线,该直线相对于载荷轴的斜率是载荷-变形曲线弹性阶段相对于载荷轴斜率的2倍,该直线与载荷-变形曲线交点所对应的载荷值称为极限载荷。
2 温度场分析 2.1 模型建立本文以某极地科考船为研究对象,在舷侧模型构建时,x方向为船长方向,采用1/2+1+1/2的模型尺寸,即在中间部分使用一个全加强肋骨间距模型,而在前后两端则采用半加强肋骨间距模型,总长6 m。y方向为船宽方向,全宽44.6 m,z方向沿船型深方向,取向上为正方向,高11.8 m,见图2。后续分析主要基于2个加强肋骨之间,其余部分用来消除边界带来的影响。
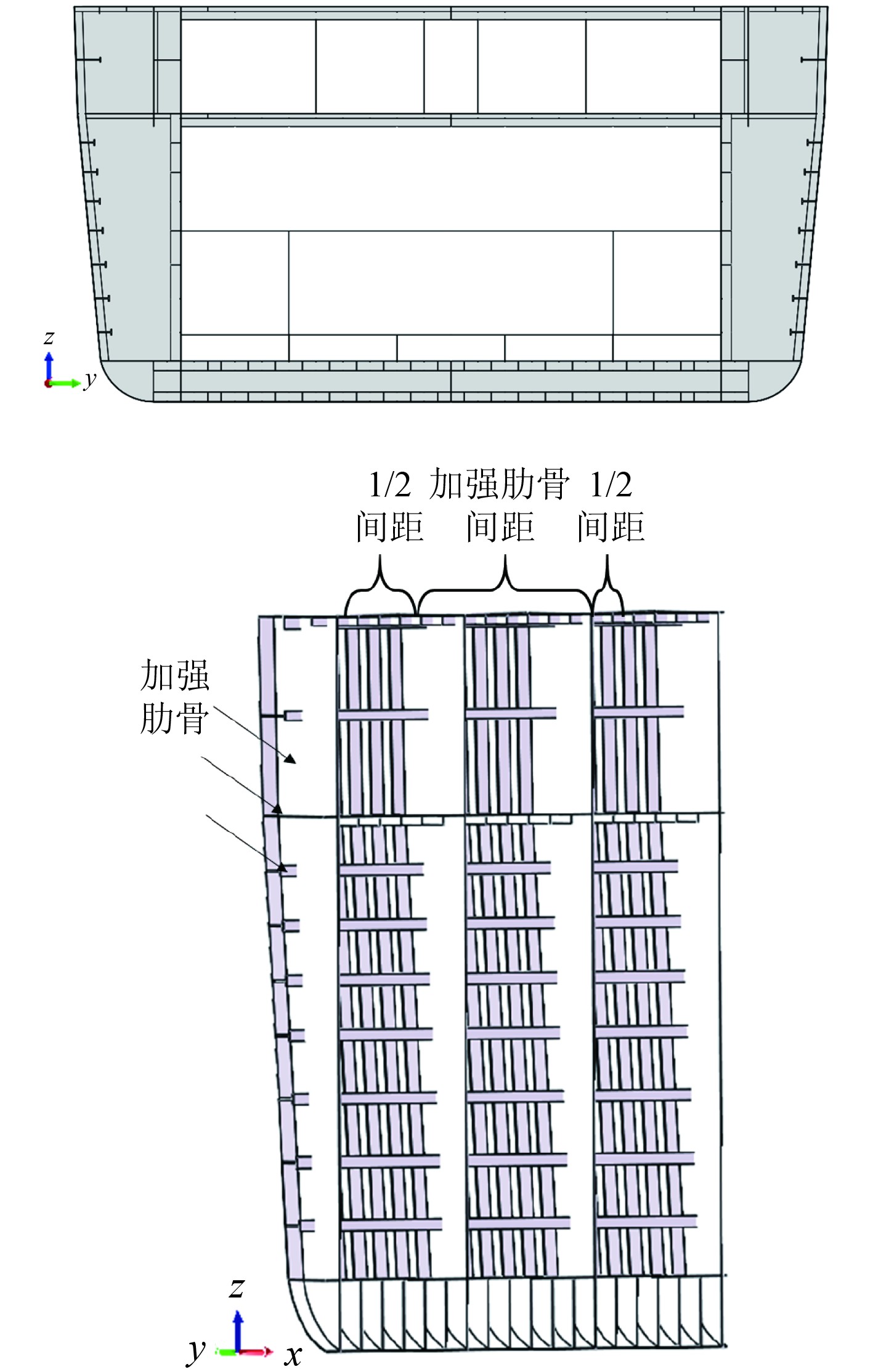
|
图 2 舱段模型 Fig. 2 Module model |
温度应力的计算基于材料的热物理性能参数。不同材料的热物理性能参数不同,环境温度变化引起的膨胀或收缩量就不同。舱段结构用钢EH36,参考相关资料[15 − 17]其热物理性能参数如表1所示。
|
|
表 1 材料热物理性能参数 Tab.1 Thermophysical parameters of the material |
在正常气候条件下,北极东北航道夏季气温一般不低于−10℃,冬季平均气温在−20℃~−40℃,极端低温可达−60℃,而北极海水温度基本维持在−2℃以上。基于这些温度条件,设定了3种温度工况(见表2),以模拟不同温度下船体结构的响应行为。
|
|
表 2 计算工况 Tab.2 Computational working condition |
采用VOF模型进行数值模拟仿真计算,选择层流模型。采用压力的隐式算子分裂(PISO)算法和PRESTO压力离散进行计算处理,时间步长设为5 s,时间步数设为
如图3所示,当舷侧初始温度为0 ℃,海水温度为0 ℃,空气温度为−10 ℃时,在前
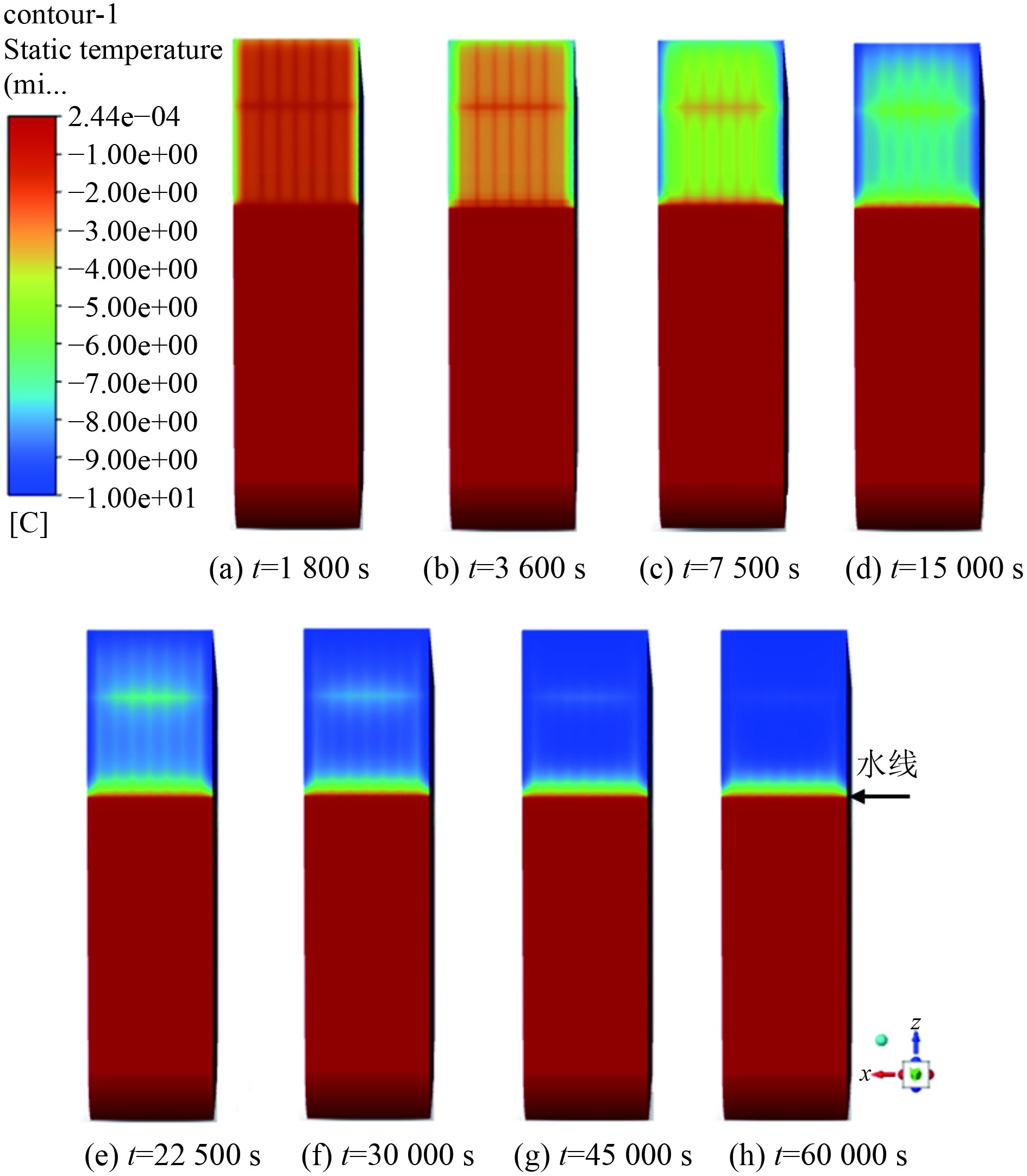
|
图 3 环境温度−10 ℃舷侧温度变化云图 Fig. 3 Temperature nephogram of side plate at temperature −10 ℃ |
为明确温度变化,在舱段外板上布置监测点,a、b、c为舷侧外板与肋骨接触位置,7.85为水线处,8.60为二甲板处,在水线以下布置一组监测点,在水线与二甲板之间间隔0.25布置监测点,在二甲板之上间隔1.00布置监测点,如图4所示。
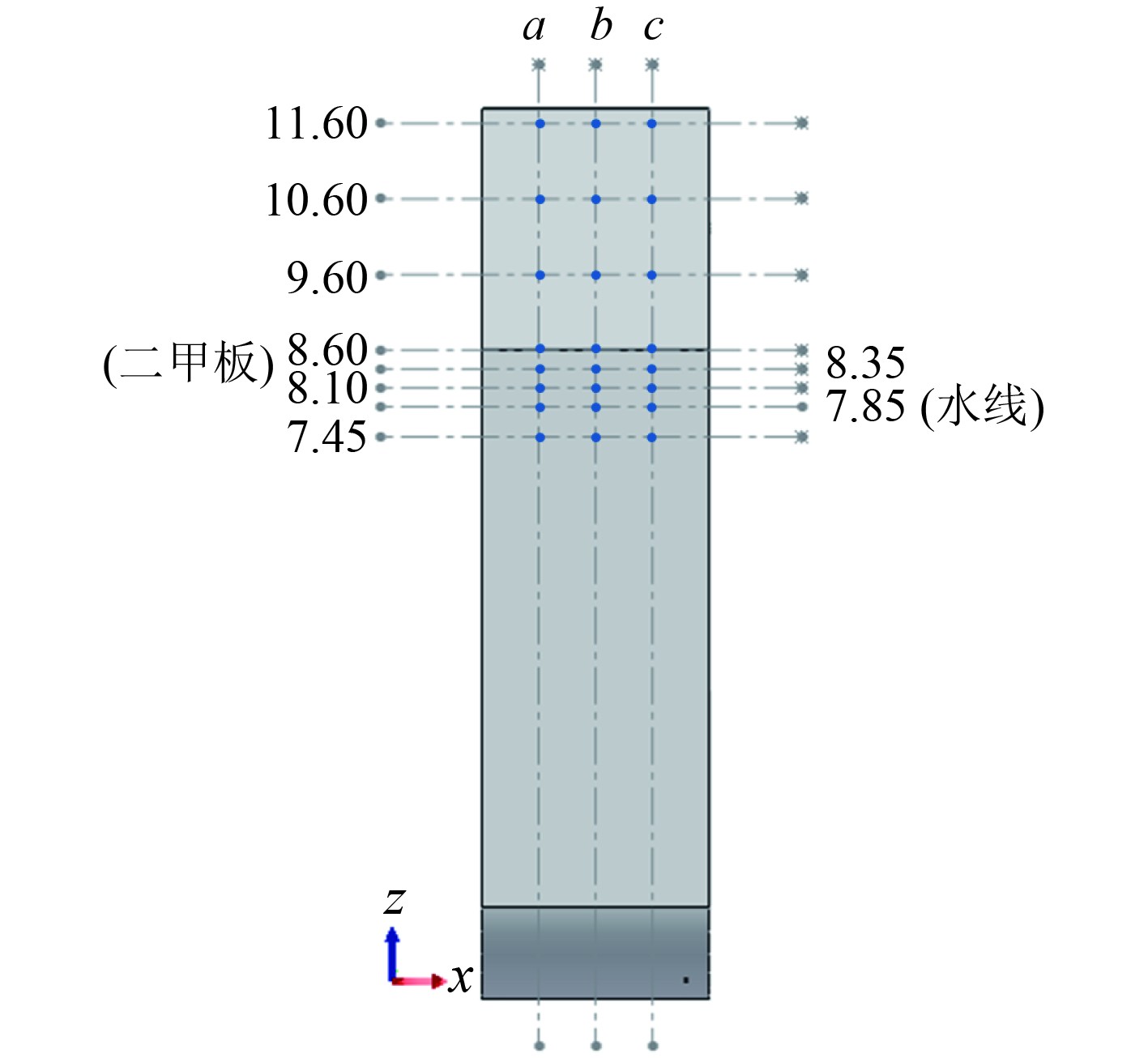
|
图 4 监测点位置布置 Fig. 4 Location of monitoring points |
各高度下a、b、c点的温度变化,见图5(a)。在水线及水线以下位置,a、b、c点温度变化趋势一致。型深8.10 b点在

|
图 5 监测点温度变化曲线 Fig. 5 Temperature curves of monitoring points |
在b处各高度的温度变化,见图5(b)。水线以下仅受海水温度的影响,温度稳定于0 ℃;水线以上至二甲板处即受到海水温度影响又受到空气温度的影响产生明显的温度梯度,型深7.85处的温度稳定在−2 ℃,型深8.10处的温度稳定在−6 ℃,型深8.35处的温度稳定在−8 ℃,型深8.10处温度稳定于−9 ℃;二甲板以上位置受环境温度影响明显,最终趋于环境温度−10 ℃。
在环境温度为−10℃的情况下,温度在横向上由外向内传递,在垂向上,水线以下稳定于海水温度,水线至二甲板处产生明显的温度梯度,二甲板以上稳定于环境温度。改变环境温度,稳定后舷侧各高度平均温度如表3所示。
|
|
表 3 稳定后舷侧外板垂向位置平均温度 Tab.3 Average temperature in the vertical position of the side plate after stabilization |
稳定后,舷侧外板在环境温度不同的情况下,水线以下温度均为海水温度0℃,水线处的温度大致为环境的1/6,水线以上至二甲板处,存在明显的温度梯度,二甲板以上位置逐渐趋于环境温度。
在无风无浪的低气温环境下,船舶舷侧受低温影响明显,水线附近存在明显的温度梯度。舷侧垂向温度以水线为界,水线以下部分受海水温度的影响更多,温度在0℃左右;水线处即受海水温度的影响又受空气温度的影响,环境温度改变,水线处最终稳定的温度也随之改变;水线以上部分,与空气接触,更多受到环境的影响,从水线往上逐渐趋于环境温度。
3 低温作用下的极限承载能力分析首先确定冰载荷大小,载荷板施加位置以及局部精细网格尺寸,然后以环境温度为−10℃、−30℃、−60℃下产生的温度应力为基础,在舷侧外板上施加冰载荷,研究温度应力与冰载荷联合作用下船体舷侧极限承载能力,通过与无温度应力下的极限载荷进行对比,探讨低温环境对船体结构极限载荷的具体影响。
在研究舷侧的极限承载能力时,将材料视为理想弹塑性,忽略应变硬化影响,舷侧及舷侧肋骨、舷侧纵桁采用高强度钢EH36,参考文献[18 − 20],设定材料密度
根据式(3)~式(5),计算可得载荷板宽2.68 m,高0.74 m,计算冰载荷为5.94 MPa,为得到充分发展的载荷-变形曲线,载荷板的压力值从0开始线性增大,实取最大载荷为12 MPa。
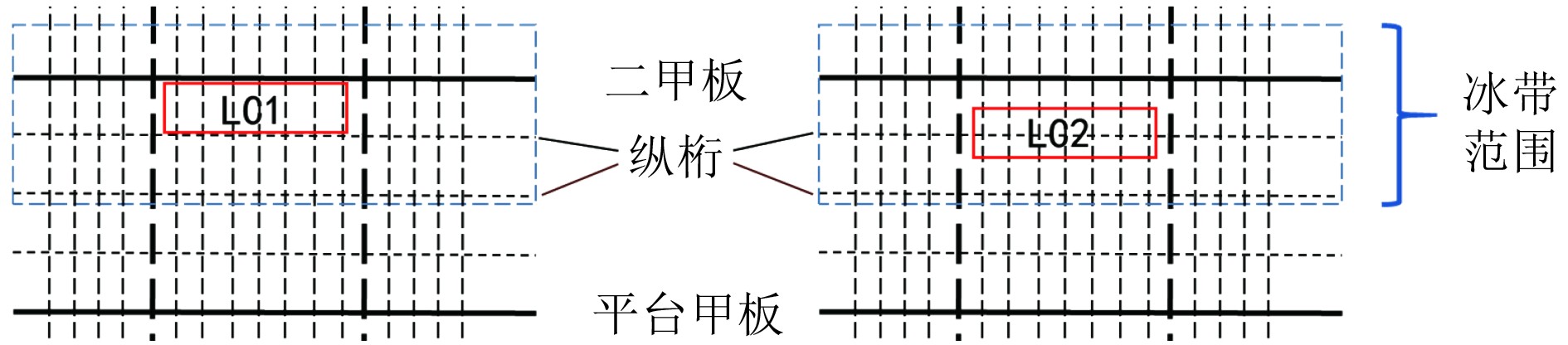
冰载荷以虚拟载荷板的方式施加在舷侧外板上,且施加位置为使所校核的构件发生最大位移的地方。本文将载荷板施加在板格中心、纵桁跨中(见图6),研究舷侧外板的极限承载能力。
|
图 6 加载示意图 Fig. 6 Loading location |
根据船舶结构形式,将相对变形统一定义为构件相对于其支撑构件的变形,以忽略船体结构整体弹性变形的影响,如图7所示。

|
图 7 各位移点示意图 Fig. 7 Diagram of displacement points |
此工况下的相对变形为:
| $ \delta = {\delta _1} - \frac{{{\delta _2} + {\delta _3}}}{2} ,$ | (7) |
| $ \delta = {\delta _4} - \frac{{{\delta _5} + {\delta _6}}}{2}。$ | (8) |
为了研究分析合适的网格尺寸,选择无环境温度影响,以局部最精细网格30 mm×30 mm模型计算结果作为基准,比较60 mm×60 mm和120 mm×120 mm 2种局部精细网格模型计算结果的差别。
表4所示为3种局部精细网格模型对极限载荷的影响,120 mm×120 mm局部精细网格模型计算得到的极限载荷差别达到24.41%,60 mm×60 mm局部精细网格模型计算得到的极限载荷差别仅为4.35%,后续研究均采用60 mm×60 mm局部精细网格精度,既保证计算的准确性,也能节省很多计算资源。
|
|
表 4 局部精细网格对极限载荷影响比较 Tab.4 Comparison of the influence of local fine meshes on limit loads |
仅考虑冰载荷对舷侧的影响,舷侧受到持续的冰载荷而发生变形。图8为无温度时的载荷-变形曲线,通过两倍弹性斜率法,确定舷侧的极限强度为6.24 MPa。

|
图 8 无温度载荷-变形曲线 Fig. 8 Load-deflection curve of no temperature |
如图9所示,在极限状态下,最大应力出现在二甲板与舷侧外板接触位置以及肋骨与舷侧外板接触位置,为364 MPa。通过设置变形比例因子,放大显示变形区域,载荷板在船宽方向(Y轴正方向)上向船体内侧凹陷,最大变形11.33 mm,冰载荷产生的应力为压应力。在船长方向(X轴方向)上,变形趋势由载荷板中央向两侧递减,最大变形位于载荷板中央。

|
图 9 无温度下极限状态应力变形云图 Fig. 9 Stress nephogram and deformation nephogram in the limit state in the absence of ambient temperature |
当考虑环境温度时,使用CFD-Structure Interpolator,将2.2计算的温度结果从体单元映射到壳单元模型中,导入的温度载荷在水线附近存在明显温度梯度(见图10)。

|
图 10 温度梯度 Fig. 10 Temperature gradient |
仅受环境温度影响时,舷侧外板在二甲板处存在最大温度应力(见图11)。当温度为−10℃、−30℃和−60℃时,产生的最大应力分别为31.84 MPa、96.59 MPa和193.67 MPa。随着环境温度的降低,产生的最大应力逐渐增大。

|
图 11 温度应力 Fig. 11 Stress of temperature |
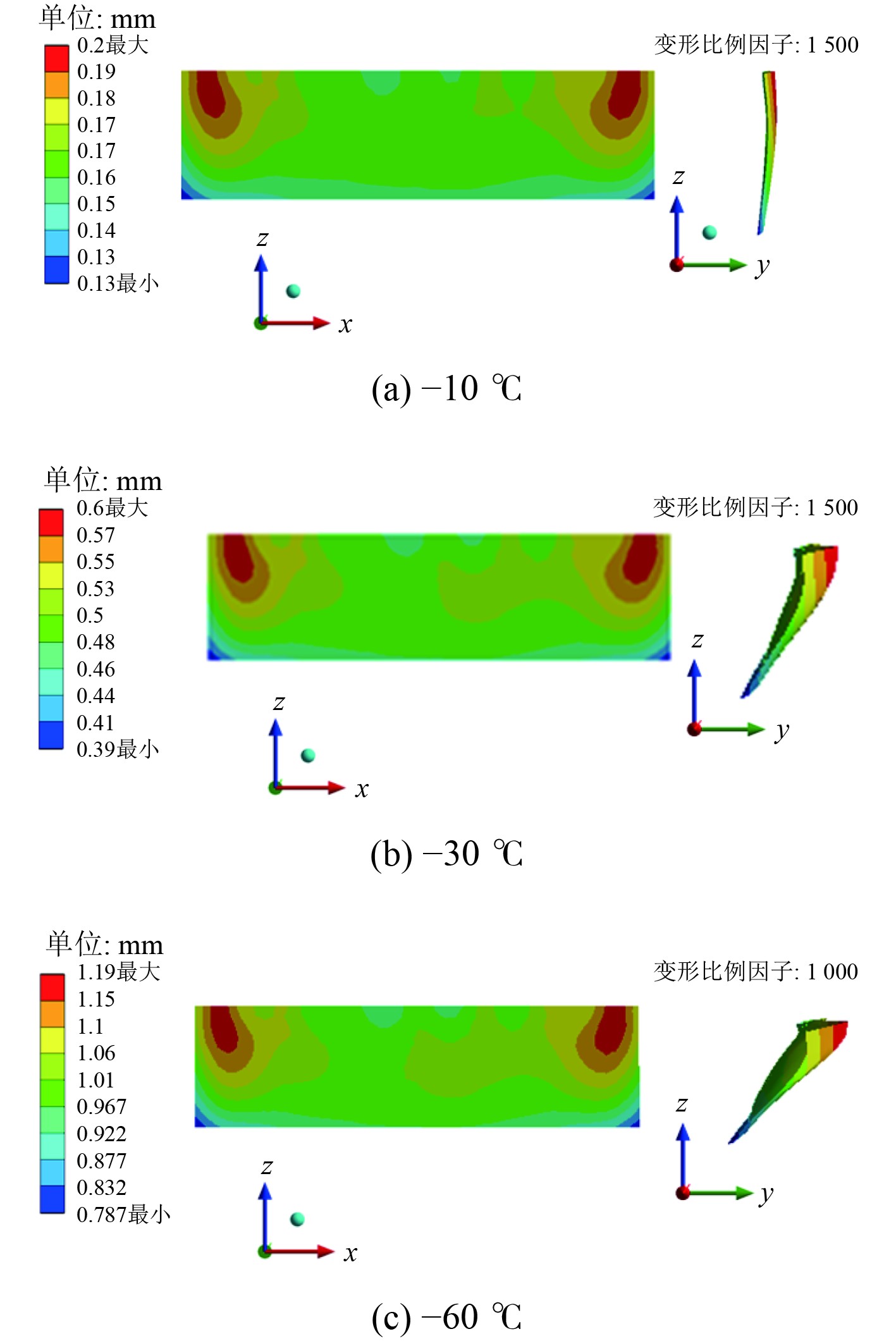
在温度应力的影响下,载荷板发生变形(见图12)。设置变形比例因子,放大显示变形区域,可以观察到在各温度下,载荷板产生向舷侧内部(Y轴正方向)的凹陷,温度应力表现为压应力。−10℃时,载荷板产生0.20 mm的最大变形;−30℃时,载荷板产生0.60 mm的最大变形;−60℃时,载荷板产生1.19 mm的最大变形。
|
图 12 载荷板变形 Fig. 12 Deformation of the load plate |
在温度应力的基础上,向载荷板上施加压力,随着压力的逐步增加,舷侧最大应力在温度应力之后经历了短暂的缓慢增长,然后迅速增大。同时,最大应力的位置逐渐从二甲板位置向载荷板移动。由于冰载荷不断增加,舷侧外板的应力最终达到屈服强度。
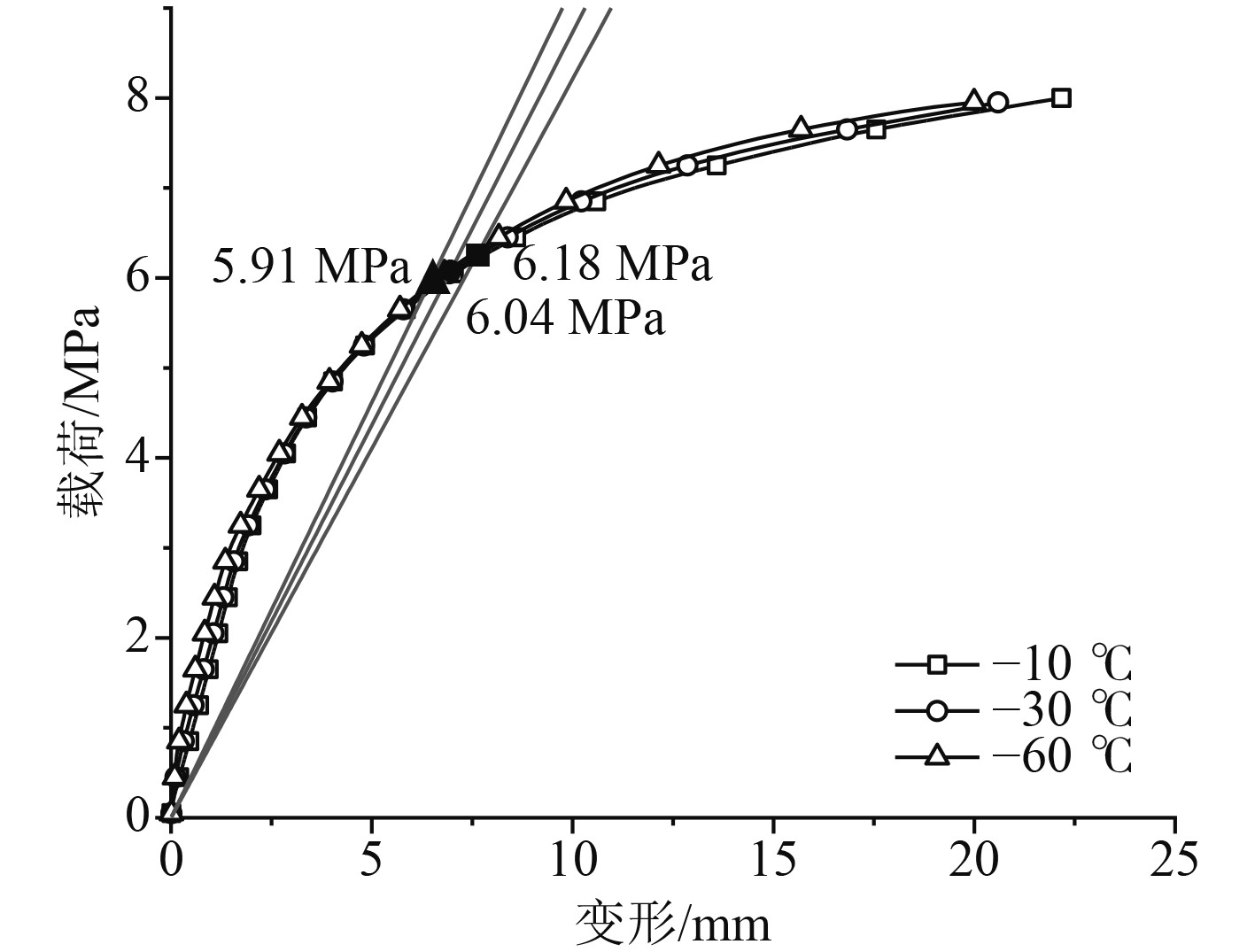
将仿真得到的数据绘制载荷-变形曲线,通过2倍斜率法,确定舷侧的极限载荷(见图13)。以无温度时的极限载荷为基准,−10℃,舷侧外板的极限载荷为6.18 MPa,相较于无温度时的极限载荷下降了0.96%;−30℃,舷侧外板的极限载荷为6.04 MPa,与无温度时的相比,此时下降了3.21%;−60℃,舷侧外板的极限载荷为5.91 MPa,下降了5.29%。随着环境温度的降低,舷侧的极限承载能力下降。
|
图 13 载荷-变形曲线 Fig. 13 Load-deflection curves |
各温度下极限状态时的应力变形云图(见图14~图15),最大应力位置与无温度时的位置分布一致,位于二甲板与舷侧外板接触位置以及肋骨与舷侧外板接触位置。最大变形也与无温度时的位置一致,位于载荷板中央,向舷侧内部凹陷。

|
图 14 极限状态下应力云图 Fig. 14 Stress nephogram in the limit state |

|
图 15 极限状态下变形云图 Fig. 15 Deformation nephogram in the limit state |
对于加载区在水线附近且无强构建支撑的舷侧外板来说,无温度影响时,舷侧外板的极限载荷为6.24 MPa,当存在环境温度,温度产生的压应力与冰载荷产生的压应力叠加,使得环境温度越低,其极限载荷也越小。
3.3.2 LC2极限载荷LC2用于研究加载区在水线附近且有纵桁支撑的船舶舷侧极限承载能力。如图16所示,在无环境温度影响下,舷侧外板极限载荷8.81 MPa;以无温度时的极限载荷为基准,−10℃时,舷侧外板的极限载荷下降0.57%,降至8.76 MPa;−30℃时,舷侧外板的极限载荷下降1.82%,达8.65 MPa;−60℃时,舷侧外板极限载荷仅8.41 MPa,与无温度相比下降4.54%。
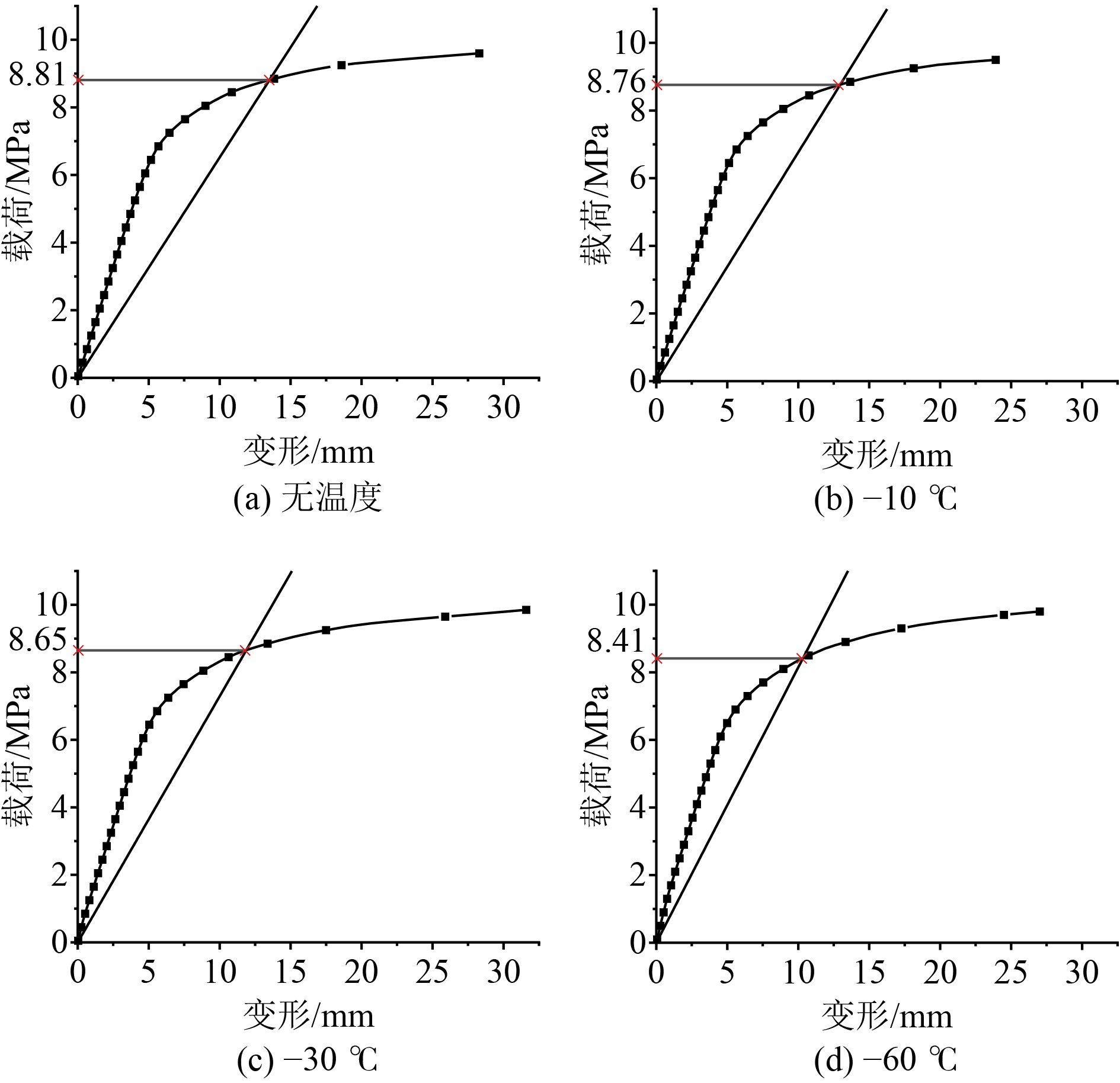
|
图 16 载荷-变形曲线 Fig. 16 Load-deflection curves |
将LC1与LC2的极限载荷汇总(见表5)。在强构建的支撑下,船舶舷侧的极限承载能力上升。但总体趋势保持不变,随着环境温度的下降,极限载荷减小。因此,对极地船舶结构设计和安全性评估时,应充分考虑温度效应的影响,确保在低温条件下船体结构的安全性和可靠性。
|
|
表 5 不同工况下的极限载荷 Tab.5 Limit loads under different operating conditions |
本文研究了在低温下,舷侧外板垂向温度变化,以此温度梯度下产生的温度应力为基础,在不同位置施加冰载荷,利用两倍弹性斜率法,确定舷侧外板的极限载荷。研究和讨论了低温环境对舷侧外板极限承载能力的影响,得出以下结论:
1)在仅受环境温度影响下,舷侧温度变化一致。在水线至二甲板处既受到海水温度的影响又受到环境温度的影响,产生明显的温度梯度。
2)环境温度降低,温度应力增大,舷侧的极限承载能力下降。温度产生的温度应力和作用在舷侧外板的冰载荷叠加,船体结构更容易达到其屈服强度,从而极限载荷降低。
3)强构件的支撑有利于舷侧极限承载能力的提升。当载荷板位于水线附近并配有强构件支撑下的极限载荷普遍大于无强构件支撑的极限载荷。
| [1] |
TAKASHI Y, KUMIKO T. Rapid change of the arctic climate system and its global influences - overview of grene arctic climate change research project (2011–2016)[J]. Polar Science, 2020, 25: 100548. |
| [2] |
MARCIANESI F, AULICINO G A, WADHAMS P. Arctic sea ice and snow cover albedo variability and trends during the last three decades[J]. Polar Science, 2021, 28: 100617. |
| [3] |
JASPER N H. Temperature-induced stresses in beams and ships[J]. Journal of the American Society of Naval Engineers, 1956, 68(3): 485-497. DOI:10.1111/j.1559-3584.1956.tb05265.x |
| [4] |
杜忠仁. 船体纵向构件的热应力计算与比较衡准[J]. 中国造船, 1991, 2: 58-67. DU Z R. Calculation method and comparative evaluation of the thermal stress in longitudinal hull structural components[J]. Shipbuilding of China, 1991, 2: 58-67. |
| [5] |
滕晓青, 顾永宁. 单壳双底货船舱段结构瞬态温度场和热应力[J]. 船舶力学, 2003, 2: 51-60. TENG X Q, GU Y N. Transit temperature field and thermal stresses of hold structures of single side shell and double bottom vessels[J]. Journal of Ship Mechanics, 2003, 2: 51-60. |
| [6] |
程玉莹. 极地环境载荷作用下船舶起重机结构设计与分析[D]. 大连: 大连海事大学, 2022.
|
| [7] |
MOATSOS I, DAS P K. Modelling the effect of extreme diurnal temperature changes on ship structures for the assessment of structural reliability using load combination techniques[C]//14th International Offshore and Polar Engineering Conference, 2024.
|
| [8] |
MIHKEL K. Load carrying capacity of ice-strengthened frames under idealized ice load and boundary conditions[J]. Marine Structures, 2018, 58: 18−30.
|
| [9] |
陆锁芳. 冰载下冰带区域板格强度快速评估方法研究[D]. 上海: 上海交通大学, 2019.
|
| [10] |
曾佳, 王燕舞, 郑文青, 等. 极区船舶冰带构件极限载荷评估[J]. 船舶工程, 2019, 41(7): 5-11. ZENG J, WANG Y W, ZHENG W Q, et al. Limit load assessment for ice belt structure of polar ships[J]. Ship Engineering, 2019, 41(7): 5-11. |
| [11] |
贺福, 刘晖, 刘俊. 冰载荷空间分布对舷侧结构响应的影响[J]. 船舶工程, 2021, 43(7): 13-17+135. HE F, LIU H, LIU J. Influence of ice load spatial distribution on the response of side structure[J]. Ship Engineering, 2021, 43(7): 13-17+135. |
| [12] |
中国船级社. 钢质海船入级规范[S]. 2023.
|
| [13] |
IACS. Requirements Concerning Polar Class [S]. 2011.
|
| [14] |
TRAFI. Finnish-Swedish Ice Class Rules [S]. 2010.
|
| [15] |
那城炜. 东北寒区碾压混凝土坝温度应力仿真研究[D]. 沈阳: 沈阳农业大学, 2020.
|
| [16] |
李继中. 考虑低温影响的LNG船极限强度与剩余极限强度研究[D]. 上海: 上海交通大学, 2016.
|
| [17] |
陈章兰, 熊云峰, 蔡振雄. EH36船用钢焊接角变形有限元分析[J]. 船舶工程, 2007(6): 62-64. CHEN Z L, XIONG Y F, CAI Z X. FEA of welding angular distortion of EH36 marine steel[J]. Ship Engineering, 2007(6): 62-64. |
| [18] |
KE W, LI W, YONG Z L, et al. Experimental study on low temperature fatigue performance of polar icebreaking ship steel[J]. Ocean Engineering, 2020, 216: 107789. DOI:10.1016/j.oceaneng.2020.107789 |
| [19] |
周塞北. 冰区船舶起重机械结构强度分析[D]. 镇江: 江苏科技大学, 2017.
|
| [20] |
孙雨薇. 低温下船体结构反复碰撞损伤研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
 2025, Vol. 47
2025, Vol. 47
