鱼雷按照使用方式可分为自导鱼雷和线导鱼雷[1],线导鱼雷是由发射平台通过线导通道传输指令控制其导向目标的水中兵器。由于线导鱼雷可以在发射后的攻击过程中根据遥控命令不断调整航行姿态,相较自导鱼雷在攻击远距离和机动目标时易于取得较理想的攻击效果。根据攻击时已经获取的目标信息情况,线导鱼雷可以采用不同的导引方法计算遥控参数。方位导引法依赖目标信息少,使用条件易于满足,是经常使用的导引方法。
自导鱼雷攻击弹道在鱼雷发射时确定,而线导鱼雷发射后还可以进行导引,在提升鱼雷攻击能力的同时带来了攻击弹道的不确定性。为了能够快速制定线导鱼雷攻击方案以及确定鱼雷最佳发射时机,需要在鱼雷发射前预知线导鱼雷攻击弹道。在发射艇和目标都是进行匀速直航运动情况下,本文提出了一种基于推算方位的线导鱼雷方位导引预估弹道计算方法,使用目标运动要素推算的目标方位序列,采用方位导引方法以及新构建的预估弹道计算模型,计算线导鱼雷方位导引预估弹道。
1 线导鱼雷方位导引方法线导鱼雷导引方法包括前置点导引、方位导引和修正方位导引等[2 − 4],在实际使用时需要根据现实条件选择合适的导引方法。方位导引法是将线导鱼雷导向目标当前方位并与目标逐渐接近的一种导引方法[5],具有依赖目标信息少、操作控制简单等特点。
假设,
|
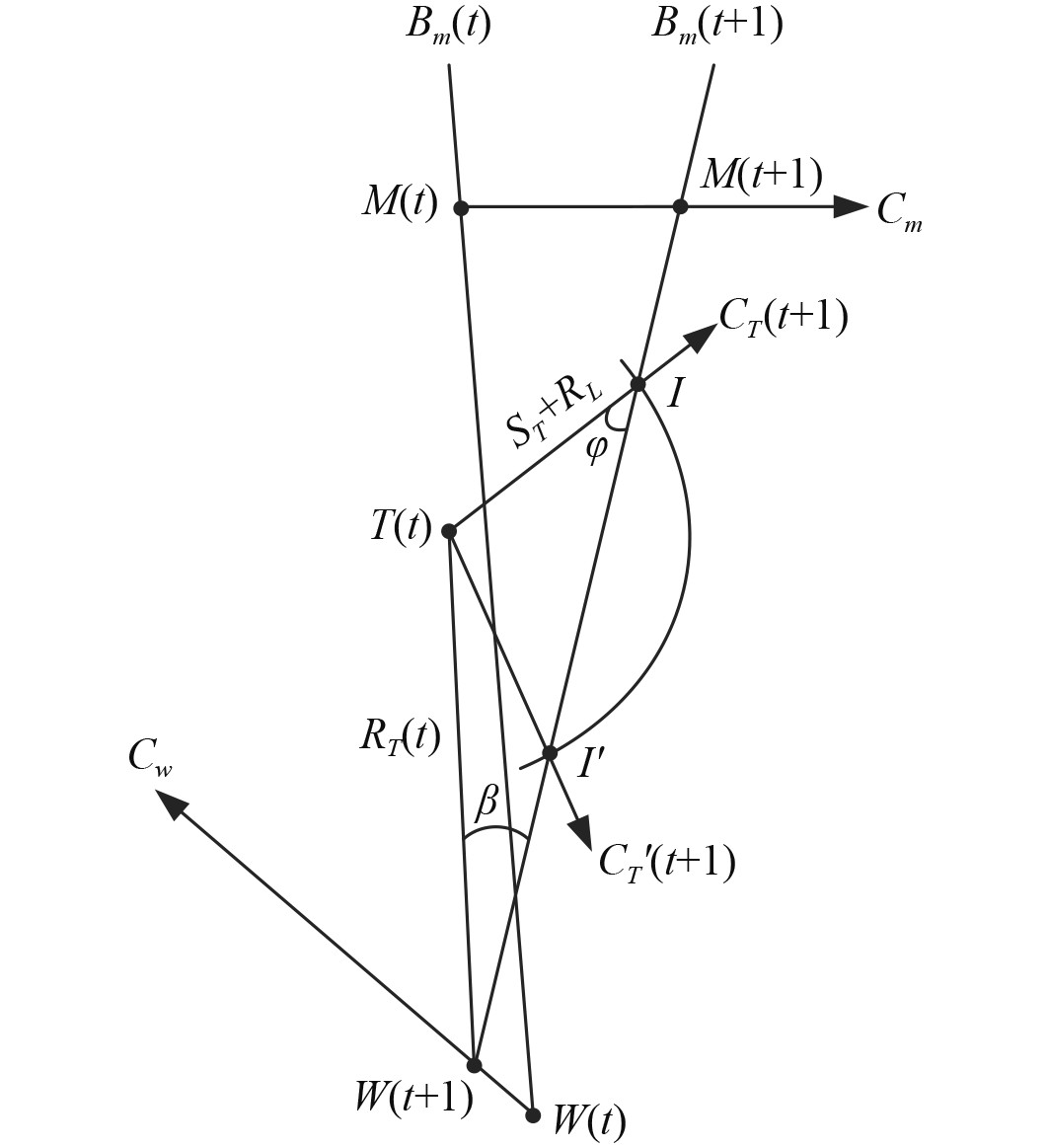
图 1 方位导引示意图 Fig. 1 Azimuth guidance diagram |
| $ \frac{{{R_T}(t)}}{{\sin (\varphi )}} = \frac{{{S_T} + {R_L}}}{{\sin (\beta )}},$ | (1) |
| $ \varphi = \arcsin \frac{{{R_T}(t) \times \sin (\beta )}}{{{S_T} + {R_L}}},$ | (2) |
| $ {C_T}(t + 1) = {B_m}(t + 1) + \varphi 。$ | (3) |
根据方位导引原理,鱼雷发射后是远离发射平台运动,取鱼雷航向为
本文主要研究利用目标运动要素推算目标方位进而预估线导鱼雷方位导引弹道方法,目标运动要素误差是影响要素推算方位准确性的主要因素。
2.1 目标运动要素目标运动要素主要包括目标方位(
要素误差是指实际用于计算的目标运动要素与目标真实运动要素的差值。目标距离误差
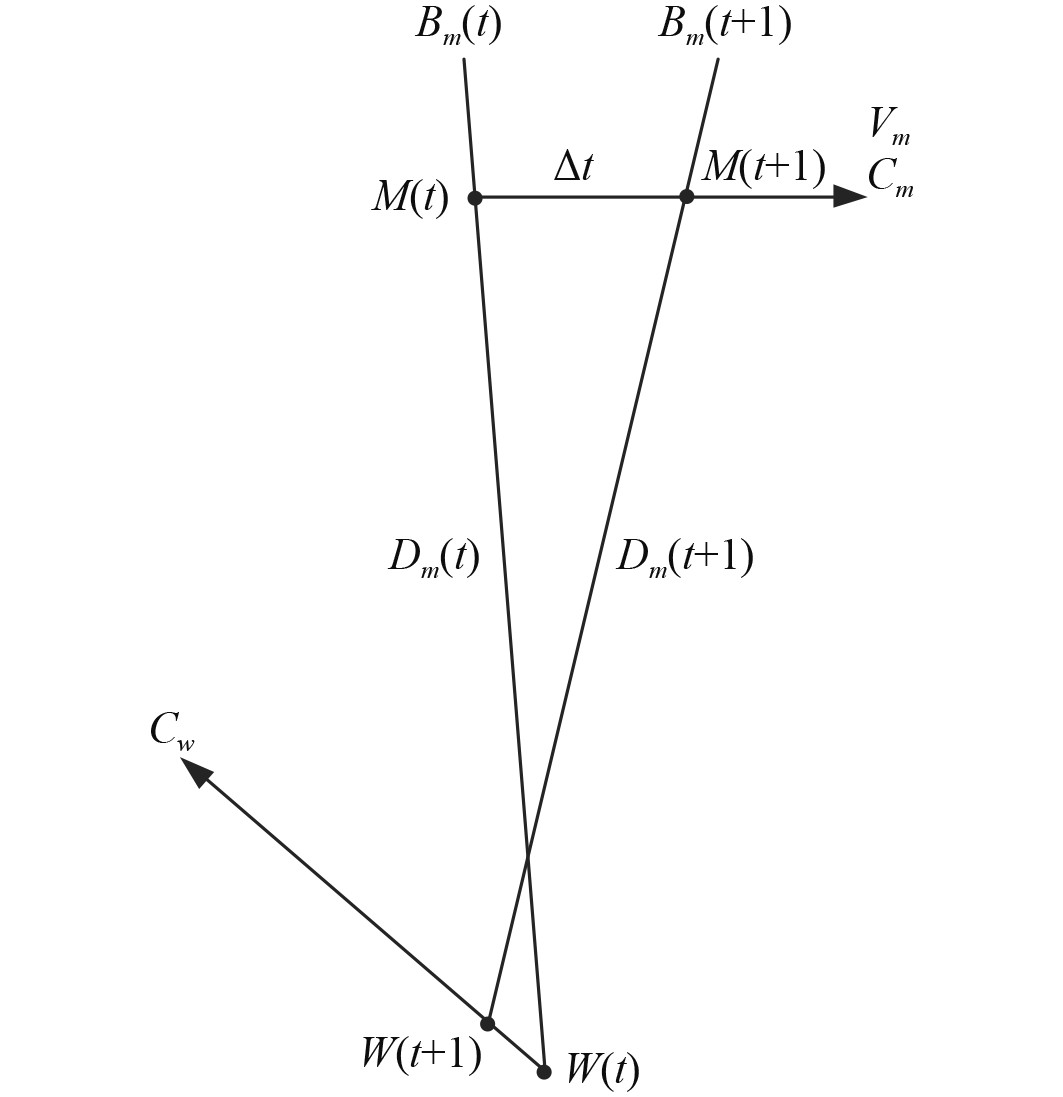
已知目标方位、距离、航速和航向以及发射平台航速、航向等信息,可以建立目标运动模型[9],采用目标运动要素推算目标方位,主要包括3个步骤:首先,在大地坐标系下根据现时刻发射平台位置坐标、目标方位以及目标距离信息计算现时刻目标位置信息;然后,根据现时刻目标位置信息、目标航速、目标航向和时间间隔,计算下一个时刻目标位置信息;最后,根据下一个时刻发射平台位置坐标以及目标位置信息计算新的目标方位和距离信息。目标运动要素推算目标方位示意图如图2所示。
|
图 2 目标运动要素推算方位示意图 Fig. 2 Target motion elements calculated target orientation diagram |
具体计算公式如下:
| $ \left\{ \begin{gathered} {X_m}(t) = {X_w}(t) + {D_m}(t) \times \sin ({B_m}(t)),\\ {Y_m}(t) = {Y_w}(t) + {D_m}(t) \times \cos ({B_m}(t)),\\ \end{gathered} \right. $ | (4) |
| $ \left\{ \begin{gathered} {X_m}(t + 1) = {X_m}(t) + \Delta t \times {V_m} \times \sin ({C_m}),\\ {Y_m}(t + 1) = {Y_m}(t) + \Delta t \times {V_m} \times \cos ({C_m})。\\ \end{gathered} \right. $ | (5) |
| $ {B_m}(t + 1) = \arctan \frac{{{X_m}(t + 1) - {X_w}(t + 1)}}{{{Y_m}(t + 1) - {Y_w}(t + 1)}},$ | (6) |
| ${\begin{split} {D_m}(t + 1) = \sqrt {{{\left[ {{X_m}(t + 1) - {X_w}(t + 1)} \right]}^2} + {{\left[ {{Y_m}(t + 1) - {Y_w}(t + 1)} \right]}^2}} \end{split}}。$ | (7) |
式中:(
线导鱼雷发射后首先开始执行初始弹道,然后才能进行线导导引。预估线导鱼雷导引弹道,首先需要预估鱼雷完成初始弹道后位置信息,然后根据推算的目标方位序列,使用线导鱼雷方位导引计算方法,按照导引周期计算鱼雷预估位置点序列信息,生成线导鱼雷预估弹道。
3.1 预估鱼雷完成初始弹道后位置鱼雷执行完成初始弹道后的位置信息计算方法如下:
1)计算鱼雷执行完成初始直航段[9]后位置坐标
| $ \left\{ \begin{gathered} {X_{T0}} = {X_{w0}} + {S_0} \times \sin ({C_{w0}}),\\ {Y_{T0}} = {Y_{w0}} + {S_0} \times \cos ({C_{w0}})。\\ \end{gathered} \right. $ | (8) |
2)计算鱼雷执行一次转角时圆心位置坐标
| $ \left\{ \begin{gathered} {X_O} = {X_{T0}} + {R_T} \times \sin \left({C_{w0}} + \frac{\text{π}}{2} \times \mathrm{sign}({\omega _1})\right),\\ {Y_O} = {Y_{T0}} + {R_T} \times \cos \left({C_{w0}} + \frac{\text{π}}{2} \times \mathrm{sign}({\omega _1})\right)。\\ \end{gathered} \right. $ | (9) |
3)计算鱼雷执行完成一次转角后位置坐标
| $ {\left\{ \begin{gathered} {X_T}(0) = {X_O} + {R_T} \times \sin \left({C_{w0}} + {\omega _1} + \frac{\text{π}}{2} \times \mathrm{sign}( - 1 \times {\omega _1})\right),\\ {Y_T}(0) = {Y_O} + {R_T} \times \cos \left({C_{w0}} + {\omega _1} + \frac{\text{π}}{2} \times \mathrm{sign}( - 1 \times {\omega _1})\right)。\\ \end{gathered} \right.} $ | (10) |
式中:(
假设,鱼雷进行第
1)根据上述线导鱼雷方位导引方法计算式(1)~式(3)中鱼雷导引航向为
| $ {C_T}(n) = {B_m}(n) + \varphi 。$ | (11) |
2)鱼雷完成一次方位导引后位置坐标为
| $ \left\{ \begin{gathered} {X_T}(n) = {X_T}(n - 1) + \Delta t \times {V_T} \times \sin ({C_T}(n)),\\ {Y_T}(n) = {Y_T}(n - 1) + \Delta t \times {V_T} \times \cos ({C_T}(n)) 。\\ \end{gathered} \right. $ | (12) |
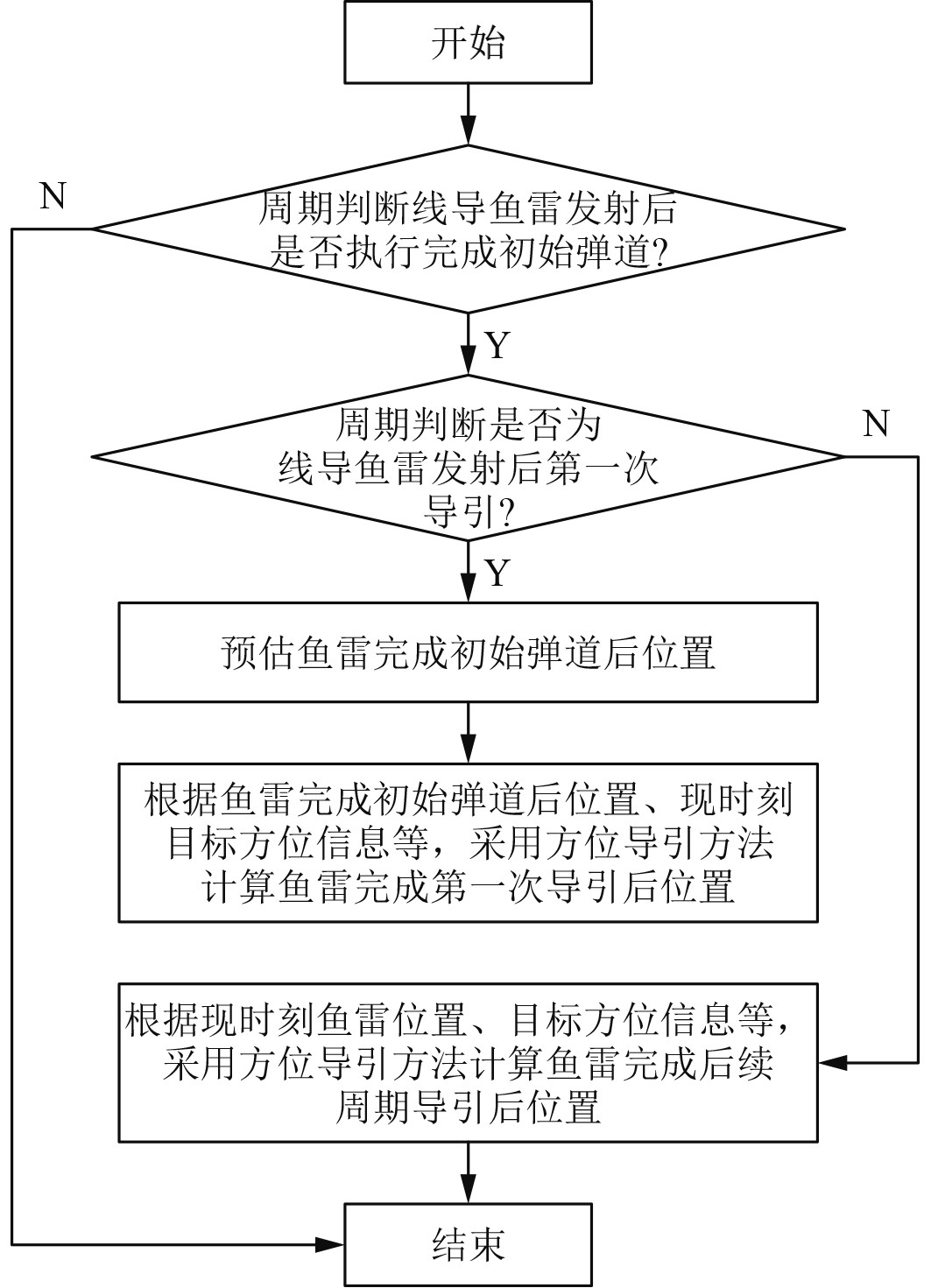
预估鱼雷导引弹道计算流程如图3所示。
|
图 3 预估鱼雷导引弹道计算流程图 Fig. 3 Flow chart of calculation of estimated torpedo guided trajectory |
假设发射平台和目标都是进行匀速直航运动情况下,根据已发表的文献资料选择典型的鱼雷攻击态势对预估鱼雷方位导引弹道计算方法进行仿真验证。
4.1 仿真态势根据目标航速高、中、低,目标距离远、中,目标舷角中、小,设计12个典型态势进行仿真测试。
1)发射平台态势:航速为6 kn,航向为20°;
2)目标具体态势如表1所示。
|
|
表 1 目标态势信息表 Tab.1 Target situation information table |
分2种情况对推算使用的目标运动要素增加误差:
1)针对目标航向、航速、距离三要素中单个要素输入增加固定误差处理
①目标航向误差
②目标航速误差
③目标距离误差
2)针对目标航向、航速、距离三要素分三档增加正态分布随机误差处理
①第一档:目标航向误差
②第二档:目标航向误差
③第三档:目标航向误差
根据上述12个典型态势进行仿真测试,按照误差设置情况,分为2个部分完成,设置鱼雷自导方式为尾流,鱼雷速度取40 kn[10],尾流长度取180
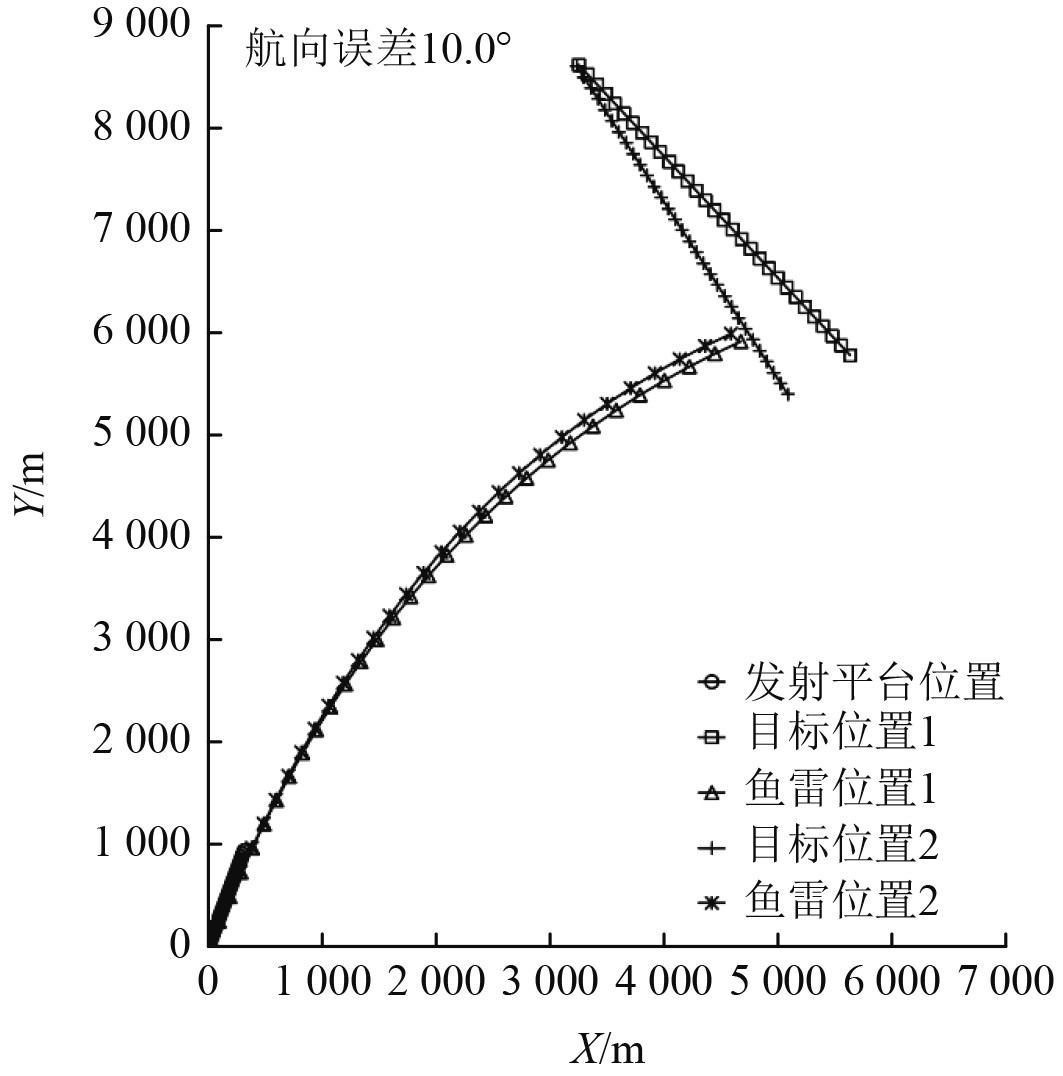
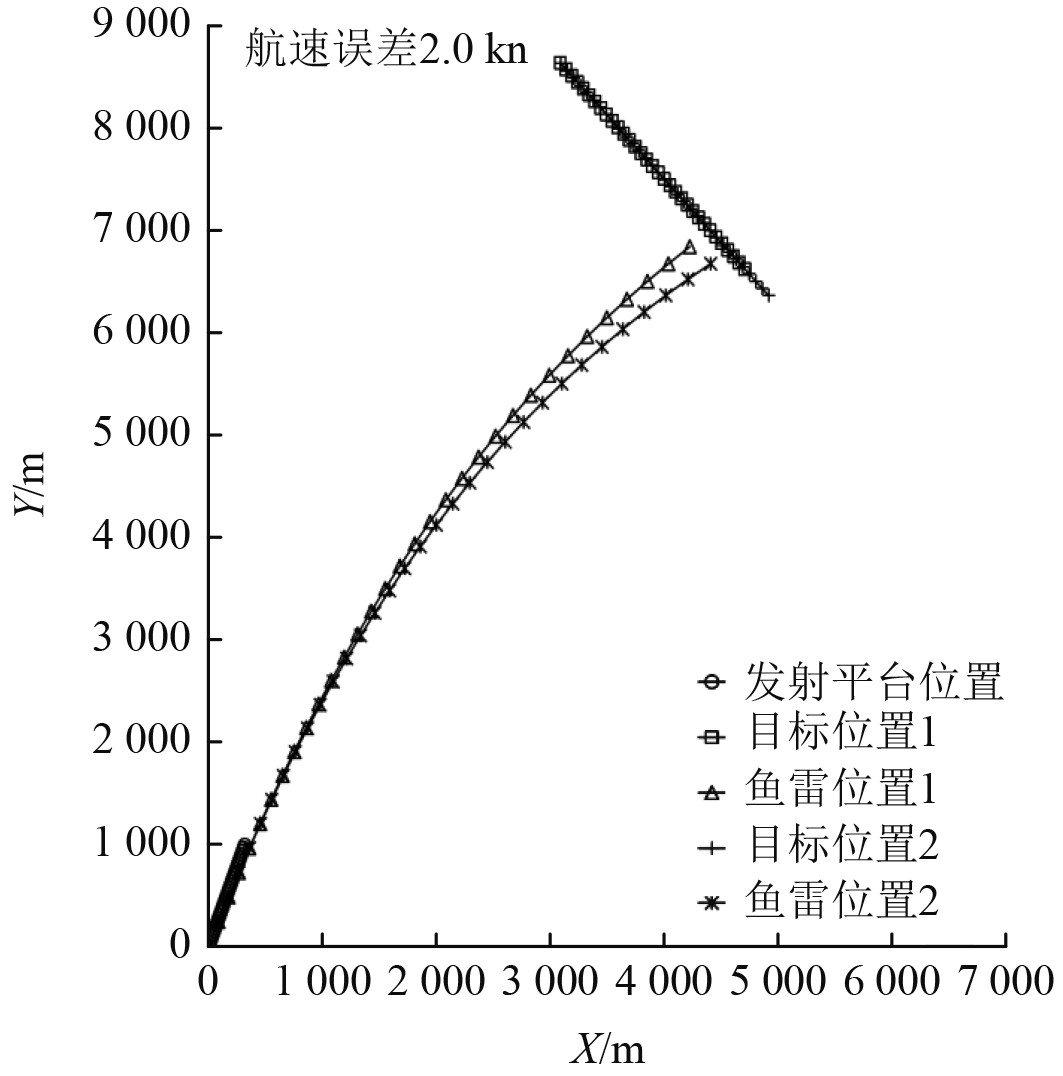
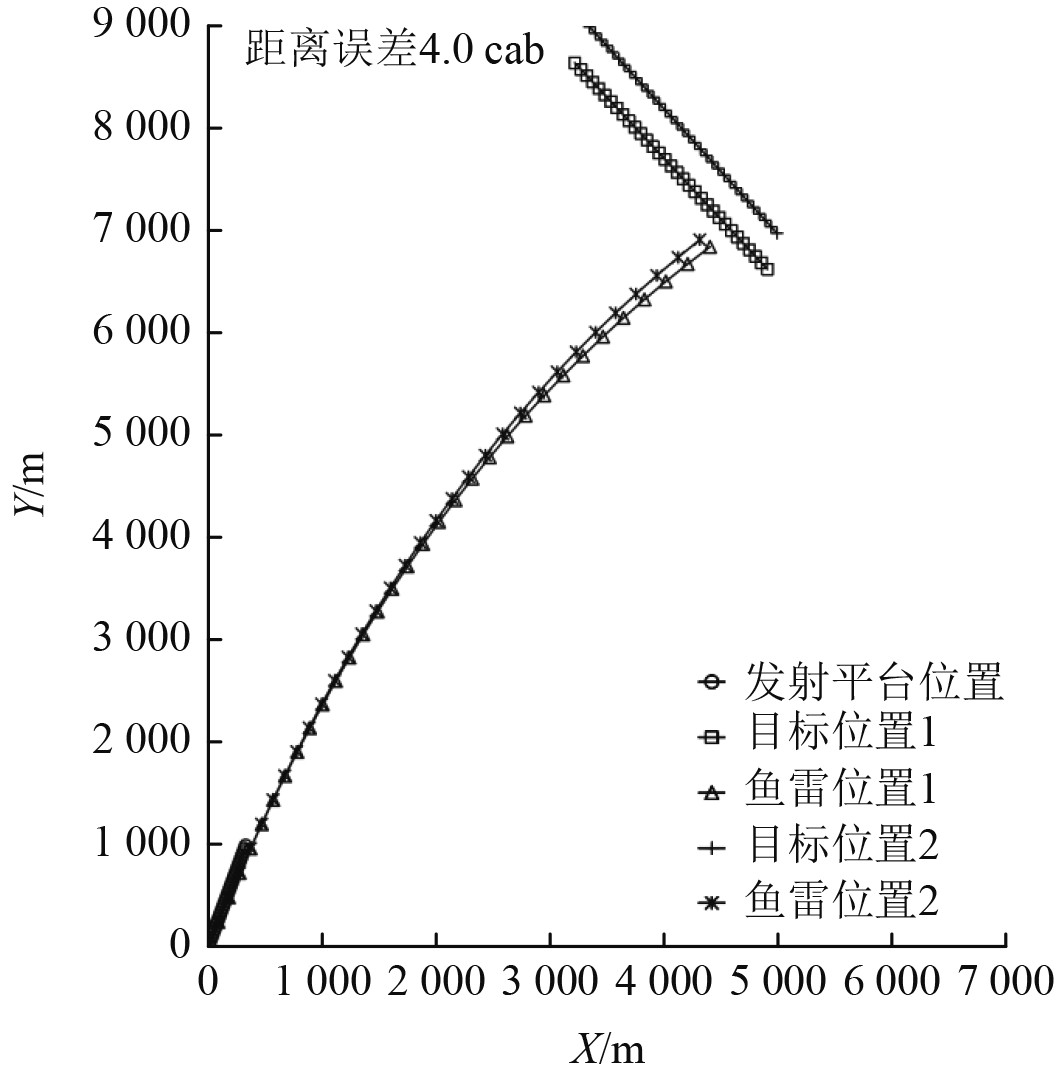
1)固定误差处理测试,针对目标航向、航速和距离3个推算方位输入要素,按照误差设置分别增加固定误差后推算方位并进行预估弹道计算,并与无误差输入要素推算方位预估弹道进行比较,仿真测试示意图分别如图4~图6所示(目标位置1和鱼雷位置1为无误差情况下仿真结果;目标位置2和鱼雷位置2为增加误差情况下仿真结果)。弹道一致情况下统计3个推算方位输入要素的取值范围,测试统计情况见表2。
|
|
表 2 预估弹道情况统计表1(单项目标运动要素固定误差推算方位) Tab.2 Estimated trajectory statistics table 1 (Single object motion element fixed error to calculate the orientation) |
|
图 4 方位导引预估弹道示意图1(固定目标航向误差推算方位) Fig. 4 Azimuth guidance projected trajectory diagram 1 (Fixed target course error to calculate target bearing) |
|
图 5 方位导引预估弹道示意图2(固定目标航速误差推算方位) Fig. 5 Azimuth guidance projected trajectory diagram 2 (Fixed target speed error to calculate target bearing) |
|
图 6 方位导引预估弹道示意图3(固定目标距离误差推算方位) Fig. 6 Azimuth guidance projected trajectory diagram 3 (Fixed target distance error to calculate target bearing) |
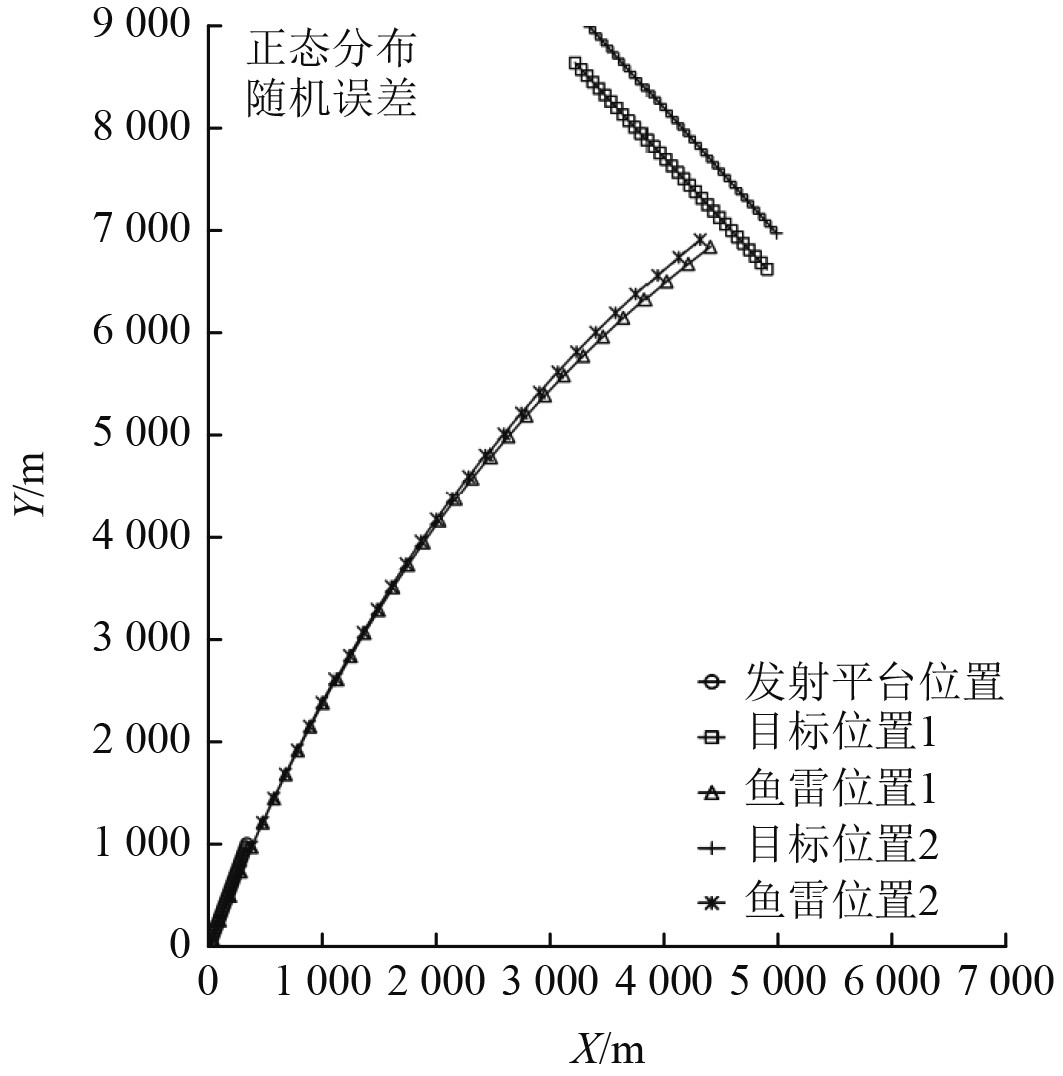
2)随机误差处理测试,针对目标航向、航速和距离3个推算方位输入要素按照误差设置,分别增加随机误差后推算方位并进行预估弹道计算,并与无误差输入要素推算方位预估弹道进行比较,仿真测试示意图如图7所示(目标位置1和鱼雷位置1为无误差情况下仿真结果;目标位置2和鱼雷位置2为增加误差情况下仿真结果)。统计弹道一致情况出现的次数,每个态势分三档误差各测试100次(每个态势共测试300次),测试情况见表3。
|
图 7 方位导引预估弹道示意图4(目标运动要素随机误差推算方位) Fig. 7 Azimuth guidance projected trajectory diagram 4 (Target orientation is calculated by random error of target motion elements) |
|
|
表 3 预估弹道情况统计表2(目标运动要素随机误差推算方位) Tab.3 Estimated trajectory statistics table 2 (Random error of target motion element to calculate orientation) |
经过仿真测试,在推算方位使用的目标运动要素输入误差较小情况下,使用本方法预估的线导鱼雷方位导引弹道与期望弹道(无目标要素输入误差仿真预估弹道)一致概率较高,可以满足在线导鱼雷发射前预知攻击弹道的需求。具体情况如下:
1)固定要素误差处理测试
①仅存在航向误差。中舷角态势比小舷角态势对航向误差容忍范围大。最大为[−20.0,8.0],单位:(°);小舷角态势情况下,低速目标对航向误差容忍范围较大,最大为[−5.0,4.0],单位:(°)。
②仅存在航速误差。中舷角态势比小舷角态势对航速误差容忍范围小,最小为[−0.5,0.5],单位:kn;小舷角态势情况下,高速中距离目标对航速误差容忍范围较大,最大为[−1.5,1.5],单位:kn;低速情况下,远距离小舷角目标对航速误差容忍范围较大,最大为[−1.5,1.5],单位:kn。
③仅存在距离误差。中舷角态势比小舷角态势对距离误差容忍范围小,最小为[−1.0,1.0],单位:cab;远距离情况下,对目标距离误差容忍范围较大;低速情况下,对目标距离误差容忍范围较大;低速远距离情况下,对目标距离误差容忍范围最大为[−14.0,18.0],单位:cab。
2)随机误差处理测试
①第一档随机误差:针对高速中距离目标弹道一致概率偏低,其它情况下弹道一致概率很高。
②第二档随机误差:弹道一致概率偏低,针对远距离中速和低速目标弹道一致概率略高。
③第三档随机误差:弹道一致概率太低,不可用。
5 结 语本文提出一种基于推算方位的线导鱼雷方位导引预估弹道计算方法,经过仿真测试验证,针对匀速直航目标在推算方位使用的目标运动要素输入误差较小情况下(目标航向误差均方差取值为2°;目标航速误差均方差取值为0.2 kn;目标距离误差均方差取值为真实初距的1%),使用本方法预估的线导鱼雷方位导引弹道与期望弹道一致概率较高,可以满足在线导鱼雷发射前预知攻击弹道的需求。系统通过图形方式直观的把预估弹道以及攻击态势展示出来,可以为指挥人员制定鱼攻方案以及选择鱼雷攻击时机提供决策参考。
| [1] |
孟庆玉, 张静远, 宋保维. 鱼雷作战效能分析[M]. 北京: 国防工业出版社, 2003.
|
| [2] |
司广宇. 潜艇指控系统理论与应用[M]. 北京: 电子工业出版社, 2018.
|
| [3] |
王顺杰, 丁文强, 朱伟良. 目标对抗条件下自导+线导鱼雷连射方法[J]. 火力与指挥控制, 2020, 45(5): 82-86. WANG S J, DING W Q, ZHU W L. Research on the method of homing and wire-guided torpedo continuous fire under target countermeasure condition[J]. Fire Control & Command Control, 2020, 45(5): 82-86. DOI:10.3969/j.issn.1002-0640.2020.05.014 |
| [4] |
王顺杰, 许兆鹏, 朱伟良, 等. 潜射线导鱼雷蛇形弹道设计及仿真研究[J]. 兵工学报, 2020, 41(1): 196-201. WANG S J, XU Z P, ZHU W L, et al. Snake-like trajectory design and simulation of submarine-launched wire-guided torpedo[J]. Acta Armamentarii, 2020, 41(1): 196-201. DOI:10.3969/j.issn.1000-1093.2020.01.023 |
| [5] |
李家腾, 邱长卿, 范学满. 一种基于目标指示的现在时刻推算方位导引法[J]. 软件, 2021, 42(10): 50−53. LI J T, QIU C Q, FAN X M. A current moment calculated azimuth guidance method based on target indication[J]. Software, 2021, 42(10): 50−53. |
| [6] |
张永峰, 李志伟. 声呐探测对潜艇鱼雷武器系统发现概率的影响[J]. 水下无人系统学报, 2017, 24(4): 359-364. ZHANG Y F, LI Z W. Influence of sonar detection on detection probability of submarine torpedo weapon system[J]. Journal of Unmanned Undersea Systems, 2017, 24(4): 359-364. |
| [7] |
王顺杰, 张玉玲, 罗向前. 目标运动要素误差对尾流自导鱼雷齐射影响[J]. 指挥控制与仿真, 2020, 42(3): 52-56. WANG S J, ZHANG Y L, LUO X Q. Influence of target motion parameter error on wake hominy torpedo salvo[J]. Command Control & Simulation, 2020, 42(3): 52-56. DOI:10.3969/j.issn.1673-3819.2020.03.010 |
| [8] |
李长文, 毛俊超, 初磊. 目标运动要素稳定性的图形表达探讨[J]. 鱼雷技术, 2016, 24(2): 137-140. LI C W, MAO J C, CHU L. Discussion on graphic expression of stability of target motion factors[J]. Torpedo Technology, 2016, 24(2): 137-140. |
| [9] |
李家腾, 刘剑, 范学满. 基于目指信息的潜射线导鱼雷环形搜索方案研究[J]. 舰船电子工程, 2021, 41(10): 24-29. LI J T, LIU J, FAN X M. Research on circular search scheme of submarine launched wire-guided torpedo based on target indication information[J]. Ship Electronic Engineering, 2021, 41(10): 24-29. DOI:10.3969/j.issn.1672-9730.2021.10.006 |
| [10] |
徐继华, 袁富宇. 基于折线简化的方位导引方法的可用性研究[J]. 指挥控制与仿真, 2017, 39(2): 31-35. XU J H, YUAN F Y. Research on usability of directional guidance method based on simplification of polyline[J]. Command Control & Simulation, 2017, 39(2): 31-35. DOI:10.3969/j.issn.1673-3819.2017.02.007 |
| [11] |
野学范, 朱伟良, 张靖康, 等. 一种改进的线导+尾流自导鱼雷导引方法[J]. 火力与指挥控制, 2015, 40(9): 172-175. YE X F, ZHU W L, ZHANG J K, et al. An improved guidance method for wire-guided + wake-homing torpedo[J]. Fire Control & Command Control, 2015, 40(9): 172-175. DOI:10.3969/j.issn.1002-0640.2015.09.042 |
 2025, Vol. 47
2025, Vol. 47
