船舶主机排烟温度是衡量船舶燃烧效率、热能利用状况以及设备健康状态的重要参数之一。作为船舶能源消耗和环境排放的关键指标,排烟温度不仅直接反映了燃烧能量的利用效率,还与船舶机械设备的运行状况息息相关。高排烟温度往往意味着燃烧效率降低或设备内部存在故障,从而可能导致燃料消耗的增加、排放污染物浓度的上升,以及设备寿命的缩短。因此,准确监测和控制船舶主机排烟温度对于优化燃烧过程、降低燃料消耗、减少温室气体和有害物质的排放具有至关重要的作用。
为了提高船舶主机排烟温度预测精度和适应性,学者们在该领域开展了一系列相关研究,并取得了显著成果。传统方法方面,研究人员采用了统计学方法和时间序列分析方法。张跃文等[1]通过建立时间序列AR模型实现了对船舶主机排烟温度变化趋势的预测。邹永久等[2]提出一种改进的灰色预测模型GM(1,1)和AR模型相结合的组合模型,取得了较高的预测准确性和稳定性。然而,由于船舶主机排烟温度受到多个因素的影响,传统方法在处理非线性、非平稳等复杂问题时存在一定的局限性。
近年来,随着深度学习技术的飞速发展,其在船舶主机排烟温度预测领域展现了显著的优势,特别是基于长短期记忆(Long Short Term Memory,LSTM)神经网络的方法得到了广泛的应用与认可。LSTM神经网络能够有效处理序列数据,具有记忆长时间依赖信息的能力,因此在预测复杂的时序数据方面具有独特的优势。Zhang等[3]采用LSTM神经网络,结合影响主机排烟温度的因素,建立了多输入多输出的模型,提高了船舶主机排烟温度的预测精度。Zhu等[4]基于深度学习算法建立预测模型,并验证了其在船舶主机排烟温度预测中的有效性和准确性。此外,还有其他一些值得关注的研究成果。如Li等[5 − 7]基于注意力机制和LSTM,提出一种船舶排烟温度预测新方法。为了进一步提高预测性能,混合模型和融合算法逐渐成为研究的重点。研究人员通过结合传统时间序列分析方法与机器学习模型,构建出具有更强泛化能力和适应性的预测模型。例如,将时间序列分解方法(如经验模态分解EMD)与LSTM结合,能够有效分离不同时间尺度的特征,并对复杂的船舶工况数据进行分层次分析,显著提升了预测效果[8]。
尽管这些新兴方法在船舶主机排烟温度预测方面取得了显著的成果,但仍存在一些挑战和问题,如复杂多样化数据特征提取、不同航行工况下模型的泛化能力和鲁棒性等。因此,本文提出一种基于时间序列分解和混合模型的排烟温度预测模型,在现有方法的基础上,结合多种时间序列分析技术,旨在突破现有方法的局限,提高船舶主机排烟温度的预测精度和可靠性,为船舶主机的运行管理提供更为精确的参考。
1 模型基本原理 1.1 CEEMDAN分解方法CEEMDAN(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise)是一种改进的经验模态分解(EMD)方法,用于信号处理和数据分析,是对传统的EMD方法进行改进和优化的一种技术,可提取出排烟温度信号中不同尺度的振动模式和成分,为船舶主机排烟温度预测分析和建模提供更准确和详细的数据[9 − 11]。CEEMDAN方法具体分解过程如下:
1)引入自适应噪声。添加自适应白噪声到原始信号
2)获取第1个本征模态分量和余量
| $ {\text{IM}}{{\text{F}}_{\text{1}}}\left( t \right) = \frac{1}{K}\sum\nolimits_{i = 1}^K {{\text{IMF}}_1^i\left( t \right)},$ | (1) |
| $ {{{r}}_{{1}}}(t) = {{y}}(t) - {\text{IM}}{{\text{F}}_{\text{1}}}\left( t \right)。$ | (2) |
式中:
3)余量信号加入噪声后继续进行EMD分解
| $ {\text{IM}}{{\text{F}}_j}\left( t \right) = \frac{1}{K}\sum\nolimits_{i = 1}^K {{E_1}\left[ {{r_{j - 1}}\left( t \right) + {\varepsilon _{j - 1}}{E_j}\left( {{\delta _{j - 1}}\left( t \right)} \right)} \right]},$ | (3) |
| $ {{{r}}_j}(t) = {{{r}}_{j - 1}}(t) - {\text{IM}}{{{F}}_j}\left( t \right)。$ | (4) |
式中:
4)迭代直至满足停止条件。重复进行分解过程,直到余量信号为单调信号为止。每次迭代中,使用新的噪声引入和分解方法,以改善分解结果。CEEMDAN方法最终将原始信号分解成多个IMF和1个剩余项
| $ {{y}}(t) = \sum\nolimits_{i = 1}^n {{\text{IM}}{{\text{F}}_i}\left( t \right)} {\text{ + res}}(t)。$ | (5) |
ARMA算法(Autoregressive Moving Average,自回归滑动平均)是一种经典且广泛应用的时间序列分析方法[12 − 13],常用于建立能够描述和预测时间序列数据的模型。该模型结合了自回归(AR)和滑动平均(MA)2种模型的优势,具有较强的灵活性和适应性。在AR部分,模型通过当前值与其前期值之间的自相关性来进行预测,即通过过去的数据推断未来的变化趋势;而在MA部分,模型则通过分析随机误差项的滞后移动平均效应,来纠正预测中的随机波动。通过这种结合,ARMA模型能够较好地捕捉时间序列数据中的自相关结构和短期的随机扰动,有效提高预测的精度和可靠性。
ARMA模型的数学表示为:
| $ \begin{aligned} y\left( t \right) = &c + {\phi _1}y(t - 1) + {\phi _2}y\left( {t - 2} \right) + ... + {\phi _p}y\left( {t - {{p}}} \right) + \\ &\varepsilon \left( t \right) + {\theta _1}\varepsilon \left( {t - 1} \right) + {\theta _2}\varepsilon (t - 2) + ... + {\theta _q}\varepsilon \left( {t - {{q}}} \right)。\\ \end{aligned} $ | (6) |
式中:
ARMA模型在时间序列分析中具有广泛的应用,可以用于预测时间序列数据的未来趋势和行为,识别数据中的周期性和趋势,以及进行异常检测和模型诊断等,尤其适用于平稳时间序列数据的分析与建模。
1.3 LSTM算法LSTM算法是一种循环神经网络的变体,用于处理序列数据的建模和预测。相比传统的循环神经网络,LSTM引入了记忆单元和门控机制,能够更好地捕捉长期依赖关系。记忆单元通过门控机制选择性地存储和遗忘信息,以便更好地处理序列中的长期依赖。这种机制使得LSTM在处理和预测序列数据时具有较强的记忆和学习能力,能够更好地处理时序信息[14 − 17]。LSTM结构图如图1所示。LSTM模型的性能在很大程度上取决于其结构参数的选择,尤其是层数和单元数。本文采用交叉验证法和网格搜索策略对LSTM的层数和单元数进行调优。

|
图 1 LSTM结构图 Fig. 1 Structure diagram of LSTM |
LSTM在许多领域具有广泛的应用,包括自然语言处理、语音识别、时间序列预测等,尤其在处理具有长期依赖关系的复杂序列数据方面表现出色。在船舶主机排烟温度预测中,LSTM可以学习和建模非平稳时间序列的动态特征,从而实现对未来排烟温度的准确预测。通过捕捉温度序列中的长期依赖关系和动态变化模式,LSTM可以提供更精确的预测结果,对船舶运行状态监测和维护提供有价值的信息。
1.4 ADF检验ADF(Augmented Dickey-Fuller)检验是一种常用的单位根检验方法,用于判断时间序列数据的平稳性。基于自回归模型(AR)的线性关系,通过拟合时间序列数据的回归模型并计算统计量,来评估序列中是否存在单位根(非平稳性)。根据统计量与临界值的比较,可以得出对时间序列数据平稳性的结论,以指导后续分析和建模工作[18]。平稳性是构建高精度预测模型的基础,若数据序列不平稳,则可能影响预测结果的准确性。ADF检验在船舶主机排烟温度预测等领域具有重要意义。通过ADF检验,可以有效检测数据的平稳性,进而为后续的建模工作提供依据,帮助研究人员选择合适的预测方法和模型,如采用差分或其他数据预处理技术,提升模型的稳定性和预测性能。
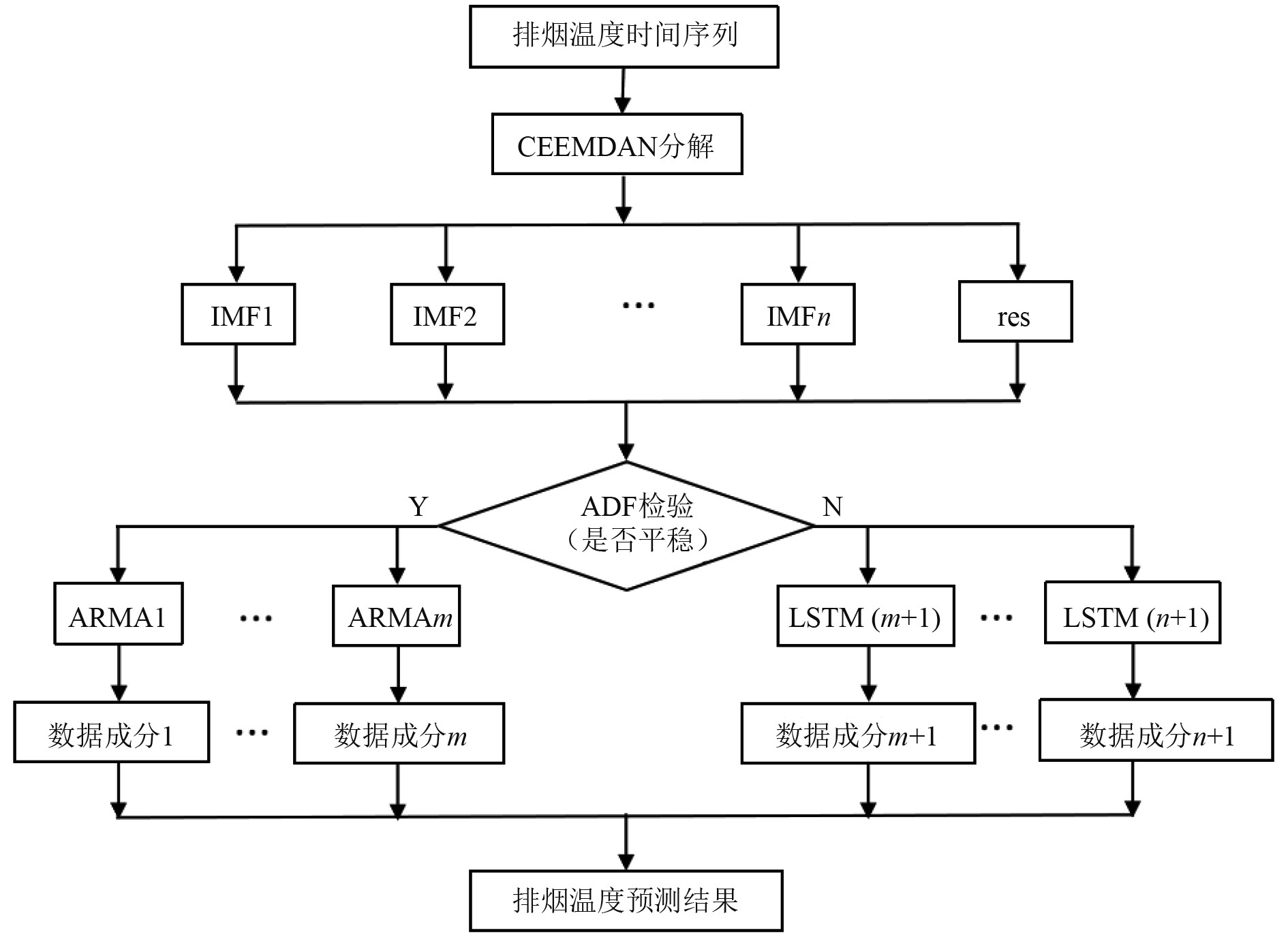
2 组合预测模型新的船舶主机排烟温度组合预测模型基于时间序列分解和混合预测模型建立,综合应用了CEEMDAN方法、ADF检验、ARMA和LSTM算法。具体步骤如下:
1)CEEMDAN分解。使用CEEMDAN方法对船舶主机排烟温度原始数据进行分解,将非线性非平稳时间序列分解为若干个本征模态函数(IMF)和1个趋势项。通过自适应地提取不同频率成分来描述数据,更好地捕捉数据的内在规律。
2)ADF检验。每个IMF和趋势项都有各自的局部特征时间尺度。低波动性序列包含更多的线性特征,而高波动性序列可被认为是非线性的序列。使用ADF检验,以5%作为判断数据稳定性的阈值,将线性分量和非线性分量分离。
3)ARMA模型预测。对于通过ADF检验被判定为线性的IMFs,使用ARMA模型进行预测。ARMA模型利用历史数据和滑动窗口方法建立模型,通过自回归和滑动平均的组合来捕捉时间序列数据的自相关性和移动平均特征。
4)LSTM模型预测。对于通过ADF检验被判定为非线性的IMFs和趋势项,采用LSTM神经网络进行预测。LSTM模型具有记忆和学习能力,能够有效地捕捉非线性的时序特征。
5 )预测结果叠加。将ARMA模型和LSTM模型的预测结果进行叠加,得到最终的船舶主机排烟温度预测结果。
该组合预测模型综合考虑了数据的平稳性与非平稳性特征,结合了线性和非线性预测方法的优势。在线性部分,模型能够有效捕捉数据中的趋势和周期性变化,而在非线性部分,模型则通过算法应对数据中的非线性关系。组合模型的优势在于能够将线性和非线性方法分别应用于适合的特征层次,从而在处理复杂数据时兼顾不同特性的影响。通过这种分而治之的策略,模型不仅提升了对不同特征数据的适应性,还有效降低了由单一模型引入的预测误差。这种多层次、多角度的建模方法,提升了模型应对复杂系统数据预测的能力。其流程图如图2所示。
|
图 2 组合预测算法流程图 Fig. 2 Flow chart of combined prediction algorithm |
本文采用的数据来自于某远洋实习船,主机型号为6S35 MC,连续采集670个该船主机1号缸排烟温度值,采样间隔10 min。具体数据如图3所示,该段数据包含了2次主机排烟温度显著波动过程,2次波动并非由测量设备不稳定或外部环境干扰引起,而是由于船舶主机工况调整导致,反映了主机运行状态的真实变化,具有较强的代表性。为确保数据的准确性和完整性,本文对数据进行了预处理,排除了测量设备异常导致的噪声数据,保留了具有实际意义的工况变化数据。

|
图 3 实测主机排烟温度序列 Fig. 3 Exhaust temperature sequence of main engine |
利用CEEMDAN方法对采集到的实船主机排烟温度数据进行分解,共得到9个IMF和1个趋势项,分解结果如图4所示。其中理想信号剔除了高频噪声,由IMF5-IMF9数据和趋势项叠加获得。

|
图 4 CEEMDAN分解结果 Fig. 4 Decomposition results of CEEMDAN |
对分解后的IMFs进行ADF检验,IMF1至IMF7数据的给定ADF统计量值小于5%临界值,p-value值在0.05的显著性水平以下,通过平稳性检验,判定为平稳序列。而IMF8、IMF9和趋势项数据的给定ADF统计量值超出5%临界值,p-value值在0.05的显著性水平以上,未能通过平稳性检验,属于非平稳信号。
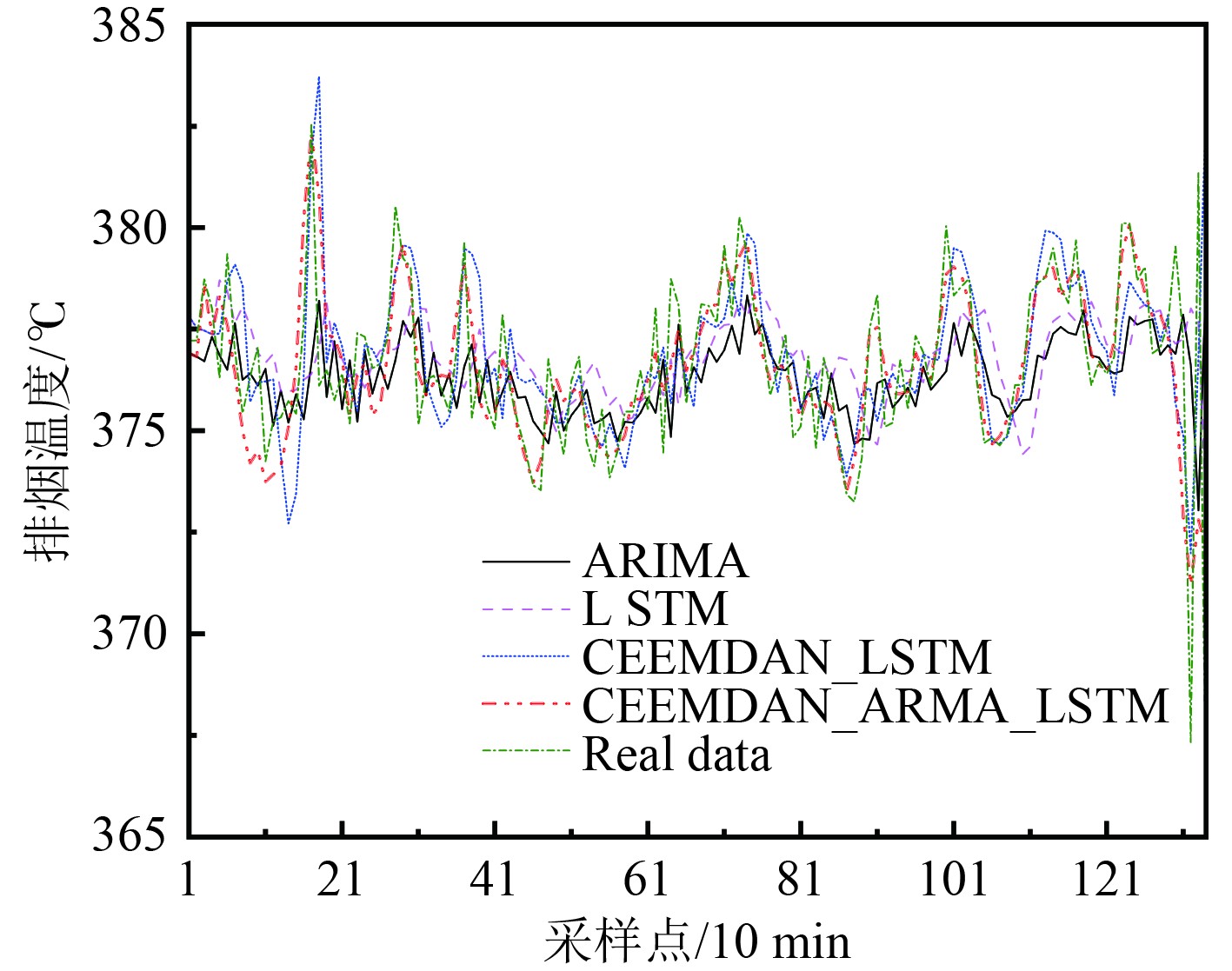
3.3 算法预测结果分析与评价将采集到的船舶主机排烟温度序列前80%数据(536个)作为训练数据,经过CEEMDAN分解和ADF检验后,分别训练ARMA模型和LSTM模型。利用训练好的模型进行预测,将结果叠加后得到后20%数据(134个)的预测值。同时分别利用差分自回归滑动平均模型(Autoregressive Integrated Moving Average,ARIMA)模型、LSTM模型和CEEMDAN-LSTM模型对时间序列数据进行预测,与基于时间序列分解和混合模型(CEEMDAN-ARMA-LSTM模型)的预测结果作对比。预测结果如图5所示。
|
图 5 各模型预测结果对比图 Fig. 5 Comparison of prediction results of each model |
对船舶主机排烟温度预测结果进行评价时,选取RMSE(均方根误差)和MAE(平均绝对误差)作为预测精度评价指标。RMSE指标能够较好地反映预测模型的整体拟合情况,并能够对异常值产生较大的惩罚。MAE指标更加关注预测误差的绝对大小,能够提供对预测误差的直观理解。通过综合考虑这2个评价指标,可以更全面地评估和比较不同预测模型的性能[19 − 20]。
| $ {\text{RMSE}} = \sqrt {\frac{1}{n}{{\sum\nolimits_{i = 1}^n {\left( {{y_{i}^\prime} - y_i} \right)} }^2}}, $ | (7) |
| $ {\text{MAE}} = \frac{1}{n}\sum\nolimits_{i = 1}^n {\left| {{y_{i}^\prime} - y_i} \right|} $ | (8) |
式中:
表1为各预测模型预测结果误差统计。通过对比可知,CEEMDAN-ARMA-LSTM混合模型预测精度与ARIMA模型、LSTM模型、CEEMDAN-LSTM模型相比有大幅提升,均方根误差(RMSE)降低约30%,平均绝对误差(MAE)降低约35%。
|
|
表 1 各模型预测误差 Tab.1 Prediction errors of each model |
由于船舶主机排烟温度预测属于实时性要求较高的控制系统,耗时对模型的实际应用至关重要。在实验中记录了不同模型的训练时间和预测时间,并将其作为性能评价的重要指标之一。在保证预测精度的前提下,本文选择了较为简化的LSTM结构和优化的ARMA阶数,以降低模型的计算复杂度和运行时间。实验证明,组合模型在预测精度显著提升的同时,其耗时控制在可接受范围内,相比于单一LSTM模型,组合模型降低了约15%的运行时间。
4 结 语本文利用CEEMDAN分解方法降低了船舶主机排烟温度原始数据的波动性和复杂性,通过对原始数据进行分解,提取出多个不同频率的信号分量,从而能够更加精准地分析数据的时间序列特性。为了进一步提高预测的精度,通过ADF检验将各分解信号分为平稳信号和非平稳信号2类。然后,充分发挥ARMA模型在处理平稳时间序列方面的优势以及LSTM模型在处理非线性、非平稳数据中的强大能力,对不同信号分量进行预测,提高了组合模型的预测精度。
通过该组合预测模型的构建,能够更准确地获得船舶主机排烟温度的变化趋势,显著提高了预测精度。该方法不仅为船舶主机运行状态的监测与维护管理提供了科学依据,还为船舶系统性能优化和安全管理提供了有效的评估手段,具有重要的实用价值和广泛的应用前景。
| [1] |
ZHANG Y W, ZOU Y J, LIU Z F, et al. Prediction of ship main engine exhaust gas temperature using AR model[J]. Appl. Mech. Mater. 2015, 696: 244−248.
|
| [2] |
邹永久. 基于RKGM-AR模型的船舶柴油机热力参数趋势预测研究[D]. 大连:大连海事大学, 2014.
|
| [3] |
ZHANG Y, LIU P, HE X, et al. "A prediction method for exhaust gas temperature of marine diesel engine based on LSTM[C]//, " 2020 IEEE 2nd International Conference on Civil Aviation Safety and Information Technology, (CASIT) 2020, 49−52.
|
| [4] |
ZHU L, LI C, WU Q. Ship main engine exhaust temperature prediction based on deep learning algorithm[C]// Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), 632-636.
|
| [5] |
LI J, LIU Y, GAO Z. Ship exhaust temperature prediction based on attention mechanism and LSTM[C]// Proceedings of the 2020 International Conference on Artificial Intelligence and Big Data (ICAIBD), 78−83.
|
| [6] |
焦品博, 王海燕, 孙超, 等. 基于长短期记忆网络的船舶主柴油机性能预测[J]. 内燃机学报, 2021, 39(3): 250-256. |
| [7] |
刘满强, 吴杰. 基于ICEEMDAN与POA-SVM的感应电机故障诊断[J]. 现代制造工程, 2024(5): 127-137. |
| [8] |
LI J. "Hybrid model combining EMD and LSTM for marine exhaust temperature prediction " [J]. Ocean Engineering, 2023.
|
| [9] |
李洪涛. 基于MI-CEEMDAN-RF-LGBM的风功率预测分析[J]. 电力与能源, 2024, 45(2): 239-242. |
| [10] |
史永胜, 施梦琢, 丁恩松, 等. 基于CEEMDAN–LSTM组合的锂离子电池寿命预测方法[J]. 工程科学学报, 2021, 43(7): 985-994. |
| [11] |
常智慧, 徐耀松. 基于CEEMDAN与INGO优化BiLSTM的短期电力负荷预测 [J/OL]. 控制工程, 1-92024-10-07].
|
| [12] |
王瑞, 高强, 逯静. 基于CEEMDAN-LSSVM-ARIMA模型的短期光伏功率预测[J]. 传感器与微系统, 2022, 41(5): 118-122. |
| [13] |
朱利明, 卓静超, 邢世玲. 基于CEEMDAN-NAR-ARIMA组合模型的桥梁结构健康监测应变预测[J]. 科学技术与工程, 2020, 20(4): 1639-1644. DOI:10.3969/j.issn.1671-1815.2020.04.052 |
| [14] |
张雪, 肖秦琨. CEEMDAN组合DISPSO-LSTM的短期电力负荷预测[J]. 西安工业大学学报, 2021, 41(4): 461-469. |
| [15] |
李杰, 孟凡熙, 牛明博, 等. CEEMDAN-WPE-CLSA超短期风电功率预测方法研究[J]. 大连交通大学学报, 2024, 45(2): 101-108. |
| [16] |
张淑娴, 江文韬, 陈玉花, 等. 基于二次模态分解的LSTM短期电力负荷预测[J]. 科学技术与工程, 2024, 24(7): 2759-2766. |
| [17] |
文博, 陈芳芳, 胡道波, 等. 基于完全集成经验模态分解和模糊熵分频的短期风电功率预测[J]. 科学技术与工程, 2023, 23(25): 10835-10845. |
| [18] |
冯建强, 宋昆仑. 基于CEEMDAN-LSTM的桥梁变形时间序列预测研究[J]. 地理空间信息, 2023, 21(7): 40-43. |
| [19] |
简定辉, 李萍, 黄宇航, 等. 基于CEEMDAN-LSTM-CNN网络的短期电力负荷预测[J]. 电工电气, 2023(6): 1-6. |
| [20] |
向玲, 刘佳宁, 苏浩, 等. 基于CEEMDAN二次分解和LSTM的风速多步预测研究[J]. 太阳能学报, 2022, 43(8): 334-339. |
 2025, Vol. 47
2025, Vol. 47
