0 引　言

近几年，智能船舶已成为全球航运领域研究的热点^[1]。船舶自主避碰是智能船舶的关键问题，主要涉及感知与识别技术、决策与规划技术、执行与控制系统等，而船舶避碰决策算法是决策与规划技术中的核心^[2]。

国内外学者对此进行了深入研究。倪生科等^[3]提出一种基于多种群的遗传算法，不仅避免了遗传算法调参难的问题，还使种群向着符合避碰规则的方向进化。曾勇等^[4]将粒子群算法和遗传算法相融合，将其运用到多船避碰当中，融合后的算法具有提高收敛精度和加速全局寻优的特点。周双林等^[5]把深度学习运用到船舶避碰当中，通过设计船舶避碰奖励函数，保证避碰决策在符合避碰规则下进行。马杰等^[6]基于人工势场法和速度障碍法研究了内河水域的船舶避碰问题，其仿真实验表明在规则约束下该方法可以在内河水域实现动静态障碍物的避碰。苗鹏等^[7]采用按需分层和动态分布适应度策略对多目标遗传算法进行改进，加快了收敛速度。Ning等^[8]建立一种改进的模糊动态碰撞风险度模型，通过权重法和约束法对解空间进行限制，实现船舶的自主避碰。翁建军等^[9]利用模拟退火算法对海上风电水域的船舶避碰进行研究，通过升温退火法避免算法陷入局部最优情况。宁君等^[10]提出一种混合粒子群算法的船舶避碰决策方法，通过引入高斯位置变异来克服算法容易陷入局部最优的局限，利用自适应参数策略提高粒子的局部搜索能力。Wu等^[11]针对拥堵海域的船舶避碰提出了一种改进的遗传算法，确保本船的避碰操作符合避碰规则的规定。

上述文献在船舶避碰决策方面取得了一些成果，但相关研究与避碰规则的结合不够，对多船避碰的解决也缺乏验证。针对上述问题，本文提出自适应遗传模拟退火（Genetic Simulated Annealing Algorithm，GSA）算法。首先利用遗传算法全局搜索能力强的特点对初始解空间进行搜索，再用模拟退火算法对搜索出的解进行退火操作，不仅避免算法陷入局部最优解陷阱，而且加快了搜索解的速度。同时对遗传算法的交叉和变异操作，引入自适应策略，进一步避免算法过早收敛。在目标函数的构建上，运用多目标函数优化理论，综合考虑海上避碰、航行经济型和安全性等要素。

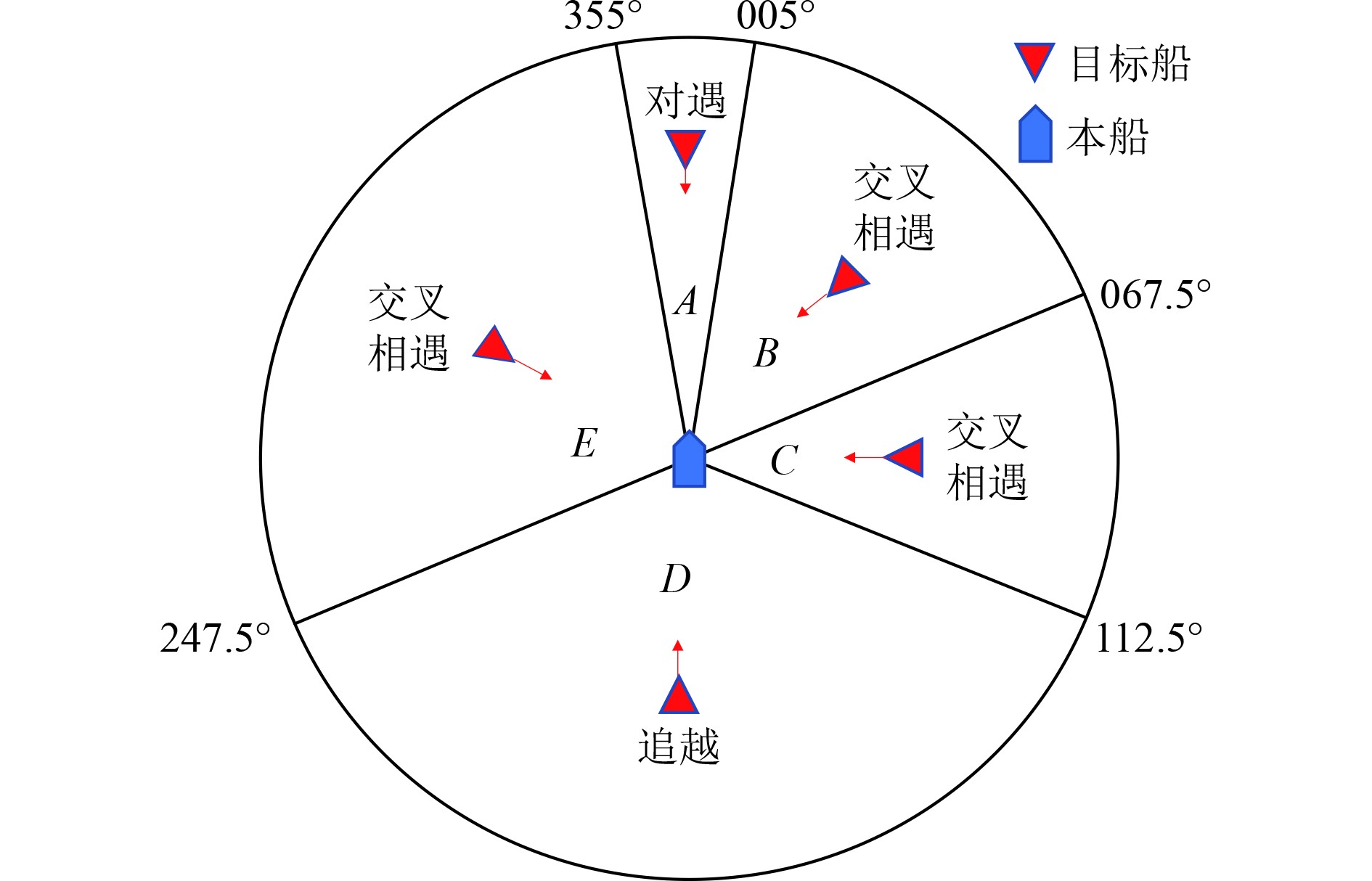
1 船舶避碰理论 1.1 船舶会遇态势识别模型

根据《国际海上避碰规则》对两船会遇的态势进行划分，把两船会遇局面划分为对遇、交叉和追越3种情况，其中交叉局面又细分为左舷交叉、右舷小角度交叉和右舷大角度交叉，并且规则对上述情况都进行了定性描述。船舶会遇态势识别模型如图1所示。

根据避碰规则中第二章第13～15条的说明，把两船会遇情况分为了上述5种情况。当目标船位于A区时，此时与本船构成对遇局面，按照规则要求，本船和目标船都应右转避让；当目标船位于B区时，目标船作为直航船，本船应右转避让且尽量从目标船船尾后方驶过；当目标船位于C区时，本船作为让路船，应左转旋回避让；当目标船位于D区时，此时构成追越局面，本船保速保向行驶，目标船作为让路船应右转避让；当目标船位于E区时，本船直航，目标船右转进行避让。

1.2 船舶相对运动参数

在船舶避碰决策中，必须依赖本船与他船之间的相对运动来判断两船之间的危险程度。因此，通过船载设备探知本船与障碍船的运动参数，并计算出两船之间的相对运动参数显得至关重要。

本文建立如图2所示的坐标系，假设本船的初始位置、航向和航速分别为$ (\mathit{x_{\mathrm{0}},y_{\mathrm{0}}}) $、$ {c}_{0} $和$ {v}_{0} $，障碍船的初始位置、航向和航速分别为$ \left(\mathit{x_t,y_t}\right) $、$ {c}_{t} $和$ {v}_{t} $。然后通过以下公式计算两船之间的相对运动参数。

1）本船在x轴与y轴方向的速度分量表达式为：

$ \left\{ \begin{gathered} {v_{x0}} = {v_0}\sin ({c_0})，\\ {v_{y0}} = {v_0}\cos ({c_0})。\\ \end{gathered} \right. $

(1)

2）目标船在x轴与y轴方向的速度分量表达式为：

$ \left\{ \begin{gathered} {v_{x{\text{t}}}} = {v_t}\sin ({c_t})，\\ {v_{yt}} = {v_t}\cos ({c_t})。\\ \end{gathered} \right. $

(2)

3）目标船相对于本船的速度$ {v}_{R} $的表达式为：

$ \left\{ \begin{gathered} {v_{xR}} = {v_{xt}} - {v_{x0}}，\\ {v_{yR}} = {v_{yt}} - {v_{y0}}。\\ \end{gathered} \right. $

(3)

$ {v_R} = \sqrt {{v_{xR}}^2 + {v_{yR}}^2}。$

(4)

4）本船与目标船之间的距离$ {R}_{D} $的表达式为：

$ {{\mathit{R}}_{\mathit{D}}} = \sqrt {{{({x_0} - {x_t})}^2} + {{({y_0} - {y_t})}^2}}。$

(5)

5）目标船相对本船的相对速度航向$ {\phi }_{R} $的表达式为：

$ {{\phi }_{R}=\left\{\begin{aligned}&\displaystyle\frac{{\text{π}} }{2},{v}_{xR}\geqslant 0,{v}_{yR}=0\\ &\displaystyle\frac{3{\text{π}} }{2},{v}_{xR} < 0,{v}_{yR}=0\\ &\displaystyle\rm ta{n}^{-1}\left(\displaystyle\frac{\mathit{{v}_{xR}}}{\mathit{{v}_{yR}}}\right)+\alpha,\mathit{{v}_{yR}}\ne 0\end{aligned}\text{ ，}\right.\\ \;\; \alpha =\left\{\begin{aligned}&0,{v}_{xR}\geqslant 0,{v}_{yR}\geqslant 0,\\ &{\text{π}}, {v}_{yR} < 0,\\ &2{\text{π}}, {v}_{xR} < 0,{v}_{yR}\geqslant 0。\end{aligned}\right. }$

(6)

6）目标船相对于本船的真方位$ {\alpha }_{t} $的表达式为：

$ \begin{array}{l}\alpha_t=\left\{\begin{aligned} & \displaystyle\frac{\text{π}}{2},x_t-x_0\geqslant0,y_t-y_0=0 \\ & \displaystyle\frac{3\text{π}}{2},x_t-x_0 < 0,y_t-y_0=0 \\ & \rm{t}an^{-1}\displaystyle\frac{\mathit{x_t}-\mathit{x_{\mathrm{0}}}}{\mathit{y_t}-\mathit{y\mathrm{_0}}}+\beta,\mathit{y_t}-\mathit{y_{\mathrm{0}}}\ne0\end{aligned}\text{，}\right. \\ \\ \beta=\left\{\begin{array}{l}0,x_t-x_0\geqslant0,y_t-y_0\geqslant0, \\ \text{π},y_t-y_0 < 0, \\ 2\text{π},\text{ }x_t-x_0 < 0,y_t-y_0\geqslant0。\end{array}\right.\end{array} $

(7)

7）目标船相对本船的相对方位$ {\theta }_{t} $的表达式为：

$ {\theta _t} = {\alpha _T} - {c_0} 。$

(8)

通过本船的AIS设备能够获取本船和目标船的运动参数，可以求出本船与目标船的最近会遇距离D_cpa和最近会遇时间T_cpa。

1.3 船舶碰撞危险度模型

引入船舶碰撞危险度（Collision Risk Index，CRI）作为评估船舶碰撞风险的指标。CRI的取值受到多种因素的影响，本文主要考虑了最近会遇距离D_cpa、最近会遇时间T_cpa，船速比（K）、相对距离（D），以及相对方位（B）对CRI的影响，构建出碰撞危险度CRI的表达函数，其表达式为：

$ {\begin{array}{c}CRI = {\omega }_{1}{U}_{Dcpa} + {\omega }_{2}{U}_{Tcpa} + {\omega }_{3}{U}_{K} + {\omega }_{4}{U}_{D} + {\omega }_{5}{U}_{B}。\end{array} }$

(9)

式中：$ {U}_{Dcpa} $、$ {U}_{Tcpa} $、$ {U}_{K} $、$ {U}_{D} $和$ {U}_{B} $分别为最近会遇距离、最近会遇时间T_cpa、船速比（K）、相对距离（D），以及相对方位（B）的风险隶属函数。

上述5个因素对船舶碰撞危险度的影响按照$ {U}_{Dcpa} > {U}_{Tcpa} > {U}_{K} > {U}_{D} > {U}_{B} $顺序递减，因此5个因素权重$ \omega $值应按照这个顺序进行取值，且$ {\omega }_{1}+{\omega }_{2}+{\omega }_{3}+{\omega }_{4}+ {\omega }_{5}=1 $。

2 自适应遗传模拟退火算法

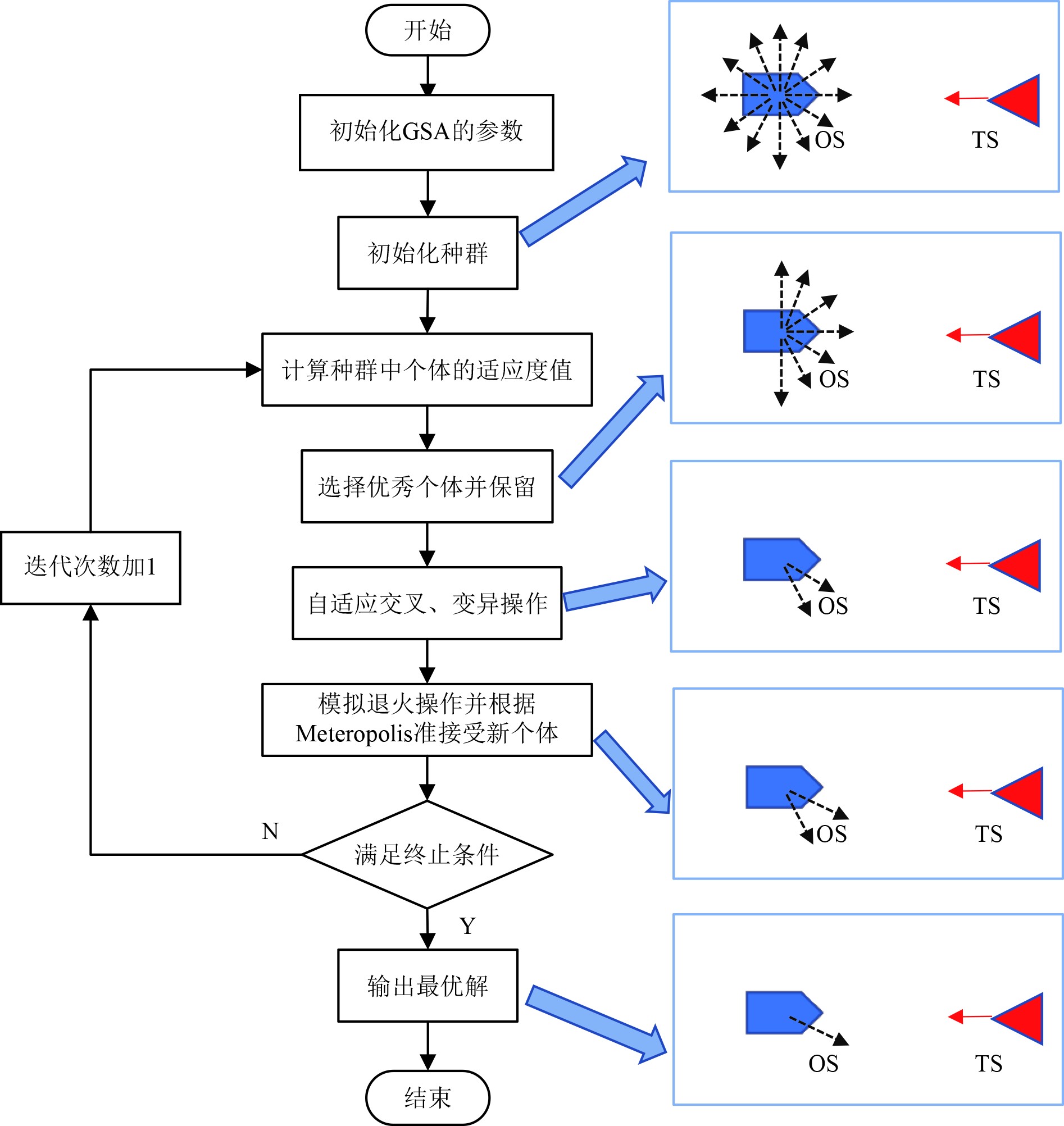
遗传算法具有较强的全局搜索能力，却也容易陷入局部最优解的情况。而模拟退火算法采用接受劣解的策略具有摆脱局部最优解的能力，但搜索范围相对较小。因此，本文将自适应遗传算法和模拟退火算法结合起来，构成自适应遗传模拟退火算法。通过自适应遗传算法得到新的种群后，将新种群适应度前20%的个体拿出，对这些个体的部分基因加入扰动，然后计算这些个体的适应度值，并采用Metropolis准则来判断新个体是否采用。改进后的GSA算法将2种算法的优点结合起来，从而在更短的时间内获得更优的解，其算法流程图如图3所示。

2.1 船舶避碰目标函数构建

船舶避碰航线规划需要考虑各种影响因素，建立各影响因素的评价函数。基于自适应遗传模拟退火算法，本文构建综合适应度函数来衡量避碰路径规划的效果。避碰路径规划优化中影响因素的目标如下:

1）船舶安全目标函数构建

在避碰路径规划过程中，要尽可能地保证本船与避碰船舶间碰撞危险度值尽可能小，保证本船能够安全完成避碰操作，构建的船舶安全目标函数如下：

$ \begin{array}{c}{f}_{1}\left(x\right)={\rm min}CRI。\end{array} $

(10)

式中：$ {f}_{1}\left(x\right) $为船舶安全目标函数，此函数值的大小直接反应了规划避碰路径的安全性，函数值越小，说明此时的避碰路径最安全。

2）航行经济目标函数构建

在避碰路径规划中，除了要考虑船舶安全的因素外，船舶航行的经济性也不可忽视。船舶在进行避碰操作时，如忽略经济效益，易导致避碰角度过大，且在避碰结束后的复航也更加困难。因此，本文在保证船舶安全的基础上，构建的船舶经济目标函数如下：

$ {{f_2}\left( x \right) = {\rm{min}}\sum\limits_{i = 1}^n {\sqrt {{{\left( {{x_{i + 1}} - {x_i}} \right)}^2} + {{\left( {{y_{i + 1}} - {y_i}} \right)}^2}} } - {f_d}}。$

(11)

式中：$ {f}_{2}\left(x\right) $为船舶经济目标函数，公式右边的求和项为本船航行的起点，避碰转向点，复航点和终点的各段距离之和；$ {f}_{d} $为本船从起点不进行避碰径直驶向终点的距离，两者之差即为本船避碰所消耗的距离函数。

根据《国际海上避碰规则》中“早，大，宽”的避让原则，一旦发现本船作为让路船，本船应尽早地采取大幅度的避让行动。根据要求，本文设置当$ CRI > 0.5 $ 时，即为本船的避让时机，且避让的角度限制在15°～60°。根据上述描述，本文的决策目标函数设置为：

$ \begin{array}{c}F\left(x\right)={\alpha }_{1}{f}_{1}\left(x\right)+{\alpha }_{2}{f}_{2}\left(x\right)。\end{array} $

(12)

式中：$ {\alpha }_{1}、{\alpha }_{2} $ 为比例系数，用于调节安全目标函数和经济目标函数的比例系数。对于个体的每条路径，$ F\left(x\right) $值越小，说明避碰效果越满意。

在遗传模拟退火算法当中，用适应度函数来评价个体的好坏，适应度越高，说明个体越优秀，被保留下来的机会也更大。因此，本文设计的适应度函数为目标函数的倒数。

2.2 自适应机制设计

遗传算法是一种受生物进化和遗传机理启发而来的优化算法，交叉和变异的概率对于遗传算法有着重要的影响。本文采取了自适应的交叉和变异方法，该方法对于适应度高的个体，会通过减小交叉概率和变异概率来保护优良基因不被破坏；对于适应度低的个体，则增大交叉概率及变异概率以便快速产生适应度高的个体。交叉概率的计算公式为：

${ P_c=\left\{\begin{aligned} & \displaystyle\frac{P{_{c\mathrm{max}}}-P{_{c\mathrm{min}}}}{1+\mathrm{e}\mathrm{x}\mathrm{p}\left(\lambda\displaystyle\frac{f^\prime-f\mathrm{_{avg}}}{f\mathrm{_{max}}-f\mathrm{_{avg}}}\right)}+P{_{c\mathrm{min}}}，f^\prime \geqslant f_{\mathrm {avg}}，\\ & P{_{c\mathrm{max}}}-\displaystyle\frac{P\mathrm{_{cmin}}}{1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\lambda\left(f\mathrm{_{max}}-f\mathrm{_{avg}}\right)\right]}，f^\prime < f_{\mathrm {avg}}。\end{aligned}\right.} $

(13)

式中：$ P_{c\mathrm{min}} $和$ \mathrm{P}_{\mathrm{\mathit{c}}\mathrm{m}\mathrm{a}\mathrm{x}} $分别为设计的交叉概率的下限和上限；$ f_{\mathrm{avg}} $为交叉时2个父代个体适应度较大的值，f_{avg}为当代种群的平均适应度值，$ f_{\mathrm{max}} $为当代种群的最大适应度值，$ \lambda $为1个常数。

变异概率的计算公式为：

$ P_m=\left\{\begin{aligned} & \displaystyle\frac{P_{m\mathrm{m}\mathrm{a}\mathrm{x}}\left(f_{\mathrm{m}\mathrm{a}\mathrm{x}}-f\right)}{f_{\mathrm{m}\mathrm{a}\mathrm{x}}-f_{\mathrm{a}\mathrm{n}\mathrm{g}}}+P_{m\mathrm{m}\mathrm{i}\mathrm{n}}, \; f\geqslant f_{\mathrm{a}\mathrm{n}\mathrm{g}}, \\ & P_{m\mathrm{m}\mathrm{a}\mathrm{x}}, \; f < f_{\mathrm{a}\mathrm{n}\mathrm{g}}。\end{aligned}\right. $

(14)

式中：$ P_{m\mathrm{min}} $和$ P_{m\mathrm{max}} $分别为预设的变异概率最小值和最大值；$ f $为变异个体的适应度值；$ f_{\mathrm{ang}} $为当代种群的平均适应度值；$ f\mathrm{_{max}} $为当代种群的最大适应度值。

3 仿真实验

本文研究的是在开阔水域的船舶避碰问题，且海上环境良好，不考虑风、浪、流对船舶操纵的影响。根据《国际海上避碰规则》的描述，当本船作为让路船时，如果仅仅通过转向操作就可以进行避碰，可以不改变本船的航速。因此，本文设定本船作为让路船，只通过改变航向进行避碰，而目标船则作为直航船，均保持原有的航速和航向航行。

算法的相关参数如下：初始种群设为200个，最大迭代次数100代，风险隶属函数影响比例$ {\omega }_{1}、{\omega }_{2}、{\omega }_{3}、{\omega }_{4}、{\omega }_{5} $的值分别为0.4、0.3、0.1、0.1和0.1。模拟退火过程中设定初始温度 为100，降温速率$ \mu $为0.9。

本文涉及的仿真实验均在Matlab仿真平台上进行，为验证本算法在多船会遇态势下的有效性，设计了三船和四船的会遇实验。

3.1 三船会遇实验仿真

三船会遇实验中，本船与2艘目标船分别形成对遇和右舷小角度交叉情况，本船和目标船的相关参数如表1所示。

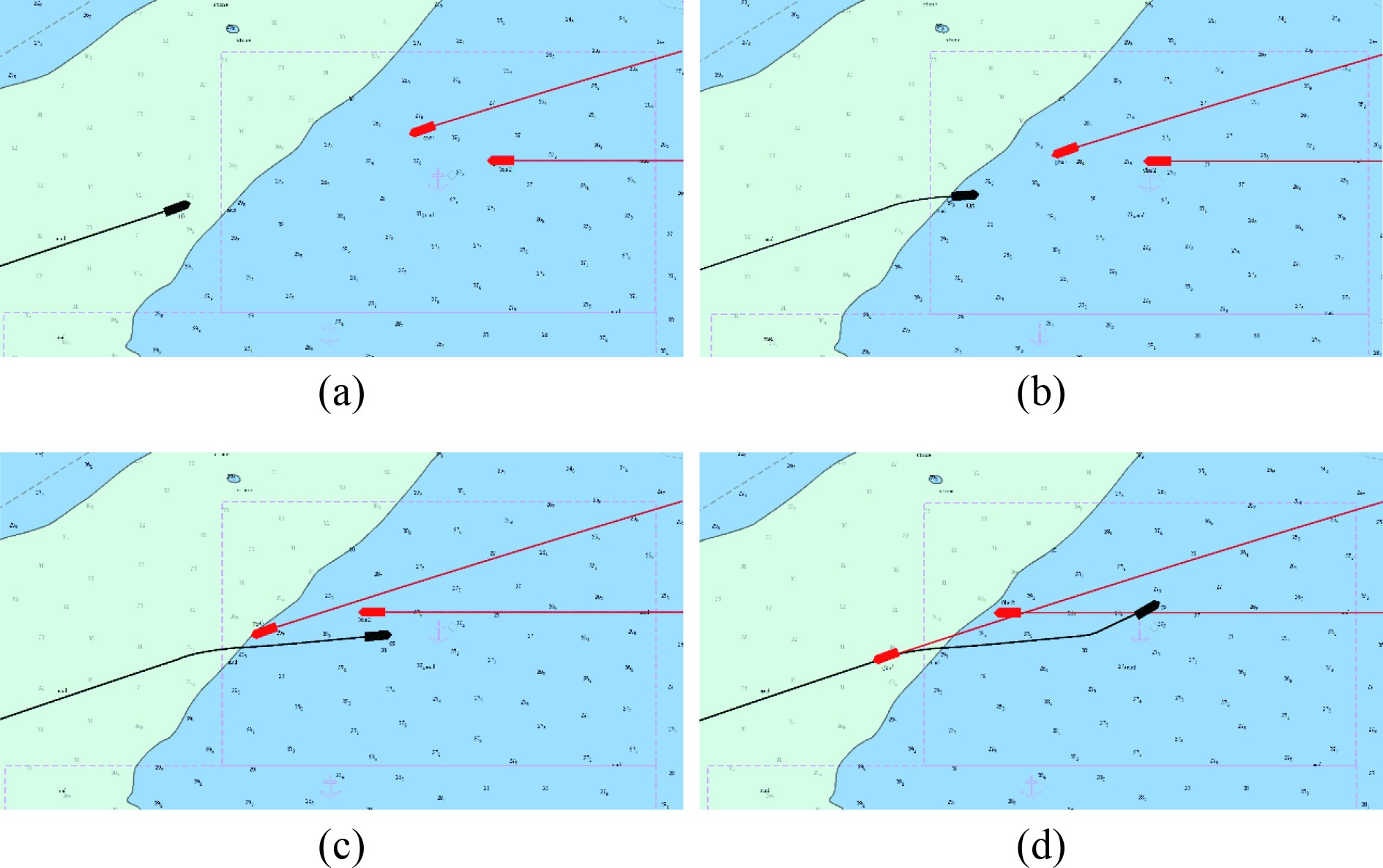
本文在仿真过程的4个时间点截取了本船的最优避碰路径，仿真结果如图4所示。

图4中当本船和其他两船会遇时，本船作为让行船，先避开CRI值较大的目标船1，避开目标船1准备复航时发现复航角度会导致本船与目标船2发生碰撞，因此重新计算本船的转向角度和复航时间，保证本船可以安全的避开2艘目标船。图5为本船和2艘船在整个过程中的距离变化情况，本船和2艘目标船间的最近会遇距离均大于1.5 n mile，符合海上避碰的要求。

本文还与标准遗传算法进行了对比，通过对10次仿真结果求取平均值得到了自适应遗传模拟退火算法和标准遗传算法的适应度函数变化情况，如图6所示。可以看到，本算法对比遗传算法，其寻优能力更强，算法的收敛速度也更快。

3.2 四船会遇实验仿真

四船会遇实验中，本船和3艘目标船分别构成对遇、右舷小角度交叉和右舷大角度会遇情况，4艘船的运动参数如表2所示。

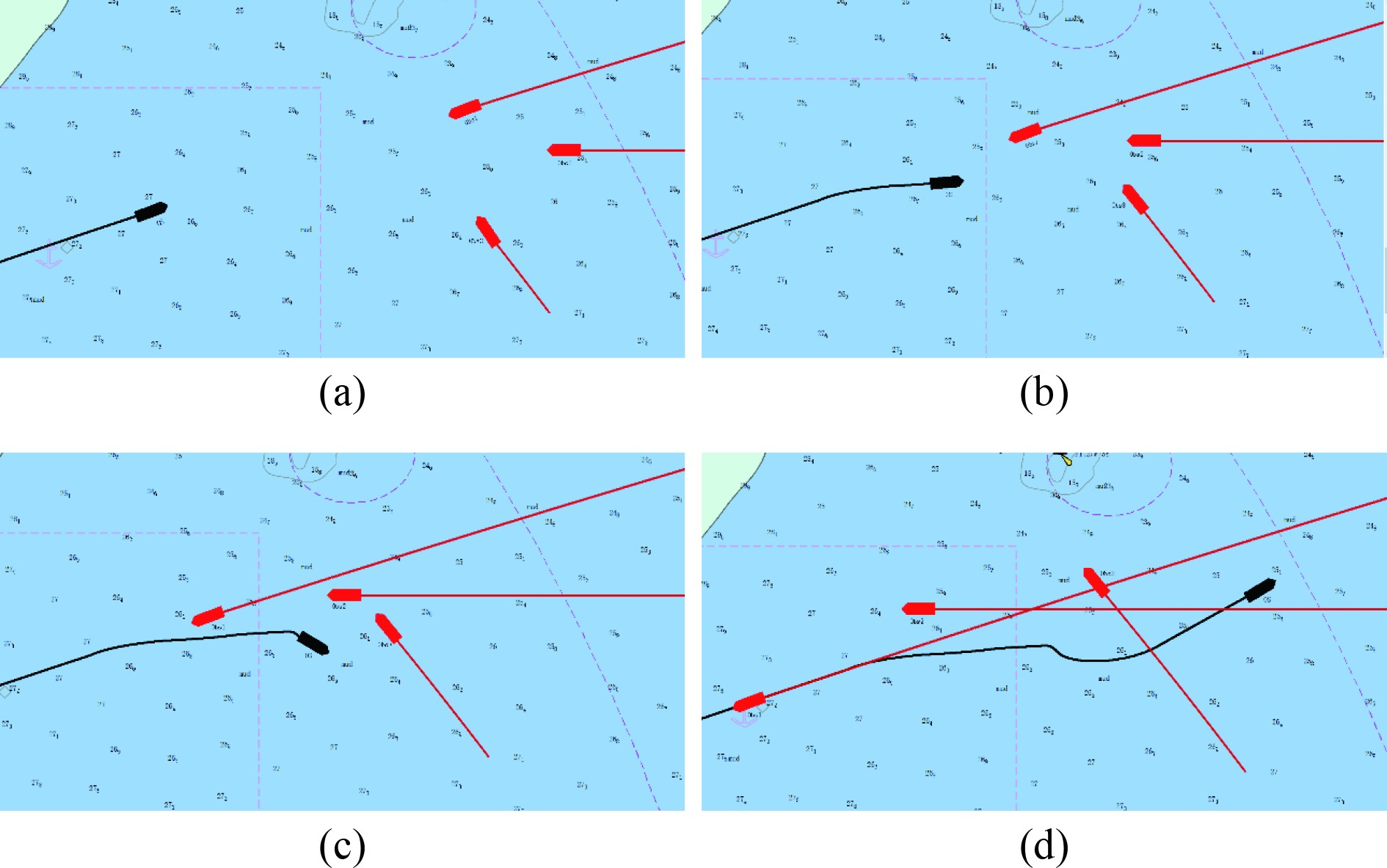
本文在仿真过程的4个时间点截取了本船的最优避碰路径，仿真结果如图7所示。

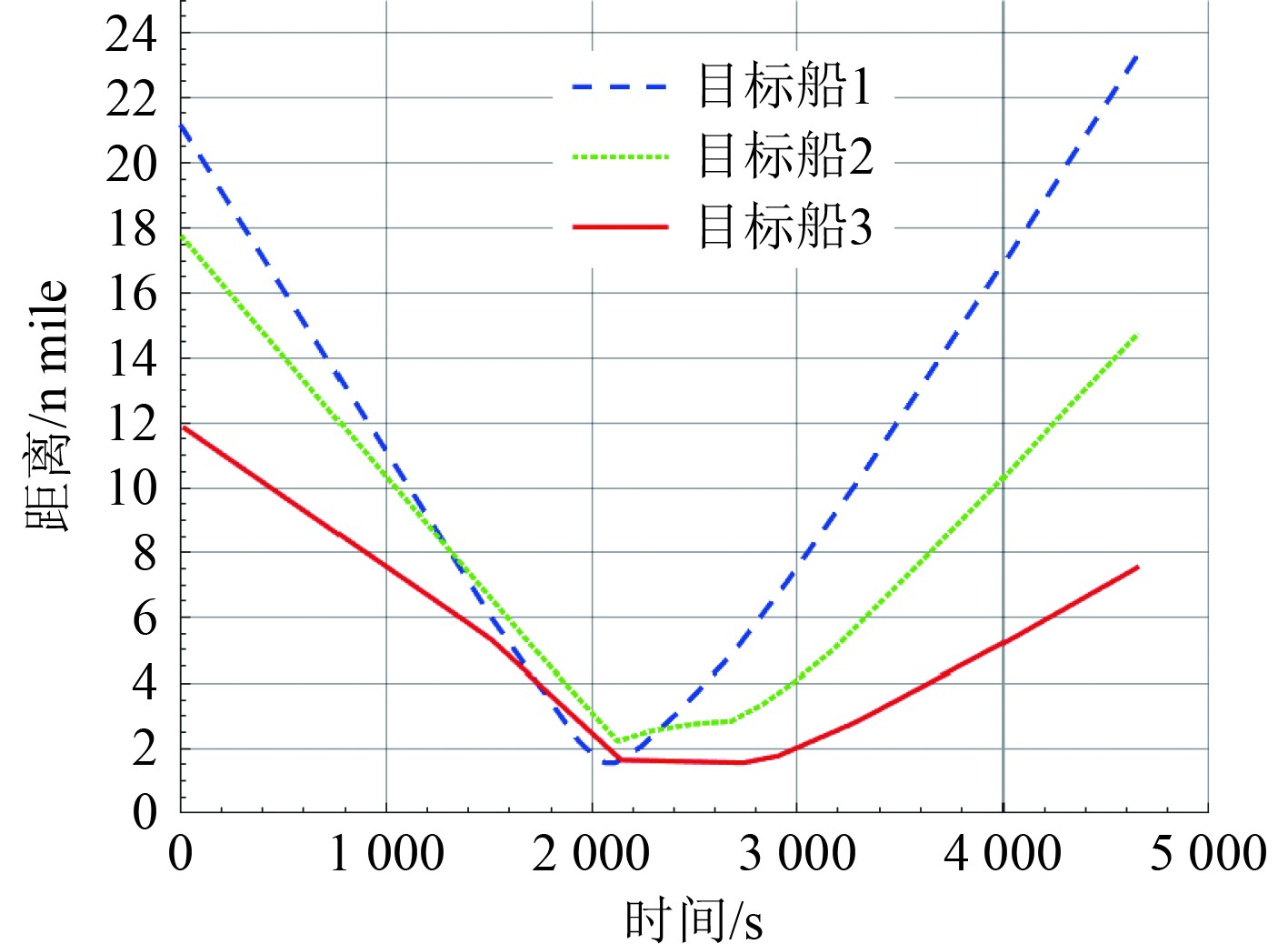
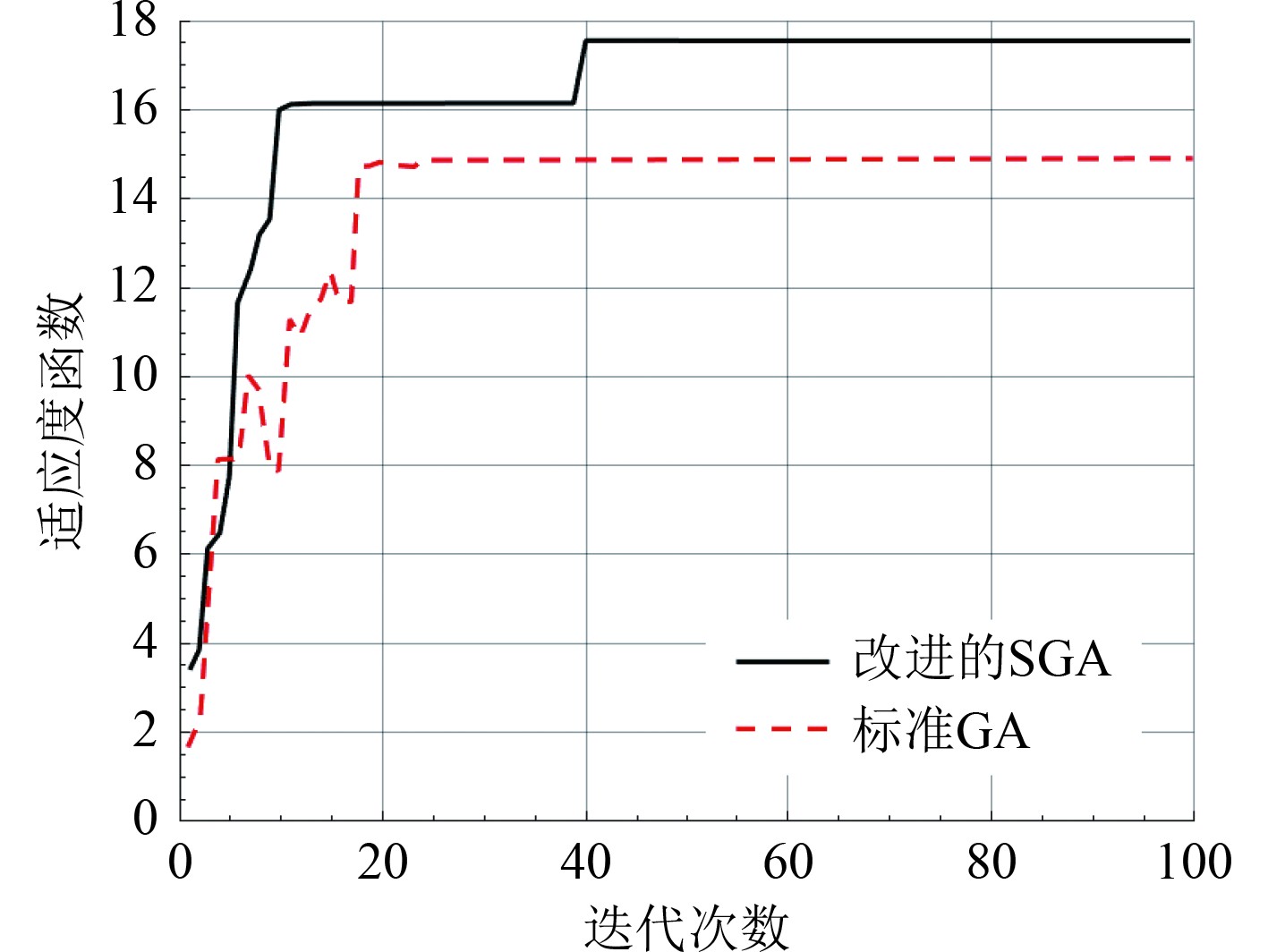
在四船会遇局面中，本船在避开目标船1和目标船2后，发现继续沿着该航向会与目标船3发生碰撞，因此调用算法计算出避碰时机和避碰角度，在避开目标船3后，再进行复航操作。图8为本船和3艘目标船之间的距离变化情况，本船与3艘目标船间的距离均大于1.5 n mile，也符合避碰的要求。图9为四船会遇下本船避开第3艘目标船的适应度函数变化曲线，由于本算法在遗传算法当中嵌入了模拟退火算法，且引入了自适应交叉和变异操作，使得算法能够跳出局部最优陷阱。

4 结　语

本文提出一种改进的遗传模拟退火算法，用于处理在开阔水域多船会遇局面下的船舶避碰决策问题。该算法通过自适应策略对遗传算法的交叉和变异算子进行改进，并在遗传算法中嵌入模拟退火算法，增强算法的局部搜索能力。在船舶避碰决策上，以D_CPA、T_CPA、相对距离、相对方位、船速比作为 计算的基础，在目标函数的构建上，统筹考虑了船舶安全性、航行经济性和避碰规则。仿真实验结果表明：本算法相较于传统遗传算法，具有迭代速度快，寻优能力强的特点，能为船舶驾驶人员在多船会遇态势下的避碰操纵提供参考依据。

在后续的研究中，应综合考虑本船作为直航船，以及他船作为让路船且未遵守《国际海上避碰规则》而导致出现紧急局面的情况。因此，在处理多船会遇时，需要进一步研究本船和目标船不协调避碰的问题。