0 引　言

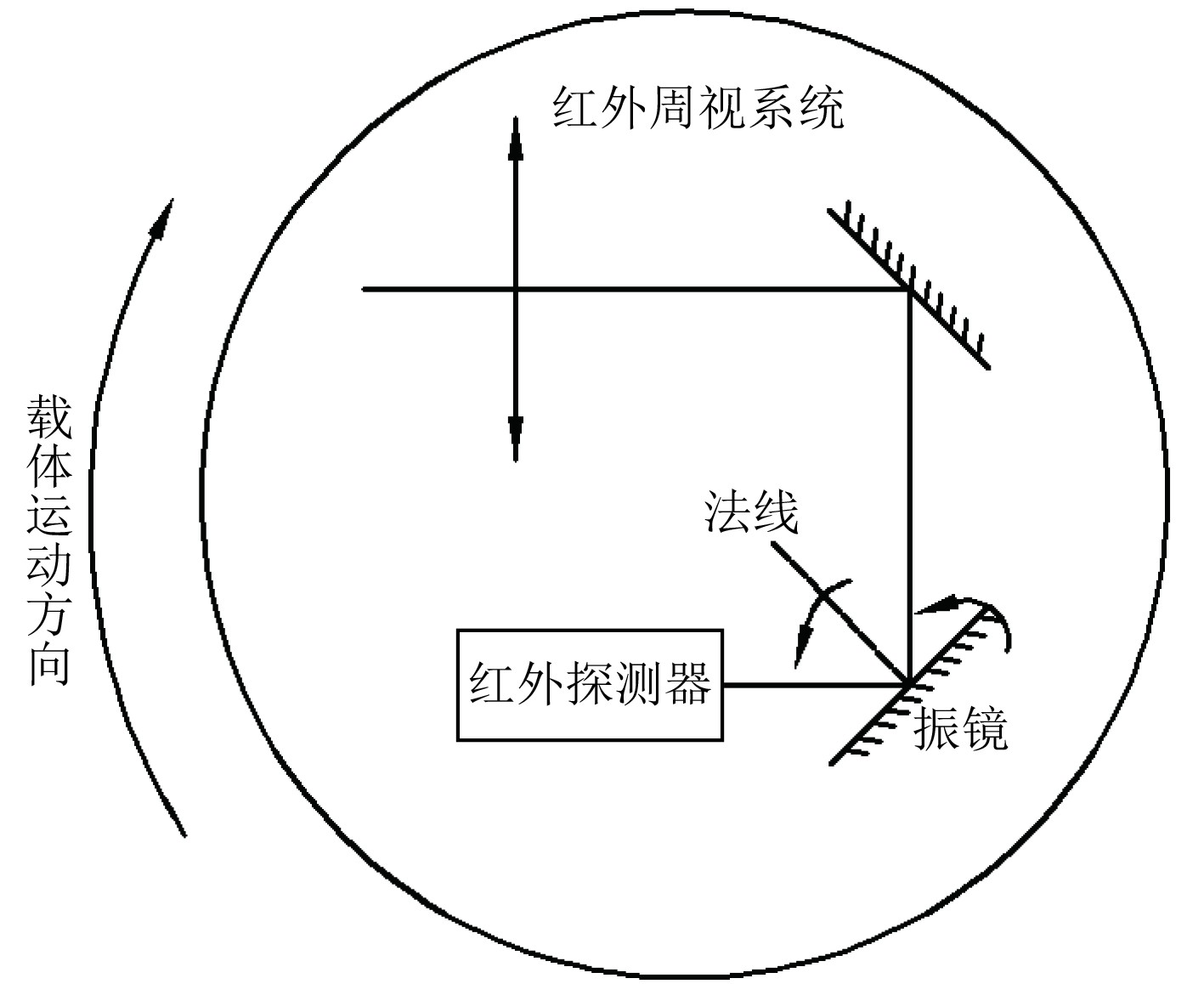
随着光电技术的发展，新一代潜艇光电桅杆通常配备面阵红外热像仪、可见光摄像机、激光测距机等多种成像传感器，并通过旋转实现全方位搜索最终实现周视图像的获取。面阵红外热像仪需要凝视成像，其探测器积分时间长，在载体高速转动，无补偿措施的情况下，在积分时间内物方空间与探测器发生相对运动，图像会产生拖尾^[1]，严重影响图像清晰度。当面阵红外热像仪振镜补偿时法线运动平面与载体运动平面完全平行，可以实现完全补偿，这是通用红外像移补偿问题，如图1所示。针对其他复杂情况，引入了惯性稳定技术，用以隔离载体扰动，使得图像或光轴在惯性空间保持稳定^[2]，从而解决红外像移问题。

光电桅杆系统由于受空间限制，其面阵红外热像仪多采用反射镜实现多次光路折叠，该类系统可以通过反射镜转动，使光线反向运动，抵消由于载体高速运动引起的像移，从而完成像移补偿^[3]。但该类通过反射镜转动的光学式像移补偿成像技术^[1]，在扫描成像过程中除像移现象还会发生图像旋转^[4]。本文介绍了面阵红外中振镜法线运动平面与载体运动平面不能平行的特殊结构，针对积分时间内面阵红外的像移问题和扫描成像过程中的像旋问题，本文提出一种新型的二级光学稳定补偿结构，采用振镜内补偿的方式实现红外周视成像系统的二级光学稳定。

针对积分时间内面阵红外的像移问题解决方法，扫描成像中像旋问题解决方法的技术路线和控制方法介绍较多，但同时针对该2个问题对具体像移和像旋量的分析和补偿策略介绍和详细论述较少。本文提出一种新型的二级光学稳定补偿结构，采用振镜内补偿的方式实现红外周视成像的二级光学稳定，并具体介绍了补偿策略。

1 系统介绍

新一代光电桅杆中的红外周视成像系统，多采用面阵光电传感器替代线阵光电传感器，国外光电桅杆头均采用光电传感器和窗口随壳体转动的方式，本文提出一种超半球蓝宝石窗口，且窗口与外壳固定，传感器在内部并随设备旋转的光电桅杆头。面阵红外热像仪因为传感器的积分时间长，在扫描过程中会出现明显的拖尾现象，导致图像模糊^[5]。光电桅杆头受潜艇出水使用、便捷收纳等多方面的影响，属于细长型结构^[6]。该结构形式下要实现红外热像仪、可见光摄像机、激光测距机等多传感器的布置，光电桅杆头的整体布局受限较大。红外周视成像系统可在面阵传感器光路中加入一组扫描振镜组，扫描振镜会根据主平面反射镜的扫描运动进行一定规律的方位和俯仰扫描补偿运动^[7]，保证光电传感器在积分时间内焦平面相对景物静止不动，即光轴在惯性空间内指向不变，从而使红外清晰成像。

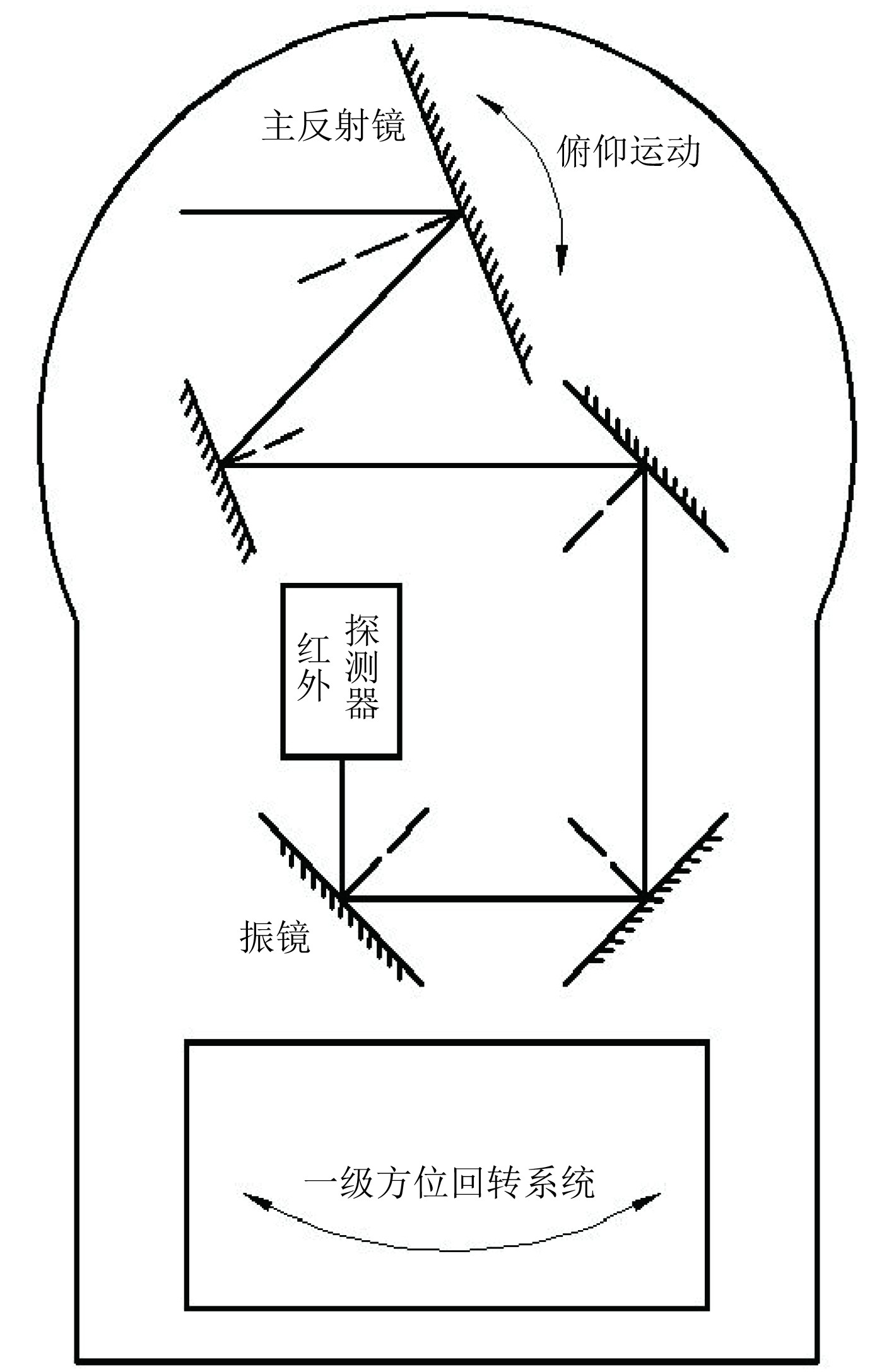
如图2所示，该光电桅杆头采用超半球窗口与外壳固定不动，内部采用整体回转的探测机构。内部回转探测机构分为一级主反射镜稳定和内部二级振镜稳定，内部回转探测机构整体位于一级方位系统上，外部一级主反射镜还能做俯仰运动，二级振镜置于光学通道中。目标和背景的红外辐射入射到一级主反射镜平面上，通过折转光路和光学系统到达二级振镜，最后进入传感器内部光路并到达探测器焦平面上。一级主反射镜随系统整体以一定方位角速度做匀速回转扫描，俯仰方向在一定范围内也可连续运动。为了消除载体摇摆引起的瞄准线晃动，外部一级主反射镜需根据载体摇摆在惯性空间内进行方位和俯仰的一级稳定，保证方位的惯性空间匀速扫描与俯仰视轴的稳定^[2]，内部二级振镜随整体方位旋转，并在积分时间内进行某规律的二次补偿，保持光轴的指向不变。

2 稳定技术

通用面阵红外系统像移问题，一般都是振镜补偿时，振镜法线运动平面与载体运动平面完全平行，通过振镜与载体反方向旋转来补偿由于探测器积分时间不够造成的像移。

本文主要介绍面阵红外中振镜法线运动平面与载体运动平面不能平行的特殊结构，运用理论分析的方法，计算该结构形式下一级方位旋转后，二级振镜的补偿策略。验证通过二级振镜法线运动面与载体运动面不平行的角度补偿，能否解决像移和像旋问题。通过建立理论模型，计算载体运动后，针对不同位置光线，振镜的补偿策略，即振镜的补偿方向和补偿角度量问题。最终分析载体按某速度匀速运动时，能否通过振镜某方向上一维补偿，使最大像面偏移量在满足使用可接受的范围内。

该系统中一级稳定控制完成了一级主反射镜在惯性空间里的方位角匀速回转扫描和俯仰角一级稳定^[7]。由于载体运动，积分时间内使目标在像面上发生位置移动和旋转，所以需要内部二级扫描振镜根据一级主反射镜的扫描运动进行一定规律的方位和俯仰补偿运动，即二级稳定，保证红外探测器在积分时间内焦平面光轴指向静止不动。

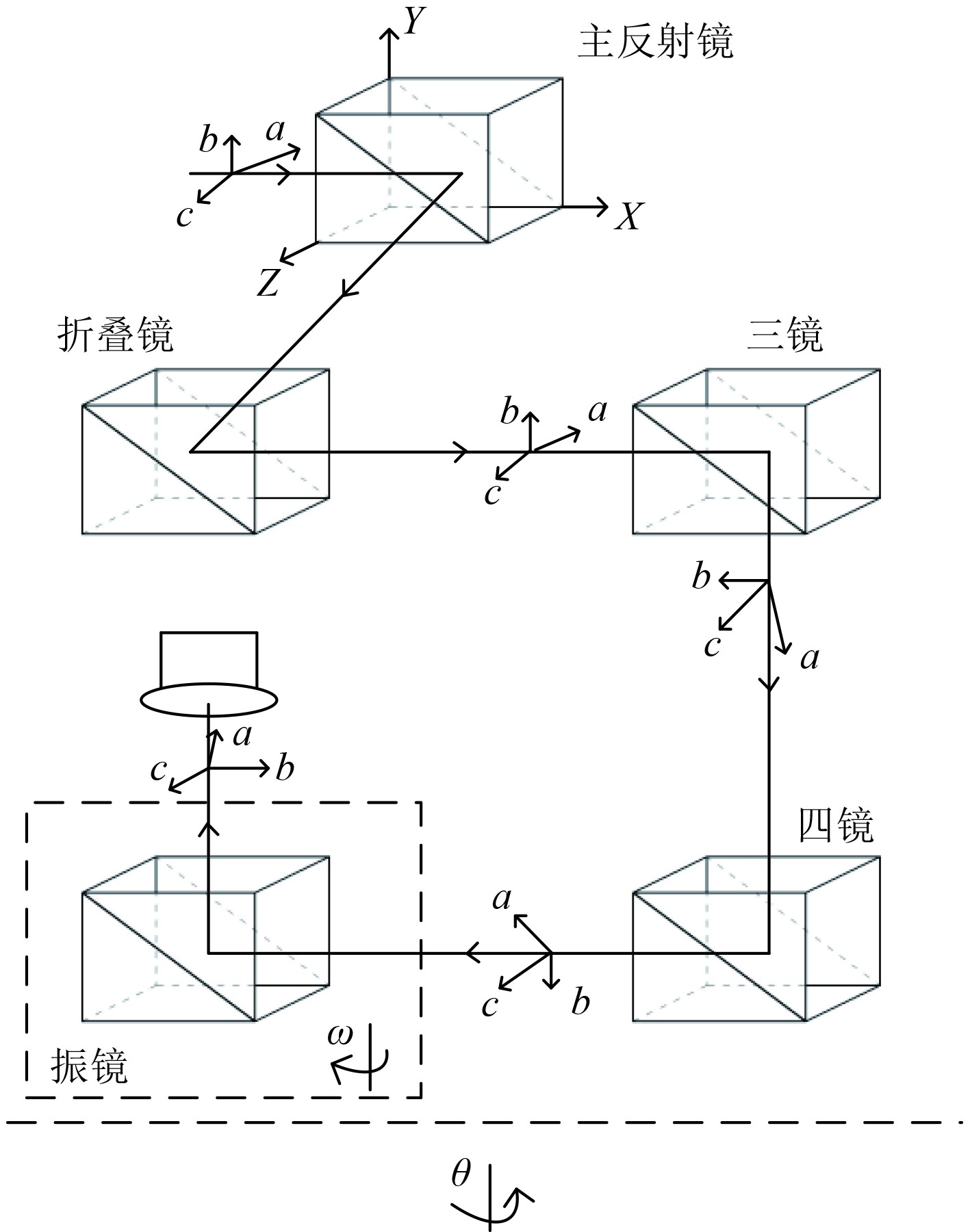
3 模型建立及计算 3.1 模型建立

根据图3建立光电桅杆捷联稳定光路模型和坐标系关系，假设光电桅杆的方位平台搭载所有设备逆时针转为θ，振镜顺时针补偿为ω。该红外系统为焦距50 mm/200 mm双视场，640 × 512，15 μm面阵探测器。

以红外探测器像面坐标系为参考坐标，要实现像移补偿，即要保持原入射向量经过振镜补偿后在相机坐标系中保持不变。

矢量形式的反射定律为：

$ \left[\begin{array}{*{20}{c}}A'_x \\ A'_y \\ A'_z\end{array}\right]=\left[\begin{array}{*{20}{c}}1-2N_x^2 & -2N_xN_y & -2N_zN_x \\ -2N_xN_y & 1-2N_y^2 & -2N_yN_z \\ -2N_zN_x & -2N_yN_z & 1-2N_z^2\end{array}\right]\left[\begin{array}{*{20}{c}}A_x \\ A_y \\ A_z\end{array}\right]。$

(1)

式中：$ {N_x} $、$ {N_y} $、$ {N_z} $为平面反射镜法线在坐标系上的分量；$ {A_x} $、$ {A_y} $、$ {A_z} $为入射向量在坐标系上的分量；$ {A_x}^\prime $、$ {A_y}^\prime $、$ {A_z}^\prime $为出射向量在坐标系上的分量。

一级主反射镜与XOZ面夹角为β，一级主反射镜与XOZ面夹角β零位值为62.5°；折叠反射镜法线与水平成62.5°；三镜、四镜和振镜法线与水平成45°。$ A $、$ {A_0} $定义为主光线向量，$ {A_1} $定义为俯仰面内正边缘光线，由矢量形式的反射定律可知各反射镜法线单位向量和出射矩阵为：

$ \overrightarrow{\boldsymbol{A}}=\left(\begin{array}{*{20}{c}}1 \\ 0 \\ 0\end{array}\right)。$

(2)

式中：$ A $为原主光线单位向量。

$ \overrightarrow{A_0}=\left(\begin{array}{*{20}{c}}\cos\theta \\ 0 \\ \sin\theta\end{array}\right)。$

(3)

式中：$ {A_0} $为原主光线单位向量经过逆时针旋转θ角后形成的向量。

$ \overrightarrow{A_1}=\left(\begin{array}{*{20}{c}}\cos\alpha \\ \sin\alpha \\ 0\end{array}\right)。$

(4)

式中：$ {A_1} $为原俯仰面内正边缘光线单位向量；α为红外系统垂直半视场角。

$ \overrightarrow{A_{10}}=\left(\begin{array}{*{20}{c}}\cos\alpha\cos\theta \\ -\sin\alpha \\ \cos\alpha\sin\theta\end{array}\right)。$

(5)

式中：$ {A_{10}} $为原俯仰面内正边缘光线单位向量经过逆时针旋转θ角后形成的向量；α为红外系统垂直半视场角。

$ \overrightarrow{N_{10}}=\left[\begin{array}{*{20}{c}}-\sin\beta \\ -\cos\beta \\ 0\end{array}\right]。$

(6)

式中：$ {N_{10}} $为主反射镜的法线单位向量；β为主反射镜与XOZ面夹角。

$ \boldsymbol{M}_{10}=\left[\begin{array}{*{20}{c}}\cos(2*\beta) & -\sin(2*\beta) & 0 \\ -\sin(2*\beta) & -\cos(2*\beta) & 0 \\ 0 & 0 & 1\end{array}\right]。$

(7)

式中：$ \boldsymbol{M}_{10} $为主反射镜的出射矩阵；β为主反射镜与XOZ面夹角。

$ \overrightarrow {{N_{20}}} = \left[ {\begin{array}{*{20}{c}} {\sin 62.5^\circ } \\ {\cos 62.5^\circ } \\ 0 \end{array}} \right]。$

(8)

式中：$ {N_{20}} $为折叠镜的法线单位向量。

$ \boldsymbol{M}_{20}=\left[\begin{array}{*{20}{c}}\cos125^{\circ} & -\sin125^{\circ} & 0 \\ -\sin125^{\circ} & -\cos125^{\circ} & 0 \\ 0 & 0 & 1\end{array}\right]。$

(9)

式中：$ \boldsymbol{M}_{20} $为折叠镜的出射矩阵。

$ \overrightarrow {{N_{30}}} = \left[ {\begin{array}{*{20}{c}} { - \sin 45^\circ } \\ { - \cos 45^\circ } \\ 0 \end{array}} \right] 。$

(10)

式中：$ {N_{30}} $为三镜的法线单位向量。

$ \boldsymbol{M}_{30}=\left[\begin{array}{*{20}{c}}0 & -1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1\end{array}\right]。$

(11)

式中：$ \boldsymbol{M}_{30} $为三镜的出射矩阵。

$ \overrightarrow {{N_{40}}} = \left[ {\begin{array}{*{20}{c}} { - \sin 45^\circ } \\ {\cos 45^\circ } \\ 0 \end{array}} \right]。$

(12)

式中：$ {N_{40}} $为四镜的法线单位向量。

$ \boldsymbol{M}_{40}=\left[\begin{array}{*{20}{c}}0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{array}\right]。$

(13)

式中：$ \boldsymbol{M}_{40} $为四镜的出射矩阵。

$ \overrightarrow {{N_5}} = \left[ {\begin{array}{*{20}{c}} {\sin 45^\circ } \\ {\cos 45^\circ } \\ 0 \end{array}} \right] 。$

(14)

式中：$ {N_5} $为振镜的法线单位向量。

$ \boldsymbol{M}_5=\left[\begin{array}{*{20}{c}}0 & -1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1\end{array}\right]。$

(15)

式中：$ \boldsymbol{M}_5 $为振镜的出射矩阵。

$ \overrightarrow {{N_{50}}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\sqrt 2 }}{2}\cos \omega } \\ {\dfrac{{\sqrt 2 }}{2}} \\ {\dfrac{{\sqrt 2 }}{2}\sin \omega } \end{array}} \right] 。$

(16)

式中：$ {N_{50}} $为振镜顺时针补偿ω角后的法线单位向量。

$ \boldsymbol{M}_{50}=\left[\begin{array}{*{20}{c}}\sin^2\omega & -\cos\omega & -\sin\omega\cos\omega \\ -\cos\omega & 0 & -\sin\omega \\ -\sin\omega\cos\omega & -\sin\omega & \cos^2\omega\end{array}\right]。$

(17)

式中：$ \boldsymbol{M}_{50} $为振镜补偿ω角后的出射矩阵。

3.2 俯仰零位时主光线补偿计算

当β = 62.5时，入射向量$ A $经过该5组反射镜后输出光线方向向量为：

$ \overrightarrow{A''}=\boldsymbol{M}_5\cdot\boldsymbol{M}_{40}\cdot\boldsymbol{M}_{30}\cdot\boldsymbol{M}_{20}\cdot\boldsymbol{M}_{10}\cdot A\text{ = }\left[\begin{array}{*{20}{c}}0 \\ 1 \\ 0\end{array}\right]。$

(18)

当β = 62.5时，入射向量$ {A_0} $经过该5组镜反射（振镜补偿ω角后）输出光线方向向量为：

$ \begin{split}\overrightarrow{A_0''}=\; & \boldsymbol{M}_{50}\cdot\boldsymbol{M}_{40}\cdot\boldsymbol{M}_{30}\cdot\boldsymbol{M}_{20}\cdot\boldsymbol{M}_{10}\cdot A_0= \\ \; & \left[\begin{array}{*{20}{c}}-\sin\omega\sin(\theta+\omega) \\ \cos(\theta+\omega) \\ \cos\omega\sin(\theta+\omega)\end{array}\right]。\end{split} $

(19)

若要完全补偿，则需要$ {A_0} $ = $ A $，即应有式(18)等于式(19)，即：

$ \left[ {\begin{array}{*{20}{c}} { - \sin \omega \sin (\theta + \omega )} \\ {\cos (\theta + \omega )} \\ {\cos \omega \sin (\theta + \omega )} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \\ 0 \end{array}} \right] 。$

(20)

因为积分时间内载体运动角度ω ≠ 0，要使式(20)成立，则只能是ω + θ = 0。由于初始时定义平台搭载所有设备逆时针转θ，振镜顺时针补偿ω，所以应该是ω = −θ，即当主反射镜β = 62.5时，振镜与平台同方向1∶1角度补偿可实现主光线完全补偿。

3.3 俯仰零位时边缘光线计算

当β = 62.5时，入射向量$ {A_1} $经过该5组反射镜后输出光线方向向量为：

$ \overrightarrow{A_1''}=\boldsymbol{M}_5\cdot\boldsymbol{M}_{40}\cdot\boldsymbol{M}_{30}\cdot\boldsymbol{M}_{20}\cdot\boldsymbol{M}_{10}\cdot A_1\text{ = }\left[\begin{array}{*{20}{c}}\sin\alpha \\ \cos\alpha \\ 0\end{array}\right]。$

(21)

式中：$ {A_1}^{\prime \prime } $为原俯仰面内正边缘光线单位向量经过5组反射镜后的输出向量；α为红外系统垂直半视场角。

当β = 62.5时，入射向量$ {A_{10}} $经过该5组镜反射（振镜补偿ω角后）输出光线方向向量为：

$ \overrightarrow{A_{10}''}=\boldsymbol{M}_{50}\cdot\boldsymbol{M}_{40}\cdot\boldsymbol{M}_{30}\cdot\boldsymbol{M}_{20}\cdot\boldsymbol{M}_{10}\cdot A_{10}。$

(22)

$ {A_2} $定义为方位面内正边缘光线，则有：

$ \overrightarrow {{A_2}} = \left( {\begin{array}{*{20}{c}} {\cos \alpha } \\ 0 \\ {\sin \alpha } \end{array}} \right) 。$

(23)

式中：α为红外系统方位半视场角。

$ \overrightarrow {{A_{20}}} = \left( {\begin{array}{*{20}{c}} {\cos (\alpha + \theta )} \\ 0 \\ {\sin (\alpha + \theta )} \end{array}} \right) 。$

(24)

式中：α为红外系统方位半视场角；θ为载体逆时针转动的角度。

当β = 62.5时，入射向量$ {A_2} $经过该5组反射镜后输出光线方向向量为：

$ \overrightarrow{A_2''}=\boldsymbol{M}_5\cdot\boldsymbol{M}_{40}\cdot\boldsymbol{M}_{30}\cdot\boldsymbol{M}_{20}\cdot\boldsymbol{M}_{10}\cdot A_2\text{ = }\left[\begin{array}{*{20}{c}}0 \\ \cos\alpha \\ \sin\alpha\end{array}\right]。$

(25)

式中：$ {A_2}^{\prime \prime } $为原方位面内正边缘光线单位向量经过5组反射镜后的输出向量；α为红外系统垂直半视场角。

当β = 62.5时，入射向量$ {A_{20}} $经过该5组镜反射（振镜补偿ω角后）输出光线方向向量为：

$ \begin{split}\overrightarrow{A_{20}''}=\; & \boldsymbol{M}_{50}\cdot\boldsymbol{M}_{40}\cdot\boldsymbol{M}_{30}\cdot\boldsymbol{M}_{20}\cdot\boldsymbol{M}_{10}\cdot A_{20}= \\ \; & \left[\begin{array}{*{20}{c}}-\sin\omega\sin(\alpha+\omega+\theta) \\ \cos(\alpha+\omega+\theta) \\ \cos\omega\sin(\alpha+\omega+\theta)\end{array}\right]。\end{split} $

(26)

式中：$ {A_{20}}^{\prime \prime } $为振镜补偿ω角后，原方位面内正边缘光线单位向量经过5组反射镜后的输出向量；α为红外系统垂直半视场角；θ为载体逆时针转动的角度。

向量$ {A_{20}}^{\prime \prime } $与向量$ {A_2}^{\prime \prime } $相比，在X轴的分量不再为0，所以向量$ {A_{20}}^{\prime \prime } $与向量$ {A_2}^{\prime \prime } $相对于YOZ面有旋转ξ，如图4所示。

计算ξ的正切值如下：

$ \mathrm{tan}\xi=\left(\frac{A''_x}{A''_z}\right)=-\mathrm{tan}\omega。$

(27)

式中：ξ为向量$ {A_{20}}^{\prime \prime } $与向量$ {A_2}^{\prime \prime } $相对于YOZ面的旋转角度；$ {A_x}^{\prime \prime } $、$ {A_z}^{\prime \prime } $分别为向量在X轴和Z轴上的分量；ω为振镜补偿角度。

所以由上可知，像点发生旋转，且有像旋角度与旋转角存在ξ = −ω的关系。

由此可计算方位正边缘光线偏离量如下：

$ \sigma=2\times(640\times0.015/2)\times\sin(\xi/2)，$

(28)

$ \xi=-\omega=\theta=vt。$

(29)

式中：ξ为向量$ {A_{20}}^{\prime \prime } $与向量$ {A_2}^{\prime \prime } $相对于YOZ面的旋转角度；σ为方位正边缘光线偏离量；ω为振镜补偿角度；θ为载体逆时针转动的角度；v为载体运动速度；t为积分时间。

3.4 主反射镜俯仰角与补偿角的关系 3.4.1 中心主光线

假设载体转动速度v为60°/s，积分时间t为4 ms，载体转动角度y = 0.24°；俯仰镜角度为b；第二反射镜角度为φ = 62.5°，第三、四、反射镜，振镜初始角度为c = 45°，振镜补偿角为ω = z。

主光线入射向量与主反射镜的俯仰角有关，向量$ B $和$ {B_0} $如下，补偿后的初始向量表示如下：

$ \overrightarrow {{B}} = \left( {\begin{array}{*{20}{c}} {\cos (2*({{b }-}\varphi ))} \\ { - \sin (2*({{b }-}\varphi ))} \\ 0 \end{array}} \right) ，$

(30)

$ \overrightarrow {{B_0}} = \left( {\begin{array}{*{20}{c}} {\cos (y)\cos (2*({{b }-}\varphi ))} \\ { - \sin (2*({{b }-}\varphi ))} \\ {\sin (y)\cos (2*({{b }-}\varphi ))} \end{array}} \right) 。$

(31)

式中：b为俯仰镜角度；φ = 62.5°为常量；y为载体在积分时间内转动的角度。

主光线$ B $和$ {B_0} $入射镜组的出射目标向量$ {B_c} $和$ {B_{0c}} $表示为：

$ \mathit{\overrightarrow{{B}_{{c}}}}=M_5\cdot M_{40}\cdot M_{30}\cdot M_{20}\cdot M_{10}\cdot B，$

(32)

$ \overrightarrow {{{{B}}_{{{0c}}}}} = {M_{50}} \cdot {M_{40}} \cdot {M_{30}} \cdot {M_{20}} \cdot {M_{10}} \cdot B 。$

(33)

令$ {B_{0c}} = {M_{50}} \cdot {B_x} $，计算化简$ {B_c} $和$ {B_x} $如下所示：

$ \overrightarrow {{B_c}} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 0 \end{array}} \right) ，$

(34)

$ \overrightarrow{B_x} = \left( \begin{array}{*{20}{c}}-\text{co}\text{s}^{\text{2}}\text{(2}\varphi-2b)\mathrm{cos}(y)-\mathrm{si\text{n}}^{\text{2}}\text{(2}\varphi-2b) \\ 1/2*\sin(4\varphi-4b)\mathrm{cos}(y)-1/2*\sin(4\varphi-4b) \\ \text{cos(2}\varphi-2b)*\mathrm{sin}(y)\end{array} \right)。$

(35)

式中：b为俯仰镜角度；φ=62.5°为常量；y为载体在积分时间内转动的角度。

振镜绕Y轴旋转ω角后矩阵为$ \boldsymbol{M}_{50} $，$ {B_{0c}} $化简表示为：

$ {\begin{gathered} {B_{0c}} = \left[ \begin{gathered} {{ - \sin}^{{2}}}{{({{z}})(\cos}^{{2}}}{{(2 \varphi - 2{{b}}) \cos({{y}}) + \sin}^{{2}}}{{(2 \varphi - 2{{b}})) - }} \\ {{\cos({{z}})({\cos}}^{{2}}}{{(2 \varphi - 2{{b}})\cos({{y}}) + \sin}^{{2}}}{{(2 \varphi - 2{{b}})) - }} \\ {{1/2\sin(2{{z}})(\cos}^{{2}}}{{(2 \varphi - 2{{b}})\cos({{y}}) + \sin}^{{2}}}{{(2 \varphi - 2{{b}})) - }} \\ \end{gathered} \right. \\ {\text{ }}\left. \begin{gathered} \begin{split}{1/2\cos({{z}})\sin (4 \varphi - 4 {b} )}&(\cos({{y}}) - 1) - \\ & 1/2\sin(2{{z}})\cos(2\varphi - 2{{b}})\sin({{y}}) \end{split} \\ {{\sin({{z}})\cos(2 \varphi - 2{{b}})\sin({{y}})}} \\ \begin{split}{1/2\sin( {z}})(\sin(4 \varphi - 4{{b}})&\cos({{y}}) + \sin(4 \varphi - 4 {b})) + \\ & \cos^{{2}}{{({{z}})\cos(2}}\varphi {{ - 2{{b}})\sin({{y}})}}\end{split} \\ \end{gathered} \right] \\ \end{gathered}。} $

(36)

式中：b为俯仰镜角度；φ = 62.5°为常量；y为载体在积分时间内转动的角度；z为振镜补偿角。

若想完全补偿，则补偿后的出射向量$ {B_{0c}} $应与$ {B_c} $相等，即式(34)与式(36)相等；令$ {B_{0c}} $向量第二项为f，则应有f=1，同时第一项和第三项等于0。绘制以俯仰角变化量和补偿角为变量的f表达式图形如图5所示，求解一条最佳的曲线使得f = 1，同时代入该曲线计算向量$ {B_{0c}} $的第一项和第三项，该值与0的差值情况为补偿剩余量。可求得某旋转速度下，一次主反射镜与二次振镜补偿角度的关系曲线。

$ {{y}} = s(1){x^2} + s(2)x + s(3)。$

(37)

式中：y为振镜补偿角度；x为主反射镜当前俯仰角度；s(1)、s(2)、s(3)分别为解算出的二次曲线系数。

3.4.2 边缘主光线

$ {A_3} $定义为方位面内正边缘光线，定义半视场角为α，俯仰镜角度为b；第二反射镜角度为φ = 62.5°，第三、四反射镜，振镜初始角度为c = 45°，振镜补偿角为ω = z。

$ \overrightarrow {{A_3}} = \left( {\begin{array}{*{20}{c}} {\cos \alpha } \\ 0 \\ {\sin \alpha } \end{array}} \right) ，$

(38)

$ \overrightarrow {{A_{30}}} = \left( {\begin{array}{*{20}{c}} {\cos (\alpha + \theta )} \\ 0 \\ {\sin (\alpha + \theta )} \end{array}} \right)。$

(39)

式中：$ {A_3} $为方位面内正边缘光线；α为红外半视场角；θ为载体逆时针转动的角度。

入射向量$ {A_3} $经过该5组反射镜后输出光线方向向量化简为：

$ \begin{split}\overrightarrow{A_3''}=\; & \boldsymbol{M}_5\cdot\boldsymbol{M}_{40}\cdot\boldsymbol{M}_{30}\cdot\boldsymbol{M}_{20}\cdot\boldsymbol{M}_{10}\cdot A_3= \\ \; & \left[\begin{array}{*{20}{c}}\text{ - sin(2}\varphi-2b)*\mathrm{cos}(\alpha\text{)} \\ \text{cos(2}\varphi-2b)*\mathrm{cos}(\alpha\text{)} \\ \sin\alpha\end{array}\right]。\end{split} $

(40)

式中：$ {A_3}^{\prime \prime } $为入射向量$ {A_3} $经过该5组反射镜后输出向量；φ = 62.5°为常量；b为俯仰镜角度；α为红外半视场角。

入射向量$ {A_{30}} $经过该5镜反射补偿后输出光线方向向量化简为：

$ \begin{array}{l}\overrightarrow{A_{30}^{''}}=M_{50}\cdot M_{40}\cdot M_{30}\cdot M_{20}\cdot M_{10}\cdot A_{30}= \\ \left[\begin{array}{l}\rm{-}\sin^2\omega\rm{cos(2}\varphi-2b)*cos(\alpha+\theta\rm{)}- \\ \cos\omega\rm{cos(2}\varphi-2b)*\mathrm{cos}(\alpha+\theta\rm{)}- \\ \sin\omega\cos\omega\rm{cos(2}\varphi-2b)*cos(\alpha+\theta\rm{)}- \\ \cos\omega\rm{sin}(\rm{2}\varphi-2b)*\mathrm{cos}(\alpha+\theta\rm{)}-\sin\omega\cos\omega\rm{sin}(\alpha+\theta\rm{)} \\ \sin\omega\rm{sin(}\alpha+\theta\rm{)} \\ \sin\omega\rm{sin(2}\varphi-2b)*cos(\alpha+\theta\rm{)+}\cos^2\omega\rm{sin(}\alpha+\theta\rm{)}\end{array}\right]。\end{array} $

(41)

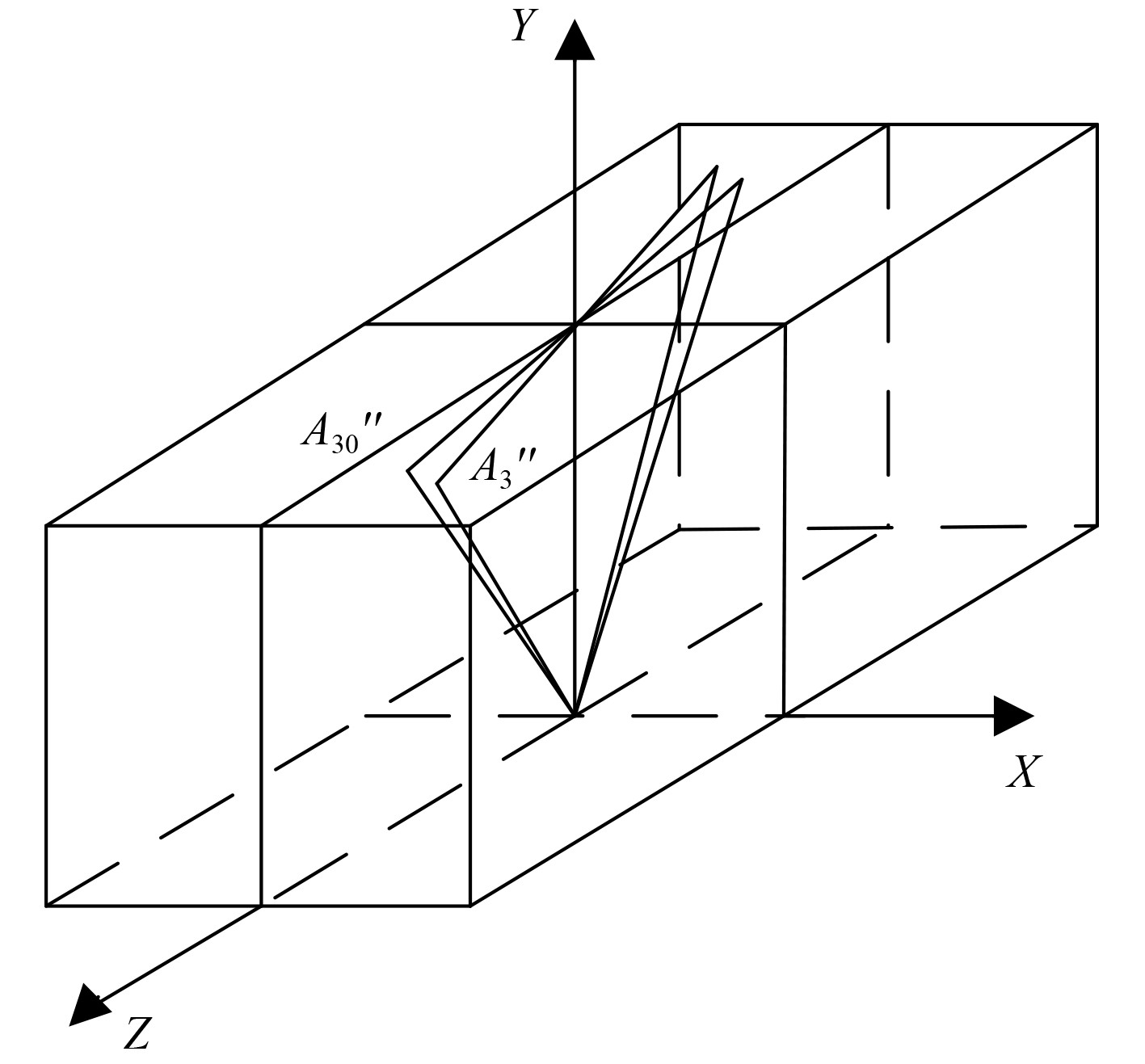
式中：$ {A_{30}}^{\prime \prime } $为入射向量$ {A_{30}} $经过该5组反射镜后输出向量；φ = 62.5°为常量；b为俯仰镜角度；α为红外半视场角；θ为载体逆时针转动的角度；ω为振镜补偿角。

向量$ {A_{30}}^{\prime \prime } $与向量$ {A_3}^{\prime \prime } $相比，2个向量均为空间向量，所以向量$ {A_{30}}^{\prime \prime } $与向量$ {A_3}^{\prime \prime } $相对于YOZ面有旋转ξ（即靶面上的旋转），相对于XOZ面有旋转η（即靶面离焦的距离），如图6所示。

$ \begin{split}\xi=\; & \arcsin(A_{xA30}/\mathrm{sqrt}(A_{zA30}^2+A_{xA30}^2))- \\ \; & \arcsin(A_{xA3}/\mathrm{sqrt}(A_{zA3}^2+A_{xA3}^2))。\end{split}$

(42)

式中：$ {A_{xA30}} $、$ {A_{zA30}} $分别为向量$ {A_{30}} $在X轴和Z轴的分量；$ {A_{xA3}} $、$ {A_{zA3}} $分别为向量$ {A_3} $在X轴和Z轴的分量。

3.4.3 主光线入射面阵

文中3.4.1节和3.4.2节均计算为特殊光线情况，现在考虑以主反射镜旋转中心，入射不同视场角的入射光线阵，该阵以主光线为旋转中心，以半对角线边缘视场上光线为母线旋转得到。求经过该5组反射系统，到达像面的出射光线阵。该出射向量在像面上相对位置的偏离为像移大小。该出射向量偏离像面的离焦量为像面畸变值。

根据面阵光线的计算模型可知，当载体方位按60°/s转动时，振镜若不进行角度补偿时，其红外系统短焦中心和边缘约产生整体平移，偏离值约185.6 μm，长焦中心和边缘约产生整体平移，偏离值约618.8 μm。且在主反射镜与水平成90°时偏移量最小，主反射镜与水平成57.5°时偏移量最大（见图7）。

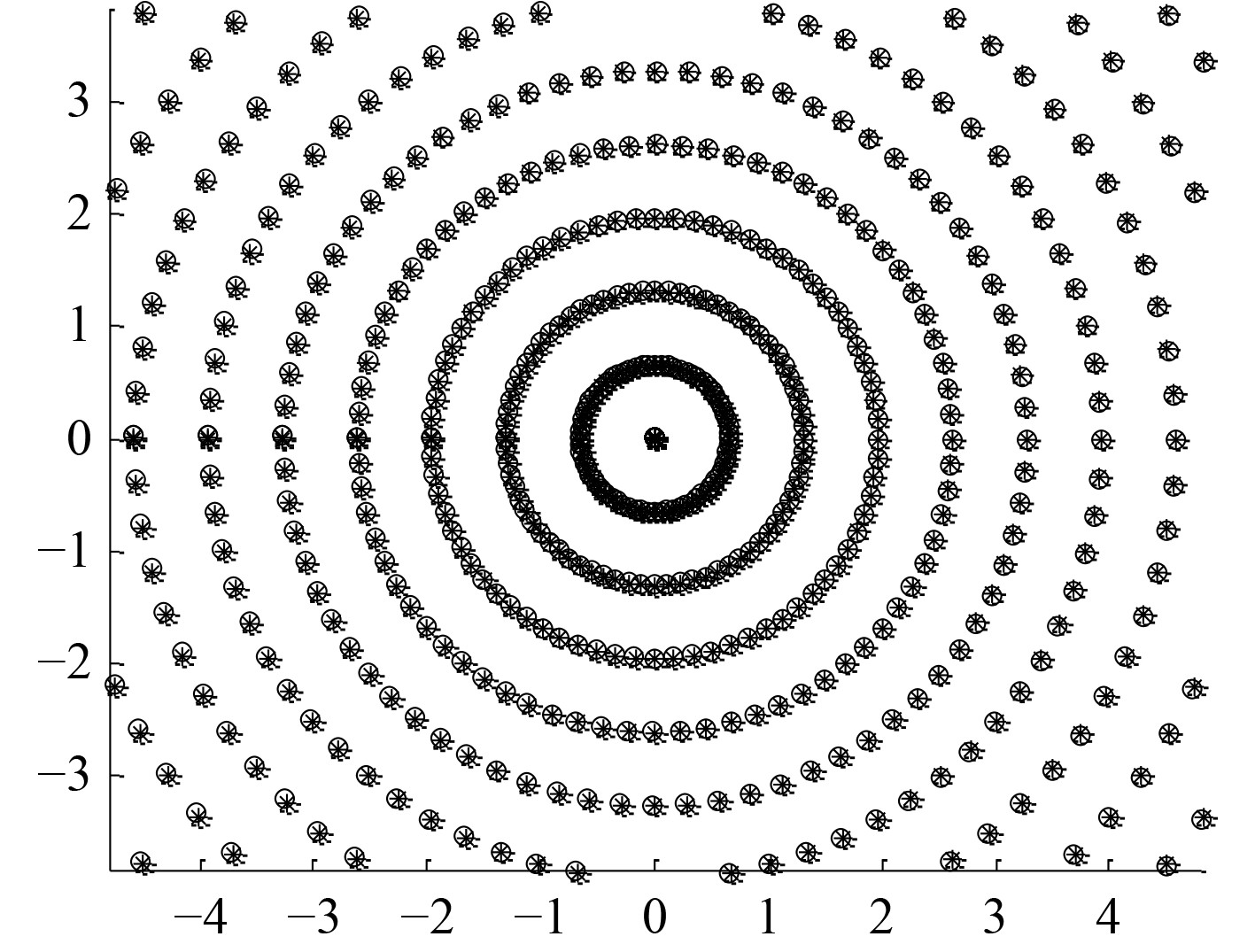
当振镜按照与主反射镜俯仰角的关系曲线进行角度补偿时，其短焦补偿结果中心偏离最大值1.6 μm，长焦补偿结果中心偏离最大值5.4 μm，不同视场角边缘主光线会产生最大值30 μm偏离。该偏离情况基本认为图像可以清晰成像，该补偿策略可行（见图8）。

3.5 补偿结果

通过该模型建立和理论计算结果可认为：当一级主反射镜与XOZ面夹角β为62.5°时，该模型下可以通过振镜与载体同方向同角度完成平台转动后对原目标主光线的补偿。

当一级主反射镜与XOZ面夹角β为62.5°时，通过振镜与载体同方向同角度补偿后，载体转动后对原目标边缘光线会产生补偿角度大小的偏转。

该模型下振镜的补偿角度与主反射镜和XOZ面夹角β有关，除β为62.5°时能通过振镜与平台同方向同角度1∶1完成补偿；其他角度下不能通过振镜与平台同方向同角度1∶1补偿完成补偿，可以通过一定比例关系进行补偿，通过计算解出补偿角与俯仰角的关系曲线。

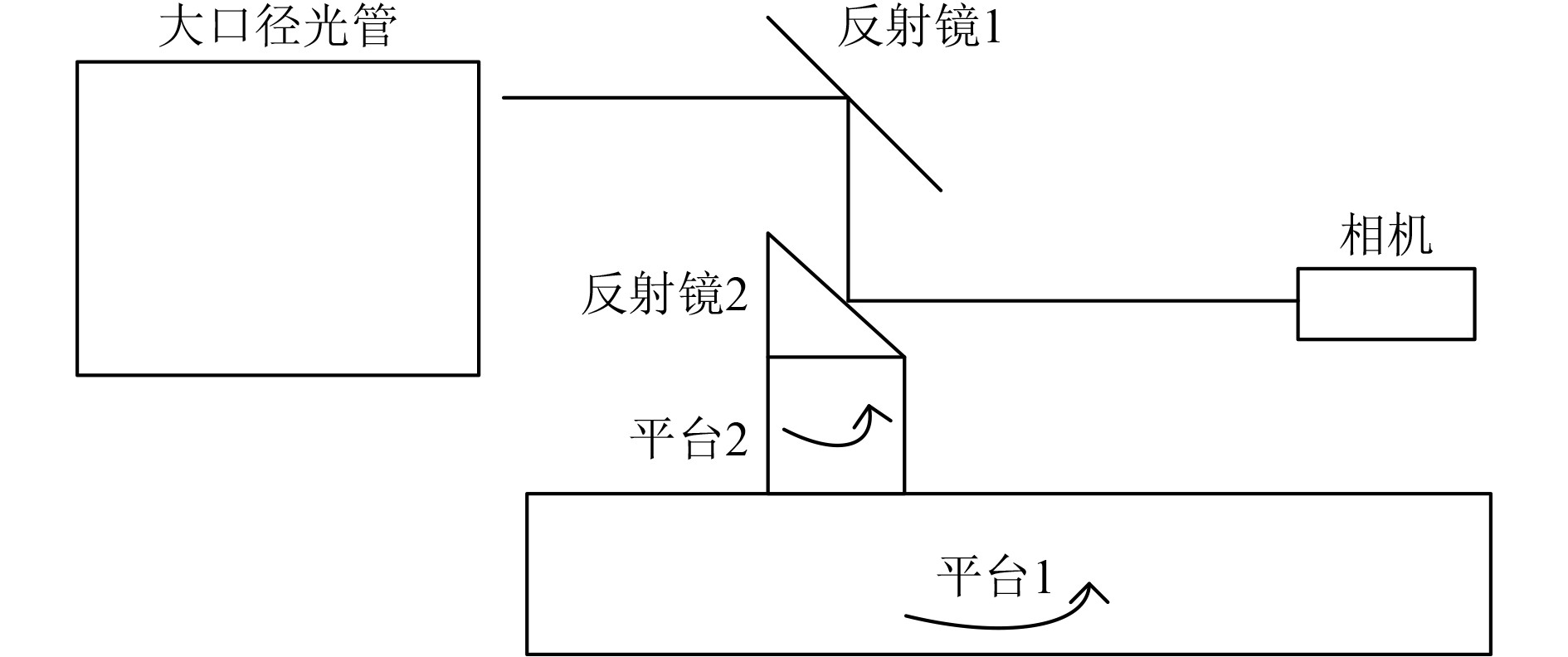
4 验证情况 4.1 双反射镜验证 4.1.1 双反射镜验证方法

分析和验证双反射镜结构，转台方位旋转后，能否通过非法线方向旋转进行方位补偿。试验平台搭建：在一维方位平台上搭建2个45°反射镜和1个摄像机，一维方位平台整体搭载设备水平转动，用其中一个反射镜进行补偿，检查其补偿方向和补偿角度（见图9）。

验证方法：1）将相机置于平台1上，调节平台1使相机十字丝与大口径光管十字丝对准。2）在平台一上架设反射镜1，反射镜2和平台2，调整反射镜1和平台2，使相机看到的反射十字丝与相机十字丝对准。并记录平台2的当前角度（α₁，β₁）。3）顺时针转动平台一1°，检查平台2水平转动能否使相机看到的反射十字丝与相机十字丝重合。记录平台转动方向和角度（α₂，β₂）。

4.1.2 双反射镜验证结果

计算当平台1转动角度θ = 1，平台2补偿角度ω = −1时，入设向量$ A $经过图8两反射镜模型后的出射向量$ {A^{\prime \prime }} $有如下式成立：

$ {A^{\prime \prime }} = {M_{50}} \cdot {M_{10}} \cdot {A_0} = \left[ \begin{gathered} 0.999\;999\;953\;6 \\ 0.000\;304\;586\;5 \\ - 0.000\;002\;657 \\ \end{gathered} \right] 。$

(43)

由此可见，该输出向量$ {A^{\prime \prime }} $与目标向量$ A $差距非常小。

当平台1顺时针转1°，平台2顺时针补偿1°，相机观察到的反射十字丝像与相机十字丝基本重合。当平台1逆时针转1°，平台2逆时针补偿1°，相机观察到的反射十字丝像与相机十字丝基本重合。

则此理论计算与实际验证情况相符，该模型正常，验证结果正常。

4.2 多反射镜验证 4.2.1 多反射镜验证方法

建立如图2所示的多反射镜模型，分析该光路结构形式下，红外热像仪是否通过相同的补偿策略补偿方位转动积分时间不够造成的图像模糊。平台逆时针转θ，五镜顺时针补偿ω。

4.2.2 多反射镜验证结果

主反射镜角度为62.5°时，可以通过五镜与平台同方向同角度补偿完成平台转动后对原目标主光线的补偿，该模型下可以通过五镜与平台同方向同角度补偿后，平台转动后对原目标边缘线产生补偿角度大小的偏转。主反射镜在他角度下，不能通过五镜与平台同方向同角度1∶1补偿完成补偿，但当已知主反射镜俯仰角度和载体转动速度时，可以通过第3章解算补偿策略，按其策略补偿后中心图像基本无影响，边缘图像清晰度可接受。

5 结　语

本文针对面阵红外中振镜法线运动平面与载体运动平面不能平行的特殊结构，运用理论分析的方法，计算该结构形式下一级方位旋转后，二级振镜的补偿策略。验证通过二级振镜法线运动平面与载体运动面不平行的角度补偿，解决像移和像旋问题。对中心主光线、边缘主光线的向量计算公式进行了推导和分析，并对面阵入射光线进行了Matlab仿真，根据计算和仿真结果，该模式下可以通过二级振镜同方向一定规律运动实现像移补偿，且该运动规律还与当前外部一级主反射镜的俯仰角相关。该补偿并非为完全补偿，而是存在一定的偏转剩余量。

该模型论证通过后，可将该光学结构形式应用于光电桅杆产品中，解决光电桅杆整体方位旋转时水密和气密问题，同时该结构形式还有利于多光路整合，有利于光电桅杆的小型化设计。