0 引　言

在“双碳战略”的背景下，水路运输业正大力向绿色智能化发展。相较于传统燃油船，电动船舶具有零排放、高效率、低噪声的特点^{[1 − 2]}，受到了国家的高度重视。电动船舶在降低排放的同时，省去了主机与配套设施的安装费用。而相应的，储能电池组的性能与寿命则成为了影响船舶营运和安全的核心因素之一。动力电池的重要参数包括荷电状态（SOC）、健康状态（SOH）等。其中SOC代表电池剩余电量，同时也是SOH等估计算法运行的基础参数，在电池管理系统（BMS）中具有极为重要的意义。

船用动力电池BMS调研结果显示，现有的船用储能系统大多使用估算总输出电荷量的安时积分法配合基于开路电压与SOC对应关系的静置修正实现电池荷电状态估计。然而目前的电流检测手段均具有一定的误差，通过端电压实施静置修正则会受到静置时间与温度的影响。船舶航行状态下，电池持续放电，在到达下一港口前无法提供SOC静置修正所需的条件，传感器误差持续累积易使SOC估计大幅度偏离真实值。锂电池需在特定的SOC范围内充放电才能满足性能、寿命与安全性的要求。错误的SOC估计会使BMS系统将SOC引导至安全范围外，降低电池使用寿命，并提高过充、过放的潜在风险。若为船舶与电池的安全，则只能压缩SOC运行区间，降低电池容量利用率，提供更大的容错范围。

近年来众多学者对电池SOC估计进行了研究。叶惠丽等^[3]针对船用电池管理需求，利用扩展卡尔曼滤波估计电池SOC状态，在精度上取得了一定的提升。刘巨等^[4]将LSTM神经网络与扩展卡尔曼滤波相结合，有效降低了SOC估计值与实际值的偏差。对于现有船用BMS系统而言，SOC估计精度的提升能有效提高电池组的管理效果，并更精准地预测和控制电池状态，以优化电池容量利用率、延长电池寿命。卡尔曼滤波（KF）属于贝叶斯滤波的一种，即利用系统模型修正观测误差，提高电池SOC估计精度^[5]。然而KF与其针对非线性系统优化的衍生类型，应用于具有高度非线性特征的电池系统均会存在一定的精度损失^[6]。同时，现有船用BMS系统大多以微型MCU作为控制核心，对算力资源的消耗较为敏感。如LSTM等神经网络难以在现有环境下运行，无法为船用储能系统提供实质性的提升。因此，本文以提高电池SOC估计精度并优化算力资源消耗为核心目标，提出融合多时间尺度在线辨识与FOA优化粒子滤波的SOC估计方法。利用基于多时间尺度的递推最小二乘法（MTS-FFRLS）在线辨识电池状态，优化船用大容量电池的参数辨识效果。同时使用适合于非线性系统且经果蝇优化算法（FOA）改进的粒子滤波（PF）进行SOC估计，在优化估计效果的同时降低种群数量与计算复杂度，以提高估计方法在实际环境下的应用价值。

1 动力电池模型及模型方程的建立

动力电池内部发生极为复杂的电化学反应过程且具有高度的非线性^[7]。考虑模型计算量与参数辨识难度，为提高算法适应性，本文使用二阶Thevenin等效电路模型作为粒子滤波载体。二阶等效模型相较一阶模型增加一个并联RC网络，能更好地模拟电池输入输出变化，其结构如图1所示。

图1模型关系方程如下：

$ \left\{\begin{aligned} & U_{\text{ocv}}=U+R_{\text{int}}\cdot\mathrm{I}+U_1+U_2，\\ & {I}\text{ = }\displaystyle\frac{U_1}{R_{\text{ct}}}+C_{\text{dl}}\displaystyle\frac{\mathrm{d}U_1}{\mathrm{d}t}，\\ & {I}\text{ = }\displaystyle\frac{U_2}{R_{\text{diff}}}+C_{\text{diff}}\displaystyle\frac{\mathrm{d}U_2}{\mathrm{d}t}。\end{aligned}\right. $

(1)

式中：$ {U}_{\mathrm{o}\mathrm{c}\mathrm{v}} $为电池开路电压；$ {R}_{\mathrm{i}\mathrm{n}\mathrm{t}} $为电池内阻；$ {R}_{\mathrm{c}\mathrm{t}} $为传荷电阻；$ {C}_{\mathrm{d}\mathrm{l}} $为双电层电容；$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $、$ {C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $分别为扩散电阻、扩散电容；U为电池端电压；I为工作电流；$ {U}_{1} $、$ {U}_{2} $分别为2个RC并联电路端电压。

选取SOC与RC并联电路端电压$ {U}_{1} $、$ {U}_{2} $为预测值，利用安时积分法及式(1)构建PF状态空间模型如下：

$ \left\{\begin{aligned} & {\rm{SOC}}_k={\rm{S}OC}_{k-1}-\displaystyle\frac{\eta\cdot\Delta t\cdot I_{k-1}}{C_{ }}+w_k，\\ & U_{1k} = e^{\frac{-\Delta t}{R_{\text{ct}}C_{\text{dl}}}}\cdot U_{1k-1}+I_{k-1}R_{\text{ct}}\left(1-e^{\frac{-\Delta t}{R_{\text{ct}}C_{\text{dl}}}}\right)+w_k，\\ & U_{2k} = e^{\frac{-\Delta t}{R_{\text{diff}}C_{\text{diff}}}}\cdot U_{2k-1} + I_{k-1}R_{\text{diff}}\left(1 - e^{\frac{-\Delta t}{R_{\text{diff}}C_{\text{diff}}}}\right) + w_k。\end{aligned}\right. $

(2)

$ U_k+R_{int}I_k=U_{\text{ocv}}(SOC_k)-U_{1k}-U_{2k}+v_k。$

(3)

式中：$ \Delta t $为离散时间步长；C为电池总电荷量；$ \eta $为库伦效率；$ U_{\mathrm{ocv}} $为电池k时刻荷电状态对应的开路电压（OCV）；$ {w}_{k} $、$ {v}_{k} $均为模型误差与观测噪声。

2 电池模型参数辨识

电池模型的参数辨识方法包括离线辨识和在线辨识^[8]，由于电池状态会随环境与自身因素改变，因此使用带遗忘因子的递推最小二乘法（FFRLS）在线辨识模型参数，以提高算法在不同工况与电池全生命周期下的估计效果。本文以EVE 280 Ah 磷酸铁锂（LFP）电池为实验对象，进行混合功率脉冲特性实验（HPPC），测试电流1 C，每隔5% SOC测量一次，结果如图2所示。

2.1 电池模型参数初始值辨识

基于FFRLS的参数在线辨识是一个自适应过程，为使初始时辨识参数快速收敛，选取电池90% SOC下端电压零输入响应与零状态响应数据进行离线辨识，并将其设置为电池满电状态的模型初值。端电压特性曲线如图3所示。

图中，$ {U}_{{a}{b}} $、$ {U}_{{c}{d}} $、$ {U}_{{e}{f}} $、$ {U}_{{g}{h}} $均为$ {R}_{\mathrm{i}\mathrm{n}\mathrm{t}} $导致的端电压瞬变，$ {U}_{{b}{c}} $、$ {U}_{{f}{g}} $与$ {U}_{{d}{e}} $、$ {U}_{{h}{i}} $分别为零状态响应与零输入响应过程。由式(1)可推算$ {R}_{\mathrm{i}\mathrm{n}\mathrm{t}} $与$ {U}_{1} $、$ {U}_{2} $计算公式如下：

$ {R_{{\text{int}}}} = \frac{{({U_{{a}}} - {U_{{b}}}) + ({U_{{d}}} - {U_{{c}}}) + ({U_{{f}}} - {U_{{e}}}) + ({U_{{g}}} - {U_{{h}}})}}{{4I}}，$

(4)

$ \left\{\begin{aligned} & U_1(t)=U_1(0)\cdot e^{\frac{-t}{R_{\text{ct}}C_{\text{dl}}}}+IR_{\text{ct}}\left(1-e^{\frac{-t}{R_{\text{ct}}C_{\text{dl}}}}\right)，\\ & U_2(t)=U_2(0)\cdot e^{\frac{-t}{R_{\text{diff}}C_{\text{diff}}}}+IR_{\text{diff}}\left(1-e^{\frac{-t}{R_{\text{diff}}C_{\text{diff}}}}\right)。\end{aligned}\right. $

(5)

结合开路电压与内阻分压，将式(4)、式(5)代入式(1)并拟合曲线后，可辨识模型参数$ {R}_{\mathrm{c}\mathrm{t}} $、$ {C}_{\mathrm{d}\mathrm{l}} $、$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $、$ {C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $。最后获得90% SOC下电池等效模型参数为$ {R}_{\mathrm{i}\mathrm{n}\mathrm{t}} $ = 0.000348 Ω、$ {R}_{\mathrm{c}\mathrm{t}} $ = 0.00044 Ω、$ {C}_{\mathrm{d}\mathrm{l}} $ = 20106 F、$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $ = 0.00011 Ω、$ {C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $ = 20347 F。

2.2 基于多时间尺度的FFRLS参数在线辨识

锂电池的观测量包括 $ {U}_{\mathrm{o}\mathrm{c}\mathrm{v}} $、U以及电流I 。根据式(1)构建 $ {U}_{ocv} $-U与I的传递函数，并通过双线性变换将连续函数离散化获得适用于数字系统的差分方程。传递函数与差分方程为：

$ G(s)=\frac{U_{\text{ocv}}(s)-U(s)}{I(s)}=R_{\text{int}}+\frac{R_{\text{ct}}}{1+\tau_1s}+\frac{R_{\text{diff}}}{1+\tau_2s}，$

(6)

$ \begin{aligned}U_{\text{ocv}}(k)-U(k)= & \alpha_1[U_{\text{ocv}}(k-1)-U(k-1)]+ \\ & \alpha_2[U_{\text{ocv}}(k-2)-U(k-2)]+ \\ & \alpha_3I(k)+\alpha_4I(k-1)+\alpha_5I(k-2)，\end{aligned} $

(7)

$ \left\{\begin{aligned} & \alpha_1=\displaystyle\frac{-bT-2a}{T^2+bT+a}\text{，}\alpha_2=\displaystyle\frac{a}{T^2+bT+a}，\\ & \alpha_3=\displaystyle\frac{cT^2+dT+aR_{int}}{T^2+bT+a}\text{，}\alpha_4=\displaystyle\frac{-dT-2aR_{int}}{T^2+bT+a}，\\ & \alpha_5=\displaystyle\frac{aR_{int}}{T^2+bT+a}，\\ & a=\tau_1\tau_2\text{ ，}b\text{ = }\tau_1+\tau_2\text{，}c\text{ = }R_{\text{int}}+R_{\text{ct}}+R_{\text{diff}}，\\ & d=R_{int}(\tau_1+\tau_2)+R_{\text{ct}}\tau_2+R_{\text{diff}}\tau_1。\end{aligned}\right. $

(8)

式中：$ {\tau }_{1} $、$ {\tau }_{2} $分别为$ {R}_{\mathrm{c}\mathrm{t}}{C}_{\mathrm{d}\mathrm{l}} $与$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}}{C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $；$ \alpha_{1～}\alpha_5 $均为模型辨识参数；U为电池端电压；I为负载电流；$ U\mathrm{_{ocv}} $为电池开路电压。U与I均为传感器测量参数，$ {U}_{\mathrm{o}\mathrm{c}\mathrm{v}} $则由OCV-SOC关系曲线获得。式(7)中$ \alpha_{1～}\alpha_5 $的计算公式如式(8)所示，联立等式消除中间变量T可解析电池模型5项基本参数。递推最小二乘法运行时数据会持续累积易导致内存溢出和数据饱和^[9]，因此采用带遗忘因子的递推最小二乘法（FFRLS）进行参数辨识。FFRLS只截取少量历史数据，并通过遗忘因子调节参数跟踪速度，具有更高的运算效率与鲁棒性。FFRLS公式如下：

$ \left\{\begin{aligned}&\hat{\theta}(k)=\hat{\theta}(k-1)+K(k)[U(k)-\varphi(k)\hat{\theta}(k-1)^{\mathrm{T}}]，\\ &K(k)=P(k-1)\varphi(k)[\lambda+\varphi\mathrm{^T}(k)P(k-1)\varphi(k)]^{-1} ，\\ &P(k)=\lambda^{-1}[I-K(k)\varphi^{\mathrm{T}}(k)]P(k-1)。\end{aligned}\right. $

(9)

$ \left\{{\begin{gathered}\hat{\theta}=[\alpha_1\text{ }\alpha_2\text{ }\alpha_3\text{ }\alpha_4\text{ }\alpha_5]\text{ }，\\ \boldsymbol{\varphi}(k) = [U\mathit{_{{b}}}(k - 1)\text{ }U\mathit{_{{b}}}(k - 2)\text{ }I\mathit{_{{b}}}(k)\text{ }I\mathit{_{{b}}}(k - 1)\text{ }I\mathit{_{{b}}}(k - 2)]。\\ \end{gathered}} \right. $

(10)

式中：$ \hat{\theta } $、φ分别为模型状态向量与系统输入；U为观测向量；K为算法增益；P为系统协方差；$\lambda $为遗忘因子；$ U_b $、$ I_b $分别为电池端电压与工作电流；I为系统同维数的单位矩阵。

电池模型存在2个RC并联环节，但其特征频率并不相同。在普遍使用大容量电池的船舶储能中，特征频率的差异会愈加明显，并最终影响参数辨识效果。为研究其对不同频率的响应特性，使用电化学阻抗谱（EIS）法测定280 Ah电池在不同频率正弦电压激励下的特征阻抗。测试结果如图4所示。图中频率信号包括：a、b、c、d四阶段，分别为200～500 Hz（超高频）、50～200 Hz（高频）、10～50 Hz（中频）以及0.1～10 Hz（低频）。Z_Re代表电阻，Z_Im代表电抗。其中高频、低频范围内阻抗呈现明显的变化特征，分别对应$ {R}_{\mathrm{c}\mathrm{t}} $、$ {C}_{\mathrm{d}\mathrm{l}} $与$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $、$ {C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $并联电路的特征频段。若以同一时间尺度辨识全部参数，则容易导致某一环节出现数据饱和或发散。因此引入多时间尺度辨识策略，使辨识频率与各参数特征频段一致，以提高参数辨识精度与稳定性。

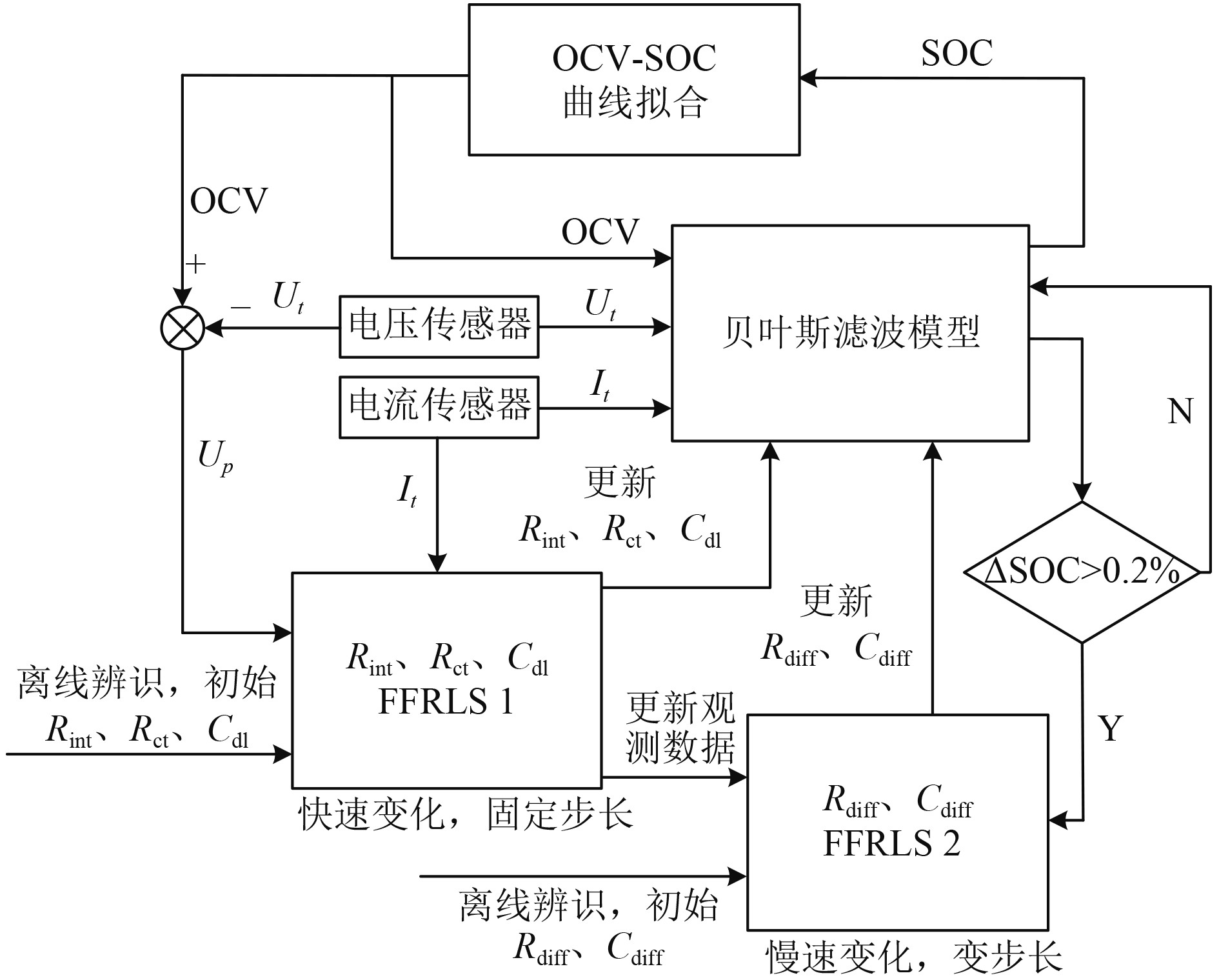
图5为多时间尺度参数辨识流程，首先以离线辨识结果为初始值，并建立2个独立的FFRLS系统。FFRLS1和贝叶斯滤波模型以100 Hz的频率运行，实时更新$ {R}_{\mathrm{i}\mathrm{n}\mathrm{t}} $、$ {R}_{\mathrm{c}\mathrm{t}} $、$ {C}_{\mathrm{d}\mathrm{l}} $与SOC估计值。当$ \Delta\mathrm{SOC} $超过0.2%时FFRLS2运行，在宏观尺度上辨识并更新$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $、$ C_{\rm diff} $。

3 基于FOA优化的改进粒子滤波算法 3.1 粒子滤波算法及运算矩阵的建立

粒子滤波（PF）是一种基于贝叶斯估计和蒙特卡罗方法的近似值求解方法，用于在测量值存在误差的情况下利用模型从观测数据中估计系统状态。与KF利用积分运算实现状态估计不同，PF首先通过实验数据获取模型与观测误差的经验分布，然后生成一组相似分布的随机粒子，通过重要性分布函数计算粒子权重，并依据权重对粒子进行迭代，获取模型状态的后验概率期望，即参数估计值。PF的状态空间模型为：

$ \left\{\begin{array}{*{20}{l}}x_k=A_kx_{k-1}+B_ku_k+w_k，\\ y_k=C_kx_k+D_ku_k+v_k。\end{array}\right. $

(11)

式中：$ {\mathit{x}}_{k} $为状态变量；$ {\mathit{u}}_{k} $为系统输入；$ {\mathit{y}}_{k} $为观测变量；$ {\mathit{w}}_{k} $、$ {\mathit{v}}_{k} $分别为模型误差与观测误差。由式(2)、式(3)可得$ {\mathit{A}}_{k} $、$ {\mathit{B}}_{k} $、$ {\mathit{C}}_{k} $、$ {\mathit{D}}_{k} $的具体参数。

3.2 基于FOA算法优化的粒子滤波实现过程

粒子滤波总共包括5个步骤：1）利用先验分布函数得到初始粒子；2）根据观测值利用重要性分布函数更新粒子权值；3）归一化粒子权值；4）依据权值进行重采样得到N个新粒子；5）计算后验概率期望，获取状态估计。

粒子滤波以大数定律作为支撑，因其随机粒子以及概率估计的特性，使其适用于非线性系统，相比于泰勒级数展开以及无迹变换等扩展KF算法，拥有更高的综合性能。但PF算法在多次运行后易出现粒子贫化，即多数粒子权重趋近于0，无法有效反应后验分布^[10]。粒子贫化会降低PF算法的估计效果，同时增加相同估计精度下所需的初始种群数量，极大地提高了芯片的算力资源消耗。因此本文使用轻量化且解值多样性丰富的果蝇优化算法（FOA），改进重采样过程。在提高估计精度的同时，降低算法所需的种群数量与重采样次数，优化算力资源消耗，提高PF算法适应性。

基于FOA的改进PF算法运算步骤如下：

1）初始化粒子种群。由先验概率分布生成粒子集{x₀⁽ⁱ⁾,i = 1,2,3,…,N}，粒子初始权值$ {\omega }_{0}^{i} $设为1/N。

2）粒子权值计算。依据大量实验经验，锂电池测量误差近似为高斯分布，因此使用似然概率作为重要性分布函数，粒子权值计算公式如下：

$ L(\theta)=\frac{1}{\sqrt{2\text{π}}\sigma}\mathrm{e}^{\left(-\frac{(y(i)-\theta^{\mathrm{T}}x(i))^2}{2\sigma^2}\right)}。$

(12)

式中：σ为观测矩阵标准差；y (i)为观测量；θ为观测矩阵；x(i)为k时刻粒子i对应的状态量；L(θ)为粒子x(i)在当前观测下出现的概率，即粒子权值。

3）归一化权值。

$ {\bar \omega _k}^{(i)} = \frac{{{\omega _k}^{(i)}}}{{\displaystyle\sum\nolimits_{i = 1}^N {{\omega _k}^{(i)}} }} 。$

(13)

式中：$ {\omega }_{k}^{\left(i\right)} $为粒子i的权值。通过上述计算使各粒子权值归一化。

4）基于FOA优化的粒子重采样。

果蝇优化算法（FOA）旨在模拟果蝇寻找食物的过程，果蝇通过食物的气味浓度搜寻目标，并通过果蝇位置的移动、迭代、优化获取最优解。FOA计算过程如下：

步骤1　初始化种群：将PF算法依据先验概率分布生成的粒子作为果蝇初始种群。

步骤2　种群适应度评估：通过计算种群适应度评估粒子贫化程度，计算公式如下：

$ N=\frac{1}{\displaystyle\sum_{ }^{ }\omega_k^{(i)}}。$

(14)

式中：$ {\omega }_{k}^{\left(i\right)} $为粒子i的归一化权值；N为种群适应度。N越小，粒子贫化越严重。

步骤3　果蝇个体位置更新：自然环境中果蝇虽会沿着气味浓度最大的方向前进但个体之间会存在差异，通过式(15)模拟个体独立行为，向最优值趋近的同时提高种群多样性。

$ \left\{ {\begin{array}{*{20}{l}} \begin{split} {\alpha _k}^{{{(i)}}}{\text{ = }}&w \cdot \sigma \cdot {\text{RAND[ - 1,1]}} + \\ &v \cdot (pbes{t_{k - 1}} - {x_{k - 1}}^{(i)}) \cdot {\text{RAND[0,1]}} \\ \end{split}，\\ {{x_k}^{(i)} = {x_{k - 1}}^{(i)} + {\alpha _k}^{{{(i)}}}} 。\end{array}} \right. $

(15)

式中：σ为系统标准差；pbest为个体最优估计位置；w、v为个体权重与学习因子；RAND[a,b]代表a,b之间的随机数；$ {x}_{k} $为个体位置。

步骤4　重复进行步骤2、步骤3，迭代优化种群适应度，当N高于阈值或达到最大重采样次数时停止迭代。

5）输出最优估计值。

$ \overline{x}_k=\sum\limits_{i=1}^N\omega_k^{(i)}\hat{x}_k^{(i)}。$

(16)

式中：$ {\hat x}_k $为经过FOA迭代的粒子；$ {\omega }_{k}^{\left(i\right)} $为粒子归一化权值；${\bar x_k}$为当前电池组SOC的最优估计值。

4 算法验证

为验证算法性能，本文以EVE 280Ah LFP电池为测试对象，搭建实验平台。平台包括：BMS主控板（STM32F407ZGT6）、分流器（SH-T300A）、电子负载（IT8516C）、EVE 280Ah LFP电池和上位机。以某船舶BMS系统电流历史数据为测试条件，在室温25℃风冷的条件下使用电子负载模拟船舶单簇电池放电情况，并通过RTOS系统记录不同算法下CPU利用率。电池SOC运行区间为20%～80%，电流、电压采样频率为100 Hz。

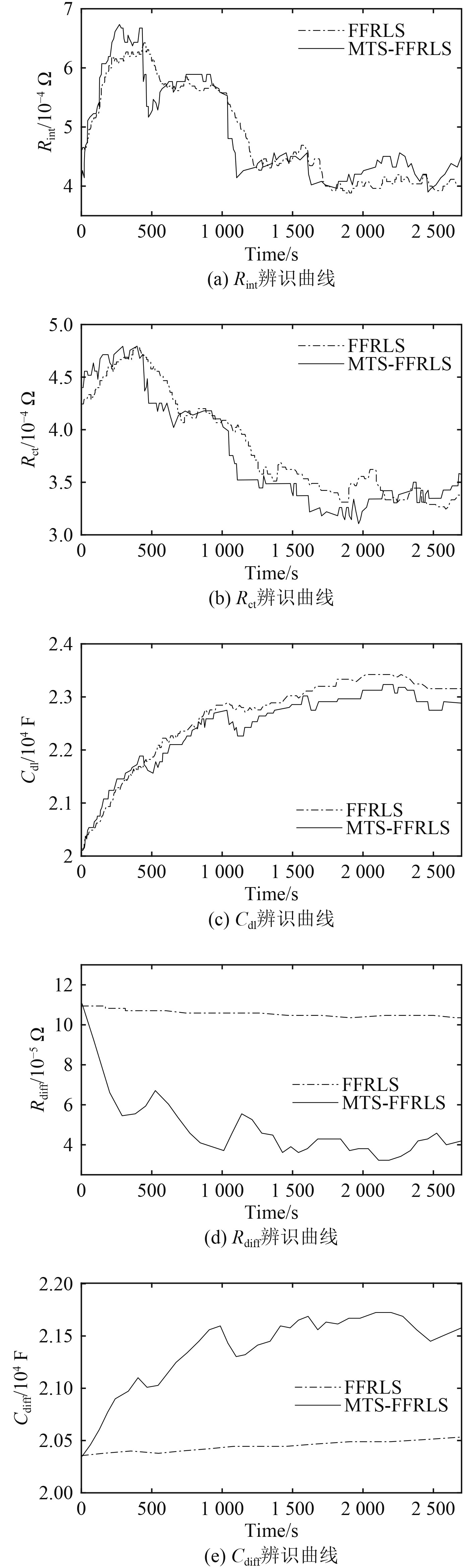
针对电池参数辨识，分别以FFRLS与MTS-FFRLS算法在相同工况下辨识电池参数，并取70%～75% SOC内的辨识结果对比算法性能，参数辨识曲线如图6所示。3个高频参数$ {R}_{\mathrm{i}\mathrm{n}\mathrm{t}} $、$ {R}_{\mathrm{c}\mathrm{t}} $、$ {C}_{\mathrm{d}\mathrm{l}} $在2种算法下均收敛并呈现相同趋势，证明在线辨识算法具备随电池状态变化实时辨识参数的能力。在FFRLS下，算法运行频率远高于$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $和$ {C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $的特征频率，FFRLS已产生数据饱和，无法有效辨识电池状态。而MTS-FFRLS由于引入了多时间尺度辨识策略，$ {R}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $、$ {C}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}} $的辨识结果较为清晰，且变化规律与$ {R}_{\mathrm{i}\mathrm{n}\mathrm{t}} $、$ {R}_{\mathrm{c}\mathrm{t}} $、$ {C}_{\mathrm{d}\mathrm{l}} $基本一致，数据有效且辨识精度优于FFRLS，更适应船用大容量电池参数的时变特性。

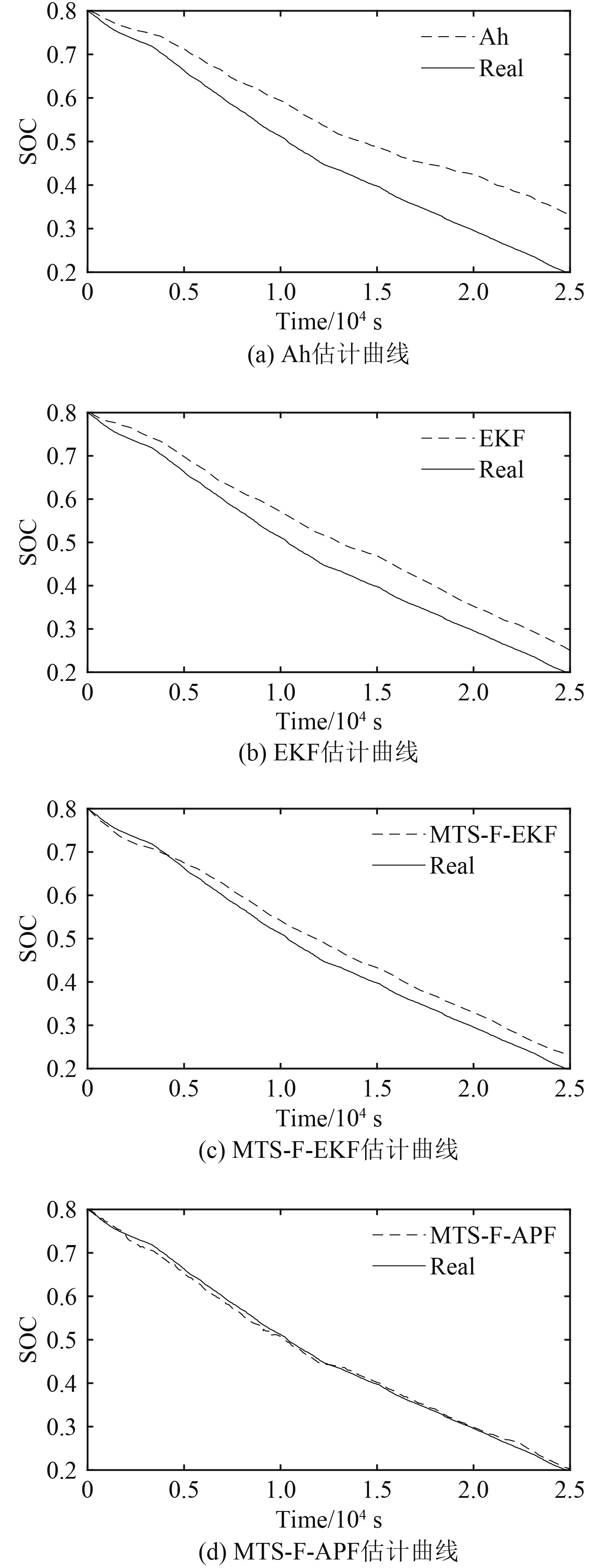
图7为电池在不同算法下的SOC估计结果，以高精度电子负载编程数据为真实值绘制4组对照曲线。算法包括：安时积分法（Ah），基于离线辨识的扩展卡尔曼滤波（EKF）,基于MTS-FFRLS的扩展卡尔曼滤波（MTS-F-EKF）以及基于MTS-FFRLS的FOA优化粒子滤波（MTS-F-APF）。Ah算法由于传感器及测量元件误差持续累积，导致最终估计结果大幅度偏离真实值。EKF算法在Ah算法的基础上引入电池模型校正传感器误差，但由于模型参数固定和EKF算法误差，SOC估计仍明显偏离真实值。MTS-F-EKF算法通过在线辨识电池参数，优化了SOC估计效果，但由于EKF算法自身应用于非线性系统的精度损失，导致SOC估计相对真实值仍具有一定的误差。MTS-F-APF算法由于非线性滤波算法的引入，曲线相较于前者估计误差最小，与真实值跟随最紧密。

图8与表1分别为各算法SOC估计误差曲线与估计误差统计表。可知，Ah算法、EKF算法均具有较大误差。EKF算法在引入MTS-FFRLS后平均绝对误差下降了0.0236，平均相对误差下降了5.44%，均方根误差下降了0.0241。进一步使用改良的非线性滤波算法，MTS-F-APF相较MTS-F-EKF平均绝对误差下降了0.0155，平均相对误差下降了4.42%，均方根误差下降了0.0186。

表2为算法的CPU利用率对比。经FOA优化的MTS-F-APF算法在相同估计精度下，种群数量缩小至普通粒子滤波算法MTS-F-PF的1/3，CPU利用率降低了约17%，有效缩小了估计方法的算力资源消耗。在主流BMS控制器多任务处理的环境下具有更高的适应性与应用价值。

5 结　语

针对现有船舶动力电池组SOC估计存在的不足，本文提出一种基于FOA优化粒子滤波的SOC估计方法，并通过实验测试验证了该估计方法的有效性与优势，得到如下结论：

1）针对电池模型参数辨识，本文在传统离线辨识基础上，引入了改良的MTS-FFRLS在线辨识算法。利用多时间尺度辨识策略提高了船用大容量储能电池参数辨识效果，提升了SOC估计算法中电池状态预测的实时性与预测精度。

2）针对传统滤波算法应用于非线性系统的精度损失，本文提出经FOA优化的粒子滤波算法。实验结果表明，通过MTS-FFRLS与FOA优化粒子滤波联合运行，在实验条件下可将SOC估计的均方根误差控制在0.0058，相较普通粒子滤波CPU利用率下降了17%。在有效提升SOC估计精度的同时，降低了粒子滤波算法所需的算力资源消耗。

SOC估计精度的提升，能在保证船舶及电池安全的前提下提升电池组容量利用率，并更精确地控制电池充放电过程，提高动力电池组的整体寿命。实验结果表明，所提算法具有在主流MCU上的运行能力，消耗少量算力的同时表现出较高的精度与计算稳定性，可为船用动力电池管理系统的设计提供一定参考，优化动力电池组综合性能。